Híbrido rat-race miniaturizado para la banda ISM 2,4 GHZ
Miniaturized Rat-Race Hybrid for 2,4 GHZ ISM Band
Sebastián Rodríguez Paez1, Arturo Fajardo Jaimes2, Carlos Ivan Paez Rueda3
1Ingeniero electrónico, magíster en Electrónica, profesor de cátedra de la Pontificia Universidad Javeriana, Bogotá, Colombia. Contacto: jrodriguezp@javeriana.edu.co.
2Ingeniero electrónico, magíster en Electrónica, profesor asistente de la Pontificia Universidad Javeriana, Bogotá, Colombia. Contacto: fajardoa@javeriana.edu.co
3Ingeniero electrónico, especialista en Docencia e Investigación Universitaria, magíster en Eléctrica, profesor asociado de la Pontificia Universidad Javeriana, Bogotá, Colombia. Contacto: paez.carlos@javeriana.edu.co
Fecha de recepción: 31 de agosto de 2013 Fecha de aceptación: 16 de mayo de 2014
Clasificación del artículo: investigación
Financiamiento: Pontificia Universidad Javeriana
Resumen
En este artículo se presenta el diseño, la implementación y la evaluación de un híbrido Rat-race miniaturizado, construido en un substrato CER-60 con líneas de transmisión (LxTx) tipo micro-cinta, siguiendo una curva de llenado fractal novedosa. Este circuito es el resultado principal del proyecto de investigación PS 3206 financiado por la Vicerrectoría Académica de la Pontificia Universidad Javeriana. El híbrido desarrollado logra una miniaturización del 73 %, opera en la banda ISM 2,4 GHz, con una frecuencia de operación óptima de 2,56 GHz y un ancho de banda fraccio-nalde 17,15%.
Palabras clave: circuitos acopladores, circuitos de microondas, microcinta.
Abstract
This paper presents the design, implementation and evaluation of a miniaturized Rat-race hybrid implemented in substrate CER-60 with microstrip transmission lines in a novel space-filling curve. This circuit is the main research's result of the project PS 3206funded by the Pontificia Universidad Javeriana. The hybrid achieves a miniaturization of 73 %, it operates in the 2.4 GHz ISM band, with an optimum operating frequency 2.56 GHz and a fractional band width of17.15%.
Keywords: coupling circuits, microwave circuits, microstrip.
Introducción
Los sistemas de comunicaciones inalámbricos están conformados por circuitos digitales, circuitos de señal mixta y circuitos de radio frecuencia (RF). La evolución de los procesos de fabricación de los circuitos digitales ha producido una reducción significativa en los tamaños de este tipo de circuitos, aunque en contraste los circuitos de RF han disminuido muy poco su tamaño (Pucel, 2012).
Antes de 1950 los dispositivos de microondas usaban guías de onda. El uso de esta tecnología implicaba dimensiones físicas muy grandes, impidiendo la portabilidad de los equipos. Con la aparición de la tecnología de microcinta y la mejora en los procesos de fabricación de materiales dieléctricos, surgió la tecnología conocida como HMIC (Hibrid Microwaves Integrated Circuits), la cual utiliza una placa de sustrato metalizada para dar soporte a los componentes del circuito (resistencias, condensadores, transistores, chipsets, etc.) y para contener los campos producidos por su interconexión. En 1967 esta tecnología evolucionó a los MMIC monolíticos (MMIC). En esta tecnología los circuitos de microondas activos o pasivos se fabrican en un sustrato semiconductor por una combinación de técnicas que incluyen la difusión, la evaporación, la implantación y otros medios (Pucel, 2012). Hoy en día la tecnología MMIC es usada ampliamente para implementar sistemas electrónicos embebidos en los dispositivos de comunicación móviles que operan en la banda de la microondas (He-Xiu Xu, Guang-Ming Wang y Ke Lu, 2011), en los cuales uno de los principales retos para aumentar su portabilidad es la miniaturización de sus componentes (Chiou, Tsai, Wu y Kuo, 2008).
El híbrido de 180° es un circuito usado en una gran variedad de sistemas de RF. De forma convencional se implementa a través de un acoplador Rat-race (He-Xiu Xu et al., 2011). En esta implementación, las dimensiones físicas del híbrido son proporcionales a longitud de onda (λ) de operación del acoplador. Recientemente se han realizado múltiples esfuerzos para lograr su miniaturización en la banda de bajas frecuencias de microondas (Chiou et al, 2008; Ghali y Mo-selhy, 2004b; Jen-Tsai Kuo, Yi-Chyun Chiou y Juo-Shiuan Wu, 2007; Wen-Ling Chen y Guang-Ming Wang, 2007). Estos esfuerzos en reducción de tamaño se concentran en aquellas implementaciones que se pueden fabricar con facilidad en tecnología MMIC. Por lo tanto, la investigación se ha focalizado en implementaciones basadas en tecnologías planares de LxTx.
Los primeros esfuerzos por lograr la miniaturización del acoplador tipo Rat-race utilizaban componentes concentrados para reducir la longitud física de las LxTx sin disminuir su longitud eléctrica, o bien remplazaban completamente las LxTx por componentes concentrados. El principal problema de estas aproximaciones es que se aumenta el costo y la complejidad de fabricación en un proceso MMIC. En tiempos más recientes se pueden destacar tres diferentes técnicas de diseño: la primera utiliza LxTx artificiales con elementos concentrados (Wei-Shin Tung, Hsu-Hsiang Wu y Yi-Chyun Chiang, 2003), la segunda se enfoca en el uso de LxTx artificiales (Chao-Hsiung Tseng y Hsiang-Ju Chen, 2008; Chiou et al., 2008; Jen-Tsai Kuo et al., 2007) y la tercera utiliza LxTx con geometrías fractales (Chen y Wang, 2008; Ghali y Moselhy, 2004b; Rao, Subramanian y Kamki, 2010; Wen-Ling Chen y Guang-Ming Wang, 2007). En esta última técnica se usa la propiedad de las curvas de llenado fractales de incrementar su perímetro manteniendo confinada su área. Usando esta técnica se ha reportado miniaturización del 85%, con un ancho de banda fraccional de 25 % (Ghali y Mo-selhy, 2004b) y miniaturización del 81,5%, con una ancho de banda fraccional de 33% (Rao et al., 2010).
En la mayoría de las investigaciones sobre miniaturización no se hace un análisis del impacto de esta en los parámetros de mérito del híbrido, en gran parte por que no existe una forma estándar de comparación, ni una definición precisa de tales parámetros. En los últimos años han aparecido algunos trabajos que comparan diferentes métodos de miniaturización (Duxiang Wang, Huynh, Hakansson, Ming Li y Shaofang Gong, 2008; Psychogiou y Hesselbarth, 2010). Estos se concentran en la comparación de parámetros de mérito de las salidas del híbrido (Rodríguez, Fajardo y Páez, 2011), o bien se proponen un grupo de parámetros de mérito que permiten comparar varias de las dimensiones de operación del circuito.
Lo que sigue se divide de la siguiente forma: en la segunda sección del artículo se introduce el concepto de curvas de llenado. En la tercera sección se presenta la metodología usada para definir la curva de llenado sectorizada aplicada a la miniaturización propuesta. Adicionalmente, se presenta el diseño y la implementación computacional del híbrido novedoso. Finalmente, en la cuarta sección se hace una comparación detallada del híbrido miniaturizado y el híbrido convencional, ambos diseñados e implementados en substrato CER60 para la banda ISM de 2,4 GHz.
Curvas de llenado fractales
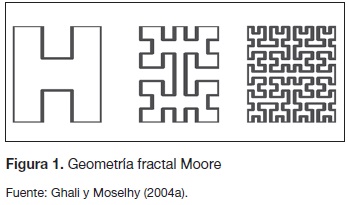
En 1975 Mandelbrot introdujo el término fractal para describir una nueva geometría, opuesta a la geometría euclidiana y con características de forma especiales. Por ejemplo, en un objeto fractal todas sus partes tienen la misma forma o estructura que el todo, aunque pueden presentarse a diferente escala y estar ligeramente deformadas. Las curvas de llenado de espacio pueden ser consideradas como parte del mundo fractal (Sagan, 1996). Estas curvas fueron introducidas por Pea-no en 1890, mucho antes de que el término fractal fuera inventado. Después de las curvas propuestas por Peano, aparecieron otras familias de curvas de llenado (p. ej., Hilbert, l89l; Moore, 1900; Osgood, 1903; Lehesgue, 1904; Sierpinski, 1912 y Wunderlich, 1954). Todas estas curvas tienen la característica de poder llenar el espacio planar completamente con una sola curva continua (Sagan, 1996). Las curvas de llenado fractales tienen la característica particular de aumentar su perímetro manteniéndose confinadas en la misma área (ver figura 1), lo cual las hace atractivas para la miniaturización de estructuras electromagnéticas. Recientemente algunas de estas curvas se han utilizado para reducir el tamaño de los dispositivos electromagnéticos y de los dispositivos electrostáticos (Chen y Wang, 2008; Ghali y Moselhy, 2004b; Moselhy, Ghali, Ragaie y Haddara, 2003).
Metodología
Aplicación sectorizada de curvas de llenado en el híbrido Rat-race
La implementación convencional del híbrido de 180° es conocida como Rat-race y tiene tres segmentos de longitud eléctrica de λ 4 y un segmento de longitud eléctrica de 3 λ /4 (Ludwig y Bogda-nov, 2008). Esta implementación se ilustra en la figura 2a. Para el diseño geométrico del híbrido novedoso se usaron curvas de llenado abiertas que permitieran hacer un remplazo de cada traza fundamental de su figura geométrica básica del convencional. Por esta razón, se generó un hexágono inscrito en el círculo que lo dividió en sub-áreas, en la que se confinaría la curva abierta de llenado fractal, como se ilustra en la figura 2b. Estas curvas formarían los segmentos 0,25 λ y 0,75 λ de las LxTx presentes en el circuito, esta construcción se ilustra en la figura 2c.
Para buscar las soluciones óptimas al problema propuesto, se implementó un programa que genera las diferentes curvas de llenado bajo la estructura propuesta, remplazando cada línea del hexágono por una curva de llenado fractal abierta. Con esta metodología se analizaron las curvas de llenado tipo Gosper, Koch, Sierpinski y Moore, introduciendo variaciones en la simetría de construcción de la curva de llenado (Sagan, 1996). En la figura 3 se observan algunos ejemplos de los fractales analizados, ilustrando todas las posibles simetrías, manteniendo la misma curva fractal. En la figura 4 se ilustran las curvas de llenado implementadas manteniendo la simetría constante. De forma adicional se estudió la combinación de fractales, utilizando en cada sub-área una curva de llenado particular. En esta última forma de remplazar las rectas del polígono se buscó que los fractales se complementaran en el llenado del área aumentado el perímetro, como se ejemplifica en la figura 5. Finalmente, para comparar de forma simple las figuras fractales generadas, se definió una métrica cuantitativa basada en el cálculo del área del cuadrado en que se confinaba la figura fractal y el porcentaje de relación con el área de una circunferencia de perímetro equivalente, para así determinar cuál lograba la mayor miniaturización.
Diseño del híbrido fractal novedoso
A partir del espacio de búsqueda obtenido se realizó un análisis cualitativo de las geometrías que presentaban porcentajes de miniaturización mayores al 70 %, para escoger aquellas que tuvieran características que facilitaran su implementación y la ubicación de los puertos de RF, que presentaran mínima cercanía entre líneas para disminuir posibles acoples electromagnéticos y que no presentaran cruces. Posteriormente estas geometrías se analizaron con Ansoft Designer®, utilizando como dieléctrico un substrato cerámico llamado CER10, el cual gracias a su alta permitividad (sr = 10) permite disminuir simultáneamente la longitud física y el ancho de las LxTx involucradas en el diseño del dispositivo. A través de la simulación se analizó el comportamiento electromagnético de las geometrías seleccionadas. Para cada geometría se realizó un análisis paramétrico del perímetro total de la estructura y de la posición de los puertos, con el fin de que la frecuencia de operación fuera de 2,45 GHz. A partir del análisis comparativo de las simulaciones de las diferentes estructuras y sus parámetros de mérito, se escogió la estructura mostrada en figura 6b. Finalmente, se generaron los archivos de fabricación, tanto de la estructura propuesta como de la implementación convencional, ilustrados en la figura 7. Esta estructura produjo un porcentaje de miniaturización entre 73 y 68%, dependiendo de la métrica que se escoja para su cálculo, como se ilustra en la figura 8.
Resultados Y discusión
Para un análisis comparativo global en las figura 9 y 10 se presentan los parámetros de dispersión experimentales y simulados. Analizando los resultados es posible concluir que la simulación captura casi todas las dinámicas de los híbridos, sin errores significativos. De igual forma, se observa que existe un aumento de la frecuencia de operación experimentalmente medida con respecto al valor simulado. En la figura 11 se muestran los híbridos implementados.
Para analizar el impacto de la miniaturización sobre los parámetros de mérito se utilizó la taxonomía propuesta por Rodríguez et al. (2011). En este artículo se define la frecuencia de operación óptima del híbridofo) como la frecuencia que minimiza una función de costos asociada al error cuadrático medio de las diferencias de fase deseadas en los puertos de salida, definiendo los puertos de suma como los puertos asociados a un desbalance de fase de 0° y los puertos de resta como aquellos asociados a un desbalance de fase de 180 °. Esta función de costos se rescribe por conveniencia en la ecuación (1).
En los híbridos ideales existe una frecuencia en la cual el desbalance de fase, el desbalance de magnitud, las pérdidas de inserción y las pérdidas de retorno son mínimos. Sin embargo, para un sistema híbrido de 180 ° generalizado, no necesariamente existe una frecuencia en la que coincidan estos fenómenos, por lo que para su evaluación se propuso una función de costos descrita por la ecuación, a fin de definirfo Esta función contempla tanto el desbalance de fase como el desbalance de magnitud. Los valores de wp y wm son pesos que le permiten al diseñador ponderar la importancia de los errores definidos en la función de costos. En esta investigación la función de costo se evalúa con wp2=1 ywm2=(5/0,5). Esta escogencia se puede interpretar como que una variación
de fase 5° es equivalente a desbalance en la amplitud de 0,5 dB. Esta relación en particular es un valor típico usado para la evaluación del ancho de banda de los híbridos de este tipo (Caillet, Clenet, Sharaiha y Antar, 2009; Yang, Chen y Bao, 2010).
Adicionalmente, los parámetros propuestos por Rodríguez et al. (2011) suponen un alto grado de simetría en la estructura, donde el desempeño global se puede describir a partir del comportamiento de algunos de sus puertos. Para el caso de un híbrido generalizado, es importante contemplar la simetría del circuito y medirla para verificar la validez de los parámetros propuestos.
A fin de medir la simetría del circuito se propone una comparación directa de las magnitudes y fases de los parámetros de dispersión del híbrido, que se resume en un parámetro de simetría denominado A. Esta comparación se centra en la comparación de los puertos de suma (1 y 2) entre sí y los puertos de resta (3 y 4) entre sí.
Los errores de simetría son tratados como vectores. La medida de simetría propuesta se calcula como el valor medio de los errores de cada parámetro de dispersión analizado, siguiendo la ecuación para su cálculo. Finalmente, se propone como medida general de simetría el valor máximo de los promedios de asimetría de fase y amplitud calculados en los puertos suma (Σ) y resta (∑), siguiendo la ecuación para su cálculo. En la tabla 1 se presenta un resumen de todos los parámetros de mérito de los prototipos implementados (ver figura 11). Es importante aclarar que los valores de los parámetros son calculados para frecuencia de operación óptima que minimiza la función de costos descrita por la ecuación, y que el ancho de banda fraccional se define para todos los parámetros como el rango de frecuencia que cumple el criterio de operación determinado del parámetro sobre la frecuencia de operación.
La miniaturización del 73 % del híbrido produce un impacto en el ancho de banda del dispositivo, donde el ancho de banda fraccional se reduce en un 45%. De igual manera, se observa cómo a pesar de que el híbrido sigue funcionando en la banda ISM de 2,4 GHz, la frecuencia en la cual funciona de forma óptima se mueve hacia frecuencias más altas, lo que implica que para un funcionamiento simétrico en el punto de operación la reducción de ancho de banda es mayor a la que se reporta en la tabla 1.
En cuanto a la asimetría del circuito, esta no se ve afectada significativamente con la técnica de miniaturización usada. Adicionalmente, se observa que la asimetría producida en la fase es mucho mayor que la asimetría en las magnitudes de los parámetros de dispersión. En cuanto a los parámetros de mérito relacionados con pérdidas de retorno del dispositivo, se observa que el comportamiento del híbrido novedoso y del convencional es similar, con variaciones poco significativas en cuanto a las pérdidas de retorno, siempre menores allO % del parámetro y conservando su ancho de banda. De igual manera, se observa que el rango de frecuencias en el que el aislamiento es menor a -20 dB y es muy similar para los dos circuitos. Por su parte, el aislamiento en la frecuencia de operación del híbrido novedoso se reduce hasta en un 33%, alcanzando el valor de -33,76 dB. Es importante aclarar que en la mayoría de las aplicaciones este valor es suficiente para que los diferentes circuitos que usan este dispositivo funcionen apropiadamente. Se puede concluir que a pesar de que el impacto de la miniaturización es significativo en el aislamiento en la frecuencia de operación, no es relevante en el desempeño del híbrido. Finalmente, se observa una disminución de los anchos de banda en los cuales las pérdidas de inserción son tolerables (2 dB<IL<4 dB), con un detrimento hasta de un 37%. Este comportamiento se puede explicar por las pérdidas del dieléctrico.
El impacto más significativo de la miniaturización se presenta en los parámetros de mérito a la salida. Se encuentra un desbalance de magnitud que alcanza variaciones en sus parámetros de hasta 43 % en la frecuencia de operación, manteniendo casi el mismo rango de operación en ambos híbridos. Por su parte, el desbalance de fase reporta una reducción del ancho de banda fraccional de hasta el 34%, más aun en el rango de frecuencias en las cuales el desbalance de fase es ΡΙΣ<±10° o ΡΙΔ<180°±10°, que es aquel que limita la operación del circuito como híbrido. Para entender el origen de estos resultados se analiza en detalle la figura 12, donde se presentan los desbalances de fase y magnitud de los híbridos implementados en el ancho de banda de interés. En esta figura se observa cómo en el híbrido miniaturizado, el punto óptimo para mínimo desbalance de fase se encuentra entre 2,5 y 2,7 GHz, mientras que el punto óptimo de desbalance de fase se encuentra entre 2,4 y 2,5 GHz. Por lo tanto, no es posible conseguir a la misma frecuencia un buen desempeño de desbalance de fase y desbalance en magnitud simultaneo. Este efecto se presenta al realizar la miniaturización del híbrido y muestra el efecto negativo de este proceso en el desempeño del circuito.
En la figura 13 se presentan las magnitudes de los parámetros de dispersión asociados al puerto suma y al puerto resta. Se observa cómo el comportamiento general de ambas implementaciones es muy similar. Sin embargo, en la implementación fractal los fenómenos de máximo aislamiento, mínimas pérdidas de retorno y mínimas pérdidas de inserción no ocurren en la misma banda de frecuencias, a diferencia del híbrido convencional en el cual estos fenómenos se presentan en la misma banda. Este fenómeno produce un decremento en el desempeño del híbrido miniaturizado, como se ha discutido previamente.
Conclusiones
En este artículo se presentó el diseño, la implementación y la evaluación de un híbrido Rat-race miniaturizado, siguiendo una curva de llenado fractal novedosa. El híbrido opera en la banda ISM 2,4 GHz, con una frecuencia de operación óptima de 2,56 GHz y un ancho de banda fraccional de 17,15%. La técnica de miniaturización propuesta alcanza una reducción de hasta el 73 % de miniaturización, utilizando un 27% del área del híbrido convencional. Esta miniaturización produce un impacto en casi todos los parámetros de mérito del híbrido, siendo los parámetros asociados a pérdidas de retorno, aislamiento e inserción los menos afectados, con un promedio de variación de 6, 14 y 12%, respectivamente. Por otra parte, el principal impacto de la miniaturización en el sistema es la disminución del ancho de banda fraccional en un 45 %.
El impacto de la miniaturización se debe a que el híbrido miniaturizado no genera desbalance de fase mínimo, desbalance de magnitud mínimo, máximo aislamiento, mínimas pérdidas de retorno y mínimas pérdidas de inserción, en el mismo rango de frecuencias. Por lo tanto, al momento de diseñar el híbrido miniaturizado es necesario definir claramente lo que se necesita en la aplicación específica, para lograr el mejor desempeño del sistema. La comparación sistemática de los híbridos implementados a través de los parámetros de mérito propuestos por Rodríguez et al. (2011) y los utilizados en este artículo simplifica la comparación y permite analizar el impacto de la miniaturización en su desempeño.
Financiamiento
El presente trabajo fue financiado por la Vicerrectoría Académica de la Pontificia Universidad Javeriana como parte del proyecto de investigación PS 3206.
Agradecimientos
Los autores desean agradecer al Departamento de Electrónica de la Pontificia Universidad Javeriana por el apoyo en software y hardware necesario para la investigación actual.
Referencias
Caillet, M., Clenet, M., Sharaiha, A. y Antar, Y. M. M., "A Compact Wide-Band Rat-Race Hybrid Using Microstrip Lines", Microwave and Wireless Components Letters, IEEE, Vol. 19, No. 4, 2009, pp. 191-193.
Chao-Hsiung, T. y Hsiang-Ju, C., "Compact Rat-Race Coupler Using Shunt-Stub-Based Artificial Transmission Lines", Microwave and Wireless Components Letters, IEEE, Vol. 18, No. 11, 2008, pp. 734-36.
Chen, W. y Wang, G., "Exact Design of Novel Miniaturized Fractal-Shaped Branch-Line Couplers Using Phase-Equalizing Method", Microwaves, Antennas & Propagation, IET, Vol. 2, No. 8, 2008, pp. 773-80.
Chiou, Y., Tsai, C., Wu, J. y Kuo, J., Miniaturization Design for Planar Hybrid Ring Couplers, Art of Miniaturizing RF and Microwave Passive Components, International Microwave workshop, 2008, pp 19-22.
Duxiang, W., Huynh, A., Hakansson, P., Ming, L. y Shaofang, G., "Study of Wideband Microstrip 90° 3-dB Two-Branch Coupler with Minimum Amplitude and Phase Imbalance", Microwave and Millimeter Wave Technology, 2008, ICMMT 2008, International Conference, Vol. 1, pp. 116-19.
Ghali, H. y Moselhy, T., Design of fractal rat-race coupler, Microwave Symposium Digest. Vol. 1, 2004, pp. 323-326.
Ghali, H. y Moselhy, T. A., "Miniaturized Fractal Rat-Race, Branch-Line, and Coupled-Line Hybrids", Microwave Theory and Techniques, IEEE Transactions, Vol. 52, No. 11, 2004b, pp. 2513-20.
He-Xiu, X., Guang-Ming, W. y Ke, L., "Mi-crostrip Rat-Race Couplers", Microwave Magazine, IEEE, Vol. 12, No. 4, 2011, pp. 117-29.
Jen-Tsai, K., Yi-Chyun, C. y Juo-Shiuan, W., Miniaturized Rat Race Coupler with Microstrip-to-CPW Broadside-Coupled Structure and Stepped-Impedance Sections, 2007, Microwave Symposium, 2007, pp. 169-172.
Ludwig, R. y Bogdanov, G., RF Circuit Design: Theory & Applications (2nd Ed.), Prentice Hall, 2008.
Moselhy, T., Ghali, H., Ragaie, H. F. y Haddara, H., Investigation of Space Filling Capacitors, Microelectronics, Proceedings of the 15th International Conference, 2003, pp. 287-290.
Psychogiou, D. y Hesselbarth, J., "Comparing Miniaturization Techniques for Microstrip 180° Hybrid Ring Junctions", Microwave Symposium (MMS), 2010 Mediterranean, pp. 29-32.
Pucel, R. A., "Looking back at Monolithic Microwave Integrated Circuits", Microwave Magazine, IEEE, Vol. 13, No. 4, 2012, pp. 62-76.
Rao, P. H., Subramanian, J. y Kamki, M., "Miniaturized Broadband Microstrip Fractal Rat-Race Coupler with Shunt Stubs", Microwave and Optical Technology Letters, Vol. 52, No. 289, 2010.
Rodríguez, S., Fajardo, A. y Páez, C. I., "Characterization of the Branch-Line and Rat-Race Ideal Hybrids through their Merit Parameters", Circuits and Systems (LASCAS), 2011, IEEE Second Latin American Symposium, pp. 1-4.
Sagan, H., Space-Filling Curves, Springer-Verlag, 1996.
Wei-Shin, T., Hsu-Hsiang, W. y Yi-Chyun, C., "Design of Microwave Wide-Band Quadrature Hybrid Using Planar Transformer Coupling Method", Microwave Theory and Techniques, IEEE Transactions, Vol. 51,No. 7, 2003, pp. 1852-56.
Wen-Ling, C. y Guang-Ming, W., Design of Novel Miniaturized Fractal-Shaped Branch-Line Couplers, Microwave Conference, 2007, pp. 1-3.
Yang, Y., Chen, J. y Bao, Z., "Broadband Compact Rat-Race Hybrid and its Application to Mixers", Microwaves, Antennas & Propagation, IET, Vol. 4, No. 12, 2010, pp. 2001-07.