Comunicaciones Técnicas
Matemático, Universidad Nacional de Colombia; Ingeniero de Sistemas y Computación, Universidad Distrital Francisco José de Caldas; Especialista en Sistemas de Información Geográfica, Instituto Geográfico Agustín Codazzi- Universidad Distrital Francisco José de Caldas; Profesor de Matemáticas de la Universidad Distrital Francisco José de Caldas. Facultad del Medio Ambiente y Recursos Naturales. Proyecto curricular de Ingeniería Forestal. Profesor de Sensores Remotos de la misma Universidad en la Especialización en S. I. G.
En algunas ocasiones mis alumnos preguntan el porque se les enserian ciertos tipos de ecuaciones diferenciales, además quieren saber acerca de sus aplicaciones en el campo de la Ingeniería Forestal y debido a mi formación no temática en este campo no les puedo responder con exactitud a este tipo de inquietudes. Pero en días pasados se acercó un colega, él si Ingeniero Forestal, a indagarme precisamente por la solución de una ecuación diferencial que es utilizada en uno de los cursos de último semestre que él imparte.
Como se sabe, en los artículos y textos, aparece sólo la ecuación y a continuación su solución, debido a que interesa es sólo su aplicación y se supone que el lector podría llegar a ella sin contratiempos. Sin embargo, dicha suposición no es del todo cierta, puesto que a esta altura se ha olvidado, por falta de práctica, el proceso que conduce a la solución.
Es de indicar que el proceso completo de esta solución no es la primera vez que se da, ya que el mismo se ha presentado varias veces y aquí se trata de recordarlo.
La ecuación que se va a solucionar se emplea como modelo para el estudio del crecimiento de fustales , o árboles que tienen diez o más centímetros de diámetro a la altura del pecho en un bosque.
El modelo también se emplea para describir y simular de manera aproximada el crecimiento del bosque, comenzando en su etapa de régimen transitorio y logrando estimar su turno y el tiempo que los árboles permanecen en cada categoría diamétrica (tiempos de paso). López A. etal. (1993) .
En este artículo se ofrece la solución completa paso por paso de la ecuación diferencial de Bernoulli. Agradezco a mi alumna Karla Rodríguez por su desinteresada colaboración en la transcripción manual de la engorrosa solución.
En las últimas tres décadas se ha intensificado la tala indiscriminada de bosques, tanto por parte de los usuarios que han obtenido permisos del estado, como por los colonos y nativos que presionan sobre los bosques en busca de subsistencia, trayendo como consecuencia la destrucción de grandes áreas boscosas, la extinción de ricas selvas y de valiosísimas especies, pensando quizás que el recurso forestal es inagotable.
Debido a que algunos de nuestros bosques poseen una composición florística y faunística bastante rica, se debe propugnar por su conservación por medio de un aprovechamiento racional, basado en un plan de manejo sustentado en el conocimiento del comportamiento de estos bosques. La complejidad del sistema para llegar a conocerlo e intervenirlo y garantizar su soste nibilidad, los altos costos que implica investigarlo y el peligro de ocasionar daños irreparables robustecen la necesidad de establecer un modelo de simulación para conocer su comportamiento. López A. et al. (1993).
El primero en formular una teoría sobre el crecimiento orgánico basada en principios biológicos fue von Bertalanffy. Para él « el crecimiento se basa en la acción encontrada de procesos anabólicos y catabólicos. El organismo crece cuando la formación sobrepasa a la degradación y se detiene cuando ambos procesos se equilibran». Además, se puede suponer, que en muchos organismos, el catabolismo es proporcional al volumen (peso) y el anabolismo es proporcional a la superficie. Sus ideas parten de considerar a los sistemas vivos como sistemas abiertos. Para medir el crecimiento del bosque el modelo planteado, puede tomar como variables de respuesta las siguientes:
(a) El área basal (AB), que se define como la suma de las áreas seccionales de los árboles a la altura del pecho, por unidad de superficie del bosque y sus unidades son m 2/ha.
(b) La densidad, se define como el número de árboles fustales (NA) por hectárea y su unidad de medida es árboles/ha.
(c) El diámetro a la altura del pecho (DAP), que se calcula a partir de registros de la circunferencia a la altura del pecho (CAP) medida para fustales, así: DAP = CAP / IC y sus unidades son cm/árbol.
Para su teoría de crecimiento von Bertalanffy propuso la ecuación:
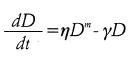
donde:
N = variable de nivel o de respuesta (Puede ser AB, DAP o NA)
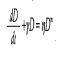 = Cambio de nivel en el tiempo (tasa bruta de crecimiento)
= Cambio de nivel en el tiempo (tasa bruta de crecimiento)
n,y = Constantes de anabolismo y catabolismo. (Tasas de síntesis y degradación).
m = Medida de las velocidades metabólicas.
Do = Valor inicial de D en el tiempo to.El modelo que se va a solucionar se propone para la variable respuesta DAP. Su ecuación es:
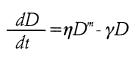
La solución que se obtiene es el diámetro D en función de la edad, así para los árboles muestreados no se conozca esta relación. En dicha solución:
A = Valor límite máximo o estado uniforme (asíntota) que toma la función de crecimiento.
k = Medida adimensional de la tasa de crecimiento con que se llega a la asíntota.
Solución completa
Con la condición inicial t =O , D =Do se tiene:
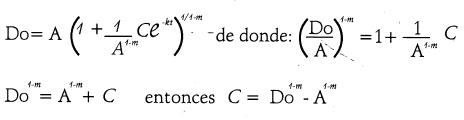
Reemplazando en la solución general se tiene:

DEL VALLE, JORGE I. 1986. La ecuación de crecimiento de von Bertalanffy en la determinación de la edad y el crecimiento de árboles tropicales. Revista Facultad Nacional de Agronomía. Vol XXXIX. No. 1.
LOPEZ, AURA. 1993. Modelos Matemáticos para describir el crecimiento de un bosque primario en el Bajo Calima. Universitas Javeriana. Cali. No. 10.