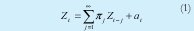
Análisis comparativo de las técnicas de series de tiempo ARIMA y ANFIS para pronosticar tráfico Wimax
Comparative analysis of the time series techniques ARIMA and ANFIS for Wimax traffic forecast
Octavio Salcedo
Director del grupo de investigación Internet Inteligente,
Universidad Distrital.
Cesar Augusto Hernández Suárez
Pertenece al grupo de investigación Internet Inteligente y al grupo ARMOS, Universidad Distrital
Luis Fernando Pedraza Martinez
Pertenece al grupo de investigación GISSIC,
Universidad Militar Nueva Granada.
En este documento se presenta el procedimiento y el resultado principal de un estudio comparativo basado en el uso de un modelo autoregresivo y una técnica de inteligencia artificial, aplicadas en una tarea de predicción de una serie de datos de tráfico Wimax. Los métodos de predicción de series de tiempo comparados son: el modelo ANFIS (Sistema de Inferencia Difuso Basado en Redes Adaptativas) y el modelo ARIMA (Modelos Autoregresivo Integrados de Medias Móviles).
El objetivo del artículo es presentar datos significativos que muestren el desempeño de cada una de las anteriores técnicas bajo el criterio de la suma del error cuadrático medio y el tiempo de procesamiento requerido. Como resultado de este estudio, se comparan los modelos ARIMA desarrollados bajo la plataforma RATS con respecto los modelos ANFIS desarrollados mediante MATLAB.
Palabras claves:
ANFIS, ARIMA, autocorrelación, estocástico, modelo de tráfico, serie de tiempo, Wimax.
This paper presents the procedure and the main result of a comparative study based on the use of a autoregressive model and a technique artificial intelligence applied to the task of predicting a series of traffic data Wimax. The prediction methods of time series compared are: the ANFIS model (Adaptive Network based Fuzzy Inference System) and the ARIMA model (autoregressive integrated moving average).
The goal of this article is to present significant data showing the performance of each of the above techniques at the discretion of the shape of the root mean square error and time-processing required. As a result of this study, are compared the models ARIMA developed under the platform RATS with regard to ANFIS models developed under the software MATLAB.
Key words:
ANFIS, ARIMA, autocorrelation, stochastic, time series, traffic model, Wimax.
1. Introducción
En el campo de la ingeniería algunas veces las series de tiempo resultan ser una buena herramienta para estimar el tráfico de una red. Este estudio presenta un acercamiento para la construcción de una serie Wimax usando ARIMA de orden 18 y ANFIS.
El estudio de series de tiempo tiene como objetivo central desarrollar modelos estadísticos que expliquen el comportamiento de una variable aleatoria que varía con el tiempo, o con la distancia, o según un índice; y que permiten estimar pronósticos futuros de dicha variable aleatoria.
Por ello, el manejo de las Series de Tiempo es de vital importancia en planeación y en áreas del conocimiento donde evaluar el efecto de una política basada sobre una variable, y/o conocer predicciones de sus valores futuros, aportan criterios que disminuyen el riesgo en la toma de decisiones o en la implementación de políticas futuras [5].
Una serie de tiempo es una sucesión de un proceso estocástico Zt generado al obtener una y solo una observación de cada una de las variables aleatorias que definen el proceso estocástico. Estas observaciones son tomadas a intervalos de tiempo o de distancia iguales, según lo indica el índice t que genera la sucesión. En este sentido, la serie es una realización de un proceso estocástico. Para esta investigación se tomaron datos de tráfico de una red de datos Wimax a intervalos constantes de 15 minutos durante aproximadamente 10 días, los datos de tráfico tienen unidades dadas en paquetes por segundo.
En el contexto de Series de Tiempo, pronosticar significa predecir valores futuros de una variable aleatoria basándose en el estudio de la estructura definida por las observaciones pasadas de variables que explican su variación, suponiendo que la estructura del pasado se conserva en el futuro [14].
2. Modelos de tráfico
2.1 ARIMA
Los métodos de pronóstico pueden clasificarse en dos grandes bloques: métodos cualitativos o subjetivos y métodos cuantitativos. Debido a que el objetivo es desarrollar un modelo de tráfico y compararlo con la técnica ANFIS basada en redes adaptativas, se escogió los métodos cuantita- tivos de series de tiempo, estos métodos modelan las series de tiempo estudiando la estructura de correlación que el tiempo, o el índice, o la distancia induce en las variables aleatorias que originan la serie. [7] [8] [13].
Dentro de los métodos cuantitativos existen varios tipos de series de tiempo, entre los que se destacan: los modelos autorregresivos (AR), modelos de promedio móvil (MA), modelos autorregresivos y de promedio móvil (ARMA), modelos autorregresivos e integrados de promedio móvil (ARIMA), modelos autorregresivos e integrados de promedio móvil estaciónales (SARIMA), modelos autorregresivos e integrados de promedio móvil fraccionales (FARIMA) y modelos multivariados (VARMA).
Para explicar la estructura de correlación entre las observaciones de una serie estacionaria se consideran básicamente dos modelos, el modelo autorregresivo en la ecuación 1 y el modelo de media móvil en la ecuación 2.
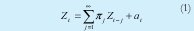
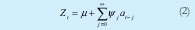
Donde el ruido blanco (at) es una variable aleatoria con media cero, varianza constante, incorrelacionadas entre sí y con los valores pasados de la serie.
Estos dos modelos básicos para series estacionarias se combinan para producir los modelos ARMA (p, q).
En general las series de tiempo no son estacionarias pero por medio de transformaciones de varianza y de diferencias pueden ser transformadas en estacionarias. Los modelos ARIMA resultan de integrar la serie estacionaria ARMA (p, q) estimada, con respecto a las diferencias y las transformaciones que fueron necesarias para convertirla en una serie estacionaria. [3].
En resumen los modelos ARIMA estudian la estructura de correlación entre las observaciones de una serie y basándose en la estructura estimada calcula los pronósticos y los respectivos intervalos de predicción.
2.2 ANFIS
ANFIS tiene una estructura tipo red, similar al de una red neuronal la cual mapea las entradas a través de funciones de pertenencia y sus parámetros asociados, y luego a través de las funciones de pertenencia de la salida y los parámetros asociados a la salida, este sistema puede interpretarse como el mapeo entradasalida. Los parámetros asociados a las diferentes funciones de pertenencia cambian a través del proceso de aprendizaje. La combinación de parámetros (o su ajuste) es realizada por un vector gradiente el cual provee una medida, que también ajusta el sistema de inferencia obtenido para él, modelando el conjunto de datos entrada-salida para un conjunto de parámetros dado. Una vez el vector gradiente es obtenido, cualquiera de las muchas rutinas de optimización podría ser aplicada con el fin de ajustar los parámetros así como para reducir la medida del error (definida en este caso por la suma del cuadrado de la diferencia entre el valor de entrada y el de la salida obtenida). En la presente investigación, ANFIS utiliza el algoritmo llamado propagación hacia atrás para estimar los parámetros de la función de pertenencia [11].
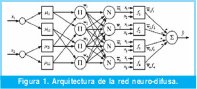
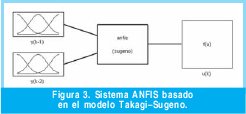
La estructura ANFIS aquí descrita es basada en el modelo TakagiSugeno, el cual según lo demostrado en [12], se puede representar como redes neuronales difusas de 5 capas. Este ejemplo de una red neuro-difusa de 5 capas se muestra en la Figura 1. La primera capa se utiliza para la fusificación de las entradas. En la segunda capa, se calcula el peso de cumplimiento de las reglas difusas. La tercera capa es la capa de normalización. En la cuarta capa, los valores de las reglas de los consecuentes son calculados y multiplicados por el peso de cumplimiento de las respectivas reglas y la quinta capa realiza la desfusicación [10].
3. Desarrollo de los modelos de tráfico
En la Figura 2 se muestra la traza de tráfico Wimax capturada y la cual se pretende modelar a partir de las técnicas ARIMA y ANFIS.

De la Figura 2, se observa que la media de los datos de tráfico está lejos de cero y que su varianza no es constante, dos aspectos que hacen no estacionaria esta serie. A pesar de lo anterior, se desarrollo la prueba de Dickey-Fuller de raíz unitaria para comprobar si realmente es no estacionaria, los resultados de esta prueba se muestran a continuación:
Dickey-Fuller Unit Root Test, Series TRÁFICO_REAL
Regression Run From 2007:01:15//62 to 2007:01:21//95
Observations 828
With intercept with 60 lags
T-test statistic -1.49785
Critical values: 1%= -3.443 5%= -2.867 10%= -2.569
Según el criterio de DickeyFuller, la serie no es estacionaria, ya que el valor absoluto del test es menor al valor absoluto del valor crítico del 5%.
3.1. Modelo ARIMA
El modelo ARIMA de esta investigación se desarrollo a partir de la metodología Box Jenkins, de la siguiente forma:
1. Por medio de transformaciones y/o diferencias se estabiliza la varianza, y se elimina la tendencia y la estacionalidad de la serie,obteniéndose así, una serie estacionaria.
2. Para la serie estacionaria obtenida se identifica y se estima un modelo que explica la estructura de correlación de la serie con el tiempo.
3. Al modelo hallado en el punto 2, se le aplica transformaciones inversas que permiten establecer la variabilidad, la tendencia y la estacionalidad de la serie original.
4. El modelo estimado se valida a través de la correlación de sus residuales, si estos llegan a presentar correlación es necesario volver a estimar nuevamente los parámetros, es decir se regresa al punto 2. El anterior procedimiento iterativo se repite hasta que finalmente no exista correlación significativa entre los residuales. [2] [9].
El modelo obtenido se describe en la ecuación (3)
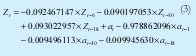
3.2. Modelo ANFIS
Si se utiliza en el entrenamiento del modelo neuro-difuso dos muestras anteriores (y(k-1) y y(k-2)) de la señal a predecir (y(k)), se tienen dos universos de entrada (y(k-1) y y(k-2)), donde cada uno posee dos conjuntos sigmoidales (mf1 y mf2), y un universo de salida (u(k)) con 4 con juntos lineales de salida (mf1, mf2, mf3 y mf4), (Figura 3). Esto permite ajustar a su vez las siguientes reglas:

3.2.1. Algoritmo de Entrenamiento "Propagación Hacia Atrás"
A continuación se realiza una breve descripción del algoritmo utilizado para el entrenamiento de los parámetros de las funciones de pertenencia. Dado un par de parejas de entrenamiento:
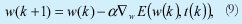
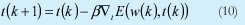
Donde

5. Repetir, regresando al paso No.2 [16].
Como resultado este algoritmo entrena los parámetros de los antecedentes (datos anteriores) y los consecuentes, haciendo que ANFIS sea un modelo de gran adaptabilidad.
4. Resultados
El objetivo de esta sección es evaluar los modelos de tráfico desarrollados en esta investigación en el capitulo anterior. Para lo cual se usa el error cuadrático medio, la desviación estándar en valor absoluto y el tiempo de procesamiento. Para este último parámetro es necesario mencionar que el equipo de cómputo utilizado tiene las siguientes características: un procesador AMD de 2.4 Ghz de frecuencia de un solo núcleo, Memoria RAM DDR de 1.0 GB en capacidad y 400 Mhz en el bus de datos, tarjeta de gráfica Nvidia 6100 y disco duro de 7.200 rpms.
Las pruebas de ambos modelos se desarrollaron en el equipo anteriormente descrito y los resultados son condensados en las posteriores tablas. Sin embargo dichas pruebas se estimaron bajo dos software distintos MATLAB y RATS.
4.1. ANFIS
Se decidió evaluar el modelo con dos cantidades de muestras anteriores, luego con tres, cuatro, cinco y por último de seis datos de tráfico anteriores al dato actual, estos fueron implementados en el software Matlab.
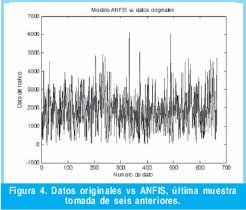
Los resultados permiten afirmar que ha medida que aumenta el numero de muestras se mejora la exactitud de la predicción. En la Figura 4 se puede observar que el nivel de exactitud del modelo es demasiado bajo.
En la Tabla I se presentan los resultados del modelo ANFIS para el total de muestras utilizadas, evaluando los parámetros planteados inicialmente.
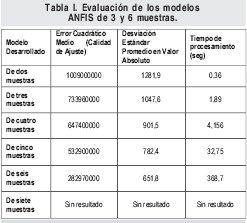
Aquí se decide tomar la desviación estándar promedio en valor absoluto como variable de medida en razón en que a no ser así, este parámetro permite cancelar los errores entre sí. Los valores en la calidad de ajuste muestran como un dato atípico podría sancionar seriamente la evaluación de un modelo según este criterio, razón por la cual también se decidió adicionar el parámetro de desviación estándar promedio en valor absoluto.
Al realizar las pruebas para siete muestras anteriores el sistema durante aproximadamente 30 minutos no obtiene dato alguno.
4.2. ARIMA
El modelo ARIMA (18,1,18) se desarrollo a través del software RATS, con este mismo software se desarrollaron las pruebas.
Para este modelo fue necesario realizar una transformación a la serie original, de una diferencia, con el software RATS, con el objetivo de volver estacionaria la serie. Esto último se comprobó analíticamente a través del criterio de la raíz unitaria, cuyo resultado es el siguiente:
Dickey-Fuller Unit Root Test, Series DTRÁFICO_REAL
Regression Run From 2007:01:15//63 to 2007:01:21//95
Observations 827
With intercept with 60 lags
T-test statistic -6.03666
Critical values: 1%= -3.443 5%= -2.867 10%= -2.569
Según el criterio de Dickey-Fuller, la serie es estacionaria, ya que el valor absoluto del test es mayor al valor absoluto del valor crítico del 5%.
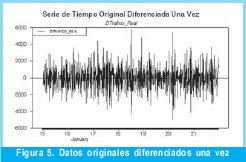
Aunque se realizaron transformaciones de dos diferencias y logarítmicas diferenciadas, con resultados satisfactorios se opto por tomar la primera diferencia en razón de perder únicamente una muestra de tráfico. La serie original luego de diferenciarse una vez se muestra en la Figura 5.
En la Tabla II se presenta los resultados arrojados por el modelo ARIMA
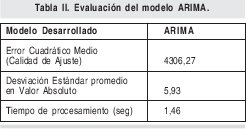
Del análisis de las Tablas I y II, se puede concluir que el modelo ARIMA es mejor tanto en la exactitud de los pronósticos como en el tiempo de procesamiento, esto último se puede atribuir a que el modelo ARIMA a pesar de ser de orden 18 solo procesa tres muestras anteriores la 6,10 y 18, y además el software RATS está basado en código sin interfaz grafica mejorando sustancialmente los tiempos de procesamiento.
Con respecto a la relación que existe entre el orden del modelo ARIMA y el numero de rezagos (muestras anteriores), que hace que el modelo sea mas eficiente que el ANFIS, es debido a las pruebas previas de la metodología BOX-JENKIS permiten estimar los rezagos que realmente son significativos. Lo anterior se logra a través la correlacion de los residuales del modelo. En la figura 6 se muestra uno de los tantos correlogramas que fue necesario correr para estimar adecuadamente los pronósticos de la serie.
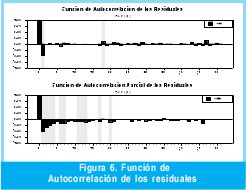
Los rezagos sombreados indican un nivel de significancia alto dentro del modelo, sin embargo, luego de varias iteraciones algunos rezagos pierden significancia y otros aumentan. Como se describió en la metodología BOX-JENKINS la iteración termina una vez que no existe correlación entre los residuales. Como lo muestra la F igura 7 obtenida al final de la iteración del modelo ARIMA (se realizaron cinco iteraciones).
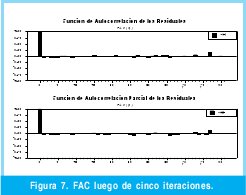
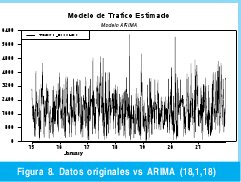
En la Figura 8 se puede observar la serie estimada a partir del modelo ARIMA.
5. Conclusiones
De los resultados obtenidos en la Tabla 1 y de las figuras correspondientes, se concluye que el modelo ANFIS crece en exactitud a medida que se tienen en cuenta más datos de tráfico anteriores al actual, sin embargo la gran desventaja es su costo computacional el cual es demasiado elevado (mucho mayor al del modelo ARIMA); cuando se intento obtener la grafica para 10 muestras anteriores e incluso para 7 muestras anteriores el tiempo de procesamiento llego a los 25 minutos sin mostrar aun resultado alguno. Lo anterior deja al modelo ARIMA como el mejor modelo por encima de los no correlacionados y de los modelos basados en redes neuronales, porque aunque estos lleguen a tener una exactitud parecida el costo computacional es mucho más elevado. Lo anterior en razón a que el modelo ARIMA analiza a través de correlogramas los rezagos con mayor grado de significancia y toma únicamente estos para estimar el dato siguiente en lugar de realizar este proceso con todos los anteriores al orden del modelo.
Los modelos correlacionados desarrollados a partir de las series de tiempo no experimental una relación tan compacta y su tratabilidad matemática se ve comprometida, debido a los rezagos del modelo y sus componentes aleatorias, sin embargo permiten modelar el tráfico Wimax con una precisión y exactitud realmente significativa, debido a que son capaces de capturar los efectos de la correlación a costos computacionales razonables. Lo anterior permite a los modelos de series de tiempo ofrecer un alto desempeño en la caracterización de tráfico Wimax.
Referencias bibliográficas
[1] ALZATE, Marco Aurelio. Modelos de tráfico en análisis y control de redes de comunicaciones. En: Revista de ingeniería de la Universidad Distrital Francisco José de Caldas. Bogotá. Vol. 9, No. 1 (Junio 2004); p. 63-87.
[2] BOX, G. E. P. y JENKINS, Gwilym M. Time series analysis: Forecasting and control. Revised Edition. Oakland, California: Editorial Holden-Day, 1976.
[3] BROCKWELL, P.J. On continuous-time ARMA processes. En: Handbook of statistics. Elsevier, Amsterdam: Vol. 19, 2001. p. 249-276.
[4] CAMERANO FUENTES, Rafael. Teoría de colas. Bogota: Fondo de publicaciones Universidad Distrital Francisco José de Caldas, 1997.
[5] CORREA MORENO, Emilia. Series de tiempo: conceptos básicos. Medellín: Universidad Nacional de Colombia, Facultad de Ciencias, Departamento de matemáticas, 2004.
[6] COUCH, L. Digital and analog communication system. New Jersey: Prentice Hall, 2001.
[7] DAVIS, R. A. Maximum likelihood estimation for MA(1) processes with a root on or near the unit circle. In: Econometric theory. Vol. 12, 1996. p. 1-29
[8] DETHE, Chandrashekhar y WAKDE D.G. On the prediction of packet process in network traffic using FARIMA time series model. Department of Electronics, College of Engineering, India. 2003.
[9] GUERRERO GUZMAN, Víctor Manuel. Análisis estadís- tico de series de tiempo económicas. Segunda edición. México: Editorial Thomson, 2003.
[10] HALANG, Z. Li and CHEN, G. Integration of fuzzy logic and chaos theory. Springer, 2006.
[11] JANG, J.-S. ANFIS: Adaptive-network-based fuzzy inference systems. En: IEEE Transactions on systems, man, and cybernetics. Vol. 23, 1993.
[12] JANG, J.-S. and MIZUTANI, Sun E. Neuro-fuzzy and soft computing--A computational approach to learning and machine intelligence. Prentice Hall, 1997.
[13] MAKRIDAKIS, Spyros G.; WHEELWRIGHT, Steven C. y HYNDMAN, Rob J. Forecasting: methods and applications. Tercera edición. USA: Editorial Wiley, 1997.
[14] PAJOUH, Danech. Methodology for traffic forescating. The French National Institute for Transport and Safety Research (INRETS). Arcuel. 2002.
[15] STALLINGS, William. Comunicaciones y redes de computadores. Séptima edición. Madrid: Prentice Hall, 2004.
[16] ZAK, S. Systems and control. Oxford: oxford university Press, 2003.
Octavio José Salcedo Parra
Ingeniero de sistemas de la Universidad Autónoma de Colombia en 1994, Magíster en teleinformática de la Universidad Distrital Francisco José de Caldas. Magíster en economía de la Universidad de los Andes.Actualmente se encuentra adelantando estudios de doctorado en informática con énfasis en sociedad del conocimiento en la Universidad Pontifica de Salamanca. Director y fundador del grupo de Investigación en Internet Inteligente. Es director de la revista Ingeniería y docente de la Universidad Distrital. ojsalcedop@unal.edu.co
César Augusto Hernández Suárez
Ingeniero electrónico de la Universidad Distrital, Colombia. especialista en interconexión de redes y servicios telemáticos de la Universidad Manuela Beltrán. Candidato a magíster en ciencias de la información y las comunicaciones de la Universidad Distrital. Se desempeñó como docente investigador en la Universidad Manuela Beltrán durante 3 años donde desarrolló varios proyectos aprobados y financiados por Colciencias, dentro de los cuales esta el proyecto Sistema Electrónico Mecánico para la enseñanza de la lectoescritura del Braille para el cual se encuentra en curso la patente de invención. Actualmente se desempeña como docente de planta en la Universidad Distrital en el área de la electrónica digital y el procesamiento digital de señales. Lctsubasa@gmail.com
Luis Fernando Pedraza Martínez
Ingeniero electrónico de la Universidad Distrital, Colombia. magíster en ciencias de la información y las comunicaciones de la Universidad Distrital. Se desempeño como docente en el área de control en Universidades como Cooperativa de Colombia y Distrital. Es director del grupo de investigación «Semaforización Inteligente». Actualmente se desempeña como docente de planta en la Universidad Militar Nueva Granada en el área de comunicaciones. luis.pedraza@umng.edu.co