Ruido de disparo
SHOT NOISE
Alvaro Betancourt Uscátegui
Dos temas serán siempre de permanente búsqueda y tratamiento. Uno, la información y otro el ruido: en el primero se tratará de maximizar, mientras que en el segundo su objeto es minimizarlo, en ambos casos con el propósito de tener mejores resultados. El ruido intrínseco puede dividirse en dos grandes categorías: el ruido "shot" o de disparo que es el propósito de este documento y, el ruido térmico. Aún cuando los orígenes físicos de los dos son distintos, a nivel de estructura de ruido de formas de onda son similares.
Palabras Clave:
ruido, ruido de disparo.
Two topics will always be searching and treatment. One, the information and the other the noise: In the first one, the objetive will be to maximize, while in the other is to minimize it, in both cases the purpose is to obtain the better results. Intrinsic noise was separated in two major categories: shot noise that is the purpose of this paper, and, thermal noise. The physical origins of theses two categories are distinct, but the structures of noise waveform are similar.
Key words :
noise, shot noise.
INTRODUCCION
Aunque el ruido externo de acoplamiento pudiera ser eliminado con la ayuda de un circuito, un mínimo nivel de ruido existirá producido por fuentes de ruido intrínsecas. Si el valor rms de estas fuentes de ruido puede ser definido, el valor instantáneo de amplitud puede predecirse en términos de probabilidad. En casi todos los dispositivos electrónicos se encuentra presente el ruido intrínseco. Tanto el ruido shot estudiado extensivamente por Schottky [1] como el ruido térmico conocido como ruido Johnson, en honor de J.B. Johnson [2] pueden representarse como un tren de pulsos aleatorios consistente en una secuencia de pulsos similares distribuidos en el tiempo. En ambos casos el mecanismo responsable es controlado por la naturaleza pues el ruido no puede eliminarse por sí mismo.
El ruido de disparo fue primer mecanismo del ruido eléctrico reconocido. El descubrimiento proviene con el funcionamiento del tubo al vacio y se observó en la forma de fluctuación de una corriente espontánea de placa d-c. [1]. Como quiera que los electrones se emiten aleatoriamente desde el cátodo, lo que acarrea una carga q, el flujo de corriente resultante es granular en un sentido microscópico, dando lugar a la fluctuación aleatoria alrededor del valor medio.
Se pretende en este artículo efectuar una revisión del ruido de disparo. En la primera parte se presenta una introducción de base al ruido de disparo y del ruido en general. Se describe posteriormente la presencia del ruido de disparo en varios dispositivos. Finalmente, se muestran resultados experimentales obtenidos por diferentes autores como técnica de medida [3].
GENERALIDADES DEL RUIDO DE DISPARO
El ruido de disparo es la corriente de ruido asociada con el flujo de corriente directa en una barrera de potencial. Causado por la fluctuación de corriente alrededor de un valor promedio resultante de la emisión aleatoria de electrones o agujeros. Con el objeto de entender la naturaleza de ruido de disparo, es conveniente considerar un diodo térmico en el que se emiten electrones al azar desde el cátodo y se desplazan al ánodo bajo la influencia del campo eléctrico. La corriente asociada con la cadena de electrones fluctúa aleatoriamente sobre un nivel, dichas fluctuaciones son debidas a la naturaleza discreta del proceso de emisión.
Se encuentra presente en tubos, transistores, diodos y dispositivos de estado sólido En tubos, el ruido proviene de la emisión aleatoria de electrones desde el cátodo mientras que en los semiconductores es debido a la difusión aleatoria de portadores a través de la base del transistor y a la generación y recombinación de pares de electrónhueco [4].
Teóricamente fue analizado en su trabajo pionero por W. Schottky [l] observando que el valor rms del ruido de disparo es:
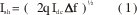
donde q = la carga del electrón, 1.59 x 10-19 Culombios
Idc= la corriente directa, en Amperios,
Δf = el ancho de banda, en Hz,
En la figura No. 1 se muestra un gráfico de la corriente de ruido de disparo vs. la corriente de diodo [3].
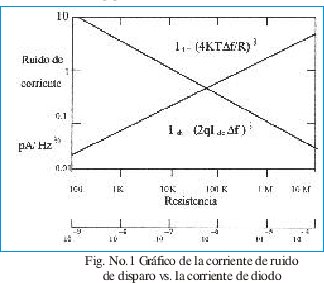
La densidad espectral de potencia del ruido de disparo es constante con la frecuencia y la amplitud tiene una distribución gaussiana. Es proporcional a la raíz cuadrada del ancho de banda y es un ruido blanco. Al dividir la ecuación (1) por la raíz cuadrada del ancho de banda se obtiene
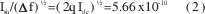
Significa que el ruido de corriente por la raíz cuadrada del ancho de banda es sólo una función del flujo de corriente d.c., y puede ser determinada la cantidad de ruido.
En la tabla No. 1 se muestra las fluctuaciones relativas de acuerdo con las corrientes.
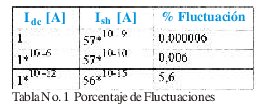
La densidad espectral de potencia del ruido de disparo es aplicable a los diodos de unión de p-n, a los transistores bipolares, a los diodos de metal semiconductor, cargados a través de los portadores en la barrera de potencial [5].
El ruido de disparo es muy útil cuando una fuente que tiene un espectro de ruido blanco es similar al ruido térmico midiendo la temperatura del ruido de un amplificador o cualquier componente lineal del receptor para esa materia.
RUIDO DE DISPARO EN DIODOS Y EN LOS TRANSISTORES BIPOLARES
Van der Ziel [6] propuso la base de una línea analógica de transmisión distribuida R-C. Fue considerado como un diodo ideal en el que la capa de deflexión combinación- generación y los efectos de la superficie es despreciable mostrando que el ruido puede ser representado por una corriente generadora en paralelo con la unión cuya densidad espectral depende de la corriente terminal y de la unión de conductancia.
La expresión de la densidad espectral para este generador de corriente de ruido en paralelo tiene la forma 2qIdc y para la polarización aplicada (Idc=0) que simplifica a la fórmula de Nyquist para el ruido térmico en un componente pasivo con una conductancia igual de la unión. El comportamiento V-I de la unión es notada por la ecuación ya familiar:
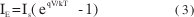
donde IE es la corriente terminal, Is es la corriente de saturación inversa, q la magnitud (carga) del electrón y V es el voltaje aplicado. Si son consideradas separadamente las dos corrientes que conforman IE;
IE= I1 + I2 (4)
donde I1= -Is. Es causado por los portadores minoritarios generados térmicamente,
I2= Is eqV/kT (5)
que representa la difusión de portadores mayoritarios a través de la barrera. Cada corriente tiene ruido de disparo y la corriente directa representan el flujo opuesto.
Con polarización inversa de la corriente de ruido de disparo, I1 domina puesto que I2 tiende a cero. Cuando el diodo es polarizado en directo, la corriente del ruido de disparo I2 domina. Para polarización cero no hay ninguna corriente externa, I1 e I2 son iguales y opuestas. El significado del valor al cuadrado del ruido de disparo es dos veces la corriente de polarización inversa del ruido de disparo;
Ish2= 4qIs Δf (6)
Un circuito equivalente que representa el ruido de disparo para una unión pn de polarización directa se muestra en figura No. 2. Desde el punto de vista matemático significa que el cuadrado del ruido de disparo es igual al ruido térmico para una unión no polarizada e igual a un medio del voltaje del ruido térmico en una polarización de unión.
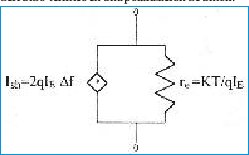
A temperatura ambiente re = 0.026/IE. El voltaje del ruido de una unión polarizada en directo es el producto del ruido de corriente de disparo , Ish y de la resistencia del diodo.
El comportamiento del ruido de una selección aleatoria de transistores de silicio fue reportado por [7] quién encontró que el ruido mínimo a frecuencias de audio es mejor que 0.5 dB. Sin embargo, todavía el problema de exceso de ruido a frecuencias bajas e intermedias es tema de investigación.
Una teoría del ruido en la unión fue propuesta por [8], en la que se invoca la difusión del portador de carga originada localmente y fluctuaciones aleatorias en la población de los portadores.
LA TEORIA DE DIFUSION DE RUIDO EN UNA UNION de P-N
El mismo autor [8] plantea que un diodo ideal de unión es aquel en el que la capa de recombinación-generación y los efectos de la superficie son despreciables, y cuya característica de corriente/ voltage es descrita por la ecuación de Shockley (3).
El ruido en el diodo es representado por un generador de corriente en paralelo con la unión y cuya densidad espectral es:
Si(f) = 2q (IE + 2Is) + 4KT (Gj -Go) (7)
donde Gj es la conductancia de la unión y
Go = dIE / dV = q / KT (IE + Is) (8)
siendo Go el valor de baja frecuencia de Gj.
La ecuación (7) es la expresión de la fórmula de Van der Ziel para el ruido en una unión ideal p-n; tiene ciertas propiedades: a bajas frecuencias y sometido con fuerte polarización directa o inversa se reduce a la forma familiar del ruido de disparo 2qI E y 2qIs respectivamente mientras que para cero polarización se simplifica a 4kGj.
RUIDO DE DISPARO EN UNA UNION DE JOSEPHSON
El Ruido en el efecto Josephson, producido cuando la corriente que fluye a través de la unión es mayor que la corriente crítica, fue investigado de manera teórica por [9] encontrando que el sistema es inestable con respecto a las fluctuaciones de fase y tiene el efecto de ampliar el ancho de banda de la radiación emitida de la unión, en lugar de que sea una simple frecuencia. Este tratamiento predice una fluctuación en la corriente que fluye a través de la unión.
Un argumento de ruido de disparo que lleva a un resultado más preciso es empleado por [10]. La corriente que fluye a través de la unión consiste de electrones normales donde la magnitud de la carga sobre cada uno es q mientras que los pares de electrones la magnitud de carga es 2q.
Así, en la unión la corriente total es
i = in + ip = in1 - in2 + ip1 - ip2 (9)
donde in= in1 - in2 es la corriente neta de electrones normales en tanto que ip = ip1 - ip2 es la corriente neta de electrones apareados a través de la unión, (flujo de corriente en ambas direcciones).
Cada uno de los cuatro componentes de corriente en el lado derecho de la ecuación muestra el ruido de disparo, dado que son independientes y las densidades espectrales de potencia de in y de ip son respectivamente
Sin(f ) = 2q (In1 + In2)
( 10 )
y Sip(f ) = 4q (Ip1+ Ip2)
Finalmente se llega a la expresión para la densidad espectral:
Si(f) = 2qIn + 4qIp ( 11 )
RUIDO DE DISPARO EN TRANSISTORES
Van der ziel [11] describe que si se asume por simplicidad que el transistor es de tipo p-n-p en el que toda la corriente es transportada por los portadores huecos, la corriente de emisor IE está compuesta de una parte por IES eqV/kT debido a los huecos inyectados en la base, donde V es el voltaje emisor-base, y de otra parte por -IBE debida a los huecos generados en la región de base y colectada por el emisor.
La corriente del emisor Ic consiste en una parte de αFIES eqV/kT debido a la colección de huecos inyectados por el emisor, donde el F es el factor de amplificación de la corriente, y de otra parte a IBC debida a los huecos generados en la región baja y colectada por el colector. Por tanto,
IE= IES eqV/kT - IBE ( 12 )
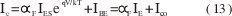
donde Ico= αF IBE + IBC y es la corriente saturada de colector .
La conductancia LF del emisor gebo es
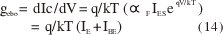
La transconductancia de LF es gmo
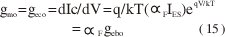
y el factor de amplificación de corriente de LF es
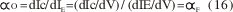
Todas estas corrientes muestran el ruido de disparo. A bajas frecuencias
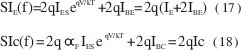
Como quiera que las corrientes IE e Ic tienen en común el componente αF IES eqV/kT, estas presentan el ruido de disparo.
RUIDO DE LUZ EN DIODOS LUMINISCENTES DE ESTADO SOLIDO Y LASER DE ESTADO SOLIDO
Esta parte se limita a los diodos de luz y diodos láser y su funcionamiento es tratado por [11]. En los diodos Luminiscentes se presenta el ruido de disparo, debido a los por tadores que cruzan la barrera y que se recombinan posteriormente.
Para describirlo es necesario tomar una serie de eventos que ocurren a la tasa promedio n y además que n es un número fluctuante de eventos que ocurren durante un segundo dado. Para este proceso de fluctuación es posible mostrar que:

Si estos eventos son independientes y ocurren al azar - proceso de Poisson o proceso de ruido de disparo se encuentra que:

Un proceso que satisface esta condición da como resultado el ruido de disparo. Si, similarmente es aplicada a la emisión del fotón, se aprecia que el proceso de emisión de fotón es un proceso de ruido de disparo. Si todos los electrones inyectados se recombinan bajo generación de un fotón y son emitidos, entonces la tasa de emisión de los fotones np es igual a la tasa n de inyección de electrones de tal manera que;
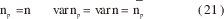
y los fotones emitidos muestran ruido de disparo.
En el caso de ruido de disparo de la emisión espontánea de ruido en laseres, puede ser considerado un láser como un generador de amplitud estable, así que la radiación emitida obedece estadísticamente a procesos de Poisson y

y los dispositivos muestran ruido de disparo de los fotones emitidos. Una de las razones para que el láser debiera mostrar el ruido de disparo es el considerar un láser ideal con 100 % de eficiencia y pérdida óptica cero; entonces, la tasa n de emisión de fotones es igual a la tasa de bombeo W. Como quiera que esta tasa puede representarse como una serie de eventos aleatorios independientes, entonces:
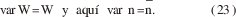
Si hay pérdidas ópticas de forma tal que la parte de los o˜ quántum producidos es realmente emitido, se tiene que

desde el var W = W entonces n muestra el ruido de disparo.
MEDIDA DEL FACTOR DE RUIDO CON UN DIODO DE RUIDO
Tal como se describe en [5] un buen método para medir el factor del ruido cuando el ancho de banda es desconocido, es usar un diodo de ruido como una fuente de ruido blanco. El circuito que mide el ruido se muestra en figura No. 3, I dc es la corriente directa a través del diodo de ruido y Rs es la resistencia de fuente. El ruido de disparo en el diodo es:
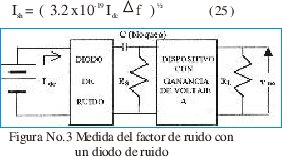
Usando el teorema de Thevenin, el ruido de disparo del generador de ruido es reemplazado por Vsh (generador de voltaje) en serie con Rs, y

El voltaje corresponde al ruido térmico de la resistencia de la fuente y es debido al ruido en el dispositivo. Así que la expresión es:
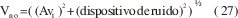
Aunque la corriente del diodo puede fluir, es incrementada hasta que la salida del ruido dobla - el voltaje de salida rms y el incremento llega a 3 dB, se obtiene:
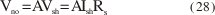
sustituyendo Vno en la expresión del factor del ruido tenemos,
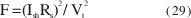
reemplazando Ish y Vt= (1.6 x 10-20 ΔfRs)½ se obtiene:
F = 20Idc Rs ( 30 )
y se aprecia que, el factor del ruido es función sólo de la corriente directa a través del diodo y del valor de la resistencia de la fuente.
RUIDO DE DISPARO EN n + - UNIONES
Los autores Macucci y Pellegrini [12] describen la medición del ruido de disparo en casi todas las uniones ideales en n+ p , usan un sencillo amplificador operacional mostrado en figura No. 4. El amplificador operacional es un PMI OP17; dispositivo que es un amplificador de entrada de FET de bajo ruido caracterizado por un valor pequeño de las corrientes de polarización de entrada.
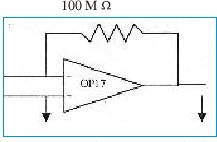
Los diodos probados, citan los autores eran uniones n+-p con un proceso tecnológico particular que apuntó a reducir la impureza tanto como fuera posible para un comportamiento casi ideal para ambas características I-V. La unión se ha mantenido a una temperatura constante de 0°C, con corrientes que van desde 136 pA a 100 nA.
Como se muestra en figura No. 5 los puntos representan los valores de SIB que fueron obtenidos para el caso crítico, el valor más bajo de corriente de polarización fue de 136pA. El ruido de disparo teórico ( líneas punteadas ) tiene una densidad espectral SIB = 2qI = 43.57x10/-30 A2 Hz, el cual corresponde a un pequeño porcentaje de los valores medidos. El ruido del amplificador está representado por la línea continua.
El aumento puede notarse a frecuencias cercanas de 1 Khz. En este caso a la frecuencia de 1 Khz el ruido del amplificador SID era doce veces más grande que los SIB del diodo.
Finalmente describieron que de acuerdo con lo mejor de su conocimiento, el nivel de ruido de disparo evaluado con su método está lejos de la medida directa más pequeña en uniones del p-n con una exactitud comparable.
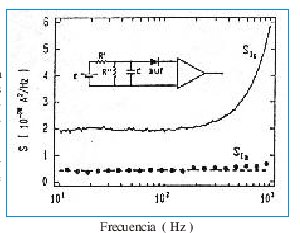
Figura No. 5 Densidad espectral SIB del ruido de disparo de una unión n+-p polarizada en directo con una corriente de 136 pA
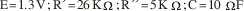
POTENCIA DE RUIDO DE DISPARO SUB-POISSON
La mayoría de los textos sobre dispositivos electrónicos informan que no se presenta ruido de disparo en las resistencias metálicas, sólo ruido térmico y el ruido dependiente de frecuencia conocido como ruido 1/f. Sin embargo, Marc de Jong [13] en un estudio y experimentaciones sobre el mismo, describe que en dispositivos pequeños esta afirmación ya no tiene total consistencia.
Aunque han habido algunas predicciones teóricas acerca del ruido de disparo en resistencias metálicas, la evidencia experimental ha sido difícil obtener. Trabajos de [14] sobre medidas del ruido muy exactas para las resistencias de película delgadas muestran la existencia de varios regímenes claramente diferenciables de ruido.
El reciente progreso en la tecnología de nanofabricación ha revivido el interés en el ruido de disparo, en particular a nivel de nanoestructuras y de las resistencias que permiten hacer las medidas en escalas de longitud que anteriormente eran experimentalmente inaccesibles. Cálculos recientes muestran que el ruido de disparo existe en dicho tipo de resistencias aunque a niveles más bajos que en una unión túnel.
Es la denominada potencia de ruido de disparo sub-Poisson, S, de una resistencia metálica y que es función de su longitud L. Los autores investigaron en una estructura de semiconductor en donde la longitud era aproximadamente de 17 micrones. Los experimentos realizados por [14] fueron hechos en películas metálicas delgadas con longitudes entre 1 micrón y 7 nanomicrones y a temperaturas entre 50 y 400 mK. Los resultados confirman que el ruido de disparo está cerca del valor de 0.87eI por longitudes que corresponden al régimen caliente del electrón, siendo esta la primera vez que el ruido de disparo ha sido medido con exactitud para poder distinguir entre estos dos regímenes.
MEDIDAS OPTICAS BASADAS EN LASER
Las medidas ópticas basadas en el láser son una tecnología fundamental [15]. Los límites de la mayoría de estas medidas son el conjunto de ruido y de señales espurias de uno u otro tipo. Las perturbaciones ocasionadas por el viento, el sonido, la vibración mecánica, el ruido térmico, el ruido de disparo, el excesivo ruido de láser, son algunos ejemplos de ruido comunes que pueden no estar correlacionados con los datos. Antes que ruido hay usualmente señales ópticas espúreas debido por ejemplo a modulaciones propias de láser desde el frente de la superficie de reflexión o modulaciones de amplitud residual. Están frecuentemente correlacionadas con los datos y se introduce un error sistemático.
REDUCCION DE RUIDO
La mayoría de las tecnologías más sofisticadas de medidas ópticas consisten principalmente de la manera como se mejora la relación señal a ruido y la forma como éstas son realizadas depende específicamente de la aplicación.
La eficacia de un sistema de retroalimentación está dada por su ganancia de error. Si un haz de láser de 40 dB por encima del ruido de disparo a una frecuencia de modulación fm es alimentado en dicho sistema, la ganancia de error del sistema a fm debe ser menor que un 1% si el rendimiento de salida alcanza el ruido de disparo. Esto ocurre usualmente alrededor de un 1% de los 3dB del ancho de banda del sistema, además, un sistema de retroalimentación con un ancho de banda de 1 MHz podría estar limitado a modulación de frecuencias de 10 Khz.
SUPRESOR DE REALIMENTACION DE RUIDO
La posibilidad de lograr excelente desempeño, puede realizarse con un balanceo electrónico por ajuste para el substrato y un criterio electrónico sencillo para encontrar un perfecto balance, son los elementos básicos de un supresor de ruido, solo resta adicionar realimentación negativa. En la figura No.6 se presenta un esquema de un dispositivo que utiliza dichas ideas[15].
Los transistores Q1 y Q2 son un par diferencial de transistores bipolares BJT que mejora la separación de la corriente (Q3es una etapa de cascada para prevenir inestabilidad debido a CR1 y la unión A1). El integrador A2 sensa la salida de A1 y ajusta la relación de corriente de Q1/Q2 (vía ΔV be) para mantenerlo a cero voltios. El lazo de realimentación puede ser tan rápido o tan lento como se desee, dado que la cancelación efectiva del ancho de banda no depende de la realimentación del ancho de banda f C , solamente de la f T de los transistores.
En el artículo [16] cita el autor que el circuito tiene otra salida, a partir A2, la cual se muestra con la ecuación

y se presenta otra salida que es la razón logarítmica de las fotocorrientes de señal y de muestreo :

El factor KT/q es eliminado por la selección del divisor de voltaje.
APLICACIONES
Varias técnicas muy puntuales existen para tratar de eliminar el ruido de disparo limitado en las mediciones ópticas, pero son pocas las usadas fuera del laboratorio. La importancia de este dispositivo es que permite realizar medidas de rutina dado su costo.
SEÑALES DE RUIDO EN EL CIELO
Es bien interesante mostrar que SCO-X-1 fue la primera fuente de descubrimiento y única con rayos x más brillantes en el cielo [17]. Escasos diez años atrás, una extraña señal fue detectada desde la fuente de rayos x SCO-X-1. Denominada "oscilaciones quasi periódicas" (ó QPO´s) estos pulsos de rayos x difíciles de encontrar van y vienen como el viento, con duración de unos pocos cientos de segundos, de manera repetida, pero ligeramente diferente cada vez. Durante estos cientos de segundos, ráfagas externas de luz van y vienen como en la rotación de un faro aproximadamente una vez cada segundo.
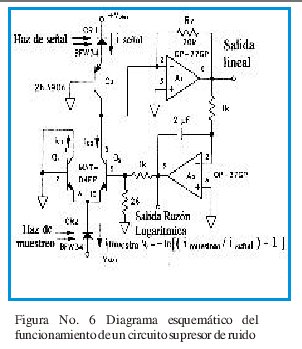
La naturaleza exacta del proceso que da origen a estas señales particulares es desconocida y la teoría más cercana es la llamada ruido de disparo. La gran variedad de efectos presentes en estas fuentes (tales como cambios en las propiedades espectrales) la hace tanto más difícil cuanto más interesante su explicación. En la figura No. 7 se muestra el telescopio Rossi XTE con el que pueden obtenerse nuevos resultados para conocer más sobre estas misteriosas señales.
Lo cierto es que la naturaleza proveerá más sorpresas sobre estos rayos x. Si bien SCO X-1 ha sido la fuente de rayos x más nítida en el cielo (excluyendo el sol), citan los autores que se necesita observar más su variabilidad sobre escalas de tiempo más cortas (de un milésimo de segundo) para comprender en detalle qué está sucediendo. Durante este corto período, solo unos pocos fotones pueden ser colectados con satélites actuales, y los datos parecen "ruidosos".
CONCLUSIONES
De las diferentes aplicaciones de fuentes del ruido probablemente lo más conocido es su uso en la medida de interferencia en el campo de la electrónica y sistemas. La meta es la reducción de ruido. Se ha llevado a cabo una breve revisión del desarrollo histórico y generalidades del ruido de disparo, su presencia en algunos fenómenos tales como: en diodos, transistores, uniónes pn, josephon, laser, en resistencias delgadas metálicas, ruido en el cielo; los métodos de medida y de cancelación así como algunos resultados experimentales realizados por diferentes autores.
BIBLIOGRAFIA
[1] Schottky W., Ann. Phys., vol. 57, pp. 541-567, (1918).
[2] Jonhson, J.B.,Thermal agitation of electricity in conductors, Phys. Rev. ,vol. 32 ,pp. 97-109,(1928).
[3] Motchenbacher C.D. and Fitchen F. C., Low-Noise Electronic Design, Wiley, NewYork, (1973).
[4] Ott H.W., Noise Reduction Techniques in Electronic Systems Wiley, New York, pp. 208-218, (1976).
[5] van der Ziel A., Noise, Prentice Hall, Englewood Cliffs,N.J., pp. 210 ,(1954).
[6] van der Ziel A., Theory of shot noise in junction diodes and junction transistors, Proc. IRE, 45, pp. 1011 (1957).
[7] Faulkner E.A., and Harding D.W., Some measurements on low noise transistors for audio frequency applications, The Radio and Elect. Eng., 36, pp. 31-33 ,(1968).
[8] Faulkner E.A., and Buckingham M. J. , The theory of inherent noise in p-n junction diodes and bipolar transistors, The Radio and Elect. Eng.,44, pp.125-140,(1974).
[9] Stephen, Noise in the a.c. Josephson effect, Phys, Rev. 182, pp. 531-538, (1969).
[10] van der Ziel and Chenette R., Noise in solid state devices, in Advances in Electronics and Electron Physics, 46, pp. 313-383, (1978)
[11] van der Ziel A., Noise in solid-state devices and lasers,Electrical Noise; Fundamental & Sources, IEEE PRESS, N.Y., pp. 237-265, (1977).
[12] Macucci M. and Pellegrini B., Very Sensitive Measurement Method of Electron Device Current Noise, IEEE Transactions on Instrumentation and Measurement, vol . 40, No.1, pp. 7-12, (1991).
[13] De Jong Marc, " Sub-Poissonian shot noise" Physics world, 1996, p.p 22.
[14] Steinbach A, Martinis, J., Devoret M, Physics Rev. Lett. 76, (1996).
[15] Habbs.P "Shot noise limited optical measurement at baseband witer noise laser" Laser Noise SPIE ´roc.1991
[16] Hoobs P., Reaching the shot noise, Optics & Photonics News, p.p.17-23,( 1991).
[17] http://chandra.harvard.edu/xray_source,1998
Alvaro Betancourt Uscátegui
Ingeniero Electrónico Universidad Distrital, Especialista en Telecomunicaciones Móviles, Universidad Distrital, Msc. Ciencias Financieras y Sistemas, U. Central, Magister en Informatique Apliquée, Ecole Polytechnique de Montreal, Canada., Profesor Facultad de Ingeniería Universidad Distrital Francisco José de Caldas , abetancourt@atlas.udistrital.edu.co