Academia y Desarrollo
Determinación de la proyección Equiárea para Sistemas de Información Geográfica
Pedro Omar Castañeda
Profesor Especialización en SIG, Universidad Distrital Francisco José de Caldas
Se presenta una metodología general de selección de un sistema de proyección cartográfico diseñado por TISSOT. Se aplica para seleccionar una proyección EQUIÁREA para ser utilizada en aplicaciones con SISTEMAS DE INFORMACIÓN GEOGRÁFICA o todo aquello que utilice una base cartográfica y que obtenga como resultados el cálculo de áreas y distancias.
Como esta base cartográfica generalmente esta construida con una proyección CONFORME, se define el factor que debe afectar a los datos conformes para que produzcan resultados equiáreos y equidistantes, tomando como parámetros la proyección EQUIÁREA seleccionada.
INTRODUCCIÓN
La tecnología de los SISTEMAS DE INFORMACI&Oacuxte;N GEOGRÁFICA, se ha desarrollado ampliamente en los últimos años, de tal manera que las aplicaciones se hacen en todos los campos profesionales y uno de sus principales objetivos es la homogeneización y estandarización de la información con el único fin de mejorar su manejo en procura de una acertada respuesta de los fenómenos que se presentan en el manejo de los Recursos Naturales.
Los diferentes estudios sobre el manejo de los Recursos Naturales, utilizando los S.I.G., pretenden identificar las áreas que son utilizadas, afectadas, mejoradas, transformadas y todas aquellas que tienen que ver con su cambio. Para esto los S.I.G. toman como base la Cartografía existente, la cual ha sido elaborada con un Sistema de proyección conforme. Dicha proyección como es obvio pensar no permite calcular áreas y distancias exactas.
Por lo anterior se desarrollo un trabajo de investigación que pretende solucionar dicho problema.
La investigación se desarrolla en tres etapas: en la primera se efectúo el estudio detallado para seleccionar la proyección EQUIÁREA de una región cualquiera, para lo cual se aplico la teoría de Tissot; en segunda instancia, mediante cálculos numéricos se efectúa una comparación entre la proyección EQUIÁREA seleccionada y la proyección conforme existente, tomando como guía una poligonal geodésica, finalmentecomo los datos varían se determino la metodo- logía para convertir los datos conformes en los equiáreos.
Los resultados anteriores pueden ser aplicados a cualquier región del globo terráqueo.
ANTECEDENTES
Los SISTEMAS DE INFORMACIÓN GEOGRÁFICA, tuvieron su base en la CARTOGRAFÍA que es la ciencia de representar, gráficamente, la superficie terrestre o parte de ella a escala, la cual involucra una serie de procesos manuales tediosos que han sido minimizados por la CARTOGRAFÍA AUTOMATIZADA (CAD) y ahora la tecnología de los SISTEMAS DE INFORMACIÓN GEOGRÁFICA (S.I.G.), además de la representación gráfica automática involucra el análisis de datos georeferenciados con el objetivo de proporcionar información óptima en la toma de decisiones a diferentes niveles.
Para el análisis de la información es necesario que los datos utilizados se encuentren referenciados de tal manera que permitan alcanzar los objetivos del S.I.G.
Los Sistemas de Información Geográfica manejan en sus módulos gráficos puntos, nodos, líneas, arcos y polígonos. Todas sus aplicaciones, generalmente, realizan cálculos de distancias y áreas sobre la base de los polígonos creados en las diferentes coberturas, pero las coordenadas de los vértices que se utilizan en éste cálculo son valores transformados por una proyección CONFORME lo cual genera error en área y para solucionar ésta distorsión se requiere que los datos sean transformados por una proyección EQUIÁREA.
En los últimos seminarios o simposios se ha planteado la necesidad de que la información cartográfica utilizada por los S.I.G. sea transformada a un sistema equiáreos, teniendo en cuenta que la Cartografía de un país o comarca se elabora utilizando una proyección conforme.
MARCO TEÓRICO
La representación de la superficie terrestre o parte de ella en un medio plano genera una serie de distorsiones que la CARTOGRAFÍA debe resolver.
Dichas distorsiones se presentan debido a que la superficie terrestre se encuentra en un espacio tridimensional y su representación gráfica se hace en un medio bidimensional, lo cual no permite una representación exacta presentándose deformaciones en ángulo o forma, en área, distancia y en dirección, para lo cual la CARTOGRAFÍA ha desarrollado sistemas que permiten eliminar una o varias de estas distorsiones. Estas son las PROYECCIONES CARTOGRAFÍCAS, en donde se encuentran proyecciones CONFORMES que representan verdaderas formas o ángulos en el mapa, proyecciones EQUIÁREAS con las cuales se puede calcular verdaderas áreas, proyecciones EQUIDISTANTES en donde las distancias son verdaderas en el mapa y proyecciones AZIMUTALES que permiten representar verdaderas direcciones.
Un sistema de proyección que elimine todos los tipos de deformación es imposible generar, pero se pueden ajustar varias de estas, sin embargo no se puede construir un mapa que a su vez sea CONFORME Y EQUIÁREO, si se es conforme se debe ser consiente que se deforma el área y viceversa.
Disponiendo de un gran paquete de proyecciones, primero se efectúa una selección teórica, en la cual se analiza:
Por medio de este proceso se seleccionan un pequeño grupo de proyecciones, luego mediante un proceso analítico - gráfico - matemático se selecciona la proyección definitiva.
Esta metodología fue diseñada por TISSOT Su teoría básica consiste en:
Las ecuaciones aquí definidas se aplican a las diferentes proyecciones seleccionadas en la primera etapa y se escoge aquella que mejor cumpla con las condiciones impuestas al mapa (véase anexo: teoría básica de Tissot).
Para tal fin, a las proyecciones seleccionadas se les calcula los vectores de deformación individual y el resultante el cual se utilizara en la selección de la proyección definitiva.
METODOLOGÍA
El propósito fundamental del proyecto es describir la metodología de selección de un sistema de proyección EQUIÁREO para cualquier comarca para ser utilizados en aplicaciones de S.I.G. y luego determinar un factor que permita convertir la información existente (conforme) en EQUIÁREA que garantice calcular áreas y distancias verdaderas.
Para el proceso de selección, como se indico anteriormente, implica dos pasos fundamentales:
PROCESO TEÓRICO
Del conjunto general de proyecciones (planas o azimutales, cilíndricas y cónicas) existentes se selecciona aquellas que se consideren cumplan con las siguientes características:
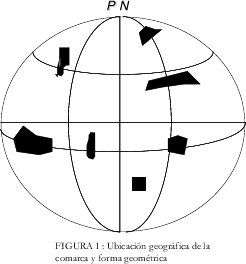
•POR UBICACIÓN GEOGRÁFICA DE LA COMARCA
Esta puede estar en la zona ecuatorial, en latitudes medias o cerca al polo.(véase figura No. 1).

• POR FORMA GEOMÉTRICA DE LA COMARCA
Puede ser regular o irregular la cual puede ser alargada en sentido sur-norte o este-oeste o inclinado.
•POR LA PROPIEDAD DEL MAPA
Puede ser conforme, equiáreo, equidistante o azimutal o cualquier combinación excepto conforme-equiáreo, que como ya se sabe es imposible generar.
De este estudio se selecciona un pequeño grupo de proyecciones de las cuales debe finalmente escogerse la proyección definitiva por un proceso matemático.
PROCESO MATEMÁTICO.
Definir mediante un gráfico aproximado la comarca a mapear y determinarle una poligonal geodésica que la circunscriba lo mejor posible con un vértice central que se tomara como centro de proyección.
•A las proyecciones seleccionadas teóricamente se les define sus ecuaciones de transformación de coordenadas geográficas a planas X,Y, los semiejes de la elipse indicatriz de Tissot a,b y las ecuaciones de distorsión en ángulo, área, longitud y dirección. (Véase anexo: teoría básica de TISSOT).
•Para la poligonal geodésica se define una tabla de valores de coordenadas geográficas (latitud y longitud), la cual se aplica a las anteriores proyecciones en lo cual se calcula los semiejes a y b de la elipse indicatriz de Tissot y con estos los vectores de deformación.
•Teniendo en cuenta el objetivo del mapa y la propiedad que debe cumplir se identifican los vectores de deformación que intervienen y se define uno resultante que garantice el propósito del mapa.
•Para seleccionar la proyección definitiva se toma el vector de no deformación y aquella proyección que más se acerquen a este será la "PROYECCIÓN SELECCIONADA".
Hasta aquí se ha seleccionado la proyección, que para el caso es una EQUIÁREA. Ahora veamos cual es el proceso para transformar los datos existentes en los equiáreos.
Lo primero que se debe es determinar las cuadrículas de las dos proyecciones, lo cual pueden presentar:
Para el primer caso se debe determinar el punto de corte de las dos cuadrículas y calcular el ángulo que forman, luego definir sus ecuaciones de transformación. (véase figura No. 2).
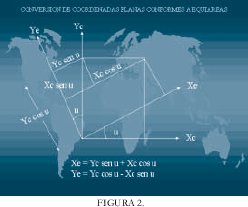
De la gráfica 2 se deduce:
Xe = Yc Sen u + Xc Cos u
Ye = Yc Cos u - Xc Sen u
Xe y Ye: Coordenadas EQUIÁREAS.
Xc y Yc: Coordenadas calculadas con la proyección CONFORME
Con las coordenadas Xe,Ye se deben hacer los cálculos de áreas y distancias en las aplicaciones de los S.I.G..
Para el segundo caso estas ecuaciones no se pueden aplicar.
Si las cuadrículas son paralelas o coinciden se utilizan los vectores de deformación definidos por Tissot.
Aquí una vez calculadas las áreas y distancias, en cada aplicación, con la proyección CONFORME estos se afectan por un FACTOR, que ha sido definido con los vectores de deformación de la proyección CONFORME y la proyección EQUIÁREA.
La definición de este FACTOR se efectúa mediante un ejercicio de aplicación a una poligonal Geodésica, a la cual se le calcula con ambas proyecciones sus coordenadas planas (X,Y), sus áreas y sus vectores de deformación. Mediante un análisis detallado se debe encontrar un FACTOR que al afectar el área calculada con la proyección Conforme de el área de la proyección EQUIÁREA, con un margen de error muy pequeño.
Aquí es muy importante haber seleccionado adecuadamente la proyección EQUIÁREAS y los vectores de deformación que intervienen en el Factor.
EJERCICIO DE APLICACIÓN
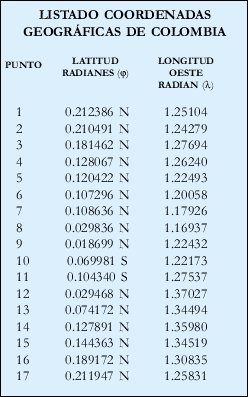
Se determino una poligonal geodésica de 17 puntos para el mapa de COLOMBIA con centro de proyección el observatorio Astronómico de Bogotá.
Para hacer un poco menos compleja la aplicación, se tomaron proyecciones derivadas, considerando la tierra esférica, con lo cual se tomo como radio medio 6.738,388 Kilómetros.
PROYECCIONES SELECCIONADAS TEORICAMENTE
1. CILÍNDRICA NORMAL EQUIÁREA
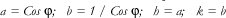
2. CILÍNDRICA OBLICUA EQUIÁREA
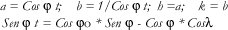
3. CILÍNDRICA TRANSVERSA EQUIÁREA
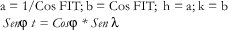
CENTRO DE PROYECCIÓN
LATITUD φ=o = 4 35' 56.57" N
LONGITUD λ=o = 74 04' 51.30" W
4. CÓNICA EQUIÁREA DE LAMBERTS
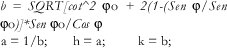
5.- CÓNICA EQUIÁREA DE BONNE
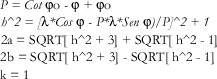
a y b Son los semiejes de la elipse Indicatriz de Tissot
h y k Son las distorsiones longitudinales a lo largo del paralelo y meridiano respectivamente.
Las proyecciones cónicas se incluyeron, aunque no cumplen con la primera condición teórica, porque son usadas en otras regiones.
De acuerdo con la teoría de Tissot se tiene:
VDA: VECTOR
DISTORSIÓN EN ÁNGULO = b/a
VDL: VECTOR
DISTORSIÓN EN LONGITUD = L
Para las cuatro primeras proyecciones L = b Para la cónica de BONNE se aplica la ecuación.
VDR: VECTOR
DISTORSIÓN RESULTANTE Se define por la suma vectorial de los dos anteriores. La distorsión por dirección para las cuatro primeras proyecciones equivale a 90 grados y para la cónica de Bonne es muy pequeño, por lo tanto no se considero en los resultados.
Como todas son proyecciones son EQUIÁREAS su vector de deformación es igual a uno (1).
Una vez realizados los cálculos se tiene:
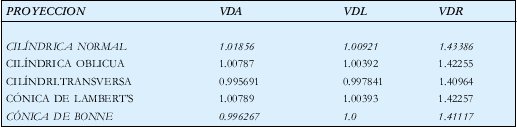
Teniendo en cuenta que el vector de no deformación en cada caso debe ser igual a uno, se toma como parámetro de comparación la raíz de 2, o sea, 1.41421.
De acuerdo a esto el vector resultante que más se acerca a este valor es la de la "CÓNICA EQUIÁREA DE BONNE", por lo tanto es la proyección seleccionada.
DETERMINACIÓN DEL FACTOR DE CONVERSIÓN.
El mapa general de Colombia usa actualmente la proyección CONFORME DE GAUSS, que tiene como ecuaciones derivadas a partir de la esfera las siguientes:
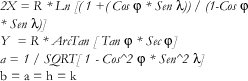
La proyección EQUIÁREA DE BONNE tiene las siguientes ecuaciones:
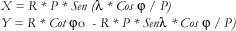
Aplicando estas dos ecuaciones a la poligonal anterior y al observar sus coordenadas planas X,Y se ve que sus cuadrículas coinciden y que por lo tanto su estudio se debe realizar por los vectores de deformación, para lo cual se tiene los siguientes resultados:

VDÁREA:
VECTOR DISTORSIÓN ÁREA= a * b En el presente estudio se realizo diferentes análisis entre los anteriores resultados y de acuerdo a estos se encontró que el factor más apropiado y técnico es la relación de los vectores resultantes. Partiendo de que la teoría conceptual y matemática de Tissot se fundamento principalmente en las relaciones escalares.
Por lo tanto: FACTOR = VECTOR RESULTANTE CONFORME/VECTOR RESULTANTE EQUIÁREA ÁREA EQUIÁREA = ÁREA CONFORME / FACTOR
Por lo tanto: FACTOR = 1.73581 / 1.7299 = 1.00342 ÁREA EQUIÁREA = 1.199.610 Km2/1.00342 = 1195520 Km2
Si se compara este resultado con la de BONNE existe una pequeña diferencia que con relación al tamaño de la comarca es despreciable.
La definición de si el FACTOR multiplica o divide al área conforme, se determina del estudio preliminar. Una vez definido el FACTOR este se puede aplicar a cualquier problema o resultado obtenido con los Sistemas de Información Geográfica.
En una segunda aplicación efectuada al mapa de Colombia, mediante un contrato de investigación entre el autor y el Instituto Geográfico Agustín Codazzi, se determino que una corrección más aproximada, al error en el cálculo del área, se lograría corrigiendo las coordenadas de cada vértice por el factor de variación presentado, en área, en cada uno de ellos.
Lo anterior se planteo al considerar que las deformaciones que se presentan en el mapa, son variables dependiendo de la distancia del centro de proyección y cada vértice. Luego una forma de distribuir el error es modificar o alterar las coordenadas de cada vértice, que han sido transformadas por una proyección conforme, por la diferencia entre uno (valor que resulta de multiplicar los semiejes a y b de la elipse, cuando se utiliza una proyección EQUIÁREA) y el valor que resulte del producto de a y b de la proyección conforme. Con estas coordenadas corregidas se debe calcular el área definitiva
Esta etapa final se encuentra en estudio, ya que no se dispone de las ecuaciones de los semiejes a y b de la proyección de Gauss desarrollada sobre el elipsoide.
Se espera que un futuro muy próximo se pueda publicar los resultados obtenidos en el último planteamiento.
CONCLUSIONES
El adoptar un sistema de proyección equiáreo para la base cartográfica que deben utilizar los Sistemas de Información Geográfica, permitirá determinar con mayor precisión la información obtenida en sus aplicaciones.
Es obvio pensar que como la información cartográfica existente se encuentra definida por una proyección conforme, su cambio seria muy costoso por lo tanto adoptar las soluciones aquí planteadas, el de afectar los datos por un factor, facilitara su proceso y su costo es bajo.
Seguramente lo complejo será definir inicialmente el factor para la comarca o el país, pero una vez determinado todo tipo de aplicación que realice en esa zona se le aplica el mismo factor.
ANEXO:
Selección Analítica y Matemática
TEORÍA BÁSICA DE TISSOT
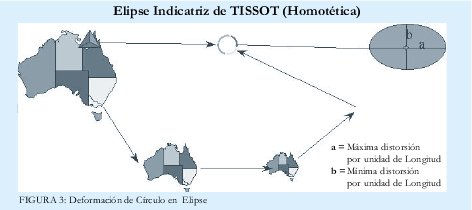
La teoría básica de TISSOT se fundamento en tomar un punto definido sobre la superficie terrestre y tomarlo como un círculo infinitesimal y proyectarlo sobre un plano (mapa). Se demostró que este círculo sobre una superficie tridimensional al proyectarse sobre una bidimensional se transformaba en una ELIPSE cuya característica geométrica es ser Homotética en donde sus semiejes a y b representan la máxima y mínima deformación por unidad de longitud. A esto se llamo la "ELIPSE INDICATRIZ DE TISSOT".
La anterior teoría se aplica de dos formas:
1. Defínase sobre la comarca o país a mapear una poligonal geodésica y a cada punto o vértice aplíquesele la teoría.
2. Tómese la comarca o país y redúzcase en escala hasta llegar a un punto, a este se le aplica la teoría anterior. (figura No. 3).
En el primer caso cada vértice de la poligonal es una elipse y a cada una se le determina sus deformaciones.
En el segundo caso la comarca o país es una elipse y aquí se determina las distorsiones a toda la comarca.
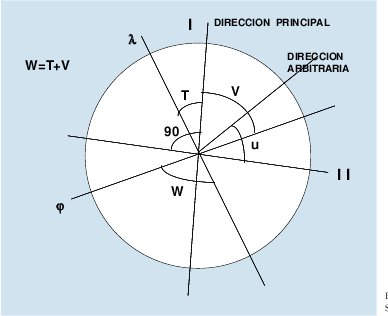
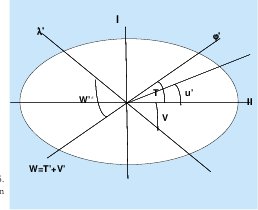
El desarrollo matemático de esta teoría se fundamenta haciendo relaciones escalares; de tal manera que se relacionan los elementos de proyección con los elementos de referencia tanto gráfica como geométricamente. (figura No. 4 y 5)
Por medio de lo anterior se determinan las ecuaciones con las cuales se calculan las magnitudes de deformación en ángulo, área, longitud y dirección.
De la última figura No. 6 mediante relaciones geométricas y trigonométricas se obtiene:

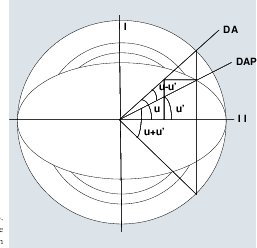
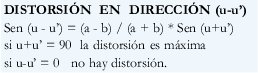
Los semiejes a y b están definidos por los elementos Gaussianos de la proyección y la superficie de referencia y estos a su vez están en función de las derivadas parciales de las ecuaciones de las coordenadas planas X e Y de cada proyección.
REFERENCIAS
[1] CASTAÑEDA G, PEDRO Y OTROS. Estudio de sistemas de proyección cartográficas y su selección. 1975. Universidad Distrital.
[2] DEETZ H,CHARLES Y OTRO. Elementos de proyección de mapas. 1944. Publicación TC- 289 Washington, D.C.
[3] RAISZ, ERWIN. Cartografía.
[4] I.G.A.C. Resultados de la red geodésica de Colombia.
[5] ROZO, DARIO Y OTRO. Selección de la proyección de Colombia. 1940. I.G.A.C.