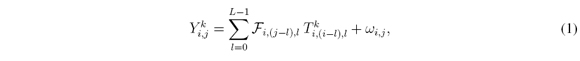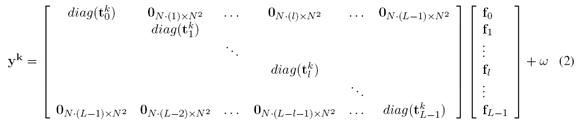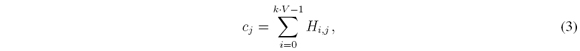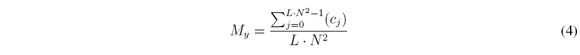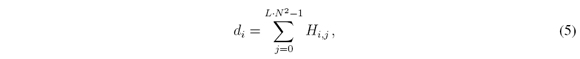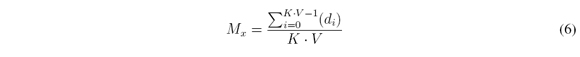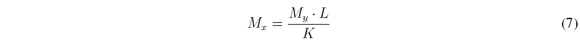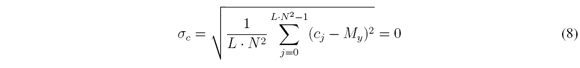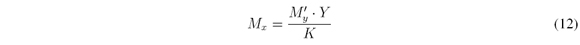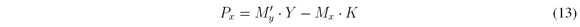DOI: http://dx.doi.org/10.14483/udistrital.jour.reving.2016.2.a06
A Compressive System Matrix Design in Spectral
Imaging by a Homogenization Algorithm
Diseño de la Matriz de un Sistema Compresivo en Imágenes
Espectrales por Medio de un Algoritmo de Homogeneización
Camilo Noriega
Universidad Industrial de Santander. camilo.noriega@correo.uis.edu.co
Yuri Mejía
Universidad Industrial de Santander. yuri.mejia@correo.uis.edu.co
Henry Arguello
Universidad Industrial de Santander.henarfu@uis.edu.co
Received: 07-11-2015. Modified: 08-04-2016. Accepted: 22-04-2016.
Abstract
Context: Compressive spectral imaging systems (CSI) use a focal plane array (FPA) to measure twodimensional (2D) coded projections of a three-dimensional (3D) spatiospectral scene. A reconstruction algorithm based on compressive sensing theory exploits the projections to retrieve the underlying 3D scene. Compressive sensing relies on two principles: Sparsity and incoherence. Higher incoherence drives to better-reconstructed image quality. In CSI systems, a random design of the coded
apertures elements guarantees a high incoherence between the sensing matrix and the representation basis. However, when a coded aperture is designed completely random, it is possible that some voxels not be sensed at all or they be sensed more than once.
Method: This paper presents a random algorithm for a colored coded apertures design by homogenizing defined parameters of the colored coded aperture snapshot spectral imaging system (C-CASSI) representative matrix. Homogenization parameters guarantee that all voxels are sensed at least once. The homogenization is achieved by weighting the selected parameters of the matrix, in this case, the average of unblocking elements per column and the average of unblocking elements per row.
Results/Conclusions: Simulations show a higher performance in the PSNR of the reconstructed images by using the proposed approach, as compared to traditional random coded apertures.
Keywords: Colored coded apertures, C-CASSI, spectral images, random algorithms.
Acknowledgements: The authors gratefully acknowledge the Vicerrectoría de Investigación y Extensi
ón of the Universidad Industrial de Santander for supporting this research registered under the project title: Diseño y simulación de una arquitectura de tomografía computarizada para el sensado compresivo de imágenes de Rayos X, (VIE 1803 code).
Language: English.
Resumen
Contexto: Los sistemas de muestreo compresivo de imágenes espectrales (CSI, por su sigla en inglés)
cuentan con una matriz de plano focal (FPA) para medir proyecciones codificadas bidimensionales (2D) de una escena espacio-espectral de tres dimensiones. Un algoritmo de reconstrucción basado en la teoría de muestreo compresivo aprovecha las proyecciones para recuperar la escena 3D. La teoría de muestreo compresivo se basa en dos principios: dispersión e incoherencia. Un alto grado de incoherencia conduce a mayor calidad en las reconstrucciones. En los sistemas CSI, un diseño aleatorio de las aperturas codificadas asegura una alta incoherencia entre la matriz de muestreo y la base de representación dispersa. Sin embargo, si un código de apertura se diseña completamente aleatorio es probable que algunos voxeles no sean muestreados en absoluto, o, por el contrario, que la información sea muestreada redundantemente.
Método: Este artículo presenta un algoritmo aleatorio para el diseño de las aperturas codificadas de color por medio de la homogeneización de los parámetros de la matriz representativa del sistema de muestreo de imágenes espectrales basado en aperturas codificadas de color (C-CASSI, por su sigla en inglés). Los parámetros de homogeneización garantizan que todos los voxeles sean muestreados al menos una vez. La homogeneización se logra mediante la ponderación de algunos parámetros de la
matriz representativa, en este caso, el promedio de elementos de paso por columnas y por filas.
Resultados/Conclusiones: Las simulaciones muestran que usando el método propuesto se obtiene una mejora en la calidad en términos de PSNR con las imágenes reconstruidas en comparación con las aperturas aleatorias tradicionales. Palabras clave: Aperturas codificadas de color, C-CASSI, imágenes espectrales, algoritmos aleatorios.
Agradecimientos: Los autores agradecen a la Vicerrectoría de Investigación y Extensión de la Universidad
Industrial de Santander por apoyar esta investigación registrada bajo el título del proyecto:
Diseño y simulación de una arquitectura de tomografía computarizada para el sensado compresivo de
imágenes de Rayos X, (Código VIE 1803).
1. Introduction
Imaging spectroscopy requires sensing the spectral signatures of a scene. A spectral image is represented as a three-dimensional (3D) array called data cube (2D-spatial x 1D-spectral). Constructing the spectral data cube using traditional imaging spectroscopy has the disadvantage of scanning a number of zones that grows linearly in proportion to the desired spatial or spectral resolution. In contrast, compressive spectral imaging systems (CSI) capture the 3D spatio-spectral information
of a scene by measuring 2D coded projections on a focal plane array (FPA). The amount of information required in CSI is much lower than in the linear scanning case [1], [2] Finally, an algorithm based on l1 - l2 norms reconstructs the data cube [3].
Some CSI systems apply the compressive sensing theory (CS) for reconstructing the data cube. CS relies on two principles: Sparsity and incoherence. Sparsity indicates that spectral images found in nature can be concisely represented in some basis Ψ with just a small number of coefficients. Incoherence refers to the structure of the sampling waveforms used in CS that have a dense representation in the basis Ψ [4], [5]. Randomness can be an effective sensing mechanism inasmuch as random matrices are widely incoherent with any fixed basis Ψ. Higher incoherence drives to better-reconstructed image quality [3].
The colored coded aperture snapshot spectral imager (C-CASSI) is one example of CSI sensor with two main components, a colored coded aperture and a dispersive element [2], [6]. The projections
measured in C-CASSI are given by y =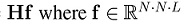 is the vector representation of a hyperspectral signal
is the vector representation of a hyperspectral signal 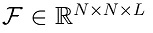 with L and N x N representing the spectral and spatial resolution, respectively, and H is a
with L and N x N representing the spectral and spatial resolution, respectively, and H is a 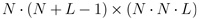 matrix where the colored coded aperture entries and the dispersive element determine its structure; H is the Câ CASSI representative system matrix.
matrix where the colored coded aperture entries and the dispersive element determine its structure; H is the Câ CASSI representative system matrix.
The traditional CASSI systems use completely random blocking-unblocking coded apertures. The traditional approaches may cause multiple or null sensing of a voxel information. In traditional CASSI, the blocking-unblocking coded aperture elements are fabricated with opaque or transparent materials, modulating the light from the scene spatially [6], [7]. Microlithography and
coating advances allow constructing multi-patterned arrays of optical filters. These filter arrays have been recently used as colored coded apertures in applications such as multi-focusing, depth estimation [8], deblurring, and matting [9]. The colored coded apertures module the scene spatially and spectrally. The spectral modulation over each detector pixel consists of the pass off some wavelengths. A random colored coded aperture reaches better-reconstructed image quality than a traditional blocking-unblocking coded aperture[2].
Previous works have based their research on the direct design of colored coded apertures based on a hard understanding optimization problem which requires high computation processing, then it is necessary the use of genetic algorithms [2], [10], [11]. However, there are not studies that design the apertures through the representative system matrix H. This work develops a random algorithm that designs H, and then constructs a set of colored coded apertures using a simpler algorithm than the algorithms in the literature. First, the proposed algorithm homogenizes H such that all columns have the same sum, i.e. the standard deviation of the average of unblocking elements per column is zero. Second, the algorithm distributes the unblocking elements per row, reducing the standard deviation of the average of unblocking elements per row, after the homogenization of the unblocking elements in columns. With this aim, the algorithm creates a set of auxiliary matricesWi with
the information of H that directly affects the total sum of a column and the sum of a row on the ith iteration, this construction is detailed later in this paper. Then Wi is first homogenized by columns and then by rows. Finally, the information taken in H is replaced by the new one in Wi. This design guarantees that all voxels are sensed equally. Simulations show the improvement attained by the proposed approach regarding reconstruction peak signal-to-noise ratio (PSNR). We remark that this is an extended version of a short paper recently published in theWorkshop on Engineering Applications -WEA2015- that was held in Bogotá, September 2015 [12].
This article is organized as follows: Section 2 explains the C-CASSI architecture and the disadvantages of the traditional coded apertures. In section 3, the algorithm that designs the representative system matrix (H) is introduced. Simulations and results are presented in section 4. Finally, conclusions are drawn in section 5.
2. Colored Coded Apertures in C-CASSI
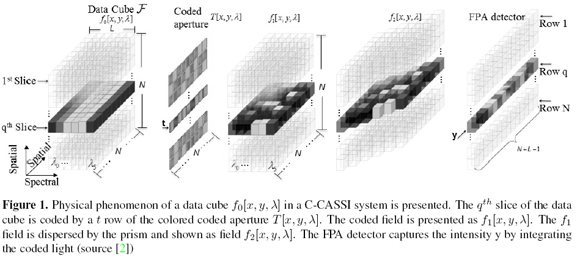
The physical sensing phenomenon in the C-CASSI system for L = 6 spectral bands is depicted in Figure 1 where a colored coded aperture replaces the traditional blocking-unblocking mask, and the optical elements are represented by their effect on the discretized data cube [6], [7]. Each pixel
of the colored coded aperture has a band-pass filter. The physical sensing phenomenon is described as follows: the discrete data cube f0[x, y, λ], where [x; y]are the spatial coordinates and λ is the wavelength, is coded spatially and spectrally by the colored coded aperture T[x, y, λ] resulting in the coded field f1 [x, y, λ]. The coded field is spectrally dispersed by a dispersive element before it impinges on the focal plane array as f2 [x, y, λ]. Briefly, every spectral slice of where the data cube is spatially and spectrally modulated by the coded aperture and dispersed by the dispersive element [6], [7]. The integration of the field f2 [x, y, λ] over the spectral range sensitivity of the detector realizes the compressive measurements across the FPA. f0 [x, y, λ]can be written in index form as F where i and j are the spatial coordinates, and l determines the lth spectral plane. Let Tk[x, y, λ]be the kth coded aperture used in the kthmeasurement. The indexation of Tk[x, y, λ] is Tki,j,l ∈; {1,0}, where 0 represents the blocking elements and 1 the unblocking
elements. The colored coded aperture is a tridimensional matrix whereas the traditional blockingunblocking coded aperture is a two-dimensional matrix. The indexed kthFPA measurement also called shot, can be expressed as
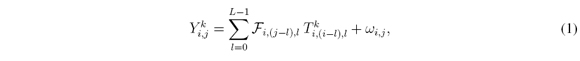
where Y k i,jis the intensity at the (i, j)thposition of the detector in the kthmeasurement whose dimension is N x (N + L - 1). F is a N x N x L spectral data cube and ωijis the white noise of the sensing system. It is possible to rewrite Equation 1 in matrix notation as yk = Hk f + ω , and its expansion as
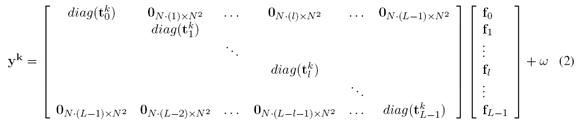
where ykis a V - long vector representation of Y k i,jwith V = N (N +L-1) tk
l is the vectorization of the 3D colored coded aperture T k i,j,lat the 2D lthspectral plane through the lexicographical order as (T k i) j = T k (j-r∙N) for j = 0,…,N2 - 1 and r = [j/N] ∙ diag (t k l ) is an N2 x N2 diagonal matrix whose entries are the t k l vectors. f is a vector representation of the data cube as
f = vec([f0,…, fL-1]) ∙ fl is the vectorization of the lthspectral band. fl and y kare also ordered lexicographically [2].
The set of K shots is then assembled as y = [(y 0)T ,…,(yK-1)T ]T , where T represents the transpose matrix. The projections in C-CASSI can be alternatively expressed as y=HΨθ=Aθ where the matrix A=HΨ is the sensing matrix and θ is an S-sparse representation of f on the basis Ψ.The underlying data cube is reconstructed as f = Ψ(argmin ║ y - HΨθ ║2 + т ║θ║1) where т
is a regularization constant and H = [(H0)T],…, (HK-1)T ]T [11].
The colored coded apertures lead to a richer structure of the matrices Hk inasmuch as their entries are less correlated. Figure 2 shows a random colored coded aperture-based H matrix for K = 2, N = 6 and L = 3. Ones (unblocking elements) are shown as white squares elements. Each row represents the coded aperture modulation effect and the prism dispersion on every spectral band of the data cube. Columns represent the times a particular voxel on a specific band is sensed. The right bar is a gray-scale indicator of the unblocking elements on every row.
For this particular case, the bar has four different values, black, dark gray, light gray and white, meaning zero, one, two and three unblocking elements in such row respectively. For instance,
Figure 2 depicts the case where a row has three
unblocking elements. Bottom bar symbolizes the sum of the unblocking elements per column, having the same color convention as the right bar. The figure highlights the case where there are
two unblocking elements in a column.
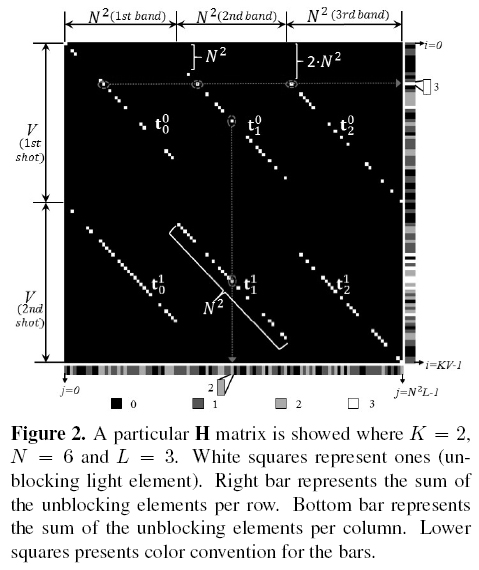
As will be shown later in this paper, the main contribution is to homogenize the unblocking elements in H i.e. to reduce the standard deviation to zero of the average of unblocking elements per column by adding or erasing unblocking elements in H if it is necessary, guaranteeing that all voxels be sensed equally. Then, minimize the standard deviation of the average of unblocking elements per row but without adding or erasing more unblocking elements.
3. Proposed Algorithm for Homogenization of Representative System Matrix
It is possible to construct the coded aperture set from the system measurement H matrix. In this work a design of the set of colored coded apertures through the homogenization of the H matrix is presented for data cubes with dimensions N xN xL and N > L. Homogenization is based on two statistical parameters of H, the average of unblocking elements per column (My) and the average of unblocking elements per row (Mx).
3.1. Column and Row Homogenization of H
Let c = [c0,…, cL∙N2-1] be a vector such that
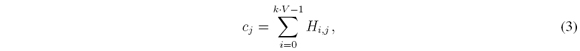
where j = 0,…,L N2 - 1 and Hi, is the H element of the ijthrow and jthcolumn with H ∈; ℝ K∙VxN2∙L. Let the average of unblocking elements per column be defined as
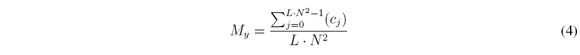
Myis the average of times a particular voxel on a specific band is sensed through the Kshots. It will be required that all the voxel be sensed equally.
Like the columns, the average of unblocking elements per row follows the same structure. Let d=[d0,…, dk·V - 1 ]be a vector such that
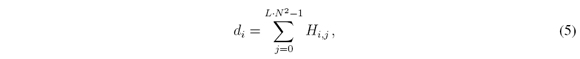
where i = 0,…,KV - 1. Let the average of unblocking elements per row be defined as
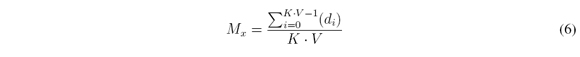
However, since H structure allows at most Kunblocking elements per row and Lper column, Myand Mxare not independent, in fact, they are related as
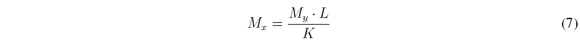
The homogenization of the representative C-CASSI system matrix is solved with the proposed random algorithm which receives as parameters the H matrix, the number of shots K and a userdefined amount of unblocking elements per column M'y. Hence, the algorithm achieves that cj = M'yfor all j, where j = 0,…,L N2-1. As a consequence My = M'y . Then, the standard deviation of the average unblocking elements in columns is
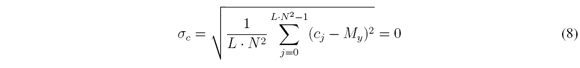
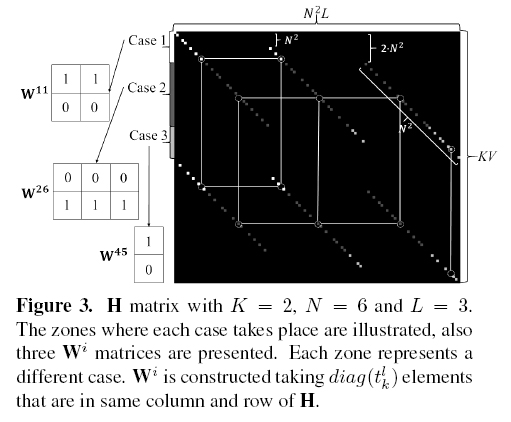
The prism effect is modeled in H by the shifting of the diagonals on each band; this helps to differentiate three zones in the H matrix. The zones are defined according to the first shot. The Vrows are partitioned into the three zones as follows: since 0 to N ∙ (L-1) - 1, since N ∙ (L-1) to N2-1and since N2to V-1for the first, second and third zone respectively. Figure 3 depicts the three zones. Taking into account the zones of H, the problem is reduced to homogenize auxiliary matrices Wi that vary in size with at most K x Ldimension and i = 0,…, V - 1instead of H ∈; ℝ K·V N2 L. Every zone is related to a case in the main algorithm because the zones determine dimension and elements of the Wi matrices; the main algorithm makes Viterations, and on each iteration the algorithm constructs Wias follows:

where si = [i/N], si ∈; {0,…,L-1}and gi = si-N +1. If i-si<0or i-(gi +k)∙N < 0, with k = 0,…,L-1, then such column does not exist in Wi, i.e. the matrix Wihas a variable width depending on the ith row, getting at maximum L columns.
Figure 3 shows where each case takes place.
The H matrix presented in Figure 3 is
another example for K = 2, N = 6and L = 3. Visually a Wimatrix is constructed taking diag(tlk)elements that are in same column and row of H according to the case. In particular Figure 3 presents the matrices for i = 11(case 1), 26 (case 2) and 45 (case 3), where it depicts how the row length of
Wichanges in cases 1 and 3, but in case 2 it
is constant having Lcolumns. The number of rows is always K.
The main algorithm constructs the Wimatrices from H and sends them to the Algorithm 1 WHomogenization, which will be the algorithm that makes the homogenization of Wi. Then, WHomogenizationreceives as parameters Wi, the number of shots Kand the amount of unblocking elements per column M'y. It uses the relation in the Equation 7 to find Mxin rows of Wionce it has
homogenized the columns. Nevertheless Equation 7 outputs a rational number not always integer, for this reason, to reduce the standard deviation of the average of unblocking elements per row on every Wimatrix the algorithm recalculates Mxas
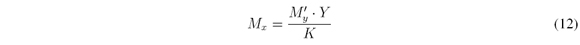
where Yis the number of the columns of Wi. Then, to guarantee the average does not change as it has been calculated in Equation 7 it is necessary that some rows have an extra unblocking element. The number of rows that will have the extra element is calculated as:
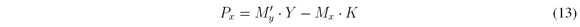
The Algorithm 1 has these considerations into account.
The procedure of Algorithm 1 is as follows: If Sis negative, the function SetRandOnesColrandomly changes │S│ blocking elements for unblocking elements. On the contrary, if Sis positive the function SetRandOnesCol randomly removes Sunblocking elements turning them into blocking until there are M'yunblocking elements on the jthcolumn. The function zeroscreates a vector of zeros, and the function SetRandOnesColRowrandomly selects an unblocking element on the ith row and turns it into a blocking element, then relocates that unblocking element randomly on the
same column only being restricted by the rows where S > 0.

The Algorithm 1 returns a Wimatrix with i = 0,…, V - 1where all its columns have the same number of unblocking elements and where the amount of unblocking element per row only differs between them with at best + 1. Finally,
the homogenized Wii is reinserted in H by the main algorithm.
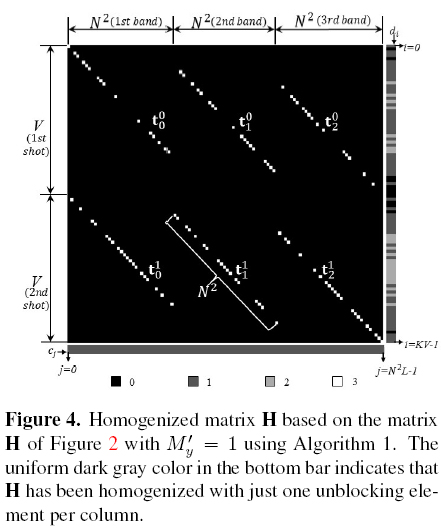
Figure 4 shows the homogenization of the
H matrix in Figure 2 using Algorithm 1 with My = 1. Indeed, the uniform dark gray color in bottom bar indicates that H has been homogenized
with one unblocking element per column. This way the homogenized H matrix has σc = 0.
4. Simulations and Results
4.1. Experimental Design
To verify the C-CASSI colored coded aperture designs, a set of compressive measurements is simulated using the model in Equation 1. These measurements are constructed employing a test spectral data cube acquired by a monochromator using wavelength steps of 1 nm, a bandpass filter (transmission
window 450-670nm), and a CCD camera AVT Marlin F033B, pixel pitch of 9.9μm, and 14 bits pixel depth. The resulting test data Fhas 256x256 pixels of spatial resolution and L = 16spectral bands in the range 461nm to 596nm.
Given the designed colored coded apertures, the compressive sensing GPSR (Gradient Projection for Sparse Re-construction) algorithm is used to recover the data cube [13]. The basis representation is set as the Kronecker product of two bases Ψ= V⊗Ψ 2D , where V is the 1D-DCT basis and Ψ 2D is the 2D-Wavelet Symmlet 8 basis.
The Algorithm 1 is used to homogenize the representative system H matrix with M'y= 1. The designed colored coded aperture sets, derived from the homogenized H matrix, are used in capturing the C-CASSI compressive measurements and in the corresponding image reconstruction. The performance of the designed apertures set is compared with a random colored coded apertures set that has the same transmittance as the designed and with a 50% transmittance blocking-unblocking coded apertures set, where the percentage of ones and zeros of the coded aperture is determined by the transmittance [14].
4.2. General Results
Three different sets of experiments were done. The sets of tests were: consistency in reconstructions related to the homogenization algorithm, noise in the measurements and the sparsity effect of the scene. The noise added to the measurements was Gaussian with zero mean. Assuming y as the average value of the measurement y and noise as the standard deviation of the noise signal, the Signal to Noise Ratio (SNR) is giving by SNR=10log10(μy=σnoise). The sparsity ratios are calculated as S/N2Lwhere Sis the number of non-zero elements of the underlying data cubes. The reconstructions quality of the three different coded apertures sets are compared for 3, 4, 8, and 12
shots (K) with SNR values of 5dB, 10dB, and 40dB and using the data cube with 5%, 10% 30% and 100% as the sparsity levels. The quality of reconstructions of simulated experiments is compared
using the peak-signal-to-noise ratio (PSNR) [15].
4.2.1. Consistency in reconstructions
The table I indicates the mean PSNR of the reconstructed images and their standard deviation, in pharentesis,
having a direct variation with the mean value

Different homogenized coded apertures are generated by the Athlgorithm 1 because it uses stochastics methods. The consistency in reconstruction was evaluating the standard deviation of the reconstruction quality produced by the different apertures. Table I presents the summary of ten experiments that were performed by the filter ensembles: blocking-unblocking filter, random colored filter, and homogenized filter, for 3, 4, 8 and 12 shots, with 100% of sparsity level and with SNR of 0dB. Table I indicates the mean PSNR of the reconstructed images and their standard deviation having a direct variation with the mean value. The PSNR values obtained with the homogenized coded apertures are higher than those achieved with the random colored coded apertures. The blocking-unblocking coded apertures obtained the lowest values of PSNR. The reconstructions of original data cubes zoomed versions, as it would be viewed by a Stingray F-033C CCD Color Camera, are depicted in Figure 5. Figure 5b shows the zoomed reconstructions of the data cube by taking four shots using the designed colored coded aperture set, Figure 5c using the random colored coded aperture set and Figure 5d using Blocking-Unblocking coded aperture set.

4.2.2. Noise in measurements
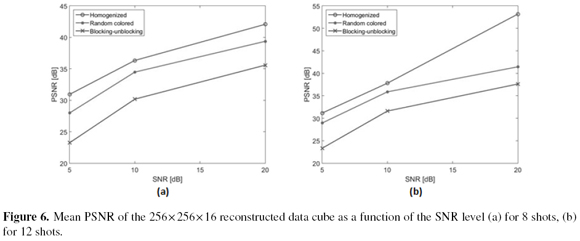
The SNR values added to the measurements were 5dB, 10dB and 40dB. Ten experiments were performed for every set of tests. A set of tests was comprised with the three filter ensembles, a noise level and an amount of shots. Figure 6 shows the mean PSNR of the reconstruction for the different coded aperture sets as a function of the noise levels in measurements for 8 shots (a) and 12 shots (b). Figure 6 depicts that even for the noisy input signal with SNR of 5dB, the PSNR attained to the homogenized coded apertures is higher than the PSNR attained to the blocking-unblocking apertures and the random colored coded apertures.
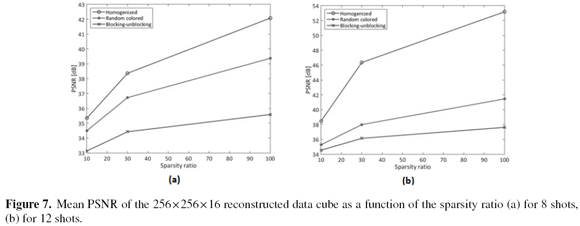
4.2.3. Sparsity Analysis
The sparsity ratios used are 0.05, 0.1, 0.3 and 1. Figure 7 determines the effect of the sparsity in the random and homogenized designs. Figure 7 presents the PSNR attained to the three filter ensembles as a function of the sparsity ratio. The reconstruction quality obtained with homogenized coded apertures outperforms up
to 11.74dB compared with the random colored coded aperture and up to 15.56 compared with the blockingunblocking apertures.
5. Conclusions
It has been proposed a random algorithm for a design of the representative system matrix. The proposed algorithm gets the standard deviation of the average of unblocking elements per column reaches zero. The algorithm also minimizes the standard deviations of the average of unblocking elements per row without
losing the randomness of the design. This method is important because it proposes a different approach to optimize coded apertures. Although the proposed algorithm is a stochastic method for the design of colored coded apertures, the quality of reconstructions with the homogenized apertures varies 0.05 dB. The PSNR increases rapidly for the homogenized colored coded apertures with the number of measurement shots and the sparsity ratio. In particular, the improvement in PSNR obtained with the homogenized coded apertures is up to 11.74dB compared to the obtained with the random colored coded aperture and up to 15.56 compared with the obtained using blocking-unblocking apertures. In general, the homogenized coded apertures sets achieve a higher image reconstruction quality even when the measurements have additive noise. Three shots or less, make the homogenized apertures less efficient to get good reconstructions than random apertures with the same transmittance, this because the homogenization method does not count with too much freedom to
replace the unblocking elements making that the new apertures have big kernels of unblocking elements, and as a consequence lowering the incoherence. Four or more shots make that the homogenized apertures be superior to the non-designed coded apertures. As future work, it is expected to develop incoherence theoretical actions to prove the effectiveness of the homogenization in the representative system matrices.
References
[1] D. Kittle, K. Choi, A. Wagadarikar, and D. J. Brady, "Multiframe image estimation for coded aperture snapshot spectral imagers" Appl. Opt., vol. 49, no. 36, p. 6824, Dec. 2010.
[2] H. Arguello and G. R. Arce, "Colored Coded Aperture Design by Concentration of Measure in Compressive Spectral Imaging" IEEE Trans. Image Process., vol. 23, no. 4, pp. 1896-1908, Apr. 2014.
[3] E. J. Cand'es and M. B. Wakin, "An Introduction To Compressive Sampling" IEEE Signal Process. Mag., vol. 25, no. 2, pp. 21-30, Mar. 2008.
[4] D. L. Donoho, "Compressed sensing" IEEE Trans. Inf. Theory, vol. 52, no. 4, pp. 1289-1306, Apr. 2006.
[5] G. R. Arce, D. J. Brady, L. Carin, H. Arguello, and D. S. Kittle, "Compressive Coded Aperture Spectral Imaging: An Introduction" IEEE Signal Process. Mag., vol. 31, no. 1, pp. 105-115, Jan. 2014.
[6] A. Wagadarikar, R. John, R. Willett, and D. Brady, "Single disperser design for coded aperture snapshot spectral imaging" Appl. Opt., vol. 47, no. 10, pp. B44-B51, 2008.
[7] H. Arguello, H. Rueda, Y. Wu, D. W. Prather, and G. R. Arce, "Higher-order computational model for coded aperture spectral imaging" Appl. Opt., vol. 52, no. 10, p. D12, Apr. 2013.
[8] S. Kim, E. Lee, M. H. Hayes, and J. Paik, "Multifocusing and Depth Estimation Using a Color Shift Model-Based Computational Camera" IEEE Trans. Image Process., vol. 21, no. 9, pp. 4152-4166, Sep. 2012.
[9] Y. Bando, B.-Y. Chen, and T. Nishita, "Extracting Depth and Matte Using a Color-filtered Aperture" in ACM SIGGRAPH Asia 2008 Papers, New York, NY, USA, 2008, pp. 134:1-134:9.
[10] H. Arguello and G. R. Arce, "Code aperture optimization for spectrally agile compressive imaging" J. Opt. Soc.Am. A, vol. 28, no. 11, p. 2400, Nov. 2011.
[11] H. Arguello and G. R. Arce, "Rank Minimization Code Aperture Design for Spectrally Selective Compressive Imaging" IEEE Trans. Image Process., vol. 22, no. 3, pp. 941-954, Mar. 2013.
[12] C. Noriega, Y. Mejía, and H. Arguello, "A random algorithm for designing the system matrix in compressive spectral imaging by homogenizing its structure" in 2015 Workshop on Engineering Applications - International Congress on Engineering (WEA), 2015, pp. 1-6.
[13] M. A. T. Figueiredo, R. D. Nowak, and S. J. Wright, "Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems" IEEE J. Sel. Top. Signal Process., vol. 1, no. 4, pp. 586-597, Dec. 2007.
[14] D. F. Galvis-Carreño, Y. H. Mejía-Melgarejo, and H. Arguello-Fuentes, "Efficient reconstruction of Raman spectroscopy imaging based on compressive sensing" DYNA, vol. 81, no. 188, pp. 116-124, Dec. 2014.
[15] H. F. R. Chacon, C. A. V. García, and H. A. Fuentes, "Single-pixel optical sensing architecture for compressive hyperspectral imaging" Rev. Fac. Ing., vol. 0, no. 73, pp. 134-143, Nov. 2014.
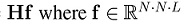 is the vector representation of a hyperspectral signal
is the vector representation of a hyperspectral signal 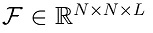 with L and N x N representing the spectral and spatial resolution, respectively, and H is a
with L and N x N representing the spectral and spatial resolution, respectively, and H is a 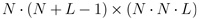 matrix where the colored coded aperture entries and the dispersive element determine its structure; H is the Câ CASSI representative system matrix.
matrix where the colored coded aperture entries and the dispersive element determine its structure; H is the Câ CASSI representative system matrix.