COMPUTATION OF EFFECTIVE PROPERTIES IN TWO-PHASE PIEZOCOMPOSITES WITH A RECTANGULAR PERIODIC ARRAY
submitted date: October 2013
received date: November 2013
accepted date: January 2014
Ransés Alfonso Rodríguez
Bachelor in Mathematics in the Faculty of Mathematics and Computers Sciences at the University de La Habana, Cuba. Current position: Junior Professor at the Centro de Estudios Matemáticos del Instituto Superior Politécnico José Antonio Echevarría, Cuba. ralfonso@cemat.cujae.edu.cu
Julián Bravo Castillero
Bachelor in Mathematics Education, Instituto Superior Pedagógico Enrique José Varona, La Habana, Cuba. Bachelor in Mathematics, MSc in Mathematics, and PhD in Mathematics Faculty of Mathematics and Computers Sciences at the Universidad de La Habana, Cuba. Current position: professor in the Faculty of Mathematics and Computers Sciences at the Universidad de La Habana, Cuba. jbravo@matcom.uh.cu
Renald Brenner
Ph D en Mechanics in Université Paris Nord, 2001, Researcher at the Institut Jean Le Rond d’Alembert, UPMC-CNRS, UMR 7190, 4 place Jussieu, 75005 Paris, France. renald.brenner@upmc.fr
David Guinovart Sanjuán
Bachelor in Mathematics Faculty of Mathematics and Computers Sciences at the Universidad de La Habana, Cuba. Current position: Junior Professor Faculty of Mathematics and Computers Sciences at the Universidad de La Habana, Cuba. davidgs@matcom.uh.cu
Raúl Guinovart Díaz
Bachelor in Mathematics Education, Instituto Superior Pedagógico Enrique José Varona, La Habana, Cuba. MSc in Mathematics, and PhD in Mathematics Faculty of Mathematics and Computers Sciences at the Universidad de La Habana, Cuba. Current position: professor Faculty of Mathematics and Computers Sciences at the Universidad de La Habana, Cuba. guino@matcom.uh.cu
Reinaldo Rodríguez Ramos
Bachelor in Mathematics Education, Instituto Superior Pedagógico Enrique José Varona, La Habana, Cuba. PhD in Mathematical-Phisycs Sciences, Facultad de Matemática y Mecánica. Universidad Estatal de Moscú, Rusia. Professor Faculty of Mathematics and Computers Sciences at the Universidad de La Habana, Cuba. reinaldo@matcom.uh.cu
Abstract
Based on the Asymptotic Homogenization Method, the electromechanical global behavior of a two-phase piezoelectric unidirectional periodic fibrous composite is investigated. The composite is made of homogeneous and linear transversely isotropic piezoelectric materials that belong to the symmetry crystal class 622. The cross-sections of the fibers are circular and are centered in a periodic array of rectangular cells. The composite state is anti-plane shear piezoelectric. Local problems that arise from the two-scale analysis using the Asymptotic Homogenization Method are solved by means of a complex variable, leading to an infinite system of algebraic linear equations. This infinite system is solved here using different truncation orders, allowing a numerical study of the effective properties. Some numerical examples are shown.
Key words
Periodic composites, asymptotic homogenization method, effective properties, infinite systems.
1. Introduction
Periodic composite materials made of reinforced unidirectional fibrous embedded in a polymeric matrix are often found in a wide range of applications. An important problem is to compute their global (or effective) properties as a function of the physical and geometric characteristics of the components. The asymptotic homogenization method (AHM) is a mathematical tool for examining both macroscopic and microscopic properties of this class of heterogeneous media and has been applied to many areas. The formal procedure of the AHM is based on the combination of the two-scales method combined with average techniques of the perturbation theory.
From a mathematical point of view, the method guarantees that the solution of a family of problems with periodic and rapidly oscillating coefficients, depending on a microstructural small parameter ε , converges to the solution of the homogenized problem as ε → 0 The coefficients of the homogenized problem are not rapidly oscillating and are called effective coefficients of the composite. However, to compute the effective coefficients it is necessary to solve the so-called local problems, which involves, for instance, partial differential equations with periodic boundary conditions and conditions on the interfaces between the matrix and the fibrous composite. Consequently, AHM provides a mathematical model to give answers to engineering problems but does not provide analytical or numerical algorithms to compute the effective properties.
In this work, AHM is applied to obtain semi- analytical formulae for the elastic, piezoelectric and dielectric permittivity, which represent effective properties of a reinforced composite with circular cylindrical shaped fibers, also with a rectangular array distribution in a matrix. Both, fibers and matrix, are characterized by homogeneous and linear transversely isotropic piezoelectric materials belonging to the symmetry crystal class 622. The results are a generalization of those published in [1], where the same problem on the square periodic cell was investigated.
2 Problem formulation and basic equations
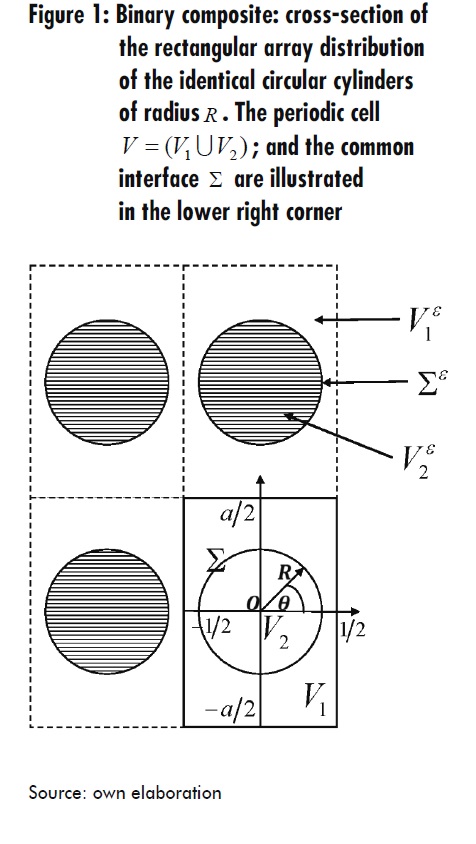
A two-phase fibrous composite consisting of identical circular cylinders embedded in a matrix is considered here. Both components are homogeneous and linear transversely isotropic piezoelectric materials belonging to the symmetry crystal class 622. The axis of transversely symmetry coincides with the fibers direction, which is taken as the Ox3 -axis. The periodic distribution of the fibers follows a rectangular array, as observed in Figure 1. The governing equations are the equilibrium equations of linear elasticity and the quasi-static approximation of Maxwell’s equations in the absence of free conduction currents. For the mechanical displacement, w = (w1 ,w2 ,w3 ) and the electric field E = (E1 , E2 , E3).
The constitutive relations of the linear piezoelectricity theory are as follows:
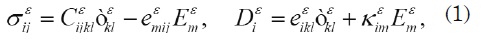
where σεij ε σ is the stress tensor;∈εij is the linearized strain; and Dεi the electric displacement.
The material properties of the piezoelectric medium are described by the following coefficients: elastic Cεijkl piezoelectric eεikl and dielectric kεij The super-index ε indicates the periodic and rapidly oscillating variation of the original fields. The material functions satisfy the usual symmetry and positivity conditions (see, for instance, [2]). The convention summation over repeated indexes is assumed. The Latin indexes runs from 1 to 3.
The equilibrium equations on the composite are represented by
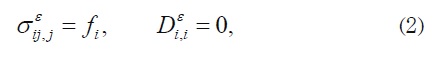
where fi corresponds to the body forces and the comma notation means partial differentiation. The following geometric relations have been used
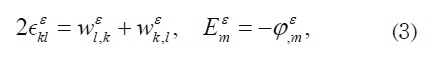
where Φε is an electric potential.
Perfect contact conditions are assumed on the interface ∑ ε between the fibers and the matrix:
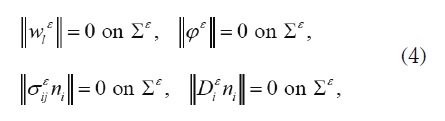
where n = (n1 ,n2 ) is the outer unit normal vector to ∑ε, and ||•|| = •(1) − •(2) denotes the contrast around ∑ε, taken from the matrix to the fiber.
Equations (1)-(4), are established are established in the region occupied by composite Ωε , which must be completed with appropria ted boundary conditions. For instance, one can assume homogeneous boundary conditions like W1ε = 0, φε = 0, on ∂Ωε Hereinafter, when “the problem (1)-(4), is mentioned”, it means that such homogeneous conditions are considered.
3. Homogenization and models for the local problems and effective coefficients
In this problem the small parameter ε could be considered ε = l/L where l is the distance between the centers of two neighboring cylinders and L is the diameter of the composite. In this type of problem it is possible to distinguish two spatial scales: one of them defined by the global (or slow) variable x , and the other one is the local (or fast) variable y= x/ε
In order to obtain the homogenized problem, the solution of the solution of (1)-(4), is sought is sought as follows:
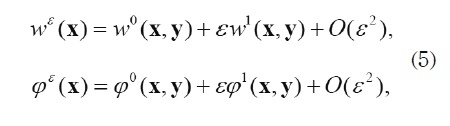
where w0, w1, φ 0, φ 1 are V - periodic functions with respect to the fast variable y.
Substituting (5) in the problem (1)-(4), applying the chain rule differentiation formula, and equating to zero, the terms corresponding to equal powers of ε(ε-2, ε-1, ε0.....) are obtained, which correspond to a recurrent family of partial differential equations. From the term corresponding to ε-2 it is possible to conclude that w0 and φ0 do not depend on the fast variable, i.e.: w0= w0(x) and φ0 = φ0(x) On the other hand, from the equations associated to ε-1 the local problems are obtained. The solutions to these problems play an important role to compute the effective properties. Finally, working with the system corresponding to ε0 it is possible to derive the “homogenized problem” and the formulae for the computation of the effective coefficients as functions of the solution of the local problems
Summarizing the relevant results, the homogenized problem can be written in the composite Ω0 in the following form:
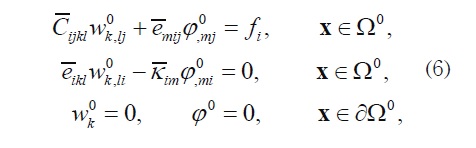
where the effective coefficients can be calculated from the formulae
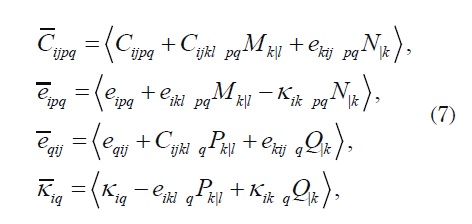
where “|” is used to denote partial differentiation with respect to the fast variable yl y whereas the local functions pq M k , pq N, q P k y qQ are the V -periodic solutions of the following local problems on the periodic cell V :
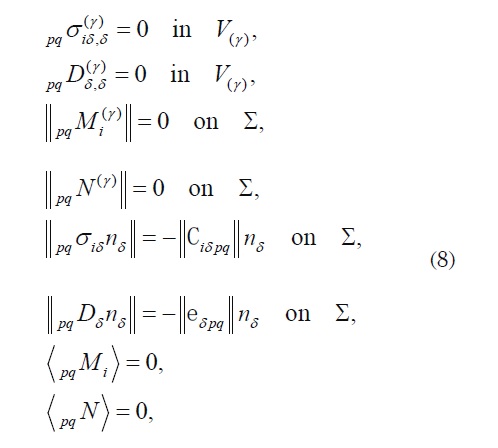
With the local constitutive relations given by
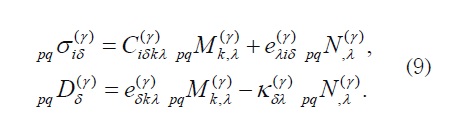
The Greek indexes run from 1 to 2.
Problem qL : Find the V-periodic functions q P k and qQ such that:
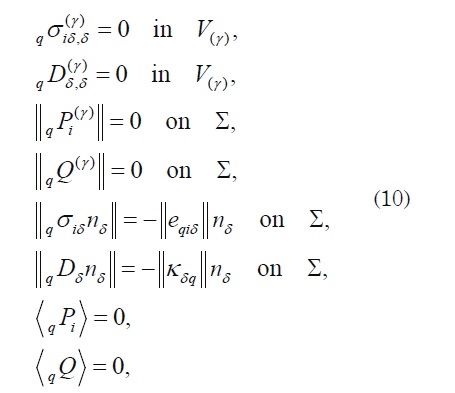
where
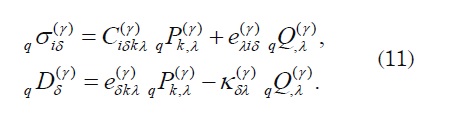
A more detailed explanation of this asymptotic process for a more general case can be found in [3].
3.1 About the “antiplane” problems for the symmetry crystal class 622
In this section the homogenization model will be specified for the particular case of components with transversely isotropic piezoelectric of 622 crystal symmetry. In particular, we are interested in the solution of the “antiplane” problems (13L, 23L, 1L, 2 L) because the “plane” problems (11L, 22L, 33L, 12 L, 3L) are the same as those investigated in [4]. The relevant constitutive relations are
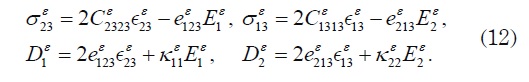
Only three material properties are involved here, namely: the longitudinal shear modulus ρε = Cε1313 = Cε2323 the transverse permittivity constant tε = kε11 = kε22, and the shear stress piezoelectric coefficient s'ε = eε213 = -eε123
The solution of the “antiplane” local problems allows obtaining the effective properties
C1313, C2323, e213, e123, k11 and k22For instance, with the solutions 1P and 1Q of the local problem 1L it is possible to compute the effective coefficients:
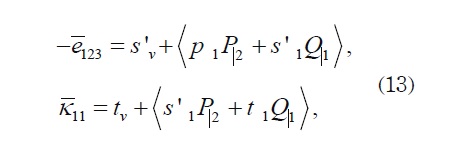
where
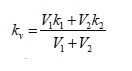
with V2 = πR2 and 1 V 2 = a In the following, the pre-index “1” will be eliminated for simplicity. The local displacement 1 P ≡ P and the local potential 1 Q ≡ Q are solutions of the following local problem 1L
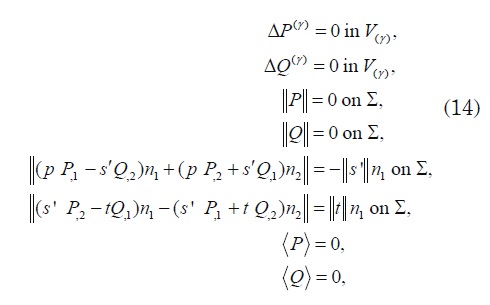
where Δ is the two-dimensional Laplacian. Therefore, the solutions Pγ and Qγ (γ = 1,2) are doubly periodic harmonic functions of the complex variable z = x1 + ix2 defined in the rectangular cell where V =V1U V21∩ V2 = Ø with periods ω1=1 and ω2= ai
3.2 Solution of the local problem 1L
The solution of is sought as follows:
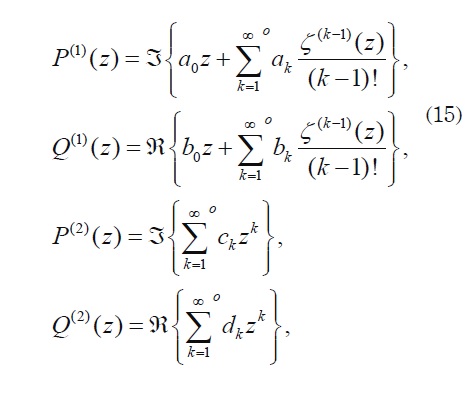
where ak bk ck and d k are real and undetermined coefficients, ζ(z) is the quasiperiodic Weierstrass Zeta function; whereas ζk(z) denotes their k-th derivative of periods ω1 and ω2 The superscript “ o ” on the summation indicates that the summation is carried out only over the odd indexes. P(ϒ) is an even function of Θ with z= ReiΘ and Q(ϒ) is an odd function of θ Expressions for the undetermined constants a0 and b0 appearing in P(1) and Q(1) , respectively, can be obtained from the quasi-periodicity of ζ(z)
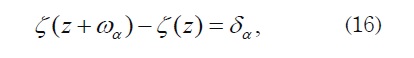
where δα = 2ζ(ωα/2) and the Legendre’s relation is fulfilled (see, for instance, [5]). The Laurent expansion about the origin for P(1) and Q(1) is
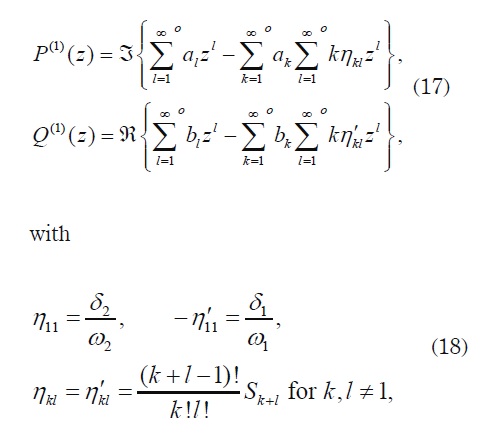
and the lattices sum Skis defined by
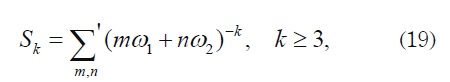
where the prime on the summation means that the double summation excludes the term m = n = 0 . The series are absolute and uniformly convergent. The conditions on the interface in (14) are used now to derive the following relations between the undetermined coefficients
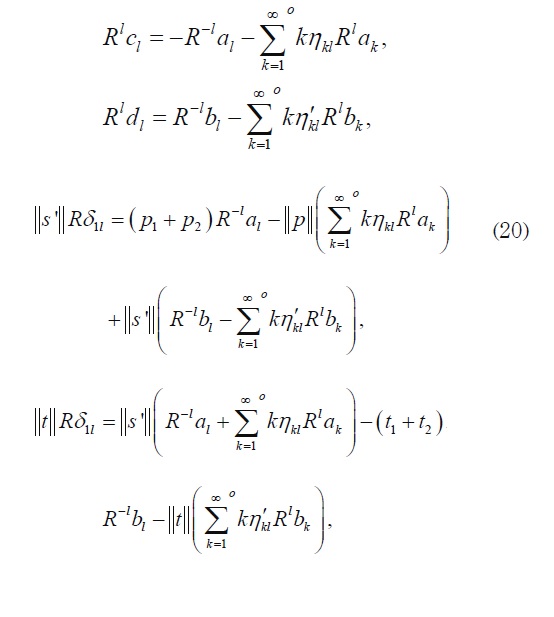
for l =1,3,5,… As we can note, the coefficients ak and bk, from the last two equations of (20), are solutions of an infinite system of linear algebraic equations.
On the other hand, based on certain transformations, as in [1], it is possible to modify to obtain
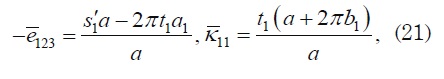
where only residues a1 and b1 of P(1) and Q(1) , respectively, are relevant for computing e123 and k11.
3.2.1 Solution of the infinite system
To solve the infinite system (20) it is convenient to introduce the following change of variables
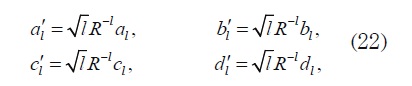
to rewrite (20) as follows:
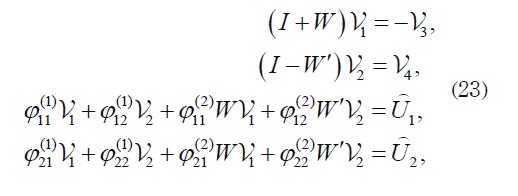
where I es identity Matrix, and the components of matrices W y W' for k=l=1 are
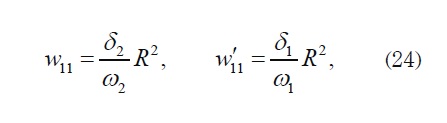
and in other case
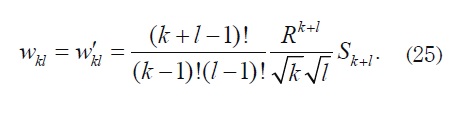
So both matrices W and W′ are real, symmetric, and bounded, and consequently we can use classical results from the theory of infinite systems. Furthermore,
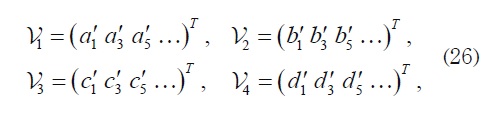
and all components of U1 and U2 are zero except the first ones which are equal to −Rχpand −Rχt respectively, where The non-symmetric 2× 2 matrices Φ(1) and Φ (2) can be defined by
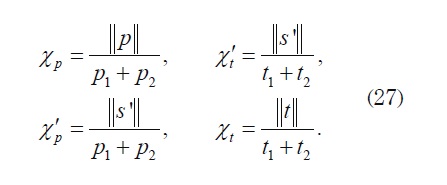
The non-symmetric 2× 2 matrices Φ(1) and Φ(2) can be defined by
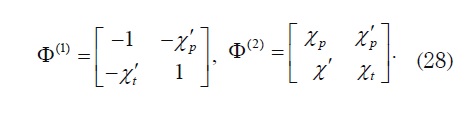
Therefore, the third and fourth equations of (23) can be transformed in
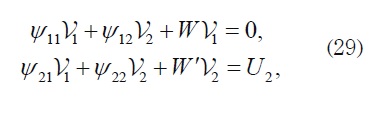
where only the first component of U2 is nonnull, and equal to −R , and
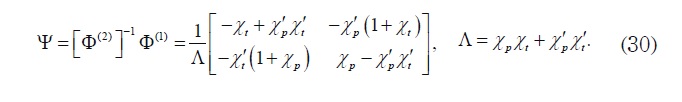
Now we can analyze the behavior of the effective coefficients for different orders of truncation of the infinite system (29). The general form of the components of the principal matrix - H = hij - of (29) can be defined as follows
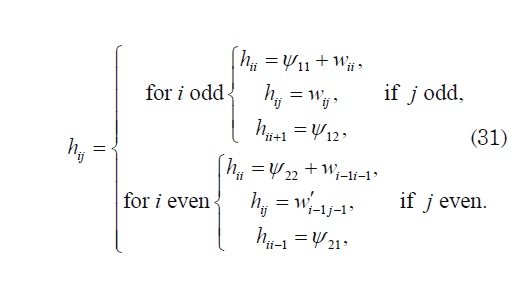
3.2.2 Generalization to other antiplane problems
Solving the local problem 1L one can obtain only the coefficients e123 e and k11. This is why we need to solve the other “antiplane” local problems so as to obtain the remaining effective coefficients. For instance, from 2L we can compute e123 e and k11 from 23L it is possible to obtain e123 and C2323 and from 13L we can compute e213 and C1313.
The methodology used in the previous subsections is then applied to solve these local problems, with the aim of computing the effective coefficients C2323, e213 and κ22
4. Numerical examples
In this section some numerical examples will be presented in order to illustrate the efficiency of the method described above. Firstly, we will show comparisons with the results reported in [1] for computations of the effective coefficients in the limit case of a square cell (a =1) . Secondly, for the rectangular cell with a = 2 , some comparisons are made with results derived from the Fast Fourier Transform numerical method. These last numerical results illustrate that the present work involves an extension of the results published in [1].
In both cases we use the same data taken from [1], which are as follows: for the matrix (collagen) p1 =1,4GPa t1/Ε0 = 2.825 units, and d1 = 0,062 pC/N; whereas for the fibers (collagen-hydroxyapatite (HA)) p2 = 2,697 GPa, t2/Ε0= 2.509 units, and d2 = 0,041pC/N.Ε0= 8,854×10−12 C2/N·m2
4.1 Case of a =1
In this subsection, we reproduce the numerical results published in [1]. In fact, Figure 2 shows the semi-analytical results of the present model that reproduce those published in Figure 2, page 5774 of [1]. The results derived from the present model corresponds to an order of truncation n0 = 4.
4.2 Case of a = 2
The main goal of this subsection is to illustrate the effectiveness of the present semianalytical model for a rectangular array (a ≠ 1) . In this case the effective properties don’t preserve the symmetry of the phases, i.e., when we compute e123/s`1and e213/s`1 they will be different. The same will happen when we obtain k11/t1 and k22/t1 or c1313/p1 and c2323/p1 as illustrated in Figure 3.
Moreover, this semi-analytical model shows its quality when we compare with the results via the Fast Fourier Transform method (FFT) (see, for instance, [5-8]). The results of such comparison are shown in Figure 3. The expected effect of the rectangular array periodic distribution, for a = 2 , in the orthotropic global behavior is revealed.
5. Concluding remarks
A methodology was developed for obtaining semi-analytical expressions to compute the effective properties derived from the “antiplane” local problems of a two-phase piezoelectric unidirectional periodic fibrous composite made of homogeneous and linear transversely isotropic piezoelectric materials, which belong to the symmetry crystal class 622. The crosssections of the fibers are circular and are centered in a periodic array of rectangular cells. The efficiency of such methodology was verified by reproducing the results published in [1] for the particular case of a square cell.
The main difficulties found in this study are linked with the non-nullity of the lattices sums related to the considered rectangular geometry, which is a considerable source of non-null coefficients in the principal matrix of the infinite system. The effective properties depend on the fiber radius “ R ”, which is less than 1/ 2; on the physical properties of each phase as well as on the length “ a ” of the rectangular cell that appears revealed in the matrix Ψ of the system (30). The methodology is based on elements from the theory of complex variables, from lattices sums, and from the theory of infinite systems of algebraic equations.
The authors are very grateful to the Organizing Committee of the IX Congreso Internacional de Electrónica, Control y Telecomunicaciones for their invitation and support. This work was finished during a visit of Dr. R. Brenner to the Faculty of Mathematics and Computers Sciences at the University of Havana, and was supported by the Priority Solidarity Fund (FSP Cuba 2011-26) project. The PNCB project is also acknowledged.
References
[1] E . López-López, F. J. Sabina, J. Bravo- Castillero, R. Guinovart-Díaz y R. Rodríguez- Ramos, “Overall electromechanical properties of a binary composite with 622 symmetry constituents. Antiplane shear piezoelectric state”, International Journal of Solids and Structures, Volume 42, pp. 5765-5777, 2005.
[2] J. Bravo-Castillero, J. A. Otero, R. Rodríguez- Ramos y A. Bourgeat, “Asymptotic homogenization of laminated piezocomposite materials”, International Journal of Solids and Structures, Volume 35, Issue 5-6, pp. 527-541, 1998.
[3] L. M. Sixto-Camacho, J. Bravo-Castillero, R. Brenner, R. Guinovart-Díaz, H. Mechkour, R. Rodríguez-Ramos y F. J. Sabina, “Asymptotic homogenization of periodic thermo-magneto-electro-elastic heterogeneous media”, Computers and Mathematics with Applications, Volume 66, pp. 2056-2074, 2013.
[4] G. G. Nava-Gómez, H. Camacho-Montes, F. J. Sabina, R. Rodríguez-Ramos, L. Fuentes, R. Guinovart-Díaz, “Elastic properties of an orthotropic binary fiber-reinforced composite with auxetic and conventional constituents”, Mechanics of Materials, Volume 48, pp. 1-25, 2012.
[5] S. Lang, Complex Analysis, New York: Springer-Verlag, 1993
[6] H. Moulinec y P. Suquet, “A numerical method for computing the overall response of nonlinear composites with complex microstructure”, Comput. Methods Appl. Mech. Engrg., Volume 157, pp. 69-94, 1998.
[7] J. C. Michel, H. Moulinec y P. Suquet, “A computationl scheme for linear and nonlinear composites with arbitrary phase contrast”, International Journal for Numeriacl Method in Engineering, Volume 52, pp. 139-160, 2001.
[8] R . Brenner, “Numerical computation of the responze of piezoelectric composites using Fourier transform”, Physical Review, 2009.
[9] R . Brenner, “Computational approach for composite materials with coupled constitutive laws”, Journal of Applied Mathematics and Physics, vol. 61, nº 5, pp. 919- 927, 2010.