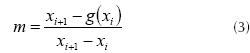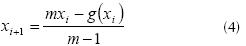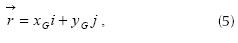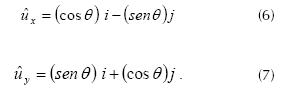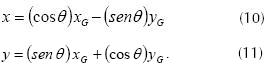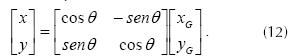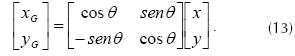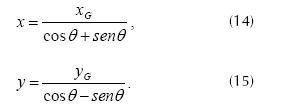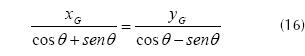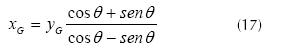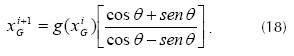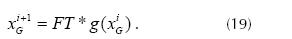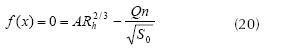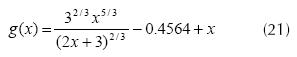Formulations to overcome the divergence of iterative method of fixed-point in nonlinear equations solution

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a14

Formulations to overcome the divergence of iterative method of fixed-point in nonlinear equations solution

Formulaciones para superar la divergencia del método de iteración de punto fijo en la solución de ecuaciones no lineales

Wilson Rodríguez Calderón*,
Myriam Rocío Pallares-Muñoz**

* Civil Engineer, Master on Numerical Methods in Engineering, Universidad Cooperativa de Colombia, Bogotá, Colombia. Contact: wilson.rodriguezca@campusucc.edu.co
** Civil engineer, Master on Numerical Methods in Engineering, Surcolombiana University, Neiva, Colombia. Contact: myriam.pallares@usco.edu.co

Fecha de recepción: 25 de febrero de 2014 Fecha de aceptación: 19 de enero de 2015

Citation / Para citar este artículo: Rodríguez Calderón, W., & Pallares Muñoz, M. R. (2015). Formulations to overcome the divergence of iterative method of fixed-point in nonlinear equations solution. Revista Tecnura, 19(44), 191-199. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a14

Abstract

When we need to determine the solution of a nonlinear equation there are two options: closed-methods which use intervals that contain the root and during the iterative process reduce the size of natural way, and, open-methods that represent an attractive option as they do not require an initial interval enclosure. In general, we know open-methods are more efficient computationally though they do not always converge. In this paper we are presenting a divergence case analysis when we use the method of fixed point iteration to find the normal height in a rectangular channel using the Manning equation. To solve this problem, we propose applying two strategies (developed by authors) that allow to modifying the iteration function making additional formulations of the traditional method and its convergence theorem. Although Manning equation is solved with other methods like Newton when we use the iteration method of fixed-point an interesting divergence situation is presented which can be solved with a convergence higher than quadratic over the initial iterations. The proposed strategies have been tested in two cases; a study of divergence of square root of real numbers was made previously by authors for testing. Results in both cases have been successful. We present comparisons because are important for seeing the advantage of proposed strategies versus the most representative open-methods.

Keywords: divergence, fixed point, linear convergence, open methods, quadratic convergence, root equations.

Resumen

Cuando se requiere encontrar la solución de una ecuación no lineal existen dos grandes alternativas: los métodos cerrados que usan intervalos que contienen la raíz y durante su proceso iterativo reducen su tamaño de manera natural, y los métodos abiertos que son una buena opción por no requerir un intervalo inicial que la encierre. En general, se sabe que los métodos abiertos son más eficientes computacionalmente aunque no siempre convergen. Este trabajo presenta el estudio de uno de los casos de divergencia cuando se usa el método abierto de iteración de punto fijo; se trata de una aplicación típica de hidráulica de canales cuando se requiere calcular el tirante normal en un canal rectangular haciendo uso de la fórmula clásica de Manning. Para solucionar el problema de divergencia se proponen dos estrategias (desarrolladas por los autores) que permiten modificar la función de iteración realizando formulaciones adicionales que parten del método original y su teorema de convergencia. Aunque la ecuación de Manning se resuelve con otros métodos como el de Newton, cuando se usa el de iteración de punto fijo se presenta una situación interesante de divergencia que puede solucionarse y además obtener convergencia superior a la cuadrática en las iteraciones iniciales. Situaciones de divergencia monotónica como la que se presenta en este artículo han sido estudiadas con las estrategias propuestas con resultados satisfactorios. En el artículo se presentan comparaciones para reconocer las ventajas de las estrategias propuestas frente a los métodos abiertos más representativos.

Palabras clave: convergencia cuadrática, convergencia lineal, divergencia, métodos abiertos, punto fijo, raíces de ecuaciones.

Introduction

When we want to determine the roots or zeros of an equation, that is, values of x which cause f(x) = 0, it is possible using two ways: analytical direct methods that are restricted to particular cases such as classical quadratic equation, or numerical methods which covering a broad spectrum, for example, solving algebraic equations, transcendental and polynomial. In general, there are two philosophies work for finding roots of equations: closed and open methods (Akai, 2004) (Nakamura, 1997) (Chapra & Canale, 2007).

Intervals that enclose or contain the root are used by closed methods. These methods reduce the work interval using a particular criterion for each method; such is the case of the bisection methods and false position or false rule. These methods perform so well, however, we know their convergence is too slow even in some cases is deficient. Therefore, we cannot generalize about the benefits of a method over another. Rather than have a large battery of methods that can be used in case of failure or improper behavior of convergence. There is also the possibility of finding new methods including modifications to existing.

Iterations of closed methods always generate approximations ever closer to the root; therefore, we say they are convergent because they are progressively closer to the root as they advance calculation cycles. Meanwhile, the open methods are based on iteration formulas requiring only a starting point or pair of values that need not necessarily enclose the root. This quality provides important advantages; however, a difficulty arises that is related to the divergence of the methods, so it is necessary to plan alternatives to face the problem, especially when we know it is worth doing, since, in general, when the open methods converge, they do so more quickly than closed methods (Press, Teukolski, & Vetterling, 2012).

Open methods using a general strategy of successive substitutions. Examples of these methods are Newton, Secant and the method of fixed point iteration. On this last method the attention of this article focuses, as there is a whole mystique around the divergence of this method and the alternatives for improvement (Heath, 2002). Perhaps the easiest way to overcome this divergence is another method but worth undertaking efforts to get it to work, as its advantages of simplicity and flexibility make it an interesting method for apply in real cases.

Methodology

The term "method of successive substitutions" refers to a broad class of iterative schemes for nonlinear equations. However, the interest of this work focuses on the method of fixed point iteration.

If starting the basic equation f(x) = 0 may be written as equation (1),

so we could write an iterative scheme in terms of equation (2),

where the iteration index i = 0,1,2, ... and x0 is the initial estimate of the root. This method is called fixed point iteration and its great advantage is the simplicity and the flexibility to choose the form of g(x). However, it has serious difficulties in cases where the iterative formula does not always converge for g(x) chosen arbitrarily.

To ensure convergence of the iterative scheme for the interval containing the root, 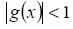condition must be satisfied.

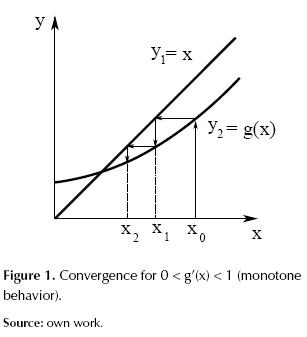
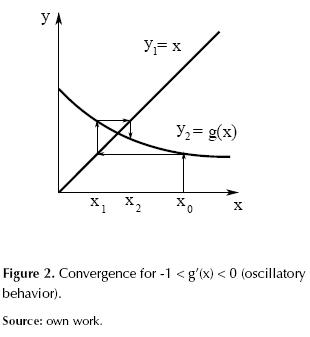
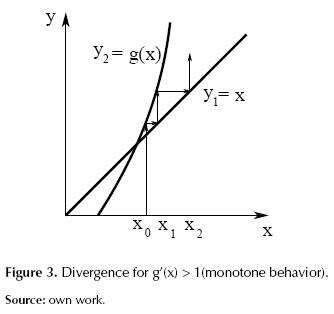
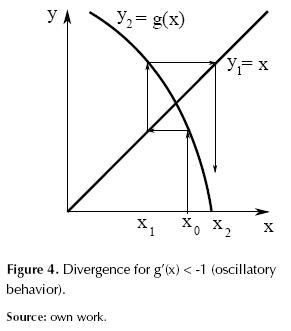
Figures 1 to 4 illustrate how g’(x) affects the convergence of the method such that: if 0 < g’(x) < 1 is asymptotic convergence, and if 1 < g’(x) < 0 is oscillatory convergence. Otherwise, the method diverges. By extension of this analysis it can be demonstrated that the convergence speed increases as g’(x) approaches zero.

Resolving divergences shown in figures 3 and 4 is interesting. For this, two strategies which are applied to a particular case are proposed.

Proposed strategies

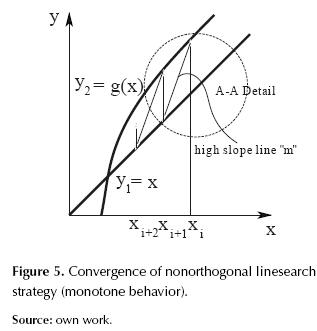
Strategy number 1. Nonorthogonal linesearch

Based on the case of figure 3, we propose use non-orthogonal linesearch instead using the search orthogonal directions as in the method of fixed-point iteration. This strategy should aim to generate a convergent iterative scheme.

From figure 5 we can observe graphically that the strategy in principle has the possibility to converge and that the proposed method can enclose to the root at least intuitively (intersection of y1 and y 2) as shown.

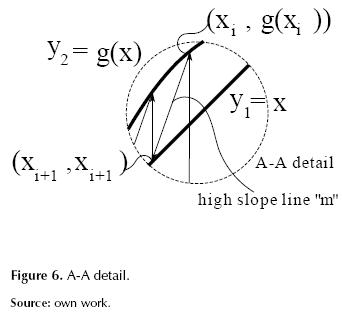
From figure 6 an expression for m is obtained in the form of equation (3),

Starting from equation (3) it is possible to get x_i+1 by means of the equation (4),

Equation (4) represents the generalized iteration formula to overcome the problems of divergence in the cases of figures 3 and 4, according to the following recommendations:

1) If a positive value m (figure 3) is required, we must use m > 1, preferably beginning to test values ​​m = 2, 3, ..., If a positive value m (figure 3) is required, use m > 1, preferably beginning to test values m = 2, 3, ..., because we must search a high slope higher than the slope of y1 line (m = 1) and large enough to cross the line y1 in a point before the intersection between y1 and y2, as shown in figure 6.

2) If a negative value m (figure 4) is required, we must use m ≤ 1, preferably beginning to test with values m = -1, -2, -3, ... , because a high slope must be found. In this case using linesearch with slope m = -1 is not prohibited because these would be perpendicular to y1, therefore, intersection with y1 is guaranteed.

These two recommendations have been drawn from simple approaches and have been implemented in several examples to establish its performance.

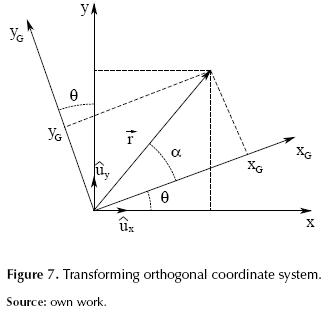
Strategy number 2. Rotation of reference system XY and determination of iteration formulas in the new system (Strategy of rotated axes)

In this case we take an arbitrary point (x, y) in the coordinate system XY and we seek a relationship with the coordinates of the point in a system rotated an angle θ.

According to figure 7 we can see that vector ‘r’ can be represented by equation (5).

and the unit vectors ux and uy are expressed by equations (6) and (7) respectively.

Equations (8) and (9) are obtained from the projection of a vector,

Equations (10) and (11) are obtained operating appropriately,

Writing equations (10) and (11) in matrix form, the system of equations (12) is obtained.

Establishing the inverse relationship in the form of equation (13) is possible because they are orthogonal systems.

Equations (14) and (15) are obtained when we apply an arbitrary point on the line

Knowing that equations (14) and (15) correspond to the line y = x we can establish relationships between x_G and y_G in the rotated system through matching. Equation (16) demonstrates this consideration.

Solving for x, equation (17) is obtained.

However, if the classic strategy of root finding for method of fixed point iteration is developed in the rotated system, we have y_Gi+1 = g(x_Gi), where the superscripts indicate the iteration and the subscripts indicate the reference coordinate system. An iteration formula is obtained when we apply this reasoning to equation (17). This expression can be used in the rotated system also in the original system using equation (10).

Equation (18) shows the final iteration expression obtained in the coordinate system when is rotated an angle ‘θ’.

The factor in square brackets can be set as a constant called FT because the angle A is a constant. So the expression (18) can be simplified and we can get the equation (19).

The results of equation (19) can be transferred to the XY system to get the value of the root, even if g(x) does not meet the convergence condition described above; however, when we moved to the system rotated coordinate we are doing a transformation and a reformulation and this allows convergence.

RESULTS AND DISCUSSION

In order to present evidence about the performance of the proposed methods we developed one of the cases where we found divergence problems with the method of fixed point iteration. This is the Manning equation that is a problem where the analyst solves the normal height in rectangular open-channel-flow.

The starting equation is of the form described by equation (20):

In (20) equation (20), A is the channel area; also A = bx, where b is the base of channel and x is the normal height. Meanwhile:

Q = channel flow

S₀ = channel slope

N = Manning coefficient rugosity

In general, Q, n and S₀ are constants. One particular solution for this equation is obtained when Q = 5m³/s, n = 0.015, S₀ = 0.003, b = 3 m.

Equation (21) provides g(x) in general form as g(x) = f(x)+x, so,

Using previous testing by Newton’s method we can get the root x = 0.7323. Substituting this value in the scheme of fixed-point iteration we can know g(x) is divergent and therefore, seeking a solution to the problem is necessary.

The results of the two proposed strategies are described. The implementation of the formulations was developed in a spreadsheet.

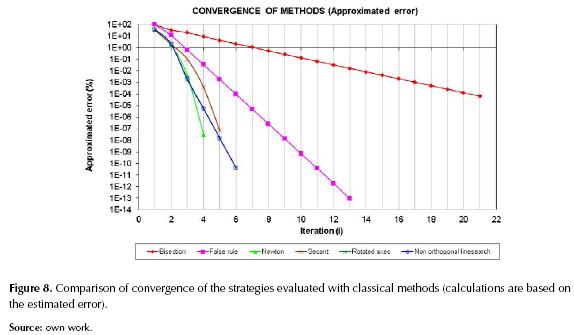
The most interesting analysis that can probably be done is the convergence curve vs. other classical methods mentioned in the introduction that can be reviewed in references (Mathews & Fink, 2011), (Burden & Faires, 2011). Figures 8 and 9 show these curves, these are used as a performance comparison of the methods.

The methods exhibit similar behavior in the convergence when we use the approximate error which is calculated at an each iteration taking the value of the previous iteration. Comparison is important to look over the advantage of proposed strategies versus the most representative methods.

Figure 8 shows how the two alternatives evaluated far exceed the speed of convergence of the methods of bisection and False Rule.

We can see that the proposed alternatives exceed the convergence of Secant method and Newton's method in the first iterations. Note these methods are known for having high speed of convergence. However, in the end, Newton’s method exhibits lower relative error than the proposed strategies, although the orders of magnitude of the errors are very low. So, we can say that the proposed strategies are very competitive.

Similar situation is presented when g(x) is the function who allows getting the square root of a number. A study of divergence in this case was made previously by authors for testing about the proposed strategies.

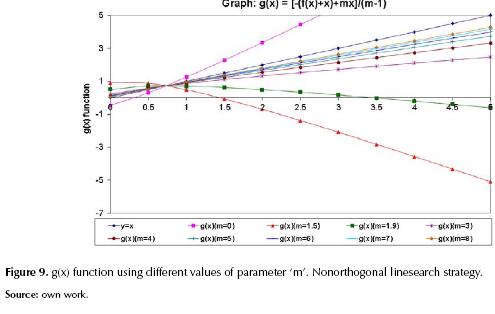
The behavior of the nonorthogonal linesearch strategy is explained by figure 9.

Figure 9 indicates that event of divergence reported in figure 3 is presented when m = 0, however, when we use m = 1.5 the curvature is inverted. Meanwhile, the curve g(x) tends to become straight and nearest to line y = x when higher values of 'm' are used. We can say, there is an optimum value of 'm' (in present case is 1,9) which was used for the calculation. The reason is, insofar as g(x) tends to have horizontal slope in the vicinity of the fixed point (that is, it tends to the root of f(x)) the optimum condition of iteration fixed point (g’(x) = 0) is reached.

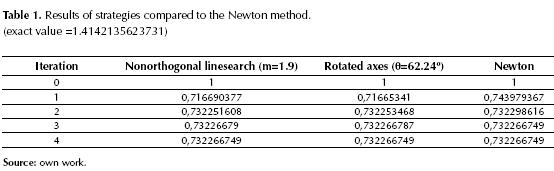
In table 1 the results of the first four iterations of the methods are recorded.

Conclusions

From the results in table 1 we can see that the proposed strategies are working properly. Just look at the insignificant differences when comparing the results with those of Newton method.

We present comparisons because are important for seeing the advantage of proposed strategies versus the most representative open-methods.

The proposed strategies have been tested in two cases. A study of divergence of square root of real numbers was made previously by authors for testing. Results in both cases have been successful.

The strategies developed show significant advantages in both implementation and precision-accuracy. Most importantly is, they solve the divergence properly and they fit to convergence rates that are very attractive for solving problems in science and engineering.

An interesting advantage of the proposed search strategies is that it isn't necessary to know the derivatives of the function or enclose the desired root likewise the computational cost is certainly lower than of Newton and Secant methods.

We hope make an extended study to characterize more functions. The goal will be enlarge the understanding of proposed strategies to known its adaptability in different situations. Later a study of convergence generalized must be developed.

ACKNOWLEDGMENT

Thanks to Cooperativa University and Surcolombiana University for the support given to this research.

References

Akai, T. J. (2004). Métodos Numéricos Aplicados a la Ingeniería. México: Limusa Willey.

Burden, R. L., & Faires, D. J. (2011). Análisis Numérico. México: Cengage Learning Editores S.A.

Chapra, S. C., & Canale, P. R. (2007). Métodos Numéricos para Ingenieros. México: McGraw-Hill.

Heath, M. T. (2002). Scientific Computing: An Introductory Survey. Boston: McGraw-Hill.

Mathews, J. H., & Fink, K. D. (2011). Métodos Numéricos con Matlab. México: Cengage Learning Editores S.A.

Nakamura, S. (1997). Análisis Numérico y Visualización Gráfica con Matlab. México: Pearson Education.

Press, W. H.; Teukolski, S. A., & Vetterling, W. T. (2012). Numerical Recipes In C: The Art Of Scientific Computing. London: Cambridge University Press.