DOI:
https://doi.org/10.14483/23448393.2264Published:
2001-11-30Issue:
Vol. 7 No. 1 (2002): January - JuneSection:
Science, research and developmentUso de la Transformada Wavelet para el Estudio de Tráfico Fractal en Redes de Comunicaciones
Keywords:
Transformada wavelet, Tráfico Autosimilar, Detección y Estimación, Síntesis de Movimiento Browniano Fraccional. (es).Downloads
References
P. Abry and D. Veitch. Wavelet Analysis of Long-Range-Dependent Traffic. IEEE Trans. Information Theory, 44(1):2-15, 1998.
P. Abry, P. Flandrin, M. Taqqu and D. Veitch. Wavelets for the Analysis and Synthesis of Scaling Data, In "Self-Similar Network Traffic and Performance Evaluation", K. Park and W. Willinger, editors. John Wiley and Sons, New York, 2000.
P. Abry, D. Veitch and P. Flandrin Long-Range Dependence: Revisiting Aggregation with Wavelets. Blackwell publishers ltd. 1999
M. Alzate. Obtención de Bases Wavelets Ortonormales Mediante el Diseño de Bancos de Filtros de Reconstrucción Perfecta. IV Simposio de Procesamiento de Señales, Universidad de los Andes, 1995.
M. Alzate. Modelos de Tráfico en Redes de Comunicaciones. Reporte de Investigación de la Maestría en Teleinformática de la Universidad Distrital, marzo de 1995.
M. Alzate. Generation of Simulated Fractal and Multifractal Traffic. IX Congreso Nacional de Estudiantes de Ingeniería de Sistemas, Bogotá, 2000.
M. Alzate. Introducción al Tráfico Autosimilar en Redes de Comunicaciones. Revista INGENIERIA, Universidad Distrital,Vol. 6 No. 2, 2001.
I. Daubechies. Ten Lectures on Wavelets. SIAM'92. Philadelphia, 1992.
R. Dijkerman and R. Mazumdar. Wavelet representation of stochastic processes and multiresolution stochastic models. IEEE Trans. Signal Proc. 42:1640-1652, July 1994
P. Fieguth and A. Willisky. Fractal estimation using models on multiscale trees. IEEE Trans. Signal Proc. 44:1297-1300, 1996.
P. Flandrin. Wavelet Analysis and Synthesis of Fractional Brownian Motion. IEEE Trans. Inf. Theory, 38:910-917, 1992.
V. Frost and B. Melamed. Traffic Modeling for Telecommunications Networks. IEEE Commun. Mag. 32(3):7081, 1994.
A. Gilbert, W. Willinger and A. Feldman. Scaling analysis of conservative cascades with application to network traffic. IEEE Trans. Information Theory, 45(3):971-991, 1999.
P. Huang, A. Feldmann and W. Willinger. A Non-intrusive, Wavelet-based Approach To Diagnosing Network Performance Problems. Proceeding of ACM SIGCOMM Internet Measurement Workshop 2001, San Francisco, November 2001
Internet Traffic Archive. BC_pAug89, http://www.acm.org/ sigcomm/ITA/index.html.
W. Leland, M. Taqqu, W. Willinger and D. Wilson. On the selfsimilar nature of Ethernet Traffic. IEEE/ACM Trans. Networking, 2:1-15, 1994.
S. Ma and C. Ji. Modeling Heterogeneous Network Traffic in Wavelet Domain. IEEE/ACM Trans. Networking, 9(5):634-649, 2001.
D. McDysan. QoS and Traffic Management in IP and ATM networks. McGrawHill, NY, 2001.
H. Michiel and K. Laevens. Teletraffic Engineering in a broadband era. Proceedings of the IEEE, december 1997.
M. Parulekar and A. Makowski. M/G/ Input Processes. Proc. IEEE Infocom'97, 1997.
V. Paxson and S. Floyd. Wide-Area Traffic: The Failure of Poisson Modeling. IEEE/ACM Trans. Networking, 3:226-244, 1995.
R. Riedi, et. al. A Multifractal Wavelet Model with Application to Network Traffic. IEEE Trans. Inf. Theory, 45(3):992-1018, 1999.
M. Schwartz. Broadband Integrated Networks. Prentice Hall, UpperSaddle River, 1996.
A. Tewfik and M. Kim. Correlation structure of the discrete wavelet coefficients of fractional brownian motion. IEEE Trans. Info. Theory, 38:904-909, 1992.
B. Tsybakov and N. Georganas. Self-Similar Processes in Communications Networks. IEEE Trans. Inf. Theory, 44(5):17131725, 1998.
D. Veitch and P. Abry. A Wavelet-Based Joint Estimator of the Parameters of LRD. IEEE Trans. Inf. Theory, 45(3):878-897, 1999.
W. Willinger and V. Paxson. Where Mathematics meets the Internet. Notices of the American Mathematical Society, Vol. 45, No.8, August 1998, pp. 961-970
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Ingeniería, 2002-00-00 vol:7 nro:1 pág:11-24
Uso de la Transformada Wavelet para el estudio de tráfico fractal en redes de comunicaciones
Marco Aurelio Alzate Monroy
Resumen
En ingeniería de redes es necesario que los modelos de tráfico capturen las principales características estadísticas del tráfico moderno. En este sentido, los modelos autosimilares son los únicos que representan las complejas estructuras de correlación que este tráfico moderno exhibe en un amplio rango de escalas de tiempo. Desafortunadamente, la gran variabilidad de estos modelos dificultan enormente su análisis matemático. La transformada wavelet se ha venido conviritiendo en una poderosa herramienta para dicho análisis, pues elimina las complejas correlaciones al generar una serie de procesos independientes e idénticamente distribuidos que representan el tráfico original. En este artículo se hace una presentación sencilla y de manera tutorial tanto de la transformada wavelet como de su aplicación al estudio del tráfico autosimilar, en continuación de un artículo previo donde se presentaron de igual manera los conceptos más básicos sobre este tipo de tráfico [7]. El objetivo es ofrecer al lector mejores herramientas para iniciar el estudio del tema y, porqué no, para conducir su propia investigación al respecto.
Palabras clave:
Transformada wavelet, Tráfico Autosimilar, Detección y Estimación, Síntesis de Movimiento Browniano Fraccional.
Abstract
Traffic models must capture the main statistical properties of modern network traffic. In this sense, self-similar processes are the only ones that capture the complex correlation structures exhibited by modern traffic in a wide range of time scales. Unfortunately, because of its high variability, these models are not easily tractable. However, the wavelet transform can represent these ill-behaved processes as a sequence of independent and identical distributed subprocesses, so it has became a powerful tool for self-similar traffic analysis. This paper describes, in a tutorial manner, both the wavelet theory and its application in the analysis of self-similar traffic. It is a continuation of a previous paper [7] describing the basic concepts of self-similarity. The objective of the paper is to provide the reader with better tools for studying the subject in the specialized literature and, maybe, for conducting his/her own research.
Key words:
Wavelet Transform, Self-Similar Traffic, Detection and Estimation, FBM Synthesis.
I. INTRODUCCIÓN
El principal objetivo de la ingeniería de redes de comunicaciones es la optimización del uso de los recursos en la red al tiempo que se garantiza una calidad de servicio dada. Un aspecto importante por considerar en la búsqueda de este objetivo es el modelamiento del tráfico.
Durante las primeras décadas de la tecnología de las telecomunicaciones fue suficiente con caracterizar el número de llamadas telefónicas como un proceso de Poisson y representar la duración de cada llamada como una variable aleatoria exponencialmente distribuida y completamente independiente de la duración de otras llamadas. Posteriormente, la transmisión de datos introdujo una mayor complejidad debido a los tiempos de espera y a los esquemas de acceso al medio de transmisión. Ahora que los distintos servicios de comunicaciones se integran en redes únicas de banda ancha (convergiendo hacia una plataforma universal IP), no es suficiente con caracterizar el número y la duración de las llamadas sino también la variabilidad en el ancho de banda que ocupa el flujo de información durante cada llamada. Por supuesto, ahora el concepto de llamada es más general y puede significar una conexión TCP, una sesión FTP o Telnet, un datagrama UDP, una conversación VoIP, un flujo RTP, etc.
Para representar todas estas características del tráfico sobre las nuevas redes de comunicaciones, se han desarrollado diferentes modelos que tratan de capturar el efecto de las ráfagas con las que se presenta este tráfico moderno. En general, estos modelos se pueden dividir en dos categorías: modelos markovianos que sólo presentan dependencia de rango corto (procesos ON/OFF en los que los períodos de actividad e inactividad están exponencialmente distribuidos[23], procesos markovianamente modulados (de Poisson o determinísticos)[5], modelos gaussianos autoregresivos [12], modelos de flujo y de difusión [19], etc.), y modelos que exhiben dependencia de rango largo (modelos de movimiento browniano fraccional (FBM) [7], procesos ON/OFF en los que los períodos de actividad e inactividad tienen una distribución con cola pesada [7], modelos M/Pareto/ [20], modelos Farima (fraccionales autoregresivos integrales de promedios móviles) [25], modelos wavelet multifractales [22], etc.).
El primer tipo de modelos representó un avance importante sobre el modelo simple de llegadas Poisson y tiempos de servicio exponenciales, el cual fue el único que se utilizó durante casi un siglo. Sin embargo, recientemente se ha evidenciado de una manera empírica la presencia de fractalidad en el tráfico de las redes modernas de telecomunicaciones, con lo cual se invalidan muchos de los procedimientos de diseño y control de redes basados en los modelos markovianos de tráfico. En efecto, esos procedimientos sólo contemplan la correlación que existe en el rango de tiempo correspondiente al RTT (Round-TripTime, tiempo que tarda un mensaje en ir del origen al destino más el tiempo que tarda el reconocimiento en retornar al origen), cuando ahora sabemos que esta correlación se extiende sobre un amplio rango de escalas de tiempo. Esta estructura de correlación puede conducir a la "depedencia de rango largo", la cual tiene un impacto significativo sobre el comportamiento de las colas en elementos de red como multiplexores y enrutadores que no se puede predecir con los modelos markovianos de tráfico. Por eso se hace tan importante el estudio de la segunda clase de modelos de tráfico. Dentro de este estudio deben incluirse actividades de investigación (incluyendo investigación matemática fundamental) para comprender las implicaciones (aún desconocidas) de la fractalidad del tráfico en el desempeño de las redes y, sobre todo, para desarrollar mecanismos prácticos y eficientes de control de tráfico y de congestión que permitan garantizar una determinada calidad de servicio a cada usuario. Tres de las principales áreas de investigación son (1) la detección de fenómenos de escala en trazas muestrales de tráfico, incluyendo la estimación de los parámetros correspondientes, (2) el mismo modelamiento físico del tráfico que permita explicar las causas de la fractalidad, y (3) el análisis de desempeño bajo tráfico fractal, orientado al diseño de mecanismos de control de tráfico y asignación de recursos.
Con respecto a la detección de fractalidad a partir de trazas muestrales de tráfico, ha sido necesario desarrollar nuevas técnicas de estimación de parámetros. En efecto, recordemos que la primera manifestación de fractalidad es una altísima variabilidad, fácilmente caracterizable mediante varianzas infinitas, y una compleja estructura de correlación que impide cualquier suposición de independencia, de manera que ni la ley de los grandes números ni el teorema del límite central (corazón de casi todos los métodos estadísticos de detección y estimación) son aplicables al análisis de las trazas muestrales de tráfico fractal. Esta dificultad ha conducido al desarrollo y la adopción de técnicas de estimación basadas en wavelets, las cuales presentan muchas ventajas como robustez ante tendencias determinísticas, eficiencia computacional, clasificación de diferentes regímenes de escala, etc. [2]
Con respecto al modelamiento mismo del tráfico autosimilar, se han propuesto algunos modelos que facilitan el análisis del comportamiento de las colas en los elementos de la red, otros que han sido motivados por los mismos procesos dinámicos que se suceden dentro de la red y algunos más que se basan en diferentes técnicas para generar dependencia de rango largo. Por ejemplo, el modelo ON/OFF es una abstracción matemática que proporciona un fundamento físico al explicar una posible causa de la fractalidad en el tráfico. Sin embargo, este modelo supone independencia entre los procesos ON/OFF cuando es evidente que estos procesos interactúan íntimamente en los puntos de congestión. Al incluir esta dependencia, se evidencian ciertos fenómenos de escala multiplicativa que se observa sobre muchas escalas pequeñas de tiempo (fracciones del tiempo de transmisión de un paquete). Esta multifractalidad se puede modelar directamente en el dominio de la escala, nuevamente mediante la transformada wavelet [22].
Con respecto al análisis de desempeño, control de tráfico y asignación de recursos, se ha encontrado que el comportamiento dinámico de las colas en los elementos de red ante tráfico de entrada fractal es fundamentalmente diferente a los sistemas con tráfico markoviano. En particular, la distribución del número de paquetes en espera de servicio tiene una cola que decrece subexponencialmente (ya sea en forma weibulliana o polinómica). Estos resultados implican que la estrategia de asignar más capacidad en los buffers para disminuir la pérdida de paquetes es inútil, pues una muy pequeña reducción en la tasa de pérdidas implicaría un costo exagerado en el retardo de los paquetes. Sin embargo todos estos resultados son asintóticos de una manera u otra, cuando los límites asintóticos difícilmente se alcanzan en la realidad; se concentran en medidas de desempeño de primer orden cuando las medidas de segundo orden son aún más importantes en comunicaciones multimedios; no tratan sobre las medidas de desempeño en régimen transiente, que es lo más importante en la práctica ya que la convergencia a un estado estable es tan lenta que resulta inútil para propósitos de ingeniería; ignoran los fenómenos de realimentación tales como los esquemas de control de flujo en TCP; etc. En síntesis, a pesar de los ingentes esfuerzos de eminentes investigadores, casi todo está por hacer en esta área. Y, nuevamente, la transformada wavelet podría constituir una útil herramienta para analizar el comportamiento de las colas de espera directamente en el dominio de la escala[17]. Por otro lado, es posible sintetizar eficientemente grandes trazas muestrales de tráfico mediante técnicas basadas en wavelets, lo cual es importante para estudio de desempeño mediante simulación [22].
Así pues, el método de la transformada wavelet se ha constituido en una importante herramienta para detección, estimación, síntesis, modelamiento y análisis de tráfico fractal. Por esta razón, en este artículo se ha querido hacer una presentación sencilla y de manera tutorial tanto de la transformada wavelet como de su aplicación al estudio del tráfico fractal. Los conceptos más básicos sobre tráfico fractal (autosimilitud, dependencia de rango largo, distribución con cola pesada, FBM, etc.) ya se presentaron brevemente en un artículo anterior [7]. En este artículo continuamos dicha esposición con la esperanza de ofrecer al lector mejores herramientas para iniciar el estudio del tema y, porqué no, para conducir su propia investigación al respecto. Por supuesto, si queremos hacer un estudio serio de la aplicación de la transformada wavelet en el modelamiento de tráfico fractal, debemos ubicarnos al nivel de abstracción matemática que se necesita y por eso la presentación de los conceptos no puede dejar de ser formal. En consecuencia, supondremos que el lector posee un conocimiento general sobre teoría de sistemas y señales (en particular, espacios vectoriales), teoría de probabilidades y fundamentos básicos de procesos estocásticos, al nivel con que se estudian en un programa de ingeniería electrónica, de telecomunicaciones o de sistemas. Igualmente se supone que el lector conoce los conceptos elementales de autosimilitud, aunque sea al nivel básico con que se expusieron en [7].
En la sección 2 se hará una introducción a la transformada wavelet de una manera muy tutorial, incluyendo análisis multiresolución, la transformada wavelet discreta (DWT) y el algoritmo rápido para el cálculo de la DWT mediante bancos de filtros. En la tercera sección se estudia la DWT de procesos autosimilares, enfatizando el hecho de que la invarianza a la escala de las bases wavelet hace de la DWT una técnica ideal para estudiar fenómenos invariantes a la escala y, en particular, que los coeficientes wavelet forman un conjunto de procesos estocásticos independientes e idénticamente distribuidos. Estas propiedades se usan en la sección 4 para detectar, identificar y estimar los fenómenos de escala que se presenten en trazas de tráfico real, mediante el sencillo y eficiente método del diagrama LogEscala, haciendo notar cómo sin ningún esfuerzo adicional podemos eliminar tendencias determinísticas. La sección cinco introduce un método de síntesis de movimiento browniano fraccional mediante el cálculo de la IDWT y, por último, se presentan algunas conclusiones.
II. INTRODUCCIÓN AL ANÁLISIS DE SEÑALES MEDIANTE WAVELETS
En esta sección hacemos una introducción tutorial a la transformada wavelet y el análisis multiresolución.
2.1 De Fourier a la Transformada Wavelet Continua
Todos estamos bien familiarizados con la transformada de Fourier (TF), definida para una señal de energía finita x(t) mediante
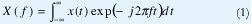
X(f) es una representación, en el dominio de la frecuencia, de la señal x(t), la cual está definida en el dominio del tiempo. La transformación (1) hace evidentes algunas características de la señal que no se pueden observar fácilmente en el dominio original, es una operación lineal definida por el producto interno de la señal con el conjunto de las ondas senoidales, es invertible y es unívoca. Sin embargo, tal como está definida, la TF presenta dos dificultades importantes: Primero, la señal debe conocerse en todo instante, inclusive en el futuro; segundo, la transformada no ubica en el tiempo los distintos componentes espectrales. Aunque la primera dificultad se podría controlar suponiendo que la señal x(t) es idénticamente cero por fuera del intervalo que nos interesa, la segunda dificultad sólo se puede resolver suponiendo que la señal es estacionaria, esto es, que cada componente frecuencial permanece inmodificable durante todo el intervalo de tiempo de interés. Por supuesto, son muy escasas las ocasiones en que se quieren estudiar señales estacionarias. Por estas razones se han buscado transformaciones capaces de indicarnos la composición espectral de una señal x(t) alrededor de un instante de tiempo t0. El primer aporte importante en este sentido fue la Transformada de Fourier en Tiempo Corto (TFTC) definida mediante (2), la cual se construye calculando la transformada de Fourier de segmentos consecutivos de la señal, obtenidos mediante el desplazamiento de una "ventana" de tiempo g(t) cuya longitud es lo suficientemente pequeña como para considerar que cada segmento es estacionario.
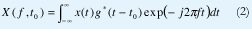
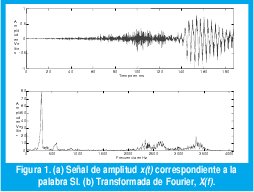
Las señales de voz son un buen ejemplo de falta de estacionariedad, como se muestra en la figura 1 con la palabra "SI". Aproximadamente los primeros 130 ms corresponden al fonema /S/ y los últimos 40 ms son del fonema /I/. Entre los 130 y los 145 ms se presenta la transición entre ambos fonemas. La falta de estacionariedad es evidente: mientras el fonema /S/ corresponde a una señal aleatoria de alta frecuencia y baja amplitud, el fonema /I/ es casi senoidal (tiene un único componente frecuencial bien definido de gran amplitud). Sin embargo, al aplicar la transformada (1), aunque podemos determinar con claridad la frecuencia de la /I/ a 300 Hz y la composición frecuencial de la /S/ entre 2200 y 3700 Hz, no podríamos determinar cuándo se presentaron esas frecuencias sin mirar simultáneamente la señal en el tiempo.
Aplicando la TFTC con ventanas de 20 ms, obtenemos una representación en el plano tiempo-frecuencia que ofrece la información que queremos, como muestra la figura 2. Obsérvese cuán fácil es ubicar ahora cada fonema tanto en el tiempo como en la frecuencia.
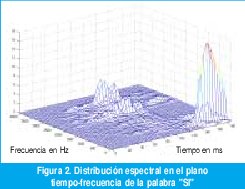
Existen dos interpretaciones para la TFTC (figura 3): Fijando un t0, la TFTC es la TF de x(t)g(t-t0), un segmento específico de la señal x(t) seleccionado mediante la ventana g(t-t0). Escogiendo diferentes valores de t0, podemos construir distintas "cintas" en el plano tiempo-frecuencia como muestra la figura 3(a), donde el ancho de cada cinta, t, depende de la forma y el ancho de la ventana. Por otro lado, como g(t) se escoje de manera que su contenido espectral sea tan parecido a un impulso en f=0 como sea posible (para evitar distorsiones espectrales en X(f,t)), se trata de un filtro pasabajos cuyo ancho de banda f está determinado por la forma y la longitud de la ventana. Así pues, para una frecuencia fija f0, la TFTC es la convolución entre x(t) exp(-j2pf0t) y g(t), lo cual se puede interpretar como un filtro pasabanda centrado en f0. Escogiendo diferentes valores de f0 podemos construir distintas "cintas" en el plano tiempo frecuencia como muestra la figura 3(b).
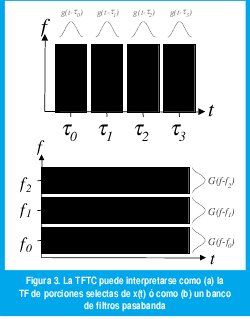
Así pues, mediante la TFTC podemos ubicar los fenómenos que se suceden en la señal tanto en la frecuencia como en el tiempo. ¿Qué tan exactamente los podemos ubicar? La señal original x(t) tiene una resolución infinita en el tiempo y cero en la frecuencia en cuanto que podemos ubicar cualquier fenómeno en el tiempo con infinita precisión pero sin saber sobre su composición espectral. Correspondientemente, la TF X(f) tiene una resolución infinita en la frecuencia y cero en el tiempo. Desafortunadamente, la resolución de la TFTC X(f,t) no se puede seleccionar arbitrariamente debido al principio de incertidumbre de Heissenberg, según el cual el producto Δf Δt siempre será mayor a 1/4 π, donde Δf es la mínima distancia (en Hz) a la que pueden estar dos componentes frecuenciales antes de que se vuelvan indistinguibles y t es la mínima distancia (en segundos) a la que pueden estar dos impulsos antes de que se vuelvan indistinguibles. Así pues, mediante la TFTC hemos "cuadriculado" el plano tiempo frecuencia pues, una vez seleccionada la ventana, la resolución en tiempo y la resolución en frecuencia permanecen constantes para cualquier posición de la ventana en el tiempo y para cualquier frecuencia central del filtro pasabanda.
Dicho de otra manera, la TFTC hace un análisis con "ancho de banda constante", como muestra la figura 4(a). La respuesta al impulso de cada uno de los filtros tienen una duración constante, pues se trata de simples traslados en frecuencia del espectro de la ventana g(t). Esta no es una característica deseable pues, en señales no estacionarias, suelen suceder fenómenos transientes de corta duración a altas frecuencias y de larga duración a bajas frecuencias. Tómese, por ejemplo, una señal de audio. Un semitono alrededor del LA de 110 Hz ocupa sólo 6 Hz, mientras que alrededor del LA de 880 Hz cada semitono es de cerca de 53 Hz. Siendo así, lo ideal sería tener una alta resolución en frecuencia (f pequeño) para frecuencias bajas, así perdamos resolución en el tiempo (Δt grande), y una alta resolución en tiempo (Δt pequeño) para frecuencias altas, así perdamos resolución en la frecuencia (Δf grande). Esto se conseguiría dividiendo el plano tiempo-frecuencia como muestra la figura 4(b).
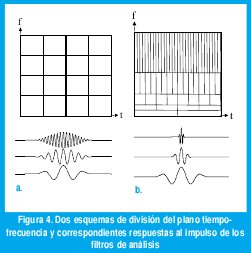
Aquí los anchos de banda de cada filtro son proporcionales a la frecuencia central, con lo que se consigue un análisis con "factor de calidad Q constante". En este caso, la duración de la respuesta al impulso de los filtros se hace más pequeña para filtros de frecuencia más alta, con lo que se consigue un "análisis multiresolución".
Nótese en la figura 4(b) cómo la respuesta ideal de los filtros de análisis son versiones dilatadas de la respuesta de un filtro prototipo. Esta propiedad motiva la definición de lo que son las wavelets: Unas señales bien ubicadas tanto en el tiempo como en la frecuencia (por eso el nombre de "onditas") que se construyen mediante la dilatación o contracción de una "wavelet madre". La dilatación o contracción se obtiene de acuerdo con un parámetro de escala, α como muestra la siguiente ecuación.
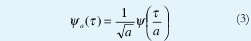
La escala es la relación que existe entre las frecuencias centrales de la wavelet madre y de las wavelets derivadas, de manera que, en este contexto, el dominio de la frecuencia se puede cambiar por el dominio de la escala. De esta manera, se puede definir la transformada wavelet continua de una manera semejante a (2), donde la respuesta al impulso de los filtros corresponde a las wavelets escalizadas, como muestra la siguiente ecuación.
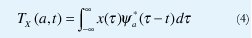
La transformada wavelet continua es, pues, el conjunto de coeficientes
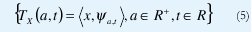
que comparan, mediante productos internos, la señal x a ser analizada con un conjunto de funciones de análisis
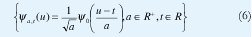
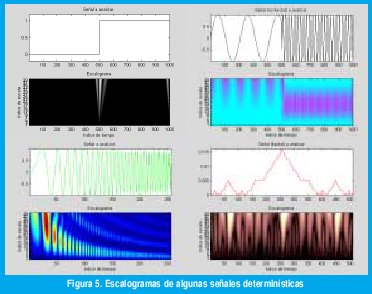
La figura 5 muestra algunos "escalogramas", representaciones de |TX(a,t)|2, para diferentes funciones en el tiempo. Nótese cómo a bajas escalas (altas frecuencias) tenemos una excelente resolución en el tiempo y podemos ubicar los instantes en que se presentan los fenómenos transientes en las señales analizadas. Igualmente a altas escalas (bajas frecuencias) se obtiene con mejor detalle la composición frecuencial de las señales. La primera señal es un escalón para el cual el escalograma permite determinar no solo el instante en el que se dio el paso sino la dispersión frecuencial que dicha discontinuidad produce. La segunda señal corresponde a otro escalón pero no en la amplitud de una señal dc sino en la frecuencia de una onda senoidal, para la cual el escalograma permite detectar la composición de cada segmento y el instante de la transición. La tercera señal es una onda "chirp" y la cuarta, de sumo interés para nosotros, es una señal fractal derivada del copo de nieve de Von Koch. Obsérvese cómo, a escalas pequeñas se pueden apreciar los detalles de las últimas iteraciones mientras a escalas grandes se observa la forma general de la figura fractal. Aquí podemos apreciar con claridad dónde reside la utilidad de la transformada wavelet para el análisis de las señales fractales: la familia de wavelets de análisis posee, en sí misma, la característica de invarianza a la escala propia de los fenómenos fractales y los mismos coeficientes de la transformada wavelet reflejan la invarianza de la señal analizada.
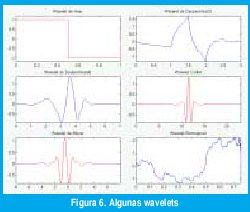
La wavelet madre y0(t) se escoje de manera tal que tanto su duración en el tiempo como su dispersión en la frecuencia estén relativamente limitados, esto es, se trata de pequeñas ondas con soporte limitado en el tiempo en las que casi toda su energía se encuentra dentro de una banda limitada de frecuencias. Por supuesto, no se puede tener un soporte finito en tiempo y una banda limitada en frecuencia, pero sí se pueden tener onditas bien localizadas en tiempo y en frecuencia, de manera que con los desplazamientos ψ0(t-t0) se puedan seleccionar los instantes de tiempo en los que queremos analizar una señal y con las dilataciones ψ0(t/a)√a se pueda definir la escala de tiempo (o, equivalentemente, el rango de frecuencias) sobre la cual vamos a observar la señal. Además de estar bien localizadas en el tiempo y en la frecuencia, las wavelet madres deben satisfacer la condición de admisibilidad /ψ0(t)dt= 0, la cual muestra que se trata de señales pasabanda oscilantes u "onditas". La figura 6 muestra algunas waveletes que cumplen con estas propiedades.
La condición de admisibilidad permite invertir la transformada wavelet continua:
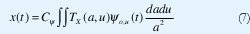
donde Cψ es una constante que depende de ψ0. Esta fórmula de reconstrucción demuestra que la transformada wavelet continua posee toda la información originalmente contenida en la señal x(t). Sin embargo, representa en un espacio bidimensional tiempo-escala la información contenida en un espacio unidimensional, de manera que se trata de una transformación redundante en la que los coeficientes vecinos en el plano tiempo-escala tienen mucha información en común. Existe una teoría matemática conocida como el Análisis MultiResolución (MRA) que demuestra la posibilidad de hacer un muestreo crítico del plano tiempo-escala para escoger entre los {TX(a,t)=<x, ψa,t>, a∈R+, t∈R}, un conjunto discreto de coeficientes que retengan la información total en x(t). Este procedimiento de muestreo define la transformada wavelet discreta, DWT.
2.2 Transformada Wavelet Discreta
Un análisis multiresolución (MRA) es un conjunto de subespacios vectoriales anidados {Vj}j∈Z que satisface las siguientes propiedades:

Para comprender estas propiedades, obsérvese que los Vj son subespacios de aproximación del espacio de señales de energía finita (o funciones de cuadrado integrable L2(R)). El conjunto de funciones de escala desplazadas {Φ0(t-k), k∈Z} es linealmente independiente y genera el espacio V0, pero las funciones desplazadas no son necesariamente ortogonales (base Riesz). Correspondientemente, y teniendo en cuenta la propiedad 3, el conjunto de funciones
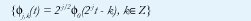
constituye una base Riesz para el subespacio Vj. El análisis multiresolución consiste, precisamente, en projectar la señal de interés x(t) sobre cada uno de lo subespacios de aproximación Vj:
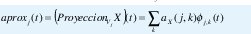
Pero como Vj está contenido en Vj-1, approxj(t) es una aproximación mas burda de x(t) que approxj-1(t). Más aún, debido a la primera parte de la propiedad 1, en el límite cuando j→∞ la aproximación no contiene ninguna información sobre la señal original. La idea cen- tral del análisis multiresolución es, precisamente, estudiar la señal a partir de aproximaciones más y más burdas, donde en cada aproximación se cancelan algunas de las altas frecuencias o de los "detalles" de la señal original. Estos detalles (la información que se elimina de una aproximación a la siguiente), equivalen a
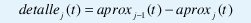
y se pueden obtener directamente mediante la proyección de x(t) sobre el conjunto de subespacios
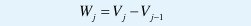
llamados los subespacios wavelet. Más aún, la teoría del análisis multiresolución muestra la existencia de una función ψ0(t), llamada la wavelet madre y obtenida a partir de Φ0(t), tal que el siguiente conjunto de funciones forman una base Riesz para Wj:
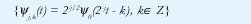
esto es,
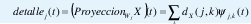
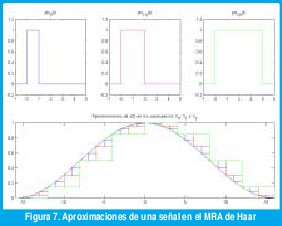
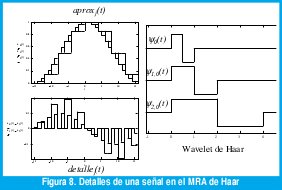
Por ejemplo, una función de escala Φ0(t) muy simple es aquella que vale 1 si 0 ≤ t ≤ 1 y vale 0 para cualquier otro instante de tiempo. La figura 7 muestra las aproximaciones en los espacios V0, V1 y V2 generados por esta función de escala (dilatada y desplazada). La wavelet madre correspondiente ψ0(t) se llama "wavelet de Haar" (Figura 6(a)). Los detalles correspondientes a las aproximaciones de la figura 7 se pueden apreciar en la figura 8.
Teóricamente, j puede ir de -∞ a + ∞. Pero en la práctica nos limitamos α∈j {0,1,2,,J}y reescribimos las aproximaciones como un conjunto de detalles a diferentes resoluciones junto con una aproximación final de muy baja resolución perteneciente al subespacio VJ:
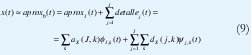
Si x(t) pertenece a V0, tendremos x(t)=aprox0(t) en la anterior ecuación. En cualquier otro caso, la selección de V0 implica una pérdida inevitable de información. Sin embargo, después de esta proyección inicial, no hay ninguna pérdida adicional de información puesto que, al variar J, simplemente estamos decidiendo si ponemos más información en los detalles (J grande) o más información en la aproximación final (J pequeño).
Ahora ya podemos definir la transformada discreta wavelet. Dada una función de escala Φ0(t) y una wavelet madre ψ0(t) correspondiente, la DWT es el conjunto de coeficientes
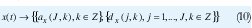
definidos mediante el producto interno de la señal x(t) con los conjuntos de funciones ΦJ,k(t) y ψj,k(t). Un resultado interesante es que el conjunto de coeficientes dX(j,k) constituye un muestreo de los coeficientes de la transformada wavelet continua donde las muestras se toman en la llamada grilla diádica,

El parámetro j, que es el logaritmo en base dos de la escala α=2j, se denomina "ocatava" y la escala se suele referenciar mediante su correspondiente octava.
2.3 Cálculo rápido de la DWT
Los coeficientes wavelet dX(j,k) han sido definidos mediante el producto interno continuo entre la señal a analizar y las versiones dilatadas y desplazadas de la wavelet madre. Sin embargo, gracias a la estructura anidada de los subespacios de aproximación, los coeficientes αX(j,k) y dX(j,k) pueden calcularse mediante una convolución en tiempo discreto que involucra a la secuencia αX(j-1,k) y dos filtros digitales h(n) y g(n), como muestra la figura 9 para el caso J=4.
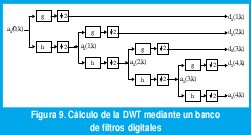
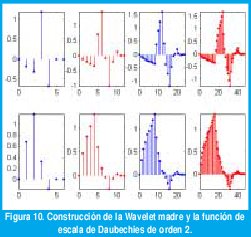
Los coeficientes de los filtros h y g se obtienen a partir de la wavelet madre ψ0 y la función de escala Φ0. La respuesta en octavas se obtiene mediante los submuestreadores (↓2), los cuales eliminan una de cada dos muestras de la entrada. Mediante el uso de técnicas de procesamiento digital de señales multitasa tales como el uso de redes polifásicas, el costo computacional del cálculo de la DWT mediante bancos de filtros submuestreados puede hacerse menor que el costo computacional del cálculo de la transformada rápida de Fourier, FFT. Para la reconstrucción de la señal se usan filtros de espejo en cuadratura con supermuestreadores (↑2), los cuales insertan un cero entre cada par de muestras de la entrada. La figura 10 muestra cómo el banco de filtros de reconstrucción puede usarse para generar la misma función de escala y la wavelet madre.
III. TRANSFORMADA DWT DE PROCESOS AUTOSIMILARES
Primero que todo debemos recordar que la teoría de wavelets se desarrolló inicialmente para el análisis de señales determinísticas de energía finita. Cuando se aplica sobre procesos estocásticos, tanto las secuencias de aproximación como las secuencias de detalle constituyen nuevos procesos estocásticos con característica estadísticas particulares. En el caso que nos interesa, si el proceso de entrada es estacionario de segundo orden, la transformada wavelet forma un campo aleatorio de segundo orden siempre que la función de escalización satisfaga ciertas condiciones respecto a la estructura de correlación del proceso analizado. En nuestro caso, es suficiente con asumir que tanto las funciones de escalización como las wavelets decaen exponencialmente rápido en el dominio del tiempo, con lo cual aseguramos que las estadísticas de segundo orden de la transformada wavelet existan para todos los procesos estocásticos que se utilizan como modelos de tráfico.
Recordemos también que un proceso X={X(t),t∈R} es autosimilar con parámetro H>0 si los procesos {X(at), tR} y {aHX(t), t∈R} tienen las mismas distribuciones de dimensión finita. En este caso decimos que X es H-ss. Este proceso no puede ser estacionario, pero puede tener incrementos estacionarios. Decimos que X es autosimilar con parámetro H>0 y con incrementos estacionarios (oH-sssi) si es H-ss y las distribuciones de dimensión finita de sus incrementos {X(t+h)- X(t), t∈R} no dependen de t. Un proceso H-sssi tiene media cero y varianza E[X(t)2]=Φ2|t|2H. El FBM, por ejemplo, es el único proceso gaussiano H-sssi. Con H=½ se convierte en un simple movimiento browniano. La dependencia de rango largo se asocia, en cambio, con procesos estacionarios. Un proceso estacionario de varianza finita X posee dependencia de rango largo (LRD) si su densidad espectral ⌈X(f) satisface la relación

donde 0 < < 1 y c #0. La ecuación (11) implica que la autocorrelación rX(k)=E[X(j)X(j+k)] satisface la relación

Las ecuaciones (11) y (12) son equivalentes e implican que la autocorrelación rX(k) decae tan lentamente que

Existe una íntima relación entre los procesos autosimilares y los procesos con dependencia de rango largo: Los incrementos de cualquier proceso H-sssi tienen dependencia de rango largo si ½<H<1, donde H y α están relacionadas mediante
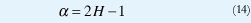
Pues bien, ahora describiremos algunas propiedades de la transformada wavelet de procesos Hss, Hsssi y LRD. Aunque, en general, se trata de propiedades no triviales cuya deducción está muy lejos de los alcances de este artículo, de alguna manera se puede decir que provienen de las siguientes dos características fundamentales de la transformada wavelet:
1. Las bases wavelet se obtienen de la dilatación de la wavelet madre. Esta dilatación es, esencialmente, un operador de cambio de escala, de manera que la familia de funciones de análisis de la transformada wavelet tienen una propiedad intrínseca de invarianza a la escala.
2. La wavelet madre tiene un número N≥1 de momentos desvanecientes, esto es,

donde N se puede escoger libremente seleccionado una ψ0 adecuada.
Las propiedades que nos interesan son resultados (no triviales) de estas dos características y las vamos a presentar en un contexto generalizado para procesos H-ss, H-sssi o LRD. De este manera se verá inmediatamente la gran versatilidad de la transformada wavelet para analizar todos los posibles fenómenos de escala:
Sea X un proceso estocástico que presenta algún fenómeno de escala. Entonces los coeficientes wavelet de X exhiben las siguientes dos propiedades:
1. El conjunto {dX(j,k), k∈Z} es un proceso estacionario para cada octava j si el número de momentos desvanecientes de la wavelet madre ψ0 es N≥(a-1)/2. La varianza de dX(j,k) reproduce con exactitud el comportamiento de escala subyacente, dentro de un rango de octavas j1≤ j j2:
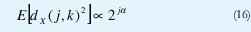
donde j1, j2 α y dependen del tipo de comportamiento de escala del proceso original X, así:
(a) Si X es H-sssi, entonces α=2H+1, j1=∞ y j2=∞+.
(b) Si X es LRD, entonces α=2H-1, j2=+∞ y jt debe identificarse a partir de los datos obtenidos.
(c) En el caso de un proceso estacionario de segundo orden general que obedece a una ley de potencia como en (11) en un rango de frecuencias ft ≤f≤ f2 (en cuyo caso se denomina proceso 1/f), αcorresponde a la ley de potencia de la ecuación 11 y el rango de escalas (j1, j2) debe obtenerse a partir de (f1, f2).
2. A pesar de reproducir el comportamiento de escala como en (16), los coeficientes {dX(j,k), k∈Z} no exhiben ningún tipo dependencia estadística de rango largo si el número de momentos desvanecientes de la wavelet madre ψ0 es N≥ a/2. Más aún, entre mayor sea N, menor es la correlación en cuanto que
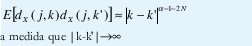
Esta condición es tan significativa que se ha reportado la validez de la siguiente idealización:
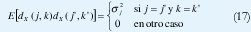
Esto es, cada coeficiente wavelet es una variable aleatoria no-correlacionada con ninguna otra variable ni dentro de su misma escala ni en otras escalas.
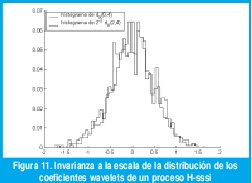
Estas dos propiedades son las que hacen de la DWT una herramienta tan poderosa en la detección,estimación, síntesis y modelamiento de tráfico autosimilar. Las figuras 11 y 12 ilustran estas dos propiedades para el caso de un proceso H-sssi (FBM). En este caso, el comportamiento de escala es la invarianza de las distribuciones de dimensión finita, de manera que los coeficientes wavelet deben satisfacer la siguiente relación:
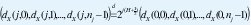
donde nj es el número de coeficientes en la octava j, como efectivamente se puede verificar en la figura 11. Para este caso particular, y como consecuencia directa e inmediata de la invarianza a la escala de la distribución de los coeficientes wavelet, la ecuación (16) toma la siguiente forma:
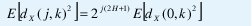
Para verificar la idealización (17), la figura 12 muestra la función de autocorrelación de los coeficientes de escala 0 y las funciones de correlación

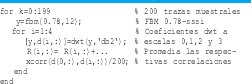
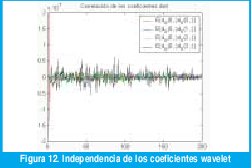
con otras escalas. Se aprecia fácilmente cómo la única correlación apreciable corresponde a la de la escala cero con desplazamiento de tiempo cero (la varianza de dX(0, :). Todos los demás coeficientes de correlación están en el orden de 10-8.
Existe una importante extensión del primera propiedad que no desarrollaremos en este artículo por falta de espacio. Se trata de los procesos de escala cuyo comportamiento no se puede describir mediante un único exponente sino, por ejemplo, mediante la generalización H=H(t). Aquí también la transformada wavelet resulta una poderosa herramienta de análisis. Por ejemplo, con movimiento browniano multifraccional, la evolución temporal de H puede determinarse mediante la transformada wavelet continua usando la propiedad E[TX(a,t)2] a2H(t)+1 para bajas escalas α → 0, que es una versión de (16) con dependencia del tiempo. Otra clase de procesos con múltiples exponentes son los procesos multifractales, en los que la misma dependencia temporal de H es también fractal, por lo que se prefiere seguir las variaciones estadísticas de H. Aquí el uso de la transformada wavelet es aún más fundamental en cuanto que los incrementos involucrados en el estudio de la variabilidad de H para una traza muestral son, en sí mismos, coeficientes de un tipo particular de transformada wavelet. Un último ejemplo es el de las cascadas multiplicativas introducidas por Mandelbrot hace 30 años pero recientemente utilizadas en modelamiento de tráfico autosimilar; aquí la transformada wavelet (introducida una década después de las cascadas multiplicativas en un contexto muy diferente) reproduce el mecanismo de generación de cascadas multiplicativas propuesto por Mandelbrot.
IV. DETECCIÓN, IDENTIFICACIÓN Y ESTIMACIÓN DE INVARIANZAS A LA ESCALA MEDIANTE LA TRANSFORMADA WAVELET
En esta sección mostraremos cómo pueden usarse las dos propiedades estadística (16) y (17) para detectar, identificar y estimar los comportamientos de escala de un proceso estocástico. La principal herramienta en estas actividades es el diagrama LogEscala.
4.1 El Diagrama LogEscala
La propiedad (17) constituye la gran ventaja estadística del análisis en el dominio wavelet pues, gracias a ella, podemos medir promedios temporales y usarlos como estimaciones de los correspondientes promedios estadísticos. En efecto, la falta de correlación entre los coeficientes wavelet asegura que los estimadores temporales tengan una varianza pequeña. Así, por ejemplo, podemos estimar la varianza del proceso dX(j, ) mediante el siguiente estimador,
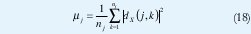
donde nj es el número de coeficientes en la octava j (recordemos que el valor esperado de dX(j,k) es cero debido a la condición de admisibilidad,∫ψ0(t)dt=0). La varianza de µj decrece con 1/nj y, de hecho, es un estimador no polarizado y asintóticamente eficiente (de mínima varianza). En consecuencia, la variable µj puede interpretarse como una manera óptima de "comprimir" en un sólo número el comportamiento de segundo orden de X en la octava j. Más aún, nuevamente por la propiedad (17), los distintos µj son prácticamente independientes entre sí, de manera que ganamos un desacoplamiento entre los análisis del comportamiento de X a diferentes octavas.
La propiedad (16), por otro lado, muestra cómo la varianza del proceso dX(j, ), de la cual µj es un estimador, decae hiperbólicamente con la octava j. Esto sugiere la idea de que el exponente de escala, α, puede extraerse de la pendiente de la gráfica de yj≡log2(µj) como función de la octava j. Esta gráfica, acompañada de los correspondientes intervalos de confianza, se conoce como Diagrama LogEscala.
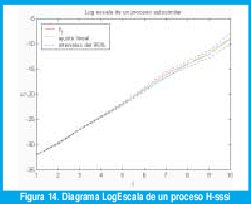
Por supuesto, el hecho de que, en general, E[log(·)] # log(E[·]) hace que la estimación deba hacerse con un poco más de cuidado que la simple medición de la pendiente en el diagrama LogEscala. Las figuras 13 y 14 muestran dos ejemplos de diagramas LogEscala, uno correspondiente a un proceso LRD y otro a un proceso H-sssi. Lo primero que debe observarse es que, por la naturaleza misma del operador de dilatación en la DWT, el número nj de coeficientes de detalle en la octava j se reduce a la mitad con cada incremento en j y, consecuentemente, los intervalos de confianza se hacen cada vez más grande a medida que usamos mayores escalas. Segundo, obsérvese que la primera información que podemos obtener del diagrama LogEscala es el tipo de dependencia de la escala que posee el proceso analizado. Esto es, el comportamiento de escala no se supone, sino que se detecta mediante la observación de regiones de alineación en la gráfica, esto es, rangos de escalas en las que los yj caen sobre una línea recta (dentro de las posibles variaciones estadísticas, por supuesto). La estimación de los parámetros correspondientes se puede hacer mediante un análisis de regresión lineal sobre las regiones de alineación. Finalmente, la identificación del tipo de proceso se obtiene interpretando el valor estimado dentro del contexto del rango de alineación observado. Enseguida describimos mejor cada proceso.
4.1.1 Detección
No es posible saber a priori sobre cuáles escalas exista alguna propiedad invariante a la escala, si es que existe alguna. Por detección nos referimos a la identificación de regiones de alineación (j1,j2), en donde existan propiedades invariantes a la escala. Este no es un problema fácil, pues la invarianza a la escala suele ocurrir en forma asintótica. De hecho, la región de alineación es un concepto más ligado a los intervalos de confianza para yj que la alineación propiamente dicha de los yj. De hecho, observar alineación en los yj durante dos o tres escalas no es necesariamente significativo, pues a tres o cuatro puntos aleatorios no les queda difícil alinearse por casualidad. Pero si la línea de regresión cae siempre dentro de los intervalos de confianza, ya podemos asegurar (con la confianza especificada) que la alineación no es casual. Esta heurística de aceptar el alineación sólo si la curva de regresión cae dentro de los intervalos de confianza ayuda a evitar dos posibles errores: (1) pasar por alto una región de alineación debido a la alta variabilidad de los yj cuando, en realidad, dentro de los intervalos de confianza existe un buen alineación (este error se suele presentar cuando la pendiente es muy pequeña, de manera que sólo se grafica un pequeño rango de valores en el eje vertical, incrementando en tamaño aparente de las variaciones), y (2) la inclusión errada de escalas adicionales a la izquierda de j1, debido a que, para el ojo, parecen continuar la tendencia de la línea recta cuando en realidad los intervalos de confianza son muy pequeños y no dejan apreciar que la curva de regresión está por fuera de ellos.

4.1.2 Identificación
Una vez seleccionado un rango de escalas (j1, j2), es importante identificar el tipo de fenómeno de invarianza a la escala que se presenta en la secuencia analizada (si en un proceso H-ss, un proceso LRD o un proceso 1/f generalizado). Para esto se debe interpretar el valor estimado de α dentro del contexto del rango de escalas de la región de alineación (ayudándose, si es posible, con otras propiedades conocidas de la serie de tiempo analizada). Por ejemplo, si está en el rango (0,1) y la región de alineación va de algún j1 hasta la máxima octava utilizada en la descomposición wavelet, se puede decir que la secuencia corresponde a un proceso LRD con exponente de escala . En la figura 13, por ejemplo, se observa alineación desde la octava 4 en adelante y el exponente de escala se estima en 0.56, por lo que podría tratarse de un proceso LRD (tal vez el proceso de incrementos de un proceso 0.78-sssi). Si tenemos razones para pensar que el proceso analizado es estacionario (por ejemplo si se trata de una secuencia de tiempos entre llegada de paquetes), no cabrían dudas de que se trata de un proceso LRD. Otro ejemplo importante es cuando se obtiene un valor de &alph; >1 sobre un rango de octavas que incluye las mayores escalas, como en la figura 14. Dicho valor excluye cualquier proceso LRD y puede indicar que se requiere de un modelo autosimilar o asintóticamente autosimilar (lo cual también implica que los datos son no estacionarios). En este caso el exponente se puede reexpresar como el parámetro de Hurst, H(α1)/2. En la figura 14 se observa alineación en todo el rango de escalas con un valor estimado de α de 2.57, pudiéndose tratar de un proceso 0.79-sssi. Por supuesto, la conclusión de no-estacionariedad debe cotejarse con otra información adicional que tengamos sobre la secuencia. Por ejemplo, si se trata de un proceso acumulativo como el número total de bytes que han llegado a un enrutador hasta el instante t, la no estacionariedad no sólo es plausible sino que, como conclusión del análisis, es una información adicional importante. Pero si estamos seguros, por alguna razón adicional, que el proceso es estacionario, podemos resolver la paradoja de dos posibles maneras: Utilizar un modelo estacionario que presenta una ley de potencia 1/f sobre un amplio rango de escalas que van más allá de la máxima octava en que pudimos descomponer el proceso, o aceptar la evidencia empírica de no estacionariedad y revisar los postulados que nos hacían suponer que el proceso debe ser estacionario. Existen otras posibilidades: si j1=1 y hay una octava de corte superior j2, será mejor interpretar la naturaleza fractal de la traza muestral en cuestión. O, si existe más de una región de alineación, debemos concluir un fenómeno de "biescala" como, por ejemplo, una naturaleza fractal de la traza muestral a pequeñas escalas, con cierto exponente, y una dependencia de largo rango que produce una región de alineación a altas octavas con otro exponente de escala.
4.1.3 Estimación
Debido a la propiedad (16), la medición de se reduciría a determinar la pendiente sobre la región de alineación en el diagrama LogEscala, lo cual se podría conseguir, en un contexto de estimación estadística típico, mediante regresión lineal, definiendo la hipótesis E[yj]=aj+b, donde b es una constante real. Sin embargo esta condición no se satisface en general, debido a que, E[log(·)]# log(E[·]), como se mencionó antes. Esta dificultad se puede resolver introduciendo un factor correctivo g(j), de manera que redefiniendo yj=log(µj)-g(j), se consiga E[yj]=αj+b. Por ejemplo, si el proceso X se puede suponer gaussiano, el factor de corrección sería
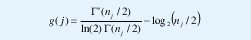
donde ⌈(z) es la función Gamma. El estimador no polarizado de mínima varianza se obtiene, entonces, mediante la regresión ponderada
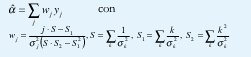
donde todos los índices de las sumas van de j1 a j2.
4.2 Discriminación de tendencias determinísticas
En muchas situaciones de interés práctico, la suposición de que los datos que se tienen se pueden describir completamente mediante un modelo invariante a la escala es demasiado restrictiva para ser realista. Un caso particular es cuando el proceso observado Y(t) es el resultado de un proceso de escala X(t) contaminado con una tendencia determinística T(t), la cual se puede modelar como un polinomio de orden p. En este caso se pueden perder características importantes tales como la estacionariedad de los incrementos, con lo que se perjudicaría la estimación del exponente de escala. Peor aún, cuando estas tendencias determinísticas con ley de potencia se añaden a procesos markovianos estacionarios, pueden parecerse a estructuras de correlación de tipo LRD, conduciendo a conclusiones completamente equivocadas. En consecuencia, sería muy deseable poder eliminar estas posibles tendencias o, al menos, poder evaluar y controlar sus efectos. Nuevamente, las wavelets ofrecen un método fácil y versátil para resolver (parcialmente) este problema.
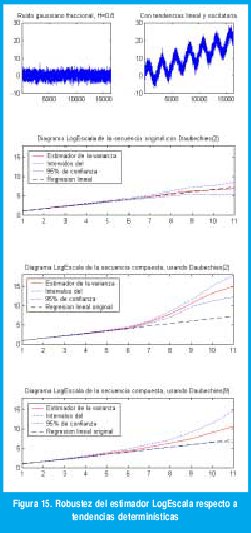
La versatilidad de las wavelets, en este caso, viene de la condición de admisibilidad ∫ψ0(t)dt=0, la cual hace que la wavelet sea ortogonal a valores medios distintos de cero. Usando la ecuación (15), esta característica se puede generalizar diciendo que, si se usa una wavelet madre con N momentos desvanecientes, el análisis es ortogonal a polinomios de orden menor que N. En otras palabras, la eliminación de tendencias polinómicas de orden p se puede garantizar usando una wavelet madre con N p+1. No se necesita nada más! La eliminación de las tendencias polinómicas es exacta, pero vale la pena hacer notar que el procedimiento sigue siendo valido con tendencias no polinómicas (por ejemplo, tendencias oscilatorias). La figura 15 muestra ruido gaussiano fraccional con H=0.8 (esquina superior izquierda) contaminado con una tendencia lineal y otra sinusoidal (esquina superior derecha). Usando la wavelet de Daubechies con dos momentos desvanecientes (Haar), la tendencia lineal se elimina pero la tendencia oscilatoria afecta la estimación de la potencia de escala, pues la regresión correcta se sale de los intervalos de confianza después de la octava 5. La wavelet de daubechies con nueve momentos desvanecientes casi elimina ambas tendencias y permite una estimación correcta, =0.59 (la línea de regresión permanece dentro de los intervalos de confianza hasta la escala 10).
V. SÍNTESIS DE MOVIMIENTO BROWNIANO FRACCIONAL MEDIANTE LA TRANSFORMADA WAVELET
Existen diferentes métodos para generar trazas muestrales de FBM que no se basan en wavelets. Entre ellos, el método de Cholesky genera autosimilitud con exactitud, pero su inmenso costo computacional lo hace inadecuado para generar muchas muestras de tráfico, como se necesita para experimentos de simulación, por ejemplo. En consecuencia, se han desarrollado métodos de síntesis de procesos aproximadamente autosimilares con cargas computacionales más razonables (el método de síntesis espectral, la superposición de procesos ON/OFF, el desplazamiento del punto medio, etc.). Aunque estos métodos se implementan de una manera práctica, no se pueden controlar los errores debidos a la aproximación y nisiquiera es posible saber cuál propiedad del FBM se ha podido perder con la aproximación.
Existen diferentes métodos para generar trazas de diferentes procesos estacionarios del tipo 1/f basados en wavelets. En [2] se describe un método que se basa en una expansión wavelet exacta de FBM, con el que se generan trazas aproximadas pero con errores controlados, que reproduce exactamente las características más claves como estacionariedad de los incrementos, autosimilitud y dependencia de rango largo y que, además, lo hace de una manera computacionalmente muy eficiente. El método logra su eficiencia mediante el uso de la transformada wavelet discreta inversa (IDWT), la cual se puede calcular eficientemente mediante el banco de filtros de la figura 16.
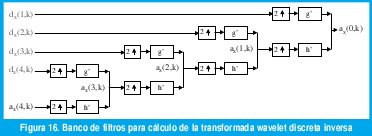
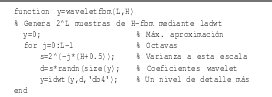
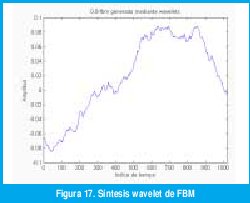
De acuerdo con las propiedades (16) y (17), las entradas dX(j,k) de los filtros de síntesis son vectores aleatorios independientes conformados por secuencias de variables aleatorias gaussianas independientes e idénticamente distribuidas con media cero y varianza σ22j(2H+1). Por supuesto, dos aspectos importantes son el diseño mismo de las wavelets que dan origen a los filtros de síntesis h' y g' y la obtención de la aproximación de máxima escala, αx(J,k). Aunque el método requiere muchas consideraciones acerca de la expansión wavelet exacta para dar precisión a la serie generada, la idea básica se muestra en la figura 17. Por supuesto, el procedimiento mostrado requiere muchos refinamientos, para los cuales el lector se debe referir a [2].
VI. CONCLUSIONES
El modelamient o de tráfico autosimilar presenta muchos retos a los que se les puede encontrar respuesta utilizando la transformada wavelet. Esta transformada consiste en la proyección de una señal sobre el espacio vectorial generado mediante funciones bases que se obtienen de la dilatación y el desplazamiento de una función pasabanda prototipo, bien localizada tanto en el tiempo como en la frecuencia, llamada la wavelet madre. Puesto que esta dilatación es, esencialmente, un operador de cambio de escala, la familia de funciones de análisis de la transformada wavelet tienen una propiedad intrínseca de invarianza a la escala. Es esta propiedad la que hace del análisis wavelet una herramienta naturalmente apropiada para el estudio de fenómenos de escala como la autosimilitud y la dependencia de largo rango.
Dentro de las muchas ventajas que tienen las técnicas basadas en wavelets para el estudio del tráfico autosimilar podemos contar las siguientes:
•Las wavelets ofrecen un marco teórico unificado igualmente aplicable a procesos autosimilares, procesos con dependencia de rango largo, trazas muestrales fractales, etc. Cada modelo aplicable se puede diferenciar observando el rango se escalas sobre el que se presenta la invarianza y el valor estimado del correspondiente exponente de escala.
•Las wavelets permiten dividir el proceso analizado, de una manera bien controlada, en diferentes subprocesos a diferentes escalas, donde cada subproceso se comporta mucho mejor que el proceso original en el sentido de la variabilidad extrema del proceso analizado que contrasta con la independencia de los subprocesos obtenidos. Por ejemplo, las herramientas estadísticas clásicas no se pueden aplicar sobre procesos LRD, pero sí sobre las secuencias de coeficientes wavelet, lo cual permite el diseño de estimadores simples y eficientes.
•El número de momentos desvanecientes se puede escoger mediante la selección de la wavelet madre, y con él podemos controlar la falta de autocorrelación en los coeficientes y eliminar el efecto de las tendencias determinísticas en los procesos de entrada.
•Los bancos de filtros de análisis y de síntesis proporcionan una gran ventaja computacional para el análisis y la síntesis de procesos autosimilares.
•El concepto matemático de la multiresolución y el concepto físico de la escala comparten una afinidad estructural que posibilita todas las bondades de la transformada wavelet para análisis de tráfico autosimilar.
Por supuesto, son muchas las áreas de investigación que quedan por desarrollar, desde la detección automática de los rangos de octavas en los que se presenta invarianza a la escala, hasta análisis de desempeño de redes directamente en el dominio de la escala.
REFERENCIAS BIBLIOGRÁFICAS
[1] P. Abry and D. Veitch. Wavelet Analysis of Long-Range-Dependent Traffic. IEEE Trans. Information Theory, 44(1):2-15, 1998.
[2] P. Abry, P. Flandrin, M. Taqqu and D. Veitch. Wavelets for the Analysis and Synthesis of Scaling Data, In "Self-Similar Network Traffic and Performance Evaluation", K. Park and W. Willinger, editors. John Wiley and Sons, New York, 2000.
[3] P. Abry, D. Veitch and P. Flandrin Long-Range Dependence: Revisiting Aggregation with Wavelets. Blackwell publishers ltd. 1999
[4] M. Alzate. Obtención de Bases Wavelets Ortonormales Mediante el Diseño de Bancos de Filtros de Reconstrucción Perfecta. IV Simposio de Procesamiento de Señales, Universidad de los Andes, 1995.
[5] M. Alzate. Modelos de Tráfico en Redes de Comunicaciones. Reporte de Investigación de la Maestría en Teleinformática de la Universidad Distrital, marzo de 1995.
[6] M. Alzate. Generation of Simulated Fractal and Multifractal Traffic. IX Congreso Nacional de Estudiantes de Ingeniería de Sistemas, Bogotá, 2000.
[7] M. Alzate. Introducción al Tráfico Autosimilar en Redes de Comunicaciones. Revista INGENIERIA, Universidad Distrital,Vol. 6 No. 2, 2001.
[8] I. Daubechies. Ten Lectures on Wavelets. SIAM'92. Philadelphia, 1992.
[9] R. Dijkerman and R. Mazumdar. Wavelet representation of stochastic processes and multiresolution stochastic models. IEEE Trans. Signal Proc. 42:1640-1652, July 1994
[10] P. Fieguth and A. Willisky. Fractal estimation using models on multiscale trees. IEEE Trans. Signal Proc. 44:1297-1300, 1996.
[11] P. Flandrin. Wavelet Analysis and Synthesis of Fractional Brownian Motion. IEEE Trans. Inf. Theory, 38:910-917, 1992.
[12] V. Frost and B. Melamed. Traffic Modeling for Telecommunications Networks. IEEE Commun. Mag. 32(3):70- 81, 1994.
[13] A. Gilbert, W. Willinger and A. Feldman. Scaling analysis of conservative cascades with application to network traffic. IEEE Trans. Information Theory, 45(3):971-991, 1999.
[14] P. Huang, A. Feldmann and W. Willinger. A Non-intrusive, Wavelet-based Approach To Diagnosing Network Performance Problems. Proceeding of ACM SIGCOMM Internet Measurement Workshop 2001, San Francisco, November 2001
[15] Internet Traffic Archive. BC_pAug89, http://www.acm.org/sigcomm/ITA/index.html.
[16] W. Leland, M. Taqqu, W. Willinger and D. Wilson. On the self- similar nature of Ethernet Traffic. IEEE/ACM Trans. Networking, 2:1-15, 1994.
[17] S. Ma and C. Ji. Modeling Heterogeneous Network Traffic in Wavelet Domain. IEEE/ACM Trans. Networking, 9(5):634-649, 2001.
[18] D. McDysan. QoS and Traffic Management in IP and ATM networks. McGrawHill, NY, 2001.
[19] H. Michiel and K. Laevens. Teletraffic Engineering in a broadband era. Proceedings of the IEEE, december 1997.
[20] M. Parulekar and A. Makowski. M/G/ Input Processes. Proc. IEEE Infocom'97, 1997.
[21] V. Paxson and S. Floyd. Wide-Area Traffic: The Failure of Poisson Modeling. IEEE/ACM Trans. Networking, 3:226-244, 1995.
[22] R. Riedi, et. al. A Multifractal Wavelet Model with Application to Network Traffic. IEEE Trans. Inf. Theory, 45(3):992-1018, 1999.
[23] M. Schwartz. Broadband Integrated Networks. Prentice Hall, UpperSaddle River, 1996.
[24] A. Tewfik and M. Kim. Correlation structure of the discrete wavelet coefficients of fractional brownian motion. IEEE Trans. Info. Theory, 38:904-909, 1992.
[25] B. Tsybakov and N. Georganas. Self-Similar Processes in Communications Networks. IEEE Trans. Inf. Theory, 44(5):1713- 1725, 1998.
[26] D. Veitch and P. Abry. A Wavelet-Based Joint Estimator of the Parameters of LRD. IEEE Trans. Inf. Theory, 45(3):878-897, 1999.
[27] W. Willinger and V. Paxson. Where Mathematics meets the Internet. Notices of the American Mathematical Society, Vol. 45, No.8, August 1998, pp. 961-970
Marco Aurelio Alzate Monroy
Ingeniero Electrónico de la Universidad Distrital en 1989 y Máster en Ingeniería Eléctrica de la Universidad de los Andes en 1991. Entre 1989 y 1992 fue docente-investigador en la División de Investigación del ITEC, Telecom, y luego se vinculó a la Facultad de Ingeniería Electrónica de la Universidad Distrital, donde actualmente se desempeña como Profesor. En este momento adelanta su disertación doctoral en Ingeniería Eléctrica y de Computadores en la Universidad de Maryland, USA.
Creation date:
License
From the edition of the V23N3 of year 2018 forward, the Creative Commons License "Attribution-Non-Commercial - No Derivative Works " is changed to the following:
Attribution - Non-Commercial - Share the same: this license allows others to distribute, remix, retouch, and create from your work in a non-commercial way, as long as they give you credit and license their new creations under the same conditions.




2.jpg)