TOMA DE DECISIONES BASADAS EN EL ALGORITMO DE DIJKSTRA

TOMA DE DECISIONES BASADAS EN EL ALGORITMO DE DIJKSTRA

Una Solución para Radios Cognitivos

DECISION MAKING BASED ON THE DIJKSTRA´S ALGORITHM

A Solution for Cognitive Radio

Laura Méndez Martínez ¹, Enrique Rodriguez-Colina ¹, R. Carolina Medina Ramírez ¹

¹ Universidad Autónoma Metropolitana, Iztapalapa (UAM-I)

menlaunez@xanum.uam.mx , erod@xanum.uam.mx , cmed@xanum.uam.mx

Recibido: 23/10/2013 - Aceptado: 22/12/2013

Resumen

Una de las funciones que realiza un ‘Radio Cognitivo’ es la toma de decisiones sobre el espectro radioeléctrico, esto a partir del análisis que realiza de su entorno. En este trabajo de investigación, se propone un método para la toma de decisiones para la selección de una banda en el espectro radioeléctrico que cumpla con ciertos criterios requeridos para una aplicación. Esta toma de decisiones se basa en un algoritmo de búsqueda del camino más corto similar al Algoritmo de Dijkstra. Para encontrar el camino más corto, el cual representa a la banda de frecuencia requerida, se especifican los atributos o parámetros a considerar para cada una de las bandas de acuerdo a una aplicación en particular o servicio requerido. A estos atributos o parámetros se les asignan valores es decir, pesos que determinan la prioridad e importancia para cada servicio. El algoritmo propuesto basado en Dijkstra, evalúa los parámetros del conjunto de bandas disponibles considerando el peso asignado, e indica la banda a seleccionar y que cubre con los criterios de la toma de decisiones. Se realizaron simulaciones por computadora para caracterizar los servicios identificados como mejor esfuerzo ‘Best Effort’ y tiempo real ‘Real Time’, obteniendo como resultado una latencia reducida que representa un tiempo práctico para ser implementado en un Radio Cognitivo en su toma de decisiones. Se observó también que los tiempos mostraron una mejora al ser comparados con los resultados obtenidos al implementar el Algoritmo de AHP¹.

Palabras clave: Toma de decisiones para Radios Cognitivos, Algoritmo de Dijkstra, Analytic Hierarchy Process (AHP¹).

Abstract

One of the functions that Cognitive Radio performs is the spectrum decision making, this is considering the analysis of its environment. This work proposes an algorithm for the selection of a band in the spectrum based on the idea of the Dijkstra’s Algorithm. In order to find the shortest path, which corresponds to the selection of a spectrum band, it is required to specify the attributes or parameters to consider for each of the bands according to the application or service required. Values, i.e., weights, are allocated to each attribute which determine the priority or significance of each service. The proposed algorithm based on Dijkstra evaluates the parameters that characterize a collection of bands considering the weights assigned and, this indicates which band should be selected according to the decision making criteria. Computer simulations were performed to characterize the Best Effort and Real Time applications. These resulting in latency reduction in the selection process of the band which represents a practical time for the algorithm implementation in a Cognitive Radio for the decision making process. It was also observed that the selection time acquired improves in contrast to the results obtained by implementing the AHP¹ Algorithm.

Keywords: Selection a band, Decision making, Dijkstra algorithm based, Analytic Hierarchy Process (AHP¹).

1. INTRODUCCIÓN

Los constantes avances tecnológicos han contribuido en el aumento del uso de dispositivos móviles, actualmente existe un mayor número de usuarios que utilizan las comunicaciones móviles y redes inalámbricas, originando nuevos problemas de comunicación debido a la saturación e interferencia en el espectro radioeléctrico de uso libre, mientras que otros espacios de frecuencia no son aprovechados en su totalidad [1].

Ante la problemática surgida por el auge de las comunicaciones inalámbricas y a la mala administración del espectro radioeléctrico, surge el concepto de Radio Cognitivo, que tiene como objetivo aprovechar mejor el espectro radioeléctrico, permitiendo utilizar los huecos del espectro radioeléctrico, conocidos en la literatura como ‘white spaces’ [2].

Un Radio Cognitivo (RC), se puede definir como un asistente de redes inalámbricas lo suficientemente inteligente para detectar las necesidades del usuario y brindarle los recursos de comunicación más adecuados [3].

En general un RC debe realizar las siguientes funciones para resolver la asignación dinámica del espectro [4]:

• Monitorización del espectro (sensing): consiste en identificar las bandas disponibles de frecuencia o ‘white spaces’.

• Toma de decisiones sobre el espectro: una vez que se han identificado las frecuencias disponibles, se puede seleccionar la banda de frecuencias más apropiada de acuerdo a parámetros de servicios o aplicaciones requeridas.

• Compartir el espectro: es la capacidad de compartir los recursos del espectro con varios usuarios, evitando la interferencia que pudiera ser originada por la superposición de señales.

• Movilidad del espectro: en el instante que el RC detecta a un usuario primario¹, debe desocupar la banda de frecuencia en uso y continuar con la comunicación a través de otra banda disponible.

En este artículo se propone un algoritmo que permite seleccionar una banda de frecuencias, como lo debe hacer la Función de Toma de Decisiones de un RC. Para realizar el proceso de toma de decisión se considera la evaluación de algunos de los atributos de las bandas disponibles, con la finalidad de elegir la banda que mejor se adapte al servicio o aplicación solicitada. Los atributos considerados en este estudio son: el ancho de banda, la interferencia, la ocupación y la calidad de la banda. Los atributos considerados se tomaron de un trabajo previo [7] y así tener la posibilidad de que los algoritmos de toma de decisiones puedan ser comparados. Durante el proceso de toma de decisión se consideran los servicios de mejor esfuerzo o ‘Best Effort’ (BE) y de tiempo real ‘Real Time’ (RT).

El algoritmo se basa en la idea de encontrar la mejor ruta o camino más corto como lo hace el Algoritmo de Dijkstra, donde el camino más corto corresponde a seleccionar la mejor banda, para ello se debe asignar un “peso” a cada uno de los atributos de las bandas disponibles a evaluar.

Una de las contribuciones de esta propuesta es la disminución en los tiempos de ejecución para la toma de decisiones debido a que el algoritmo propuesto requiere menor poder de cómputo. Esto a diferencia de otros algoritmos empleados en los radios cognitivos y otras propuestas como es el caso del proceso Analítico Jerárquico (AHP¹, por sus siglas en inglés).

A continuación en la Sección 2 de este artículo se describe el algoritmo AHP¹, con el cual se comparan los resultados obtenidos con el algoritmo propuesto. En la Sección 3 se describe el Algoritmo de Dijkstra y las características que sirvieron de base para nuestra propuesta. En la Sección 4 se describe el algoritmo propuesto ATDDiM (Algoritmo de Toma de Decisiones con Dijkstra Modificado). En la Sección 5 se presentan los resultados obtenidos y finalmente en la Sección 6 se presentan conclusiones.

2. Proceso Analítico Jerárquico (AHP¹)

AHP¹ es un método para la toma de decisiones con criterios múltiples, su principal característica es que modela la toma de decisión mediante una jerarquía, en cuyo vértice superior se encuentra el objetivo o problema a resolver. En los niveles intermedios, se representan los criterios o parámetros utilizados en la toma de decisiones. En cada uno de los niveles de la jerarquía AHP¹, se realizan comparaciones entre pares de elementos del mismo nivel, de acuerdo a la importancia o contribución de cada uno de ellos y de acuerdo al elemento del nivel superior al que están ligados. Para realizar este proceso de comparación se asignan prioridades o pesos a cada uno de sus elementos [5].

Para la implementación del modelo AHP¹ se tienen los siguientes pasos [6]:

1. Definir el objetivo que se quiere alcanzar, establece los criterios para alcanzar el objetivo planteado y desarrollar un modelo con una estructura jerárquica utilizando diversos factores o atributos que contribuyan para la toma de decisiones.
2. Se establece la prioridad para cada uno de los factores de cada subnivel, para posteriormente introducirlos en una matriz de comparación por pares.
3. A través de ciertos cálculos se determinan los factores de mayor importancia.

En [7] los autores proponen utilizar el Algoritmo AHP¹ para modelar la selección de una banda, evaluando así, los atributos de: ancho de banda, interferencia, ocupación y calidad, asignando un peso a cada atributo que permita cubrir los requisitos de calidad de servicio (QoS). Así mismo estos autores evalúan los servicios de BE y RT por medio de simulación y los mismos pesos asignados en [7] son considerados para nuestro modelo. Esto con la finalidad de realizar una comparación en el desempeño de cada algoritmo para la selección de una banda.

3. Algoritmo de Dijkstra

El Algoritmo de Dijkstra permite encontrar el camino más corto entre dos vértices de un grafo [8]. Para describir el algoritmo partimos de la definición de un grafo, como la representación gráfica de un conjunto de nodos o vértices unidos por enlaces llamados aristas o arcos.

Se tiene un grafo G = (V,E) como un conjunto de vértices V donde V = {v0, v1, … , vn-1} y un conjunto de aristas E que unen los vértices, a los cuales se les asocia un peso.

El orden de complejidad del Algoritmo de Dijkstra es de O(n2). A continuación se describe el pseudocódigo del algoritmo en los siguientes pasos [8 - 9]:

1. Definir un vector D, para guardar las distancias e inicializarlo con un valor infinito relativo, ya que las distancias son desconocidas en un principio, excepto para el vértice inicial v0, el cual tiene una distancia de cero.
2. Sea a, el vértice actual. Se recorren todos los vértices adyacentes, marcando los ya visitados y los no visitados vj.
3. Si la distancia desde v0 hasta vj guardada en el vector D, es mayor que la distancia desde v0 hasta a sumada a la distancia desde a hasta vj, se sustituye el valor de la distancia Dj por el valor de distancia Da + d(a,vj) es decir: Si (Dj > Da + d(a, vj)) entonces (Dj= Da + d(a, vj))
4. Se marca el vértice a como vértice ya visitado y se toma como próximo vértice a visitar al de menor valor en el vector D, repitiendo el Paso III mientras existan vértices no marcados.

Para nuestra propuesta del Algoritmo de Toma de Decisiones con Dijkstra Modificado (ATDDiM), se considera la idea de encontrar el camino más corto, tras una asignación de pesos, para modelar la selección de una banda dentro de un conjunto de bandas disponibles tras la evaluación los atributos mencionados.

4. Modelo propuesto

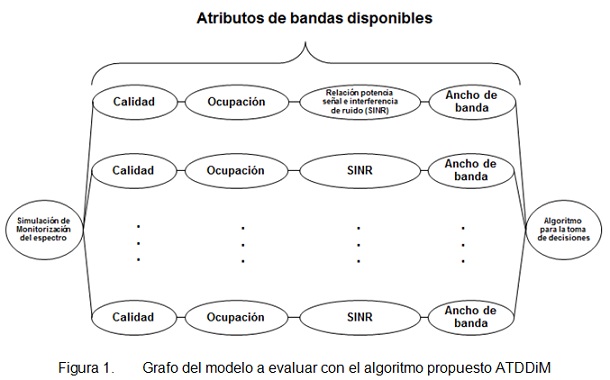
Retomando la idea de encontrar el camino más corto de un grafo de acuerdo al Algoritmo de Dijkstra, se propone el grafo de la figura 1 a evaluar con nuestro modelo.

En la figura 1, los círculos corresponden a los vértices, que representan los atributos a evaluar para cada una de las bandas, los vértices se encuentran unidos por líneas que corresponden a las aristas que unen a cada vértice, a los cuales se les asigna un peso, de acuerdo a los requerimientos del servicio a evaluar: BE o RT, los vértices y aristas forman caminos que representan a las bandas disponibles y sus atributos, los cuales serán evaluados para determinar el camino más corto, es decir, seleccionar la mejor banda del espectro.

Definimos al grafo de la figura 1, como G=(V,E) donde V son los vértices que representan los atributos a evaluar asignándoles un peso y, las aristas E, que unen los vértices. En el Algoritmo de Dijkstra, podemos representar los caminos formados por los vértices y aristas de dos formas [10]:

1. Por medio de una Matriz Adyacente M: tenemos una matriz de tamaño NxN, donde cada elemento de M[i,j] almacena la longitud entre el vértice i y el vértice j. Si su valor es infinito significa que no existe arista entre esos vértices y M[i,j]=0. Su complejidad es de O(n2).
2. Por medio de una Lista Adyacente L: se utiliza un vector de tamaño N (un elemento para cada vértice) donde L[i], almacena la referencia a una lista de los vértices adyacentes o contiguos a i. Esta lista almacenará también la longitud de la arista que va desde i al vértice adyacente. Su complejidad es de O(n).

Para nuestro modelo utilizamos la estructura de una Lista Adyacente debido a que el orden de complejidad es menor, lo cual para nuestro caso es mejor que si implementáramos una Matriz de Adyacencia de tamaño NxN.

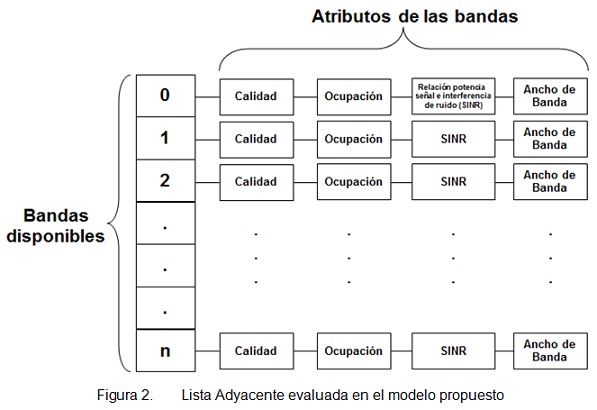
Primero definimos una Lista Adyacente L, de tamaño N para representar el número de bandas disponibles, donde cada L[i], contiene los atributos o parámetros a evaluar de cada banda. La figura 2 muestra la Lista Adyacente evaluada en nuestro modelo.

En la Lista Adyacente evaluada en nuestro modelo, se observa que el tamaño de la lista L corresponde a las bandas disponibles, ver figura 2. Donde a cada banda se le asigna un identificador que va de cero a n, el cual permite, identificar la banda seleccionada como el camino más corto. A cada banda se le asocia con sus atributos a evaluar, por medio de un peso que se especificará más adelante.

Como ya se menciona en la Sección 2, en nuestra propuesta implementamos los siguientes atributos: ancho de banda, interferencia, calidad y ocupación del canal, para cubrir los atributos de QoS para los servicios de BE y RT, con la finalidad de poder comparar nuestros resultados con los resultados obtenidos por el modelo AHP¹ propuesto en [7]. Sin embargo, el modelo puede adaptarse para la evaluación de distintos atributos de acuerdo al servicio solicitado.

A continuación se describe el pseudocódigo del algoritmo ATDDiM propuesto en los siguientes pasos:

1. Definir una variable valor_minimo con un valor infinito relativo, es decir un valor tan grande que no se pueda obtener durante nuestra evaluación, ya que esta variable nos permite tener un valor de referencia al realizar nuestra primer comparación, con el valor que se obtiene al realizar nuestra primer evaluación en el proceso de selección.
2. Recorremos nuestra Lista Adyacente hasta evaluar cada una de las bandas disponibles.
3. Para cada banda almacenada en la Lista Adyacente L:

   1. evaluamos cada uno de sus atributos, al sumar todos sus pesos asignados, para obtener el valor de la distancia de esta ruta o camino y se asigna a una variable valor_peso para posteriormente compararse con el valor almacenado en la variable minimo.

      Si (valor_peso < minimo) minimo=valor_peso guardamos el identificador asignado a nuestra banda, de acuerdo al modelo que se describe en la figura 2.

4. Al terminar de recorrer la Lista Adyacente desplegamos el identificador de la banda que corresponde al camino más corto, con un valor o peso final de sus atributos almacenado en la variable minimo.

5. Simulación y resultados

Para evaluar el algoritmo propuesto ATDDiM, se realizó una simulación de la Función de Monitorización del espectro que realiza un RC, generando valores aleatorios de detección de energía, y los posibles valores de cada atributo de las bandas disponibles.

Los valores aleatorios son variables de tipo flotante dentro de un intervalo entre 1 y 10. Cada uno de los valores generados para cada atributo se evalúa junto con un peso fijo, el cual es asignado de acuerdo a la prioridad que tiene cada atributo para cada servicio requerido.

Con la finalidad de comparar el algoritmo propuesto ATDDiM, contra el modelo de AHP¹ que se presenta en [7], asignamos los pesos propuestos para BE y RT de la tabla 1.

En la tabla 1, se observa que para el caso de BE el peso asignado para SINR y Ancho de Banda son mayores con respecto al caso de RT. Sin embargo, para RT la asignación de peso es mayor para los atributos de calidad y ocupación de la banda. El peso de los atributos cambia de acuerdo a los requerimientos solicitados por cada servicio de comunicación.

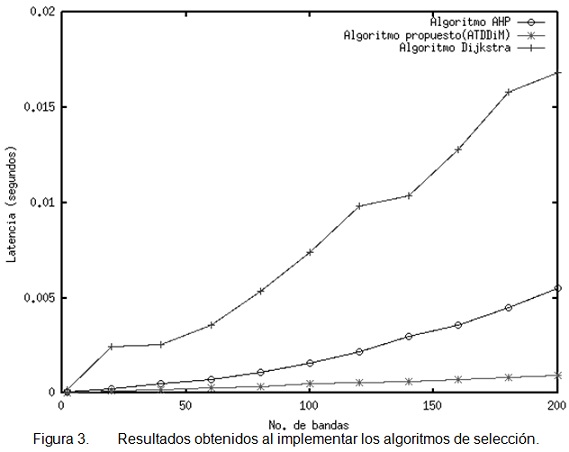
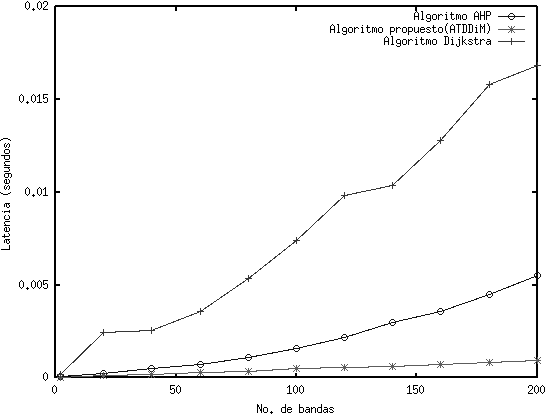
Al evaluar los valores aleatorios generados para cada atributo en conjunto con su peso asignado, el algoritmo propuesto ATDDiM, presenta una reducción en los tiempos de ejecución para el proceso de selección de la banda, como se puede apreciar en la figura 3.

En la figura 3 se muestran los tiempos de ejecución obtenidos de la simulación del proceso de selección de la banda, al implementar los algoritmos: de Dijkstra, el propuesto ATDDiM y el Algoritmo de AHP¹, considerando una selección desde 2 hasta 200 bandas de frecuencia.

Como se puede observar, los tiempos obtenidos al implementar ATDDiM, son menores al compararlos con el Algoritmo de Dijkstra y los resultados obtenidos por el Algoritmo AHP¹. Esto se debe a que nuestra propuesta implementa una estructura de Lista Adyacente donde el tamaño de la lista L está en función del número de bandas disponibles y sus atributos, permitiendo con ello reducir la complejidad del algoritmo al realizar menos operaciones durante la evaluación de los atributos de cada banda. Esto a diferencia del Algoritmo de AHP¹ en el cual se utiliza una estructura con una matriz de tamaño NxM, donde N representa el número de atributos a evaluar y M el número de bandas disponibles. La mejora en operaciones también es con respecto al Algoritmo de Dijkstra el cual implementa una Lista Adyacente, que a diferencia de nuestro modelo, el tamaño de la lista L varía en función al número de vértices y no al número de bandas disponibles. Como se explica en la Sección IV, la Lista Adyacente para Dijkstra almacena una lista de los vértices adyacentes o contiguos del grafo a evaluar, por lo tanto, al ser más grande el tamaño de la lista L, implica un mayor número de cálculos para cada vértice, lo cual eleva los tiempos de ejecución en el proceso de selección de la banda con respecto a la propuesta ATDDiM.

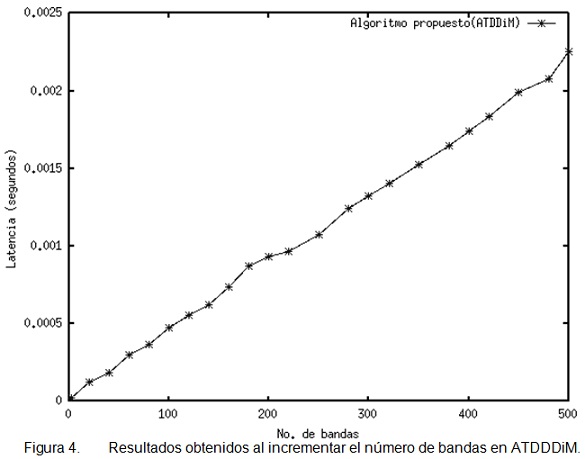
Al implementar ATDDiM, se incrementó el número de bandas disponibles, para observar el comportamiento que presenta ante un número mayor de bandas. Los resultados obtenidos se describen en la figura 4.

De acuerdo a la gráfica de la figura 4, se observa que el tiempo de ejecución del proceso de selección de la banda, presenta un comportamiento lineal, variando muy poco el incremento en el tiempo al variar de cero hasta 500 bandas disponibles, lo que nos indica que el tiempo permanece casi constante a pesar de evaluar un número mayor de bandas con respecto a los otros algoritmos estudiados. La figura 4 muestra este hecho hasta 200 bandas para los tres algoritmos, mientras que la figura 5 muestra el detalle hasta 500 bandas a elegir como las adecuadas para las aplicaciones sugeridas.

Conclusiones

Los resultados obtenidos con la propuesta del Algoritmo de Toma de Decisiones con Dijkstra Modificado (ATDDiM) muestran una reducción en los tiempos de ejecución con respecto a los algoritmos AHP¹ y Dijkstra. Durante la simulación se consideraron cuatro atributos para evaluar los servicios Best Effort y Real Time, para determinar la banda que se adapta mejor a los requerimientos solicitados para cada caso. Además, el modelo propuesto puede adaptarse a diferentes atributos, así como ajustarse a un número mayor de atributos, teniendo en cuenta que se deberán ajustar la asignación de pesos o prioridades de acuerdo al servicio solicitado o disponible.

Nuestra simulación muestra que el algoritmo propuesto puede utilizarse en la Toma de Decisiones en un Radio Cognitivo ya que presenta tiempos de latencia que se pueden llevar a la práctica. Además, no presenta un incremento significativo en el tiempo de selección cuando se incrementa el número de bandas evaluadas, esto comparado con los algoritmos de AHP¹ y Dijkstra.

Como trabajo futuro se planea implementar la propuesta con valores experimentales de la detección de energía y llevarlo a una aplicación utilizando radios programables (GNU-Radios).

Reconocimientos

Los autores agradecen el apoyo brindado por el Programa PROMEP de la Secretaría de Educación Pública de México y al Consejo Nacional de Ciencia y Tecnología (CONACyT). También agradecen a la Universidad Distrital Francisco José de Caldas, por la invitación a participar en el IX Congreso Internacional de Electrónica, Control y Telecomunicaciones.

Referencias

1. FCC, Spectrum policy task force report. Proceedings of the Federal Communications Commission (FCC '02), Washington, DC, USA, November 2002.
2. A. De Domenico, E. C. Strinati, M. G. Di Benedetto; A survey on MAC strategies for cognitive radio networks, Communications Surveys & Tutorials, IEEE, 2012.
3. A.M. Wyglinski, M Nekovee, Y. T. Hou; Cognitive Radio Communications and Networks Principles and Practice, ISBN: Elsevier, San Diego California, 2010.
4. Ian F. Akyildiz, Won-Yeol Lee, Kaushik R. Chwdhury; “CRAHNs: Cognitive radio ad hoc networks”, Volumen 7, 2009. Trans. Roy. Soc. London, vol. A247, pp. 529–551, April 2009.
5. N. Uchida, K. Takahata, Xiaolin Zhang, K. Takahata, Y. Shibata; Min-Max based AHP¹ method for route selection in cognitive wireless network, International Conference on Network-Based Information Systems (NBis), pp. 22-27, 2010.
6. Wang Xinil, Ma. Jianghua; Application and research of analytic hierarchy process in project investment appraisal and decision-making, International Conference on E-Bussiness and Information System Security, EBISS, pp 1-4, 2009.
7. E. Rodriguez-Colina, P. Ramirez, A. Carrillo; Multiple attribute dynamic spectrum decision making for cognitive radio networks, International Conference on Wireless and Optical Communications Networks (WOCN), pp 1-5, 2011.
8. F. Dongkai Fan, Ping Shi; Improvement of Dijkstra's algorithm and its application in route planning, Internacional Conference on Fuzzy System and Knowledge Dicovery (FSKD), pp. 1901-1904, 2010.
9. N. Jasika, N Alispahic, A. Elma, K. Ilvana, L. Elma, N. Nosovic; Dijkstra's shortest path algorithm serial and parallel execution performance analysis, Proceedings on International Convention MPRO, pp 1811-1815, 2012.
10. F. Riaz, Ali, K.M; Applications of graph theory in computer science, International Conference on Computational Intelligence, Communication Systems and Networks (CICSyN), pp 142-145, 2011.