DOI:
https://doi.org/10.14483/udistrital.jour.redes.2015.2.a03Publicado:
2015-12-26Número:
Vol. 6 Núm. 2 (2015)Sección:
InvestigaciónSOLUCIÓN DE LA ECUACIÓN NO LINEAL DE SCHRODINGER (1+1) EN UN MEDIO KERR
Palabras clave:
ecuación de Schrodinger no lineal, óptica no lineal, solitones (es).Descargas
Resumen (es)
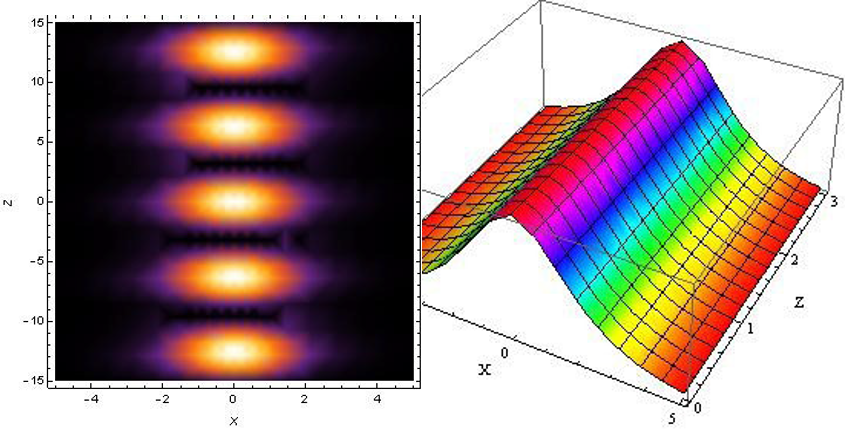
Se presenta un marco teórico y se muestra una simulación numérica de la propagación de solitones. Con especial atención a los solitones ópticos espaciales, se calcula analíticamente el perfil de solitón correspondiente a la ecuación Schrodinger no-lineal para un medio Kerr. Los resultados muestran que los solitones ópticos son pulsos estables cuya forma y espectro son preservados en grandes distancias.
Solution of the nonlinear Schrodinger equation (1+1) in a Kerr medium
ABSTRACT
This document presents a theoretical framework and shows a numerical simulation for the propagation of solitons. With special attention to the spatial optical solitons, we calculates analytically the profile of solitón corresponding to the non-linear Schrodinger equation for a Kerr medium. The results show that the optical solitons are stable pulses whose shape and spectrum are preserved at great distances.
Keywords: nonlinear optics, nonlinear Schrodinger equation, solitons.
Referencias
P.G. Drazin and R. S. Johnson. “Solitons: an Introduction”, Cambridge: Ed. Cambridge University Press, pp. 1-17, 1996.
D. J. Korteweg and G. de Vries. “Philosophical Magazine, 5th series”, vol. 39, 422- 443, 1895.
N. J. Zabusky and M. D. Kruskal. “Interaction of solitons in a collision less plasma and the recurrence of initial states”, Phys. Rev. Lett., vol 15, 240-243, 1965.
S. López, M. Esparza, G. Lem y J. C. Gutiérrez. “Ondas solitarias no lineales: una introducción a los solitones ópticos espaciales”, Rev. Mex. Fis., vol 60, 39-50, 2014.
Y. Kivshar and G. Agrawal. “Optical solitons”, USA: Ed. Academic Press, 2003.
M. Segev. “From the Guest Editor-Solitons: A Universal Phenomenon of Self-Trapped Wave Packets”, Opt. Photonics news, vol.13, 27, 2002.
F. Wise and P. Di Trapani. “Spatiotemporal Solitons”, Opt. Photonics news, vol. 13, 28-32, 2002.
F. V. Kusmartsev. “Application of catastrophe theory to molecules and solitons”, Phys. Rep., vol. 183, 1-35, 1989.
T. Herr, V. Brasch, J. D. Jost, C. Y. Wang. “Temporal solitons in optical microresonators”, Nature Photonics, vol. 8, 145-152, 2014.
F. V. Kusmartsev. “Application of catastrophe theory to molecules and solitons”, Phys. Rep., vol. 183, 1-35, 1989.
M. Rho, A. Goldhaber and G. Brown. “Topological solitón bag model for baryons”, Phys. Rev. Lett., vol. 51, 747, 1983.
J. M. Soto y C. Mejía. “Optical solitons in dissipative media”, Óptica Pura y Aplicada, vol. 44, 425-431, 2011.
G. Torres, J. Sánchez, M. Iturbe, G. García, M. Torres y C. Triviño. “Guías de onda generadas por solitones ópticos espaciales”, Rev. Mex. Fis., vol 41, 662-694, 1995.
E. Arévalo, C. Ramírez y A. Guzmán. “Solitones en fibras ópticas”, Rev. Momento, vol. 11, 9-16, 1995.
S. López, M. Esparza, G. Lem y J.C. Gutiérrez. “Ondas solitarias no lineales: una introducción a los solitones ópticos espaciales”, Rev. Mex. De física, vol. 60, 39-50, 2011.
J. Jackson. “Classical Electrodynamics”, USA: Ed. Jhon Wiley and Sons, 3th edition, pp. 237-241, 1998.
A. Sepulveda. “Electromagnetismo”, Medellín: Ed. Universidad de Antioquia, pp. 270-271, 2008.
G. Stephenson. “Introducción a las ecuaciones en derivadas parciales”, España: Ed. Reverte, pp. 119-140, 1982.
S. López, Y. V. Kartashov, V. Vysloukh and L. Torner. “Method to generate complex quasi-nondiffracting optical lattices”, Phys. Rev. Lett., vol. 105, 031902, 2010.
B. Karasozen, C. Akkoyunlu and M. Uzunca. “Model order reduction for nonlinear Schrödinger equation”, Appl. Math. and Comp., vol. 285, 509-519, 2015.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Licencia
Reconocimiento – NoComercial – CompartirIgual (by-nc-sa): No se permite el uso comercial de la obra original, las obras derivadas deben circular con las mismas condiciones de esta licencia realizando la correcta atribución al autor.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional












