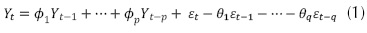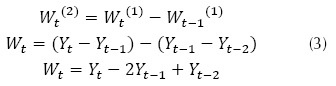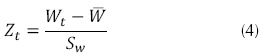DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a07Publicado:
01-04-2017Número:
Vol. 21 Núm. 52 (2017): Abril - JunioSección:
Estudio de casoAplicación de modelo ARIMA para el análisis de series de volúmenes anuales en el río Magdalena
Applying ARIMA model for annual volume time series of the Magdalena River
Palabras clave:
Modelo estadístico, modelo auto regresivo, serie de tiempo (es).Palabras clave:
Statistical model, autoregressive model, time series (en).Descargas
Referencias
Bowerman, B. (2009). Pronósticos, series de tiempo y regresión: un enfoque aplicado. 4a. ed. México: Centro Ixtapaluca Edo. de México, CENGAGE Learning.
Box, G. E. P., y Jenkins, G. M. (1970). Time series analysis: forecasting and control, 1976. ISBN: 0-8162-1104-3.
Calle, E.; Angarita, H. y Rivera, H. (2010). Viabilidad para pronósticos hidrológicos de niveles diarios, semanales y decadales en Colombia. Ingenieria e Investigación, 30(2), 178-187.
Chatfield, C. (2003). The Analysis of Time Series: An Introduction. 6a. ed. Boca Raton, Florida: Chapman and Hall/CRC.
De Arce, R. y Mahía, R. (2003). Modelos Arima. Programa CITUS: Técnicas de Variables Financieras.
García M., B. y Baena E., R. (2015). El doble meandro abandonado del Guadalquivir en Cantillana (Sevilla): cambios de trazado y evolución geomorfológica. Geographicalia, (53), 101-119.
Guerrero, V. (2003). Análisis estadístico de series de tiempo económicas. 2a. ed. México, D.F.: Thomson.
Hildebrand, D. (1998). Estadística aplicada a la administración y a la economía. Serie de probabilidad y estadística. 3a. ed. México, D.F.: Addison Wesley Longman..
Ideam (2001). Primera Comunicación Nacional ante la Convención Marco de las Naciones Unidas sobre Cambio Climático. Bogotá, D. C.
Krajewski, L.; Ritzman, L. y Malhotra, M. (2008). Administración de operaciones. 8a. ed. México: Pearson Educación.
Lehner, B.; Döll, P.; Alcamo, J.; Henrichs, T. y Kaspar, F. (2006). Estimating the impact of global change on flood and drought risks in Europe: a continental, integrated analysis. Climatic Change, 75(3), 273-299.
Mauricio, J. (2007). Introducción al análisis de series temporales. Madrid: Universidad complutense de Madrid.
Ocampo, E.; Cabrera, A. y Ruiz, A. (2006). Pronóstico de bolsa de valores empleando técnicas inteligentes. Revista Tecnura, 9(18), 57-66.
Organización Meteorológica Mundial (OMM) (2003). Servicios de Información y Predicción del Clima y Aplicaciones Agrometeorológicas para los países andinos. Ginebra- Suiza.
Pabón, D. (1997). Variabilidad climática. En: Técnicas agrometeorológicas en la agricultura operativa de América Latina (pp. 99-103). Ginebra, Suiza: Organización Meteorológica Mundial.
Panel Intergubernamental sobre Cambio Climático (IPCC) (2007). Informe de síntesis. Contribución de los Grupos de trabajo I, II y III al Cuarto Informe de evaluación del Grupo Intergubernamental de Expertos sobre el Cambio Climático. Suiza.
Pinilla, L.; Pérez G., A. y Benito, G. (1995). Cambios históricos de los cauces de los ríos Tajo y Jarama en Aranjuez. Geogaceta, 18(10), 101-104.
Vargas, J.; Hernández, C. y Aponte, G. (2012). Comparación del modelo FARIMA y SFARIMA para obtener la mejor estimación del tráfico en una red Wi-Fi. Revista Tecnura, 16(32), 84-90.
Velásquez, J.; Dyner, I. y Souza, R. (2008). Modelado del precio spot de la electricidad en Brasil usando una red neuronal autorregresiva. Ingeniare. Revista Chilena de Ingeniería, 16(3), 394-403.
Yaglom, A. (1955). Correlation theory of processes with random stationary nth increments. Matematicheskii Sbornik (N. S.), 37(79), 141-196.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2017.2.a07
Aplicación de modelo ARIMA para el análisis de series de volúmenes anuales en el río Magdalena
Applying ARIMA model for annual volume time series of the Magdalena River
Gloria Amaris1, Humberto Ávila2, Thomas Guerrero3
1 Ingeniera civil, magíster en Ingeniería Civil, estudiante Doctorado en Ciencias de la Ingeniería. Pontificia Universidad Católica de Chile. Departamento de Hidráulica y Ambiental. Santiago de Chile. Contacto: geamaris@uc.cl
2 Ingeniero civil, especialista en ríos y costas, magíster en Recursos Hídricos, magíster en Estadística, doctor en Recursos Hídricos. Docente de la Universidad del Norte, Departamento de Ingeniería Civil y Ambiental. Barranquilla, Colombia. Contacto: havila@uninorte.edu.co
3 Ingeniero civil, magíster en Ingeniería Civil, docente asistente de la Universidad Francisco de Paula Santander Ocaña. Ocaña, Norte de Santander, Colombia. Contacto: teguerrerob@ufpso.edu.co
Fecha de recepción: 29 de agosto de 2016 Fecha de aceptación: 15 de febrero de 2017
Cómo citar: Amarís, G.; Ávila, H. y Guerrero, T. (2017). Aplicación de modelo ARIMA para el análisis de series de volúmenes anuales en el río Magdalena. Revista Tecnura, 21(52), 88-101. doi: 10.14483/udistrital.jour.tecnura.2017.2.a07
Resumen
Contexto: Los efectos del cambio climático, intervenciones humanas y características de los ríos, son factores que incrementan el riesgo en la población y de los recursos hídricos. Sin embargo, impactos negativos como inundaciones y desecación de ríos pueden ser identificados previamente mediante el uso de herramientas de modelación adecuadas.
Objetivos: Se estima un modelo ARIMA para el análisis de series de tiempo de volúmenes anuales (millones de m3/año) en el río Magdalena usando registros de la estación Calamar (Instituto de Hidrología, Meteorología y Estudios Ambientales de Colombia-Ideam), buscando la compatibilidad entre la hipótesis de modelación y los datos observados en el río.
Métodos: El modelo ARIMA es considerado uno de los enfoques más implementados en hidrología y estudios relacionados con variabilidad climática dado que considera registros no estacionarios.
Resultados: El pronóstico de volumen máximo del río Magdalena para los años 2013 a 2024 oscila entre 289.695 millones de m3 y 309.847 millones de m3. El pronóstico de volumen mínimo para los años de 2013 a 2024 oscila entre 179.123 millones de m3 y 157.764 millones de m3 con una tendencia de decrecimiento de 106 millones de m3 en 100 años.
Conclusiones: Los resultados de la simulación con el modelo ARIMA, comparados con los datos observados, muestran un ajuste adecuado de los valores mínimos y máximos. Esto permite concluir que, aunque estos modelos no simulan el comportamiento exacto en el tiempo, son una buena herramienta para aproximar eventos mínimos y máximos.
Palabras clave: modelo estadístico, modelo auto regresivo, serie de tiempo.
Abstract
Context: Climate change effects, human interventions, and river characteristics are factors that increase the risk on the population and the water resources. However, negative impacts such as flooding, and river droughts may be previously identified using appropriate numerical tools.
Objectives: The annual volume (Millions of m3/year) time series of the Magdalena River was analyzed by an ARIMA model, using the historical time series of the Calamar station (Instituto de Hidrología, Meteorología y Estudios Ambientales de Colombia-IDEAM), and looking for matching the modelling hypothesis with the data measured in the river.
Methods: The ARIMA model is considered one of the most implemented approaches in hydrology and studies related to climatic variability because it considers non-stationary information.
Results: The maximum volume forecasted of the Magdalena River from 2013 to 2024 oscillates between 289,695 million m3 and 309,847 million m3. The minimum volume forecast for the same period ranges from 179,123 million m3 to 157,764 million m3, with a decreasing trend of 106 million m3 in 100 years.
Conclusions: The simulated results obtained with the ARIMA model compared to the observed data showed a fairly good adjustment of the minimum and maximum magnitudes. This allows concluding that it is a good tool for estimating minimum and maximum volumes, even though this model is not capable of simulating the exact behaviour of an annual volume time series.
Keywords: statistical model, autoregressive model, time series.
INTRODUCCIÓN
Los efectos del cambio climático, las intervenciones humanas (García y Baena, 2015) y la configuración del canal (Pinilla, Pérez y Benito, 1995) son factores que afectan la hidráulica de los ríos y alteran el equilibrio de la dinámica fluvial mediante variaciones en su morfología, Lo cual trasciende a grandes distancias, tanto aguas arriba como aguas abajo de la zona de intervención. Los cambios del régimen hidrológico pueden generar un aumento en el caudal del río o desecamiento en las riveras (Lehner, etal., 2006), lo cual conlleva a impactos negativos en la población, a incrementos en la vulnerabilidad de los recursos hídricos (Ideam, 2001), además de la afectación al funcionamiento y operación de infraestructura hídrica existente y en las prácticas de gestión de recursos hídricos (IPCC, 2007).
Herramientas de modelación y predicción mediante series temporales han sido de gran utilidad para diversas áreas de investigación como: economía (Ocampo, Cabrera y Ruiz, 2006), tecnología (Vargas, Hernández y Aponte, 2012), ingeniería eléctrica (Velásquez, Dyner y Souza, 2008) e ingeniería de los recursos hídricos (Calle, Angarita y Rivera, 2010), demostrando que existe un comportamiento tendencial de las variables de diversas disciplinas que pueden relacionarse al contar con un registro histórico en una escala definida en el tiempo. Los pronósticos mediante series temporales demuestran la aplicabilidad de modelos de estimación de pronósticos de volumen, caudales o niveles a corto plazo (Pabón, 1997). Los pronósticos mediante estos análisis requieren que los objetivos sean orientados a identificar o prever los efectos generados por variación del comportamiento de los recursos hídricos ligados a la consistencia, veracidad y calidad de la información recopilada.
Las metodologías empleadas para este fin se basan principalmente en identificar, estimar y diagnosticar modelos de series temporales. Las técnicas estadísticas son implementadas en el pronóstico climático a niveles regionales y nacionales (Organización Meteorológica Mundial, 2003), las cuales incluyen análisis de esquemas generales de ciclos atmosféricos, series de tiempo, correlación, regresiones y análisis de variación climática. Entre los modelos de pronóstico más usados que consideran la relación del comportamiento de variables en el tiempo se destacan tres: i) los de regresión lineal simple y múltiple, los cuales describen tendencias lineales para pronóstico partiendo de variables explicativas; ii) los de series de tiempo, que capturan la aleatoriedad de la demanda a partir del comportamiento histórico identificando patrones elementales de la demanda (Krajewski, Ritzman y Malhotra, 2008), y iii) la técnica de Box y Jenkins (1970), en donde se establece que los datos temporales de una serie indican las características de su estructura probabilística (De Arce y Mahía, 2003).
Teniendo en cuenta la importancia de los análisis de los esquemas que definen los registros históricos, se abordó en esta investigación la temática de modelación y pronóstico. Se evaluaron los registros históricos de volumen del río Magdalena (Colombia) desde 1967 hasta 2015, de la estación Calamar (K+115). Para ello, se elaboró un modelo estadístico para representar apropiadamente la procedencia de la serie de tiempo y, de esta manera, validar que las hipótesis utilizadas en el modelo revelan la compatibilidad con la muestra observada del río, basada en la representación de la evolución de la serie, permitiendo realizar un pronóstico a corto plazo por medio de simulación.
METODOLOGÍA
Existen diversos modelos de series de tiempo (Hildebrand, 1998; Chatfield, 2003; Guerrero, 2003; Bowerman, 2009). Sin embargo, se destaca el modelo ARIMA por su simplicidad y practicidad en la modelación y pronóstico. Este modelo es considerado el enfoque más implementado en hidrología y estudios relacionados con variabilidad climática debido a que considera registros de datos no estacionarios (con tendencia). El modelo ARIMA consiste en la combinación de un término autorregresivo (AR) y un término de promedio móvil (MA) con un elemento diferenciador dado por la letra I basado en un estudio realizado por Yaglom (1955). En general estos modelos se referencian con la palabra ARIMA (p,d,q). Donde (p) se refiere al orden del modelo autorregresivo; (d), al término de diferenciación, y (q), al término de media móvil con q términos de error. La estructura general de estos modelos 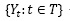 tiene la forma de un ARMA como se muestra en la ecuación (1).
tiene la forma de un ARMA como se muestra en la ecuación (1).
Donde φ corresponde al coeficiente autorregresivo a determinar, θ coeficiente de media móvil a determinar, ε término de error y Yt-p es el registro normalizado de la serie a modelar. Para el término del diferencial se debe considerar una evaluación del orden. Los diferenciales pueden ser de primer o segundo orden, siguiendo la forma mostrada en las ecuaciones (2) y (3) respectivamente.
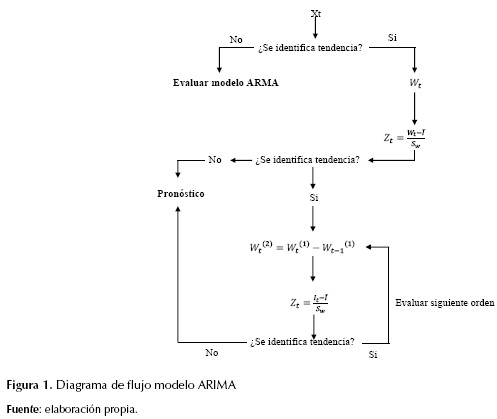
Donde Wt es el término diferenciador, Yt se refiere al registro de la serie normalizado en el tiempo t, el término Zt se refiere al dato del registro estandarizado en el tiempo t y se obtiene de la ecuación (4), promedio de los registros diferenciados, SW desviación estándar del registro diferenciado. La metodología de determinación de un ARIMA se muestra en la figura 1.
Para el objeto central de este análisis se llevó a cabo un proceso metodológico que consiste en un análisis preliminar para la determinación de la tendencia de la serie de tiempo anual. Diagnóstico considerando la función de autocorrelación (ACF) y la función de autocorrelación parcial (PACF). Selección del modelo considerando los criterios de información de Akaike (AIC), criterio de Schwarz (SBIC), el error porcentual absoluto medio (MAPE), y criterio de error cuadrático medio (ECM). Ajuste del modelo mediante verificación del comportamiento de los residuos de la serie diferenciada. Simulación de datos y, por último, generación de una serie sintética. Cabe resaltar que en la presente investigación se busca un enfoque de aproximación a una realidad la cual es reconocida como compleja y por tanto no se espera un ajuste exacto.
RESULTADOS
Análisis preliminar para la estimación del modelo
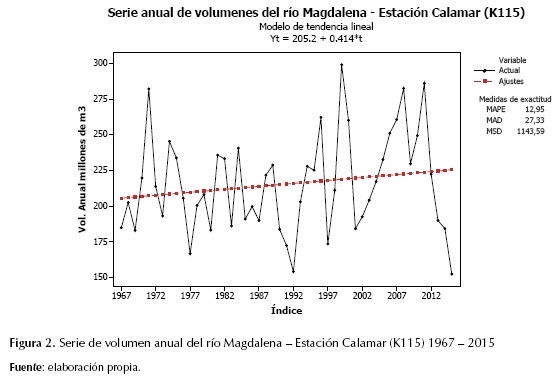
A partir de los registros históricos de volumen anual del río Magdalena, se realizó un análisis preliminar que permitió tener una idea general del tipo de modelo que podría ajustar mejor a la serie. Como primera medida se elaboró un gráfico de los registros del río en el tiempo para verificar su comportamiento (figura 2). El análisis preliminar permite detectar la necesidad de estabilizar la varianza y la media.
Diagnóstico
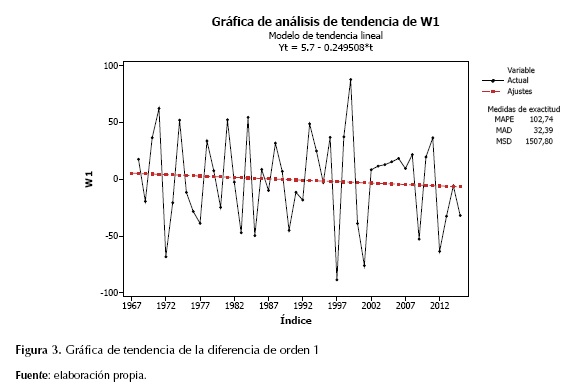
Debido a la tendencia que presentan los registros, fue necesario realizar una diferenciación de los datos para eliminarla. Una vez diferenciados los datos, se puede observar que se ha eliminado la tendencia en gran medida (figura 3). Aunque su media no es exactamente cero, es un valor pequeño que puede despreciarse en este caso.
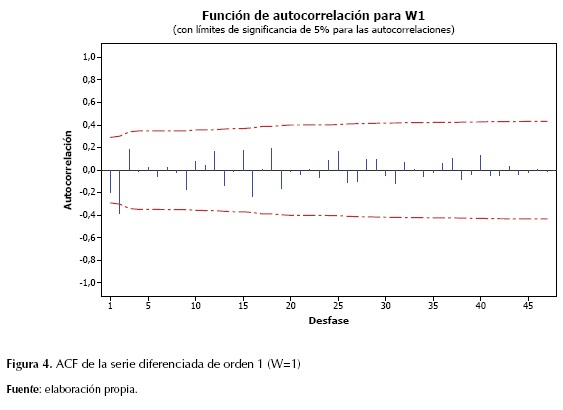
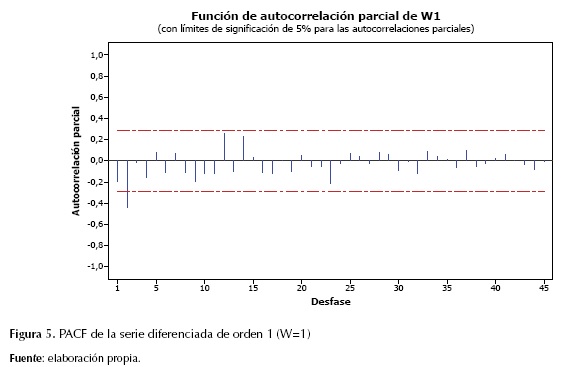
Posteriormente, se analizaron estadísticamente los registros anuales del río Magdalena, mediante la función de autocorrelación (ACF) y función de autocorrelación parcial (PACF). La finalidad de este procedimiento es llevar a cabo un análisis preliminar visual y estadístico que permita identificar un modelo con el mejor ajuste. Para cada función se analizaron 45 desfases. Gráficamente puede observarse que la función de ACF (figura 4) muestra dos barras que sobresalen en el primer segundo desfase con valores ACF de -0,198 (t estadístico: -1,37) y -0,381 (t estadístico: -2,54), demostrando la representatividad únicamente del segundo desfase. Por su parte, la PACF muestra dos barras sobresalientes en el primer y segundo desfase con un valor de PACF de -0.198 (t estadístico: -1,37) y -0,4377 (t estadístico: -3,03) respectivamente. La figura 5 muestra las dos barras sobresalientes en los desfases iniciales que decaen hacia cero, lo cual puede indicar una importante influencia del proceso de promedios móviles MA.
Selección del modelo
Después de ver el comportamiento de la serie, se realizan análisis complementarios con el fin de considerar los criterios de información de Akaike (AIC), criterio de Schwarz (SBIC), el error porcentual absoluto medio (MAPE) y criterio de error cuadrático medio (ECM) (tabla 1). Este análisis permitió seleccionar modelos entre un conjunto finito de modelos basados en la función de probabilidad (Mauricio, 2007), adicionando un término de penalización para el número de parámetros en el modelo, para evitar un sobreajuste en este.
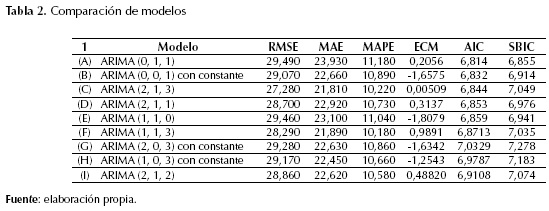
Para la determinación del mejor modelo se hace una comparación entre los mismos modelos evaluados, además de otros que tienen en cuenta el criterio de MAPE, permitiendo con esto seleccionar los que mejor se ajusten a los registros existentes (tabla 2).
De acuerdo con los criterios AIC y SBIC, se selecciona el modelo ARIMA (0, 1, 1), ya que presenta los menores valores en estos criterios (véase valores en negrilla de la tabla 2). Con el criterio MAPE se seleccionó el modelo ARIMA (1, 1, 3) pues presenta el menor valor comparado con los demás modelos (tabla 2), lo que significa que es el modelo que menos se desvía de los datos originales. Y, por último, de acuerdo con criterio ECM el modelo a seleccionar por su menor valor es el ARIMA (2, 1, 3).
Selección del modelo verificando comportamiento de residuos
De los modelos comparados mostrados en la tabla 2, se seleccionaron 3 que cumplen con los criterios de menor AIC, SBIC y ECM: ARIMA (0, 1, 1), ARIMA (1, 1, 3) y ARIMA (2, 1, 3). Para la selección del modelo con mejor ajuste se procede a realizar el análisis de los residuos de cada uno, con el fin de tomar una decisión acertada en la selección del mismo. A continuación, se muestran los estimados finales de los tres modelos seleccionados.
ARIMA (0, 1, 1)
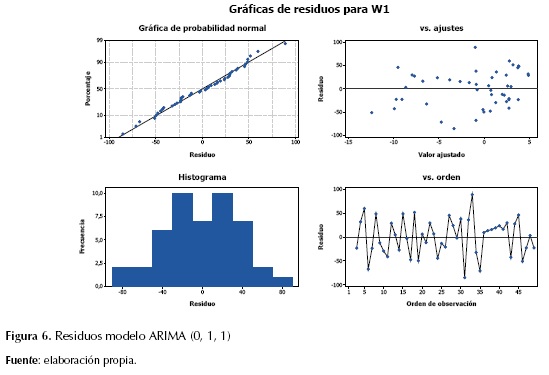
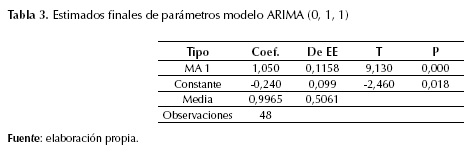
Los estimados finales de los parámetros para el modelo ARIMA (0, 1, 1), muestran que los residuos cuentan con un proceso aleatorio siguiendo una tendencia normal, media cero, con una ligera tendencia hacia el lado derecho de los ajustes (figura 6). Por otra parte, se destaca la significancia estadística del modelo, dado por el test-t mayor a 1,96 y el P-value menor a 0,05 (tabla 3).
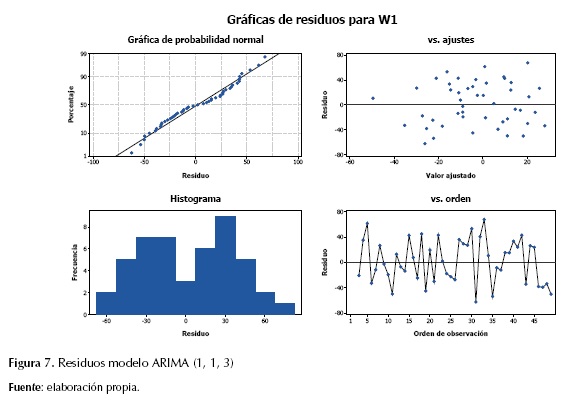
ARIMA (1, 1, 3)
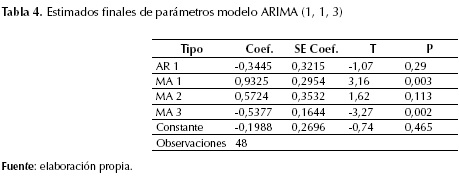
Los estimados finales de los parámetros para el modelo ARIMA (1, 1, 3) indican que los residuos siguen una tendencia normal, los valores ajustados siguen un proceso aleatorio, mostrando mayor dispersión que el modelo ARIMA (0, 1, 1). Sin embargo, los residuos no presentan una simetría (figura 6). Igualmente se destaca la significancia estadística de todos los parámetros del modelo (MA1 y MA 3), los cuales presentan mayores valores del test-t (tabla 4) para un nivel de confianza mayor al 95 %.
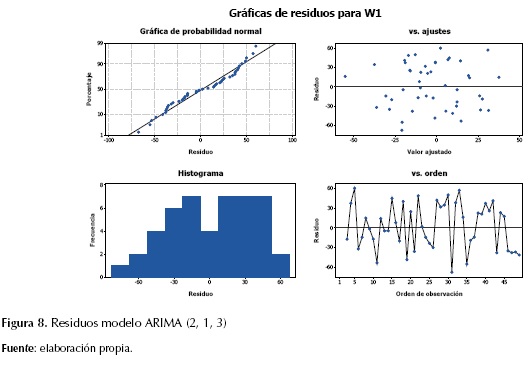
ARIMA (2, 1, 3)
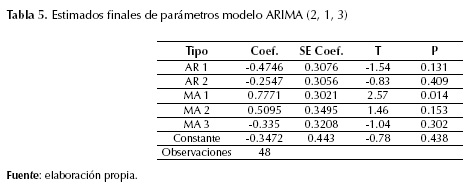
En los estimados finales de los parámetros para el modelo ARIMA (2, 1, 3), los residuos presentan un proceso aleatorio, siguiendo una tendencia normal y media cero (figura 8).
Por otra parte, se destaca que ninguno de los términos AR1, AR2, y MA2 dejan de ser significativos estadísticamente, sugiriendo que el modelo adecuado sigue un comportamiento que es descrito apropiadamente por un MA2 para un nivel de significancia estadística de 95 % (tabla 5).
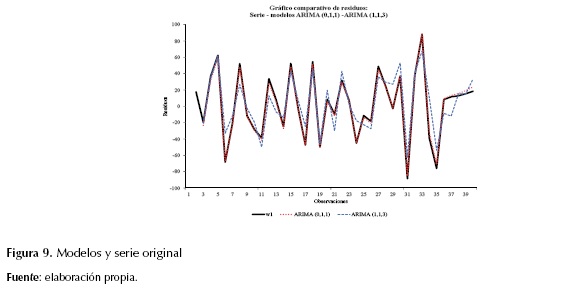
Ajuste del modelo
A partir de estos resultados, se realiza la verificación del comportamiento de los residuos de los dos modelos que presentan mayor significancia estadística. Este proceso se lleva a cabo mediante la comparación de los modelos seleccionados y el registro real diferenciado. En la figura 9 se observa que el modelo que mejor ajusta al registro real es el modelo ARIMA (0, 1, 1), indicando un modelo de media móvil de orden 1 con tendencia. Este sigue la forma descrita en la ecuación (5).
Cabe resaltar que el efecto de la tendencia para este caso será muy bajo, considerando que el coeficiente que acompaña la variable es pequeño (-0,24).
Simulación de datos
Una vez definido el modelo que representa mejor la serie MA (1) con diferencia W=1, se hizo la simulación de los datos a partir de los registros de volumen del río Magdalena, de donde se obtiene una serie sintética de 100 años.
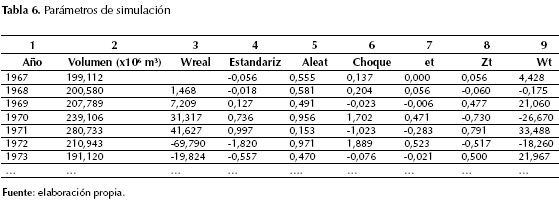
En la tabla 6 se resumen los parámetros considerados en la simulación. La columna 1 y 2 es de carácter informativo, allí se detallan los registros reales de la serie. La columna 3 muestra los datos diferenciados de la serie real obtenidos a partir de la ecuación (2). La columna 4 plantea la estandarización de los datos diferenciados, calculados a partir de la ecuación (4). La columna 5 presenta datos aleatorios generados con Excel (en total se generaron 100) que permitieran la generación de la serie sintética de 100 años. Las columnas 6 y 7 representan los términos del ruido blanco. La columna 6 presenta el choque, que no es más que el inverso de la distribución normal estándar acumulada, la cual tiene una media de cero y una desviación estándar de uno (aplicación recomendada realizarla en Excel para términos prácticos) necesario para calcular el error o ruido blanco de la ecuación (1) y ecuación (5). En la columna 7 se indica la estimación del ruido blanco calculada como: choque (columna 6) * , para esta ecuación se utilizó el valor de θ1 calculado en el ítem anterior pata el modelo ARIMA (0, 1, 1) θ1 = 1,05. La columna 8 indica la solución del modelo MA dado por la segunda parte ecuación (5). La columna 9 muestra la diferenciación de la serie simulada calculada despejando Wt de la ecuación (4).
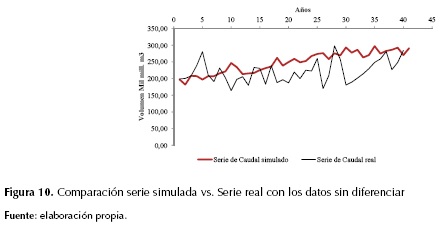
Por último, de manera esquemática, se relacionó la diferenciación simulada con el primer dato de registro real (1967) y a este se le sumó la diferencia Wt obtenida para cada año con el fin de conocer la serie en función de volúmenes. Los resultados se presentan en la figura 10. De esta se puede decir que no hay un ajuste preciso. Adicionalmente, se destaca que en el proceso de evaluación y análisis no se discrimina la influencia del fenómeno de El Niño y La Niña. Sin embargo, los análisis se realizaron en años en los que se han presentado dichos fenómenos.
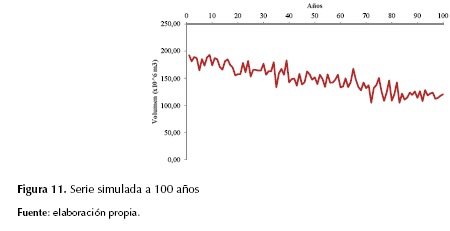
La figura 11 muestra la simulación de la serie en un rango más amplio (100 años) pronosticando un volumen mínimo del río Magdalena de 106 millones de m3 en 100 años. Esto permite considerar planes de acción a futuro para disminuir la tasa de escasez. Sin embargo, cabe destacar que estos modelos van ligados a los registros de volumen o de niveles disponibles, por tanto, se debe actualizar el modelo año a año para obtener una aproximación más exacta.
CONCLUSIONES
La simulación y pronóstico estocástico de caudales se realizó teniendo en cuenta series de tiempo, y se han evaluado los modelos más comunes en este ámbito. Mediante el análisis de los resultados se puede concluir que, para realizar un pronóstico aproximado, se debe elegir el modelo más acertado para el evento que se quiere estudiar. Como insumo de la investigación se elaboró un diagrama de flujo que considera el proceso elemental para el análisis de los modelos ARIMA.
El análisis estadístico permitió tomar una decisión del modelo escogido, el cual cumple con los parámetros requeridos de normalidad, varianza constante y aleatoriedad.
En relación al caso de estudio presentado, el pronóstico de volumen máximo del río Magdalena para el periodo 2013 a 2024 oscila entre 289.695 millones de m3 y 309.847 millones de m3. El pronóstico de volumen mínimo del río Magdalena para el periodo 2013 a 2024 oscila entre 179.123 millones de m3 y 157.764 millones de m3.
La simulación a partir del modelo ARIMA (0,1,1) demuestra que los pronósticos, desde un registro histórico, se adapta muy bien a los niveles máximos y mínimos, y se mantienen en el rango. Se concluye, entonces, que estos modelos no permiten simular el comportamiento exacto en el tiempo, pero es una buena herramienta con la cual se obtiene una aproximación de posibles eventos máximos y mínimos.
Por último, mediante los modelos de predicción estadística y simulación es posible tener aproximaciones de los comportamientos de los ríos para periodos cortos de tiempo, y que estas metodologías constituyen una herramienta que, una vez optimizada, permitirá obtener una aproximación a los cambios de ríos ante las intervenciones humanas o antrópicas. Esto implica que la utilización de modelos estocásticos para estudiar fenómenos naturales, que también son de carácter estocástico/aleatorio, es una herramienta altamente útil para la planificación, diseño y operación de problemas complejos asociados a los recursos hídricos.
REFERENCIAS
Bowerman, B. (2009). Pronósticos, series de tiempo y regresión: un enfoque aplicado. 4a. ed. México: Centro Ixtapaluca Edo. de México, CENGAGE Learning.
Box, G. E. P., y Jenkins, G. M. (1970). Time series analysis: forecasting and control, 1976. ISBN: 0-8162-1104-3.
Calle, E.; Angarita, H. y Rivera, H. (2010). Viabilidad para pronósticos hidrológicos de niveles diarios, semanales y decadales en Colombia. Ingenieria e Investigación, 30(2), 178-187.
Chatfield, C. (2003). The Analysis of Time Series: An Introduction. 6a. ed. Boca Raton, Florida: Chapman and Hall/CRC.
De Arce, R. y Mahía, R. (2003). Modelos Arima. Programa CITUS: Técnicas de Variables Financieras.
García M., B. y Baena E., R. (2015). El doble meandro abandonado del Guadalquivir en Cantillana (Sevilla): cambios de trazado y evolución geomorfológica. Geographicalia, (53), 101-119.
Guerrero, V. (2003). Análisis estadístico de series de tiempo económicas. 2a. ed. México, D.F.: Thomson.
Hildebrand, D. (1998). Estadística aplicada a la administración y a la economía. Serie de probabilidad y estadística. 3a. ed. México, D.F.: Addison Wesley Longman.
Ideam (2001). Primera Comunicación Nacional ante la Convención Marco de las Naciones Unidas sobre Cambio Climático. Bogotá, D. C.
Krajewski, L.; Ritzman, L. y Malhotra, M. (2008). Administración de operaciones. 8a. ed. México: Pearson Educación.
Lehner, B.; Döll, P.; Alcamo, J.; Henrichs, T. y Kaspar, F. (2006). Estimating the impact of global change on flood and drought risks in Europe: a continental, integrated analysis. Climatic Change, 75(3), 273-299.
Mauricio, J. (2007). Introducción al análisis de series temporales. Madrid: Universidad complutense de Madrid.
Ocampo, E.; Cabrera, A. y Ruiz, A. (2006). Pronóstico de bolsa de valores empleando técnicas inteligentes. Revista Tecnura, 9(18), 57-66.
Organización Meteorológica Mundial (OMM) (2003). Servicios de Información y Predicción del Clima y Aplicaciones Agrometeorológicas para los países andinos. Ginebra- Suiza.
Pabón, D. (1997). Variabilidad climática. En: Técnicas agrometeorológicas en la agricultura operativa de América Latina (pp. 99-103). Ginebra, Suiza: Organización Meteorológica Mundial.
Panel Intergubernamental sobre Cambio Climático (IPCC) (2007). Informe de síntesis. Contribución de los Grupos de trabajo I, II y III al Cuarto Informe de evaluación del Grupo Intergubernamental de Expertos sobre el Cambio Climático. Suiza.
Pinilla, L.; Pérez G., A. y Benito, G. (1995). Cambios históricos de los cauces de los ríos Tajo y Jarama en Aranjuez. Geogaceta, 18(10), 101-104.
Vargas, J.; Hernández, C. y Aponte, G. (2012). Comparación del modelo FARIMA y SFARIMA para obtener la mejor estimación del tráfico en una red Wi-Fi. Revista Tecnura, 16(32), 84-90.
Velásquez, J.; Dyner, I. y Souza, R. (2008). Modelado del precio spot de la electricidad en Brasil usando una red neuronal autorregresiva. Ingeniare. Revista Chilena de Ingeniería, 16(3), 394-403.
Yaglom, A. (1955). Correlation theory of processes with random stationary nth increments. Matematicheskii Sbornik (N. S.), 37(79), 141-196.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.