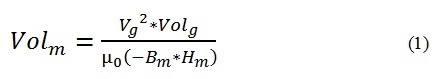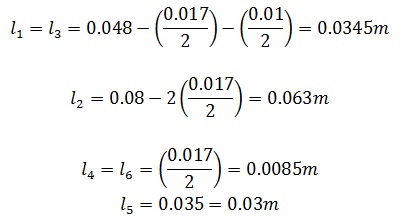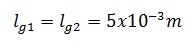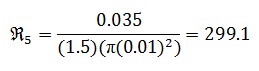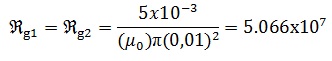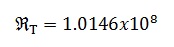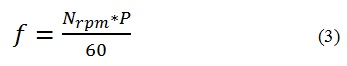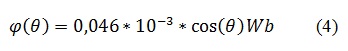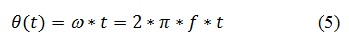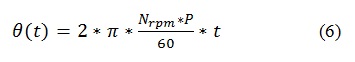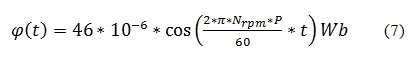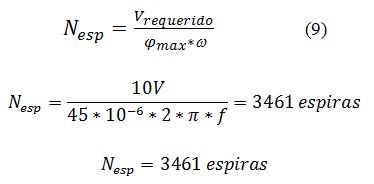DISEÑO DE UN GENERADOR DE FLUJO AXIAL USANDO EL MÉTODO DE ELEMENTOS FINITOS

DISEÑO DE UN GENERADOR DE FLUJO AXIAL USANDO EL MÉTODO DE ELEMENTOS FINITOS

AXIAL FLUX GENERATOR DESIGN BY USING THE FINITE ELEMENTS METHOD

Luisa Herrera ¹, Alexander Alarcón ¹, Edwin RivasTrujillo ¹

¹Universidad Distrital Francisco José de Caldas, Bogotá - Colombia

lufherrerag@correo.udistrital.edu.co, jaalarconv@udistrital.edu.co, erivas@udistrital.edu.co

Recibido: 27/10/2013 - Aceptado: 22/12/2013

Resumen

Este artículo presenta las simulaciones y cálculos realizados para el diseño básico de un generador de flujo axial usando el método de elementos finitos. Durante el proceso de diseño se evalúa el comportamiento electromagnético de los imanes seleccionados, se obtiene la característica B vs distancia, así mismo se define la geometría a usar para el montaje de las bobinas y los imanes, calculando el flujo máximo. Posteriormente se analiza la variación del flujo magnético dentro de la bobina en función de la posición angular, se define el número mínimo de espiras a usar por polo y se calcula la tensión inducida en la máquina asumiendo que tiene un sistema de 12 polos.

Palabras clave: Generador de flujo axial, método de elementos finitos, Campos electromagnéticos, generadores para turbinas eólicas.

Abstract

This paper shows simulations and calculations for the basic design of an axial flux generator by using the finite elements method. During the design process the electromagnetic behavior of the selected magnets is evaluated, B vs distance characteristic was obtained, same as coil and magnets geometries by calculation of the maximum magnetic flux value. Afterwards the magnetic flux in the coil was analyzed as a function of angular position, then the minimum number of turns coil required for one pole was calculated and finally the induced voltage was obtained assuming a machine with a 12 poles system.

Keywords: Axial flux generator, finite elements method, electromagnetic field, wind turbine generator.

1. INTRODUCCIÓN

Los generadores de flujo axial son máquinas eléctricas que permiten obtener señales de voltaje trifásicas o monofásicas de forma sinusoidal así como señales de voltaje DC. Se compone por un sistema de imanes permanentes que establecen un campo magnético constante B y un sistema de devanadossobre los que se produce un flujo magnético variable en el tiempo . Este flujo varía en función del tiempo gracias al movimiento relativo que se produce entre las bobinas y los imanes permanentes cuando el rotor gira.

Los generadores de flujo axial son usados para generación de energía eléctrica en turbinas eólicas y otros dispositivos de generación que tienen baja velocidad de rotación. Además permiten modificar la frecuencia de la señal de tensión, aumentando o disminuyendo el número de polos magnéticos del sistema, razón por la cual no se requiere de altas velocidades de rotación para lograr frecuencias elevadas en la señal de tensión. Esta característica lo hace ideal para su uso en turbinas eólicas de eje vertical, que no alcanzan velocidades de rotación elevadas pero si pueden tener un par de rotación alto.

Dada la importancia que está tomando este tipo de tecnología en aplicaciones relacionadas con la generación de energía eléctrica en turbinas eólicas, se plantea la necesidad de evaluar la tecnología, partiendo del diseño básico de un generador de flujo axial.

El diseño se hace con base en simulaciones de campo electromagnético estático usando el método de elementos finitos. Para esto se usa el software COMSOL MULTIPHYSICS. Durante el proceso de diseño se evalúa el comportamiento electromagnético de los imanes seleccionados, para obtener la característica B vs distancia. Luego se define la geometría a usar para el montaje de las bobinas y los imanes, calculando el flujo máximo y posteriormente se analiza la variación del flujo magnético dentro de la bobina en función de la posición angular.

Una vez obtenido el comportamiento del flujo se define el número mínimo de espiras a usar por polo y se calcula la tensión inducida en la máquina asumiendo que tiene un sistema de 12 polos.

2. CARACTERIZACIÓN DE LOS IMANES PERMANENTES

La tensión, la potencia generada, así como de la velocidad angular (w) a la que se mueve el generador depende del tipo de imanes que usa, para ello debe conocer la densidad de energía magnética del imán el cual depende del material de fabricación y de sus dimensiones [1], [2].

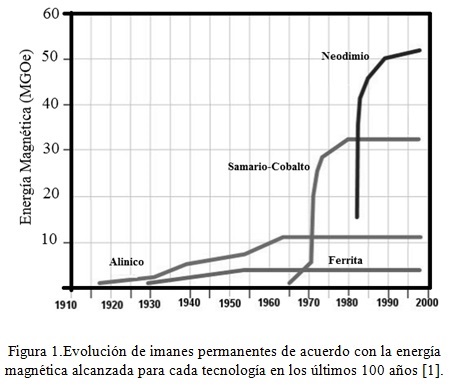
En la figura 1 se muestra la evolución de los materiales magnéticos en los últimos 100 años. Como se observa el neodimio es el material que ofrece las mejores condiciones energéticas.

El neodimio, comparado con imanes de materiales como cerámica o cobalto, requieren de un menor volumen para lograr la misma cantidad de energía magnética, lo cual indica que para una aplicación dada, se necesitarían imanes de menor tamaño de neodimio para realizar comparado con las demás tecnologías.

La relación entre el volumen (tamaño) y la densidad de campo se determina con base en la ecuación 1

“El tamaño del imán disminuye cuando aumenta la relación de energía B_m*H_m”

Dependiendo de la densidad de energía magnética del imán y de la densidad de campo es posible determinar cuál es el tamaño del imán requerido.

2.1. Características de los imanes de neodimio

Los imanes de neodimio son imanes permanentes fabricados con aleaciones de neodimio, hierro y boro, que combinados forman un compuesto cristalino tetragonal representado como Nd₂Fe₁₄B y tienen una permeabilidad magnética relativa que puede alcanzar valores de 100.000 y 300.000.

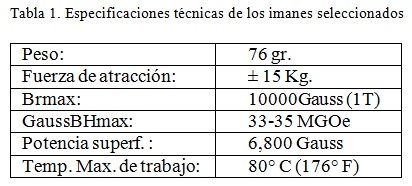
Partiendo de las especificaciones comerciales dadas por los fabricantes se seleccionó un imán de forma cilíndrica, con una densidad de energía magnética de 10000 gauss (1 T) según se ve en la tabla 1

Con los datos del iman seleccionado, inicialmente se realizan simulaciones de campo magnetico para identificar las trayectorias que siguen las lineas de campo y para determinar la forma en que disminuye la curva de campo mangnetico en funcion de la distancia fuera del material magnético [3].

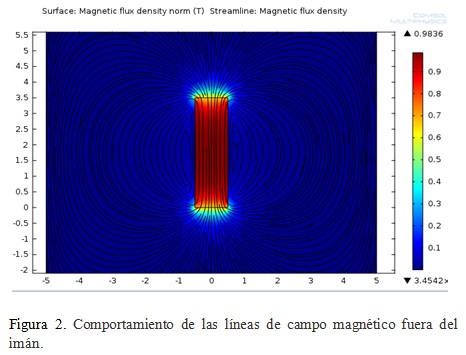
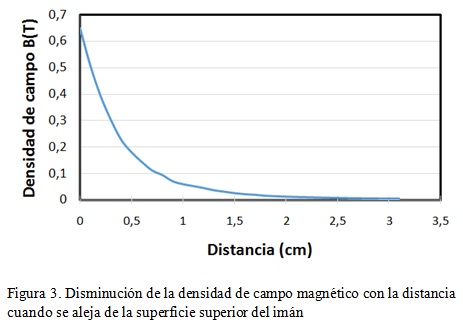
La caracterización de las lineas de campo magnético fuera del iman es necesaria ya que el campo magnético se atenua cuando aumenta la distancai a la que estan los materiales respecto de ls superficie del imán.Para identificar la trayectoria de las líneas de campo magnético se realizaron simulaciones de campo magnetico del imán seleccionado en COMSOL Multipysics que se presentan en las Figuras 2 y 3

La figura 2) muestra la trayectoria que siguen las lineas decampo magnético fuera del imán (en el aire) cuando se aplica una densidad de campo magnético igual a 10000 Gauss,encontrando que las líneas siguen trayectorias cerradas a lo largo del materialalcanzando densidades de flujo magnético máximas cercanas a los 0,65 Teslas.

La figura 3) refleja una reducción significativa en la densidad de campo magnético B a medida que aumenta la distancia, respecto a la superficie superior del imán. Esta es producida por el cambio en el material, ya que las líneas de campo salen del material magnético y se continúan su trayectoria a través del vacío, que tiene una permitividad relativa igual a 1.

3. PRINCIPIO DE FUNCIONAMIENTO DEL GENERADOR DE FLUJO AXIAL

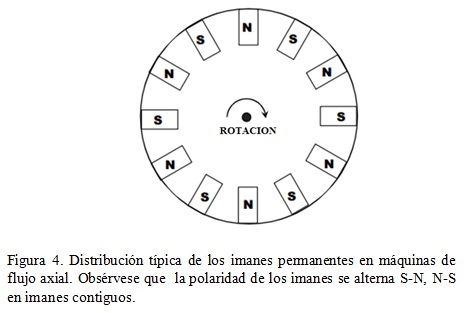
Los generadores de flujo axial funcionan debido al campo magnético generado por imanes permanentes, que se orienta en la misma dirección del eje del rotor. Los magnetos se distribuyen simétricamente alrededor del disco del rotor alternando la forma en que se orientan los polos magnéticos Norte y sur, tal como se observa en la figura 4 y figura 5

Las bobinas se distribuyen simétricamente en el estator según el tipo de generador a construir, corriente alterna (monofásico o trifásico y corriente directa).Para el diseño se deben tener en cuenta aspectos como el número de polos, tipos de imán y su densidad de energía magnética.

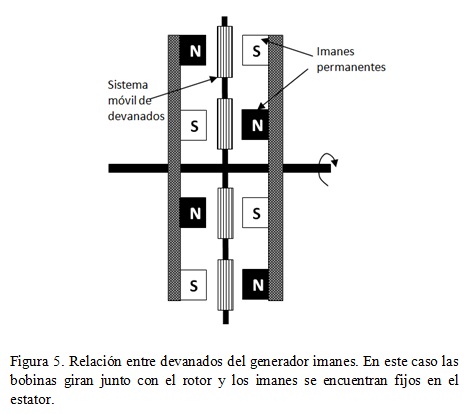
Aunque se tiene el mismo principio de funcionamiento, existen varias formas construcción que difieren en la forma de poner las bobinas, los imanes y los núcleos magnéticos.En algunos casos se instalan las bobinas en el rotor dejando los imanes fijos en el estator tal como se ve en la figura 5 y en otras versiones se hace al contrario; los imanes se mueven junto con el rotor y las bobinas se instalan fijas en el estator. En los dos casos, las bobinas ven un flujo magnético variable en el tiempo cuando el rotor gira, produciendo una tensión inducida en cada una de las bobinas de la máquina, que es proporcional a la variación del flujo con respecto al tiempo .

En cada una de estas versiones existen además, variaciones respecto a la forma de construir y ubicar las bobinas y los núcleos magnéticos.

3.1. Características y configuración geométrica usada para el diseño

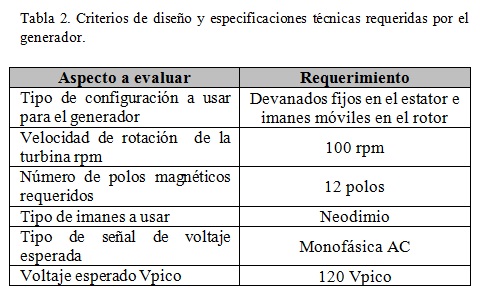
Para el diseño del generador es necesario definir aspectos como la configuración geométrica a usar, el tipo de imanes y sus características y el número de polos que se va a utilizar. Adicionalmente se requiere la velocidad de rotación esperada para la máquina, la señal de tensión y la magnitud del voltaje. Basados en estos aspectos se definen los criterios de diseño requeridos para el generador.

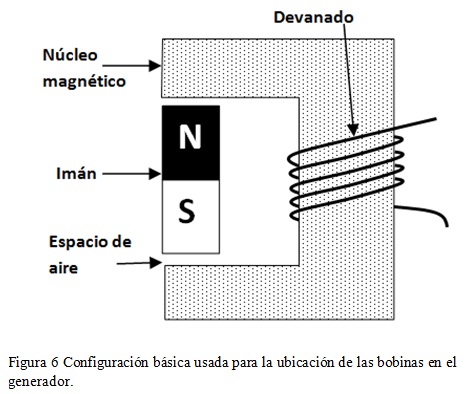
Para el diseño y simulación del generador se usa una configuración de bobinas fijas puestas en el estator y un sistema de imanes permanentes ubicados en el rotor de la máquina [4]. Existen varias configuraciones usadas para este tipo de máquinas[4], [5], [6], [7]; algunas permiten concentrar las líneas de campo aumentando el flujo magnético que pasa por el devanado y es una de estas la que se presenta en la figura 6, que indica la configuración a usar para el este caso.

Las bobinas se ponen sobre un núcleo magnético fabricado en forma de C que cierra el circuito magnético cuando el imán pasa dentro del espacio abierto tal como se ve en la figura 6.

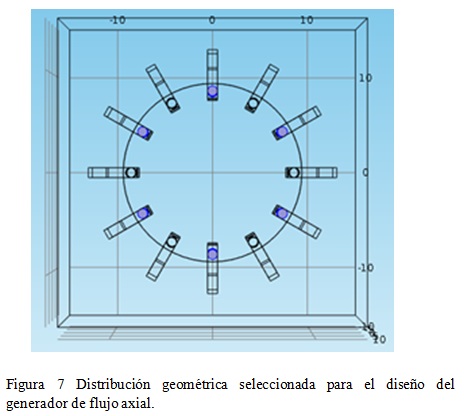
El generador está compuesto por 12 segmentos iguales distribuidas simétricamente en los 360 grados del disco del rotor (radio 10 cm), con una separación de 30 grados mecánicos entre sí tal como se ve en la figura 7.

Cada segmento se compone de un núcleo magnético que tiene 8 cm de alto, 4.8 cm de ancho y 1.5 cm de profundidad además de un imán de neodimio con un radio de 1 cm y una altura de 3.5 cm (figura 6).

3.2. Cálculos de la reluctancia del circuito magnético

Para analizar el efecto del núcleo en el circuito magnético se calcula la reluctancia con base en las características geométricas de cada segmento, ya que funcionan de manera independiente [8]. Los valores de permeabilidad magnética de los materiales se aproximan de acuerdo con valores típicos para cada material.

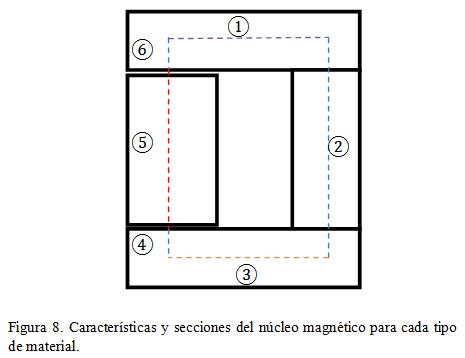
La permeabilidad magnética del neodimio (sección 5del núcleo, en la figura 8) se toma con un valor de:

μ=1.5

Y la permeabilidad del hierro (secciones 1, 2 y 3 de la figura 8) como:

μ=μ₀ μ_r=6.283185x10^-3

A continuación se presentan los cálculos de la reluctancia del circuito magnético para cada uno de los materiales que están en la trayectoria que siguen las líneas de campo magnético.Se incluyen los espacios de aire (entrehierro, secciones 4 y 6 de la figura 8).

Longitud media en metros, de las secciones que compone el núcleo magnético.

Longitud de la sección del entrehierro (aire):

Con los datos obtenidos anteriormente se calculan las reluctancias de cada una de las secciones del circuito magnético:

El área aproximada para cada núcleo ferromagnético es:

Reluctancia del imán:

Reluctancia del Aire:

Al comparar la reluctancia de cada material se observa que el aire tiene un valor muy alto comparado con el de los otros materiales, de manera que es el que determina el flujo magnético máximo que puede ver el devanado [8].

Con los valores calculados se obtiene la reluctancia total del circuito magnético.

Esta reluctancia determina el valor máximo del flujo magnético que puede ver el devanado.

Conociendo el flujo en el núcleo es posible calcular el número de espiras que requiere el devanado para lograr el voltaje requerido.

4. MODELAMIENTO DEL SISTEMA CON ELEMENTOS FINITOS

Para modelar el sistema se realiza una serie de simulaciones de las partes que componen el generador de flujo siguiendo los siguientes pasos: primero se simula uno de los segmentos que componen el generador, para establecer la trayectoria que siguen las líneas de campo dentro del núcleo magnético y para estimar la densidad de campo y el flujo magnético que ve el devanado.

Después se realizan simulaciones para el generador, incluyendo los doce segmentos que lo componen, a fin de identificar la trayectoria que siguen las líneas de campo entre los núcleos magnéticos que componen cada segmento, estimando el flujo magnético máximo que se puede obtener. Finalmente se obtiene el comportamiento del flujo magnético en función del ángulo recorrido por el devanado, cuando el generador está en rotación y se determina el número de espiras necesario para obtener el voltaje deseado.

El uso de programas como ComsolMultiphysics es cada vez más común para el diseño de máquinas eléctricas así como para evaluar el desempeño de máquinas existentes. Es usado por otros autores [10], [11], [12], quienes usan los métodos tradicionales y los métodos modernos para evaluar y comparar el funcionamiento de estas máquinas.

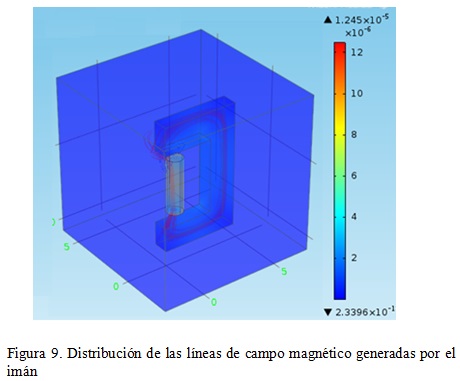
4.1. Distribución de las líneas de campo en un segmento de la máquina

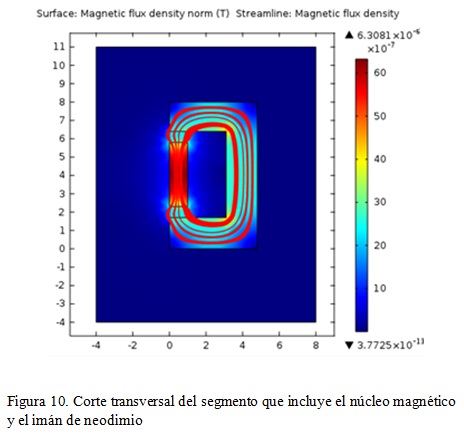
Las figuras 9 y 10 muestran las líneas de campo producidas por el imán dentro del núcleo magnético. En esta se observa que las líneas de campo circulan por el núcleo y no por el aire, mejorando así la eficiencia del sistema gracias a su baja reluctancia. Debido a esto aumenta el flujo magnético que pasa a través de las espiras del devanado, lo cual permite generar una mayor tensión inducida.

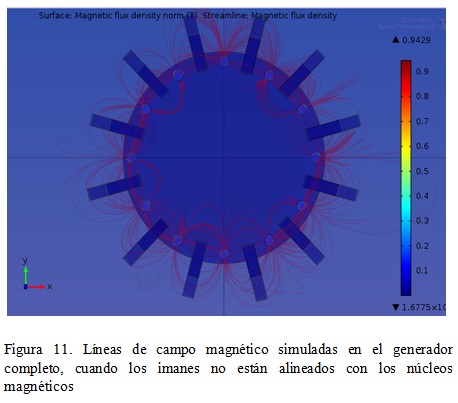
El comportamiento observado se presenta de igual forma en cada uno de los doce segmentos que componen el generador, cuando los imanes están perfectamente alineados con el núcleo durante el movimiento de rotación. Esto se ve en la figura 10, que muestra la simulación del sistema completo.

Para las demás posiciones el flujo magnético que ve la bobina depende de los dos imanes que se encuentran cerca a la posición del núcleo. Cada uno de los imanes aporta algunas líneas de campo en la dirección del núcleo haciendo que el flujo varíe según la distancia que hay entre el núcleo y el imán en movimiento.

4.2. Cálculo del flujo magnético

Para el cálculo de las tensiones inducidas es necesario conocer la forma en que varía el flujo magnético que ven las bobinas cuando la máquina está en movimiento. Para obtener el flujo se realizan simulaciones de campo magnetostático para las diferentes posiciones del núcleo respecto de los imanes, obteniendo la forma de la señale en función del ángulo recorrido.

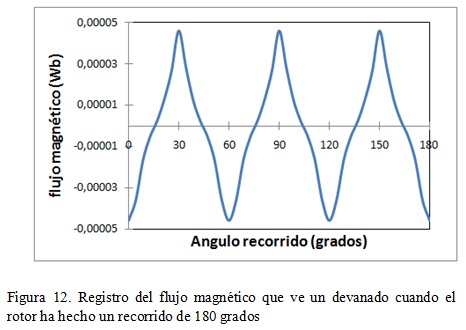
La figura 12 muestra la variación de flujo magnético que ve un devanado cuando el rotor hace un recorrido de 180 grados. Cada uno de los máximos positivos y negativos coincide con el momento en que el devanado se alinea perfectamente con un imán.

Los máximos positivos (0.046 mWb) se presentan cuando el devanado se alinea con el polo norte de un imán y el máximo negativo (-0.046 mWb) cuando se alinea con un polo sur.

Teniendo en cuenta que el generador consta de 12 imanes distribuidos simétricamente, el devanado registra una señal de frecuencia igual a seis ciclos completos por cada giro del rotor, lo que indica que para una velocidad de rotación N dada en revoluciones por minuto (rpm), se tiene un flujo magnético de frecuencia f igual a:

Donde N es la velocidad de la máquina en rpm y P es el número de pares de polos magnéticos con que se construye el generador (número de imanes dividido en 2), que para este caso es igual a 6.

Con los datos obtenidos y asumiendo que la forma de la señal sepuede representar como una función coseno, se obtiene una forma general para representar el flujo magnético que ve cada una de los doce devanados del generador:

Y expresando el ángulo en función de la velocidad de rotación de la máquina y del tiempo, se tiene una función que representa el flujo en función del tiempo donde:

Y reemplazando a f se tiene

Asumiendo que la máquina tiene una velocidad de rotación de 100 rpm el flujo queda expresado de la siguiente manera.

De esta manera se obtiene el flujo magnético en cada uno de los devanados cuando la máquina se mueve a 100 rpm.

5. Cálculo de la tensión inducida

La tensión inducida en este caso será la sumatoria de las tensiones de los doce devanados conectados en serie. Para alcanzar el voltaje deseado de 120 V, se debe tener un voltaje por bobina igual a Vdeseado/12 de manera que cada devanado debe generar 10 Voltios.

Para lograr este voltaje se calcula el número de espiras en cada devanado como se indica a continuación:

Bajo estas condiciones se puede garantizar que se obtiene un voltaje pico de salida igual a 120 voltios conectando los 12 devanados en serie siguiendo las polaridades de cada una de las bobinas de forma correcta.

De igual forma se siguen procedimientos para la construcción de muchos otros equipos basados en el funcionamiento de las máquinas de flujo axial, estos abarcan elementos como generadores eólicos, micro-turbinas de alta velocidad, motores de alto desempeño para vehículos eléctricos e incluso en vehículos de exploración extraterrestre [13], [14].

CONCLUSIONES

Al revisar el funcionamiento y características de la tecnología de generadores de flujo axial se encontró que presentan ventajas significativas desde el punto de vista mecánico y operativo, ya que permite la reducción en el tamaño de los generadores y ofrece un amplio rango de velocidades para su uso en algunos equipos, siendo las turbinas eólicas uno de los más demandan su uso en la actualidad.

Las configuraciones geométricas son siempre simétricas y fáciles de desarrollar. Gracias a esto es posible realizar simulaciones en las que se calculan la densidad de campo magnético y el flujo magnético en los materiales que componen el generador.

El método de simulación de elementos finitos permite realizar cálculos exactos de flujo magnético y conocer la distribución de las líneas de campo magnético con una gran precisión, lo cual permite mejorar las condiciones de trabajo y eficiencia de la máquina si así se requiere.

El flujo magnético visto por cada una de las bobinas presenta un comportamiento similar al de una señal senoidal, y produce una tensión inducida en las bobinas del estator que depende del número de espiras en cada segmento de la máquina así como de su velocidad de giro.

Referencias

1. B. Bochenkov, Sergey Lutz Novosibirsk; A Review Of Modern Materials Of Permanent Magnets, State Technical University, The 8th Korea-Russian International symposium on Science and Technology, IEEEXplore, Korus 2004.
2. U. S. Deshpande; Recent Advances in Materials for use in Permanent Magnet Machines -A Review, International Electric machines and drives conference, IEEEXplore, 2003.
3. Ana Mladenovic Vuckovic and Slavoljub Aleksic; Magnetic Field Determination for Different Block Permanent Magnet Systems,SER.: ELEC. ENERG. vol. 23, no. 3, pp 259-272, 2010.
4. A. Abarzúa Martínez; Aspectos de diseño de generadores sincrónicos de flujo axial para la aplicación en aerogeneradores, Memorias para optar al titulo de ingeniero Universidad de Chile, 2012.
5. W. Gonzalez, J.A. Tapia, R. Wallace, M.A. Valenzuela; Magnetic design considerations for an axial flux PM machine with field control capability, Flux magazine Cedrat technologies, No. 51, 2006,
6. C.C. Chan; Axial-Field Electrical Mahines-Design and Application, IEEETrans. on Energy Conversion, pp. 294-300, June 1987.
7. M. Aydin, S. Huang and T.A. Lipo; Axial flux permanent magnet disc machine: a review, Wisconsin Power electronics Research Center, Research Report, University of Wisconsin-Madison, 2004.
8. P. Campbell; The Magnetic Circuit of an Axial Field DC Electrical Machine, IEEE Trans. on Magnetics, pp. 1541-1543, Sept. 1975.
9. M. Cirani, C. Sadarangani and P. Thelin; Analysis of an innovative design for an axial flux torus machine, University dissertation from Stockholm: Elektrotekniska system.Division of Electrical Machines and Power Electronics, Royal Institute of Technology Teknikringen 33, Stockholm, Sweden, 2011.
10. R. Wallace, L. Moran, G. Cea, F. Peraz; Design and Construction of Medium Power Axial Flux Induction Motors, IEE Electrical Machines and Drives, pp 260-265, 1991.
11. M. Aydin, S. Husang, and T. A. Lipo; Optimum design and 3D finite element analysis of non-slotted and slotted internal rotor type axial flux PM disc machines, Power Engineering Society Summer Meeting, pp 1409-1416, 2001.
12. F. Caricchi, F. Crescimbini, O. Honorati, and E. Santini; Performance evaluation of an axial flux PM generator, Proceedings of International Conference on Electrical Machines (ICEM), pp 761-765, 1992.
13. R. J. Hill-Cottingham, P. C. Coles, J. F. Eastham, F. Profumo, A. Tenconi, G. Gianolio; Multi-disc axial flux stratospheric propeller drive, Proc. of IEEE IAS Annual Meeting Conference Record 2001, vol. 3, pp 1634-1639, 2001.
14. F. Caricchi, F. Crescimbini, O. Honorati, Modular; Axial-flux permanent magnet motor for ship propulsion drives, IEEE Trans. on Energy Conversion, vol. 14, pp 673-679, 1999.