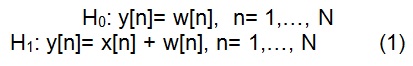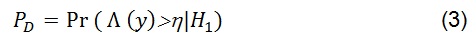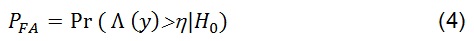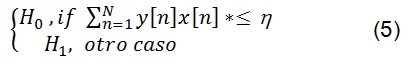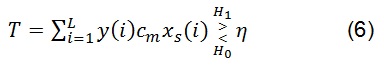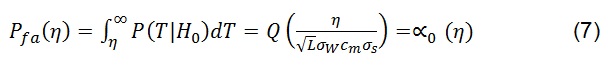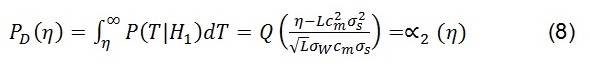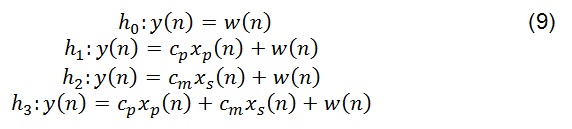EVALUACIÓN DEL DESEMPEÑO DE FILTRO ADAPTADO PARA RADIO COGNITIVA

EVALUACIÓN DEL DESEMPEÑO DE FILTRO ADAPTADO PARA RADIO COGNITIVA

MATCHED FILTER PERFORMANCE EVALUATION FOR RADIO

Danilo Alfonso López Sarmiento ¹, Octavio José Salcedo Parra ¹, René Geovani González Caballero ¹

¹Universidad Distrital Francisco José de Caldas, Bogotá - Colombia

dalopezs@udistrital.edu.co, osalcedo@udistrital.edu.co, rengoca@hotmail.com

Recibido: 24/10/2013 - Aceptado: 22/12/2013

Resumen

Este proyecto evalúa el rendimiento en la localización de filtros emparejados para la detección del espectro en Radio Cognitiva. Para resolver el problema del modelo de detección espectral se aplican dos hipótesis Ho y H1, las cuales generaron la probabilidad de detección (PD) y la probabilidad de falsa alarma (PFA) sobre una señal para un radio de ruido determinado (SNR). Se muestra como los filtros adaptados mantienen el rendimiento y el cumplimiento de los requisitos establecidos por el IEEE 802.22 en los cambios en la PFA y la potencia del ruido.

Palabras claves: Radio Cognitiva, Detección de Energía, Detección de filtros Emparejados, Radio de Ruido determinado, Probabilidad de Falsa Alarma, Probabilidad de detección.

Abstract

This project evaluates the performance of Matched Filter detection for spectrum sensing in Cognitive Radio. To solve spectral detection model problem, two hypotheses H0 and H1 are applied, which generated detection probability (PD) and false alarm probability (PFA) over a given noise ratio signal (SNR). It was shown how matched filters maintain requirements performance and compliance, according to IEEE 802.22 changes in PFA and noise power.

Keywords: Cognitive Radio, Energy Detection, Matched Filter Detection, Signal to Noise Ratio, Probability of False Alarm, Probability of Detection.

1. INTRODUCCIÓN

En el espectro electromagnético existen algunas bandas sin utilizar que se denominan espacios en blanco o bandas blancas (White Bands).La Radio Cognitiva (CR), permite utilizar estos espacios libres. El primer paso para la creación de un dispositivo CR es el desarrollo de técnicas que permitan la detección confiable de forma periódica de las partes inutilizadas del espectro, lo que se conoce como Detección Espectral (Spectrum Sensing). La premisa fundamental para el aprovechamiento de dichos espacios libres es la no interferencia con los usuarios licenciados o Usuarios Primarios, por lo que resulta evidente que para el desarrollo de futuros dispositivos, aplicaciones o sistemas basados en CR se necesita la detección de todo tipo de señales transmitidas a través del espectro.

2. DETECCIÓN DEL ESPECTRO

La Radio Cognitiva (Cognitive Radio, CR), utiliza mecanismos de aprendizaje y sensado. Percibe el entorno en el que opera mediante técnicas para detectar el espectro, posee conciencia de dicho entorno, así como de sus propias capacidades y recursos, varía y adapta, de forma inteligente, sus parámetros de transmisión/recepción, para poder actuar tanto de transmisor como de receptor, de forma autónoma. Todos los parámetros de transmisión de un CR deben poder reconfigurarse adaptándose a los cambios que se produzcan en su entorno.

2.1. Modelo del canal

El problema para sensar el espectro está en decidir que rango está disponible o no. Se debe discriminar entre dos hipótesis como se muestra en la ecuación que se relaciona en 1 [1][2][3][4]:

En donde x[n] representa la señal de un usuario primario, w[n] es el ruido y n el tiempo. La señal recibida y[n] es un vector de longitud L, en donde cada elemento del vector puede representar la señal recibida en una antena diferente. Se debe tener especial cuidado con la detección de señales muy débiles x[n]. La novedad para el sensado del espectro es la relación con la teoría de detección de tiempo establecido en donde la señal x[n] tiene una estructura que se deriva del uso de técnicas modernas de modulación y codificación en sistemas inalámbricos.

En la detección de señales, la tarea de interés, es decidir si la observación y fue generado sobre H₀ y H₁. Para esto se debe realizar una prueba estadística Λ (y) de los datos recibidos y, y comparando Λ (y) con un umbral predeterminado η como se observa en la ecuación que se referencia en 2 [1][5]:

La prueba estadística es utilizada para comprobar la disponibilidad del canal además de la precisión del detector. Para ello se determina:

• Probabilidad de detección (P_D). Probabilidad de que haya señal en el canal y se detecte correctamente.
• Probabilidad de falsa alarma (P_FA). Probabilidad de que no haya señal en el canal y el detector detecte algo.

La prueba estadística consiste en comparar el valor de la potencia, en dBm, con el valor umbral. Este valor se establece según el nivel de ruido, es decir, el valor de la densidad espectral de potencia del ruido.

El desempeño de un detector es cualificado en términos de su curva de Características de Operación de Receptor (Receiver Operating Characteristics, ROC), que genera la probabilidad de detección como se observa en la ecuación que se relaciona en 3:

Como una probabilidad de falsa alarma de acuerdo a la ecuación que se presenta en 4:

Por variación del umbral η, el punto de operación de un detector puede ser elegido en cualquier punto a lo largo de la curva ROC. Las curvas ROC es una relación entre la especificidad (Probabilidad de falsa alarma, P_FA) y la sensibilidad (probabilidad de detección, P_D) la cual está dada por 1- σ. En este caso la SNR se mantiene constante, mientras que se varía el valor del umbral (η) para obtener cada uno de los puntos de la ROC. El segundo método consiste en representar la probabilidad de detección P_D) vs. SNR para una probabilidad de Falsa Alarma determinada (P_FA) Esta curva es la más representativa en cuanto al funcionamiento real del detector, puesto que se obtiene después de fijar el umbral para garantizar una determinada P_FA) [6].

2.2. Técnica de Detección Espectral para Radio Cognitiva. Filtro Adaptado

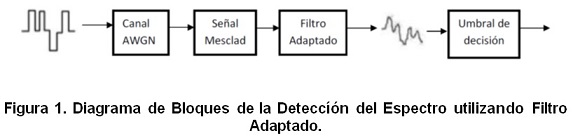
El filtro adaptado es un filtro lineal utilizado en el procesamiento digital de señales. Se utiliza para maximizar la SNR en presencia de ruido aditivo estocástico. Proporciona una detección coherente. La figura 1 muestra el diagrama de bloques en el cual una señal recibida de un UP se pasa a través de canal AWGN, luego a la señal de entrada r(t) = s(t) + n(t) se le aplica el filtro adaptado [5]. El filtro adaptado correlaciona la señal con la versión desplazada en el tiempo y el resultado de comparar la salida final del filtro adaptado y el umbral predeterminado, con lo cual determinará la presencia del usuario autorizado.

La principal característica de este filtro que es la respuesta al impulso ante una señal a la entrada , será una réplica de la señal rotada sobre el eje t=0 y retardada un tiempo , como se ve en la figura 3 tomada de [7].

Un filtro adaptado efectivamente requiere demodulación de la señal de un UP. Esto significa que la radio cognitiva tiene un conocimiento a priori de la señal de la capa Física y de la MAC de un PU, por ejemplo, Tipo y orden de modulación, forma de impulso, el formato de paquete. Tal información podría ser pre-almacenado en la memoria CR. La parte delicada es que para la demodulación tiene que lograr coherencia con la señal de usuario primario mediante la realización de temporización y sincronización de portadora, incluso ecualización de canal. Esto sigue siendo posible, ya que la mayoría de usuarios primarios tienen pilotos, preámbulos, palabras de sincronización o códigos de ensanchamiento que pueden ser utilizados para la detección coherente. Por ejemplo: la señal de TV de banda estrecha tiene piloto para portadora de audio y video, los sistemas de CDMA han dedicado códigos de ensanchamiento para canales pilotos y de sincronización; los paquetes OFDM tienen preámbulos para la adquisición de paquetes. La principal ventaja del filtro adaptado es que, debido a su coherencia este requiere menos tiempo para lograr una ganancia de procesamiento elevada [8] [9]. Sin embargo, un inconveniente significativo de un filtro adaptado es que la CR necesitaría un receptor dedicado para cada clase de UP [9].

La salida de un filtro adaptado se compara con un umbral para decidir si la señal de UP existe o no. Por tanto, la decisión binaria es [8][9][10], como se observa en 5:

Donde η es el umbral.

Para este caso, x [n] se sustituye por xp [n], que es la señal piloto del usuario primario. La ventaja principal es que el filtro adaptado necesita menos tiempo para alcanzar la ganancia de procesamiento gracias a la detección coherente. Para la demodulación, sin embargo, la CR tiene que tener temporización, sincronización de portadora e incluso ecualización del canal. Por lo tanto, la CR necesita un receptor dedicado para cada tipo de sistema primario, lo que aumenta la complejidad como un reto significativo para el uso del filtro adaptado cuando el sistema de destino está fuera de múltiples sistemas posibles, incluso para la realización programable.

En [3] se presentan dos posibles casos aplicados para el sensado del espectro utilizando Filtro Adaptado. El primero es el caso ideal, donde no hay presencia de UP, y el caso no ideal, en donde existe presencia de señales UP.

Para el caso ideal el filtro adaptado recibe una señal como la planteada en la ecuación (1), con L ≤ M, x[n]= cmxs(n). El detector óptimo es un filtro adaptado como se muestra en 6:

En donde η es el umbral. cm y xs son conocidos por el receptor SU y y(i) es Gaussina bajo ambas hipótesis, T es también Gaussiana. La Probabilidad de falsa alarma y la probabilidad de detección se relacionan en 7 y 8:

En donde .

Para el caso no ideal, el filtro adaptado recibe una de las 4 posibles señales, lo cual se puede observar en 9:

En donde n= 1, L. w(n) es el ruido, x_p (n) es la señal PU, x_s (n) es la señal SU, y c_p > 0 satisfaciendo es la ganancia del canal.

En [9] se presenta un estudio de técnicas de detección del espectro con relación a la probabilidad óptima para detección de energía, detección de filtrado adaptado, detección ciclostationario, detección basado en valores-propios, detección de conjuntos espacio-tiempo. Revisión de métodos robustos de detección y la detección del espectro Cooperativo con varios receptores. Se analizan métodos de detección que necesitan poca información previa sobre la señal de la fuente y el canal de propagación. Se discuten problemas prácticos tales como la incertidumbre de potencia de ruido, un análisis teórico con relación a la prueba de la distribución estadística y el ajuste del umbral.

En [10] se muestra un algoritmo parcial para un filtro adaptado, el cual consta de 3 pasos principales:

1. Extracción de un conjunto predeterminado de parámetros/características de la señal recibida.
2. Uso de las características extraídas para la toma de decisiones sobre la presencia de una transmisión prevista.
3. Exploración de los conocimientos adquiridos sobre los UP activos para la caracterización de espectro multi-dimensional.

En [11] se presenta una investigación referente a la robustez de algunos métodos de detección haciendo un análisis teórico y simulaciones para detectores basadas en valores propios/covarianza, detección cooperativa y detectores ciclo estacionarios. El sensado del espectro en CR tiene unos pequeños cambios especiales, con respecto a otros sistemas:

1. Un dispositivo de CR necesita detectar la señal primaria en una muy baja SNR. Se trata de superar el problema del nodo oculto: un sensor escucha una señal muy débil del transmisor primario, pero puede perturbar al receptor primario si transmite (aquí el receptor primario puede ser un nodo oculto). Para evitar la interferencia, una posible solución consiste en que el sensor debe tener la capacidad de detección a muy baja SNR. Por ejemplo, en el estándar de 802,22, el requerimiento de sensibilidad de detección está alrededor de -20dB.
2. La incertidumbre en el canal de Propagación dificulta la detección del espectro. En las comunicaciones inalámbricas, es común que el canal tenga desvanecimiento por multitrayectos y dispersión por tiempo.
3. Es difícil sincronizar la señal recibida con la señal primaria en tiempo y frecuencia. Esto provocará que algunos métodos como preámbulo/piloto sean menos eficaces.
4. El nivel de ruido puede cambiar con el tiempo y el lugar, lo que genera incertidumbre en cuanto a la detección de potencia de ruido [12], [13], [14], [15]. Esto hace que los métodos que dependen de la potencia de ruido resulten poco fiables.
5. El ruido no puede ser blanco, lo que afectará a muchos métodos con asunción al ruido blanco.
6. Puede haber interferencias procedentes de transmisores intencionales o no intencionales. Esto requiere que el detector tenga la capacidad de suprimir la interferencia mientras se identifica la señal. Aunque existen muchos métodos, algunos basados en suposiciones ideales pueden no trabajar muy bien en ambientes de radio hostiles. Se requiere que el sensado del espectro sea robusto en lo desconocido y quizás para canales con variaciones en el tiempo, ruido e interferencia.

En [16] se proporciona la aplicación de técnicas de detección de espectro y análisis de rendimiento utilizando detección de energía, filtro adaptado, detección basada en características ciclotationarias y basado en valor propio. También se realiza una comparación entre diferentes técnicas de espectro de detección sobre la probabilidad de detección base. Se evidencia que a mayores valores de SNR como 40 dB todas las técnicas dan resultados 100%. Sin embargo, en entornos ruidosos el rendimiento se degrada. Si se compara los resultados con menores valores de SNR se concluye que la detección de energía funciona mejor debido a su característica inherente. Los resultados obtenidos para la detección de filtro adaptado con 10 dB, ciclostationario con -10 dB y valor propio -20 dB. Para valores altos de SNR como 20dB y por encima de todas las técnicas dan resultados 100% pero como la relación señal a ruido reduce el rendimiento de diferentes técnicas. A menores valores de relación señal a ruido de filtro adaptado y detector de energía da resultados del 30%. En caso de que, como máximo autovalor dicha técnica de detección ofrece mejores resultados que las otras técnicas.

3. SIMULACIÓN EN MATLAB DE LA TÉCNICA FILTRO ADAPTADO PARA LA DETECCIÓN DEL ESPECTRO

En este capítulo se realiza la simulación de la técnica de detección del espectro Filtro Adaptado. Teniendo en cuenta una señal determinista con ruido blanco gaussiano, en donde tanto la señal como el ruido son complejos.

Existen diferentes tipos de detectores que se pueden utilizar en diferentes aplicaciones, como el detector bayesiano, detector de máxima verosimilitud (ML) y detector Neyman-Pearson (NP). En este trabajo se utiliza el detector NP ya que puede garantizar la probabilidad de falsa alarma (P_FA) dentro de un cierto nivel.

En las aplicaciones de arreglo de fase, es necesario decidir entre dos hipótesis, una hipótesis, llamada la hipótesis nula (H₀), establece que los datos observados se componen de sólo ruido, y la otra hipótesis (H₁.), llamada la hipótesis alternativa, establece que los datos observados se componen de una señal determinista más el ruido. Para resolverla, debe formular una regla de decisión que utiliza criterios especificados para elegir entre las dos hipótesis. Para este caso se utiliza el criterio de optimalidad Neyman-Pearson (NP).

3.1. Señal recibida y ruido

La señal recibida se asume como x(t) = s(t) + n(t), en donde s(t) es la señal y n(t) es el ruido. Asumiendo que la potencia de la señal recibida es igual a 1 watio y la potencia de ruido se determina de acuerdo a la SNR. Se presume una SNR de 10 dB, con una varianza de ruido de 0.1 watio. Se genera una forma de onda de pulso rectangular de 25 ms de duración con una PRF de 100 MHz. Se utiliza la función radareqpow para determinar la potencia máxima requerida para detectar un objetivo. La SNR se basa en una probabilidad de falsa alarma de 1-6 para un detector no coherente. Se crea un receptor y un filtro adaptado para la forma de onda rectangular.

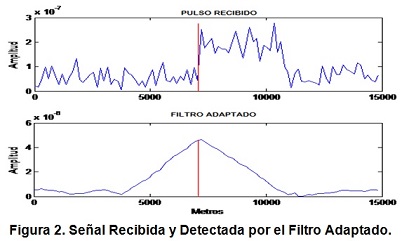
La señal del usuario primario es un pulso rectangular el cual se ha contaminado con ruido blanco gaussiano (figura 2), el detector filtro adaptado, el cual conoce las características de la señal lo detecta.

3.2. Para un receptor coherente

La señal recibida se modela como una copia de la señal original con un error de fase aleatoria.

Para maximizar la probabilidad de la detección P_D, limitando al mismo tiempo la probabilidad de falsa alarma, P_FA en un nivel especificado a. El detector NP puede estar formado como una prueba de razón de verosimilitud (LRT) de la ecuación (/7).

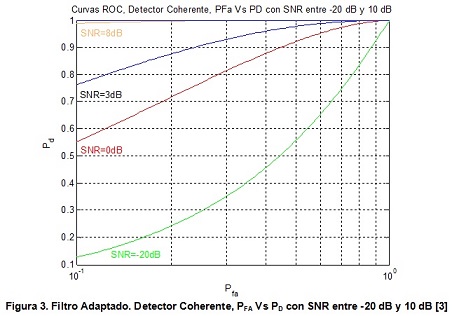
La estadística suficiente, es decir, el valor que se utiliza para comparar con el umbral de detección, para un detector coherente es la parte real de la señal recibida después del filtro adaptado. El umbral de SNR requerido para un ruido complejo, blanco gaussiano para el detector de NP se puede calcular utilizando la función npwgnthresh. Tener en cuenta que este umbral, aunque también en la forma de un valor de SNR, es diferente a la SNR de la señal recibida. El umbral SNR es un valor calculado basado en el rendimiento de detección deseada, en este caso la PFA, mientras que la SNR de la señal recibida es la característica física de la señal determinada por el entorno de propagación, la forma de onda, la potencia de transmisión, etc. Por otro lado, una falsa alarma se produce cuando la detección muestra que hay un objetivo, pero realmente no lo hay, es decir, la señal recibida pasa el umbral cuando sólo hay ruido presente. La probabilidad de error del detector para detectar un blanco cuando no lo hay se da por la P_FA. Se utilizan las curvas ROC Para ver la relación entre SNR, P_D y P_FA, (figura 3):

Se puede observar en la tabla 1 que la medida P_D = 0,1390 y P_FA = 0,0009 obtenido para el valor SNR de 3 dB se adapta a un punto teórico de la curva ROC.

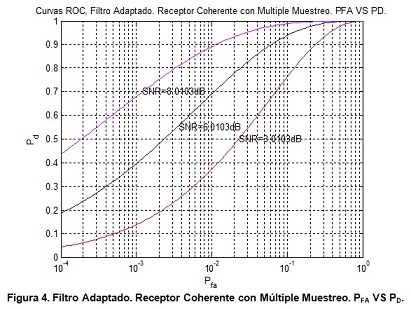
Si se puede utilizar muestreo múltiple, entonces el filtro adaptado puede producir una ganancia extra en SNR y por lo tanto mejorar el desempeño. En la práctica se puede usar un longer waveform para conseguir esta ganancia. En el caso de procesamiento de la señal en tiempo discreto, se puede obtener el muestreo múltiple incrementando la frecuencia de muestreo.

Se puede observar en la figura 4 que el punto dado de P_FA y P_D, caen a la derecha de la curva. Sin embargo, la SNR correspondiente a la curva ROC es la SNR de un muestreo simple a la salida de un filtro adaptado. Esto muestra que, se puede utilizar múltiples muestras para el desempeño en la detección, el umbral de muestreo simple en SNR no varía comparado con el caso de una simple muestra. Esto no cambia porque el valor del umbral es determinado por P_FA. Sin embargo, el umbral final T, se modifica debido a la ganancia extra del filtro adaptado. El P_FA resultante remains es el mismo comparado con el caso donde solo un muestreo es utilizado para la detección. Sin embargo, la ganancia extra del filtro adaptado genera una P_D de 0.1390 a 0.3947.

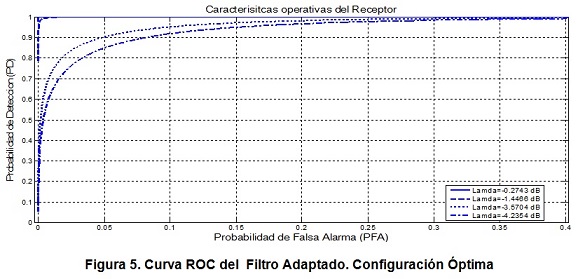
Para visualizar el desempeño del filtro adaptado se optimizan las variables de tal forma que las curvas ROC son óptimas. Para este caso se calcula el nivel de umbral teniendo en cuenta el valor deseado mínimo de la SNR y la P_FA y P_D. A continuación se presentan las curvas ROC óptimas para P_D vs P_FA y P_D vs SNR.

En la figura 5 se establece el desempeño del detector en función del valor del umbral, y se obtiene como resultado para señales con SNR = -20dB el valor del umbral es -1.4466 dB.

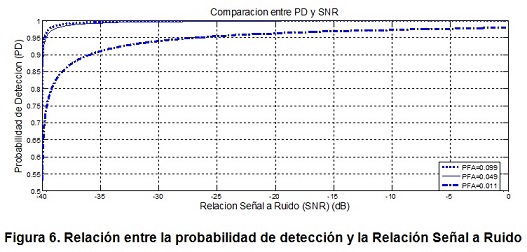
Con el valor del umbral establecido se procede a comparar el funcionamiento del detector confrontando la probabilidad de detección en función de la Relación Señal a Ruido ante variaciones en la probabilidad de falsa alarma. Los resultados obtenidos son los mostrados en la figura 6, para señales por debajo de SNR=-20 dB este detector presenta un alto grado de confiabilidad incluso para señales de hasta SNR = -40 dB cuando se tiene una P_FA =0.099, esto le da la posibilidad de tener un mayor rango de acción.

3.3. Configuración de la Tarjeta USRP N210

Para la configuración de la tarjeta USRP N210 en GNU Radio, se utilizó Linux Ubuntu 12.4, un computador personal con las siguientes especificaciones: intel Core i7, Q720, 1.6 GHz, 4 GB de RAM. Una antena con ancho de banda de 25 MHz a 1900 MHz.

La tarjeta USRP N210 se conecta utilizando el puerto gigabit Ethernet con el Computador a través de una tarjeta Gigabit Ethernet y un conversor a USB. Se instala UHD (Universal Hardware Devices) el cual proporciona el driver de host y la interfaz programable para el desarrollo de aplicaciones independientes. La tarjeta se comunica utilizando IP/UDP. La dirección IP por defecto para USRP N210 es 192.168.10.2.

Para la instalación de GNU Radio se utiliza: $ wget http://www.sbrac.org/files/build-gnuradio && chmod a+x ./build-gnuradio && ./build-gnuradio.

3.4. Limitaciones en Hardware para el Detector de Filtro Adaptado

Sólo se cuenta con una tarjeta USRP N210, la cual es utilizada como receptora de la señal a detectar. Lo ideal para realizar la implementación es tener un escenario completamente controlado, es decir contar con una tarjeta USRP adicional que funcione como transmisora en donde se estipulen todos los parámetros requeridos para que el detector funcione correctamente. Recordando que el detector de filtro adaptado debe conocer las características de la señal a detectar como: Tipo y orden de modulación, Frecuencia central, forma de impulso, el formato de paquete, etc.

3.5. Filtro Adaptado en USRP N210

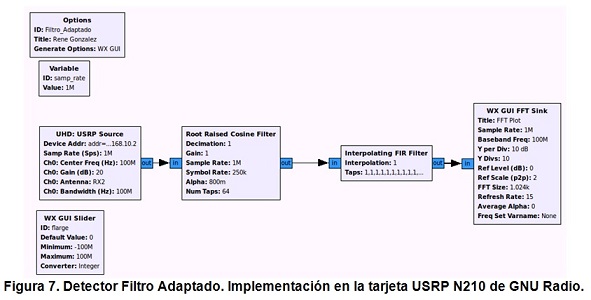
El receptor de la figura 7 tiene incluido un bloque correlacionado. Este hace uso de un filtro FIR cuyos coeficientes se determinan del código de secuencia m inverso en el tiempo, de tal manera que la convolución se convierte en una correlación. Este es el principio de un filtro adaptado. La frecuencia de trabajo es 100 MHz, sin embargo, la frecuencia real de Tx y Rx de los osciladores locales en dispositivos USRP puede desviarse de la frecuencia en unos pocos kHz.

Con el fin de sintonizar con precisión la frecuencia de los osciladores locales y reducir la diferencia de frecuencia entre el receptor y el transmisor, se utiliza los deslizadores. El desplazamiento de fase entre los dos osciladores no debe ser significativa, menos de 20 °, durante la correlación en los chips Lc [16].

Como se observa en la figura 7, se hace un llamado a la tarjeta USRP N210 a través del bloque UHD: USRP Source, configurando los parámetros de frecuencia central que para este caso de estudio es 100 MHz, la ganancia de la antena de 20 dB de acuerdo con las especificaciones. A la salida de la antena se configura el filtro correlacionado que contiene las características de la señal a sensar. En recepción la señal se convierte hacia una frecuencia menor. La configuración estándar de la FPGA incluye 4 convertidores digitales de bajada (DDC) para disminuir la tasa de muestreo (diezmado). El factor de diezmado no puede tomar cualquier valor (sólo pares entre 8 y 512) y por temas de eficiencia a veces es recomendable que sea potencia de 2 (para algoritmos como FFT). Es por esto que se realiza el proceso para cambiar la tasa de muestreo, teniendo en cuenta que la interface para el intercambio de datos entre el computador y la tarjeta es a través del puerto Gigabit Ethernet, y la tasa de muestreo de los convertidores DAC/ADC es de 400 MS/s.

4. RESULTADOS OBTENIDOS EN LA TARJETA USRP N210

En la figura 8 se muestra la configuración del sistema para la captura de información a través de la tarjeta USRP N210 y con ayuda del analizador de Espectro se visualizan los niveles de energía detectados por la tarjeta.

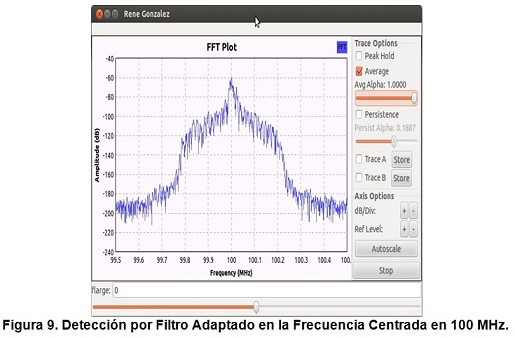
La respuesta de impulso de canal medida a la salida del filtro correlacionador de la tarjeta USRP N210 se muestra en la figura 9 sobre la frecuencia central de 100 MHz. La observación de la respuesta al impulso proporciona información útil acerca de las imperfecciones introducidas por el canal. Se nota claramente que se produce una atenuación de la señal debido a los acoples internos y filtros de la tarjeta USRP. El nivel de potencia del detector de energía es de -73 dB y el nivel de potencia del filtro adaptado es de -60 dB (figura 9).

4.1. Curvas ROC para el Filtro Adaptado

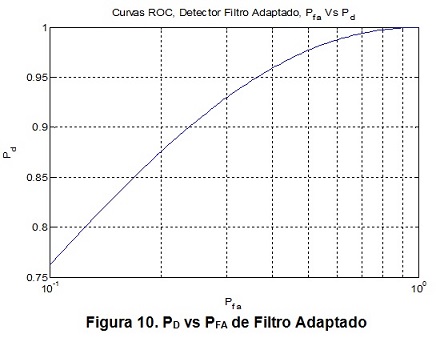
Los datos de threshold = 0.1309 y de PD = 0.7051 corresponden a la curva de PD vs P_FA de la figura 10 para el detector de Filtro Adaptado. El valor de PD es inferior al valor más bajo de P_D = 0,850 del detector de energía. Esto es debido a que se requiere de un escenario completamente controlado para la realización del filtro adaptado, con dos tarjetas USRP N210 configuradas una como transmisor y la otra como receptor, con el fin de conocer todas las características de la señal a sensar.

La figura 10 del detector de filtro adaptado corresponden claramente a las curvas ROC descritas anteriormente, evidenciando que los modelos implementados en la tarjeta USRP N210 están acordes y cumplen los requerimientos expuestos anteriormente.

CONCLUSIONES

Las curvas ROC obtenidas para el filtro adaptado están acordes con lo planteado en [17], [11] y [18], al igual que los niveles de SNR, P_D y P_FA .

Se comprobó en la configuración del filtro acoplado la característica que éste presenta al momento de tener señales contaminadas por ruidos Gaussiano de maximizar la SNR de dicha señal. De igual manera que mantienen el desempeño y cumplimiento de los requerimientos establecidos por el IEEE 802.22 ante variaciones de P_FA y potencia de ruido, llegando valores de P_FA = 0.008 y SNR = -28 dB.

La señal detectada a través de la tarjeta USRP N210 utilizando detección por filtro adaptado atenúa la señal cerca de -13 dB debido a la acción de los filtros. Para el caso del detector de energía la señal no sufre una atenuación, lo cual es comprobada con las mediciones obtenías a través del analizador de espectro.

Referencias

1. E. Axell, G. Leus, E. Larsson, H. Vincent; Spectrum sensing for cognitive radio : State-of-the-Art and Recent Advances, IEEE Signal Processing Magazine, Vol 29, Issue3 3, pp 101-116, Mayo 2012.
2. S. Ziafat, W. Ejaz, H. Jamal; Spectrum sensing techniques for cognitive radio networks: Performance analysis, Intelligent Radio for Future Personal Terminals (IMWS-IRFPT), 2011 IEEE MTT-S International Microwave Workshop Series on, pp 1-4, Daejeon, August, 2005.
3. L. Ma, Y. Li, A. Demir; Matched filtering assited energy detection for sensing weak primary users signals, Acoustics, Speech and Signal Processing (ICASSP), 2012 IEEE International Conference on, pp 3149-3152, Kyoto, March, 2012.
4. L. Pedraza, F.Forero, I.P. Páez; Detección de espectro para radio cognitiva. Revista chilena de ingeniería, Vol. 20 No 2, pp 197-210, 2012.
5. J. Ma, G. Zhao, Y. Li; Soft combination and detection for cooperative spectrum sensing in cognitive radio networks, IEEE Transactions on Wireless Communications, Vol 7, Issue 11, pp 4502-4507, 2008.
6. R. Brodersen, A. Wolisz, A. Cabric, S. Mubaraq, D. Willkomm; CORVUS : A cognitive radio approach for u sage of unlicensed spectrum, CiteSeerX, Germany, 2005.
7. T. T. Ha; Theory and design of digital communication systems, Cambridge University Press, pp 300–320, 2011.
8. Y. Chang, Y. Zeng, E. Peh, A. Tuan; Sensing-throughput tradeoff for cognitive radio networks, IEEE Transactions on Wireless Communications, Vol 7, No 4, pp 1326 - 1337 April, 2008.
9. D. Cabric, S. Mubaraq, R. Brodersen; Implementation issues in spectrum sensing for cognitive radios, Signals, Systems and Computers, 2004. Conference Record of the Thirty-Eighth Asilomar Conference on, University Of California, Berkely, pp 772 – 776, November, 2004.
10. T. Yucek, H. Arslan; Spectrum characterization for opportunistic cognitive radio systems, Military Communications Conference, 2006, MILCOM 2006, IEEE, PP 1-6, October, Whashington, 2006.
11. Y. Zeng, Y. Cahng; Robust spectrum sensing in CR, IEEE 21st international symposium on personal, Indoor and Mobile Radio Communications Workshops, Turkey, 2010.
12. A. Sonnenschein, P. M. Fishman; Radiometric detection of spread spectrum signals in noise of uncertainty power, IEEE Transaction, On Aerospace and Electronic Systems, Vol. 28, No 3, pp 654–660, 1992.
13. A. Sahai, D. Cabric; Spectrum sensing: fundamental limits and practical challenges, in Proc. IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN), Baltimore, November, 2005.
14. R. Tandra and A. Sahai; Fundamental limits on detection in low SNR under noise uncertainty, Wireless Networks, Communications and Mobile Computing, 2005 International Conference on, pp 464-469, June, 2005.
15. R. Tandra, A. Sahai; SNR walls for signal detection, IEEE Journal of selected topics in signal processing, Vol. 2, pp 4–17, Feb, 2008.
16. A. Le Naour, O. Goubet, C. Moy, P. Leray; Spread spectrum channel sounder implementation with USRP platforms, SUPELEC/IETR, Cesson-Sévigné Cedex, France, 2013.
17. Y. Zeng, Y. Liang, A. Tuan, R. Zhang; A review on spectrum sensing for cognitive radio: Challenges and solutions, Hindawi Publishing Corporation, EURASIP Journal on Advances in Signal Processing, 2010.
18. A. Ghasemi, E. Sousa; Interference aggregation in spectrum sensing cognitive wireless networks, IEEE Journal of Selected Topics in Signal Processing, Vol 2, No 1 Feb, 2008.