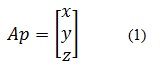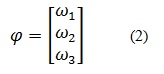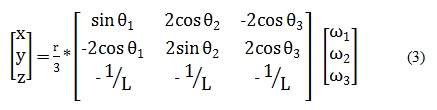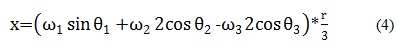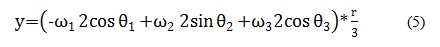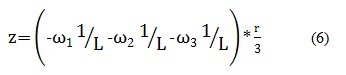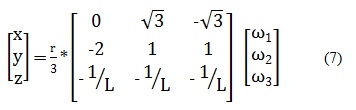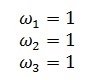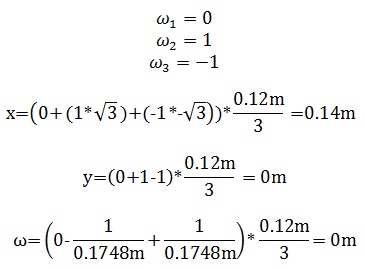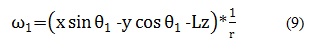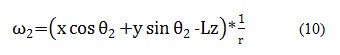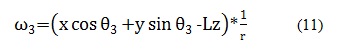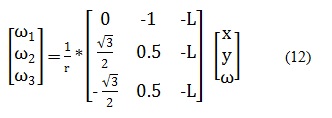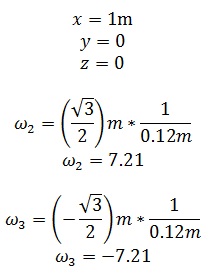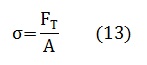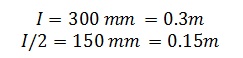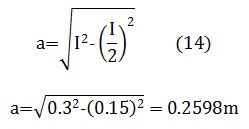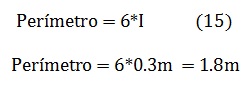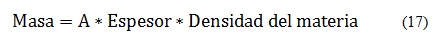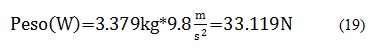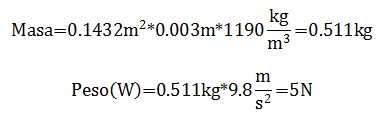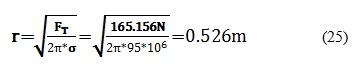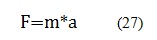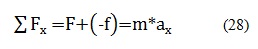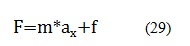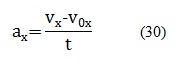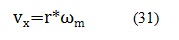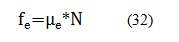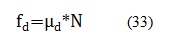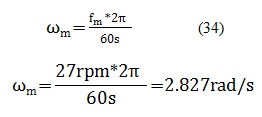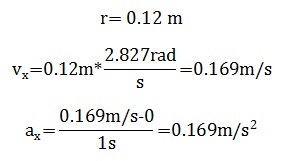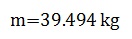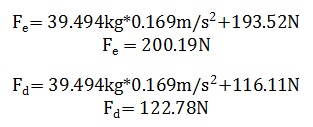DOI:
https://doi.org/10.14483/2248762X.6356Publicado:
2014-05-28Número:
Vol. 5 Núm. 1 (2014)Sección:
InvestigaciónROBOT TRANSPORTADOR Y DISTRIBUIDOR DE OBJETOS SEGÚN SU PESO
Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
ROBOT TRANSPORTADOR Y DISTRIBUIDOR DE OBJETOS SEGÚN SU PESO
CARRIER AND OBJECTS DISTRIBUTOR ROBOT ACCORDING TO OBJECT’S WEIGHT
Luis Efrén Barrero Páez 1, Andrés Felipe Villegas Caballero 2, Diana Carolina Gómez Gómez 2
1 Universidad de San Buenaventura - Colombia, 2 Universidad Manuela Beltrán
luisbarreropaez@gmail.com , felipevillegas81@gmail.com, carola369@gmail.com
Recibido: 01/10/2013 - Aceptado: 22/12/2013
Resumen
El presente artículo presenta los criterios de diseño para la construcción de un robot omnidireccional, a partir del planteamiento de modelos matemáticos, como el modelo cinemático directo e inverso, con el cual es posible interpretar que tipo de desplazamiento posee el robot y en qué circunstancias se da dicho desplazamiento; el estudio de la resistencia de materiales permite conocer si el material con el cual se pretende construir la estructura es lo suficientemente resistente para soportar no solo su propio peso, si no también el peso del objeto que debe transportar. Finalmente se establece la fuerza que deben ejercer los actuadores para vencer la fuerza de fricción. Así como el esquema de control general del proyecto y de los motores.
Palabras clave: Modelos cinemáticos, resistencia de los materiales, fuerza normal, fuerza de fricción.
Abstract
This paper shows the design criteria to build an omnidirectional robot from mathematical modeling approaches, such as: the direct and inverse kinematic model, which allows to interpret which kind of movement has the robot performed and under what kind of circumstances, the study of the material resistance will allow us to know how resistant should it be to bear not only its own weight but also the object to be transported. On the other hand the strength that must be performed by actuators to overcome the friction power. As these parameters will enable the robot move. Well as the control scheme of the project and the engines. It will also embrace the project general control and engines schema.
Keywords: Kinematic models, material strength, normal force, frictional force.
1. INTRODUCCIÓN
A través de la historia, el hombre gracias a su curiosidad e ingenio ha dado lugar a grandes inventos que han hecho de nuestra vida algo más sencillo. Como la mayoría de maquinas creadas por el hombre buscan mejorar muestro estilo de vida y a partir de la revolución industrial tan bien hacer que la industria sea más productiva por medio de la automatización, lo cual hace parte del enfoque la robótica [1]. Es por eso que la actualidad, los robots se han convertido en una excelente opción para generar producción en masa y automatizar procesos industriales, así como facilitar ciertas actividades humanas que suelen ser repetitivas [2] o de alto riesgo. Además, debido a la rapidez y precisión con la que ejecutan las tareas para las que fueron creados, incrementan la eficiencia y productividad de la compañía que los implemente.
Por lo tanto este artículo tiene como propósito mostrar el diseño de un robot omnidireccional haciendo uso de modelos matemáticos tales como los modelos cinemático inverso y directo, la segunda ley de Newton y el estudio de la resistencia del material, con el fin de que sea utilizado como base para el desarrollo de nuevas tecnologías que involucren la clasificación de objetos y el transporte de los mismos, un ejemplo de ello son las empresas que manejan encomiendas, pues dichas empresas cobran el valor de la encomienda según el peso de la misma.
Actualmente existen robots como el patentado por Porsche, utilizado para llevar objetos muy pesados como motores de automóviles, los robots creados por Kiva Systems para la distribución de mercancía [3] o el Round a Bot, es capaz de cargar hasta 200kg [4]. Sin embargo existen otras posibles aplicaciones para los robots con este tipo de configuración incluyen desde la impresión de grandes superficies, guiado de herramientas de corte para perfiles de gran tamaño hasta vehículos teledirigidos de inspección, investigación u ocio [5].
2. Modelo cinemático
Un robot omnidireccional se caracteriza porque puede moverse en cualquier dirección [6] sin necesidad de reorientación, debido a que utiliza ruedas omnidireccionales, las cuales constan de una rueda normal con rodillos ubicados de forma perpendicular a la dirección normal de la rueda. Entonces cuando se aplica una fuerza lateral, el robot se desplaza sobre los rodillos, lo que permite que haya una componente de velocidad en el eje x.
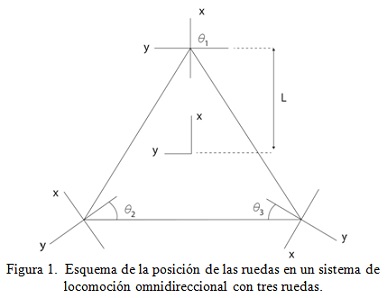
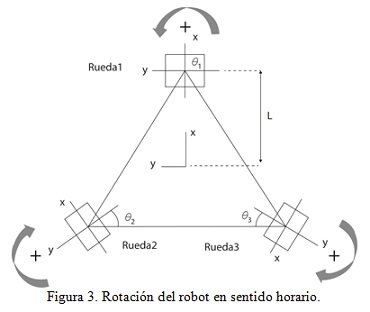
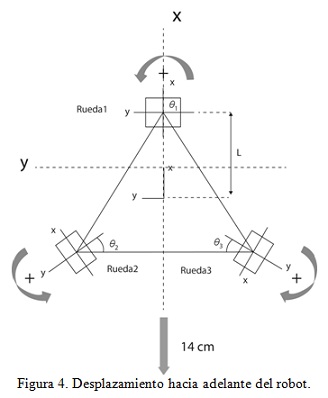
El modelo cinemático de este tipo de robot se define a partir de un triangulo equilátero en el cual se ubica una rueda en cada uno de sus vértices y por consiguiente cada rueda posee entre si un ángulo de separación de 120 grados como se muestra en la figura 1. Ahora la distancia del centro de las ruedas al centro del triangulo se denota como L, la velocidad angular de cada rueda se representa como w1, w2, w3 y por ultimo esta r que hace referencia al radio de las ruedas.
Donde los ángulos toman los siguientes valores de acuerdo a su ubicación en el triangulo equilátero:
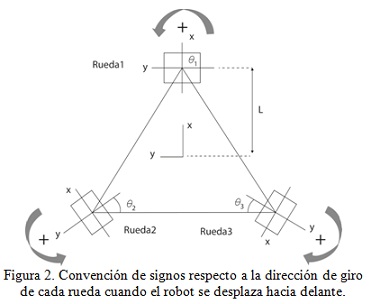
Dicho modelo cinemático se presenta de dos formas: directa e inversa. De la primera se obtiene el desplazamiento y posición del robot con respecto a los ejes x, y, z, a partir de la velocidad angular de las ruedas. Mientras que de la segunda se obtiene la velocidad angular de las ruedas a partir de la posición del robot y de su desplazamiento con respecto a los ejes de coordenadas. Sin embargo antes de realizar el análisis es necesario fijar unos parámetros, como la dirección de giro de las ruedas cuando se desplaza hacia delante, teniendo en cuenta su disposición. En este caso para las Ruedas 1 y 2, el giro es positivo cuando se realiza en contra de las manecillas del reloj, mientras que la Rueda 3 cuando giran en el sentido contrario a las manecillas del reloj, consideramos el giro con signo negativo y viceversa, como se muestra en la figura 2.
Por otro lado en el caso en que el robot gira sobre su propio eje en el sentido de las manecillas del reloj se considerara como un movimiento con signo negativo, y si se presenta el caso contrario, entonces será un movimiento con signo positivo.
A continuación se encuentran las matrices y ecuaciones que describen el modelo cinemático directo e inverso de un robot omnidireccional.
2.1. Modelo cinemático directo
A partir del modelo cinemático directo es posible conocer cuánto debe avanzar, sobre que eje de coordenadas y en qué sentido gira cada una de las ruedas con respecto a las otras.
Para este cálculo se tiene el vector de posición Ap y el vector de velocidad [6], los cuales aplican para el modelo directo e inverso y están dados como:
Ahora para hallar el vector posición se aplica la siguiente matriz:
A partir de la ecuación (3) se deducen las ecuaciones para hallar las coordenadas y el desplazamiento en x, y, z.Dichos valores se obtiene remplazando el ángulo correspondiente a la inclinación de cada una de las ruedas respecto al eje de coordenadas.
Por lo tanto para hallar el desplazamiento de cada una de las ruedas se remplaza en las ecuaciones (4), (5), (6) cada uno de los resultados obtenidos en la matriz según corresponda y el valor de L, la cual depende del tamaño del robot.
En este orden de ideas, la ecuación (7) representa el modelo cinemático directo, de la cual se concluye que el desplazamiento de la Rueda1 se rige por los valores que se encuentra en la primera columna de izquierda a derecha de la matriz 3x3, la Rueda2 se rige por la segunda columna y la Rueda3 por la tercera. Además, también muestra que el valor que toma x corresponde a la primera fila de arriba hacia abajo, y a la segunda fila y z a la tercera fila como se observa en las ecuaciones. Por lo tanto para realizar el análisis del desplazamiento se asignan valores a las variables correspondientes a la velocidad angular de cada una de las ruedas, es decir a
Inicialmente se determina el desplazamiento de las ruedas cuando el robot rota sobre si mismo, asignando los siguientes valores a las variables de velocidad angular.
A continuación se remplazan los valores de w en las ecuaciones (4), (5), (6), de lo cual se obtiene que:
Como se observa en los resultados, si remplazamos la velocidad angular para cada rueda con una unidad positiva se obtiene solo el resultado de la componente en z, la cual corresponde a la rotación del robot, con signo negativo, lo que significa que es robot está girando hacia la derecha, es decir en el sentido de las manecillas del reloj, como muestra la figura 3.
Ahora si se desea conocer el desplazamiento del robot hacia adelante solo se remplaza el valor de que corresponden a la Rueda2 y 3 respectivamente e incluimos el sentido de la rotación de cada rueda por medio del signo. La Rueda1 se le asigna el valor de cero debido a que se desplazara sobre los rodillos que posee, es decir que será “arrastrada” por el movimiento de los motores conectados a las Ruedas2 y 3.
Entonces se observa en los resultados que el robot se está desplazando solo sobre el eje x 0.14m, es decir alrededor de 14cm como se muestra en la figura 4.
2.2. Modelo cinemático inverso
A partir del modelo cinemático inverso es posible conocer a qué velocidad angular y el sentido de giro que debe tener cada una de las ruedas con respecto a las otras.
Dichos valores se obtiene remplazando el ángulo correspondiente a la inclinación de cada una de las ruedas respecto al eje de coordenadas.
Por lo tanto para hallar la velocidad angular para cada una de las ruedas se remplaza en las ecuaciones (9), (10), (11) cada uno de los resultados obtenidos en la matriz según corresponda y el valor de L, la cual depende del diseño del robot.
En el caso de la ecuaciones (8) del modelo cinemático inverso, la velocidad angular de la rueda 1 se rige por los valores que se encuentran en la primera fila de la matriz 3x3, donde el valor que toma x corresponde a la primera columna de izquierda a derecha, y a la segunda columna y z a la tercera
Por lo tanto para realizar el análisis de la velocidad angular se asignan valores a las variables correspondientes a la posición en x, y, z del robot.
Ahora se determina la velocidad angular de las ruedas cuando el robot rota sobre si mismo, asignando los siguientes valores a las variables de posición.
Y se remplaza en las ecuaciones (9), (10), (11).
Como se observa en los resultados, si remplazamos los componentes de la posición del robot se obtiene la velocidad angular para cada una de las ruedas cuando el robot gira sobre sí mismo.
Ahora si se desea conocer la velocidad angular de las ruedas involucradas en el desplazamiento del robot hacia delante solo se remplaza el valor de x, y, z en la ecuación de las Ruedas2 y 3, ya que la Rueda1 se desplazara sobre los rodillos que posee. Tampoco se incluye el valor de z, debido a que el robot no va girar sobre sí mismo.
Por lo tanto como se ve en los resultados para que el robot se desplazase hacia delante, se requiere que la magnitud de la velocidad angular sea la misma para las Ruedas 2 y 3.
Sin embargo para conseguir que el robot realice el desplazamiento deseado, el modelo matemático del mismo debe apoyarse en la lectura de los encoders, para lograr un sistema realimentado.
3. Estudio de la resistencia de materiales
Calcular la resistencia del material que se quiere utilizar en la construcción del prototipo, permite conocer si dicho material es capaz de resistir las fuerzas que actúan sobre este, mientras realiza las tareas para las cuales fue creado. Por lo tanto, con este estudio se pude determinar el material apto que garantiza una mayor vida útil del prototipo.
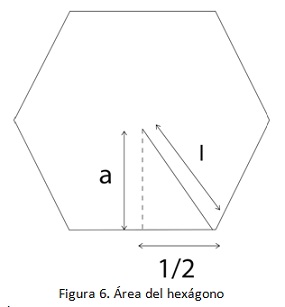
Para realizar dichos cálculos es necesario tener claro cómo va a ser el diseño de la estructura del prototipo, ya que se requiere conocer el área de cada una de las piezas que la conforman. Para este caso particular, las áreas que deben calcular son la de un hexágono, el cual corresponde a las bases de la estructura y la de un circulo, que corresponde a las varillas unidas a las bases del robot, como se ve en la figura 5.
Por lo tanto, así mismo se debe calcular el esfuerzo que debe soportar cada una de las piezas de la estructura, a partir de las sumatoria de fuerzas que actúan sobre el robot, en este caso es el peso de todos los componentes que lo conforman como motores, baterías, el circuito impreso, etc., incluso se debe incluir en los caculos el peso propio de las piezas de la estructura.
Entonces la relación a partir de la cual se obtiene el esfuerzo de cualquier material es de la forma:
Donde FT es la fuerza total en newtons, A es el área el metros cuadrados y σ es el esfuerzo del material, dado en pascales, es decir N⁄m2 [7].
A continuación se encuentra el desarrollo de los cálculos realizados para el diseño propuesto del robot, en el cual se contemplo el aluminio y acrílico para su construcción.
3.1. Área del hexágono en aluminio
Como se muestra en la figura a continuación, para hallar el área de un hexágono, es necesario hallar a, el cual se denomina apotema, utilizando el teorema de Pitágoras, ya que a junto con I e I/2 forman un triangulo rectángulo como se observa figura 6.
Los valores de I e I/2 corresponden al diseño previamente realizado del prototipo, para este caso los valores son:
Ahora para hallar la apotema, el perímetro y el área del hexágono se aplican las ecuaciones (14), (15) y (16) respectivamente como se muestra a continuación.
3.2. Peso de la base hexagonal en aluminio (con espesor de 3mm)
Ahora para hallar el peso en newtons aplicando la ecuación (17), es decir se calcula la masa de la pieza a partir del área (A), el espesor y la densidad del material como se muestra a continuación [8].
3.3. Área del hexágono inferior en acrílico
3.4. Peso de la base hexagonal en acrílico inferior (con espesor de 3mm)
3.5.Área del hexágono superior en acrílico
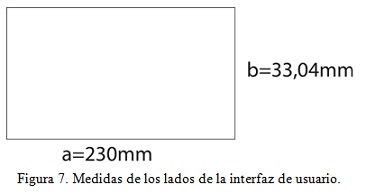
En este caso para hallar el área de la base superior en acrílico se debe restar el área rectangular ecuación (22) que corresponde a la interfaz de usuario ubicada en la parte de encima del robot como se muestra a continuación.
3.6. Peso de la base hexagonal en acrílico superior (con espesor de 3mm)
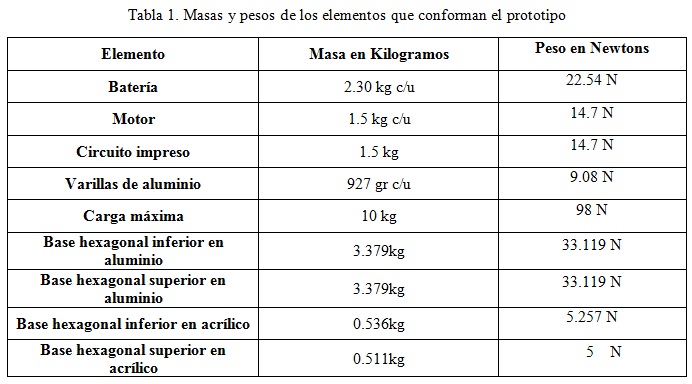
Tras haber hallado el peso de las partes que conforman la estructura del prototipo, en la tabla 1 a continuación se encuentra relacionada la masa y el peso de las piezas y dispositivos que hacen parte del robot.
3.7. Esfuerzo de base hexagonal inferior en aluminio
Entonces para determinar el esfuerzo que soportan las piezas de la estructura, utilizamos los valores del peso en newtons (tabla 1), los cuales deben sumarse para determinar la fuerza total sobre la pieza, teniendo en cuenta en la sumatoria que ítems que hacen parte del robot, afectan o ejercen alguna fuerza sobre la pieza para la cual se está calculando el esfuerzo y se aplica ecuación (13) vista previamente.
Luego, para saber si el resultado sobrepasa o no el esfuerzo como que posee como tal el material que se desea emplear, comparamos el resultado obtenido con la formula, es decir el esfuerzo que debería resistir la pieza con el esfuerzo propio del material. Por lo tanto si el esfuerzo propio del material es menor que el esfuerzo que debería soportar la pieza, entonces se concluye que el material no es apto para ser utilizado en el proyecto, ya que el peso podría deformar la pieza. Pero si por el contrario el esfuerzo del material es mayor al de la pieza, entonces el prototipo se puede construir con dicho material.
3.8. Esfuerzo de base hexagonal superior en aluminio
3.8.1. Esfuerzo de base hexagonal inferior en acrílico3.9. Esfuerzo de base hexagonal superior en acrílico
3.10. Esfuerzo de una varilla de aluminio
Ahora, en el caso de las varillas de aluminio, lo que se quiere conocer es cuánto debe medir el radio de la varilla para soportar la fuerza total que los componentes del robot hacen sobre cada una de las varillas como se muestra en la ecuación (25).
Esfuerzo para una varilla de ½ pulgada:4. Aplicación de la segunda ley de newton
Con el fin de conocer la fuerza necesaria que deben tener los motores para vencer la fuerza de fricción estática y dinámica, para lograr por consiguiente que el robot se desplace, se aplica la Segunda Ley de Newton [4]:
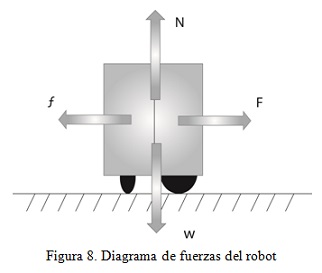
Donde F es la fuerza, m es la masa y a es la aceleración. Entonces, para identificar que fuerzas están actuando sobre el robot, se realiza un diagrama de fuerzas del mismo como se muestra en la figura 8.
Como se puede observar en la figura, sobre el robot actúa la fuerza de gravedad W y la fuerza normal N. Siendo que estas dos fuerza en una superficie plana poseen la misma magnitud pero diferente dirección, estas se anula, lo cual indica que no hay componente de fuerza en el eje y. Por otra parte, sobre el robot también actúan la fuerza de ficción f y la fuerza F que se le imprime al robot para que este se desplace, pero en este caso si hay componente de fuerza en el eje x, ya que aunque dichas fuerzas poseen direcciones contrarias, estas cuentan con diferente magnitud. Por lo tanto para hallar la fuerza mínima que deben tener los motores para mover el robot, es necesario hallar a Fx, es decir la componente de la fuerza en el eje x, a partir de las ecuaciones (28) y (29) [8]:
Donde si se despeja F se obtiene que:Sin embargo antes de aplicar las ecuaciones, se debe obtener la aceleración y la velocidad en x, así como también la fuerza de fricción estática, la cual indica la fuerza que se genera cuando un cuerpo se empieza a desplazar desde el reposo y la dinámica, la cual es la fuerza de fricción existente cuando el cuerpo ya se encuentra en movimiento [8]. Entonces para obtener los valores antes mencionados se aplican las ecuaciones (30), (31), (32). (33):
Donde Vx es la velocidad en el eje x, Vox es la velocidad en el origen, r es el radio de la rueda, Wm es la velocidad angular de la rueda en radianes/segundo, fe y fd es la fuerza de fricción estática y dinámica respectivamente, y
son los coeficientes de fricción estáticos y dinámicos [9].
Ahora, aunque no es conocido el valor de la velocidad angular en radianes, si lo es en rpm, valor el cual fue obtenido experimentalmente, contando cuantas revoluciones por minuto completo el eje del motor, cuyo resultado fue 27rpm. Por lo tanto para realizar los cálculos, primero se debe pasar los 27rpm dados como fm a radianes/segundo remplazando en la ecuación (34):
Tras obtener el valor de Wm, ahora se halla el valor de la velocidad lineal y de la aceleración:
Entonces al haber hallado el valor de la aceleración, ahora se debe obtener los valores de la fuerza de fricción estática y dinámica, pero para eso primero es necesario hallar la fuerza normal. Por lo tanto a continuación se muestra como se obtuvieron los resultados de la fuerza normal, de fricción estática y dinámica.
(Resultado obtenido de la sumatoria de las masas de la tabla 1)
Finalmente, como ya se tiene todos los valores, se aplica la ecuación deducida de la Segunda Ley de Newton para encontrar la componente de la fuerza en x para una fuerza de fricción estática y una dinámica [9]:
Por lo tanto la fuerza que deben ejercen los motores para superar la fuerza de fricción cuando el robot esta en reposo y empieza a desplazarse es igual a 200,19 N. Por otro lado, en consecuencia, los motores deben tener una fuerza de torque mínima de 122.78N para que el robot continúe desplazándose [10] [11].
5. Metodología
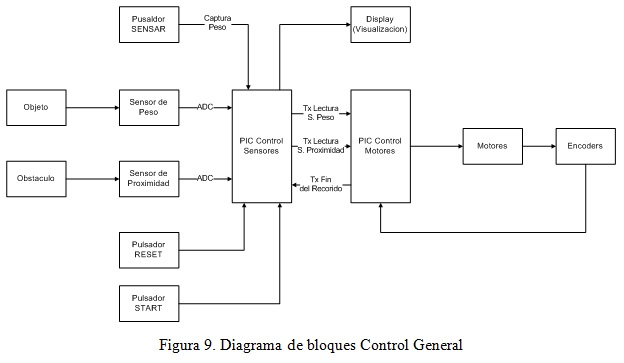
El objetivo del diseño y construcción de este prototipo es que sea capaz de llevar objetos a tres diferentes rutas, clasificándolos según el peso en un rango de 1 a 10kg máximo. Entonces para lograr que el robot cumpla su tarea se implemento un sensor de fuerza [12], encargado de medir el peso del objeto (partiendo de la premisa que el peso es una fuerza), encoders y un sensor de proximidad [13] para la detección de obstáculos. A continuación se muestra en la figura 9, el diagrama de bloques del control general que fue implementado en el robot.
Como se observa en la figura 9 las entradas del sistema llegan directamente el PIC encargado de controlar los sensores, el cual constantemente verifica los cambios que se puedan producir en las entradas. Por lo tanto cuando se produce un cambio el PIC lo visualiza y le informa al PIC encargado del control de los motores, dichos cambios, los cuales pueden representar la selección de la ruta basada en el peso del objeto o la detección de un obstáculo.
Por otra parte el control de los motores es en lazo cerrado [14], ya que por medio de los encoders se realiza la retroalimentación del sistema, indicando con el número de vueltas, cuanta distancia ha avanzado el robot. Internamente el microcontrolador usa la información obtenida de los encoders para regular el PWM [15] y por ende la velocidad de los motores.
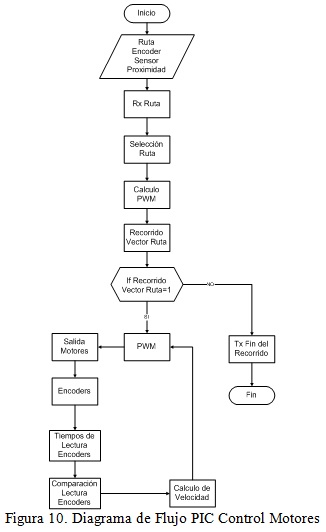
El algoritmo del PIC Control Motores posee tres variables que son ruta, encoder y sensor de proximidad, una vez el PIC recibe el código de la ruta, pasa a la selección de la misma dentro de las tres opciones con las que cuenta, luego realiza el cálculo del PWM según el ruta escogida y comienza a recorrer el vector que contiene los movimientos que debe realizar el robot, como ir hacia adelante, girar hacia la derecha o izquierda según corresponda. Mientras el vector sigue ejecutándose, entonces también se ejecutara la rutina del PWM, la cual saca un tren de pulsos por uno de los puertos del PIC y va a la etapa de potencia del robot haciendo que se muevan los motores. En este punto los encoders empiezan a recoger información del número de vueltas que ha dado el eje del motor y la envía al PIC cerrando el lazo de control, como se muestra en la figura 10.
6. Resultados
A continuación en las figuras 11, 12 y 13 se muestran la evolución en la construcción del prototipo.
En la primera figura se puede observar la realización de pruebas mecánicas al prototipo, conectando únicamente los motores a la batería con el fin de ver como se esta desplazando, es decir si lo hace en línea recta o tiende hacer una curva, lo cual se puede deber a que los componentes del robot no están simétricamente colocados, la carga no esta colocada en el centro del robot, lo cual es muy importante para conservar el centro de gravedad del mismo o que una rueda va a mayor velocidad que la otra.
En la segunda figura se realizan pruebas de movimiento con el control electrónico incorporado, con el fin de determinar si el control y el algoritmo implementado funcionan correctamente o requiere cambios.
Finalmente en la tercera figura se aprecia como se ve el robot ensamblado totalmente. Como se puede ver el robot cuenta con un panel de control conformado por el botón de Start, Reset, On-Off y un display doble de siete segmentos.
Conclusiones
Para la elaboración fue vital entender a fondo el funcionamiento del sistema de locomoción de un robot omnidireccional teniendo un modelo matemático que lo soporte, ya que esto permite predecir el desplazamiento del robot en un sistema de coordenadas, así como también permite determinar la velocidad angular con la que deben trabajar los motores, para lograr que el robot de desplace en la forma deseada, lo cual a la hora de programar el prototipo facilita dicho proceso, ya que las ecuaciones y los resultados obtenidos del modelo cinemático se pueden incorporar dentro del programa como un algoritmo, haciendo más eficaz el control sobretodo de los motores, ya que es posible conocer cuanto de debe desplazar el robot y a que velocidad para lograr su objetivo.
Por otra parte, se puede inferir que el aluminio es un material óptimo para la construcción del chasis del robot, ya que por ejemplo en el caso de la base hexagonal inferior de aluminio, la cual debe resistir sin deformarse prácticamente todo el peso en si del robot, puede llegar soportar hasta 62000N más de lo que le exige el diseño. Esto debido a que el esfuerzo que debe resistir de acuerdo con el diseño mecánico, es apenas de 1537.4Pa en comparación a 95MPa que puede llegar a resistir. Por lo tanto se trata de un material muy resistente a pesar de ser liviano. De igual manera ocurre con la base en acrílico, la cual también es bastante resistente y soporta perfectamente el peso de los elementos que provocan una fuerza sobre la misma. Por otro lado para el caso de las varillas, como se puede observar en los resultamos, cada varilla puede medir aproximadamente al menos 1mm de diámetro para lograr soportar la estructura del robot, es decir que cada varilla de media pulgada utilizada en el prototipo solo requiere un esfuerzo mínimo de 642KPa, cuando el esfuerzo del material llega hasta 95MPa, lo que indica que las varillas seleccionadas pueden resistir aun más peso y por lo tanto son más que optimas para la construcción de la estructura del prototipo.
Por otra parte al aplicar la Segunda Ley de Newton, se logro obtener la fuerza que deben tener los motores, lo cual es fundamental verificar que los motores que se escogieron son los apropiados para el proyecto o determinar la relación de reducción con el fin de lograr que el torque que proporcione el eje del motor sea el indicado para lograr que el robot se mueva. A raíz de los resultados, se observo que es necesario aplicar una mayor fuerza cuando se desea mover un cuerpo que se encuentra en reposo que uno que ya se encuentra en movimiento.
Finalmente de las pruebas realizadas al robot se puede concluir que al tratarse de un prototipo cuya forma es totalmente simétrica, la carga se debe colocar en el centro del robot para conservar el centro de masa, de lo contrario el robot tiende a frenarse o cambia la dirección de su desplazamiento.
Referencias Bibliográficas
- H. Henderson; Modern Robotics Building Versatiles Machine. Chelsea House Publishers, pp. 15-19, New York, 2006.
- J. Craig; Introducción a la Robótica. 3ed., Pearson Education, México, 2006.
- Three Engineers, Hundreds of Robots, One Warehouse. IEEE Spectrum [En linea], consultado en Septiembre 17 de 2013 Disponible en: http://spectrum.ieee.org/robotics/robotics-software/three-engineers-hundreds-of-robots-one-warehouse/0
- J. Fletcher, S. Ho, J. Kloess, R. Raj y S. Vozar; Round a Bot, holonomic Invert Pendunlum Robot. Ann Arbor, 2010.
- F. Cerro; “Vehículo compacto omnidireccional con ruedas no convencionales”, Tesis de Pregrado. Escuela Técnica Superior de Ingeniería Industrial, Barcelona, 2004.
- F. G. Pin, S. M. Killough; A New Family of Omni-Directional and Holonomic Wheeled Platforms for Mobile Robots, IEEE Trans. Rob. Autom., 10_4_, pp. 480-489, 1994.
- L. García; Modelo Cinemático y Control de Robots Móviles con ruedas, PhD Tesis, Universidad de Valencia, Valencia, 2008.
- J. Gere; Mecánica de Materiales, Thomson, 6 ed., México, 2006.
- F. Beer, R. Johnston, J. Dewolf; Mecánica de Materiales, McGraw Hill, 3 ed., México D.F, 2001.
- R. Serway; Física para Ciencias e Ingenierías. Thomson, 6 ed., Vol. I., México, 2005.
- Y. Freedman, S. Zemansky; Física Universitaria. Pearson Education, 12 ed., Vol. I., México, 2009.
- R. Palàs-Areny, J. G. Webster; Sensors and Signal Conditioning, John Wiley & Sons, 2 ed., United States of America, 2001.
- D. S. Albán, F. R. Salazar; Diseño e Implementación de Sensores de Temperatura, Presión y Proximidad en un Prototipo de Piel Sensible para Robots Compañeros, Tesis de Pregrado, Escuela Politécnica del Ejercito sede Latacunga, Latacunga, 2011.
- K. Ogata, Ingeniería de Control, Pearson Educación, 3ed., México, 1998.
- M. H. Rashid, Electrónica de Potencia, Prentice Hall, 2 ed., México, 1995.
Licencia
Reconocimiento – NoComercial – CompartirIgual (by-nc-sa): No se permite el uso comercial de la obra original, las obras derivadas deben circular con las mismas condiciones de esta licencia realizando la correcta atribución al autor.
Esta obra está bajo una licencia de Creative Commons Reconocimiento-NoComercial-CompartirIgual 4.0 Internacional