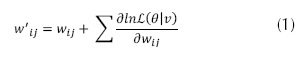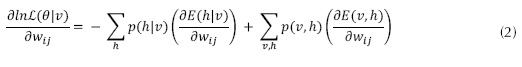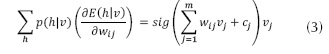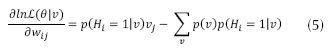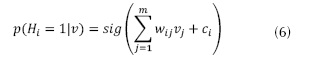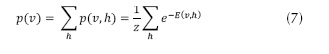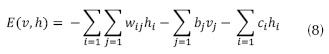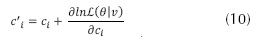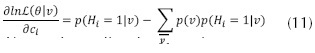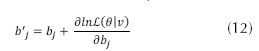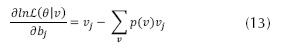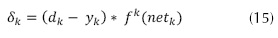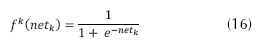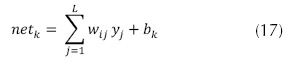DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2016.1.a03Published:
2016-01-01Issue:
Vol. 20 No. 47 (2016): January - MarchSection:
ResearchPredicción de radiación solar mediante deep belief network
Solar Insolation Prediction through Deep Belief Network
Keywords:
Accord.Net, Afforge.Net, Back propagation (BP), Contrastive Divergence (CD), Deep Belief Network (DBN), predicción de radiación solar, Restricted Boltzmann Machine (RBM), visual studio 2010 - C#. (es).Keywords:
Accord.Net, Afforge.Net, Back propagation (BP), Contrastive Divergence (CD), Deep Belief Network (DBN), Restricted Boltzmann Machine (RBM), solar insolation prediction, visual studio 2010 - C#. (en).Downloads
References
Bhardwaj, S.; Sharma, V.; Srivastava, S.; Sastry, O.S.; Bandyopadhyay, B.; Chandel S.S. & Gupta, J.R.P. (julio de 2013). Estimation of solar radiation using a combination of Hidden Markov Model and generalized Fuzzy model. Solar Energy, 93, 43-54. DOI:10.1016/j.solener.2013.03.020
De Grazia, M.; Stoianov, I. & Zorzi, M. (2012). Parallelization of Deep Networks. European Symposium on Artificial Neural Networks, Computational Intelligence (pp. 25-27). Brujas, Bélgica. Recuperado el 29 de septiembre de 2014, de: http://www.i6doc.com/en/livre/?GCOI=28001100967420
Fischer, A. & Igel, C. (enero de 2014). Training restricted Boltzmann machines: An introduction. Pattern Recognition 47(1), 25-39. DOI:10.1016/j.patcog.2013.05.025.
Gopal, S.; Woodcock, C. & Strahler, A. (febrero de 1999). Fuzzy Neural Network Classification of Global Land Cover from a 1° AVHRR Data Set. Remote Sensing of Environment 67(2), 230-243. DOI:10.1016/S0034-4257(98)00088-1.
Hernández, J.A.; Rivera, W.; Colorado, D. & Moreno-Quintanar, G. (abril de 2012). Optimal COP prediction of a solar intermittent refrigeration system for ice production by means of direct and inverse artificial neural networks. Solar Energy 86(4), 1108-1117. DOI:10.1016/j.solener.2011.12.021.
İzgi, E.; Öztopal, A.; Yerli, B.; Kemal, M. & Duran, A. (febrero de 2012). Short–mid-term solar power prediction by using artificial neural networks. Solar Energy 86(2), 725-733. DOI:10.1016/j.solener.2011.11.013.
Ji, N.; Zhang, J. & Zhang, C. (septiembre de 2014). A sparse-response deep belief network based on rate distortion theory. Pattern Recognition 47(9), 3179-3191. DOI:10.1016/j.patcog.2014.03.025.
Leconte, A.; Achard, G. & Papillon, P. (Julio de 2012). Global approach test improvement using a neural network model identification to characterise solar combisystem performances. Solar Energy 86(7), 2001-2016. DOI:10.1016/j.solener.2012.04.003.
Meng, X.; Jia, M. & Wang, T. (23 de diciembre de 2013). Neural network prediction of biodiesel kinematic viscosity at 313 K. Fuel, 121, 133-140. DOI:10.1016/j.fuel.2013.12.029.
Paoli, C.; Voyant, C.; Muselli, M. & Nivet, M. (diciembre de 2010). Forecasting of preprocessed daily solar radiation time series using neural networks. Solar Energy 84(12), 2146-2160. DOI:10.1016/j.solener.2010.08.011.
Wu, J. & Chan, C. (diciembre de 2013). Prediction of hourly solar radiation with multi-model framework. Energy Conversion and Management, 76, 347-355. DOI:10.1016/j.enconman.2013.07.067
Behrang, M.; Assareh, E.; Ghanbarzadeh, A. & Noghrehabadi, A.R. (agosto de 2010). The potential of different artificial neural network (ANN) techniques in daily global solar radiation modeling based on meteorological data. Solar Energy 84(8), 1468-1480. DOI:10.1016/j.solener.2010.05.009
Chen C.; Duan, S.; Cai, T. & Liu, B. (noviembre de 2011). Online 24-h solar power forecasting based on weather type classification using artificial neural network. Solar Energy 85(11), 2856-2870. DOI:10.1016/j.solener.2011.08.027.
Ferreira, S. & Andrade, A. (2013). Development and validation of a scale to assess the integration of the LCMS in the formative process in higher education. Information Systems and Technologies (pp. 1-10). Lisboa. Recuperado el 29 de septiembre de 2014, de: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6082328
Gaxiola, F.; Melin, P.; Valdez, F. & Castillo, O. (1 de marzo de 2014). Interval type-2 fuzzy weight adjustment for backpropagation neural networks with application in time series prediction. Information Sciences, 260, 1-14. DOI:10.1016/j.ins.2013.11.006
Hamel, P. & Eck, D. (2010). Learning features form music audio with deep belief networks. 11th International Society for Music Information Retrieal Conference (pp. 339-344). Recuperado el 29 de septiembre de 2014, de: http://ismir2010.ismir.net/proceedings/ismir2010-58.pdf?origin=publication_detail
Hinton, G.; Deng, L.; Yu, D.; Dahl, G.; Mohamed, A.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T. & Kingsbury, B. (2012). Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. Signal Processing Magazine 29(6), 82-97. DOI:10.1109/MSP.2012.2205597
Le, Q. (mayo de 2013). Building high-level features using large scale unsupervised learning. Proceedings of the 29 th International Conference on Machine Learning, (pp. 8595-8598). DOI:10.1109/ICASSP.2013.6639343.
Maas, A.L.; Hannum, A.Y. & Ng, A.Y. (2013). Rectifier nonlinearities improve neural network acoustic models. 30 th International Conference on Machine Learning, 28. Atlanta, Georgia. Recuperado el 27 de septiembre de 2014, de: http://web.stanford.edu/~awni/papers/relu_hybrid_icml2013_final.pdf
Mohamed, A.; Sainath, T.; Dahl, G.; Ramabhadran, B.; Hinton, G. & Picheny, M. (2011). Deep Belief Networks using discriminative features for phone recognition. International Conference on Acoustics, Speech and Signal Processing (pp. 5060-5063). DOI:10.1109/ICASSP.2011.5947494
Plahl, C.; Sainath, T.N.; Ramabhadran, B. & Nahamoo, D. (2012). Improved pre-training og deep belief networks using sparse enconding symmetric machines. International Conference on Acoustics, Speech and Signal Processing (pp. 4165-4168). DOI: 10.1109/ICASSP.2012.6288836.
Ramedani, Z.; Omid, M.; Keyhani, A.; Khoshnevisan, B. & Soboohi, H. (noviembre de 2014). A comparative study between fuzzy linear regression and support vector regression for global solar radiation prediction in Iran. Solar Energy, 109, 135-143. DOI:10.1016/j.solener.2014.08.023.
Santana, J.C. (junio de 2006). Predicción de series temporales con redes neuronales: una aplicación a la inflación colombiana. Revista Colombiana de Estadística 29(1), 77-92. Recuperado el 29 de septiembre de 2014, de: http://www.emis.de/journals/RCE/V29/V29_1_77Santana.pdf
Sohn, K.; Jung, D.Y.; Lee, H. & Hero, A. (2011). Efficient learning of sparse, distributed, convolutional feature representations for object recognition. Computer Vision, (pp. 2643-2650). Barcelona, España. DOI:10.1109/ICCV.2011.6126554
Stackhouse, P. (27 de septiembre de 2014). NASA Prediction of Worldwide Energy Resource (POWER). Recuperado el 27 de septiembre de 2014, de: http://power.larc.nasa.gov/
Tieleman, T. (2008). Training Restricted Boltzmann Machines using Approximations to the Likelihood Gradient. International Conference on Machine Learning (pp. 1064-1071 ). Helsinki, Finlandia. DOI:10.1145/1390156.1390290
Velilla, E.; Valencia, J. & Jaramillo, F. (28 de junio de 2014). Performance evaluation of two solar photovoltaic technologies under atmospheric exposure using artificial neural network models. Solar Energy, 107, 260-271. DOI:10.1016/j.solener.2014.04.033.
Ji, W. & Chee, K.C. (mayo de 2011). Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Solar Energy 85(5), 808-817. DOI:10.1016/j.solener.2011.01.013.
Xu, J., Yamada, K., Seikiya, K., Tanaka, R., & Yamane, Y. (octubre de 2014). Effect of different features to drill-wear prediction with back propagation neural network. Precision Engineering 38(4), 791 -798. DOI:10.1016/j.precisioneng.2014.04.007
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.1.a03
Predicción de radiación solar mediante deep belief network
Solar Insolation Prediction through Deep Belief Network
Luis Carlos Ruiz Cárdenas1, Darío Amaya Hurtado2, Robinson Jiménez Moreno3
1 Ingeniero en Mecatrónica, estudiante de maestría en Ingeniería en Mecatrónica. Asistente de Investigación en el Grupo de Aplicaciones Virtuales GAV, Bogotá D.C., Colombia. Contacto: u1801196@unimilitar.edu.co.
2 Ingeniero Electrónico, especializado en Automatización Industrial, magister en Teleinformática, doctor en Ingeniería Mecánica. Docente de tiempo completo en la universidad Militar Nueva. Bogotá, Colombia. Contacto: dario.amaya@unimilitar.edu.co.
3 Ingeniero Electrónico, magister en Automatización Industrial, estudiante de Doctorado en Ingeniería. Docente de la Universidad Militar Nueva Granada. Bogotá, Colombia. Contacto robinson.jimenez@unimilitar.edu.co.
Fecha de recepción: 16 de octubre de 2014 Fecha de aceptación: 18 de septiembre de 2015
Cómo citar: Ruiz Cárdenas, L. C., Amaya Hurtado, D., & Jiménez Moreno, R. (2016). Predicción de radiación solar mediante deep belief network. Revista Tecnura, 20(47), 39-48. doi: 10.14483/udistrital.jour.tecnura.2016.1.a03
Resumen
El desarrollo continuo de las herramientas computacionales ofrece la posibilidad de realizar procesos con la capacidad de llevar a cabo actividades con mayor eficiencia, exactitud y precisión. Entre estas herramientas se encuentra la arquitectura neuronal, Deep Belief Network (DBN), diseñada con el propósito de colaborar en el desarrollo de técnicas de predicción para hallar información que permita estudiar el comportamiento de los fenómenos naturales, como lo es la radiación solar. En el presente trabajo se presentan los resultados obtenidos al manejar la arquitectura DBN para predicción de radiación solar, la cual se simula mediante la herramienta de programación Visual Studio C#, indicando el nivel de profundidad que posee esta arquitectura, como afecta la cantidad de capas y de neuronas en el entrenamiento y los resultados obtenidos para poder predecir los valores deseados en el 2014, con errores cercanos al 2 % y mayor rapidez para el entrenamiento, respecto a errores obtenidos por métodos convencionales de entrenamiento neuronal, que se encuentran por el 5% y que a su vez llevan largos periodos de entrenamiento.
Palabras Clave: Accord.Net, Afforge.Net, Back propagation (BP), Contrastive Divergence (CD), Deep Belief Network (DBN), predicción de radiación solar, Restricted Boltzmann Machine (RBM), visual studio 2010-C#.
Abstract
The continued development of computational tools offers the possibility to execute processes with the ability to carry out activities more efficiently, exactness and precision. Between these tools there is the neural architecture, Deep Belief Network (DBN), designed to collaborate in the development of prediction technics to find information that allows to study the behavior of the natural phenomena, such as the solar insolation. This paper presents the obtained results when using the DBN architecture for solar insolation prediction, simulated through the programming tool Visual Studio C#, showing the deep level that this architecture has, how it affects the number of layers and neurons per layer in the training and the results to predict the desired values in 2014, with errors close to 2% and faster to training, respect to errors obtained through conventional methods for neural training, which are about 5% and take long periods of training.
Keywords: Accord.Net, Afforge.Net, Back propagation (BP), Contrastive Divergence (CD), Deep Belief Network (DBN), Restricted Boltzmann Machine (RBM), solar insolation prediction, visual studio 2010-C#.
Introducción
El avance en las herramientas computacionales ha permitido desarrollar aplicaciones para analizar el comportamiento de un sistema en condiciones futuras, basadas en arquitecturas de redes neuronales, como la arquitectura multi-layer perceptron (MLP) (Behrang, Assareh, Ghanbarzadeh y Noghrehabadi, 2010; Paoli, Voyant y Muselli, 2010), time delay neural network (TDNN) (Wu Ji, 2011), generalized fuzzy model (GFM) (Bhardwaj, Sharma y Srivastav, 2013) o fuzzy linea regression (FLR) (Ramedani, Omid, Keyhani, Khoshnevisan, Soboohi, 2014)Una de las principales temáticas abordadas por este tipo de arquitecturas es la de predicción de radiación solar, desarrollada por Ramedani, Omid, Keyhani, Khoshnevisan, Soboohi, (2014) y Wu Chan (2013), la cual surge para proyectar una adecuada generación de energía fotovoltaica en cada día del año, como se insinúa en Behrang, Assareh, Ghanbarzadeh y Noghrehabadi (2010) y Wu Ji (2011), teniendo en cuenta, el efecto que pueden llegar a tener las variables meteorológicas como velocidad del viento (m/s), temperatura mínima, media y máxima (°C) (İzgi, Öztopal y Yerli, 2012), precipitación (mm/dia) y humedad relativa (%), en el comportamiento de la radiación horizontal diaria (KWh/m2/día) (Bhardwaj, Sharma y Srivastav, 2013), tomando como base la información que suministra la NASA para cada día del año (Stackhouse, 2014; Chen, Duan, Cai y Liu, 2011).
En el presente trabajo se exponen los beneficios que en la actualidad puede llegar a tener la implementación de la arquitectura deep belief network (DBN), proponiendo una red neuronal con capas visibles y ocultas, explicando la etapa de entrenamiento no supervisado (restricted boltzmann machine, RBM) y supervisado (back propagation, BP), integrando el algoritmo de aprendizaje convergence divergence (CD) y función de activación sigmoide, encargados de ofrecer la aproximación más cercana a los datos que se necesitan predecir. Por tanto, se empleó la herramienta de programación Visual Studio C#, con las librerías Accord.Net y Aforge.Net, con las cuales se desarrolló el proceso de predicción de radiación solar en el campus de la Universidad Militar Nueva Granada (Cajicá, Cundinamarca), con coordenadas 4°56'23,3''N y 74°01'03''.8W, y se evaluaron los resultados a partir de la velocidad de entrenamiento y cálculo de la red, con la obtención de errores considerablemente mínimos, dándose a conocer como una aplicación adicional a las que se manejan en la actualidad.
Este trabajo se divide en cuatro secciones: la primera es una breve introducción a las arquitecturas DBN, en la que se exponen los avances en la generación de este tipo de algoritmos; la segunda sección hace referencia a la metodología de entrenamiento con las funciones de aprendizaje implementadas, mediante la herramienta de programación Visual Studio. Por último, se exponen y analizan los resultados relacionados con la predicción de radiación solar, integrando los errores obtenidos al entrenar la red con diferentes niveles de profundidad y cantidades de neuronas.
Metodología
La arquitectura deep belief network (DBN)
El avance en los estudios de las arquitecturas en redes neuronales se ha llevado a cabo con el propósito de entender y aprovechar los beneficios del comportamiento de diferentes eventos cotidianos en el medio ambiente, para lo cual se han implementado técnicas como el multi-layer perceptron (MLP) (Behrang, Assareh, Ghanbarzadeh y Noghrehabadi, 2010; Paoli, Voyant y Muselli, 2014), como la arquitectura básica para predicción; artificial neural network (ANN) (İzgi, Öztopal y Yerli, 2012; Leconte, Achard y Papillon, 2012); o inverse artificial neural network (ANNi) (Hernández, Rivera, Colorado y Moreno, 2012), en donde se obtienen errores cercanos entre 5 y 6 %, lo que compromete la generación de energía fotovoltaica en épocas del año con el mejor índice de absorción de la radiación solar en la superficie horizontal de la tierra.
Otras arquitecturas desarrolladas para este tipo de propósitos son: deep neuronal network (DNN), deep belief network (DBN) y convolutional neural network (CNN), sugeridas para la identificación de rostros de personas (Le, 2013), identificación de escritura e identificación del habla (Maas, 2013; Plahl, Sainath y Ramabhad, 2012; Hinton et al., 2012), reconocimiento de números telefónicos (Mohamed et al., 2011). Así, se da solución, de forma eficiente, a los problemas de aprendizaje de máquina y se obtiene una mayor abstracción de los datos que se están estudiando (Hamel y Douglas, 2010), dependiendo del nivel de profundidad que tenga la red neuronal. En el estudio de radiación solar se puede presentar un mejor comportamiento en el entrenamiento de la red, como una disminución considerable del error, para asegurar los resultados esperados por un sistema fotovoltaico.
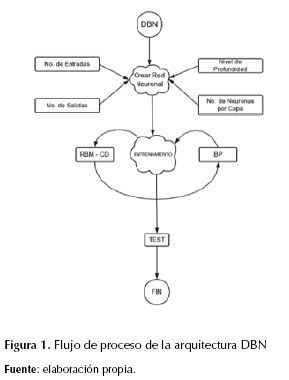
Para llevar a cabo la arquitectura DBN, se propone realizar el proceso que se expone en la figura 1, el cual parte por indicar la cantidad de variables de entrada, el número de salidas que se desea obtener, el nivel de profundidad (deep) de la red neuronal o cantidad de capas ocultas y el número de neuronas que se busca manejar por capa. Luego de definir la estructura del DBN, se adelanta el entrenamiento, que se divide en dos etapas: el no supervisado (restricted boltzmann machine, RBM), con el objetivo de entrenar capa a capa de la red y así obtener los pesos actualizados encargados de conectar capa a capa y los bias asignados a cada neurona de las capas y el supervisado con el método back propagation (BP). De esta manera, finalizó el entrenamiento de la arquitectura DBN, con los datos dispuestos para validación.
A partir del proceso de evaluación de la arquitectura DBN, se propone plantear este método para la predicción de radiación solar, con resultados cercanos al valor deseado entre el 2 y 0,1 %. Esta arquitectura permite ser operada desde herramientas de programación como Python (Hamel y Douglas, 2010; Ferreira y Andrade, 2013), Matlab (Sohn, Jung, Lee y Hero, 2011), y Visual Studio C# (De Grazia y Stoianov, 2012), donde cada una de estas posee sus propias librerías, que para el caso de Visual Studio C# maneja Accord.Net y Afforge.Net, y se usa para crear y manipular redes neuronales, como se manifiesta en el desarrollo de este trabajo.
Entrenamiento no supervisado, restricted boltzmann machine (RBM) (T4)
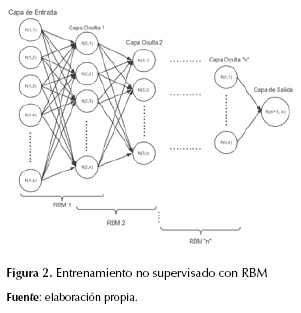
La primera etapa de entrenamiento se realiza con el método restricted boltzmann machine (RBM), que se expone en la figura 2. Este se interpreta como una red neuronal estocástica, con propiedades de predecir sin exactitud con probabilidad aleatoria (Fischer e Igel, 2014), capaz de entrenar redes multicapa.
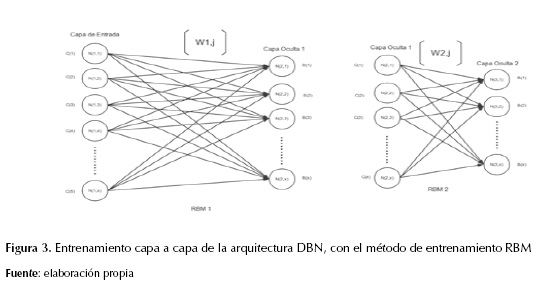
Este entrenamiento realiza el proceso capa a capa como se expone en la figura 3, sin entrenar la capa de salida. Así, se obtiene la actualización de los pesos encargados de unir la capa oculta con la capa visible, que con el algoritmo de aprendizaje contrastive divergence (CD) (Fischer e Igel, 2014; Tieleman, 2008) y la función de activación sigmoide, ofrece el de reconocimiento de patrones durante el proceso de entrenamiento.
Para el desarrollo de este método de aprendizaje, se tiene en cuenta las ecuaciones que manejan Fischer e Igel (2014). El entrenamiento no supervisado busca actualizar de forma progresiva los pesos (w'ij, wij) (Plahl, Sainath y Ramabhad, 2012), encargados de unir la capa visible (vi) con la capa oculta (hj), mediante la ecuación (1), haciendo uso de la distribución probabilística de la capa oculta a la capa visible (p(h|v)), la distribución probabilística de la capa visible a la capa oculta (p(v|h)) en la ecuación (2) y la función de energía (E) entre las mismas, manejando la ecuación (8).
Que en redes neuronales, se identifica cada término de la ecuación (2), con la ecuación (3) y la ecuación (4).
Que de forma simplificada, la probabilidad condicional i=1 de la capa oculta en una (p(Hi=1|v)) en la ecuación (5), se hace con la función de activación sigmoide (sig) de las ecuaciones (6) y (7).
Que para determinar la distribución de Gibbs (p(v)), se hace necesario hallar la función de partición (Z), con la ecuación (9):
Otras de las ventajas que tiene este tipo de entrenamiento es que, a medida que avanza, permite actualizar los bias de la capa visible (ci), correspondientes a un valor característico de las neuronas de las capas de estudio, con la ecuación (10) y los bias de la capa oculta (bj) (Ji, Zhang y Zhang, 2014), con la ecuación (13).
Entrenamiento supervisado, back propagation (BP)
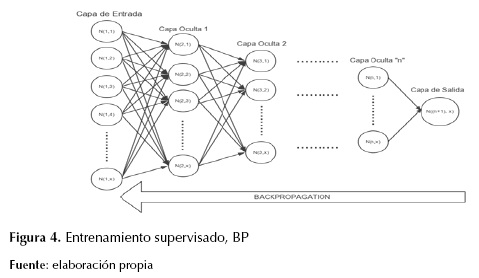
Para el desarrollo del entrenamiento supervisado con BP o sintonización fina (Hinton et al., 2012), se tiene en cuenta el proceso que se expone en la figura 4. Este entrenamiento considera el método matemático mean square error (MSE) como se maneja en Bhardwaj, Sharma, y Srivastav (2013), el cual se aplica para observar el error entre el valor deseado y el valor obtenido, devolviéndose hasta terminar el entrenamiento en la primera capa.
El desarrollo del algoritmo BP emplea la ecuación (14), para determinar el error cuadrático medio δk (Xu, Yamada y Seikiya, 2014).
Donde, el valor de error para la capa de salida δk en la ecuación (15), depende del valor deseado dk, el valor que se obtuvo yk, la salida de la función de activación sigmoide ƒk(Velilla, Valencia y Jaramill, 2014; Meng, Jia y Wang, 2013) de la ecuación (16) y el valor de cada neurona de la red netk de la ecuación (17) (Graxiola, Melin y Valdez, 2014), con los pesos wij los datos de la capa visible yj, los bias de las neuronas de la capa oculta bk.
Resultados
Teniendo en cuenta la arquitectura DBN y el flujo de proceso de entrenamiento de este tipo de red neuronal artificial, se requiere establecer la cantidad de entradas y salidas que va a tener la red neuronal. La salida de la red neuronal es la predicción de radiación solar (KWh/m2/día) del año a tener en cuenta; las variables de entrada son aquellas que pueden afectar el comportamiento de la radiación solar como lo son: velocidad del viento (m/s), temperatura mínima, media y máxima (°C) (İzgi, Öztopal y Yerli, 2012), precipitación (mm/día) y humedad relativa (%), agregando el comportamiento de la radiación horizontal diaria del año anterior (KWh /m2/día) (Bhardwaj, Sharma y Srivastav, 2013) como lo ha considerado Behrang, Assareh, Ghanbarzadeh y Noghrehabadi (2010), y Chen, Duan, Cai y Liu (2011), adquiriendo la información suministrada por la base de datos de la NASA (Stackhouse, 2014).
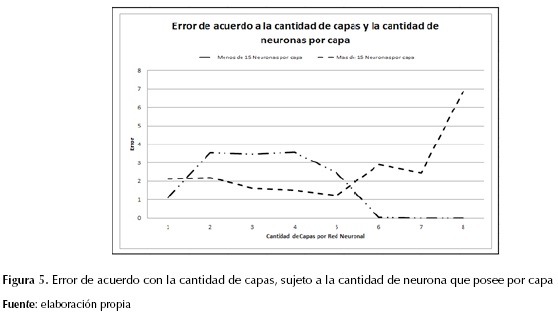
Al indicar qué parámetros rigen tanto la entrada como la salida, se agrega a la construcción de la red, la profundidad que se desea manejar, lo cual hace referencia a la cantidad de capas que va a tener la red neuronal. En la figura 5 se detallan los posibles resultados del comportamiento de la red, donde se muestra que a mayor cantidad de capas y con un menor número de neuronas por capa, se pueden obtener errores aproximados a 0. Para el caso de estudio, se propone una profundidad de 9, donde el primer nivel de profundidad tendrá 10 neuronas y en las siguientes capas desciende de a una neurona.
Al tener presente cómo será la arquitectura de la red neuronal, se toman los datos que ofrece la NASA (Stackhouse, 2014) desde 1997 al 2013, para desarrollar la etapa de entrenamiento, el cual se encarga de tomar el 80 %, correspondiente al periodo de 1997-2010, y el 20 % para validación, correspondiente al periodo de 2011-2013 como sugieren Gopal, Woodcock y Strah (1999). Para la etapa de entrenamiento no supervisado, correspondiente al método de entrenamiento RBM con el algoritmo de entrenamiento CD, el cual se encarga de aplicar de forma interna las ecuaciones (1), (10) y (11). El entrenamiento supervisado se sugiere para realizar la sintonización fina a través del método BP, para hallar el MSE que se encuentra en la ecuación (13).
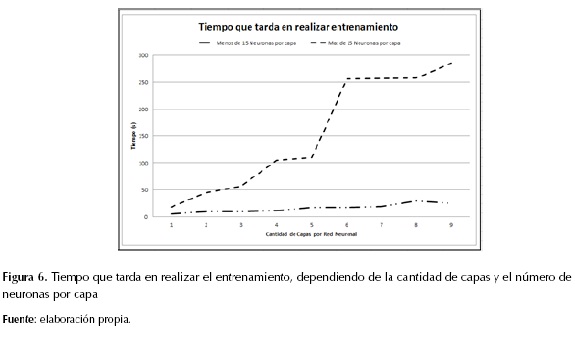
De esta manera se realiza la etapa de entrenamiento hasta llegar a la capa oculta, otorgándole un valor sólido a los pesos iniciales de la red neuronal y, a su vez, inicializando de forma adecuada los valores de las bias correspondientes a los valores asignados a cada neurona que se encuentra en cada capa o cada nivel de profundidad de la red. Así, el resultado final es una estructura de capas entrenada en cortos lapsos de tiempo como se puede observar en la figura 6, que a medida que se pueda ir aumentando la cantidad de capas tiende a tardar mucho tiempo; sin embargo, al no manejar gran cantidad de neuronas por capa, tiende a conservar el tiempo de entrenamiento.
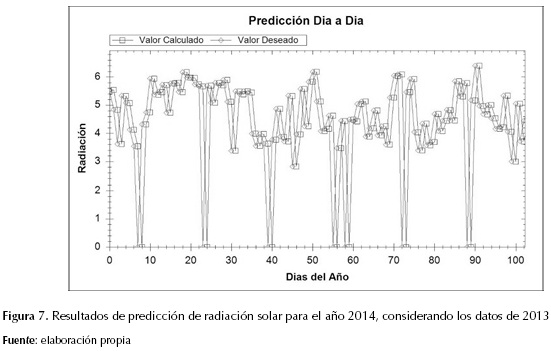
Considerando los resultados obtenidos, con la arquitectura que se propuso, el entrenamiento y la validación desarrollados, cada uno con su método y algoritmo correspondiente, se buscó predecir la radiación del año en curso (2014). Para esto se ingresó a la red los datos correspondientes al año 2013 (°C, m/s, %, mm/día y KWh/m2/día), y se obtuvieron radiaciones aproximadas a las esperadas con el año 2014, como se puede evidenciar en la figura 7.
Con el manejo de la arquitectura DBN se observó que se obtienen errores cercanos al 2,0 %; esto indica mejores resultados a los expuestos por Behrang, Assareh, Ghanbarzadeh y Noghrehabadi (2010), ya que ellos manejan las mismas entradas pero con errores cercanos a 5,21 % mediante la técnica MLP, implementando métodos matemáticos para hallar el error como el root mean square error (RMSE) y mean square error (MSE) como lo proponen Bhardwaj, Sharma y Srivastav (2013).
Conclusiones
Con los resultados obtenidos en el desarrollo de esta etapa de predicción del proyecto, se puede llegar a incrementar la integración de los sistemas fotovoltaicos a la red, debido a que es posible predecir la radiación horizontal, garantizando una adecuada generación de energía fotovoltaica sin obtener posibles pérdidas en los diferentes días del año.
Se propone, como trabajo futuro, la predicción de radiación solar, con el manejo de los datos registrados por el grupo de investigación en áreas rurales, en cada minuto, entre los que se encuentran: radiación solar horizontal, velocidad del viento, humedad relativa y temperatura del ambiente, para predecir tanto diaria como anualmente la radiación solar en este tipo de áreas donde se puede aprovechar este recurso natural y orientarlo a la población que no posee acceso a la red eléctrica convencional.
Financiamiento
Vicerrectoría de Investigaciones de la Universidad Militar Nueva Granada. Financiación del proyecto IMP_ING 1576, año 2014.
Referencias
Bhardwaj, S.; Sharma, V.; Srivastava, S.; Sastry, O.S.; Bandyopadhyay, B.; Chandel S.S. & Gupta, J.R.P. (julio de 2013). Estimation of solar radiation using a combination of Hidden Markov Model and generalized Fuzzy model. Solar Energy, 93, 43-54. DOI:10.1016/j.solener.2013.03.020
De Grazia, M.; Stoianov, I. & Zorzi, M. (2012). Parallelization of Deep Networks. European Symposium on Artificial Neural Networks, Computational Intelligence (pp. 25-27). Brujas, Bélgica. Recuperado el 29 de septiembre de 2014, de: http://www.i6doc.com/en/livre/?GCOI=28001100967420.
Fischer, A. & Igel, C. (enero de 2014). Training restricted Boltzmann machines: An introduction. Pattern Recognition 47(1), 25-39. HYPERLINK "http://dx.doi.org/10.1016/j.patcog.2013.05.025" \ t"doilink" DOI:10.1016/j.patcog.2013.05.025.
Gopal, S.; Woodcock, C. & Strahler, A. (febrero de 1999). Fuzzy Neural Network Classification of Global Land Cover from a 1° AVHRR Data Set. Remote Sensing of Environment 67(2), 230-243. DOI:10.1016/S0034-4257(98)00088-1.
Hernández, J.A.; Rivera, W.; Colorado, D. & Moreno-Quintanar, G. (abril de 2012). Optimal COP prediction of a solar intermittent refrigeration system for ice production by means of direct and inverse artificial neural networks. Solar Energy 86(4), 1108-1117. DOI:10.1016/j.solener.2011.12.021.
İzgi, E.; Öztopal, A.; Yerli, B.; Kemal, M. & Duran, A. (febrero de 2012). Short-mid-term solar power prediction by using artificial neural networks. Solar Energy 86(2), 725-733. DOI:10.1016/j.solener.2011.11.013.
Ji, N.; Zhang, J. & Zhang, C. (septiembre de 2014). A sparse-response deep belief network based on rate distortion theory. Pattern Recognition 47(9), 3179-3191. DOI:10.1016/j.patcog.2014.03.025.
Leconte, A.; Achard, G. & Papillon, P. (Julio de 2012). Global approach test improvement using a neural network model identification to characterise solar combisystem performances. Solar Energy 86(7), 2001-2016. DOI:10.1016/j.solener.2012.04.003.
Meng, X.; Jia, M. & Wang, T. (23 de diciembre de 2013). Neural network prediction of biodiesel kinematic viscosity at 313 K. Fuel, 121, 133-140. DOI:10.1016/j.fuel.2013.12.029.
Paoli, C.; Voyant, C.; Muselli, M. & Nivet, M. (diciembre de 2010). Forecasting of preprocessed daily solar radiation time series using neural networks. Solar Energy 84(12), 2146-2160. DOI:10.1016/j.solener.2010.08.011.
Wu, J. & Chan, C. (diciembre de 2013). Prediction of hourly solar radiation with multi-model framework. Energy Conversion and Management, 76, 347-355. DOI:10.1016/j.enconman.2013.07.067.
Behrang, M.; Assareh, E.; Ghanbarzadeh, A. & Noghrehabadi, A.R. (agosto de 2010). The potential of different artificial neural network (ANN) techniques in daily global solar radiation modeling based on meteorological data. Solar Energy 84(8), 1468-1480. DOI:10.1016/j.solener.2010.05.009.
Chen C.; Duan, S.; Cai, T. & Liu, B. (noviembre de 2011). Online 24-h solar power forecasting based on weather type classification using artificial neural network. Solar Energy 85(11), 2856-2870. DOI:10.1016/j.solener.2011.08.027.
Ferreira, S. & Andrade, A. (2013). Development and validation of a scale to assess the integration of the LCMS in the formative process in higher education. Information Systems and Technologies (pp. 1-10). Lisboa. Recuperado el 29 de septiembre de 2014, de: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6082328.
Gaxiola, F.; Melin, P.; Valdez, F. & Castillo, O. (1 de marzo de 2014). Interval type-2 fuzzy weight adjustment for backpropagation neural networks with application in time series prediction. Information Sciences, 260, 1-14. DOI:10.1016/j.ins.2013.11.006.
Hamel, P. & Eck, D. (2010). Learning features form music audio with deep belief networks. 11th International Society for Music Information Retrieal Conference (pp. 339-344). Recuperado el 29 de septiembre de 2014, de: http://ismir2010.ismir.net/proceedings/ismir2010-58.pdf?origin=publication_detail.
Hinton, G.; Deng, L.; Yu, D.; Dahl, G.; Mohamed, A.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T. & Kingsbury, B. (2012). Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. Signal Processing Magazine 29(6), 82-97. DOI:10.1109/MSP.2012.2205597.
Le, Q. (mayo de 2013). Building high-level features using large scale unsupervised learning. Proceedings of the 29 th International Conference on Machine Learning, (pp. 8595-8598). DOI:10.1109/ICASSP.2013.6639343.
Maas, A.L.; Hannum, A.Y. & Ng, A.Y. (2013). Rectifier nonlinearities improve neural network acoustic models. 30 th International Conference on Machine Learning, 28. Atlanta, Georgia. Recuperado el 27 de septiembre de 2014, de: http://web.stanford.edu/~awni/papers/relu_hybrid_icml2013_final.pdf.
Mohamed, A.; Sainath, T.; Dahl, G.; Ramabhadran, B.; Hinton, G. & Picheny, M. (2011). Deep Belief Networks using discriminative features for phone recognition. International Conference on Acoustics, Speech and Signal Processing (pp. 5060-5063). DOI:10.1109/ICASSP.2011.5947494.
Plahl, C.; Sainath, T.N.; Ramabhadran, B. & Nahamoo, D. (2012). Improved pre-training og deep belief networks using sparse enconding symmetric machines. International Conference on Acoustics, Speech and Signal Processing (pp. 4165-4168). DOI: 10.1109/ICASSP.2012.6288836.
Ramedani, Z.; Omid, M.; Keyhani, A.; Khoshnevisan, B. & Soboohi, H. (noviembre de 2014). A comparative study between fuzzy linear regression and support vector regression for global solar radiation prediction in Iran. Solar Energy, 109, 135-143. DOI:10.1016/j.solener.2014.08.023.
Santana, J.C. (junio de 2006). Predicción de series temporales con redes neuronales: una aplicación a la inflación colombiana. Revista Colombiana de Estadística 29(1), 77-92. Recuperado el 29 de septiembre de 2014, de: http://www.emis.de/journals/RCE/V29/V29_1_77Santana.pdf.
Sohn, K.; Jung, D.Y.; Lee, H. & Hero, A. (2011). Efficient learning of sparse, distributed, convolutional feature representations for object recognition. Computer Vision, (pp. 2643-2650). Barcelona, España. DOI:10.1109/ICCV.2011.6126554.
Stackhouse, P. (27 de septiembre de 2014). NASA Prediction of Worldwide Energy Resource (POWER). Recuperado el 27 de septiembre de 2014, de: http://power.larc.nasa.gov/.
Tieleman, T. (2008). Training Restricted Boltzmann Machines using Approximations to the Likelihood Gradient. International Conference on Machine Learning (pp. 1064-1071 ). Helsinki, Finlandia. DOI:10.1145/1390156.1390290.
Velilla, E.; Valencia, J. & Jaramillo, F. (28 de junio de 2014). Performance evaluation of two solar photovoltaic technologies under atmospheric exposure using artificial neural network models. Solar Energy, 107, 260-271. DOI:10.1016/j.solener.2014.04.033.
Ji, W. & Chee, K.C. (mayo de 2011). Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Solar Energy 85(5), 808-817. DOI:10.1016/j.solener.2011.01.013.
Xu, J., Yamada, K., Seikiya, K., Tanaka, R., & Yamane, Y. (octubre de 2014). Effect of different features to drill-wear prediction with back propagation neural network. Precision Engineering 38(4), 791 -798. DOI:10.1016/j.precisioneng.2014.04.007.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.