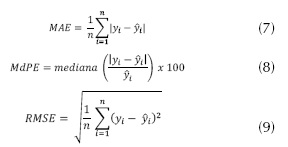DOI:
https://doi.org/10.14483/22487638.11658Published:
2017-07-01Issue:
Vol. 21 No. 53 (2017): July - SeptemberSection:
ResearchComparación de técnicas de interpolación espacial de propiedades del suelo en el piedemonte llanero colombiano
Comparison of spatial interpolation techniques to predict soil properties in the colombian piedmont eastern plains
Keywords:
bosques aleatorios, cartografía digital de suelos, hipercubo látino condicionado, oxisol (es).Keywords:
conditioned latin hypercube sampling, digital soil mapping, oxisol, random forest (en).References
Behrens, T., Zhu, A., Schmidt, K., y Scholten, T. (2010). Multi-Scale Digital Terrain Analysis and Feature Selection for Digital Soil Mapping. Geoderma, 155(3), 175-185. https://doi.org/10.1016/j.geoderma.2009.07.010
Bishop, T. y McBratney, A. (2001). A Comparison of Prediction Methods for the Creation of Field-Extent Soil Property Maps. Geoderma, 103(1–2), 149-160. https://doi.org/10.1016/S0016-7061(01)00074-X
Bray, R., y Kurtz, L. (1945). Determination of total, organic, and available forms of phosphorus in soils. Soil Science, 59(1), 39-46. https://doi.org/10.1097/00010694-194501000-00006
Breiman, L. (2001). Random Forests. Machine Learning, 45(1), 5-32. https://doi.org/10.1023/A:1010933404324
Castro, M., Costa, J., Peralta, N., y Aparicio, V. (2015). Prediction of Soil Properties at Farm Scale Using a Model-Based Soil Sampling Scheme and Random Forest. Soil science, 180, 1-12.
Giraldü, G., y Santana, E. (2014). Metodología para el pronóstico de la demanda en ambientes multiproducto y de alta variabilidad. Revista Tecnura, 18(40), 89-102. https://doi.org/10.14483/udistrital.jour.tecnura.2014.2.a07
Goovaerts, P. (1999). Geostatistics in Soil Science: State-Of-The-Art and Perspectives. Geoderma, 89(1), 1-45. https://doi.org/10.1016/S0016-7061(98)00078-0
Guyon, I., y Elisseeff, A. (2003). An Introduction to Variable and Feature Selection. Journal of Machine Learning Research, 3, 1157-1182.
Hempel, J., Hammer, R., Moore, A., Bell, J., Thompson, J., y Golden, M. (2008). Challenges to Digital Soil Mapping. Digital Soil Mapping with Limited Data (pp. 81-90). USA: Springer. https://doi.org/10.1007/978-1-4020-8592-5_7
Hengl, T., y Reuter, H. (Ed.). (2008). Geomorphometry: Concepts, Software, Applications. Amsterdam: Elsevier Science.
Hutchinson, M. (1989). A New Procedure for Gridding Elevation and Stream Line Data With Automatic Removal of Spurious Pits. Journal of Hydrology, 106(3), 211-232. https://doi.org/10.1016/0022-1694(89)90073-5
Kerry, R., y Oliver, M. (2003). Variograms of Ancillary Data to Aid Sampling for Soil Surveys. Precision Agriculture, 4(3), 261-278. https://doi.org/10.1023/A:1024952406744
Lavelle, P., Rodríguez, N., Arguello, O., Bernal, J., Botero, C., Chaparro, P., Gómez, Y., Gutierrez, A., Hurtado, M., Loaiza, S., Pullido, S., Rodríguez, Orozco, D., Flores, J., y Sanabria, Y. (2015). Indicadores químicos de calidad de suelos en sistemas productivos del Piedemonte de los Llanos Orientales de Colombia. Acta Agronómica, 64(4), 302-307.
E., Sanabria, C., Velásquez, E., y Fonte, S. (2014). Soil Ecosystem Services and Land Use in The Rapidly Changing Orinoco River Basin of Colombia. Agriculture, Ecosystems and Environment, 185(0), 106-117. https://doi.org/10.1016/j.agee.2013.12.020
Li, J., y Heap, A. (2011). A Review of Comparative Studies Of Spatial Interpolation Methods in Environmental Sciences: Performance and Impact Factors. Ecological Informatics, 6(3-4), 228-241. https://doi.org/10.1016/j.ecoinf.2010.12.003
Minasny, B., y McBratney, A. (2007). Spatial Prediction Of Soil Properties Using EBLUP With the Matérn Covariance Function. Geoderma, 140(4), 324-336. https://doi.org/10.1016/j.geoderma.2007.04.028
Olaya, V., y Conrad, O. (2009). Geomorphometry in SAGA. Developments in Soil Science, 33, 293-308. https://doi.org/10.1016/S0166-2481(08)00012-3
Oliver, M. (2010). Geostatistical Applications for Precision Agriculture. United Kingdom: Springer. https://doi.org/10.1007/978-90-481-9133-8
Pe-a, R., Rubiano, Y., Pe-a, A., y Chaves, B. (2009). Variabilidad espacial de los atributos de la capa arable de un Inceptisol del piedemonte de la cordillera oriental (Casanare, Colombia). Agronomía Colombiana, 27(1), 111-120.
R Development Core Team. (2015). R: A language and Enviroment for Stadistical Computing. Viena, Austria: R Fundation for Stadistical Computing. Recuperado de http://www.r-project.org/
Rippstein, G., Escobar, G., y Motta, F. (2001). Agroecología y biodiversidad de las sabanas en los Llanos Orientales de Colombia: CIAT.
Romero, M., Flantua, S., Tansey, K., y Berrio, J. (2012). Landscape Transformations in Savannas of Northern South America: Land Use/Cover Changes Since 1987 in the Llanos Orientales of Colombia. Applied Geography, 32(2), 766-776. https://doi.org/10.1016/j.apgeog.2011.08.010
Schmidt, K., Behrens, T., Daumann, J., Ramirez, L., Werban, U., Dietrich, P., y Scholten, T. (2014). A Comparison of Calibration Sampling Schemes at the Field Scale. Geoderma, 232, 243-256. https://doi.org/10.1016/j.geoderma.2014.05.013
Song, G., Zhang, J., y Wang, K. (2014). Selection of Optimal Auxiliary Soil Nutrient Variables for Cokriging Interpolation. PLoS ONE, 9(6), e99695. https://doi.org/10.1371/journal.pone.0099695
Toro, G., y Melo, C. (2009). Aplicación de métodos de interpolación geoestadísticos para la predicción de niveles digitales de una imagen satelital con líneas perdidas y efecto sal y pimienta. Revista Tecnura, 12(24), 55-67.
Walkley, A., y Black, I. A. (1934). An Examination of the Degtjareff Method for Determining Soil Organic Matter, and a Proposed Modification of the Chromic Acid Titration Method. Soil Science, 37(1), 29-38. https://doi.org/10.1097/00010694-193401000-00003
Webster, R., y Oliver, M. (2007). Geostatistics for Environmental Scientists. John Wiley and Sons. https://doi.org/10.1002/9780470517277
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: https://doi.org/10.14483/22487638.11658
Comparación de técnicas de interpolación espacial de propiedades del suelo en el piedemonte llanero colombiano
Comparison of spatial interpolation techniques to predict soil properties in the colombian piedmont eastern plains
Mauricio Castro Franco,1 Dayra Yisel García Ramírez,2 y Andrés Fernando Jiménez López3
1 Ingeniero Agrónomo, especialista en Sistemas de Información Geográfica, doctor en Ciencias Agrarias, estudiante de Posdoctorado en Ciencias Agrarias CONICET. Buenos Aires, Argentina. Contacto: agronomao@gmail.com
2 Ingeniera Agrícola, especialista en Gestión Ambiental Sostenible, estudiante de maestría en Producción Tropical Sostenible. Universidad de los Llanos. Villavicencio, Colombia. Contacto: dgarcia@unillanos.edu.co
3 Ingeniero Electrónico, magister en Física, estudiante de doctorado Ingeniería Mecánica-Mecatrónica Universidad Nacional de Colombia. Docente Universidad de los Llanos. Villavicencio, Colombia. Contacto: ajimenez@unillanos.edu.co
Fecha de recepción: 23 de febrero de 2017 Fecha de aceptación: 28 de abril de 2017
Cómo citar: Castro, M., García, D. y Jiménez, A. (2017). Comparación de técnicas de interpolación espadai de propiedades del suelo en el piedemonte llanero colombiano. Revista Tecnura, 21(53), 78-95, doi: 10.14483/22487638.11658
Resumen
Contexto: la interpolación espacial de propiedades del suelo en el piedemonte llanero colombiano es compleja debido al efecto simultáneo de la génesis del suelo, las características del terreno, el uso actual, y el manejo que de él se hace. Mientras las téc-nicas de interpolación vienen siendo adaptadas para tener en cuenta estos efectos, algunas propiedades del suelo son difíciles de predecir con las técnicas convencionales.
Método: en este trabajo se evaluaron seis técnicas de interpolación espacial: distancia inversa ponderada (IDW); Spline; kriging ordinario (KO); kriging universal (KU); cokriging (Ckg); y mejor predicción lineal insesgada empírica con máxima verosimilitud restringida (REML-EBLUP), a partir de la aplicación de hipercubo latino condicionado (HCLc) como es-trategia de muestreo. Se utilizaron los índices de terreno calculados a partir de un modelo digital de elevación como información auxiliar del suelo en los procedimientos de Ckg y REML-EBLUP. Para de-terminar los índices de terreno más importantes de cada propiedad se utilizó el algoritmo de bosques aleatorios (RF) y para validar las interpolaciones sobre validaciones cruzadas se usaron las métricas de error.
Resultados: los resultados soportan el supuesto de que HCLc captura adecuadamente la distribución total de la información auxiliar en condiciones del área experimental. Además, sugieren que Ckg y RE-ML-EBLUP generan mejores predicciones de la mayoría de las propiedades del suelo evaluadas.
Conclusiones: las técnicas de interpolación mixtas, teniendo también información auxiliar del suelo e índices de terreno, proporcionaron una mejora sig-nificativa de la predicción de propiedades del suelo, en comparación con las demás técnicas.
Palabras clave: bosques aleatorios, cartografía digital de suelos, hipercubo látino condicionado, oxisol.
Abstract
Context: Interpolating soil properties at field-scale in the Colombian piedmont eastern plains is cha-llenging due to: the highly and complex variable nature of some processes; the effects of the soil; the land use; and the management. While interpolation techniques are being adapted to include auxiliary information of these effects, the soil data are often difficult to predict using conventional techniques of spatial interpolation.
Method: In this paper, we evaluated and compared six spatial interpolation techniques: Inverse Distance Weighting (IDW), Spline, Ordinary Kriging (KO), Universal Kriging (UK), Cokriging (Ckg), and Resid-ual Maximum Likelihood-Empirical Best Linear Un-biased Predictor (REML-EBLUP), from conditioned Latin Hypercube as a sampling strategy. The ancil-lary information used in Ckg and REML-EBLUP was indexes calculated from a digital elevation model (MDE). The "Random forest" algorithm was used for selecting the most important terrain index for each soil properties. Error metrics were used to validate interpolations against cross validation.
Results: The results support the underlying assump-tion that HCLc captured adequately the full distri-bution of variables of ancillary information in the Colombian piedmont eastern plains conditions. They also suggest that Ckg and REML-EBLUP perform best in the prediction in most of the evaluated soil properties.
Conclusions: Mixed interpolation techniques having auxiliary soil information and terrain indexes, provided a significant improvement in the prediction of soil properties, in comparison with other techniques.
Keywords: conditioned latin hypercube sampling, digital soil mapping, oxisol, random forest.
INTRODUCCIÓN
El piedemonte llanero colombiano viene siendo sometido a una agriculturización intensiva (Romero, Flantua, Tansey, y Berrio, 2012); consecuentemente, la sostenibilidad de los servicios ecosistémicos está amenazada (Lavelle et al., 2014). Para mitigar este impacto, es imprescindible contar con técnicas que permitan determinar de manera rápida, precisa y económica, la variabilidad espacial de propiedades del suelo (Hempel et al., 2008).
Técnicas geoestadísticas y locales han sido reconocidas como técnicas convencionales de interpolación espacial para propiedades del suelo (Webster y Oliver, 2007); sin embargo, avances en teledetección han generado información auxiliar de factores formadores del suelo, que podrían aportar a la predicción espacial de propiedades del mismo. A partir de estos avances, se han desarrollado alternativas de técnicas de interpolación "mixtas", en las cuales combinan kriging e información auxiliar; numerosos trabajos han reportado que las técnicas de interpolación mixtas pueden tener alta precisión de predicción (Bishop y McBratney, 2001; Goovaerts, 1999; Oliver, 2010). Sin embargo, no se tiene evidencia de trabajos que hayan evaluado la eficiencia de predicción entre técnicas geoestadísticas, locales y mixtas, para las condiciones del piedemonte llanero colombiano.
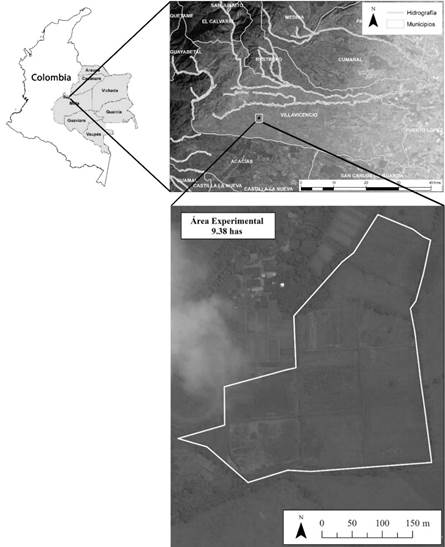
El objetivo de este trabajo fue comparar técnicas de interpolación espacial geoestadísticas, locales y mixtas de propiedades del suelo en un área experimental localizada en Villavicencio, correspondiente al piedemonte llanero colombiano, como se aprecia en la figura 1.
METODOLOGÍA
Área experimental
Este trabajo se llevó a cabo en un área agrícola de 9.38 has, localizada en Villavicencio, Meta (lat: 4.072; long: -73.580; figura 1). Los suelos del área de estudio provienen de aluviones y sedimentos aluviales heterométricos recientes, desde finos hasta gruesos y se encuentran en las distintas formas del relieve, la capacidad de retención de agua se considera de media a alta (Rippstein, Escobar y Motta, 2001); el área experimental se divide territorialmente en zonas de acuerdo a los siguientes sistemas productivos: pasturas, plátano, cultivos semestrales (maíz, soya y/o arroz), frutales y sistemas agroforestales.
Información auxiliar del suelo
Un modelo digital de elevación (MDE) fue utilizado como información auxiliar del suelo, a partir de este, índices de terreno fueron calculados utilizando el procedimiento de análisis de terreno de SAGA-GIS v2.0 (Olaya y Conrad, 2009); la tabla 1 muestra una breve descripción de cada índice (Hengl y Reuter, 2008). El MDE se obtuvo mediante la interpolación de curvas de nivel de acuerdo a la metodología ANUDEM descrita por Hutchinson (1989). La medición de curvas de nivel se realizó con una estación total SOK-KIA CX-105 (SOKKIA, Overland Park, KS). La interpolación de las curvas de nivel se realizó con la función "Topo to Raster" del módulo de Spatial Analyst de ArcGis v10.2, el MDE elaborado tuvo una resolución espacial de 10 m.
Esquema de muestreo de suelos y análisis de laboratorio
El algoritmo hipercubo latino condicionado (HCLc) fue utilizado para determinar la localización óptima de los puntos de muestreo a partir de la elevación; HCLc ha sido utilizado en la generación de cartografía digital de suelos a escala de lote (Castro, Costa, Peralta, y Aparicio, 2015; Schmidt et al., 2014). Los propósitos de utilizar HCLc como esquema de muestreo fueron: (a) evitar el uso de decisiones subjetivas en la selección de localización de muestras, (b) darle un enfoque estadístico al esquema de muestreo de suelos. Para este trabajo se decidió trabajar con 50 muestras de suelo, como cantidad suficiente para evaluar el desempeño predictivo de las técnicas de interpolación espacial (Kerry y Oliver, 2003).
Cada muestra de suelo se completó a partir de tres submuestras de 0-30 cm de profundidad, todas las muestras fueron analizadas en el laboratorio de suelos de la Universidad de los Llanos para: contenido de materia orgánica (MO; Walk-ley y Black, 1934), fósforo disponible (Pdisp; Bray y Kurtz, 1945), pH (1:1) con potenciómetro, aluminio intercambiable (Al) por el método KCL, calcio (Ca), magnesio (Mg), potasio (K), sodio (Na; extracción con acetato de amonio 1N y neutro), cobre (Cu), hierro (Fe) y manganeso (Mn; extracción con DTPA).
Selección de índices de terreno
Ckg y REML-EBLUP son métodos de interpolación espacial mixtos que requieren de variables auxiliares para optimizar la predicción espacial; debido a esto, se aplicó un método de selección de índices con mayor relación a cada propiedad del suelo (Guyon y Elisseeff, 2003).
Para la selección de índices, se implementó el algoritmo de bosques aleatorios o random forest (RF; Breiman, 2001), utilizando la librería "Ran-domForest" del software R v3.2.3. (R Development Core Team, 2015). RF calibra los parámetros "ntree" y "mtry" utilizando como método de estimación del error el "bootstrap" (Breiman, 2001). Este método consiste en tomar una cantidad establecida de muestras aleatorias (bootstrap samples) de un conjunto de datos de calibración; posteriormente, RF ajusta un árbol para cada bootstrap sample. Por cada bootstrap sample Xi, un tercio de los datos de calibración son dejados fuera de la muestra (out-of-bag; OOB), la tasa de error OOB (ERROOB) es estimada a medida que se agregan árboles al bosque. El "mtry" y "ntree" que generen el menor ERROOB deben ser elegidos para el modelo (Breiman, 2001).
La clasificación de importancia de índices se realizó mediante el cálculo de un índice de importancia, el cual se basa en el incremento del cuadrado medio del error (%incMSE), para cada árbol de regresión dentro de cada "bosque", cuando cada índice fue permutado aleatoriamente en la OOB. Mayor detalle del proceso de selección de variables con RF se encuentra en Behrens, Zhu, Schmidt, y Scholten, (2010).
Técnicas de interpolación espacial
Las técnicas de interpolación espacial seleccionadas fueron: distancia inversa ponderada (1) y Spline (2) como técnicas locales, kriging ordinario (3) y kriging universal (4) como técnicas geoestadísticas, y cokriging (5) y mejor predicción lineal insesgada empírica con máxima verosimilitud restringida (6) como técnicas mixtas. Esta selección se basó en el tipo de dato, la complejidad computacional de cada técnica y los resultados de trabajos previos (Minasny y McBratney, 2007; Peña, Rubiano, Peña, y Chaves, 2009). Las bibliotecas "automap", "gstat", "sp" y "fields" del software R v3.2.3 fueron utilizadas para ejecutar todas las técnicas de interpolación. En la tabla 2 se muestra una breve descripción de las técnicas de interpolación seleccionadas.
Evaluación de predicción
En orden de comparar la efectividad de las técnicas de interpolación, se utilizaron como métricas de error de predicción: el error medio absoluto (MAE) según la ecuación (7), la mediana del error predictivo (MdPE), mediante la ecuación (8) y la raíz del cuadrado medio del error (RMSE) por medio de la ecuación (9).
MAE determina la precisión general de la interpolación espacial, mientras RMSE es una métrica de error muy común para medir precisión de predicción, que da mayor peso a los valores extremos de los resultados; por su parte, MdPE fue utilizado en conjunto con MAE, como una métrica de error alternativa de precisión general de interpolación. En general, MdPE puede reducir el impacto que tienen los valores atípicos sobre la MAE; adicionalmente, se evaluó la diferencia entre valores interpolados y medidos en cada punto de muestreo, para esto, se calculó el error estadístico (SE) usando la ecuación (10).
RESULTADOS
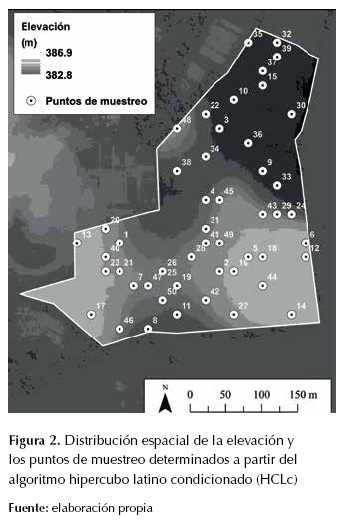
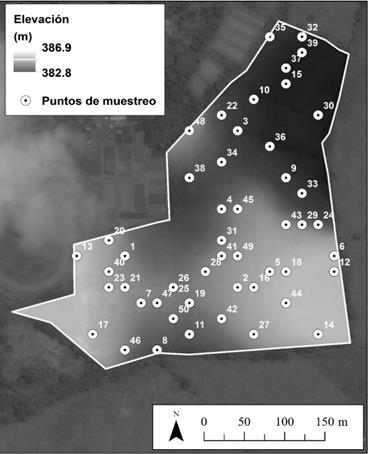
Los resultados sugieren que HCLc capturó significativamente la variabilidad espacial de la elevación utilizando 50 muestras distribuidas como se muestra en la figura 2; por lo tanto, en este trabajo se corrobora el supuesto de que HCLc puede capturar eficientemente la estructura de distribución espacial de covariables relacionadas con factores forma-dores del suelo y, por ende, es una alternativa para mejorar los esquemas de muestreo de suelos en condiciones del piedemonte llanero colombiano.
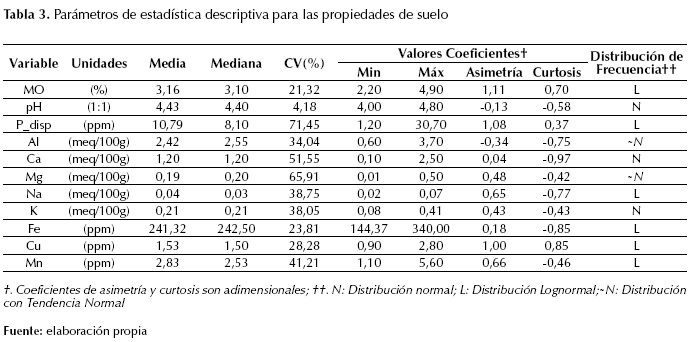
La tabla 3 muestra los parámetros de estadística descriptiva para las propiedades del suelo, los valores mínimos y máximos de pH y MO eran esperables debido a la génesis de los suelos de la zona y a las condiciones de intemperancia a las cuales se encuentra sometidos.
Excepto pH y MO, el coeficiente de variación (CV; Girald�, 2014) fue mayor al 23% para todas las propiedades del suelo; estos resultados fueron similares a los reportados por Orozco, Flores, y Sanabria. (2015), quienes plantearon que las propiedades químicas de los suelos del piedemonte llanero colombiano suelen tener alta heterogeneidad. Pdisp, Mg y Ca, en ese orden, presentaron los mayores CV, estos resultados se esperaban debido a las diferencias de uso y manejo del suelo, la aplicación de fertilizantes fosfatados, la aplicación de cal dolomita y la diferencia de tasa de absorción de P, Ca y Mg que tienen los cultivos implantados en el área experimental. Excepto MO, todos los CV de las propiedades de suelo analizadas fueron similares a los reportados por (Peña et al., 2009), ratificando los efectos de las prácticas de uso y manejo de suelo de los sistemas agropro-ductivos convencionales sobre las propiedades del suelo en el piedemonte llanero colombiano.
Las propiedades pH, Ca y K presentaron distribución normal, mientras que Al y Mg presentaron distribución con tendencia normal; las demás presentaron distribución lognormal (Tabla 3). Los coeficientes de curtosis calculados para todas las propiedades del suelo fueron diferentes a los reportados por Peña et al., (2009); a partir de este resultado, se plantea que aunque los CV puedan ser similares, la distribución de cada propiedad del suelo puede llegar a tener patrones espaciales característicos para cada área experimental.
Importancia de los índices de terreno
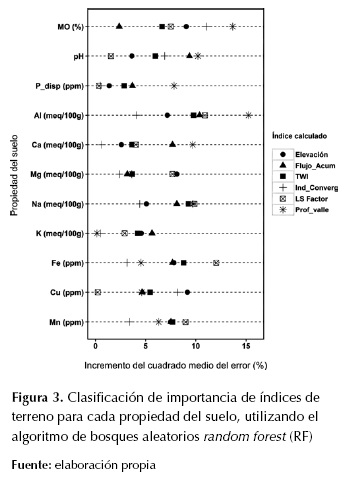
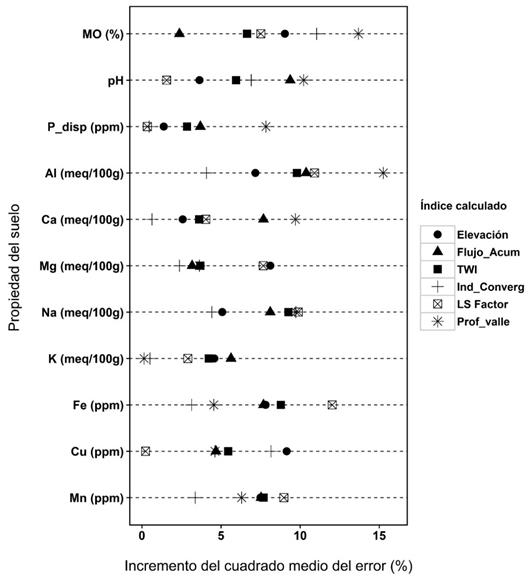
La figura 3 muestra la clasificación de importancia de los índices de terreno por propiedad del suelo, a partir de la aplicación de RF. Los índices más importantes para cada propiedad fueron utilizados
En la mayoría de las propiedades de suelo, el índice profundidad de valle (Prof_valle) e índice de convergencia (Ind_converg) fueron los de mayor y menor importancia respectivamente; el índice factor de pérdida de suelo (LS Factor) fue el segundo más importante para todas las variables, por otro lado, el índice topográfico de humedad (TWI) solo fue importante para Na. Estos índices, podrían ser los que más contribuyen a la explicación de la varianza y patrones espaciales de cada propiedad del suelo y, por ende, podrían ser utilizados dentro de funciones de pedotransferencia o para determinar patrones espaciales de indicadores de calidad del suelo (Castro et al., 2015).
Precisión de interpolación espacial
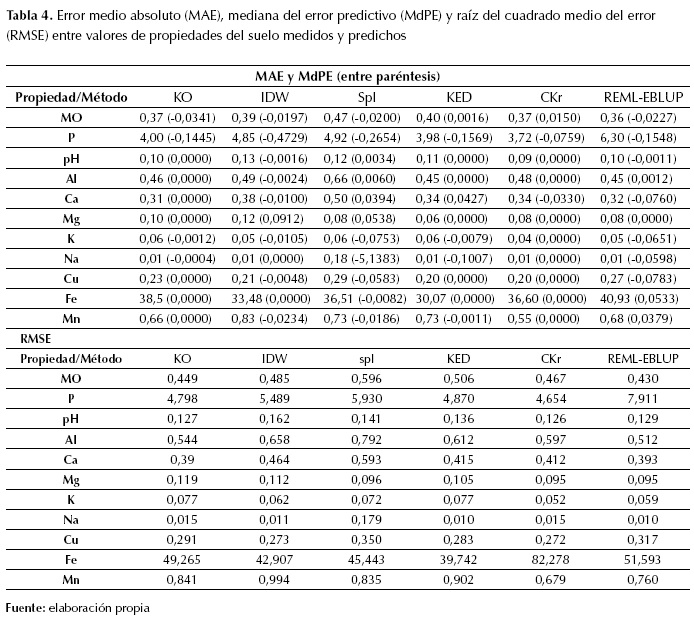
La tabla 4 muestra los MAE, MdPE y RMSE de las predicciones espaciales por propiedad del suelo y técnica de interpolación.
En general, los valores de MAE fueron moderados en todas las técnicas de interpolación, para todas las propiedades del suelo; por su parte, los valores de MdPE tuvieron mayor variabilidad, para la mayoría de las bases intercambiables. Para las interpolaciones de Pdisp y Fe, los valores de RMSE fueron considerablemente más altos y consistentes en magnitud. Las diferencias de valores de RMSE, MAE y MdPE entre propiedades, se deben al efecto del uso y manejo del suelo sobre cada propiedad del suelo, dentro del área experimental (Orozco et al., 2015).
Los valores mínimos de MAE y RMSE de la mayoría de las propiedades del suelo, se presentaron con Ckg y REML-EBLUP, al respecto, Minasny y McBratney (2007) reportaron que REML-EBLUP fue eficiente para interpolar propiedades del suelo, cuando la tendencia espacial es fuerte y el número de muestras es bajo (<200); asimismo, concluyeron que para mejorar la predicción espacial con REML-EBLUP, es prioritario hacer énfasis en las metodologías de muestreo y análisis de laboratorio de las muestras. Por su parte, Ckg, utilizando elevación como información auxiliar, ha sido escasamente reportado como una técnica de interpolación espacial eficiente de propiedades del suelo (Song, Zhang, y Wang., 2014); los resultados sugieren que técnicas de interpolación mixtas que involucren índices de terreno como información auxiliar, podrían tener mayor capacidad predictiva que las técnicas de interpolación geoestadísticas y locales, en condiciones de suelo del piedemonte llanero colombiano.
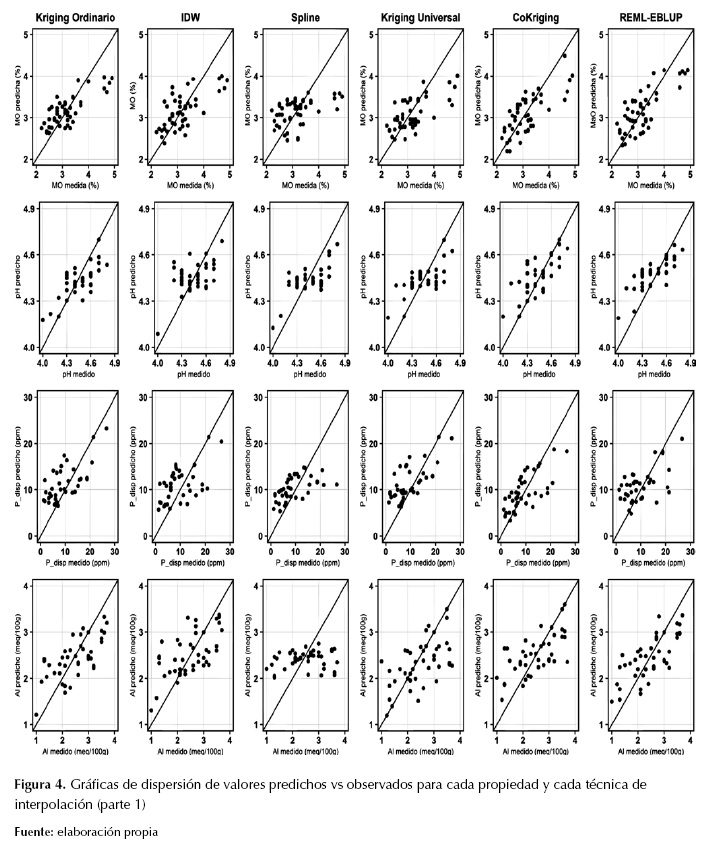
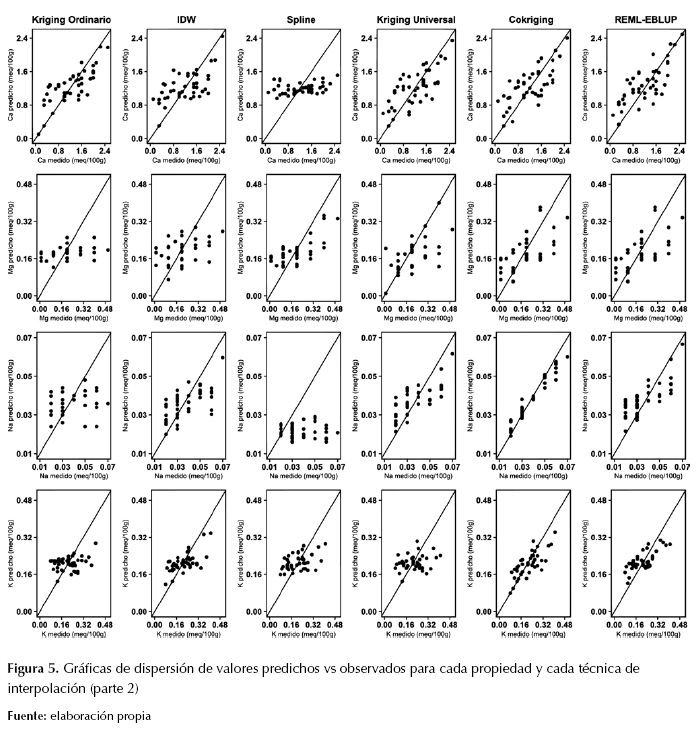
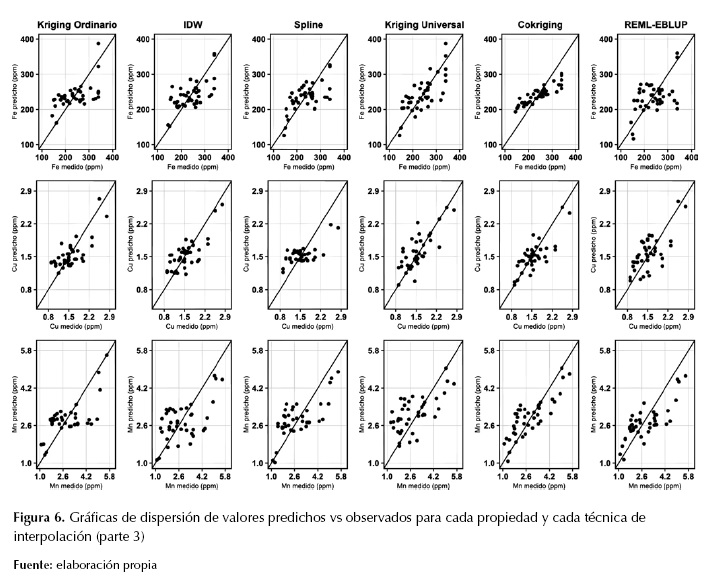
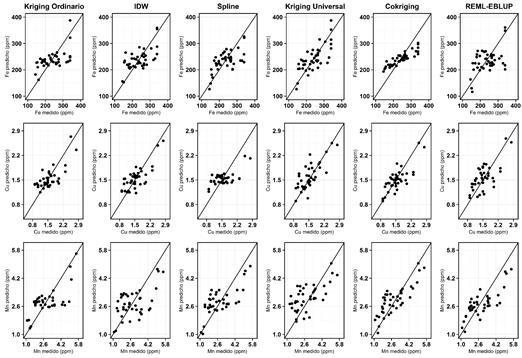
La figura 4, la figura 5 y la figura 6 muestran las diferencias entre valores predichos y observados por propiedad del suelo y técnica de interpolación; en las técnicas geoestadísticas y mixtas, la mayoría de las figuras de valores predichos observados tienen tendencia de homocedasticidad. Este resultado era esperable, ya que ha sido ampliamente discutido que IDW y Spline suelen marcar tendencia de patrones espaciales, mas no ser muy precisos en la interpolación de valores puntuales (Li y Heap, 2011). En la predicción espacial de Mg, K y Al, únicamente Ckg y EBLUP-RMSE tuvieron mayor capacidad predictiva en comparación con las demás técnicas de interpolación. En las demás propiedades, no se presentó mucha diferencia en capacidad predictiva entre las técnicas geoestadísticas y las mixtas.
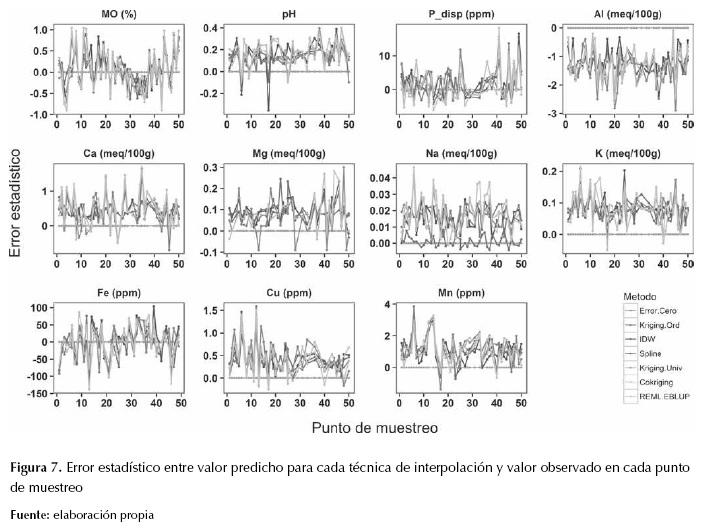
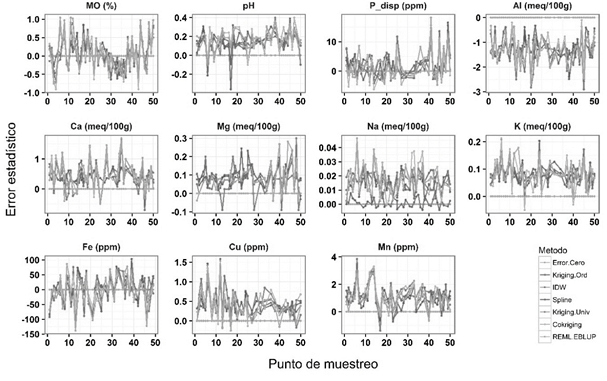
La figura 7 muestra el error estadístico (SE) entre valores interpolados y medidos en cada punto de muestreo para todas las técnicas de interpolación.
Excepto para MO, Fe y Pdisp, la SE fue alta para todas las técnicas de interpolación; por otro lado, excepto para Al, la mayoría de técnicas de interpolación presentaron tendencia a sobreestimación de valores en cada punto. Como se esperaba, las técnicas de interpolación local presentaron tendencia a predecir los valores más extremos para la mayoría de propiedades del suelo, en comparación con las demás técnicas de interpolación. En MO, entre los puntos cinco y veinte se presentó tendencia leve a la sobreestimación, mientras que en los puntos 30 al 40 a la subestimación.
Como se observa en la figura 2, de los puntos cinco al veinte tienden a estar en zonas con cultivos transitorios, mientras que los puntos 30 al 40 en zonas con cultivos perennes o sistemas agro-forestales. Estos resultados sugieren que en zonas con uso y manejo más intensivo del suelo, puede haber una tendencia a tener procesos degradativos más intensos de la MO y, por ende, esto puede afectar los patrones espaciales de la misma, (Peña et al., 2009).
En Pdisp, entre los puntos 40 y 50 se presentó tendencia leve a la sobreestimación, en comparación con los demás puntos de muestreo; de los puntos 40 a 50 se concentran en zonas con cultivos transitorios, los cuales vienen siendo fertilizados de manera continua y espacialmente desordenada. Esto, sin duda, es un cofactor a tener en cuenta para evaluar el desempeño predictivo de las técnicas de interpolación. Por último, Fe no tuvo un patrón claro de sobre o subestimación en la predicción de valores, para todas las técnicas de interpolación, lo cual era esperable debido a las fuertes condiciones de intemperancia en las que se encuentran sometidos los suelos del área experimental.
Comparación de patrones espaciales
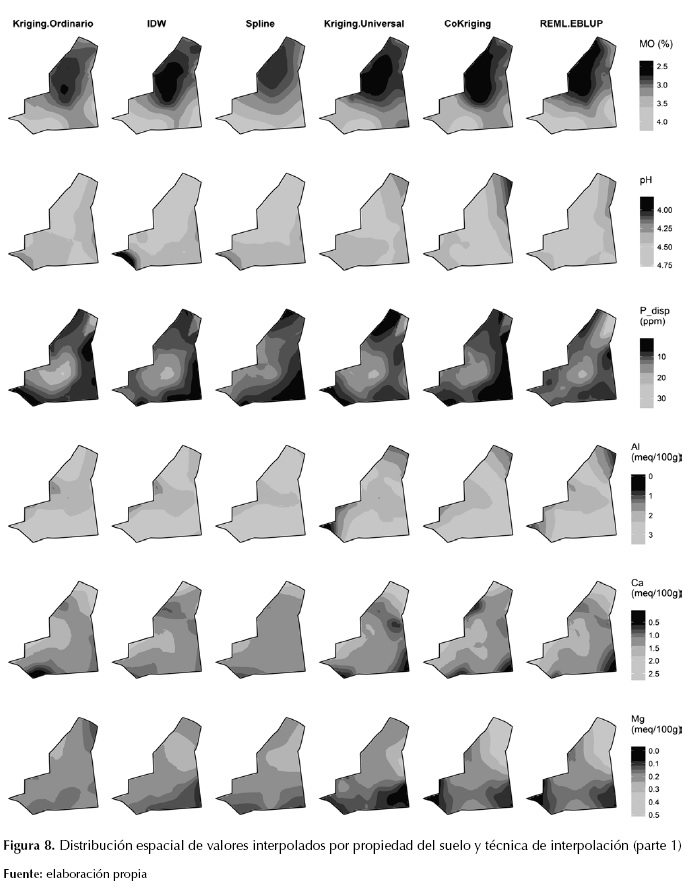
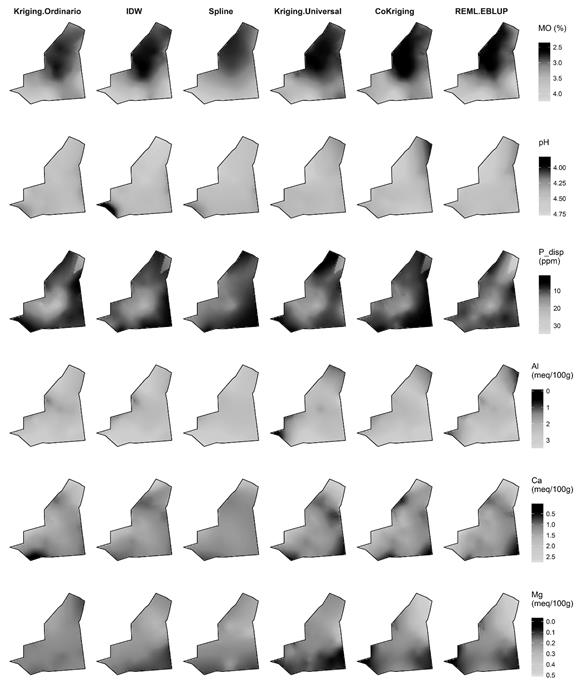
La figura 8 y la figura 9 muestran las predicciones espaciales de cada propiedad; en general, la mayoría de estas presentaron diferencias entre técnicas de interpolación. Un análisis visual determina que la predicción espacial de MO y de la mayoría de bases intercambiables presentaron mayor heterogeneidad espacial con Ckg y REML-EBLU, coincidiendo parcialmente con lo reportado por Minasny y McBratney (2007). Por su parte Al, Mg y Cu, presentó mayor heterogeneidad espacial con KU, coincidiendo parcialmente con lo reportado por Bishop y McBratney (2001). Cu, presentaron similar patrón espacial con todas las técnicas de interpolación, mientras que Ca presentó mayor heterogeneidad espacial con KO y REML-EBLUP.
Las interpolaciones con IDW y Spline tuvieron mayor homogeneidad espacial para la mayoría de propiedades del suelo, mientras que las interpolaciones con KU presentaron patrones espaciales más heterogéneos que con KO. En general, los resultados sugieren que la inclusión de índices de terreno como variables auxiliares en técnicas de interpolación mixta, puede aportar a la caracterización de los patrones espaciales de todas las propiedades del suelo en condiciones de la altillanura colombiana, excepto pH y Cu.
Los resultados permiten establecer un punto de referencia del uso de técnicas de interpolación espacial en condiciones del piedemonte llanero colombiano; no obstante, estos resultados deben ser validados para otras áreas experimentales aledañas, ya que responden exclusivamente a condiciones climatológicas, de uso y manejo del suelo y edafológicas del área experimental.
CONCLUSIONES
En este trabajo, seis técnicas de interpolación de tipo local (IDW y Spline), geoestadística (KO y KU) y mixta (Ckg y REML-EBLUP) fueron comparadas para predecir propiedades del suelo en condiciones del piedemonte llanero colombiano; los resultados validan la utilidad de HCLc como esquema de muestreo y soportan el supuesto que HCLc captura adecuadamente la distribución de información auxiliar del suelo. Por su parte, RF demostró ser adecuado para determinar los índices de terreno con mayor capacidad predictiva para cada una de las propiedades del suelo.
En general, los resultados sugieren que las técnicas de interpolación mixtas teniendo como información auxiliar del suelo e índices de terreno, proporcionaron una mejora significativa de la predicción de propiedades del suelo, en comparación con las demás técnicas; este resultado es importante para implementar estrategias de mejoramiento de la sostenibilidad de los servicios ecosistémicos del suelo, en condiciones del piedemonte llanero colombiano. Los resultados obtenidos requieren
ser validados para otras zonas y con otras fuentes de información auxiliar.
AGRADECIMIENTOS
Este trabajo se realizó en el marco del Proyecto Unillanos 2014 "Sistema de monitoreo de calidad del suelo a hiperescala (<1:2,000) en la Granja Barcelona, para la implementación de manejo sitio específico", y asesorado por integrantes del PE 1134023 INTA, Argentina.
REFERENCIAS
Behrens, T., Zhu, A., Schmidt, K., y Scholten, T. (2010). Multi-Scale Digital Terrain Analysis and Feature Selection for Digital Soil Mapping. Geoderma, 155(3), 175-185.
Bishop, T. y McBratney, A. (2001). A Comparison of Prediction Methods for the Creation of Field-Extent Soil Property Maps. Geoderma, 103(1-2), 149-160. doi: 10.1016/s0016-7061(01)00074-x.
Bray, R., y Kurtz, L. (1945). Determination of total, organic, and available forms of phosphorus in soils. Soil Science, 59(1), 39-46.
Breiman, L. (2001). Random Forests. Machine Learning, 45(1), 5-32. doi: 10.1023/a:1010933404324.
Castro, M., Costa, J., Peralta, N., y Aparicio, V. (2015). Prediction of Soil Properties at Farm Scale Using a Model-Based Soil Sampling Scheme and Random Forest. Soil science, 180, 1-12.
Girald�, G., y Santana, E. (2014). Metodología para el pronóstico de la demanda en ambientes multi-producto y de alta variabilidad. Revista Tecnura, 18(40), 89-102.
Goovaerts, P. (1999). Geostatistics in Soil Science: State-Of-The-Art and Perspectives. Geoderma, 89(1), 1-45.
Guyon, I., y Elisseeff, A. (2003). An Introduction to Variable and Feature Selection. Journal of Machine Learning Research, 3, 1157-1 182.
Hempel, J., Hammer, R., Moore, A., Bell, J., Thompson, J., y Golden, M. (2008). Challenges to Digital Soil Mapping. Digital Soil Mapping with Limited Data (pp. 81-90). USA: Springer.
Hengl, T., y Reuter, H. (Ed.). (2008). Geomorphometry: Concepts, Software, Applications. Amsterdam: Elsevier Science.
Hutchinson, M. (1989). A New Procedure for Grid-ding Elevation and Stream Line Data With Automatic Removal of Spurious Pits. Journal of Hydrology, 106(3), 21 1-232.
Kerry, R., y Oliver, M. (2003). Variograms of Ancillary Data to Aid Sampling for Soil Surveys. Precision Agriculture, 4(3), 261-278.
Lavelle, P., Rodríguez, N., Arguello, O., Bernal, J., Botero, C., Chaparro, P., Gómez, Y., Gutierrez, A., Hurtado, M., Loaiza, S., Pullido, S., Rodríguez, E., Sanabria, C., Velásquez, E., y Fonte, S. (2014). Soil Ecosystem Services and Land Use in The Rapidly Changing Orinoco River Basin of Colombia. Agriculture, Ecosystems and Environment, 185(0), 106-117. doi: http://dx.doi.org/10.1016/jagee.2013.12.020.
Li, J., y Heap, A. (2011). A Review of Comparative Studies Of Spatial Interpolation Methods in Environmental Sciences: Performance and Impact Factors. Ecological Informatics, 6(3-4), 228-241.
Minasny, B., y McBratney, A. (2007). Spatial Prediction Of Soil Properties Using EBLUP With the Matérn Covariance Function. Geoderma, 140(4), 324-336. doi: http://dx.doi.org/10.1016/j.geoderma.2007.04.028.
Olaya, V., y Conrad, O. (2009). Geomorphometry in SAGA. Developments in Soil Science, 33, 293-308.
Oliver, M. (2010). Geostatistical Applications for Precision Agriculture. United Kingdom: Springer.
Orozco, D., Flores, J., y Sanabria, Y. (2015). Indicadores químicos de calidad de suelos en sistemas productivos del Piedemonte de los Llanos Orientales de Colombia. Acta Agronómica, 64(4), 302-307.
Peña, R., Rubiano, Y., Peña, A., y Chaves, B. (2009). Variabilidad espacial de los atributos de la capa arable de un Inceptisol del piedemonte de la cordillera oriental (Casanare, Colombia). Agronomía Colombiana, 27(1), 111-120.
R Development Core Team. (2015). R: A language and Enviroment for Stadistical Computing. Viena, Austria: R Fundation for Stadistical Computing. Recuperado de http://www.r-project.org/
Rippstein, G., Escobar, G., y Motta, F. (2001). Agroeco-logía y biodiversidad de las sabanas en los Llanos Orientales de Colombia: CIAT.
Romero, M., Flantua, S., Tansey, K., y Berrio, J. (2012). Landscape Transformations in Savannas of Northern South America: Land Use/Cover Changes Since 1987 in the Llanos Orientales of Colombia. Applied Geography, 32(2), 766-776. doi: http://dx.doi.org/10.1016/j.apgeog.2011.08.010.
Schmidt, K., Behrens, T., Daumann, J., Ramirez, L., Wer-ban, U., Dietrich, P., y Scholten, T. (2014). A Comparison of Calibration Sampling Schemes at the Field Scale. Geoderma, 232, 243-256.
Song, G., Zhang, J., y Wang, K. (2014). Selection of Optimal Auxiliary Soil Nutrient Variables for Cokrig-ing Interpolation. PLoS ONE, 9(6), e99695. doi: 10.1371/journal.pone.0099695
Toro, G., y Melo, C. (2009). Aplicación de métodos de interpolación geoestadísticos para la predicción de niveles digitales de una imagen satelital con líneas perdidas y efecto sal y pimienta. Revista Tecnura, 12(24), 55-67.
Walkley, A., y Black, I. A. (1934). An Examination of the Degtjareff Method for Determining Soil Organic Matter, and a Proposed Modification of the Chromic Acid Titration Method. Soil Science, 37(1), 29-38.
Webster, R., y Oliver, M. (2007). Geostatistics for Environmental Scientists. John Wiley and Sons.
Recibido: 23 de febrero de 2017; Aceptado: 28 de abril de 2017
Resumen
Contexto:
la interpolación espacial de propiedades del suelo en el piedemonte llanero colombiano es compleja debido al efecto simultáneo de la génesis del suelo, las características del terreno, el uso actual, y el manejo que de él se hace. Mientras las técnicas de interpolación vienen siendo adaptadas para tener en cuenta estos efectos, algunas propiedades del suelo son difíciles de predecir con las técnicas convencionales.
Método:
en este trabajo se evaluaron seis técnicas de interpolación espacial: distancia inversa ponderada (IDW); Spline; kriging ordinario (KO); kriging universal (KU); cokriging (Ckg); y mejor predicción lineal insesgada empírica con máxima verosimilitud restringida (REML-EBLUP), a partir de la aplicación de hipercubo latino condicionado (HCLc) como estrategia de muestreo. Se utilizaron los índices de terreno calculados a partir de un modelo digital de elevación como información auxiliar del suelo en los procedimientos de Ckg y REML-EBLUP. Para determinar los índices de terreno más importantes de cada propiedad se utilizó el algoritmo de bosques aleatorios (RF) y para validar las interpolaciones sobre validaciones cruzadas se usaron las métricas de error.
Resultados:
los resultados soportan el supuesto de que HCLc captura adecuadamente la distribución total de la información auxiliar en condiciones del área experimental. Además, sugieren que Ckg y REML-EBLUP generan mejores predicciones de la mayoría de las propiedades del suelo evaluadas.
Conclusiones:
las técnicas de interpolación mixtas, teniendo también información auxiliar del suelo e índices de terreno, proporcionaron una mejora significativa de la predicción de propiedades del suelo, en comparación con las demás técnicas.
Palabras clave:
bosques aleatorios, cartografía digital de suelos, hipercubo látino condicionado, oxisol.Abstract
Context:
Interpolating soil properties at field-scale in the Colombian piedmont eastern plains is challenging due to: the highly and complex variable nature of some processes; the effects of the soil; the land use; and the management. While interpolation techniques are being adapted to include auxiliary information of these effects, the soil data are often difficult to predict using conventional techniques of spatial interpolation.
Method:
In this paper, we evaluated and compared six spatial interpolation techniques: Inverse Distance Weighting (IDW), Spline, Ordinary Kriging (KO), Universal Kriging (UK), Cokriging (Ckg), and Residual Maximum Likelihood-Empirical Best Linear Unbiased Predictor (REML-EBLUP), from conditioned Latin Hypercube as a sampling strategy. The ancillary information used in Ckg and REML-EBLUP was indexes calculated from a digital elevation model (MDE). The “Random forest” algorithm was used for selecting the most important terrain index for each soil properties. Error metrics were used to validate interpolations against cross validation.
Results:
The results support the underlying assumption that HCLc captured adequately the full distribution of variables of ancillary information in the Colombian piedmont eastern plains conditions. They also suggest that Ckg and REML-EBLUP perform best in the prediction in most of the evaluated soil properties.
Conclusions:
Mixed interpolation techniques having auxiliary soil information and terrain indexes, provided a significant improvement in the prediction of soil properties, in comparison with other techniques.
Keywords:
conditioned latin hypercube sampling, digital soil mapping, oxisol, random forest.INTRODUCCIÓN
El piedemonte llanero colombiano viene siendo sometido a una agriculturización intensiva (Romero, Flantua, Tansey, y Berrio, 2012); consecuentemente, la sostenibilidad de los servicios ecosistémicos está amenazada (Lavelle et al., 2014). Para mitigar este impacto, es imprescindible contar con técnicas que permitan determinar de manera rápida, precisa y económica, la variabilidad espacial de propiedades del suelo (Hempel et al., 2008).
Técnicas geoestadísticas y locales han sido reconocidas como técnicas convencionales de interpolación espacial para propiedades del suelo (Webster y Oliver, 2007); sin embargo, avances en teledetección han generado información auxiliar de factores formadores del suelo, que podrían aportar a la predicción espacial de propiedades del mismo. A partir de estos avances, se han desarrollado alternativas de técnicas de interpolación “mixtas”, en las cuales combinan kriging e información auxiliar; numerosos trabajos han reportado que las técnicas de interpolación mixtas pueden tener alta precisión de predicción (Bishop y McBratney, 2001; Goovaerts, 1999; Oliver, 2010). Sin embargo, no se tiene evidencia de trabajos que hayan evaluado la eficiencia de predicción entre técnicas geoestadísticas, locales y mixtas, para las condiciones del piedemonte llanero colombiano.
El objetivo de este trabajo fue comparar técnicas de interpolación espacial geoestadísticas, locales y mixtas de propiedades del suelo en un área experimental localizada en Villavicencio, correspondiente al piedemonte llanero colombiano, como se aprecia en la Figura 1.
Figura 1: Localización del área experimental
METODOLOGÍA
Área experimental
Este trabajo se llevó a cabo en un área agrícola de 9.38 has, localizada en Villavicencio, Meta (lat: 4.072; long: -73.580; Figura 1). Los suelos del área de estudio provienen de aluviones y sedimentos aluviales heterométricos recientes, desde finos hasta gruesos y se encuentran en las distintas formas del relieve, la capacidad de retención de agua se considera de media a alta (Rippstein, Escobar y Motta, 2001); el área experimental se divide territorialmente en zonas de acuerdo a los siguientes sistemas productivos: pasturas, plátano, cultivos semestrales (maíz, soya y/o arroz), frutales y sistemas agroforestales.
Información auxiliar del suelo
Un modelo digital de elevación (MDE) fue utilizado como información auxiliar del suelo, a partir de este, índices de terreno fueron calculados utilizando el procedimiento de análisis de terreno de SAGA-GIS v2.0 (Olaya y Conrad, 2009); la Tabla 1 muestra una breve descripción de cada índice (Hengl y Reuter, 2008). El MDE se obtuvo mediante la interpolación de curvas de nivel de acuerdo a la metodología ANUDEM descrita por Hutchinson (1989). La medición de curvas de nivel se realizó con una estación total SOKKIA CX-105 (SOKKIA, Overland Park, KS). La interpolación de las curvas de nivel se realizó con la función “Topo to Raster” del módulo de Spatial Analyst de ArcGis v10.2, el MDE elaborado tuvo una resolución espacial de 10 m.
Fuente: elaboración propia
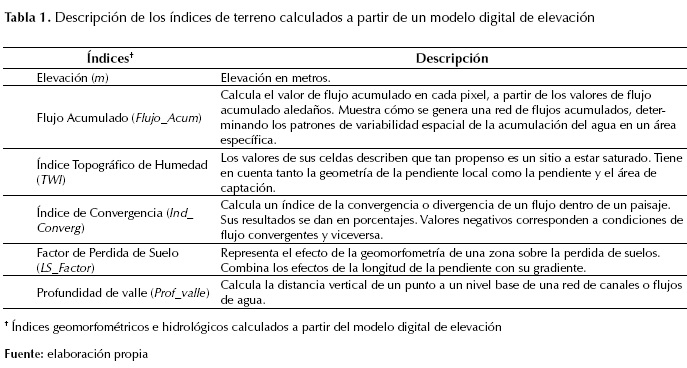
Tabla 1: Descripción de los índices de terreno calculados a partir de un modelo digital de elevación
Índices
†
Descripción
Elevación (m)
Elevación en metros.
Flujo Acumulado (Flujo_Acum)
Calcula el valor de flujo acumulado en cada pixel, a partir de los valores de flujo acumulado aledaños. Muestra cómo se genera una red de flujos acumulados, determinando los patrones de variabilidad espacial de la acumulación del agua en un área específica.
Índice Topográfico de Humedad (TWI)
Los valores de sus celdas describen que tan propenso es un sitio a estar saturado. Tiene en cuenta tanto la geometría de la pendiente local como la pendiente y el área de captación.
Índice de Convergencia (Ind_Converg)
Calcula un índice de la convergencia o divergencia de un flujo dentro de un paisaje. Sus resultados se dan en porcentajes. Valores negativos corresponden a condiciones de flujo convergentes y viceversa.
Factor de Perdida de Suelo (LS_Factor)
Representa el efecto de la geomorfometría de una zona sobre la perdida de suelos. Combina los efectos de la longitud de la pendiente con su gradiente.
Profundidad de valle (Prof_valle)
Calcula la distancia vertical de un punto a un nivel base de una red de canales o flujos de agua.
Esquema de muestreo de suelos y análisis de laboratorio
El algoritmo hipercubo latino condicionado (HCLc) fue utilizado para determinar la localización óptima de los puntos de muestreo a partir de la elevación; HCLc ha sido utilizado en la generación de cartografía digital de suelos a escala de lote (Castro, Costa, Peralta, y Aparicio, 2015; Schmidt et al., 2014). Los propósitos de utilizar HCLc como esquema de muestreo fueron: (a) evitar el uso de decisiones subjetivas en la selección de localización de muestras, (b) darle un enfoque estadístico al esquema de muestreo de suelos. Para este trabajo se decidió trabajar con 50 muestras de suelo, como cantidad suficiente para evaluar el desempeño predictivo de las técnicas de interpolación espacial (Kerry y Oliver, 2003).
Cada muestra de suelo se completó a partir de tres submuestras de 0-30 cm de profundidad, todas las muestras fueron analizadas en el laboratorio de suelos de la Universidad de los Llanos para: contenido de materia orgánica (MO; Walkley y Black, 1934), fósforo disponible (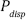 ; Bray y Kurtz, 1945), pH (1:1) con potenciómetro, aluminio intercambiable (Al) por el método KCL, calcio (Ca), magnesio (Mg), potasio (K), sodio (Na; extracción con acetato de amonio 1N y neutro), cobre (Cu), hierro (Fe) y manganeso (Mn; extracción con DTPA).
; Bray y Kurtz, 1945), pH (1:1) con potenciómetro, aluminio intercambiable (Al) por el método KCL, calcio (Ca), magnesio (Mg), potasio (K), sodio (Na; extracción con acetato de amonio 1N y neutro), cobre (Cu), hierro (Fe) y manganeso (Mn; extracción con DTPA).
Selección de índices de terreno
Ckg y REML-EBLUP son métodos de interpolación espacial mixtos que requieren de variables auxiliares para optimizar la predicción espacial; debido a esto, se aplicó un método de selección de índices con mayor relación a cada propiedad del suelo (Guyon y Elisseeff, 2003).
Para la selección de índices, se implementó el algoritmo de bosques aleatorios o random forest (RF; Breiman, 2001), utilizando la librería “RandomForest” del software R v3.2.3. (R Development Core Team, 2015). RF calibra los parámetros “ntree” y “mtry” utilizando como método de estimación del error el “bootstrap” (Breiman, 2001). Este método consiste en tomar una cantidad establecida de muestras aleatorias (bootstrap samples) de un conjunto de datos de calibración; posteriormente, RF ajusta un árbol para cada bootstrap sample. Por cada bootstrap sample Xi, un tercio de los datos de calibración son dejados fuera de la muestra (out-of-bag; OOB), la tasa de error OOB (ERROOB) es estimada a medida que se agregan árboles al bosque. El “mtry” y “ntree” que generen el menor ERROOB deben ser elegidos para el modelo (Breiman, 2001).
La clasificación de importancia de índices se realizó mediante el cálculo de un índice de importancia, el cual se basa en el incremento del cuadrado medio del error (%incMSE), para cada árbol de regresión dentro de cada “bosque”, cuando cada índice fue permutado aleatoriamente en la OOB. Mayor detalle del proceso de selección de variables con RF se encuentra en Behrens, Zhu, Schmidt, y Scholten, (2010).
Técnicas de interpolación espacial
Las técnicas de interpolación espacial seleccionadas fueron: distancia inversa ponderada (1) y Spline (2) como técnicas locales, kriging ordinario (3) y kriging universal (4) como técnicas geoestadísticas, y cokriging (5) y mejor predicción lineal insesgada empírica con máxima verosimilitud restringida (6) como técnicas mixtas. Esta selección se basó en el tipo de dato, la complejidad computacional de cada técnica y los resultados de trabajos previos (Minasny y McBratney, 2007; Peña, Rubiano, Peña, y Chaves, 2009). Las bibliotecas “automap”, “gstat”, “sp” y “fields” del software R v3.2.3 fueron utilizadas para ejecutar todas las técnicas de interpolación. En la Tabla 2 se muestra una breve descripción de las técnicas de interpolación seleccionadas.
Fuente: elaboración propia
Tabla 2: Descripción y fórmulas de las técnicas de interpolación espacial utilizados en este trabajo (Li, 2011)

Evaluación de predicción
En orden de comparar la efectividad de las técnicas de interpolación, se utilizaron como métricas de error de predicción: el error medio absoluto (MAE) según la ecuación (7), la mediana del error predictivo (MdPE), mediante la ecuación (8) y la raíz del cuadrado medio del error (RMSE) por medio de la ecuación (9).
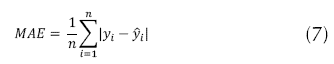
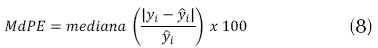
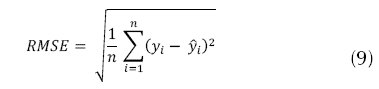
MAE determina la precisión general de la interpolación espacial, mientras RMSE es una métrica de error muy común para medir precisión de predicción, que da mayor peso a los valores extremos de los resultados; por su parte, MdPE fue utilizado en conjunto con MAE, como una métrica de error alternativa de precisión general de interpolación. En general, MdPE puede reducir el impacto que tienen los valores atípicos sobre la MAE; adicionalmente, se evaluó la diferencia entre valores interpolados y medidos en cada punto de muestreo, para esto, se calculó el error estadístico (SE) usando la ecuación (10).

RESULTADOS
Los resultados sugieren que HCLc capturó significativamente la variabilidad espacial de la elevación utilizando 50 muestras distribuidas como se muestra en la Figura 2; por lo tanto, en este trabajo se corrobora el supuesto de que HCLc puede capturar eficientemente la estructura de distribución espacial de covariables relacionadas con factores formadores del suelo y, por ende, es una alternativa para mejorar los esquemas de muestreo de suelos en condiciones del piedemonte llanero colombiano.
Figura 2: Distribución espacial de la elevación y los puntos de muestreo determinados a partir del algoritmo hipercubo latino condicionado (HCLc)
La Tabla 3 muestra los parámetros de estadística descriptiva para las propiedades del suelo, los valores mínimos y máximos de pH y MO eran esperables debido a la génesis de los suelos de la zona y a las condiciones de intemperancia a las cuales se encuentra sometidos.
†. Coeficientes de asimetría y curtosis son adimensionales; ††. N: Distribución normal; L: Distribución Lognormal; ~N: Distribución con Tendencia Normal Fuente: elaboración propia
Tabla 3: Parámetros de estadística descriptiva para las propiedades de suelo
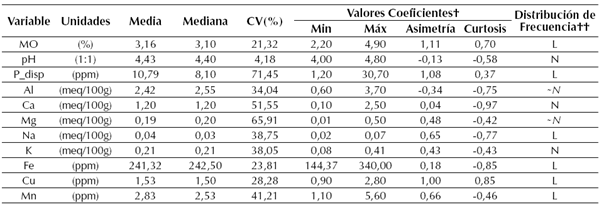
Excepto pH y MO, el coeficiente de variación (CV; Giraldü, 2014) fue mayor al 23% para todas las propiedades del suelo; estos resultados fueron similares a los reportados por Orozco, Flores, y Sanabria. (2015), quienes plantearon que las propiedades químicas de los suelos del piedemonte llanero colombiano suelen tener alta heterogeneidad. 𝑃 𝑑𝑖𝑠𝑝 , Mg y Ca, en ese orden, presentaron los mayores CV, estos resultados se esperaban debido a las diferencias de uso y manejo del suelo, la aplicación de fertilizantes fosfatados, la aplicación de cal dolomita y la diferencia de tasa de absorción de P, Ca y Mg que tienen los cultivos implantados en el área experimental. Excepto MO, todos los CV de las propiedades de suelo analizadas fueron similares a los reportados por (Peña et al., 2009), ratificando los efectos de las prácticas de uso y manejo de suelo de los sistemas agroproductivos convencionales sobre las propiedades del suelo en el piedemonte llanero colombiano.
Las propiedades pH, Ca y K presentaron distribución normal, mientras que Al y Mg presentaron distribución con tendencia normal; las demás presentaron distribución lognormal (Tabla 3). Los coeficientes de curtosis calculados para todas las propiedades del suelo fueron diferentes a los reportados por Peña et al., (2009); a partir de este resultado, se plantea que aunque los CV puedan ser similares, la distribución de cada propiedad del suelo puede llegar a tener patrones espaciales característicos para cada área experimental.
Importancia de los índices de terreno
La Figura 3 muestra la clasificación de importancia de los índices de terreno por propiedad del suelo, a partir de la aplicación de RF. Los índices más importantes para cada propiedad fueron utilizados para Ckg y REML-EBLUP.
Figura 3: Clasificación de importancia de índices de terreno para cada propiedad del suelo, utilizando el algoritmo de bosques aleatorios random forest (RF)
En la mayoría de las propiedades de suelo, el índice profundidad de valle (Prof_valle) e índice de convergencia (Ind_converg) fueron los de mayor y menor importancia respectivamente; el índice factor de pérdida de suelo (LS Factor) fue el segundo más importante para todas las variables, por otro lado, el índice topográfico de humedad (TWI) solo fue importante para Na. Estos índices, podrían ser los que más contribuyen a la explicación de la varianza y patrones espaciales de cada propiedad del suelo y, por ende, podrían ser utilizados dentro de funciones de pedotransferencia o para determinar patrones espaciales de indicadores de calidad del suelo (Castro et al., 2015).
Precisión de interpolación espacial
La Tabla 4 muestra los MAE, MdPE y RMSE de las predicciones espaciales por propiedad del suelo y técnica de interpolación.
Fuente: elaboración propia
Tabla 4: Error medio absoluto (MAE), mediana del error predictivo (MdPE) y raíz del cuadrado medio del error (RMSE) entre valores de propiedades del suelo medidos y predichos
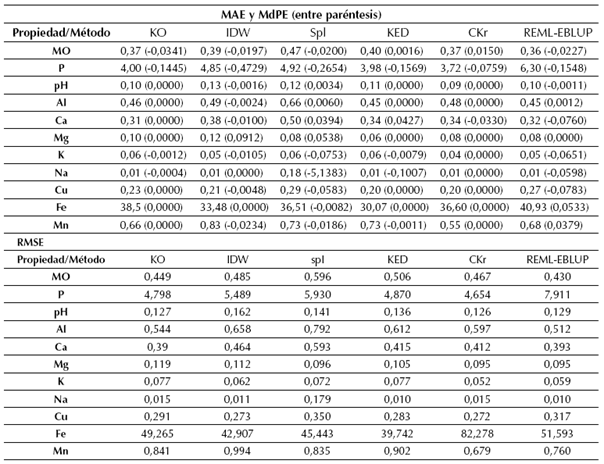
En general, los valores de MAE fueron moderados en todas las técnicas de interpolación, para todas las propiedades del suelo; por su parte, los valores de MdPE tuvieron mayor variabilidad, para la mayoría de las bases intercambiables. Para las interpolaciones de 𝑃 𝑑𝑖𝑠𝑝 y Fe, los valores de RMSE fueron considerablemente más altos y consistentes en magnitud. Las diferencias de valores de RMSE, MAE y MdPE entre propiedades, se deben al efecto del uso y manejo del suelo sobre cada propiedad del suelo, dentro del área experimental (Orozco et al., 2015).
Los valores mínimos de MAE y RMSE de la mayoría de las propiedades del suelo, se presentaron con Ckg y REML-EBLUP, al respecto, Minasny y McBratney (2007) reportaron que REML-EBLUP fue eficiente para interpolar propiedades del suelo, cuando la tendencia espacial es fuerte y el número de muestras es bajo (<200); asimismo, concluyeron que para mejorar la predicción espacial con REML-EBLUP, es prioritario hacer énfasis en las metodologías de muestreo y análisis de laboratorio de las muestras. Por su parte, Ckg, utilizando elevación como información auxiliar, ha sido escasamente reportado como una técnica de interpolación espacial eficiente de propiedades del suelo (Song, Zhang, y Wang., 2014); los resultados sugieren que técnicas de interpolación mixtas que involucren índices de terreno como información auxiliar, podrían tener mayor capacidad predictiva que las técnicas de interpolación geoestadísticas y locales, en condiciones de suelo del piedemonte llanero colombiano.
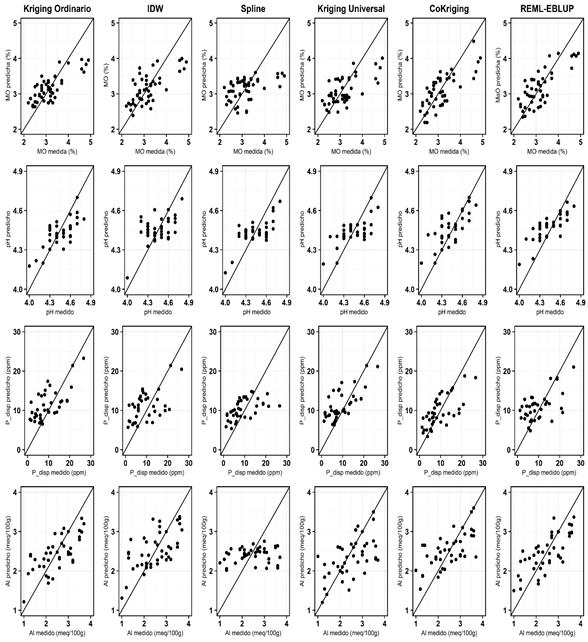
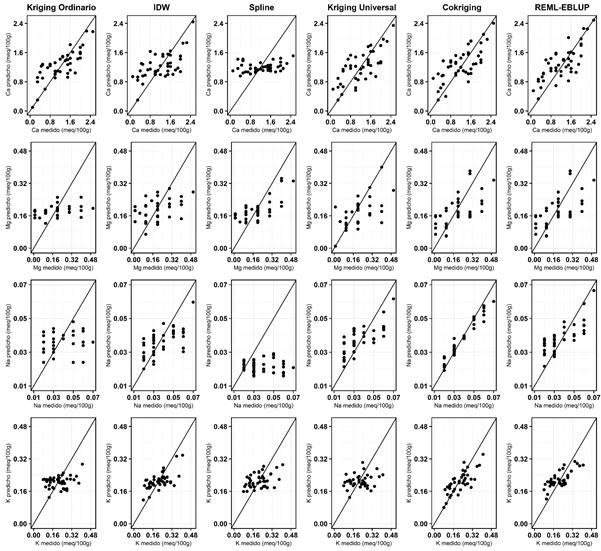
La Figura 4, la Figura 5 y la Figura 6 muestran las diferencias entre valores predichos y observados por propiedad del suelo y técnica de interpolación; en las técnicas geoestadísticas y mixtas, la mayoría de las figuras de valores predichos observados tienen tendencia de homocedasticidad. Este resultado era esperable, ya que ha sido ampliamente discutido que IDW y Spline suelen marcar tendencia de patrones espaciales, mas no ser muy precisos en la interpolación de valores puntuales (Li y Heap, 2011). En la predicción espacial de Mg, K y Al, únicamente Ckg y EBLUP-RMSE tuvieron mayor capacidad predictiva en comparación con las demás técnicas de interpolación. En las demás propiedades, no se presentó mucha diferencia en capacidad predictiva entre las técnicas geoestadísticas y las mixtas.
Figura 4: Gráficas de dispersión de valores predichos vs observados para cada propiedad y cada técnica de interpolación (parte 1)
Figura 5: Gráficas de dispersión de valores predichos vs observados para cada propiedad y cada técnica de interpolación (parte 2)
Figura 6: Gráficas de dispersión de valores predichos vs observados para cada propiedad y cada técnica de interpolación (parte 3)
La Figura 7 muestra el error estadístico (SE) entre valores interpolados y medidos en cada punto de muestreo para todas las técnicas de interpolación.
Figura 7: Error estadístico entre valor predicho para cada técnica de interpolación y valor observado en cada punto de muestreo
Excepto para MO, Fe y Pdisp, la SE fue alta para todas las técnicas de interpolación; por otro lado, excepto para Al, la mayoría de técnicas de interpolación presentaron tendencia a sobreestimación de valores en cada punto. Como se esperaba, las técnicas de interpolación local presentaron tendencia a predecir los valores más extremos para la mayoría de propiedades del suelo, en comparación con las demás técnicas de interpolación. En MO, entre los puntos cinco y veinte se presentó tendencia leve a la sobreestimación, mientras que en los puntos 30 al 40 a la subestimación.
Como se observa en la Figura 2, de los puntos cinco al veinte tienden a estar en zonas con cultivos transitorios, mientras que los puntos 30 al 40 en zonas con cultivos perennes o sistemas agroforestales. Estos resultados sugieren que en zonas con uso y manejo más intensivo del suelo, puede haber una tendencia a tener procesos degradativos más intensos de la MO y, por ende, esto puede afectar los patrones espaciales de la misma, (Peña et al., 2009).
En Pdisp, entre los puntos 40 y 50 se presentó tendencia leve a la sobreestimación, en comparación con los demás puntos de muestreo; de los puntos 40 a 50 se concentran en zonas con cultivos transitorios, los cuales vienen siendo fertilizados de manera continua y espacialmente desordenada. Esto, sin duda, es un cofactor a tener en cuenta para evaluar el desempeño predictivo de las técnicas de interpolación. Por último, Fe no tuvo un patrón claro de sobre o subestimación en la predicción de valores, para todas las técnicas de interpolación, lo cual era esperable debido a las fuertes condiciones de intemperancia en las que se encuentran sometidos los suelos del área experimental.
Comparación de patrones espaciales
La Figura 8 y la Figura 9 muestran las predicciones espaciales de cada propiedad; en general, la mayoría de estas presentaron diferencias entre técnicas de interpolación. Un análisis visual determina que la predicción espacial de MO y de la mayoría de bases intercambiables presentaron mayor heterogeneidad espacial con Ckg y REML-EBLU, coincidiendo parcialmente con lo reportado por Minasny y McBratney (2007). Por su parte Al, Mg y Cu, presentó mayor heterogeneidad espacial con KU, coincidiendo parcialmente con lo reportado por Bishop y McBratney (2001). Cu, presentaron similar patrón espacial con todas las técnicas de interpolación, mientras que Ca presentó mayor heterogeneidad espacial con KO y REML-EBLUP.
Figura 8: Distribución espacial de valores interpolados por propiedad del suelo y técnica de interpolación (parte 1)
Figura 9: Distribución espacial de valores interpolados por propiedad del suelo y técnica de interpolación (parte 2)
Las interpolaciones con IDW y Spline tuvieron mayor homogeneidad espacial para la mayoría de propiedades del suelo, mientras que las interpolaciones con KU presentaron patrones espaciales más heterogéneos que con KO. En general, los resultados sugieren que la inclusión de índices de terreno como variables auxiliares en técnicas de interpolación mixta, puede aportar a la caracterización de los patrones espaciales de todas las propiedades del suelo en condiciones de la altillanura colombiana, excepto pH y Cu.
Los resultados permiten establecer un punto de referencia del uso de técnicas de interpolación espacial en condiciones del piedemonte llanero colombiano; no obstante, estos resultados deben ser validados para otras áreas experimentales aledañas, ya que responden exclusivamente a condiciones climatológicas, de uso y manejo del suelo y edafológicas del área experimental.
CONCLUSIONES
En este trabajo, seis técnicas de interpolación de tipo local (IDW y Spline), geoestadística (KO y KU) y mixta (Ckg y REML-EBLUP) fueron comparadas para predecir propiedades del suelo en condiciones del piedemonte llanero colombiano; los resultados validan la utilidad de HCLc como esquema de muestreo y soportan el supuesto que HCLc captura adecuadamente la distribución de información auxiliar del suelo. Por su parte, RF demostró ser adecuado para determinar los índices de terreno con mayor capacidad predictiva para cada una de las propiedades del suelo.
En general, los resultados sugieren que las técnicas de interpolación mixtas teniendo como información auxiliar del suelo e índices de terreno, proporcionaron una mejora significativa de la predicción de propiedades del suelo, en comparación con las demás técnicas; este resultado es importante para implementar estrategias de mejoramiento de la sostenibilidad de los servicios ecosistémicos del suelo, en condiciones del piedemonte llanero colombiano. Los resultados obtenidos requieren ser validados para otras zonas y con otras fuentes de información auxiliar.
Acknowledgements
AGRADECIMIENTOS
Este trabajo se realizó en el marco del Proyecto Unillanos 2014 “Sistema de monitoreo de calidad del suelo a hiperescala (<1:2,000) en la Granja Barcelona, para la implementación de manejo sitio específico”, y asesorado por integrantes del PE 1134023 INTA, Argentina.
REFERENCIAS
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.