DOI:
https://doi.org/10.14483/22487638.15672Published:
2021-07-01Issue:
Vol. 25 No. 69 (2021): July - SeptemberSection:
ResearchModelo de programación entera mixta en la planeación de actividades y personal en un capítulo académico estudiantil
Spanish Mixed Integer Programming Model for Activities and Personal Planning on Student Academic Chapter
Keywords:
programación entera mixta, capítulo estudiantil, programación de actividades, asignación de personal (es).Keywords:
mixed integer programming, chapter student, scheduling activities, assignation personal (en).Downloads
References
Aarabi, M. y Hasanian, S. (2014). Capacity planning and control: A review. International Journal of Scientific & Engineering Research, 5(8), 975-985.
American Institute of Chemical Engineers (AIChE). (2017). The global of chermical engineers. https://www.aiche.org/community/membership
American Nurses Association (ANA). (2015). Code of ethics for nurses with interpretive statements. Silverspring. 10.4037/ccn2015639
American Society of Heating, Refrigerating and Air Conditioning Engineers (ASHRAE). (2017). Student Zone. Shaping Tomorrow’s Built Environment Today. https://www.ashrae.org/communities/student-zone
Ander-Egg, E. (2001). El trabajo en equipo. Editorial Progreso.
Bicova, K. y Fulemova, J. (2014). Support of effective planning in the workshop laboratory at the Department of Machining Technology in Pilsen. Procedia Engineering, 69(2014), 1008-1014. DOI: https://doi.org/10.1016/j.proeng.2014.03.083 DOI: https://doi.org/10.1016/j.proeng.2014.03.083
Domínguez M., J. (1994). Dirección de operaciones: aspectos tácticos y operativos en la producción y servicios. McGraw-Hill.
Gallego-Torres, A., Bustos-Velazco, E. y Reyes-Roncancio, J. (2020). Guided models for teaching students research in science and engineering. Tecnura, 24(66), 85-94. DOI: https://doi.org/10.14483/22487638.16133 DOI: https://doi.org/10.14483/22487638.16133
Giorgiadis, P. y Athanasion, E. (2013). Flexible long-term capacity planning in closed-loop supply chains with remanufacturing. European Journal of Operational Research, 225, 44-58. https://doi.org/10.1016/j.ejor.2012.09.021 DOI: https://doi.org/10.1016/j.ejor.2012.09.021
González Martín, M. y Génova Fuster, G. (2008). Innovación docente a la luz de Bolonia: trabajo en equipo y revisiones cruzadas para convertir al alumno en protagonista de su proceso de aprendizaje. Revista Electrónica Teoría de la Educación. Educación y Cultura en la Sociedad de la Información, 9(1), 127-141. https://doi.org/10.14201/eks.20257 DOI: https://doi.org/10.14201/eks.20257
Guevara-Bolaños, J., González-Guerrero, E. y Cavanzo-Nisso, G. (2016). Sistema de gestión del conocimiento para generación de escenarios didácticos para la diversidad. Tecnura, 20(edición especial), 108-121. DOI: https://doi.org/10.14483/22487638.11683
Guoxuan, M. y Demeulemeester, E. (2013). A multilevel integrative approach to hospital case mix and capacity planning. Computers & Operations Research, 40(9), 2198-2207. https://doi.org/10.1016/j.cor.2012.01.013 DOI: https://doi.org/10.1016/j.cor.2012.01.013
Huang, H., Lee, L., Song, H. y Thomas Eck, B. (2009). SimMan. A simulationmodel forworkforce capacity planning. Computers & Operations Research, 36, 2490-2497. https://doi.org/10.1016/j.cor.2008.10.003 DOI: https://doi.org/10.1016/j.cor.2008.10.003
Institute of Electrical and Electronics Engineers (IEEE). (2017). Advancing technology for humanity. https://www.ieee.org/membership_services/membership/renew/index_renew.html
Institute of Industrial & Systems Engineers (IISE). (2017). Student chapters. http://www.iise.org/Details.aspx?id=620
Johnson, L. y Montgomery, D. (1974). Operations research in production planning, scheduling, and inventory control. Wiley & Sons.
Kalenatic, D. (2001). Modelo integral y dinámico para el análisis, planeación y programación y control de las capacidades productivas en empresas manufactureras. Universidad Distrital Francisco José de Caldas.
Li, Y., Dai, C. y Huang, G. (2012). An interval-parameter chanceconstrained dynamic programming approach for capacity planning under uncertainty. Resources, Conservation and Recycling, 62, 37-50. https://doi.org/10.1016/j.resconrec.2012.02.010 DOI: https://doi.org/10.1016/j.resconrec.2012.02.010
Martinez-Costa, M., Mas-Machuca, M. y Benedito, E. (2014). A review of mathematical programming models for strategic capacity planning in manufacturing. International Journal of Production Economics, 153(C), 66-85. DOI: https://doi.org/10.1016/j.ijpe.2014.03.011 DOI: https://doi.org/10.1016/j.ijpe.2014.03.011
Niño-Villamizar, Y. y Román-Castillo, R. (2016). El rol de los trabajos de grado como motor de aprendizaje organizacional. El caso de los programas académicos de Tecnología Industrial e Ingeniería de Producción en la Universidad Distrital (Bogotá, D.C.). Tecnura 20(edición especial), 132-146. DOI: https://doi.org/10.14483/22487638.11685
Pinedo, M. (1995). Scheduling. Prentice Hall.
Prieto, L., Valderrama, C. y Allain-Muñoz, S. (2014). Internacionalización en casa. En C. M. Nupia (Ed.), Reflexiones para la política de internacionalización de educación superior en Colombia (pp. 159-191). Ministerio de Educación Nacional.
Ramezanian, R., Rahmani, D. y Barzinpour, F. (2012). An aggregate production planning model for two phase production systems: Solving with genetic algorithm and tabu search. Expert Systems with Application, 39, 1256-1263. https://doi.org/10.1016/j.eswa.2011.07.134 DOI: https://doi.org/10.1016/j.eswa.2011.07.134
Sánchez-Gómez, I. (2017). Propuesta de un modelo de carga docente para la optimización en asignación de recursos pedagógicos. Universidad Técnica Federico Santa María.
Taha, H. (2012). Introducción a la investigación de operaciones. Pearson.
Todorovic, J. (1995). Tehnonoloski sistemi. MRLJES.
Viles, E., Jaca, C., Campos, J., Serrano, N. y Santos, J. (2012). Evaluación de la competencia de trabajo en equipo en los grados. Revista de Ingeniería de Organización, 1(46), 67-75. DOI: https://doi.org/10.37610/dyo.v0i46.392
Zelenovic, D. (1987). The design of production systems. Naucna.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 7 de diciembre de 2020; Aceptado: 1 de abril de 2021
Resumen
Contexto:
En la actualidad es posible encontrar en diversos programas académicos en ingeniería alrededor del mundo múltiples grupos estudiantiles, como es el caso del Institute of Industrial & System Engineers (IISE), cuyo propósito es promover la formación e integración de sus miembros con la industria y el ambiente laboral, mediante la ejecución de actividades de diferente tipo y naturaleza de forma autogestionada pero empírica y con poca utilización de las escasas referencias en la literatura acerca del tema.
Método:
Este articulo presenta un modelo de programación entera mixta que identificó los parámetros de capacidad, repetitividad, retribución y temporalidad recopilados de las normas de evaluación de los capítulos estudiantiles del IISE, con los cuales fue posible formular un modelo matemático con el objetivo de maximizar el puntaje optimizando el uso del talento humano del grupo estudiantil, teniendo en cuenta las restricciones en cuanto a cantidad y repetición de cada tipo de actividad a realizar.
Resultados:
Se obtuvo un modelo de planeación y programación de personal para un horizonte anual de desempeño de un grupo estudiantil, con el cual es posible establecer una estrategia de trabajo en equipos flexibles en número y propósito para realizar las actividades con mayor puntuación ante el organismo IISE evaluador de resultados.
Conclusiones:
El modelo propuesto logra establecer un método de optimización para la selección de las actividades críticas a realizar durante un año por un capítulo estudiantil, con un uso racional del talento humano con diferenciación de comités de trabajo, tipos de dedicación y de tareas, para garantizar la flexibilidad en la asignación de miembros y el tamaño en el número de sus asociados al capítulo estudiantil.
Palabras clave:
programación entera mixta, capítulo estudiantil, programación de actividades, asignación de personal..ABSTRACT
Context:
Currently it is possible to find in various academic programs in engineering around the world multiple student groups as is the case of the Institute of Industrial & System Engineers (IISE), whose purpose is to promote the training and integration of its members with the industry and the work environment through the implementation of activities of different type and nature in a self-managed way but empirically and with little use of the few references in the literature on the subject.
Method:
Therefore, this article presents a mixed integer programming model that identifies the parameters of capacity, repetitiveness, retribution and temporality compiled from the evaluation norms of the student chapters of the IISE, with which it was possible to formulate a mathematical model with the objective of maximizing the score by optimizing the use of the human talent of the student group, taking into account the restrictions in terms of quantity and repetition of each type of activity to be performed.
Results:
It was possible to obtain a staff planning and scheduling model for an annual performance horizon of a student group, with which it is possible to establish a work strategy in flexible teams in number and purpose to perform the activities with the highest score before the IISE organization that evaluates results.
Conclusions: The proposed model manages to establish an optimization method for the selection of critical activities to be performed during a year by a student chapter with a rational use of human talent with differentiation of work committees, types of dedication and differentiation of tasks to ensure flexibility in the allocation of members and the size in the number of members associated with the student chapter.
Keywords:
mixed integer programming, chapter student, scheduling activities, assignation personal..INTRODUCCIÓN
Ante algunos señalamientos en los últimos años de formación de competencias en aprendizaje activo y cumplimiento de objetivos en estudiantes de diversas áreas de conocimiento con la conformación de grupos académicos (American Nurses Association, 2015; González Martín y Génova Fuster, 2008; Viles et al., 2012), es necesario implementar métodos que permitan la planeación y programación de las actividades por realizar en estos grupos académicos para el logro de sus metas académicas, deportivas o sociales. Esto, debido a que al revisar este aspecto en dos grupos de investigación, tres semilleros de investigación y dos capítulos estudiantiles en dos reconocidas instituciones de educación superior (IES) en Colombia, no se cuenta con técnicas de planeación para la selección y programación de actividades, sino que estas se realizan de manera empírica y cubriendo los requerimientos en un corto plazo; es decir, cubriendo las necesidades de planeación en una actividad propuesta con anticipación de máximo de un mes, sin criterios de optimización de recursos.
Por tanto, la elección de un modelo de programación entera mixta coincide con la idea de realizar una programación de tareas o actividades en diferentes periodos del horizonte de planeación para la que es necesaria la asignación de diferentes tipos de recursos (Pinedo, 1995) propia de algunos sistemas de producción (Sánchez-Gómez, 2017; Johnson y Montgomery, 1974) y educativos (Niño-Villamizar y Román-Castillo, 2016). Esto, con el fin de obtener una programación de actividades para cada mes de un año de planeación de actividades como las requeridas para el ente evaluador de este caso IISE y teniendo como elemento primario la asignación óptima de recursos (Institute of Industrial & Systems Engineers, 2017).
Se espera que el capítulo estudiantil logre los objetivos particulares en instancias académicas, deportivas o sociales (Ander-Egg, 2001), con la cual se pretende la proyección y participación en comunidades académicas de carácter profesional a nivel internacional, elemento que contribuye a la integración social y cultural de los grupos de estudiantes de diferentes nacionalidades (Prieto et al., 2014) de una manera ordenada y con criterios claros de eficiencia.
Ahora bien, en el campo de la ingeniería, estos grupos bajo la modalidad de capítulos estudiantiles son avalados por múltiples asociaciones y sociedades con diferentes líneas de especialización en ingenierías Mecánica, Química, Eléctrica, Electrónica, de Sistemas e Industrial (American Society of Heating, Refrigerating and Air Conditioning Engineers, 2017; American Institute of Chemical Engineers, 2017; Institute of Electrical and Electronics Engineers, 2017; IISE, 2017).
De esta manera, un método de planeación y programación permite una vinculación a estas sociedades y asociaciones profesionales por los capítulos estudiantiles, con un plan adecuado para la planeación y administración, programación de reuniones, alcances en el medio, comunicación, selección, reclutamiento y rotación de personal; así como participación y relacionamiento con la asociación o sociedad (IISE, 2017). Con estos será más sencillo realizar un proceso de trazabilidad que incluya la elaboración de un informe de evidencias con el detalle de las tareas y actividades adelantadas.
Finalmente, este informe del plan permitirá obtener los tres elementos por parte de la asociación o sociedad que avala: una evaluación numérica de desempeño por logros obtenidos con cada actividad; una ponderación, clasificación y comparación con otros grupos estudiantiles; así como la renovación y permanencia del grupo como asociado, con los incentivos ofertados por las asociaciones convocantes de estos grupos estudiantiles.
Por tanto este artículo pretende dar solución a las inquietudes de muchos de estos grupos estudiantiles acerca de la cantidad de recursos y miembros a emplear y asignar, en medio de las tareas emprendidas, y sus consecuencias en la organización del grupo estudiantil, tales como cuál será la mejor forma de organizar el equipo de trabajo, la dedicación horaria de cada participante en el grupo, entre otras para el caso en estudio del IISE, y su sistema de evaluación fundamentada en el informe University Chapter Activity Report (UCAR).
Estado del arte
Al realizar un análisis de correspondencia entre los requerimientos de planeación y programación de actividades para un año de desempeño por un grupo estudiantil perteneciente a un programa académico de Ingeniería Industrial en una institución de educación superior (IES) en Colombia, con la literatura disponible en problemas de programación de actividades, fue posible establecer la influencia en materia de antecedentes y fundamentos de los problemas de planeación de capacidad (capacity planning).
Planeación de capacidad (capacity planning)
Este tipo de problema considera, en una perspectiva de productividad, la capacidad como la cantidad de servicios y productos elaborados por una unidad productiva para satisfacer la demanda de la sociedad en un lapso definido (Domínguez, 1994; Kalenatic, 2001).Ante esta perspectiva, la medición de capacidad se hace a través del cálculo de la cantidad de tiempo disponible o utilizable de uno o más recursos necesarios en la fabricación de piezas o en prestación de servicios, con los cuales es posible derivar el número de unidades a fabricar o servicios a realizar, mediante la comparación entre las capacidades disponibles y requeridas en cada elemento de un sistema productivo (Kalenatic, 2001; Todorovic, 1995; Zelenovic, 1987).
En otro contexto, una segunda perspectiva -orientada a considerar la capacidad como estrategia dinámica- concibe la planeación de la capacidad como un sistema conformado por diferentes elementos que son limitados por la disponibilidad y uso de los recursos en lapsos definidos en favor del logro de objetivos y metas organizacionales, en un ámbito de competencia en las cadenas de suministro (Aarabi y Hasanian, 2014).
Los autores incorporan este aspecto en el desarrollo del modelo de programación entera mixta propuesto, al contener los elementos descritos en la literatura referentes a elementos, como el pronóstico de la demanda, la estimación de las tasas de producción, el cálculo de la capacidad requerida para el programa de actividades, teniendo en cuenta las limitaciones de capacidad y condiciones especiales del grupo estudiantil (Aarabi y Hasanian, 2014).
Adicionalmente, este enfoque seleccionado presenta casos con similitud a la solución requerida por el grupo estudiantil respecto a la programación de actividades, como las llevadas a cabo en la planeación en un laboratorio de una universidad (Bicova y Fulemova, 2014); programación de cirugías; asignación de personal médico y planeación de volumen de pacientes a servir en hospitales (Giorgiadis y Athanasion, 2013; Guoxuan y Demeulemeester, 2013); planeación de capacidad para el sistema de gestión de residuos sólidos en una población (Li et al., 2012); planeación de fuerza de trabajo para demanda con incertidumbre y niveles de inventarios con uno o varios productos y múltiples periodos de tiempo (Huang et al., 2009; Ramezanian et al., 2012).
En una revisión de tipos de modelos empleados para la representación de este tipo de problemas, se encontraron 58 estudios, de los cuales 34 son formulados como un modelo de programación entera mixta, llegando a un 60 % de uso de esta técnica, por lo cual los autores se inclinan por este tipo de modelo (Martínez-Costa et al., 2014).
De forma similar, los procedimientos de solución abarcan un enfoque de proyectos y programación de actividades (Bicova y Fulemova, 2014), programación matemática y simulación (Giorgiadis y Athanasion, 2013; Guoxuan y Demeulemeester, 2013), programación dinámica (Li et al., 2012), reglas de asignación (Huang et al., 2009) y metaheurísticas (Ramezanian et al., 2012). De estas, los autores siguen una técnica con procedimientos algorítmicos con software especializado usado en 14 de los 58 estudios señalados, siendo el método más utilizado por encima de heurísticas, metaheurísticas y otras técnicas (Martínez-Costa et al., 2014).
METODOLOGÍA
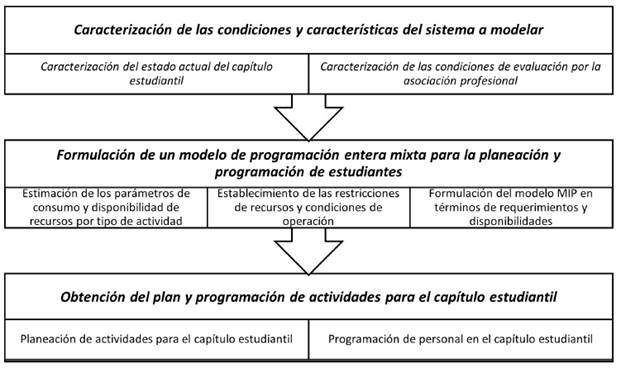
La metodología seguida para el desarrollo del modelo de planeación y programación de actividades con una técnica de programación entera mixta (MIP, por su sigla en inglés) en el capítulo estudiantil siguió tres fases que se describen en la figura 1. Estas siguen el proceso descrito en la literatura para el tratamiento de un problema con técnicas de programación matemática (Johnson y Montgomery, 1974; Taha, 2012), así como algunas de las fases propuestas para la investigación en ciencia y tecnología (Gallego-Torres et al., 2020)
Figura 1: Metodología seguida durante el estudio
Caracterización de las condiciones y características del sistema a modelar
En este aparte se reconocen las características del capítulo estudiantil como objeto de juzgamiento y de la evaluación del IISE, como escala de evaluación con condiciones y características particulares que son relevantes en la inclusión en el modelo.
Caracterización del estado actual del capítulo estudiantil
En esta etapa del proceso realizado en la investigación fue posible determinar la forma de organización, conformación y su relacionamiento interno y externo que determina su forma de actuar y, por ende, las actividades a realizar, de acuerdo con su acta de constitución y estatutos declarados en su fundación (IISE, 2017).
De esta manera, el capítulo estudiantil en el cual se realiza el estudio presenta una organización formal de cinco comités o equipos de trabajo de acuerdo con los fines operacionales identificados como clave para dar cumplimiento y generar la evidencia necesaria para cumplir los requerimientos del IISE. Estas áreas han adoptado denominaciones y tareas de publicidad [Pub], académico [Aca], finanzas y contabilidad [Fin], operaciones [Ope] y dirección [Dir]. Es de notar que cada integrante tiene diferentes formas de vinculación en dedicación horaria
Posterior al reconocimiento de la forma de organización del capítulo estudiantil se realizó la caracterización del proceso de planeación actual, el cual consistió en la elaboración de una lista de tareas posibles a realizar durante un año de gestión, estipuladas en el UCAR, las cuales se seleccionan según criterios subjetivos, como la preferencia, disponibilidad y expectativas por resultados de los miembros para realizar una u otra tarea de las fijadas inicialmente por el comité de dirección.
Luego, se procede con la estimación de unos tiempos necesarios para la planeación y ejecución de cada actividad requerida por cada comité de trabajo, así como el número máximo de actividades de cada tipo que pueden realizarse durante un periodo de operación, según las reglas de evaluación estipuladas por el UCAR.
Como resultado de este proceso es posible observar en conjunto con los integrantes que existen múltiples actividades que se ejecutan de forma lenta y poco coordinada entre los miembros de cada equipo de trabajo, ya que varios equipos pueden programar y realizar tareas para varias actividades durante una misma temporada. Esta condición implica competencia por la capacidad de los equipos de diferentes actividades, mientras en otras épocas se tienen periodos de inactividad del capítulo estudiantil, situación que implica pérdida de visibilidad y posicionamiento del grupo en el imaginario de la comunidad académica a la que pertenece.
Por tanto, este proceso ha mostrado un desgaste innecesario de recursos humanos y materiales requeridos para la realización de cada tarea, al concentrar un gran número de tareas en unas pocas temporadas, en vez de distribuirlas de manera uniforme a través del horizonte de planeación. Esto implica sobrecarga de tareas y asignación de horas para unos cuantos miembros que pertenecen a determinados grupos de trabajo, mientras otros muestran subutilización en otras temporadas.
Caracterización de las condiciones de evaluación por la asociación profesional
El IISE realiza un escalafón anual con todos los capítulos estudiantiles asociados por regiones geográficas en los cuales se evalúa en cada capítulo estudiantil la realización de actividades como la planeación y administración; la programación y ejecución de reuniones y comunicaciones con miembros internos y externos; selección y reclutamiento de miembros; eventos académicos y sociales con otros capítulos estudiantiles o profesionales; visitas industriales; asesorías; participación en proyectos y difusión de temáticas de ingeniería industrial en empresas, escuelas y organizaciones sociales; entre otras actividades (IISE, 2017).
Es de notar que estas actividades pertenecen a una clasificación genérica amplia y no definida de manera formal en tareas fijas y exactas, lo que permite a cada capítulo estudiantil confeccionar un abanico de tareas según el perfil académico, aptitudes y capacidades de sus miembros. Estas darán evidencia sobre la realización de actividades en cada uno de los aspectos de clasificación estipulados por el IISE (2017).
En cuanto a la evaluación que realiza el IISE de las actividades, existe una ponderación de cada actividad a través del documento de evaluación UCAR, que está disponible en la página web de esta asociación evaluadora. De igual forma, existe una restricción respecto al número mínimo y máximo para realizar cada tipo de actividad.
Formulación de un modelo de programación entera mixta para la planeación y programación de actividades
En este aspecto se realizaron tres actividades que contribuían a la formación de la estructura del modelo de programación entera mixta (mixer integer programming, MIP) en términos de requerimientos y disponibilidades, incluyendo las condiciones especiales que no son cuantificables en el consumo de recursos.
Estimación de los parámetros de consumo y disponibilidad de recursos por tipo de actividad
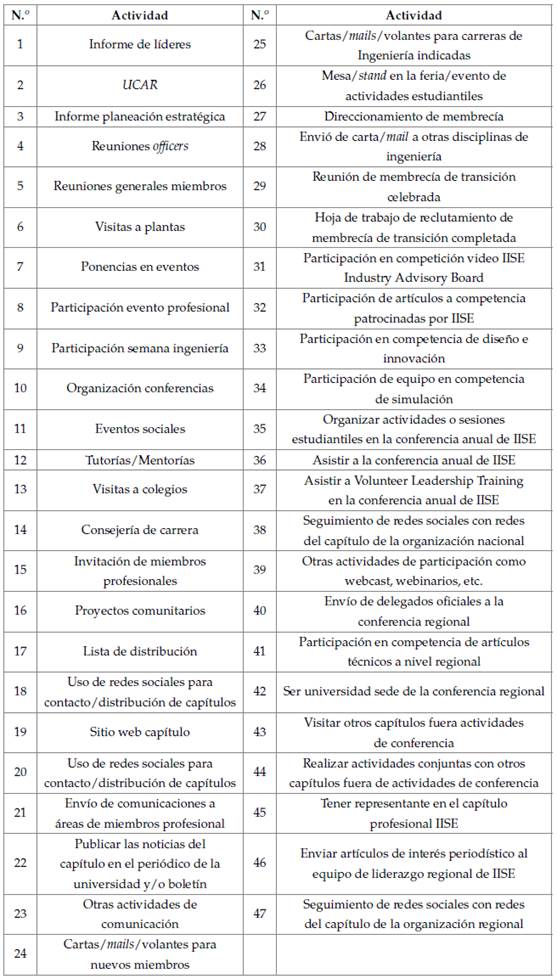
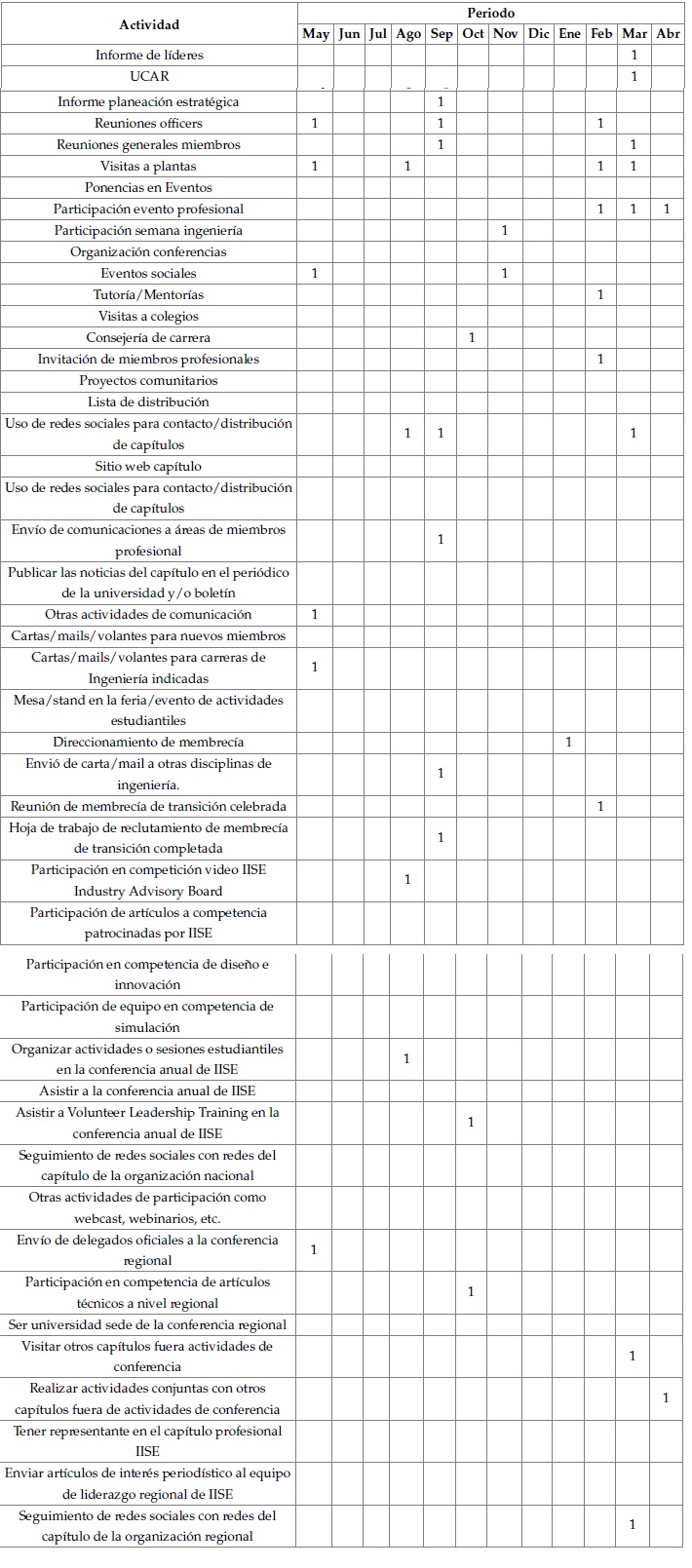
En la realización del modelo matemático se consideraron 47 actividades que abarcan tareas administrativas, reuniones de miembros, visitas con destino a industrias y a otras instituciones de educación, participación y relacionamiento en eventos académicos y con otros capítulos, labores de selección y reclutamiento de miembros, entre otras tareas, tal como se describen en el UCAR, y se detallan en la tabla 1 (IISE, 2017).
Fuente: elaboración propia.
Tabla 1: Codificación de actividades
La estimación de parámetros de consumo se realiza a partir de registros históricos de los últimos tres años de actividad del capítulo estudiantil; de esta forma se logra la estimación promedio de los tiempos de planeación y ejecución para las actividades disponibles por realizar.
En cuanto a la disponibilidad horaria, esta se calculó de acuerdo con las normas del capítulo en la cual se ha establecido con intensidades de 16, 8 y 4 horas por mes por cada integrante, los cuales se denominan con alta, media y baja dedicación respectivamente. En otro aspecto, la cantidad de integrantes por cada tipo de dedicación es de 4, 3 y 5 integrantes, luego de la convocatoria con dedicación alta, media y baja en el mismo orden y considerando como cero integrantes al inicio del horizonte de planeación.
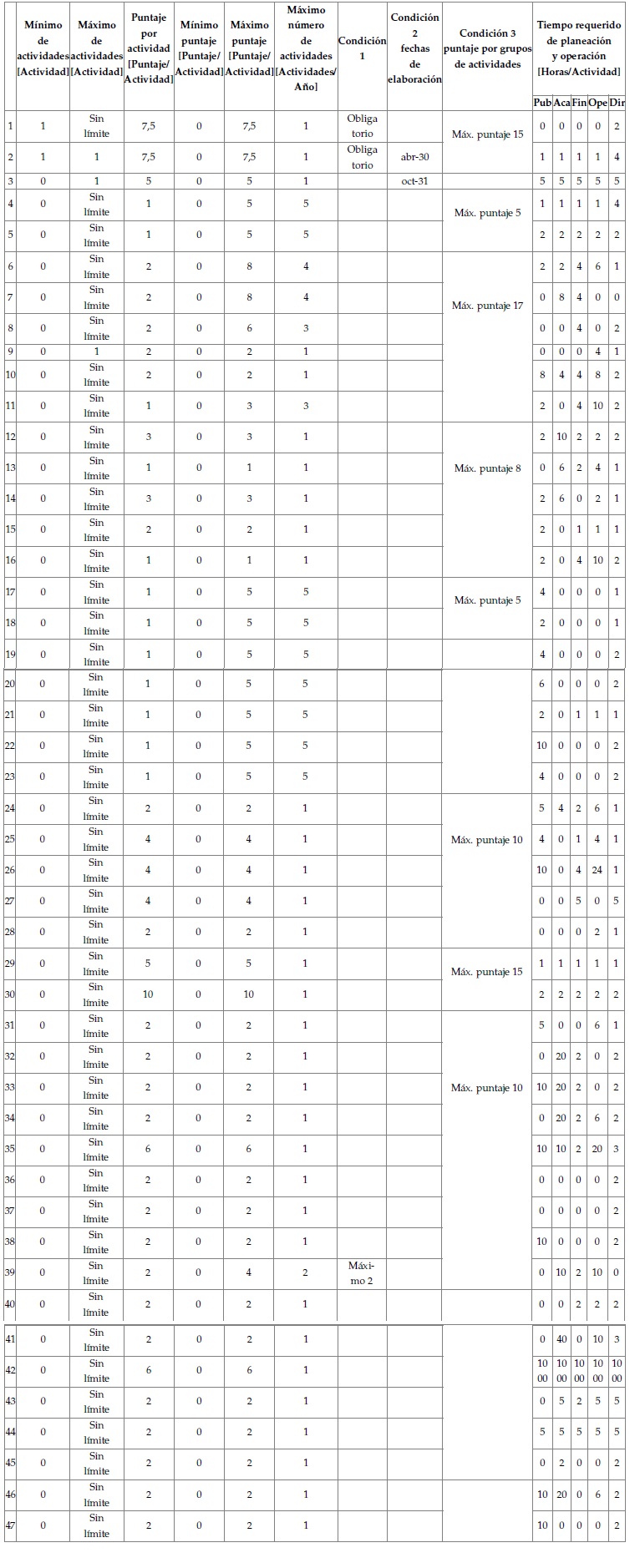
Establecimiento de las restricciones de recursos y condiciones de operación
En este aspecto, la ponderación o puntaje, y el número mínimo y máximo de actividades para cada tipo de actividad se presentan en la tabla 2, donde es posible notar que existen tres condiciones diferenciales: la primera trata de la obligatoriedad para la realización de las reuniones del capítulo estudiantil; la segunda es sobre las fechas de obligatorio cumplimiento para la entrega dela planeación e informes respecto a este proceso, y la tercera consiste en los puntajes a asignar por un conjunto de actividades que, aunque no tienen tope máximo en el número de veces a realizar, sí poseen tope en la ponderación a obtener en combinación con otras actividades similares.
Por otra parte, el modelo también contempla una baja concentración de actividades a realizar en los meses de junio, julio, diciembre y enero, los cuales en Colombia coinciden con la época de vacaciones estudiantiles, para las que tan solo se programa la realización de una única actividad de cualquier tipo.
Fuente: elaboración propia.
Tabla 2: Estimación de parámetros de tiempo, puntaje y número de actividades en el modelo matemático de programación de actividades y asignación de personal
Formulación del modelo MIP en términos de requerimientos y disponibilidades
El modelo matemático propuesto incluye una función objetivo que pretende maximizar el nivel de reconocimiento del capítulo estudiantil por su organización evaluadora, considerando para ello restricciones de capacidad de recursos disponibles, puntajes deseados y asignación de personal a grupos de trabajo. Así, es posible hallar el número, tipo y periodo a realizar cada actividad propuesta de manera racional y bajo un criterio de optimización, tal como se presentan en las ecuaciones (1) a (25):

S.A:



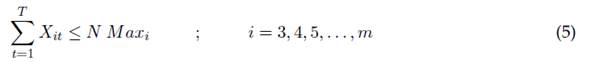
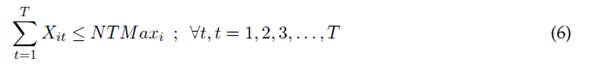
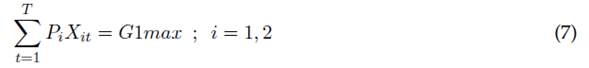

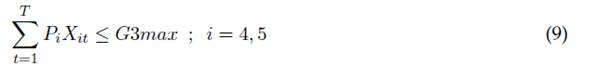
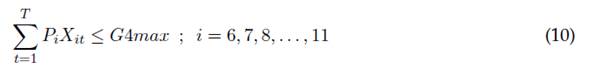
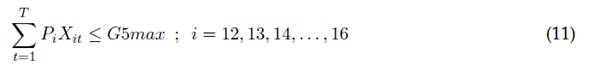
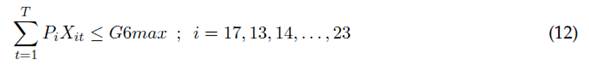
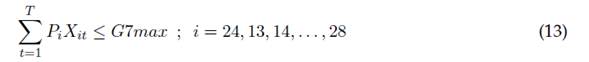
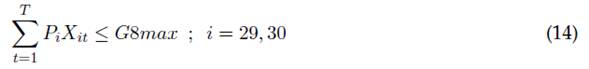
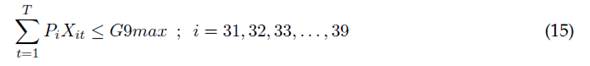
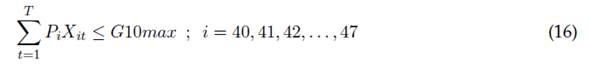
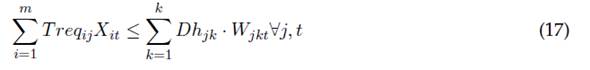
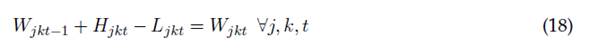

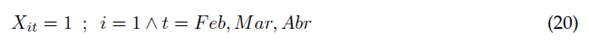
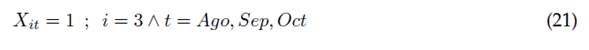
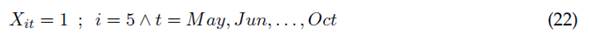
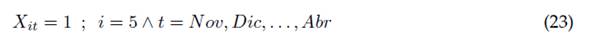


Objetivo: determinar la realización de la actividad tipo i, durante el periodo t con el propósito de maximizar el puntaje otorgado por IISE al capítulo estudiantil.
Función objetivo: el objetivo del modelo consiste en una función de maximización de puntaje a obtener por parte de la evaluación del IISE: f(X it ).
Variables de decisión:
X it : Decisión de realizar la actividad tipo i durante el mes de ejecución de actividades t; i= 1, 2, 3, …, m; t= may., jun., jul., ago., sep., oct., nov., dic., ene., feb., mar., abr.
W jkt : número de personas pertenecientes a la dedicación horaria tipo k en el grupo de trabajo j durante el mes de gestión tipo t; j= 1, 2, 3, …, n; k=1, 2, 3, …, p; t= may., jun., …, T.
H jkt : número de personas a vincular como nuevos a la dedicación horaria tipo k en el grupo de trabajo j durante el mes de ejecución de actividades t; j= 1, 2, 3, …, n; k=1, 2, 3, …, p; t= may., jun., …, T.
L jkt : número de personas a desvincular en la dedicación horaria tipo k en el grupo de trabajo j durante el mes de ejecución de actividades t; j= 1, 2, 3, …, n; k=1, 2, 3, …, p; t= may., jun., …, T.
Parámetros:
P i : puntaje que otorga el IISE por realizar una actividad tipo i en la evaluación de desempeño de capítulos estudiantiles.
PMax: puntaje máximo deseado por el capítulo estudiantil en la evaluación de desempeño otorgada por el IISE.
PMin: puntaje mínimo deseado por el capítulo estudiantil en la evaluación de desempeño otorgada por el IISE.
NMax i : cantidad máxima de actividades tipo i a realizarse durante el horizonte de planeación.
NTMax it : cantidad máxima de actividades tipo i a realizar durante el mes t.
G1Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación planeación y administración.
G2Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación planeación estratégica.
G3Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación programación del capítulo estudiantil.
G4Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación actividades del capítulo estudiantil.
G5Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación relacionamiento del capítulo estudiantil.
G6Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación comunicaciones del capítulo estudiantil.
G7Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación reclutamiento de miembros para el capítulo estudiantil.
G8Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación conversión de miembros del capítulo estudiantil al capítulo profesional.
G9Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación participación del capítulo estudiantil en las actividades mundiales del IISE.
G10Max: puntaje máximo a obtener por realizar las actividades tipo i perteneciente al grupo de evaluación participación del capítulo estudiantil en las actividades regionales del IISE.
Treq ij : tiempo de planeación requerido para la planeación y ejecución de la actividad tipo i en el grupo de trabajo tipo j.
Dh jk : disponibilidad horaria tipo k de un integrante del comité tipo j para cada periodo en el horizonte de planeación.
W0 jk : cantidad de integrantes pertenecientes al comité j al inicio del horizonte de planeación.
WMax k : cantidad máxima de personas pertenecientes a cada dedicación tipo k en el capítulo estudiantil.
Adicionalmente, el modelo caracterizado en la ecuación (1) muestra la función objetivo de maximización del puntaje obtenido por la evaluación realizada por el IISE de los capítulos estudiantiles por año. Las ecuaciones (2) y (3) establecen un límite inferior y superior de la evaluación otorgada por el IISE en la elaboración de la evaluación de desempeño, factor que puede en múltiples casos proporcionar un tamaño de los diferentes comités de trabajo tipo k, así como el tamaño total requerido del capítulo, las dedicaciones horarias de cada miembro.
La ecuación (4) muestra la obligatoriedad de realizar las actividades de planeación de actividades y elaboración del UCAR para cada horizonte de planeación del trabajo realizado por el capítulo estudiantil. En la ecuación (5) es posible restringir el número total de actividades de cada tipo i que es posible realizar durante todo el horizonte de planeación, mientras la ecuación (6) muestra una restricción acerca de la suma total de actividades de diferente tipo i a realizar durante cada periodo t. Las ecuaciones (7) a (16) presentan restricciones de agrupación de actividades a realizar durante todo el horizonte de planeación, esto es, la clasificación de actividades que son evaluadas como un conjunto de tareas, las cuales otorgan un puntaje máximo como conjunto. Se destaca que puede realizarse una combinación lineal de actividades diferente por cada grupo, durante todos los periodos de ejecución de actividades otorgando una misma evaluación.
La ecuación (17) muestra una restricción típica de capacidad de recursos, en la cual el tiempo requerido por cada comité de trabajo tipo j para planear y ejecutar todas las actividades tipo i en un periodo t está limitado por la disponibilidad de tiempo con la que cuenta cada comité de trabajo j, integrado por miembros con disponibilidad tipo k durante cada periodo t. Esta restricción es útil para capítulos estudiantiles con pocos miembros, ya que puede asignar el personal de manera eficiente a cada tipo de grupo de trabajo y establecer una prioridad de actividades, así como los requerimientos de trabajo. La ecuación (18) presenta una restricción de balance de miembros con dedicación horaria tipo k en los comités de trabajo tipo j durante los meses t, la cual hace flexible la asignación y programación de personal al interior del capítulo estudiantil, así como las necesidades de selección y reclutamiento de nuevos miembros o la programación de descansos o desvinculación del grupo estudiantil.
La ecuación (19) permite limitar el número de integrantes de cada comité de trabajo j en cada periodo t al número total de integrantes del capítulo de acuerdo con su vinculación horaria. Las ecuaciones (20) al (23) muestran en las dos primeras fórmulas la realización de actividades como la planeación e informe de evidencias para evaluación en un término de tres meses antes de su entrega y requerimiento, así como la realización de al menos una reunión de miembros por semestre en las dos últimas de estas fórmulas. Las ecuaciones (24) y (25) presentan respectivamente las restricciones lógicas y de tipo de variable del modelado matemático realizado, en las cuales las variables de personal se consideran de carácter entero, mientras las variables respecto a las actividades con carácter binario.
RESULTADOS
Ante los parámetros estimados y la formulación del modelo matemático para la programación de actividades y la asignación de personal del capítulo estudiantil, se realizó su solución a través del software GAMS® en su versión 23.9.5, en la cual se procesaron 604 restricciones con 840 variables el cual procesado en 1309 iteraciones con el algoritmo CBC. Se encontró respuesta a las interrogantes acerca del tipo de actividades y meses en las cuales estas se realizarán, el número de miembros a asignar, retirar o reclutar para cada comité y el puntaje deseado que otorgará el IISE al revisar las evidencias.
Los resultados del modelo propuesto muestran que, para alcanzar la puntuación máxima de 100 puntos, es posible realizar 28 de las 47 actividades propuestas, donde se destaca que algunas actividades importantes excluidas de la programación se relacionan con ponencias en eventos, organización de conferencias, visitas a colegios, ser universidad sede de la conferencia regional, publicar noticias del capítulo en el periódico de la universidad y/o boletín, así como la participación en competencias en diseño e innovación, simulación o artículos, debido al consumo de recurso de manera intensiva.
En otro aspecto, las actividades a realizar en una mayor cantidad de ocasiones se relacionan con las visitas a plantas con cuatro actividades, reuniones de oficiales con tres repeticiones, uso de redes sociales para contacto con tres veces y participación en eventos profesionales con igual cifra. Se destaca que solo es requerida una reunión general de miembros por semestre, tal como se estipulo en el programa lineal mixto, debido a su consumo razonable de recursos.
También se puede afirmar que el resto de las actividades es posible realizarlas una sola vez durante el año, de acuerdo con la programación obtenida; esto indica limitaciones en número o simplemente programación eficiente de recursos humanos. Ante las consideraciones ya señaladas del periodo de receso escolar, para los meses de junio, julio, diciembre y enero, se evidencia actividad únicamente en enero en la actividad de direccionamiento de membrecía; en relación a los meses con mayor actividad de acuerdo con la programación de actividades establecida, los meses de marzo con ocho actividades por realizar, septiembre con siete, mayo y febrero seis actividades serán los más congestionados y con actividad, factor que afectara a los integrantes del capítulo que tendrán que disponer de mayor dedicación en esos periodos del horizonte de planeación. Esta programación de actividades puede ser consultada en detalle en la tabla 3, en la que, mediante la asignación de un digito uno (1), se simboliza la realización de una actividad para cada periodo de tiempo, así como la falta asignación simbolizará el caso contrario de ausencia de actividad en cada periodo.
Fuente: elaboración propia.
Tabla 3: Programación de actividades del capítulo estudiantil para un año de gestión
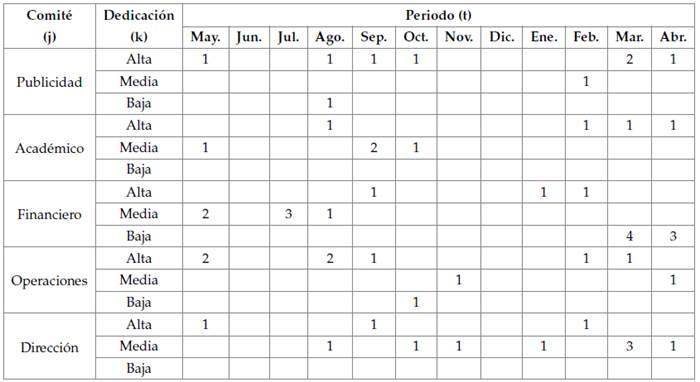
En cuanto al requerimiento de personal por cada comité, es posible afirmar que el comité de publicidad es uno de los más activos, ya que requiere en seis de los doce meses, un número de integrantes de uno o dos personas con dedicación alta, mientras en el restante de meses se requieren de forma adicional la asignación de un integrante con dedicación media y baja, según la programación de actividades.
De forma similar, el comité académico requiere en siete de los doce meses integrantes con dedicación alta y media, lo cual muestra una menor actividad, ya que este comité tendrá dos temporadas de trabajo limitadas a los meses de agosto, septiembre y octubre, en un primer lapso, y en febrero, marzo, abril y mayo, en el segundo.
Por su parte, el comité financiero requiere asignaciones de personal con las diferentes dedicaciones durante ocho meses de los doce contemplados en el horizonte de planeación, lo cual indica una carga de trabajo fluctuante, acorde a la elaboración de informes y el detalle de este tipo de actividad, tal como se requiere previo a la elaboración de los informes de gestión para la evaluación durante marzo y abril de cada horizonte de planeación.
Para el comité de operaciones, es posible afirmar un requerimiento de integrantes en ocho de los doce meses, con dedicación alta en cinco periodos de al menos uno o dos integrantes, mientras que, para los meses diferentes a la asignación con este tipo de dedicación alta, es necesario asignar un miembro con dedicación baja y media. Finalmente, el comité de dirección es requerido en nueve de los doce meses, lo que implica de uno a tres integrantes con los cuales se puede coordinar las actividades a realizar durante el horizonte de planeación.
En cuanto al número de integrantes que se asignarán por periodo, es posible afirmar que para marzo se asignarán cuatro integrantes al comité financiero, el cual es el movimiento con mayor número en toda la programación; seguido por asignación de tres integrantes a los comités de dirección en el mismo mes, y tres integrantes al comité financiero durante julio. En un análisis complementario respecto del número de integrantes por reasignar, los meses de junio, abril y septiembre presentan cifras de siete, cinco y cinco reasignaciones respectivamente, lo cual corresponde a la programación de actividades ya señalada.
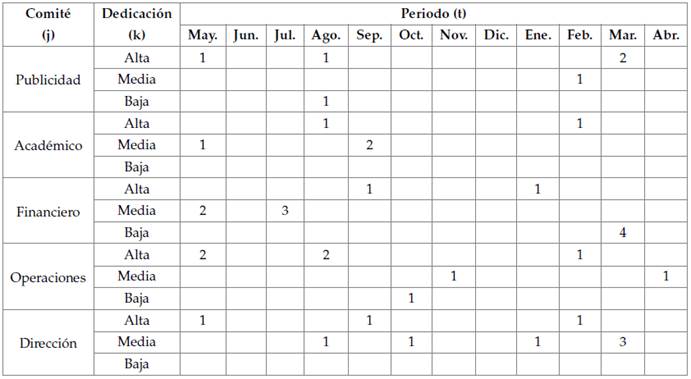
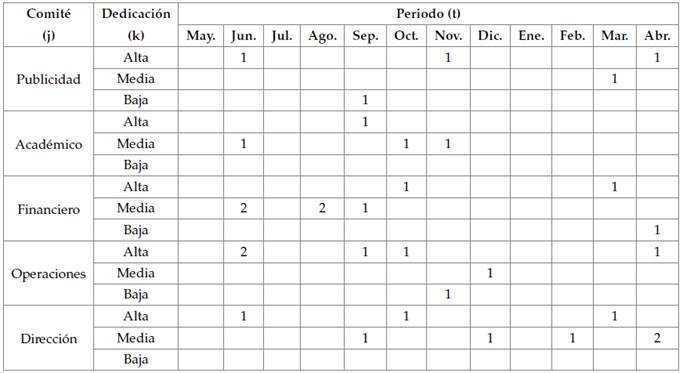
Estos comportamientos respecto al número de integrantes necesarios por asignar a cada comité bajo cada tipo de dedicación es posible verlos con detalle en la tabla 4; mientras que los miembros del capítulo que pueden ser asignados a cada comité se detallan en la tabla 5; así como los miembros que no son requeridos y pueden reasignarse se presentan en la tabla 6.
Fuente: elaboración propia.
Tabla 4: Programación de integrantes del capítulo estudiantil en comités y dedicación
Fuente: elaboración propia.
Tabla 5: Programación de ingreso de integrantes del capítulo estudiantil en comités y dedicación
Fuente: elaboración propia.
Tabla 6: Programación de reasignaciones de integrantes del capítulo estudiantil en comités y dedicación
CONCLUSIONES
A través de este proyecto de investigación fue posible obtener la programación de actividades de un capítulo estudiantil al IISE, mediante técnicas de optimización, lo cual representó un ejemplo para los estudiantes de herramientas propias de la ingeniería industrial.
Este ejercicio curricular sirve como ejemplo de modelamiento de sistemas bajo restricciones, para su réplica por otras instancias y capítulos estudiantiles en aras de mejorar el desempeño en la realización de actividades a través del uso eficiente del capital humano disponible en los capítulos estudiantiles.
El modelo presentado es de sumo interés para capítulos estudiantiles con número reducido de miembros, ya que puede mostrar cómo mejorar su desempeño y lograr evaluaciones adecuadas, aprovechando de mejor manera la disponibilidad de personal, a través de una estrategia que pretende iniciar con un proceso de adquisición de conocimiento en un sistema de gestión de conocimiento como elemento didáctico (Guevara-Bolaños et al., 2016).
En cuanto a la programación de actividades, esta es generada a través de la combinación de diferentes parámetros que pueden ser modificados por los capítulos estudiantiles según sus normas y reglas, permitiendo flexibilidad a los grupos estudiantiles respecto la dedicación horaria y labores a realizar de los miembros en cada asignación.
Con relación a los resultados obtenidos para el capítulo estudiantil en estudio, la programación de actividades sirve en este momento como parámetro mínimo e inferior de ejecución de tareas, lo cual ha repercutido en compromisos mínimos para sus integrantes con el propósito de lograr una evaluación alta ante el IISE.
Referencias
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.