DOI:
https://doi.org/10.14483/22487638.17731Publicado:
01-10-2022Número:
Vol. 26 Núm. 74 (2022): Octubre - DiciembreSección:
InvestigaciónAlgoritmo luciérnaga para la optimización de distribución en planta
Firefly Algorithm for Facility Layout Optimization
Palabras clave:
problema de distribución en planta, algoritmo luciérnaga, metaheurística, optimización combinacional (es).Palabras clave:
facility layout problem, firefly optimization, metaheuristics, combinatorial optimization (en).Descargas
Referencias
Dey, N. (2020). Applications of firefly algorithm and its variants. Springer Singapore. https://doi.org/10.1007/978-981-15-0306-1 DOI: https://doi.org/10.1007/978-981-15-0306-1
Dhillon, A., & Goyal, S. (2013). PAPR reduction in multicarrier modulations using firefly algorithm. International Journal of Innovative Research in Computer and Communication Engineering, 1(5), 1270-1275. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1074.509&rep=rep1&type=pdf
Hernández-Santibáñez, M. I., Giraldo-Correa, L. F.; Gaviria-Ramírez., L. A., Wilches-David, A. M., & Osorio-Gómez, J. C. (2017). Priorización de despachos con AHP difuso y Topsis. Revista Tecnura, 21(52), 102-110. https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a08 DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a08
Jara-Estupiñan, J., Hernández-Suárez, C. A., & Giral-Ramírez, D. A. (2020) Optimal value of past samples for decision making in cognitive radio networks. Revista Tecnura, 24(65), 13-26. https://doi.org/10.14483/22487638.15278 DOI: https://doi.org/10.14483/22487638.15278
Jati, G. K. (2011). Evolutionary discrete firefly algorithm for travelling salesman problem. In International conference on adaptive and intelligent systems. In A. Bouchachia (Ed.), Adaptive and Intelligent Systems (pp. 393-403). Springer. https://doi.org/10.1007/978-3-642-23857-4_38 DOI: https://doi.org/10.1007/978-3-642-23857-4_38
Kumar, V., & Kumar, D. (2021). A systematic review on firefly algorithm: Past, present, and future. Archives of Computational Methods in Engineering, 28(4), 3269-3291. https://doi.org/10.1007/s11831-020-09498-y DOI: https://doi.org/10.1007/s11831-020-09498-y
Kumbharana, S. N., & Pandey, G. M. (2013). Solving travelling salesman problem using firefly algorithm. International Journal for Research in Science & Advanced Technologies, 2(2), 53-57. https://www.academia.edu/download/35300356/IJRSAT-Vol2-Issue2-0002.pdf
Łukasik, S., & Żak, S. (2009). Firefly algorithm for continuous constrained optimization tasks. In N. T. Nguyen, R. Kowalczyk, & S.-M. Chen (Eds.) Computational Collective Intelligence. Semantic Web, Social Networks and Multiagent Systems (pp. 97-106). Springer. https://doi.org/10.1007/978-3-642-04441-0_8 DOI: https://doi.org/10.1007/978-3-642-04441-0_8
Patle, B. K., Pandey, A., Jagadeesh, A., & Parhi, D. R. (2018). Path planning in uncertain environment by using firefly algorithm. Defence Technology, 14(6), 691-701. https://doi.org/10.1016/j.dt.2018.06.004 DOI: https://doi.org/10.1016/j.dt.2018.06.004
Quiroga, J., Cáceres, E., & Padilla, C. (2015). Optimización de trayectorias de fresado en cavidades utilizando el algoritmo Luciérnaga. Revista de la Facultad de Ingeniería Universidad Central de Venezuela, 30(1), 93-104. http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S0798-40652015000100010
Ramírez-Ramírez, J. D., Arrieta-Giraldo, J. S., & Garcés-Ruiz, A. (2016). Distribución óptima de turbinas en parques eólicos mediante PSO considerando el efecto sombra. Revista Tecnura, 20(47), 49-55. https://doi.org/10.14483/udistrital.jour.tecnura.2016.1.a04 DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2016.1.a04
Saraei, M., Analouei, R., & Mansouri, P. (2015). Solving of travelling salesman problem using firefly algorithm with greedy approach. Cumhuriyet Üniversitesi Fen Fakültesi Fen Bilimleri Dergisi (CFD), 36(6), 267-273.
https://arastirmax.com/sites/default/files/filefield_paths/5000142870-5000238948-1-pb.pdf
Solarte, G. R., Soto-Mejía, J., & Muñoz-Guerrero, L. E. (2018). Localización del punto óptimo de partida en el problema de ruteo vehicular con capacidad restringida (CVRP). Revista Tecnura, 23(59), 27-46. https://doi.org/10.14483/22487638.13653 DOI: https://doi.org/10.14483/22487638.13653
Trachanatzi, D., Rigakis, M., Marinaki, M., & Marinakis, Y. (2020). A firefly algorithm for the environmental prize-collecting vehicle routing problem. Swarm and Evolutionary Computation, 57, 100712. https://doi.org/10.1016/j.swevo.2020.100712 DOI: https://doi.org/10.1016/j.swevo.2020.100712
Yang, X. S. (2013). Multiobjective firefly algorithm for continuous optimization. Engineering with Computers, 29(2), 175-184. https://doi.org/10.1007/s00366-012-0254-1 DOI: https://doi.org/10.1007/s00366-012-0254-1
Wu, J., Wang, Y. G., Burrage, K., Tian, Y. C., Lawson, B., & Ding, Z. (2020). An improved firefly algorithm for global continuous optimization problems. Expert Systems with Applications, 149, 113340. https://doi.org/10.1016/j.eswa.2020.113340 DOI: https://doi.org/10.1016/j.eswa.2020.113340
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 20 de enero de 2022; Aceptado: 4 de julio de 2022
ABSTRACT
Objective:
This paper presents a review of the results obtained by an optimization methodology based on the application of the firefly algorithm (FA) as a metaheuristic planning tool with the purpose of finding the optimal facility layout in order to reduce the distances and flow times between processes of the production chain.
Methodology:
By means of implementing the MATLAB script, the goal was to evaluate the FA as applied to the facility layout distribution optimization problem, conducting a test of two facility layout cases with the algorithm. The FA was applied in order to evaluate the performance with respect to the initial facility layout configuration, as well as in comparison with a conventional heuristic algorithm.
Results:
The most relevant result was the verification of the FA’s degree of efficiency regarding the convergence time, as expressed in terms of the number of cycles required to reach an optimal solution in comparison with the conventional heuristic algorithm used for validation.
Conclusions:
The total optimized distance in the plant achieves a low significant value. A reduced number of iterations is required to reach an optimal value in the case of a complex facility layout.
Keywords:
facility layout problem, firefly optimization, metaheuristics, combinatorial optimization.RESUMEN
Objetivo:
Este artículo presenta una revisión de los resultados de una metodología de optimización enfocada en la aplicación del algoritmo de luciérnaga (FA) como una herramienta de planificación metaheurística con el fin de encontrar una distribución en planta óptima para reducir las distancias y los tiempos de flujo de procesos en la cadena de producción.
Metodología:
A través de la implementación del script de MATLAB, el objetivo fue evaluar el FA aplicado al problema de optimización de diseño de distribución en planta, realizando una prueba de dos casos de diseño de instalaciones con el algoritmo. Se aplicó el FA para evaluar el rendimiento con respecto a la configuración inicial de distribución en planta, así como en contraste con un algoritmo heurístico convencional.
Resultados:
El resultado más relevante fue la verificación del grado de eficiencia del FA con respecto al tiempo de convergencia, expresado en función de la cantidad de ciclos requeridos para alcanzar una solución óptima, en comparación con el algoritmo heurístico convencional utilizado para la validación.
Conclusiones:
La distancia total optimizada en la planta logra un valor bajo significativo. Se requiere un número reducido de iteraciones para alcanzar un valor óptimo en el caso de una distribución en planta compleja.
Palabras clave:
problema de distribución en planta, algoritmo luciérnaga, metaheurística, optimización combinacional.1. INTRODUCTION
According to Hernández-Santibáñez et al. (2017) and Solarte et al. (2018), the facility layout problem (FLP) aims to obtain an optimal design for the allocation and flexible configuration of available machines, equipment, resources, and physical space in order to facilitate the movement and handling of material, as well as to allow plants to have optimized performance and production flow, i.e., with respect to a minimum production cost and total time. Traditionally, the study of such problems regarding distribution, spatial flow, and optimization has been addressed via dynamic programming techniques and combinatorial optimization, as per Jara-Estupiñán et al. (2020) and Dey (2020).
In this study, the FA is applied to such problems. This algorithm is inspired by the intermittent and rhythmic behavior of fireflies, which are winged insects capable of producing flashes of light to attract possible prey or companions. In FA applications, an initial population of fireflies must be configured at random node locations defined as a search space, where the fireflies represent a feasible solution. Each firefly’s flashing light intensity is the way to evaluate the target function to be optimized, as reported by Yang (2013).
This algorithm was introduced in 2009 by Xin-She Yang, who was inspired by the behavior and characteristics of fireflies such as their flickering. He established three essential rules:
-
Each firefly is configured to be attracted to the others regardless of its gender. Brightness is equivalent to the proportional degree of attraction. For each two blinking fireflies, the one with the lower brightness will follow to the brighter one. The attraction degree is directly related to the brightness, depends directly on the objective function, and decreases with increasing distance. If no particular firefly is brighter, they all will move randomly.
-
The brightness of a firefly is affected or determined by the objective function.
The layout optimization problem is similar to that of the traveling salesman problem (TSP): symmetric, uni-objective and Euclidean, according to González and Patle et al. (2018) and Trachanatzi et al. (2020). Configuring the layout of a plant is like outlining a movement in the XY plane. The total travel time can be determined as the time it takes to go through the process flow path plus the time at each station, as expressed in Equation (1):

where n is the quantity of workstations, tm the operation time per station, and t(x, y) the time it takes to follow the process flow path on the layout. The objective function is to optimize the time it takes to follow the process throughout the layout t(x, y), thus optimizing the cost of operation (Saraei et al., 2015; Hernández-Santibáñez et al., 2017). Here, the distance between the workstations i and j of the layout is considered to be rectilinear and corresponds to the Euclidean distance of the two points with coordinates (x i , y i ) and (x j , y j ). It can be calculated via Equation (2):

The equation to calculate the process flow on the layout plane XY (i.e., moving from point i to point j) implies a problem similar to that of the traveling agent. Therefore, the distance of the route can be calculated via Equations (3) and (4):
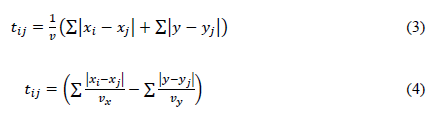
where v x and v y correspond to the process flow displacement speeds in x and y, respectively. This problem is simplified: v x and v y have the same value, so v x = v y = v.
2. METHODOLOGY
This paper applies the FA as a solving tool for combinatorial optimization problems such as the facility layout distribution problem in an industrial manufacturing plant. To this effect, many optimization algorithms have been proposed (Yang, 2013;; Łukasik & Żak, 2009). In this case, optimization can be carried out while considering the following requirements:
-
Minimizing material handling and the total distance between machines and layout stations.
-
Minimizing material flow.
-
Minimizing the total distance traveled by the material.
2.1. Firefly algorithm
In the FA discretization proposed by Jati (2011), a firefly represents a possible trajectory or path that gives an approximation to the optimal solution of the TSP, which is made up of a number of points or cities to be visited according to an order established by the fireflies’ movements. In the TSP, the function to be minimized is the length of the layout flow. Therefore, the brightest firefly is the one with the shortest path length, taking the Euclidean distance between all the layout points or nodes, in line with Wu et al. (2020), Kumar and Kumar (2018), and Saraei et al. (2015).
From the layout map containing the (x, y) coordinates corresponding to the location of each of the nodes or workstations distributed across the plant, the paths between nodes are defined, which conform a set of initial solutions that fireflies must optimize in each cycle (Yang & He, 2013).
The FA was initially implemented in continuous optimization applications such as the traveling agent problem, and later as a discretized way to solve permutation problems such as the one in this study case. The FA could be implemented in the optimization of maximization problems, taking the initial solution as a distance function xi, xj, according to the TSP model (Quiroga et al., 2015). According to Kumbharana and Pandey (2013), firefly movements must be redefined as the search space Sn, which includes all possible permutations {1, 2, …, n}. Firefly brightness I in each position x could be defined as I(x). Light intensity I(r) as seen by the other fireflies in the distance function r{ij} has an impact on the degree of attraction β. The light intensity changes according to the inverse square law equation (5), where the light source intensity is Is:

By taking a constant light absorption medium γ, the light intensity only changes as a distance function, as shown in Equation (6), where I 0 is the initial light intensity:

Avoiding singularity at r = 0 in
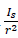 , Equation (7) is as follows:
, Equation (7) is as follows:

By taking a degree of attraction β, Equation (8) is obtained:

where β 0 denotes the maximum degree of attraction when r = 0.
The distance formula at firefly positions (x i , x j ) is applied as defined by Equation (9):
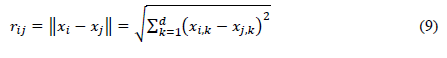
Finally, the position of each firefly i can be determined via Equation (10):
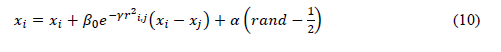
which presents two terms. In the first one, position ij of each firefly is indicated, and, in the second one, a random value is generated to arbitrarily adjust the displacement, where a smooth factor constant α and the random function are introduced.
Objective function
Each initialized path should be evaluated by an objective function with the purpose of determining its quality rate. This comprises the evaluation of the sum of each of the distances between nodes in the path in order to determine the best sequences by taking the Euclidean distance objective function, as reported by Obando-Solano et al. (2016) and Ramírez-Ramírez et al. (2016). Thus, the sum of the distance between the current node (x i , y i) and the next node (x (i+1) , y (i+1) ), including all nodes or workstations in the layout, yields the total length of the path in Equation (11):
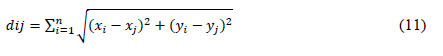
Path evaluation
The cost can be represented by the flow and distance matrix through Equation (12):

where d ij corresponds to the distance between nodes -or objective function- which corresponds to the Euclidean distance between points in this case.
The algorithm uses a maximum number of iterations as a stopping criterion. Once this value is reached, the process ends. However, not all paths can ensure that this solution is reached, but they can achieve an optimized one.
RESULTS
The experimental testing of the FA in the facility layout optimization problem was conducted in MATLAB, version 2020, running on a computer with an Intel CORE i7 and 8 GB RAM.
First, an initial solution is generated at random by each firefly. By taking initial values for parameters such as light intensity i, the initial degree of attraction 𝛽0 and 𝛾 are defined. Thus every firefly finds the brightest one. If the brightness of one firefly is lower than that of the other, it will move to the next brightest one. When a firefly moves along a path, its degree of attraction and its light intensity decreases, the best firefly is chosen as the initial solution for the next iteration based on the objective function. This condition is maintained until the end of iteration cycles is reached. Dhillon and Goyal (2013) propose an FA pseudo-code as follows:
Begin Initialize parameters: fireflies population n, objective function, maximum number of iterations, coefficients, 𝛼, 𝛽,𝛾, and initialization of fireflies x i, with n initial solutions and firefly light intensity Ii as a function of position x i, calculated by the objective function f(x i ).
While k i < Maximum Number of Iterations
for k i = 1 to n (Firefly Layout),
for k j = 1 to n (Firefly Layout),
If (Ij> Ii) moves from i to j;
Determine the degree of attraction reached as a function of distance r according to Equation (13):
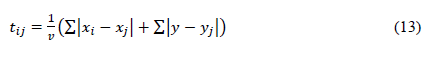
Calculate new solutions and update the light intensity.
End End
End
Select the best solution.
End
Determine the firefly with the highest light intensity.
End
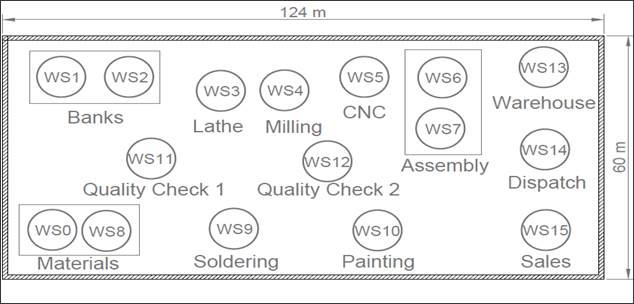
Figure 1 shows layout 1 of a mechanical factory with 15 workstations or nodes, where the path is optimized across a 124 x 60 m area. The workstations are also indicated. The previously proposed algorithm was implemented as a MATLAB script. The location coordinates (x, y) of each station were entered as vectors (x, y) in the software.
Figure 1: Initial workstations on layout 1
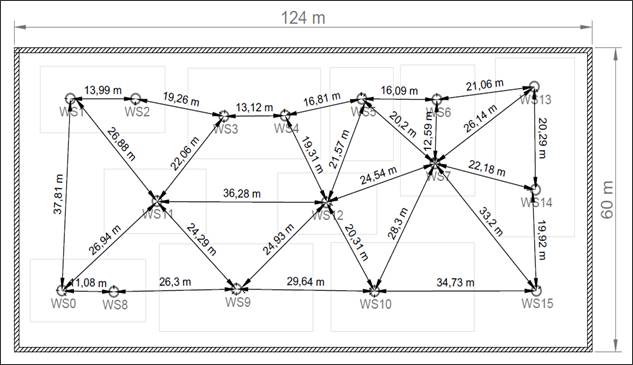
The plant layout path covers an initial distance of 283,34 m (Figure 2).
Figure 2: Initial layout 1 path distances
The assumption upon which the simulation was developed was established upon the following considerations. The algorithm ends when 50 iterations are performed. The minimum number of fireflies should be at least equal to the number of nodes or workstations, which was 100 in this case. The brightness function of the FA was set at m = 2. The weight parameters information at start were established arbitrarily: 𝛼 = 0,5, 𝛽 = 0,1, 𝛾 = 2, and 𝛽0 = = 10. The number of best solutions groups was assumed to be equal to 25% of the number of fireflies.
To determine the value of the absorptivity coefficient, the attractiveness function was estimated by varying the distance r ij and keeping 𝛽0 = 10. This value of β was chosen arbitrarily, although, during the experimentation phase, it was observed that a very large value of β drastically increases the simulation time and a very small value reduces the possibility of achieving an optimal solution. In the discretion of a firefly, movements are performed by permutating the visit sequence as a subset of the workstation nodes chosen at random by means of the random function, which in turn assume random positions (i, j); they are a subset that will be reordered. The probability that firefly i or j is permutated or moved more times is given by the brightness and the distance between fireflies. In this way, the solutions that give off less light are brought closer to those with a higher brightness.
A path is assigned to each workstation from i to j until all the nodes in the set are initialized, progressively evaluating the cost associated with each path to find the optimal value of cost or total distance in terms of the iterations performed.
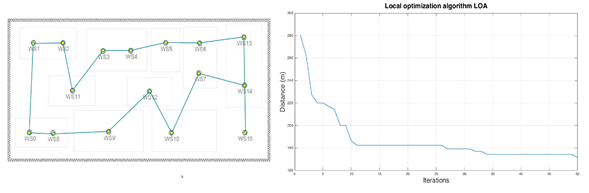
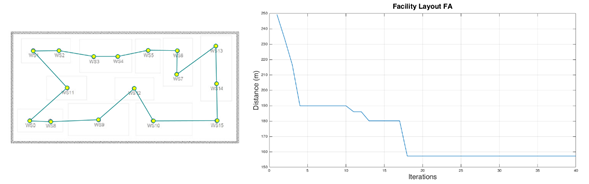
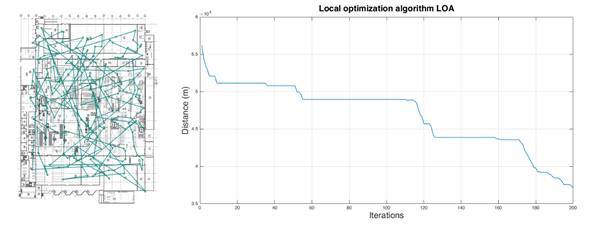
A comparison was made against a conventional nearest neighbor constructive heuristic algorithm, or Local Optimization Algorithm (LOA). The results are shown in Figures 3 and 4.
Figure 3: LOA for facility layout 1
Figure 4: FA optimization of facility layout 1
After 31 iterations of the algorithm, the best solution corresponded to the combination shown in Table 1, with 156,0187 meters for the FA and 157,21 meters with 38 iterations for the LOA. Compared with the initial configuration of the path that was at a value of 283.34 meters.
Source: Authors
Table 1: Results for facility layout 1 (LAO vs. FA)
Local Optimization Algorithm
Firefly Algorithm
Iterations
Distance (m)
Iterations
Distance (m)
46
163,8553
27
158,4811
45
158,2495
31
156,0187
42
160,3966
35
159,3212
38
157,2173
34
157,21737
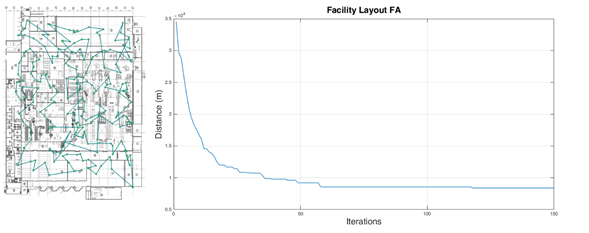
In order to evaluate the performance of the algorithm with a more robust test, a second layout corresponding to a food product factory with 200 workstations was considered. The results are shown in Figures 5 and 6.
Figure 5: LOA for facility layout 2
Figure 6: FA optimization of facility layout 2
The best solution corresponded to the combination shown in Table 2, with 8.096,936 m and 129 iterations for FA and 39.153,53 m and 200 iterations for the LOA. It is evident that, in the case of a plant with a higher degree of complexity, the FA algorithm performs better than the LOA, which, despite reaching 200 iterations, still fails to find an optimal minimum.
Source: Authors
Table 2: Results for facility layout 2 (LAO vs. FA)
Local Optimization Algorithm
Firefly Algorithm
Iterations
Distance (m)
Iterations
Distance (m)
200
40.546,77
141
8.144,797
200
40.727,99
129
8.096,936
200
40.234,65
136
8.136,360
200
39.153,53
133
8.189,162
DISCUSSION
A two-dimensional FA representation was developed, and the algorithm showed a good performance in the test scenarios. It has optimal and fast convergence with a reasonable amount of running time over ten generations once the maximum light intensity is chosen as the optimal solution.
The optimized distances associated with the layout plan in these tests were 156,0187 and 8.096,936 m, depending on the ability to optimize time, flows, and the handling of materials, among many other aspects, until a finished product is achieved. Under that premise, the scope of the results evidenced a final strategy for saving money, but also for optimizing the material flow.
The results achieved for layout 1 by the developed FA algorithm show a similar performance to that of the conventional heuristic LOA (Table 3). After the maximum number of iterations for each generation was reached in each test, the cost function was calculated in order to validate the best option.
Source: Authors
Table 3: Best performances for facility layout 1
Algorithm
Iterations
Distance (m)
LOA
38
157,2173
FA
31
156,0187
In the case of a more complex layout distribution, it is evident that the FA achieves a minimum optimum with fewer iterations than the LOA algorithm (Table 4).
Source: Authors
Table 4: Best performances for facility layout 2
Algorithm
Iterations
Distance (m)
LOA
200
39.153,53
FA
129
8.096,936
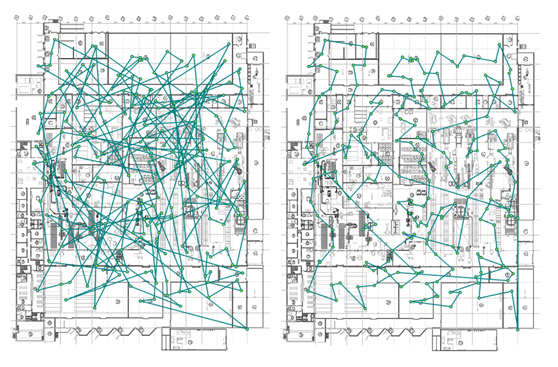
Finally, Figure 7 shows the comparison of the initial solution with respect to the optimized layout for a plant of greater complexity, which evidences how the algorithm performs the optimization task.
Figure 7: Initial solution and final plan for facility layout 2
CONCLUSIONS
In this research, the FA was used to define a model for representing the layout of a facility. It is important to define the objective function, ensuring that the best solution for the given problem is found. This algorithm offers a better path length, similar to other heuristic algorithms. In this case, a final optimized value of 156,0187 m was obtained for a simple facility layout, as well as 8.096.936 m for a complex facility layout -much better than the conventional heuristic algorithm.
The FA works particularly well at solving combinatorial problems whose feasible solution space is too large to carry out a comprehensive search with reasonable computation times. In this case, the FA achieved a significant reduction in iteration times and speed of optimization.
The potential applications of the FA in logistic and combinatorial optimization problems, as is the case of path planning, shows good promise for facilitating decision-making.
REFERENCES
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.