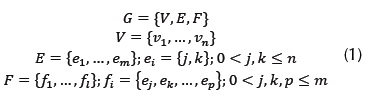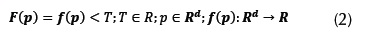DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2016.1.a01Publicado:
01-01-2016Número:
Vol. 20 Núm. 47 (2016): Enero - MarzoSección:
InvestigaciónModeling of heterogeneous objects: an approach based on implicit functions
Modelado de objetos heterogéneos: una propuesta con base en funciones implícitas
Palabras clave:
Heterogeneous objects, geometric modeling, implicit representation (en).Palabras clave:
Objetos heterogéneos, modelado geométrico, representación implícita (es).Descargas
Referencias
Alliez, P., & others. (June de 2015). 3D Mesh Generation.
Bajaj, C. (1997). Introduction to implicit surfaces. Morgan Kaufmann.
Bidarra, R., de Kraker, K. J., & Bronsvoort, W. F. (1998). Representation and management of feature information in a cellular model. Computer-Aided Design, 30(4), 301-313.
Caon, M. (2004). Voxel-based computational models of real human anatomy: a review. Radiation and environmental biophysics, 42(4), 229-235.
Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J., Fright, W. R., McCallum, B. C., & Evans, T. R. (2001). Reconstruction and representation of 3D objects with radial basis functions. Proceedings of the 28th annual conference on Computer graphics and interactive techniques, (págs. 67-76).
Chen, K.-Z., & Feng, X.-A. (2004). CAD modeling for the components made of multi heterogeneous materials and smart materials. Computer-Aided Design, 36(1), 51-63.
Cheng, J., & Lin, F. (2005). Approach of heterogeneous bio-modeling based on material features. Computer-Aided Design, 37(11), 1115-1126.
Chiu, W., & Tan, S. (2000). Multiple material objects: from CAD representation to data format for rapid prototyping. Computer-aided design, 32(12), 707-717.
De Santis, R., Ambrosio, L., Mollica, F., Netti, P., & Nicolais, L. (2007). Mechanical properties of human mineralized connective tissues. En Modeling of Biological Materials (págs. 211-261). Springer.
d'Otreppe, V., Boman, R., & Ponthot, J.-P. (2012). Generating smooth surface meshes from multi-region medical images. International Journal for Numerical Methods in Biomedical Engineering, 28(6-7), 642-660.
Fabri, A., Giezeman, G.-J., Kettner, L., Schirra, S., & Schonherr, S. (1998). On the design of CGAL, the computational geometry algorithms library.
Gómez-Mora, M., & Flórez-Valencia, L. (2013). Three-dimensional object reconstruction. Vínculos.
Gómez-Mora, M., & Flórez-Valencia, L. (2015). Surface reconstruction from three dimensional segmented domains using implicit functions. IEEE.
Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., & Stuetzle, W. (1992). Surface reconstruction from unorganized points (Vol. 26). ACM.
IRCAD. (April de 2015). http://www.ircad.fr/research/3d-ircadb-01/. http://www.ircad.fr/research/3d-ircadb-01/.
Kazhdan, M., Bolitho, M., & Hoppe, H. (2006). Poisson surface reconstruction. Proceedings of the fourth Eurographics symposium on Geometry processing, 7.
Knopf, G. K., & Al-Naji, R. (2001). Adaptive reconstruction of bone geometry from serial cross-sections. Artificial Intelligence in Engineering, 15(3), 227-239.
Kou, X. Y. (2007). Heterogeneous object modeling: A review. 284-301.
Kou, X., Tan, S., & Sze, W. (2006). Modeling complex heterogeneous objects with non-manifold heterogeneous cells. Computer-Aided Design, 38(5), 457-474.
Kumar, V. a. (1997). An approach to modeling multi-material objects. Proceedings of the fourth ACM symposium on Solid modeling and applications, 336--345.
Kumar, V., Burns, D., Dutta, D., & Hoffmann, C. (1999). A framework for object modeling. Computer-Aided Design, 31(9), 541-556.
Liu, H., Maekawa, T., Patrikalakis, N., Sachs, E., & Cho, W. (2004). Methods for feature-based design of heterogeneous solids. Computer-Aided Design, 36(12), 1141-1159.
Lorensen, W. E., & Cline, H. E. (1987). Marching cubes: A high resolution 3D surface construction algorithm. ACM siggraph computer graphics, 21, págs. 163-169.
Moustakides, G., Briassoulis, D., Psarakis, E., & Dimas, E. (2000). 3D image acquisition and NURBS based geometry modelling of natural objects. Advances in Engineering Software, 31(12), 955-969.
Ohtake, Y. a. (2013). Edge detection based multi-material interface extraction on industrial CT volumes. Science China Information Sciences, 1--9.
Ohtake, Y., Belyaev, A., Alexa, M., Turk, G., & Seidel, H.-P. (2005). Multi-level partition of unity implicits. ACM SIGGRAPH 2005 Courses, (pág. 173).
Qian, X., & Dutta, D. (2003). Design of heterogeneous turbine blade. Computer-Aided Design, 35(3), 319-329.
Schroeder, W., Martin, K., & Lorensen, B. (2006). Visualization Tollkit: An Object-Oriented Approach To 3D Graphics (4th ed.).
Shin, K.-H., & Dutta, D. (2001). Constructive representation of heterogeneous objects. Journal of Computing and Information Science in Engineering, 1(3), 205-217.
Siu, Y., & Tan, S. (2002). Source-based heterogeneous solid modeling. Computer-Aided Design, 34(1), 41-55.
Starly, B., Darling, A., Gomez, C., Nam, J., Sun, W., Shokoufandeh, A., & Regli, W. (2004). Image based bio-cad modeling and its applications to biomedical and tissue engineering. Proceedings of the ninth ACM symposium on Solid modeling and applications, (págs. 273-278).
Sun, W. a. (2002). Reasoning Boolean operation based modeling for heterogeneous objects. Computer-Aided Design, 481--488.
Sun, W., Darling, A., Starly, B., & Nam, J. (2004). Computer-aided tissue engineering: overview, scope and challenges. Biotechnology and Applied Biochemistry, 39(1), 29-47.
Sun, W., Starly, B., Nam, J., & Darling, A. (2005). Bio-CAD modeling and its applications in computer-aided tissue engineering. Computer-Aided Design, 37(11), 1097-1114.
Van Dam, A., Feiner, S. K., McGuire, M., & Sklar, D. F. (2013). Computer graphics: principles and practice. Pearson Education.
Wang, C. C. (2007). Direct Extraction of Surface Meshes from Implicitly Represented Heterogeneous Volumes. Comput. Aided Des., 35-50.
Wang, L., Yu, Y., Zhou, K., & Guo, B. (2011). Multiscale vector volumes. ACM Transactions on Graphics (TOG), 30(6), 167.
Wang, M. Y., & Wang, X. (2005). A level-set based variational method for design and optimization of heterogeneous objects. Computer-Aided Design, 37(3), 321-337.
Weiler, K. (1988). The radial edge structure: a topological representation for non-manifold geometric boundary modeling. Geometric modeling for CAD applications, 1988, 3-36.
Yuan, Z., Yu, Y., & Wang, W. (2012). Object-space multiphase implicit functions. ACM Transactions on Graphics (TOG), 31(4), 114.
Zaidi, H., & Tsui, B. M. (2009). Review of computational anthropomorphic anatomical and physiological models. Proceedings of the IEEE, 97(12), 1938-1953.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.1.a01
Modeling of Heterogeneous Objects: An Approach Based on Implicit Functions
Modelado de objetos heterogéneos: una propuesta con base en funciones implícitas
Miller Gómez-Mora1, Leonardo Flórez-Valencia2
1 System Engineer, specialist in Teleinformatics, master of Science in Information and Communications, doctor candidate in engineering. Associate professor at the Distrital University Francisco José de Caldas. Bogotá, Colombia. Contact: mgomezm@udistrital.edu.co
2 Computer and System Engineer, master in Computer and System Engineering. Degree of DEA (Diplôme d'Etudes Approfondies) in images and systems, doctor degree in images and systems. Associate professor at the Javeriana University. Bogotá, Colombia. Contact: florez-l@javeriana.edu.co
Fecha de recepción: 22 de febrero de 2015 Fecha de aceptación: 18 de septiembre de 2015
Cómo citar: Gómez-Mora, M., & Flórez-Valencia, L. (2016). Modeling of heterogeneous objects: An approach based on implicit functions. Revista Tecnura, 20(47), 15-27. doi: 10.14483/udistrital.jour.tecnura.2016.1.a01
Abstract
Modeling objects, their properties and relations is an important topic in computer science. In this sense, this research contributes to the framework of heterogeneous solid modeling, as well as the popular and intricate study of implicit solid representation. The approach presented here is broad and generic, but this article will focus on bio-CAD models, alluding to the existing extension and implementation in other fields. The overall aim of this work is to demonstrate that solid models of heterogeneous object can be built implicitly. This is shown to have promise in practical applications from biomedical computing to computer animation and engineering. The approach adopted here is based on the observation that current solid models cannot intrinsically represent multiphase geometric information along with the attribute information. This makes necessary to explore new modeling techniques in order to represent real-world objects. The availability of such modeling techniques remains central to the design, analysis, and fabrication of heterogeneous objects.
Keywords: Geometric modeling, heterogeneous objects, implicit representation.
Resumen
El modelado de objetos, sus propiedades y relaciones es un tema importante en las ciencias de la computación y la informática. En ese sentido, esta investigación busca contribuir al modelado de objetos sólidos heterogéneos, así como al complejo estudio de la representación implícita de objetos sólidos. El enfoque que aquí se presenta es amplio y genérico, pero este artículo se centra en modelos bio-CAD, aludiendo su extensión y aplicación a otros campos. El objetivo general de este trabajo es demostrar que los modelos geométricos de objetos heterogéneos se pueden representar de forma implícita. Esto promete tener gran variedad de aplicaciones prácticas desde la computación biomédica hasta la animación por computador y la ingeniería aplicada. El enfoque adoptado aquí se basa en la observación de que los modelos sólidos actuales no pueden representar intrínsecamente información geométrica multifase junto con la información de los atributos. Esto hace necesario explorar nuevas técnicas de modelado para representar objetos del mundo real. La disponibilidad de este tipo de modelos es fundamental para el diseño, análisis y fabricación de objetos heterogéneos.
Palabras clave: Modelado geométrico, objetos heterogéneos, representación implícita.
Introduction
Most objects, natural or man-made, contain multiple materials within complex volumetric structures organized in complicated geometric configurations. We refer to these objects as heterogeneous objects. Modeling heterogeneous objects can help us gain a better understanding of the physical world. The following is a set of application domains where reliable models of such objects will be of great demand:
- Reverse engineering: The geometry of a real part is scanned to create a CAD/CAM representation; this model can then be used for further editing and integration with other modeled parts, as well as for simulation purposes.
- Diagnostics: Nowadays, visualization of volume scans is an important tool in medical diagnostics. Shape and size of internal organs can be segmented from the volume data; this and additional information derived from the scans (mass density distribution, speed of blood flow, etc.) can provide much more insight into body-internal structures and processes than conventional examination methods.
- E-commerce: With the rise of Internet shopping, models of real objects need to be transmitted to potential buyers. Animation: Models of characters and props can be used in film production for creation of special effects.
Besides the reverse engineering techniques, the ongoing development in the field of medical imaging modalities such as computed tomography (CT) and magnetic resonance imaging (MRI), have made the computer aided technologies to be used extensively in modern medicine and biomedical engineering. For instance, the medical industry uses detailed models of organs in different applications such as tissue engineering, part modeling and visualization, surgical simulation and planning, as well as manufacturing of various accessories and patient specific prosthesis (Sun, Starly, Nam, & Darling, 2005). This leads to the need of new image-based bio-CAD applications to improve diagnosis, treatment and prevention of diseases.
The basic and most widely used format for generating 3D models is a volumetric voxel model (Sun, Darling, Starly, & Nam, 2004), which is currently considered to be the most accurate representation of natural objects including the human anatomy (Caon, 2004). Although voxel models produce rather realistic renderings of such objects, the memory overhead of these models is too large as to be restrictive. What's more, voxel models luck geometric representation making them unsuitable for bioengineering design and engineering analysis (Gómez-Mora & Flórez-Valencia, 2013). Consequently, extracting precise geometric models from medical images including the interfaces between different organs and tissues is important not only to visualize the internal structure of a specific region (Sun, Darling, Starly, & Nam, 2004), but also to mimic as closely as possible its properties in realistic physically-based simulations (Zaidi & Tsui, 2009).
Current situation in object representation
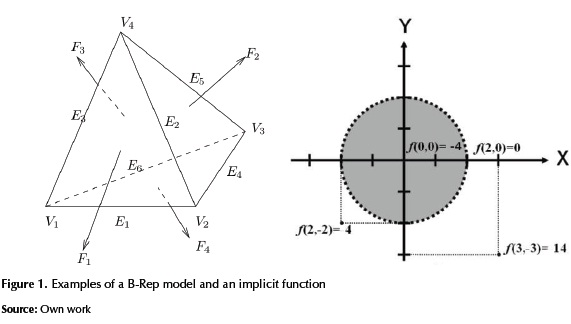
At the present time, most commercial solid modeling systems employ boundary representations (B-rep). The boundary representation model (B-Rep) is used to represent the shape of an object as a set of connected surface elements (see figure 1-left). The B-Rep model consists of geometric and topological information. The geometric information includes a description of the points belonging to the surface of an object while the topological information specifies the connections between the points on the surface. The most common type of B-Rep is the polygonal representation. A model of a polygon (G) consists of a set of vertices (V), edges (E) and faces (F) (Van Dam, Feiner, McGuire, & Sklar, 2013).
For example, figure 1-left illustrates a B-rep tetrahedral solid. B-rep representation is well suited for visual display since most modern computer video cards support hardware acceleration for polygon drawing.
Existing bio-CAD models are usually solid models defined by the bounding surfaces that enclosed the regions-of-interest (ROI) using a B-Rep, and based on the premise of material homogeneity model (Sun, Darling, Starly, & Nam, 2004). However, point membership classification for B-rep models requires a global computation, i.e. testing the position of the point in relation to each surface patch.
An approach base on implicit functions
Instead of an explicit B-Rep modeling, this research focused on an alternative representation scheme known as implicit solid modeling that offers very straightforward methods for object representation and point classification. An object can be defined by a scalar function defined on d-dimensional Euclidean space with an inequality (Bajaj, 1997):
where T is a threshold value. The subset 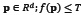 is called solid object and the subset
is called solid object and the subset 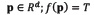 is called iso-surface (see figure 1-right). A point is classified by evaluating the implicit function at that point. If the output is negative then the point is inside; if the output is positive then the point is outside; and if the output is zero then the point lies right on the surface of the solid.
is called iso-surface (see figure 1-right). A point is classified by evaluating the implicit function at that point. If the output is negative then the point is inside; if the output is positive then the point is outside; and if the output is zero then the point lies right on the surface of the solid.
There are many ways to define f. On one hand, it can have a closed analytical form, for example, the zero level-set of the function 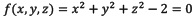 defines a sphere of radius 2, classifying the space into two half-spaces ƒ > 0 and ƒ < 0. On the other, an implicit function f can also be defines through data-driven methods taking the form of a signed distance field (Hoppe, DeRose, Duchamp, McDonald, & Stuetzle, 1992), or indicator function (Kazhdan, Bolitho, & Hoppe, 2006).
defines a sphere of radius 2, classifying the space into two half-spaces ƒ > 0 and ƒ < 0. On the other, an implicit function f can also be defines through data-driven methods taking the form of a signed distance field (Hoppe, DeRose, Duchamp, McDonald, & Stuetzle, 1992), or indicator function (Kazhdan, Bolitho, & Hoppe, 2006).
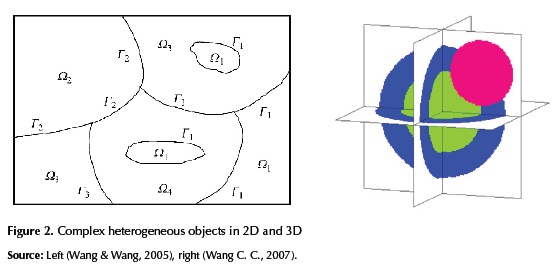
However, when multiple regions are presented inside the object (see figure 2, and figure 3-left), building and querying the implicit solid is a difficult problem.
In order to give form to the proposed research, the work focused on the following research questions:
- How to create a solid geometric model of a heterogeneous object that not only capture the outer geometry accurately, but also contain information of the inner region interfaces?
- What algorithms and methods must be introduced to be capable of implicitly representing heterogeneous objects with multiple internal regions?
Answering those two questions should also lead to answering a third question:
- How to calculate the interfaces of all inner material regions bellowing to the heterogeneous object defined by a set of unstructured labeled points in R3?
The main hypothesis that drove the research was:
- A solid modeling method based on implicit functions represents segmented multi-material volumes of heterogeneous objects efficiently and accurately.
We have taken into account that models based on an implicit representation are compact and resolution independent, and can provide specific accuracy to efficient geometry and material queries (Kou X. Y., 2007). Additionally, if the need arises, they can become explicit models using a voxel, or a finite element based representation. Because of the mathematical description, these models are concise, compact and suitable for design, simulation, and manufacturing.
Problem definition
Following the representation method in (Wang & Wang, 2005) without loss of general, a real-world object can be model as a heterogeneous solid η in a given geometric domain Ω ∈ R3 defined by a function ƒ (p) with p ∈ Ω.
If there are a total of n materials involved in Ω, the value of ƒ(p) is an integral index of material class between 0 and n (zero represents no material), which indicates the material type in Ω at p . Suppose that a region filled with the material class i is denoted by Ωi, we have that

is the complement of Ω0 in Ω. Thus, the heterogeneous object η is partitioned by regions with unique material i (see figure 2).
Suppose that the material region Ωi has a meaningful boundary surface 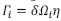 , then the interface between two material regions Ωi and Ωj is denoted by
, then the interface between two material regions Ωi and Ωj is denoted by 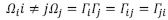 . Additionally,
. Additionally, 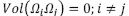 meaning that the geometric domain Ω is a partition and any two material regions do not overlap except at their shared boundary, which has zero volume.
meaning that the geometric domain Ω is a partition and any two material regions do not overlap except at their shared boundary, which has zero volume.
When the material region Ω0 is considered all the intermediate surfaces in Ω representing the geometric model of η can be defined as
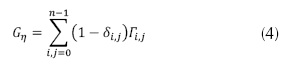
where 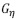 is the geometric model of η, and
is the geometric model of η, and 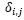 is the Kronecker delta defined to be 1 if i = j and 0 (zero) otherwise. We remark that some interfaces
is the Kronecker delta defined to be 1 if i = j and 0 (zero) otherwise. We remark that some interfaces 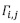 may be empty, and
may be empty, and 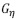 may not always be manifold, it can also be non-manifold curves and surfaces.
may not always be manifold, it can also be non-manifold curves and surfaces.
The remainder of this paper is organized as follows: Section 2 gives a brief background of composite models for representing heterogeneous objects. Section 3 lays out our method based on implicit functions. Section 4 reports results that demonstrate the effectiveness of our approach for three-dimensional segmented medical images. Section 5 draws conclusions and outlines future research.
Composite Models
Despite the diversity in the geometric and material representations, most of cited heterogeneous object models use a single (explicit, implicit, procedural or otherwise) mapping function to define the material distribution. Based on the idea of space partitions many researchers (Kumar, Burns, Dutta, & Hoffmann, 1999), (Chen & Feng, 2004), (Shin & Dutta, 2001), kou 2006, (Cheng & Lin, 2005) propose composite models to represent such objects. Intuitively, a composite model can be seen as a collection or group of sub-objects (see figure 2), each sub-object belonging to a generic material class (Wang & Wang, 2005).
Mathematically, composite models can be described as:
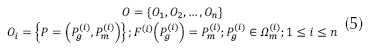
where O is a complex object, 0i is the i-th sub-object, 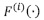 is the i-th mapping function defined in the geometric sub-domain geometric
is the i-th mapping function defined in the geometric sub-domain geometric 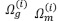 is the i-th material domain and n is the number of sub-objects.
is the i-th material domain and n is the number of sub-objects.
Assembly models
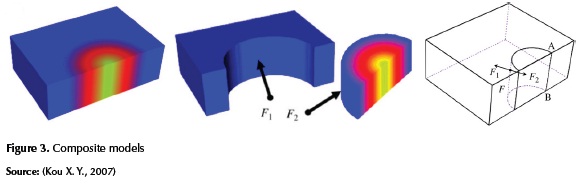
An assembly model is a natural and intuitive way to represent complex and heterogeneous objects. The whole object is modeled as a set and each part of the set is a sub-object with a unique material distribution. figure 3-center shows an assembly model of the object in figure 3-left, which is decomposed into a homogeneous solid and an FGM object.
To represent a heterogeneous object using the assembly model, spatial partitions must be established appropriate. There are at least two methods for accomplishing this. The constructive approach, which generates spatial divisions of the boundaries of existing primitives. Kumar and Dutta (Kumar V. a., 1997), and Hu and Sun (Sun W. a., 2002) proposed regularized operators (difference, intersection and union) and other operators to model the geometry of the assembly.
Alternatively, it is also possible to directly decompose existing geometries into separate components interconnected. For example, Liu (Liu, Maekawa, Patrikalakis, Sachs, & Cho, 2004) in his feature-based scheme decomposes the geometry of an object with two surfaces bounded by spheres.
Assembly models are easy to understand and implement. However, despite the intuitiveness and ease of use, assembly models also suffer some inherent disadvantages. Qian and Dutta (Qian & Dutta, 2003) noted that the use of regularized Boolean operations on the space partition leads to unnecessary operations and 3D over-segmented regions. Kou (Kou, Tan, & Sze, 2006) also showed that strong data redundancy and low consistency of assembly models are inherent problems in this type of model.
This is clearly visible from the assembly shown in figure 3-center. Here, coupling faces F1 and F2 represent the same geometric feature; however, they are represented separately and maintained in two different parts. Such separations are not only unnecessary expense of memory, but also makes the model prone to errors for certain operations. For example, after a local translation of the face F1 or F2, the material composition of a point in a neighborhood of F1 or F2 could not be assessed unambiguously, since the point can be classified randomly as within a (both) component(s) due to calculation errors. More recent cases can be seen in (Wang, Yu, Zhou, & Guo, 2011), (d'Otreppe, Boman, & Ponthot, 2012), Ohtake (Ohtake Y. a., 2013).
Cell models
Unlike assembly representations, cell models use non-manifold cell representations for modeling space partitions. The geometry is modeled essentially with non-manifold boundary representations. In figure 3-right, the non-manifold conditions occurring around the edge (border) AB, because the neighborhood of a point on the border AB is not homeomorphic to a disk in two dimensions (Weiler, 1988), whereas for an assembly model all components are topologically manifold.
According to Bidarra (Bidarra, de Kraker, & Bronsvoort, 1998) in a cell model data redundancy can be kept to a minimum through a mechanism of co-boundary. In the cell representation a topological element (for example, a face) differs from the reference sides. For example, the use of a face is actually the use of one of the two sides of the face, and each side is oriented with respect to the same geometry of the face. Either of the two side of the face that share the same border element are called co-boundary.
With a cell model, for the same example shown in figure 3-left, the boundary face is not shown separately as the case shown in figure 3-center, instead, it is represented with a single face F, as shown in figure 3-rihgt. Here F1 and F2 are oriented instances (sides) of the face F. Again, when the boundary face is subject to the same local translation as discussed above, the changes will be applied to the geometries of the face F, which is shared by F1 and F2. Therefore, consistent changes are simultaneously applied to both sides of the face (that is, F1 and F2). Thus, one can obtain the point classification and can achieve a robust assessment of the material composition.
Methodology
There are two techniques used to generate an image-based model (Moustakides, Briassoulis, Psarakis, & Dimas, 2000): The first approach builds the surface from the point cloud data, using reverse engineering methods or a commercially available reverse engineering software package. A 3D voxel model generated from segmented image slices can be used to create a point cloud data which is then triangulated to form a faceted model (Starly, y otros, 2004). An alternative method is to reconstruct a surface from serial parallel contours extracted from sequential medical images. These images are segmented into ROI and edge points around the boundary are extracted and ordered (Knopf & Al-Naji, 2001). The accuracy of the fitted surface model depends largely on the extracted edge points and the function uses to fit curves to those contours.
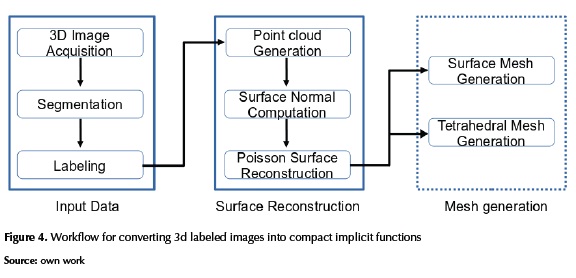
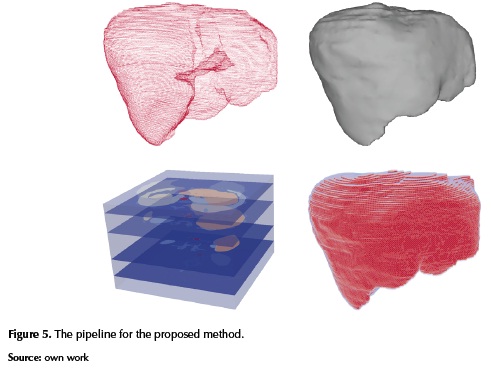
In this work, a method based on indicator functions for converting three dimensional labeled images into compact implicit functions is proposed according to the first approach presented in (Moustakides, Briassoulis, Psarakis, & Dimas, 2000), (see figure 4). As part of the method, each label is associated with a specific object (organ) of interest (see figure 5).
First, a segmented medical image is considered as input data from which a point cloud P is extracted for each object of interest (see figure 5). Secondly, an implicit surface S representing a smooth continuous three-dimensional scalar field for a specific region is reconstructed by defining an indicator function from the point cloud P, using the Poisson reconstruction method (Kazhdan, Bolitho, & Hoppe, 2006). Then, the region's surface  is represented by the zero level-set of a function
is represented by the zero level-set of a function 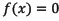 , which completely replaces the original labeled region during the meshing operations. Figure 5 depicts the pipeline for the proposal work-flow.
, which completely replaces the original labeled region during the meshing operations. Figure 5 depicts the pipeline for the proposal work-flow.
Input data
The effectiveness of a modeling method is dependent on the data set to which it is applied. One modeling method may be particularly effective for one type of data set, while being entirely useless for many others. When creating a computer model of a real-world object, the first task is to measure the relevant properties of the object. Additionally, in order to successfully build a solid model of heterogeneous objects, it is important to accurately identify and extract features of interest from this raw data (See figure 5).
Although medical image segmentation is an established and mature field, fully automatic segmentation of medical image data remains an unsolved problem (De Santis, Ambrosio, Mollica, Netti, & Nicolais, 2007). Segmenting medical data remains a challenging task due to the size of the raw data, the complexity of anatomical shapes, overlap of gray level values between neighboring tissues and organs, lack of consistently distinct boundaries and sampling artifacts and noise (Caon, 2004). Due to the above, a previously segmented medical image is considered as input data to work with. Hence, the quality of the resulting model will depend on the quality of the set of segmented images.
Surface reconstruction
Although the main requirement of all surface reconstruction methods is a set of three-dimensional points that sample the surface, working with the points alone may fail to provide an accurate surface reconstruction. To address this issue, we assume a set of normal vectors N along with the point cloud P. In other words, for each 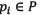 there is an accompanying normal
there is an accompanying normal 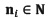 . In the field of Computer graphics the set of points P is usually obtained by laser range-finders, mechanical touch probes and computer vision techniques such as depth from stereo (Ohtake, Belyaev, Alexa, Turk, & Seidel, 2005). As in our case, the input data is a 3D segmented image (see previous subsection "Input data"); a procedure that automatically extracts the boundary points and surface normals from this image has been developed (Gómez-Mora & Flórez-Valencia, 2015).
. In the field of Computer graphics the set of points P is usually obtained by laser range-finders, mechanical touch probes and computer vision techniques such as depth from stereo (Ohtake, Belyaev, Alexa, Turk, & Seidel, 2005). As in our case, the input data is a 3D segmented image (see previous subsection "Input data"); a procedure that automatically extracts the boundary points and surface normals from this image has been developed (Gómez-Mora & Flórez-Valencia, 2015).
Based on the observation that segmented data consists of one value for points inside the object and a second value for points outside the object, the inward pointing normal field of the boundary of a solid can be interpreted as the gradient of the solid's indicator function 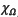 , which is often defined to have value 1 inside and value 0 outside the model, the iso-surface induced by the indicator function defines the reconstructed model
, which is often defined to have value 1 inside and value 0 outside the model, the iso-surface induced by the indicator function defines the reconstructed model 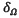 .
.
Assuming a point cloud with oriented normals, an indicator function x can be found by ensuring its gradient as-close- as-possible to the normal field N in terms of least-squares using 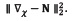 . If we apply the divergence operator to this problem, then this amounts to solving the following Poisson equation:
. If we apply the divergence operator to this problem, then this amounts to solving the following Poisson equation:
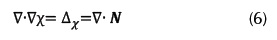
Thus, given a vector field 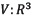 , defined by the point cloud P, the goal is to solve the scalar function
, defined by the point cloud P, the goal is to solve the scalar function 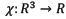 minimizing:
minimizing:
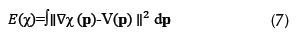
Kazhdan (Kazhdan, Bolitho, & Hoppe, 2006) directly solves for x in the spatial domain via a multi-grid approach, hierarchically solving for x in a coarse-to-fine resolution manner. This method is called Poisson surface reconstruction (PSR) and uses the Euler-Lagrange formulation, where the minimum is obtained by solving the Poisson equation:
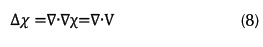
Solving the Poisson equation, the function x is obtained that approximates the indicator function. The surface S is then represented by the zero crossing of the indicator function (see figure 5-left-button, and figure 6), or with a suitable isovalue, typically the average or median value of x evaluated at all of the input points.
Mesh generation
The meshing algorithm requires to know the surface to be meshed, in this case, the implicit surfaces described as the zero level set of the indicator function. These meshes are either surface meshes approximating the boundaries of anatomical structures or volume meshes of these objects. Basically the algorithm computes a set of sample points on the surface, and extract an interpolating surface mesh from the three dimensional triangulation of these sample points. Points are iteratively added to the sample, as in a Delaunay refinement process, until some size and shape criteria on the elements of the surface mesh are satisfied (Alliez, 2015).
In (Alliez, 2015) has been clarified that if the surface is smooth enough, and if the size criteria are small enough, the algorithm guarantees that the output mesh is homeomorphic to the surface, and is within a small bounded distance from the surface. The algorithm can also be used for non-smooth surfaces but then there is no guarantee.
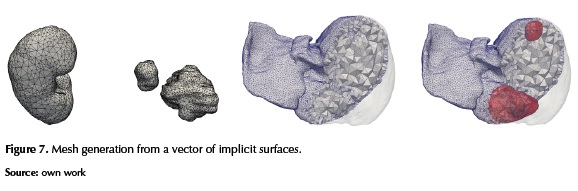
For simulation purposes one of the most important quality metrics for surface meshes is the minimal angle that avoids having flat triangles. In our experiments both the surface meshes and the volumetric meshes were constrained to have triangles with minimum angle above 30 degrees as shown in figure 7.
Figure 7-left shows surface meshes fitting the implicit surfaces of the left kidney, and two tumors located inside the liver. In figure 7-center a cut of the liver's volume mesh with two tumors is depicted, while in figure 7-rihgt the volume meshes of the tumors are added to the scene, and a superposition of volumetric meshes is rendered to show the position of the tumors in figure 7-center.
Results
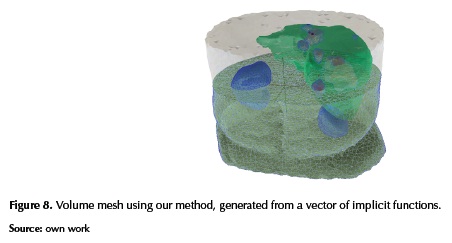
Representing multi-material interfaces begins with the generation of the indicator functions Xi that characterize each material in the volume. We do this by first isolating each material label into a separate volume, extracting boundary points and then constructing smooth implicit representations of the point clouds (see figure 8).
To establish our method's ability to handle complex geometries, we consider the reconstruction of nine different biological structures provided by IRCAD (IRCAD, 2015): a liver, the two kidney and six liver tumors, all acquired using a CT scan. The patient icom image was acquired using a CT scan with dimensions: 512x512x129; spacing: x=0.57, y=0.57, z=1.6; All the segmented structures (liver, kidneys, and tumors) have the same dimensions as the original patient dicom image, i.e., 33816576 points that are equivalent to 33 MB (see Fig 5).
We use a VTK (Schroeder, Martin, & Lorensen, 2006) implementation of the MC algorithm proposed by Lorense and Cline (Lorensen & Cline, 1987) to obtain the different point-clouds Pt. All tests were executed on a PC with an Intel R Core i7-4790 processor and 16GB of RAM. The Poisson surface reconstruction method is computed using as solver the Eigen3, version 3.2.0. The surface meshing, and volume meshing are computed using the CGAL library (Fabri, Giezeman, Kettner, Schirra, & Schonherr, 1998) (see figure 7 and figure 8).
Conclusions
Recently, modeling heterogeneous objects with intricate geometries as well as complex material distribution has attracted enormous attentions (Yuan, Yu, & Wang, 2012), Ohtake (Ohtake Y. a., 2013). This type of modeling has been considered as a hybrid type of modeling where the geometric modeling and material modeling are included (Chiu & Tan, 2000), (Siu & Tan, 2002). In this work, we have restricted our interest to the geometrical representation of heterogeneous objects as the basis for the modeling of materials and properties of the objects as it was described by Kumar (Kumar, et al., 1999). This geometric model can be used in further modeling stages where each homogeneous material component is surrounded by an implicit boundary surface.
In this paper, we have shown that an implicit representation defined in terms of indicator functions is a viable tool for solid modeling of heterogeneous objects when segmented medical images are available. Planned future work includes making a theoretical model for the creation, manipulation and querying of heterogeneous objects with the purposes of surgical planning and simulations. Additionally, we have already begun to investigate a number of ways to improve the method and procedures presented herein, as well as to explore new applications and algorithms based on a multi-material implicit representation.
Financing
This work was partially supported by the Universidad Distrital "Francisco José de Caldas" of Bogotá under Grant No. 345 of April 15, 2010.
References
Alliez, P., & others. (June de 2015). 3D Mesh Generation.
Bajaj, C. (1997). Introduction to implicit surfaces. Morgan Kaufmann.
Bidarra, R., de Kraker, K. J., & Bronsvoort, W. F. (1998). Representation and management of feature information in a cellular model. Computer-Aided Design, 30(4), 301-313.
Caon, M. (2004). Voxel-based computational models of real human anatomy: a review. Radiation and environmental biophysics, 42(4), 229-235.
Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J., Fright, W. R., McCallum, B. C., & Evans, T. R. (2001). Reconstruction and representation of 3D objects with radial basis functions. Proceedings of the 28th annual conference on Computer graphics and interactive techniques, (págs. 67-76).
Chen, K.-Z., & Feng, X.-A. (2004). CAD modeling for the components made of multi heterogeneous materials and smart materials. Computer-Aided Design, 36(1), 51-63.
Cheng, J., & Lin, F. (2005). Approach of heterogeneous bio-modeling based on material features. Computer-Aided Design, 37(11), 1115-1126.
Chiu, W., & Tan, S. (2000). Multiple material objects: from CAD representation to data format for rapid prototyping. Computer-aided design, 32(12), 707-717.
De Santis, R., Ambrosio, L., Mollica, F., Netti, P., & Nicolais, L. (2007). Mechanical properties of human mineralized connective tissues. En Modeling of Biological Materials (págs. 211-261). Springer.
d'Otreppe, V., Boman, R., & Ponthot, J.-P. (2012). Generating smooth surface meshes from multi-region medical images. International Journal for Numerical Methods in Biomedical Engineering, 28(6-7), 642-660.
Fabri, A., Giezeman, G.-J., Kettner, L., Schirra, S., & Schonherr, S. (1998). On the design of CGAL, the computational geometry algorithms library.
Gómez-Mora, M., & Flórez-Valencia, L. (2013). Three-dimensional object reconstruction. Vínculos.
Gómez-Mora, M., & Flórez-Valencia, L. (2015). Surface reconstruction from three dimensional segmented domains using implicit functions. IEEE.
Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., & Stuetzle, W. (1992). Surface reconstruction from unorganized points (Vol. 26). ACM.
IRCAD. (April de 2015). http://www.ircad.fr/research/3d-ircadb-01/. http://www.ircad.fr/research/3d-ircadb-01/.
Kazhdan, M., Bolitho, M., & Hoppe, H. (2006). Poisson surface reconstruction. Proceedings of the fourth Eurographics symposium on Geometry processing, 7.
Knopf, G. K., & Al-Naji, R. (2001). Adaptive reconstruction of bone geometry from serial cross-sections. Artificial Intelligence in Engineering, 15(3), 227-239.
Kou, X. Y. (2007). Heterogeneous object modeling: A review. 284-301.
Kou, X., Tan, S., & Sze, W. (2006). Modeling complex heterogeneous objects with non-manifold heterogeneous cells. Computer-Aided Design, 38(5), 457-474.
Kumar, V. A. (1997). An approach to modeling multi-material objects. Proceedings of the fourth ACM symposium on Solid modeling and applications, 336-345.
Kumar, V., Burns, D., Dutta, D., & Hoffmann, C. (1999). A framework for object modeling. Computer-Aided Design, 31(9), 541-556.
Liu, H., Maekawa, T., Patrikalakis, N., Sachs, E., & Cho, W. (2004). Methods for feature-based design of heterogeneous solids. Computer-Aided Design, 36(12), 1141-1159.
Lorensen, W. E., & Cline, H. E. (1987). Marching cubes: A high resolution 3D surface construction algorithm. ACM siggraph computer graphics, 21, págs. 163-169.
Moustakides, G., Briassoulis, D., Psarakis, E., & Dimas, E. (2000). 3D image acquisition and NURBS based geometry modelling of natural objects. Advances in Engineering Software, 31(12), 955-969.
Ohtake, Y. A. (2013). Edge detection based multi-material interface extraction on industrial CT volumes. Science China Information Sciences, 1-9.
Ohtake, Y., Belyaev, A., Alexa, M., Turk, G., & Seidel, H.-P. (2005). Multi-level partition of unity implicits. ACM SIGGRAPH 2005 Courses, (pág. 173).
Qian, X., & Dutta, D. (2003). Design of heterogeneous turbine blade. Computer-Aided Design, 35(3), 319-329.
Schroeder, W., Martin, K., & Lorensen, B. (2006). Visualization Tollkit: An Object-Oriented Approach To 3D Graphics (4th ed.).
Shin, K.-H., & Dutta, D. (2001). Constructive representation of heterogeneous objects. Journal of Computing and Information Science in Engineering, 1(3), 205-217.
Siu, Y., & Tan, S. (2002). Source-based heterogeneous solid modeling. Computer-Aided Design, 34(1), 41-55.
Starly, B., Darling, A., Gomez, C., Nam, J., Sun, W., Shokoufandeh, A., & Regli, W. (2004). Image based bio-cad modeling and its applications to biomedical and tissue engineering. Proceedings of the ninth ACM symposium on Solid modeling and applications, (págs. 273-278).
Sun, W. A. (2002). Reasoning Boolean operation based modeling for heterogeneous objects. Computer-Aided Design, 481-488.
Sun, W., Darling, A., Starly, B., & Nam, J. (2004). Computer-aided tissue engineering: overview, scope and challenges. Biotechnology and Applied Biochemistry, 39(1), 29-47.
Sun, W., Starly, B., Nam, J., & Darling, A. (2005). Bio-CAD modeling and its applications in computer-aided tissue engineering. Computer-Aided Design, 37(11), 1097-1114.
Van Dam, A., Feiner, S. K., McGuire, M., & Sklar, D. F. (2013). Computer graphics: principles and practice. Pearson Education.
Wang, C. C. (2007). Direct Extraction of Surface Meshes from Implicitly Represented Heterogeneous Volumes. Comput. Aided Des., 35-50.
Wang, L., Yu, Y., Zhou, K., & Guo, B. (2011). Multiscale vector volumes. ACM Transactions on Graphics (TOG), 30(6), 167.
Wang, M. Y., & Wang, X. (2005). A level-set based variational method for design and optimization of heterogeneous objects. Computer-Aided Design, 37(3), 321-337.
Weiler, K. (1988). The radial edge structure: a topological representation for non-manifold geometric boundary modeling. Geometric modeling for CAD applications, 1988, 3-36.
Yuan, Z., Yu, Y., & Wang, W. (2012). Object-space multiphase implicit functions. ACM Transactions on Graphics (TOG), 31(4), 114.
Zaidi, H., & Tsui, B. M. (2009). Review of computational anthropomorphic anatomical and physiological models. Proceedings of the IEEE, 97(12), 1938-1953.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.