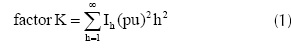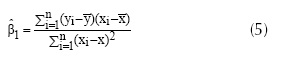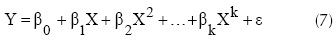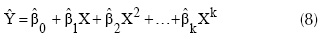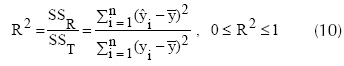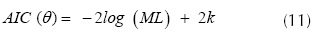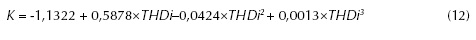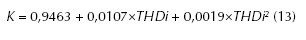Estimación del factor K en transformadores de distribución usando modelos de regresión lineal

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.2.a02

Estimación del factor K en transformadores de distribución usando modelos de regresión lineal

K factor estimation in distribution transformers using linear regression models

Juan Miguel Astorga Gómez¹, Rodrigo Alfonso Aróstica Córdova², Yuri Antonio Iriarte Salinas³

¹ Ingeniero Eléctrico,  Magister en Ciencias con Mención en Estadística Industrial, Docente de la Facultad Tecnológica, Universidad de Atacama. Copiapó, Chile. Contacto: juan.astorga@uda.cl
² Ingeniero Civil Industrial Electrónico, Docente de la Facultad Tecnológica, Universidad de Atacama. Copiapó, Chile. Contacto:  rodrigo.arostica@uda.cl
³ Profesor de Matemática y Física, Magister en Ciencias con Mención en Estadística Industrial, Docente de la Facultad de Ciencias Básicas, Departamento de Matemática, Universidad de Antofagasta. Antofagasta, Chile. Contacto: yuri.iriarte@uantof.cl

Fecha de recepción: 17 de febrero de 2015 Fecha de aceptación: 15 de febrero de 2016

Cómo citar: Astorga Gómez, J. M., Aróstica Córdova, R. A., & Iriarte Salinas, Y. A. (2016). Estimación del factor K en transformadores de distribución usando modelos de regresión lineal. Revista Tecnura, 20(48), 29-40. doi: 10.14483/udistrital.jour.tecnura.2016.2.a02

Resumen

Contexto: Debido a la incorporación masiva de equipos electrónicos a los sistemas de distribución, los transformadores de distribución están sometidos a condiciones de operación distintas a las de diseño, por causa de la circulación de corrientes armónicas. Es necesario cuantificar el efecto que producen estas corrientes armónicas para determinar la capacidad del transformador de soportar estas nuevas condiciones de operación. El factor K es un indicador que permite estimar la capacidad que tiene un transformador de soportar los efectos térmicos producidos por las corrientes armónicas. En este artículo se propone un modelo de regresión lineal para estimar el valor del factor K, a partir del contenido armónico total de corriente que se obtiene con equipos de bajo costo.

Método: Se estudian dos transformadores de distribución que alimentan cargas distintas, se registran las variables distorsión armónica total en corriente y factor K y se determina el modelo de regresión que mejor ajusta a los datos de campo. Para seleccionar el modelo de regresión se usan el coeficiente de determinación R² y el criterio de información de Akaike (AIC). Con el modelo seleccionado, se estima el factor K para las condiciones de operación real.

Resultados: Una vez determinado el modelo se pudo comprobar que tanto para la carga agrícola como para la industrial minera, el contenido de armónicos (THDi) presente supera los valores que estos transformadores pueden manejar (valor medio de 12,54 % y mínimo de 8,90 % en el caso agrícola y valor medio de 18,53 %y mínimo de 6,80 %, para el caso industrial minero).

Conclusiones: Al estimar el factor K utilizando los modelos polinomiales se determinó que los transformadores estudiados no pueden soportar la distorsión armónica total en corriente de sus cargas actuales. El factor K adecuado para los transformadores estudiados debe ser 4, esto permite que los transformadores soporten la distorsión armónica total en corriente de sus respectivas cargas.

Palabras clave: Distorsión armónica total de corriente, factor K, modelos de regresión, transformadores de distribución.

Abstract

Background: Due to massive incorporation of electronic equipment to distribution systems, distribution transformers are subject to operation conditions other than the design ones, because of the circulation of harmonic currents. It is necessary to quantify the effect produced by these harmonic currents to determine the capacity of the transformer to withstand these new operating conditions. The K-factor is an indicator that estimates the ability of a transformer to withstand the thermal effects caused by harmonic currents. This article presents a linear regression model to estimate the value of the K-factor, from total current harmonic content obtained with low-cost equipment.

Method: Two distribution transformers that feed different loads are studied variables, current total harmonic distortion factor K are recorded, and the regression model that best fits the data field is determined. To select the regression model the coefficient of determination R² and the Akaike Information Criterion (AIC) are used. With the selected model, the K-factor is estimated to actual operating conditions.

Results: Once determined the model it was found that for both agricultural cargo and industrial mining, present harmonic content (THDi) exceeds the values that these transformers can drive (average of 12.54% and minimum 8,90% in the case of agriculture and average value of 18.53% and a minimum of 6.80%, for industrial mining case).

Conclusions: When estimating the K factor using polynomial models it was determined that studied transformers can not withstand the current total harmonic distortion of their current loads. The appropriate K factor for studied transformer should be 4; this allows transformers support the current total harmonic distortion of their respective loads.

Keywords: Distribution transformers, K factor, regression models, total current harmonic distortion.

Introducción

Las cargas no lineales producen corrientes armónicas en los alimentadores de distribución y, como efecto de esto, los transformadores de distribución aumentan sus pérdidas (Daut et al., 2006). Las pérdidas por corrientes de Foucault tienen mayor significancia en las pérdidas de los transformadores de distribución, ya que al existir componentes armónicas, las pérdidas aumentan aproximadamente al cuadrado de la frecuencia (Attia, El-Metwally y Fahmy, 2010). Por lo general, los transformadores instalados en los sistemas de distribución han sido proyectados para suministrar energía a cargas que operan con frecuencias nominales. Si estos transformadores alimentan cargas no lineales y su diseño constructivo no considera la circulación de corrientes armónicas, los transformadores podrían experimentar calor excesivo en sus bobinados, reduciendo su vida útil y propiciando el corte de suministro (Yagci y Ürkmez, 2011). Para abordar el problema de las pérdidas en los transformadores de distribución se han estudiado algunas técnicas como: mitigar las componentes armónicas de las cargas que alimentan estos transformadores (Davudi, Torabzad y Ojaghi, 2011), calcular el factor K adecuado para los transformadores usando las componentes armónicas individuales de corriente (Verma, Kaushik, Prabhakar y Sengupta, 2014) y desarrollar modelos de pérdidas de transformadores por medio de elementos finitos (Faiz, Sharifian, Fakheri y Sabet-Marzooghi, 2004). Varias industrias mineras y agrícolas del norte de Chile son alimentadas por medio de transformadores de distribución cuyo factor K es igual a 1, factor que está diseñado para operar a frecuencia nominal. Dado que esta industria contiene gran cantidad de equipos de electrónica de potencia, los transformadores de distribución instalados operan en condiciones adversas de diseño. El objetivo de este trabajo es estudiar el valor adecuado del factor K que deben tener los transformadores de distribución que alimentan estas cargas, utilizando dos muestras representativas, modelos de regresión lineal, como herramienta de estimación, y distorsión armónica total de corriente, como variable de entrada. No se ha decidido utilizar a las componentes armónicas individuales de corriente como variables de entrada, porque en la práctica es más común obtener registros de distorsión armónica total de corriente por parte de los equipos de mantenimiento.

Este artículo se estructura de la siguiente manera: en la primera parte se presentan las definiciones técnicas de factor K y distorsión armónica total en corriente; se muestran las principales características de los modelos de regresión que son tratados, y se describen los indicadores que se utilizan para validar y seleccionar los modelos propuestos. Luego, se describen los resultados del procesamiento de datos de los registros para las cargas agrícola y minera; se aplican los distintos modelos de regresión; se comparan los resultados de cada modelo; se evalúa su eficiencia, y se selecciona el mejor modelo. Posteriormente, se calculan algunas estimaciones para el factor K y la distorsión armónica total en corriente usando el modelo que haya tenido el mejor ajuste. Por último, se plantean las principales conclusiones de la investigación.

Metodología

En la actualidad, los transformadores de distribución que alimentan cargas industriales manejan corrientes con alto contenido armónico. Muchos de estos transformadores han sido construidos solo para soportar el aumento de temperatura debido a las corrientes parásitas a frecuencia nominal de 50 Hz, es decir, gran parte de los transformadores de distribución tienen factor K igual a 1. En este trabajo se estima el valor del factor K que debe tener un transformador de distribución para soportar la distorsión armónica total en corriente de su carga usando modelos de regresión lineal. El análisis se realiza sobre dos transformadores de distribución, uno alimenta una carga industrial minera y el otro, una carga industrial agrícola.

Factor K

El factor K se define como un factor opcional que puede ser utilizado en transformadores y que indica la capacidad que tiene un transformador para manejar corrientes no sinusoidales (IEEE, 1998). El factor K se puede determinar según la ecuación 1.

En donde I_h(pu) es la corriente R.M.S. para la armónica de orden h (en por unidad) y h corresponde al orden de la componente armónica.

Los principales efectos de las corrientes no sinusoidales y sus consiguientes componentes armónicas en los transformadores de distribución son los siguientes: pérdidas por corrientes armónicas por el efecto I²R; pérdidas por corrientes de Eddy, las cuales aumentan proporcionalmente con el cuadrado de las corriente de carga y al cuadrado de la frecuencia, y pérdidas parásitas por efecto de corrientes armónicas en el núcleo, abrazaderas y elementos estructurales de los transformadores que aumentan proporcionalmente con el cuadrado de la corriente de carga.

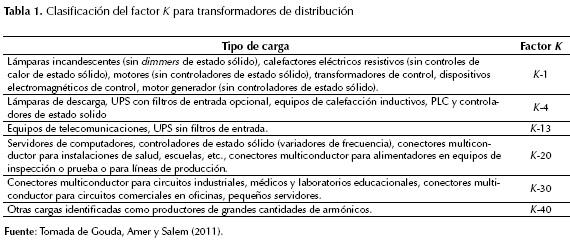
La tabla 1 muestra el factor K adecuado para transformadores de distribución según el tipo de carga que alimentan.

Distorsión armónica total en corriente (THDi)

El incremento de la tecnología disponible para el control de potencia en máquinas rotativas y la proliferación de equipos electrónicos en las instalaciones eléctricas, cuyo comportamiento es no lineal, provoca la circulación de corrientes de frecuencias que son múltiplos enteros de la frecuencia fundamental de la red (50 Hertz en Chile), llamadas frecuencias armónicas. El nivel de contenido armónico se puede medir usando el indicador Distorsión Armónica Total (THD por sus siglas en ingles), que es una relación porcentual entre el valor eficaz total de las componentes armónicas con respecto al valor eficaz de la componente fundamental. Este factor puede variar desde unas pocas unidades hasta superar el 100%.

La ecuación (2) muestra el cálculo de la distorsión armónica total en corriente, donde I_h es la magnitud de la corriente a la frecuencia de orden h e I₁ es la magnitud de la corriente a la frecuencia fundamental (Arrillaga y Watson, 2003).

Modelos de regresión lineal

Los modelos de regresión lineal son ampliamente usados en la ingeniería para el análisis de variables de entrada (independiente) y salida (respuesta) de un proceso, pues permiten estimar valores para la variable de salida en función de la variable de entrada (Montgomery, Peck y Vining, 2006). En este trabajo se estudian los modelos de regresión lineal simple y polinomial de orden 2 y 3. En ambos casos, la variable de salida es la distorsión armónica total en corriente y la variable de entrada es el factor K de transformadores de distribución.

Modelo de regresión lineal simple

La ecuación (3) muestra la representación de un modelo de regresión lineal simple, donde Y es la respuesta, X es la variable independiente, β₀ y β₁ son los parámetros del modelo o coeficientes de regresión y ε es el error del modelo.

La ecuación (4) muestra el modelo ajustado de regresión lineal simple, donde Ŷ es el valor estimado de la respuesta para la variable independiente X. Los estimadores de los parámetros del modelo son calculados por el método de los mínimos cuadrados usando las ecuaciones (5) y (6).

Modelo de regresión polinomial

Los modelos de regresión polinomial se usan cuando la variable de respuesta muestra un comportamiento no lineal (Montgomery, Peck y Vining, 2006). La ecuación 7 describe el modelo de regresión polinomial de orden k y la ecuación 8 muestra el modelo ajustado de regresión polinomial de orden k para una variable independiente. Los estimadores de los parámetros del modelo polinomial se obtienen por el método de los mínimos cuadrados usando la ecuación 9, donde y, X, X' son vectores.

Coeficiente de determinación R²

El coeficiente de determinación R² mide la proporción de la variación de la respuesta Y que es explicada por el modelo de regresión (Montgomery, Peck y Vining, 2006). El coeficiente R² se calcula usando la ecuación 10, donde SS_R es la medida de variabilidad del modelo de regresión y SS_T corresponde a la medida de variabilidad de la respuesta Y sin considerar el efecto de la variable independiente X.

Si el valor de R² se acerca a 1, entonces se tiene un buen ajuste y el modelo de regresión es capaz de explicar adecuadamente la variación de la variable de respuesta Y.

CRITERIO DE INFORMACIÓN DE AKAIKE (AIC)

El criterio de información de Akaike (AIC) es un indicador que permite seleccionar un modelo estadístico basándose en la teoría de información y en las propiedades del método de máxima verosimilitud. Cuando se comparan dos o más modelos estadísticos, se selecciona aquel que presenta el menor valor de AIC (Akaike, 1974). Para calcular el AIC se utiliza la ecuación 11, donde k es el número de parámetros del vector de parámetros θ del modelo y ML es la función de máxima verosimilitud.

Resultados

Análisis carga industrial agrícola

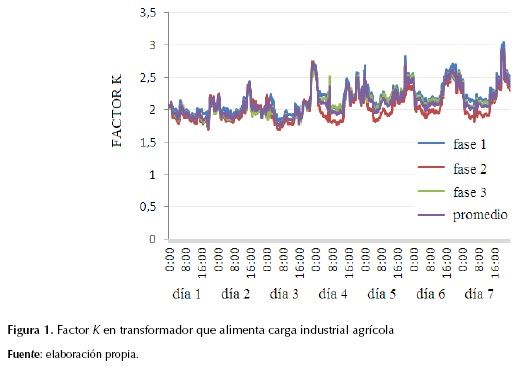
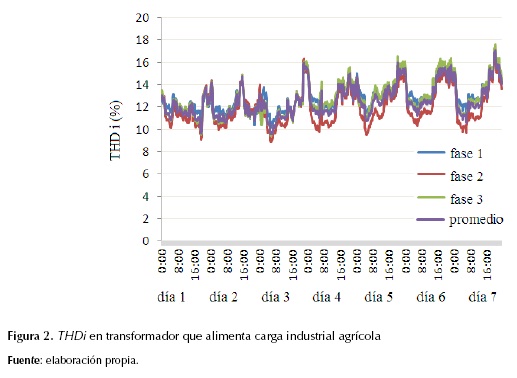
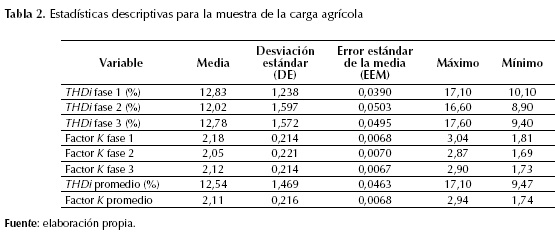
Para estudiar el transformador de distribución que alimenta la carga agrícola se registraron cada diez minutos durante siete días consecutivos las variables factor K y distorsión armónica total en corriente, usando un equipo analizador de calidad de energía. Los resultados de estos registros se pueden apreciar en las figuras 1 y 2. En la tabla 2, se presenta un resumen de los principales indicadores estadísticos por fase y promedio para el factor K y la distorsión armónica total en corriente.

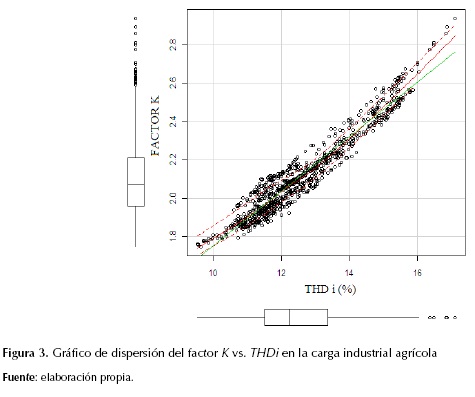
Para el ajuste de los modelos de regresión lineal se utilizan como variable independiente la distorsión armónica total en corriente promedio (THDi en la ecuación de los modelos) y como variable dependiente se usa el factor K promedio (K en la ecuación de los modelos). Usando el software de distribución libre R (R Development Core Team, 2011), específicamente el paquete Rcmdr, se obtuvieron las gráficas de dispersión y los resultados analíticos de los modelos. Por otro lado, la figura 3 muestra la dispersión de las variables factor K vs. THDi y la tabla 3 describe el desempeño de cada modelo de regresión.

De la tabla 3, se puede apreciar que el mayor valor de R² y el menor valor del AIC se obtienen con el modelo polinomial de orden 3. La ecuación 12 muestra el modelo polinomial de orden 3 que resulta ser el más adecuado para estimar el valor del factor K a partir de la distorsión armónica total en corriente en la carga industrial agrícola.

Utilizando la ecuación 12 se pueden obtener los siguientes resultados:

Cuando K=1, THDi = 5,36 %, es decir, el transformador actual (y que tiene factor K igual a 1) es capaz de soportar un contenido de distorsión armónica total en corriente no superior a 5,36 %. Sin embargo, de la tabla 2 se puede apreciar que los valores medio de THDi (12,54 %) y mínimo de THDi (8,90 %) son siempre mayores que el valor máximo que puede manejar este transformador de distribución. Ahora bien, si THDi=12,54 %, entonces K= 2,14; por tanto, y según lo indicado en la tabla 1, es recomendable reemplazar el transformador actual por otro de distribución con factor K igual a 4. Cuando K=4, THDi=19,86 %, lo que significa que al alimentar la carga agrícola con un transformador de distribución de factor K igual a 4, es posible manejar un 19,86 % de distorsión armónica total en corriente en la carga, valor superior a los valores medios y máximos de THDi de cada fase.

Análisis de carga industrial minera

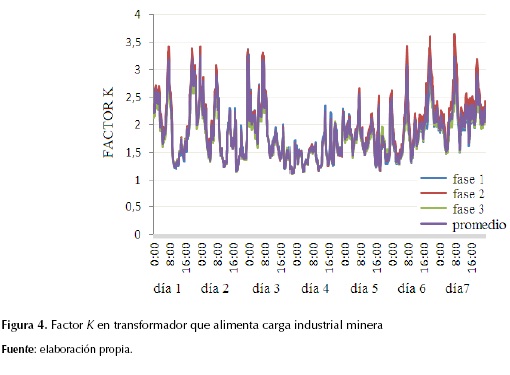
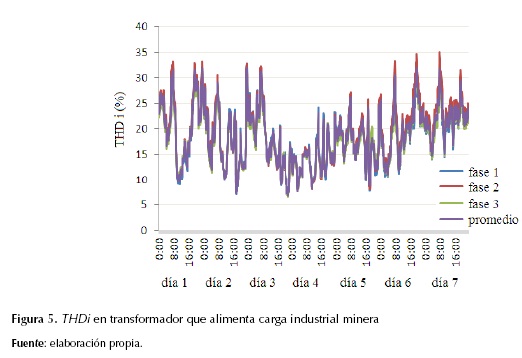
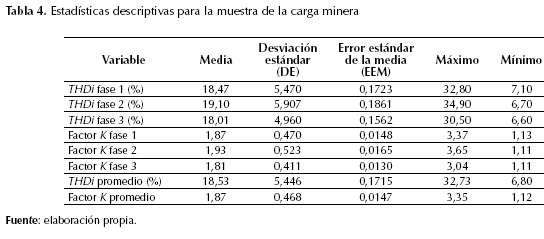
Para estudiar el transformador de distribución que alimenta la carga minera se registraron, cada diez minutos durante siete días consecutivos, las variables factor K y distorsión armónica total en corriente, usando un equipo analizador de calidad de energía. Los resultados de estos registros se pueden apreciar en las figuras 4 y 5. En la tabla 4 se presenta un resumen de los principales indicadores estadísticos por fase y promedio para el factor K y la distorsión armónica total en corriente.

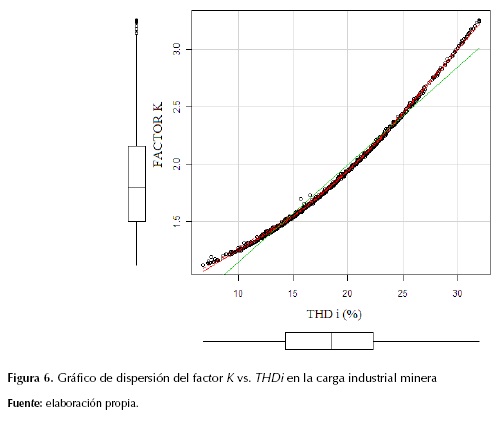
La figura 6 muestra la dispersión de las variables factor K vs. THDi y la tabla 5 describe el desempeño de cada modelo de regresión.

De la tabla 5, se puede apreciar que el mayor valor de R² y el menor valor del AIC se obtienen con el modelo polinomial de orden 3. Sin embargo, estos indicadores son muy similares en el modelo polinomial de orden 2. Por consiguiente, por su rendimiento y simplicidad se elige este modelo como el más adecuado para estimar el valor del factor K a partir de la distorsión armónica total en corriente en la carga industrial minera. La ecuación 13 muestra el modelo polinomial de orden 2.

Utilizando la ecuación 13 se pueden obtener los siguientes resultados:

Cuando K=1, THDi = 3,2 %, es decir, el transformador actual (y que tiene factor K igual a 1) es capaz de soportar un contenido de distorsión armónica total en corriente no superior a 3,2 %. Sin embargo, de la tabla 4 se puede apreciar que los valores medio de THDi (18,53 %) y mínimo de THDi (6,80 %) son siempre mayores que el valor máximo que puede manejar este transformador de distribución. Ahora bien, si THDi=18,53%, entonces K= 1,80, por tanto, y según lo indicado en la tabla 1, es recomendable reemplazar el transformador actual por un transformador de distribución con factor K igual a 4. Cuando K=4, THDi=37,4 %, lo que significa que al alimentar la carga minera con un transformador de distribución de factor K igual a 4, es posible manejar un 37,4 % de distorsión armónica total en corriente en la carga, valor superior a los valores medios y máximos de THDi de cada fase.

Conclusiones

En este artículo se mostró el uso de los modelos de regresión lineal como herramienta para estimar el valor de factor K en transformadores de distribución, a partir de la distorsión armónica total en corriente como variable independiente. Se probaron dos transformadores de distribución provenientes de la industria agrícola y minera. Ambos transformadores poseen factor K igual a 1. Se observó que los modelos polinomiales entregaron mejor rendimiento que el modelo de regresión lineal. Al estimar el factor K utilizando los modelos polinomiales se determinó que los transformadores estudiados no pueden soportar la distorsión armónica total en corriente de sus cargas actuales. El factor K adecuado para los transformadores estudiados debe ser 4. Este factor permite que los transformadores soporten la distorsión armónica total en corriente de sus respectivas cargas. Por último, se indica que el método mostrado en este estudio puede ser aplicado en empresas de distribución eléctrica que tengan instalados en sus alimentadores transformadores de distribución con factor K igual a 1, para evaluar el reemplazo de estos equipos y contribuir con la disminución de las pérdidas técnicas y la mejora en la calidad del suministro.

Financiamiento

Este trabajo fue financiado por el proyecto DIUDA 22275 de la Vicerrectoría de Investigación y Postgrado de la Universidad de Atacama Chile.

Referencias

Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716-723.

Arrillaga, J. y Watson N.R. (2003). Power system harmonics. Londres: John Wiley & Sons.

Attia, H.A.; El-Metwally, M. y Fahmy O.M. (2010). Harmonic Distortion Effects and Mitigation in Distribution Systems. Journal of American Science, 6(10), 173-183.

Daut, I.; Syafruddin, H.S.; Rosnazri, A.; Samila, M. y Haziah H. (2006). The Effects of Harmonic Components on Transformer Losses of Sinusoidal Source Supplying Non-Linear Loads. American Journal of Applied Sciences, 3(12), 2131-2133.

Davudi, M.; Torabzad, S. y Ojaghi B. (2011). Analysis of Harmonics and Harmonic Mitigation Methods in Distribution Systems. Australian Journal of Basic and Applied Sciences, 5(11), 996-1005.

Faiz, J.; Sharifian, M.B.B.; Fakheri, S.A. y Sabet-Marzooghi, E. (2004). Derating of distribution transformers for non-sinusoidal load currents using finite element method. Iranian Journal of Science And Technology, 28(3), 315-322.

Gouda O., E.; Amer, G.M. y Salem, W.A.A. (2011). A Study of K-Factor Power Transformer Characteristics by Modeling Simulation. Engineering, Technology & Applied Science Research, 1(5), 114-120.

IEEE. (1998). IEEE Recommended Practice for Establishing Transformer Capability When Supplying Non-sinusoidal Load Currents. IEEE Std C57.110-1998. http://doi.org/10.1109/IEEESTD.1998.89206.

Montgomery, D.; Peck E. y Vining, G. (2006). Introducción al análisis de regresión lineal. México: Limusa Wiley.

R Development Core Team (2011). R: A Language and Environment for Statistical Computing. Viena, Austria: The R Foundation for Statistical Computing. Recuperado de: http://www.R-project.org/.

Verma, M.K.; Kaushik, R.; Prabhakar, P. y Sengupta, M.K. (2014). Analysis of K-Rated Transformer to Make it Suitable to Handle The Harmonics Generated by Solid State Devices on The Load Side. International Journal of Emerging Technology and Advanced Engineering, 4(9), 508-514.

Yagci, M. y Ürkmez, A. (2011). The effects of linear and non-linear load son three-phase transformers supplied from different sources. Scientific Research and Essays, 6(26), 5513-5522.