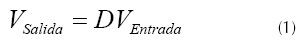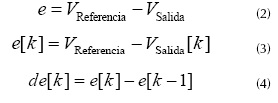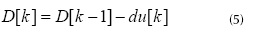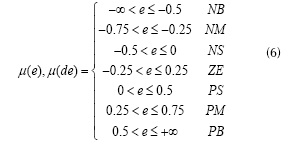Control difuso aplicado a un convertidor DC-DC buck para una carga no lineal

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.2.a10

Control difuso aplicado a un convertidor DC-DC buck para una carga no lineal

Buck DC DC converter using fuzzy logic control for no linear load

Rubén Darío Bonilla Isaza¹

¹ Ingeniero Electricista y magíster en Ingeniería de Automatización Industrial. Docente de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: rdbonillai@udistrital.edu.co

Fecha de recepción: 21 de noviembre de 2015 Fecha de aceptación: 15 de febrero de 2016

Cómo citar: Bonilla Isaza, R. D. (2016). Control difuso aplicado a un convertidor DC-DC buck para una carga no lineal. Revista Tecnura, 20(48), 117-148. http://doi.org/10.14483/udistrital.jour.tecnura.2016.2.a10

Resumen

Contexto: Este artículo presenta un sistema matemático llamado lógica difusa como técnica de control para mejorar el desempeño de un convertidor DC-DC (Buck) ante variaciones de cargas de no lineales.

Método: Para ello se construyó por medio de Simulink MATLAB un convertidor DC-DC de lazo cerrado al cual se le colocó en serie un controlador basado en lógica difusa, con entradas de control de señal de voltaje de salida y de la derivada del voltaje y como salida un valor constante que sintoniza el ciclo útil de un modulador de pulsos (PWM), que luego ajustar la tensión de salida del controlador de acuerdo a una referencia deseada. El controlador difuso fue construido con funciones de pertenencia en las que se integraron variables lingüísticas que explican cuándo un valor de voltaje de salida debe corregirse y cuándo la variación del voltaje se sale de los rangos establecidos entre -1 y 1 por ciento de variación permitida.

Resultados: Para evaluar el desempeño de este tipo de control se compara con un convertidor DC-DC con control de lazo cerrado de ganancia unitaria obteniendo un 40% de mejora en la integral de área respecto al controlador difuso con un tiempo de estabilización del orden de 0.01s. En las cargas no lineales existen fenómenos aleatorios o efectos indeseados propios de la resonancia del circuito por lo cual se emuló mediante la interrupción por ciclos de un interruptor controlado por tiempo.

Palabras clave: carga no lineal, convertidor Buck, ciclo útil, funciones de pertenencia, lógica difusa.

Abstract

Background: This paper presents a mathematical system called fuzzy logic as a control technique to improve the performance of a DC-DC converter (Buck) to changes in non-linear loads.

Method: Through Simulink MATLAB was built a DC-DC converter of closed loop, which is placed in series with a controller based on fuzzy logic. The control inputs are the voltage signal and its derivative, and the output is a constant value, which tunes the duty cycle of a pulse modulator (PWM). This adjust the output of voltage of the controller according to a desired reference. The fuzzy controller was built with membership functions in which linguistic variables that explain when a value of output of voltage must be corrected and when the voltage variation is out of the established ranges between -1 and 1 percent of allowable variation were integrated.

Results: To evaluate the performance of this type of control compared to a DC-DC converter with control of closed loop of unity gain, obtaining a 40% improvement in the integral of area regarding the fuzzy controller, with a stabilization time of 0.01s. In non-linear loads, there are random phenomena or own unwanted effects of resonance circuit, then was emulated by interrupting cycles of a time-controlled switch.

Keywords: nonlinear load, Buck converter, duty cycle, membership functions, fuzzy logic.

Introducción

La creciente demanda de tecnología ha desarrollado una carrera contra reloj para la cual los dispositivos que son más eficientes y con mayores prestaciones tendrán el éxito esperado. Una de las ventajas competitivas radica en la forma en que se controlan los procesos para los cuales están diseñados estos dispositivos. Un ejemplo actual, pero que lleva bastante tiempo implementado, son las fuentes conmutadas, las cuales se utilizan en la mayoría de los elementos de tecnología actuales, tales como TV, DVD, Smartphone entre otros. Estos dispositivos cuentan con fuentes de diferentes tipos, llamados también convertidores, con modelo de conversión DC-DC (corriente directa), AC-DC (corriente alterna) y AC-AC (corriente alterna).

Las fuentes conmutadas que usan estos principios de funcionamiento alimentan cargas de todo tipo, motivo por el cual los convertidores están sujetos a fenómenos aleatorios en las cargas no lineales o efectos indeseados propios de la resonancia del circuito (Collin, 2013). Este efecto hace que las tensiones ideales a las que fueron diseñados se vean afectadas por los comportamientos antes mencionados. Para evitar esto se realiza un control de alguna variable que afecte directamente el circuito (Asumadu & Ho, 2004). Un ejemplo, para fuentes conmutadas es la tensión de salida del convertidor donde se conecta la carga se utiliza la información que se obtiene debido a las variaciones no lineales de la carga para diseñar un control y así garantizar un error mínimo en la tensión de salida.

Una pregunta surge en este punto: ¿Qué método lograría realizar el control que permita eliminar los efectos no lineales y aleatorios de las cargas que alimenta?, y si se encuentra un método, ¿es este eficiente? Para responder la primera pregunta se requiere de investigaciones previas, las cuales se hayan enfocado en qué técnicas pueden servir para el control. La segunda se determina realizando una correlación en dos posibles escenarios. Uno de ellos, el convertidor DC-DC sin ninguna técnica de control, y otro usando una propuesta de control.

En este artículo se evaluó el método mediante lógica difusa como técnica de control para evaluar el desempeño de un convertidor DC-DC (buck) ante variaciones de cargas no lineales simulado mediante el software MATLAB.

CONVERSOR DC-DC

Los conversores DC-DC son el resultado de la conmutación en semiconductores que los hacen eficientes y económicos (Rashid, González, & Fernández, 2004). En general, como se deduce de su nombre, son dispositivos que transforman una señal de corriente continua (DC) a otra señal regulada de mayor o menor valor de corriente continua (DC). Debido a su salida regulada los conversores DC-DC también son conocidos como reguladores de conmutación (Dash & Nayak, n.d.).

Las aplicaciones académicas e industriales de los conversores son amplias por su rápida respuesta dinámica. La clasificación de los conversores es debida a los niveles de tensión de salida con respecto a la entrada, generalmente se clasifican en tres grupos (Rashid, González y Fernández, 2004):

• Conversores DC-DC reductores (buck converter): Permiten obtener en la salida una tensión menor a la señal de tensión de entrada, se conocen como conversores buck.
• Conversores DC-DC elevadores (boost converter): Permiten obtener en la salida una tensión mayor a la señal de tensión de entrada, se conocen como conversores boost.
• Conversores DC-DC reductores-elevadores: Permiten obtener en la salida una tensión mayor o menor a la señal de tensión de entrada, se conocen como conversores buck-boost, flyback y cuk.

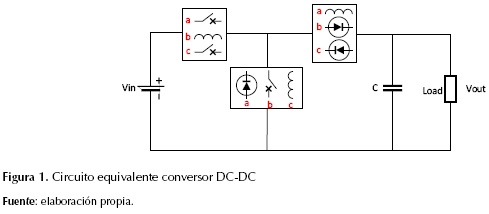
El circuito equivalente de un conversor DC-DC está compuesto por elementos activos y elemento pasivos como se muestra en la figura 1 (Elmas, Deperlioglu y Sayan, 2009), la cual ilustra cada una de las configuraciones según el tipo de conversor a implementar. Para los elementos identificados con la letra a el circuito equivalente corresponde a un conversor DC-DC buck; los elementos identificados con la letra b corresponden a un conversor DC-DC boost; y por citar un ejemplo reductor-elevador, los elementos identificados con la letra c corresponden a un conversor DC-DC buck-boost. La carga generalmente y con el objetivo de realizar el desarrollo analítico se puede modelar netamente resistiva o a partir de un modelo en serie RL.

Variables de control en un convertidor DC-DC

Un convertidor DC-DC transforma una tensión DC en otra de la misma naturaleza mediante el ajuste del ciclo útil (Dash & Nayak, n.d.). El buck, en modo continuo, es un convertidor cuya salida de tensión depende exclusivamente del ciclo útil y de la tensión de entrada (Ramot, Friedman, Langholz y Kandel, 2003; Dash y Nayak, s.f.). La relación está dada por la ecuación 1.

Donde V_salida es la tensión de salida, V_entrada es la tensión de entrada de la alimentación y D es el ciclo útil, variando 0 ≤D≤1 y para D= 0 se considera circuito abierto y D= 1 circuito cerrado.

En un convertidor DC-DC tipo buck el valor del ciclo útil se ajusta para que la tensión de salida se establezca de acuerdo con el valor de diseño que se desea (Rashid, González y Fernández, 2004). Sin embargo, al conectar una carga con la que se puede alimentar un sistema, la tensión de salida se ve afectada por el efecto mismo de la carga que se conectó (Collin, 2013). Una forma de controlar la tensión de salida dado la perturbación de la carga consiste en ajustar de forma dinámica el ciclo útil. Variar el ciclo útil a medida que la carga va exigiendo corriente al convertidor es una forma simple de lograrlo; otra manera consiste en controlar el sistema mediante la corriente que le exige la carga al convertidor; un método más complejo radica en controlar la corriente del inductor y la tensión de salida del convertidor.

FUZZY LOGIC

La lógica difusa (fuzzy logic) es una técnica matemática que permite plantear proposiciones de tipo lógico para caracterizar estados o escenarios definidos (lógica multivaluada). Respecto a la lógica binaria que establece relaciones absolutas ante un escenario ("hace calor" o "hace frío"), la lógica difusa puede establecer más estados diferentes a referencias meramente absolutas. En el mundo actual la lógica binaria funciona muy bien para los computadores, sin embargo, al intentar solucionar problemas que requieren lógica humana, se queda corta. La lógica difusa ha mostrado buenos resultados en la caracterización y resolución de problemas que con técnicas tradicionales no podían ser resueltos (Ramot, Friedman, Langholz y Kandel, 2003). Es una técnica heurística que está sujeta al diseño de la persona que desea estudiar el problema. El mismo diseñador plantea los estados y pone sus límites y restricciones. El buen entendimiento del problema, generará buena definición de reglas en la lógica difusa (Maussion y Hissel, 1998).

Las reglas son las funciones matemáticas que explican cuándo un escenario se está presentando y, por tanto, deben realizarse las tareas correspondientes. Una función de pertenencia asigna un dominio para la cual las condiciones ocurren.

Funciones de pertenencia

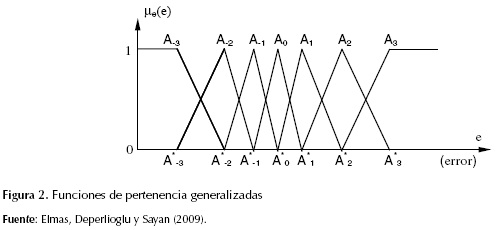
En la figura 2 se muestran funciones de pertenencia para cada intervalo en el dominio del error de un fenómeno particular. Decir que la función de pertenencia que va desde A-3 hasta A-2 y A-1 es mencionar que existen condiciones en el dominio para las cuales una función existe (Dash y Nayak, s.f.).

Cálculo del error

El error que se desea estimar es el error relativo, donde la referencia es el punto de control calculado con los parámetros del ciclo útil ajustados (Elmas, Deperlioglu y Sayan, 2009). La ecuación 2 muestra cómo se calcula en error para un sistema continuo. Debido a la discretización de la simulación en MATLAB, la ecuación 3 muestra el modo de calcular el error. En la ecuación 4 se observa también cómo se calcula la derivada del error por unidad de tiempo de simulación.

Ciclo útil

Para un convertidor tipo buck en modo continuo, el ciclo útil es la relación D cuyo dominio se encuentra entre 0 y 1, y cuyo voltaje de salida nunca superará el voltaje de entrada (ecuación 1). Para ajustar el ciclo útil sin metodologías basadas en técnicas de control, se incorpora al circuito un modulador de ancho de pulso al interruptor conectado en serie a la fuente, el ciclo útil se ajusta con la frecuencia de conmutación del PWM (Patin, 2015; Siano y Citro, 2014).

Por otro lado, la relación lineal entre el voltaje de salida y el voltaje de entrada indica que ajustando adecuadamente el ciclo útil se puede lograr un control apropiado ante variaciones en el voltaje de salida cuando existe carga en el convertidor.

El ajuste del nuevo ciclo útil después de cuantificado el error, en forma discreta, está dada por la ecuación 5.

Diversos trabajos se han desarrollado en el área de conversores y la implementación de algoritmos de fuzzy logic como estrategia de control no es algo nuevo.

Maussion y Hissel (1998) obtienen resultados preestablecidos de un control lógico difuso (sintonización) utilizando el criterio de AIE (error de integral absoluto) aplicado a un conversor DC-DC y un PMSM, asumiendo una carga lineal con lazo abierto. Las entradas de realimentación del fuzzy logic son la tensión de salida del convertidor y la derivada del error de tensión. En este trabajo se realiza una correlación entre un control PID a lazo abierto y un controlador fuzzy logic más PID. En general, este artículo presenta la información del estado inicial del conversor DC-DC con cargas lineales a lazo abierto.

Mattavelli, Rossetto, Spiazzi y Tenti (1997) muestran las potencialidades de implementar un controlador fuzzy logic en convertidores tipo buck, boost y sepic. Este trabajo menciona los modelos de control para convertidores, las variables a controlar y de cuáles variables se puede obtener información relevante para la sintonización control. Se debe recordar que la salida de tensión de un convertidor DC-DC depende de la tensión de entrada y del parámetro de ciclo útil definido en el PWM. Utilizan un controlador fuzzy logic con tres variables de control de entrada entre las que se destacan: corriente en el elemento almacenador de energía, tensión de salida y derivada de la tensión de salida para una carga lineal resistiva. Este tipo de estrategias de control pueden ser implementadas en hardware, como Gupta, Boudreaux, Nelms y Hung (1997) que utilizan un microcontrolador de 8 bits para diseñar un controlador lógico difuso. Elmas, Deperlioglu y Sayan (2009) utilizan reglas sencillas y generales, para permitirles a las personas con bajo conocimiento en el funcionamiento de convertidores DC-DC modificarlos. Este artículo toma esas reglas lingüísticas sencillas para definir las funciones de pertenencia del controlador lógico difuso. Govindaraj y Rasila (2010) muestran dos modelos para hacer control de ciclo útil del controlador DC-DC mediante realimentación a la salida del controlador difuso; la otra opción es mediante la realimentación de la salida de la tensión de salida del convertidor.

Bajo esta descripción, las investigaciones son diversificadas y recientes (Siano y Citro, 2014), sin embargo, cada autor propone técnicas de control para cargas resistivas. El objetivo de este documento es presentar los resultados obtenidos ante variaciones de cargas no lineales utilizando lógica difusa como técnica de control.

Metodología

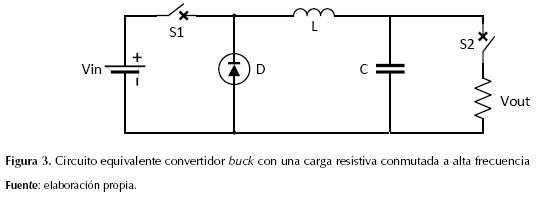
El presente documento utiliza como estudio de caso el conversor DC-DC buck y se modela la carga como una resistencia conmutada a alta frecuencia como se muestra en la figura 3 (Collin, 2013). El objetivo de la conmutación de la carga es introducir armónicos al sistema, aunque por ser un circuito basado en dispositivos semiconductores el conversor DC-DC es además una fuente de armónicos. La conmutación de la carga permite modelar una carga que sea no lineal y además al ser una carga de baja impedancia el circuito presenta variaciones en los niveles de tensión establecidos por el factor de conversión.

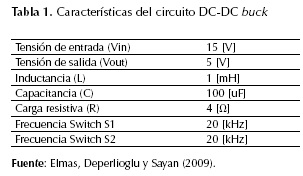
La tabla 1 muestra los valores nominales de diseño para el circuito equivalente de la figura 3.

Fuzzy logic

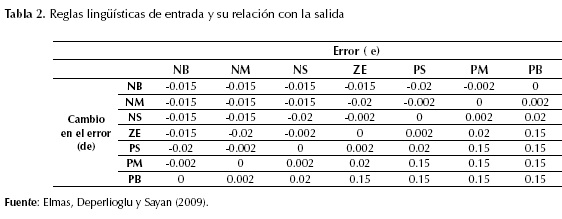
Con las reglas de pertenencia propuestas por Elmas, Deperlioglu y Sayan (2009) se plantea el control mediante el Fuzzy Logic Toolbox de MATLAB. Se utilizan dos entradas, las cuales son: el error, que se calcula restando la salida de tensión del convertidor buck del valor de referencia de tensión que se desea controlar, y la derivada del error, que se calcula aplicando el operador derivada, con una salida que denota los limites en los cuales el control debe actuar, dadas las condiciones que se establecen en la entrada del controlador lógico difuso. Las proposiciones de entrada caracterizadas por Elmas, Deperlioglu y Sayan (2009) permiten establecer relaciones entre las dos entradas y la salida. Esta caracterización se muestra en la tabla 2.

Donde NB (negative big: muy negativo), NM (negative médium: negativo medio), NS (negative small: poco negativo), ZE (zero: error cero), PS (positive small: poco positivo), PM (positive medium: positivo medio), PB (positive big: muy positivo) son las variables lingüísticas que fueron caracterizadas para el error y la derivada del error. Los valores numéricos que se encuentran en la tabla 2 y que relacionan dos posibles estados de la entrada, dan cuenta de cómo debería ser la salida cuando estas dos condiciones mencionadas ocurren.

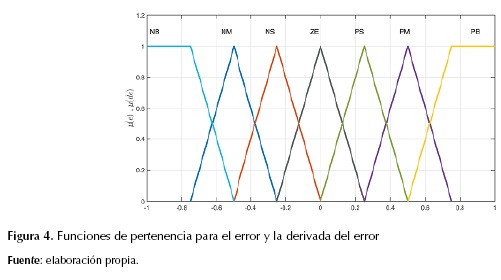
Por otro lado, las funciones de pertenencia definidas para cada una de las entradas, del error y la derivada del error, se muestran en la figura 4.

Ya que las variables lingüísticas fueron declaradas según intervalos numéricos, donde el error y la derivada del error pueden encontrarse (Elmas, Deperlioglu y Sayan, 2009), la ecuación 6 contiene los intervalos que se consideran las variables lingüísticas.

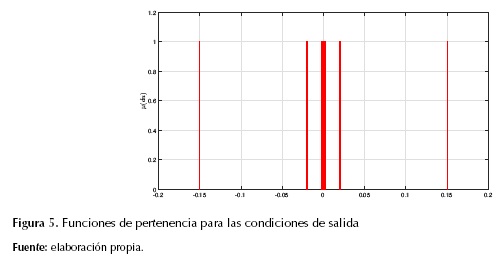
Para la función de pertenencia de salida se hallan los centroides en la intersección de las diferentes regiones formadas por las funciones de pertenencia de error y la derivada del error. La función de pertenencia de salida se muestra en la figura 5.

Con el modelo del caso de estudio y la parametrización de las funciones de pertenencia se diseñan los bloques adicionales que se requieren para el sistema de control.

Sistema de control

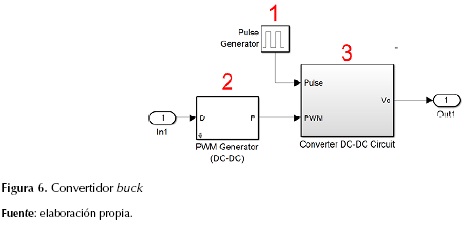
El control que se implementa mediante lógica difusa es de lazo cerrado, puesto que se toma la señal de salida para realimentar el controlador y así reajustar el ciclo útil, corrigiendo así la tensión de salida según la referencia deseada (Patin, 2015; Vindhya y Reddy, 2013). En la figura 6 se observa el convertidor DC-DC, compuesto por:

El bloque pulse generator, que sirve para simular la no linealidad de la carga que se colocó a la salida del convertidor buck.

1. El PWM Generator, que ajusta el parámetro de frecuencia de conmutación y adicionalmente se puede ajustar el ciclo útil según los parámetros que se requieran, en este caso, la variable a controlar.
2. La salida Vo, que se puede observar una rama que se utiliza para calcular el error.

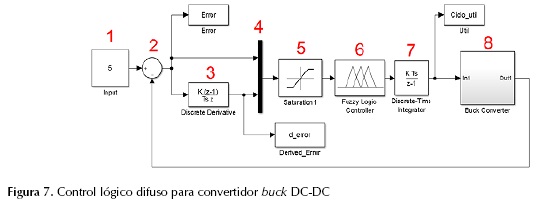
En la figura 7 se observa el sistema de control de lazo cerrado, y está compuesto por:

1. El bloque constante que representa el punto de operación el cual es la referencia ideal del convertidor buck.
2. El bloque de suma realiza la operación matemática para el cálculo del error.
3. El bloque de derivador discreto calcula la derivada del error que se requiere para la segunda entrada del bloque de lógica difusa.
4. El nodo de multiplexado que se usará para conmutar la única entrada que tiene el control de lógica difusa.
5. El bloque de saturación que se usará para definir los límites de las funciones de pertenencia.
6. El bloque de lógica difusa en el cual contiene las funciones de pertenencia.
7. Por último, como se obtiene la razón de cambio del ciclo útil se requiere realizar la integración correspondiente, la cual está en el bloque de integración discreta.

Resultados

El circuito de potencia se implementa utilizando los bloques de SimuLink que permitan realizar la simulación de circuitos eléctricos, para el control fuzzy logic se utiliza el toolbox de MATLAB que además cuenta con un bloque en SimuLink.

Conversor DC-DC Buck

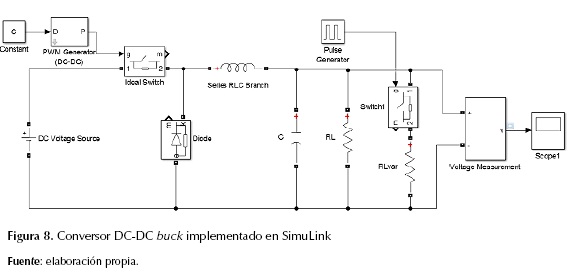
El circuito del conversor DC-DC Buck se muestra en la figura 8, cada uno de los elementos eléctricos es tomado de la librería SimRF y el simple time del bloque Powergui es ajustado para un Ts=1 us. Los interruptores utilizan bloques de la librería de Power Electronics del Simscape.

Como se muestra en el circuito de la figura 6, el conversor caso de estudio cuenta con dos interruptores, el primero se conecta en serie a la fuente de tensión de entrada y el segundo se conecta en serie a la carga; ambos interruptores son controlados por señales de entrada, el primero por una señal de modulación de ancho de pulso (PWM), señal que será ajustada por el algoritmo de lógica difusa; el segundo se controla por un generador de pulsos con un ancho de pulso del 50 %.

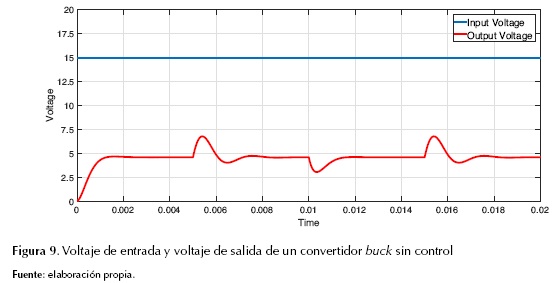
En la figura 9 se muestra la forma de onda para la señal de entrada y salida del circuito de la figura 3; la tensión DC de entrada presenta un modelo ideal sin ningún tipo de interferencia, ajustada según las características del circuito DC-DC buck mostradas en la tabla 1. La tensión de salida muestra el efecto transitorio de carga y descarga de los elementos pasivos del circuito; la tensión corresponde a un valor cercano al valor esperado de salida de la tabla 1; su valor no coincide con exactitud a los 5 V ya que para el circuito de la figura 3 se tienen en cuenta factores reales como la resistencia de amortiguación de los interruptores, resistencia interna de los interruptores y la resistencia del diodo, elementos que permiten ser parametrizados por cada uno de los bloques de SimuLink y que corresponden a pérdidas en el sistema.

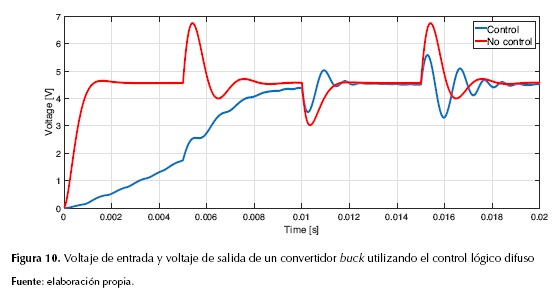
En la figura 10 se observan los resultados cuando se implementa el control mediante lógica difusa, usando las configuraciones que se mencionaron en las figuras 6 y 7.

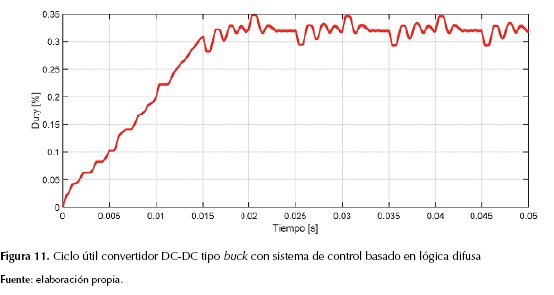
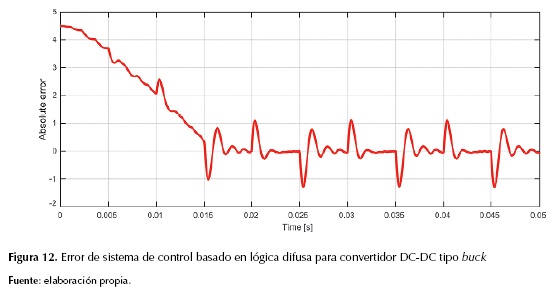
Para el modelo sin etapa de control, el circuito se sintoniza para un ciclo útil de 0.3. La figura 11 muestra el ciclo útil del sistema cuando se utiliza fuzzy logic como técnica de control; el valor máximo corresponde al 0.35 y el valor mínimo evaluado en la zona de estabilidad corresponde al 0.28. La figura 12 presenta el comportamiento del error para el tiempo de simulación establecido, como se observa en la figura 11 para instantes de tiempo superior a los 15 ms el error oscila entre -1 y 1.

Conclusiones

Un convertidor tipo buck en modo continuo presenta una relación lineal entre la tensión de salida y la tensión de entrada mediante la constante de proporcionalidad llamada ciclo útil. Este parámetro permite realizar un control simple que permite llevar el error a cero; sin embargo, puede que este no se acerque a cero dado la condición de cambio de energía de la inductancia. Podría plantearse una segunda salida de control utilizando la corriente de la inductancia para ajustar el ciclo útil de la misma forma, creando otra función de pertenencia en el controlador lógico difuso.

Para el modelo sin etapa de control, el circuito se sintoniza para una relación de ciclo útil de 0.3, esto indica que para una tensión de entrada de 15 V la salida correspondiente es de 5 V. La figura 11 muestra el ciclo útil del sistema cuando se utiliza lógica difusa como técnica de control, el valor máximo corresponde al 0.35 y el valor mínimo evaluado en la zona de estabilidad corresponde al 0.28, el valor esperado del ciclo útil para la relación 15V / 5V está contenido entre el valor mínimo y máximo del sistema con control, en términos de la variable de salida, indica que el convertidor con etapa de control tiene una salida entre 4.3 V y 4.6 V.

El error absoluto obtenido al restar la salida de tensión del convertidor buck con el valor de referencia de tensión que se desea controlar, para instantes de tiempo superior a los 15 ms oscila entre -1 y 1, esto sustenta el rango del ciclo útil obtenido.

Referencias

Asumadu, J.A. y Ho, E. (2004). A Multivariable Fuzzy Logic Controller (MFLC) for a Buck DC-DC converter. Power Electronics Specialists Conference. PESC 04. 2004 IEEE 35th Annual. Recuperado de: http://doi.org/10.1109/PESC.2004.1355141.

Collin, A.J. (2013). Advanced load modelling for power system studies.

Dash, S.S. y Nayak, B. (s.f.). Control Analysis and Experimental Verification of a Practical DC-DC Boost Converter. Journal of Electrical Systems and Information Technology. http://doi.org/http://dx.doi.org/10.1016/j.jesit.2015.08.001.

Elmas, C.; Deperlioglu, O. y Sayan, H.H. (2009). Adaptive Fuzzy Logic Controller for DC-DC Converters. Expert Systems with Applications, 36(2), 1540-1548. Recuperado de: http://doi.org/http://dx.doi.org/10.1016/j.eswa.2007.11.029.

Govindaraj, T. y Rasila, R. (2010). Development of Fuzzy Logic Controller for DC-DC Buck Converters. International Journal of Engineering Techsci, 2(2), 192-198.

Gupta, T.; Boudreaux, R.R.; Nelms, R.M. y Hung, J.Y. (1997). Implementation of a Fuzzy Controller for DC-DC Converters Using an Inexpensive 8-b Microcontroller. Industrial Electronics, IEEE Transactions on. http://doi.org/10.1109/41.633467.

Mattavelli, P.; Rossetto, L.; Spiazzi, G. y Tenti, P. (1997). General-Purpose Fuzzy Controller for DC-DC Converters. Power Electronics, IEEE Transactions on. http://doi.org/10.1109/63.554172

Maussion, P. y Hissel, D. (1998). Optimized Fuzzy Logic Controller Parameters for Open-Loop Stable or Evolutive Electromechanical Systems. Industrial Electronics Society, 1998. IECON '98. Proceedings of the 24th Annual Conference of the IEEE. http://doi.org/10.1109/IECON.1998.723938

Patin, N. (2015). 2-DC/AC Converters BT-Power Electronics Applied to Industrial Systems and Transports. Vol. 2 (pp. 35-100). Elsevier. http://doi.org/http://dx.doi.org/10.1016/B978-1-78548-001-0.50002-2

Ramot, D.; Friedman, M.; Langholz, G. y Kandel, A. (2003). Complex fuzzy logic. Fuzzy Systems, IEEE Transactions on. http://doi.org/10.1109/TFUZZ.2003.814832

Rashid, M.H.; González, M.H.R.V. y Fernández, P.A.S. (2004). Electrónica de potencia: circuitos, dispositivos y aplicaciones. Pearson Educación.

Siano, P. y Citro, C. (2014). Designing Fuzzy Logic Controllers for DC-DC Converters Using Multi-Objective Particle Swarm Optimization. Electric Power Systems Research, 112, 74-83. http://doi.org/http://dx.doi.org/10.1016/j.epsr.2014.03.010.

Vindhya, V. y Reddy, V. (2013). PID-Fuzzy Logic Hybrid Controller for a Digitally Controlled DC-DC Converter. Green Computing, Communication and Conservation of Energy (ICGCE), 2013 International Conference on. http://doi.org/10.1109/ICGCE.2013.6823461.