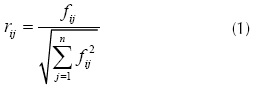Priorización de despachos con AHP difuso y Topsis

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2017.2.a08

Priorización de despachos con AHP difuso y Topsis

Dispatch prioritization using fuzzy AHP and Topsis

María Isabel Hernández Santibáñez¹, Luisa Fernanda Giraldo Correa², Lizeth Alejandra Gaviria Ramírez³, Ángela María Wilches David⁴, Juan Carlos Osorio Gómez⁵

¹ Ingeniera industrial, Universidad del Valle. Cali, Colombia. Contacto: maria.hernandez@correounivalle.edu.co

² Ingeniera industrial, Universidad del Valle. Cali, Colombia. Contacto: luisa.giraldo@correounivalle.edu.co

³ Ingeniera industrial, Universidad del Valle. Cali, Colombia. Contacto: lizeth.gaviria@correounivalle.edu.co

⁴ Ingeniera industrial, Universidad del Valle. Cali, Colombia. Contacto: angela.wilches@correounivalle.edu.co

⁵ Ingeniero industrial, especialista en Logística, magíster en Ingeniería Industrial. Profesor Titular de la Universidad del Valle. Cali, Colombia. Contacto: juan.osorio@correounivalle.edu.co

Fecha de recepción: 16 de agosto de 2016 Fecha de aceptación: 15 de febrero de 2017

Cómo citar: Hernández S., M.I.; Giraldo C. L.F.; Gaviria R., L.A.; Wilches D., A.M. y Osorio G., J.C. (2017). Priorización de despachos con AHP difuso y Topsis. Revista Tecnura, 21(52), 102-110. doi: 10.14483/udistrital.jour.tecnura.2017.2.a08

Resumen

Contexto: La limitación de recursos en las organizaciones a la hora de realizar los despachos de producto terminado, desde los centros de producción hacia las zonas de consumo, hace que sea importante definir con claridad las prioridades, de manera que dichos recursos puedan utilizarse eficientemente y garanticen los más altos niveles de satisfacción a los clientes. 

Método: En este sentido, se ha desarrollado una propuesta para priorizar los despachos de producto terminado desde un centro de distribución hacia n bodegas que involucra las herramientas multicriterio AHP difuso y Topsis. La propuesta permite definir una serie de criterios a considerar a la hora de realizar los despachos y, mediante la herramienta AHP difuso, ponderar dichos criterios dado que no todos tienen la misma importancia a la hora de tomar la decisión. Por otro lado y considerando que cada punto de destino posee unos valores diferentes de dichos indicadores se utiliza el Topsis para generar un ranking que permita establecer la prioridad a la hora de los despachos.

Resultado: La metodología propuesta ha sido aplicada en un caso de estudio y se ha encontrado que permite realizar la priorización de los despachos de manera que las bodegas más importantes, según el conjunto de criterios establecidos, son las primeras que deben ser atendidas.

Conclusiones: Esta metodología puede ser replicable a cualquier organización siempre y cuando se cuente con las personas involucradas y la claridad frente a los objetivos organizacionales de la compañía.

Palabras clave: distribución física de mercancías, logística, toma de decisiones, transporte terrestre.

Abstract

Context: The organizations present a limitation in resources when making finished product shipments from the product centers to the areas of consumption. This limitation makes it important to clearly define priorities so that those resources can be used efficiently and ensure high levels of customer satisfaction.

Method: We developed a proposal to prioritize the shipments of finished product from a distribution center to n warehouses. It involves the fuzy AHP and Topsis multi-criteria tools. The Fuzzy AHP tool allows defining a series of important criteria when making the dispatches. Additionally, it allows weighing these criteria since not all have the same importance when making the decision. Finally, we used Topsis to generate a ranking that allows us to establish the priority of dispatches, considering that each destination warehouse has different values for those criteria.

Results: The proposed methodology was applied to a case study. We found that it prioritizes the dispatches so that the most important warehouses, according to the set of established criteria, are the first to be met.

Conclusions: The proposed methodology can be replicated in different contexts and for any organization as long as there are people involved and the objectives of the of the company are clear.

Keywords: decision making, Land transportation, Logistic, Physical distribution of goods.

INTRODUCCIÓN

Según Bravo, Osorio y Orejuela (2009) se puede encontrar en la literatura una gran cantidad de investigaciones que consideran el problema de atender a los clientes ágilmente con un transporte eficiente y oportuno; sin embargo, también afirman que no se han encontrado trabajos donde se hayan definido de manera clara, indicadores que permitan planificar los despachos de la organización, apuntando a aquellas variables claves para el servicio al cliente y la gestión efectiva de los recursos de los que dispone una empresa, de manera que el despacho sea multicriterio. Así, se hace necesario para las empresas contar con herramientas que involucren los diferentes criterios mencionados en el proceso de toma de decisiones.

Este trabajo presenta, entonces, una breve revisión de la bibliografía asociada a la priorización de despachos y el uso de herramientas multicriterio para dicho fin, así como una revisión de las principales aplicaciones de las herramientas AHP y Topsis, las cuales son propuestas para el desarrollo de la metodología planteada. A continuación, se presenta la propuesta metodológica y un ejemplo de aplicación para ilustrar dicha metodología. Por último, se presentan unas conclusiones y recomendaciones sobre futuros desarrollos asociados a esta propuesta.

Revisión de la literatura

Aunque tradicionalmente muchas organizaciones asumen la priorización de los despachos como un problema asociado simplemente a la programación de camiones y a la selección de rutas, esta es una dificultad compleja que reviste atención, puesto que una mala asignación de los despachos puede generar, al mismo tiempo, inconvenientes asociados a excesos de inventarios en centros de distribución o bodegas de poca rotación, y agotados en sitios de alta demanda, o inclusive peor, agotados en zonas de mercado prioritarias en el marco de las estrategias corporativas.

Entre los trabajos revisados se pueden mencionar Bell et al. (1983); Goetschalckx (1988); Lambert y Harrington (1989); Innis y La Londe (1994); Brandão y Mercer (1997); Bowersox, Closs y Bixby Cooper (2002); Holweg (2005); Dobie (2005); Bonfill, Espuña y Puigjaner (2007); Shen y Honda (2009); Nielsena, Andersena y Pretolam (2014); Narasimhaa, Kivelevitchb, Sharmaa y Kumar (2013); Cattaruzza, Absi, Feillet y Vidal (2014), y Palhazi, Goos, Sörensen y Arráiz (2014). Sin embargo, dichos trabajos abordan la problemática considerando un solo criterio. Por tal razón, se ha planteado realizar el presente estudio, dado que se considera que tal como lo plantean Bravo, Osorio y Orejuela (2007), la situación es claramente multicriterio.

La metodología propuesta se desarrollará con base en los criterios establecidos por Bravo, Osorio y Orejuela (2007), los cuales se describen a continuación:

• Demanda: se refiere a la cantidad demandada por cada una de las bodegas, y se considerará para la prioridad aquella demanda mayor. Algunos métodos de previsión de la demanda uniproducto son abordados en Castro (2003).
• Variabilidad de la demanda: hace referencia a la desviación estándar de la demanda promedio semanal, e igual que en el caso anterior, será más prioritaria la bodega cuya variabilidad sea mayor.
• Cobertura en unidades: hace referencia a los días de cobertura del inventario actual en función del lead time y la demanda promedio medida en las mismas unidades de tiempo del lead time. La expresión matemática ha sido diseñada de manera tal que en el momento en que el valor de este indicador sea positivo, se apunta a la posibilidad de desabastecimiento y, por tanto, se hace prioritario el despacho, es decir, que a mayores valores del indicador, más prioritaria es la bodega.
• Cobertura en días: el planteamiento es equivalente al anterior, solamente que para este caso se considera el número de días que podría estar desabastecida la bodega si no se envía prontamente; por consiguiente, en la medida que el valor de este criterio sea mayor, será más prioritaria la bodega.
• Tamaño del faltante: se calcula como la diferencia entre el inventario de seguridad y el inventario efectivo. Quiere decir, entonces, que en la medida que el valor de este criterio sea mayor, será más prioritaria la bodega.
• Tamaño del pedido: equivale a la relación porcentual del inventario máximo definido menos el inventario efectivo sobre el inventario máximo, entonces, si esta relación se acerca al 100 %, mayor será la prioridad de la bodega.
• Zona de mercado: considera este criterio el hecho que algunas empresas establecen zonas geográficas estratégicas y, en ese sentido, más importantes dentro de sus planes de expansión y penetración del mercado. En este caso, se definen unos pesos de importancia, donde las zonas de mayor peso se consideran más prioritarias a la hora de programar el despacho.

Se ha considerado que estos criterios recogen los aspectos más importantes a la hora de definir la prioridad de los despachos, además se encuentra que son complementarios, pero que cada uno tiene su significado independiente y que si se miraran por separado, podrían tomarse decisiones contrarias a si se observan en conjunto, para lo cual se hace necesaria una metodología multicriterio como la propuesta en este trabajo.

En cuanto a trabajos que consideran la problemática multicriterio, se pueden mencionar Bravo, Osorio y Orejuela (2009) y Peña, Osorio y Arias (2010). Sin embargo, estos trabajos abordan la problemática utilizando una sola herramienta multicriterio (AHP y QFD difuso, respectivamente), pero, dada la naturaleza del problema, podría utilizarse exitosamente una combinación de herramientas, que para este caso se cree pueden funcionar bien: AHP difuso para la definición de las ponderaciones de cada uno de los criterios involucrados y la herramienta Topsis para la calificación de las alternativas, de manera que se tenga un ranking para que el encargado de realizar los despachos considere la prioridad marcada por dicho ranking. Así es posible obtener un mejor resultado para la organización en su conjunto, a partir de una evaluación completa del sistema.

Con respecto a aplicaciones recientes de AHP difuso y Topsis se pueden mencionar: Ball y Korukoğlu (2009); Gumus (2009); Muralidhar, Ravindranath y Srihari (2012); Awasthi y Chauhan (2012); Choudhary y Shanka (2012); Bas (2012), y Vinodh, Prasanna y Prakash (2014).

METODOLOGÍA

Se plantea entonces una metodología que utiliza la combinación del AHP difuso y Topsis para la priorización de los puntos a los cuales realizar los despachos desde el centro de distribución. Generalidades de la lógica difusa y propiedades de los números difusos pueden revisarse en Villareal y Arango (2014).

En este caso, primero se han definido los criterios, los cuales como se presentó en el apartado anterior, corresponden a los propuestos por Bravo, Osorio y Orejuela (2007). Dichos criterios son ponderados de acuerdo con la opinión de expertos, mediante la herramienta AHP en conjunto con la lógica difusa. En particular, esta última se utiliza para resolver la ambigüedad que puede estar presente en los juicios emitidos por los expertos. El tratamiento de estos juicios se hace a partir de la siguiente escala lingüística, que tiene la equivalencia con la escala de Saaty (1990) en números triangulares y su respectiva equivalencia verbal (tabla 1).

A partir de las comparaciones por pares establecidas por la metodología AHP, se obtendrá un peso ponderado para cada uno de los criterios, en función del conocimiento y experiencia de las personas que participen y que, se asume, son expertos con amplio conocimiento no solo del proceso de despacho, sino también del direccionamiento estratégico de la organización. Una vez obtenidas las ponderaciones, se procede con la metodología Topsis para establecer el orden de prioridad de las bodegas. Algunas aplicaciones de la herramienta se pueden encontrar en Behzadian, Khanmohammadi Otaghshara, Yazdani e Ignatius (2012), y Joshi y Shankar (2011).

Topsis inicia con la evaluación de cada alternativa (es decir, las bodegas que esperan los productos del centro de distribución). Las evaluaciones conseguidas son normalizadas y considerando los pesos obtenidos con el AHP difuso, se obtiene un ranking. Es importante mencionar que existen diferentes aproximaciones para la normalización, y en este caso en particular, se ha utilizado la planteada en la ecuación (1).

Donde:

r_ij es el valor normalizado para la calificación de la alternativa i frente al criterio j.

f_ij es el valor del indicador de cada alternativa i frente a cada indicador j.

Una vez obtenido el resultado de la aplicación del Topsis, el objetivo radica en realizar los despachos estrictamente en el orden establecido en el ranking, y a medida que los recursos se agoten (camiones, producto a ser enviado), programar los despachos subsecuentes corriendo nuevamente el modelo, es decir, calificando otra vez las bodegas y desarrollando la herramienta Topsis. Es importante aclarar que solamente se debe correr de nuevo el Topsis, pues el AHP recoge planteamientos de largo plazo definidos por los expertos.

De acuerdo con esto, puede apreciarse que la metodología tiene dos fases: en la cual se ponderan los criterios mediante la utilización de la herramienta AHP difuso, debe hacerse una sola vez y repetirse únicamente cuando las prioridades competitivas o las estrategias de la compañía sufran alguna modificación; y en la segunda, se aplica Topsis, debe realizarse cada vez que se vayan a programar los despachos en la organización.

Con el fin de agilizar el proceso y contribuir con su efectividad, se desarrolló una aplicación en Excel que permite correr la priorización alimentando los resultados de cada una de las bodegas a las que se espera realizar los despachos. Dicha aplicación fue diseñada para el caso de estudio, el cual se presenta en el siguiente apartado.

RESULTADOS

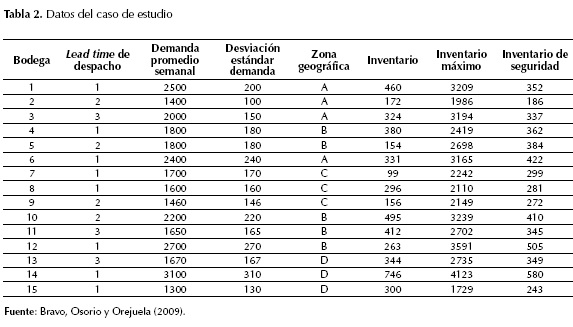
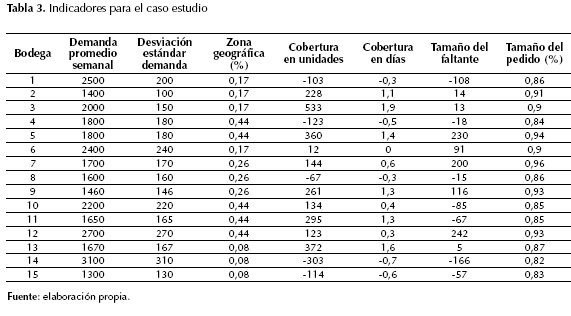
A continuación, se presenta el caso de estudio, el cual es tomado de Bravo, Osorio y Orejuela (2009) y consiste en un centro de distribución que atiende 15 bodegas de producto terminado, distribuidas en diferentes zonas geográficas con los datos que se muestran en la tabla 2. A partir de estos, se calculan los indicadores planteados que se pueden apreciar en la tabla 3.

El primer paso de la metodología planteada consiste en la ponderación de los criterios, la cual se realiza a través del AHP difuso aplicado a expertos en el tema, que, para el caso de estudio, correspondería, por ejemplo, al gerente de planta, el gerente de logística y el jefe de despachos. Mediante la utilización de la escala verbal planteada por la metodología propuesta, se obtuvieron las siguientes ponderaciones para los criterios (tabla 4).

Una vez obtenidas estas ponderaciones, las cuales se mantendrán vigentes para la organización mientras no haya cambios en las definiciones estratégicas de la compañía, se continúa con el paso 2 de la metodología, el cual consiste en la aplicación del Topsis para definir la prioridad de los despachos. Para esto, es importante normalizar el indicador, que, para este caso, se desarrolla utilizando la ecuación (1).

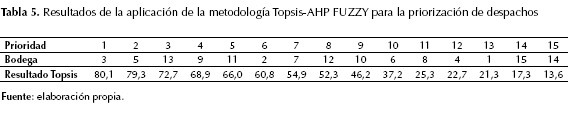
Al realizar la metodología Topsis se obtiene el ranking que prioriza las bodegas según la importancia establecida para los criterios considerados. Este ranking es el resultado final de la metodología propuesta, y define el orden estricto de prioridad para la realización de los despachos desde el centro de distribución. En la tabla 5 se presenta el ranking obtenido para el caso de estudio que se viene desarrollando. Estos resultados se discuten a continuación.

DISCUSIONES

Al observar los resultados presentados en la tabla 5, se aprecia que la bodega más prioritaria y por tanto la primera que debe ser atendida es la No. 5, dado que en el ranking ocupa el primer lugar con un valor de 89,3 %, seguida por las 12 y 7, con un valor de 75,6 % y 75 %, respectivamente.

Es importante destacar que una vez atendidas estas bodegas, el inventario efectivo cambiará y, por tanto, los valores de los indicadores, haciendo que las prioridades sean redefinidas y garantizando que con la aplicación continua de la metodología, todas las bodegas sean abastecidas en el corto y mediano plazo.

Sin embargo, atender una bodega no implica que inmediatamente vaya al final del ranking, por lo que cada vez que se vaya a realizar un nuevo despacho, debe correrse otra vez la herramienta Topsis dándole un carácter dinámico a la herramienta y al proceso, de manera que se ajuste mejor a las condiciones reales de las bodegas día a día. Se espera entonces que esta metodología se apropie por la organización y se utilice cada vez que se tenga que decidir sobre los despachos a efectuar hacia las bodegas clientes.

Es claro que esta metodología considera una situación simplificada de la realidad, pero su efectividad, a la hora de considerar todos los criterios mencionados, la convierte en un instrumento útil que puede ser ajustado a las necesidades específicas de las organizaciones.

CONCLUSIONES

La priorización de despachos es claramente un problema que debe abordarse desde el punto de vista multicriterio, y si bien no existen muchas referencias asociadas a esta situación, se considera importante desarrollar alternativas como la planteada en este documento, de manera que se fomente la investigación hacia estas aplicaciones.

La utilización del AHP difuso en conjunto con Topsis se plantea como una estrategia adecuada para el problema en mención, pues permite combinar decisiones y definiciones del largo y corto plazo de manera consistente y coherente, lográndose un resultado robusto pues satisface todos los criterios al considerar las variaciones del día a día en cada una de las bodegas clientes, pero sin perder de vista el direccionamiento estratégico de la organización y sus políticas de expansión comercial.

Aunque son herramientas matemáticas avanzadas, la integración de la propuesta planteada en este artículo puede sistematizarse fácilmente con una herramienta utilizada por casi todas las organizaciones como lo es la hoja electrónica del programa Microsoft Excel®. Es importante continuar desarrollando la herramienta para que sea posible incluir en la decisión el caso de múltiples productos y explorar en la aplicación metodológica otras formas de normalización para la herramienta Topsis.

REFERENCIAS

Awasthi, A. y Chauhan, S.S. (2012). A hybrid approach integrating Affinity Diagram, AHP and fuzzy Topsis for sustainable city logistics planning. Applied Mathematical Modelling, 36, 573-584.

Ball, S. y Korukoğlu, S. (2009). Operating system selection using Fuzzy AHP and Topsis methods. Mathematical and Computational Applications, 14, 119-130.

Bas, E. (2012). The integrated framework for analysis of electricity supply chain using an integrated SWOT-fuzzy Topsis methodology combined with AHP: The case of Turkey. Electrical Power and Energy Systems, 44, 897-907.

Behzadian, M.; Khanmohammadi Otaghshara, S.; Yazdani, M. y Ignatius, J. (2012). A state-of the-art survey of TOPSIS applications. Expert Systems with Applications, 39, 13051-13069.

Bell, W.; Dalberto, L.; Fisher, M.; Greenfield, A.; Jaikumar, R.; Kedia, P.; ...; Prutzman, P. (1983). Improving the Distribution of Industrial Gases with an On-line Computerized Routing and Scheduling Optimizer. Interfaces, 13, 4-23.

Bonfill, A.; Espuña, A. y Puigjaner, L. (2007). Decision support framework for coordinated production and transport scheduling in SCM. Computers and Chemical Engineering, 32, 1206-1224.

Bowersox, D.; Closs, D. y Bixby Cooper, M. (2002). Supply Chain Logistics Management. En: D. Bowersox, D. Closs y M. Bixby Cooper. Supply Chain Logistics Management (pp. 1-656). Nueva York: McGraw-Hill.

Brandão, J. y Mercer, A. (1997). A tabu search algorithm for the multi-trip vehicle routing and scheduling problem. European Journal of Operational Research, 100, 180-191.

Bravo, J.J.; Osorio, J.C. y Orejuela, J.P. (2007). Administración de recursos de distribución: Indicadores para la priorización en transporte. Estudios Gerenciales, 102, 101-118.

Bravo, J.J.; Osorio, J.C. y Orejuela, J.P. (2009). Modelo para la priorización dinámica de despachos de vehículos utilizando el proceso analítico jerárquico. Revista Facultad de Ingeniería de la Universidad de Antioquia, 48, 201-215.

Castro, C.A. (2003). Una estructura para la selección de modelos de gestión de inventarios de artículos individuales cuando la demanda es determinística. Revista Tecnura, 13(7), 83-93.

Cataruzza, D.; Absi, N.; Feillet, D. y Vidal, T. (2014). A memetic algorithm for the Multi Trip Vehicle Routing Problem. European Journal of Operatioanl Research, 236, 833-848.

Choudhary, D. y Shanka, R. (2012). An STEEP-fuzzy AHP-Topsis framework for evaluation and selection of thermal power plant location: A case study from India. Energy, 42, 510-521.

Dobbie, K. (2005). A proactive strategy for Motor Freight Carriers. Transportation Journal, 44, 37-53.

Goetschalkx, M. (1988). A decision support system for dynamic truck dispatching. International Journal of Physical Distribution & Material Management, 18, 3442.

Gumus, A.T. (2009). Evaluation of hazardous waste transportation firms by using a two-step fuzzy-AHP and TOPSIS methodology. Expert Systems with Applications, 18, 4067-4074.

Herrera, M.F. y Osorio, J.C. (2006). Modelo para la gestión de proveedores utilizando AHP difuso. Estudios Gerenciales, 99, 69-88.

Holweg, M. (2005). An investigation into supplier responsiveness: Empirical evidence from the automotive Industry. The International Journal of Logistics Management, 16, 96-119.

Innis, D. y La Londe, B. (1994). Customer Service: The Key to Customer Satisfaction, Customer Loyalty, and Market Share. Journal of Business Logistics, 15, 1-27.

Joshi, R.B. y Shankar, R. (2011). A Delphi-AHP-TOPSIS based benchmarking framework for performance improvement of a cold chain. Expert Systems with Applications, 38, 10170-10182.

Lambert, D. y Harrington, T. (1989). Establishing Customer Service Strategies within the Marketing Mix: More Empirical Evidence. Journal of Business Logistics, 10, 44-60.

Muralidhar, P.; Ravindranath, K. y Srihari, V. (2012). Evaluation of Green Supply Chain Management Strategies Using Fuzzy AHP and Topsis. IOSR Journal of Engineering, 2, 824-830.

Narasimhaa, K.V.; Kivelevitchb, E.; Sharmaa, B. y Kumar, M. (2013). An ant colony optimization technique for solving min-max Multi-Depot Vehicle Routing Problem. Swarm and Evolutionary Computation, 13, 63-73.

Nielsena, L.; Andersena, K.A. y Pretolam, D. (2014). Ranking paths in stochastic time-dependent networks. European Journal of Operational Research, 236, 903-914.

Palhazi, D.; Goos, P.; Sörensen, K.y Arráiz, E. (2014). An iterated local search algorithm for the vehicle routing problem with backhauls. European Journal of Operational Research, 237, 454-464.

Peña, M.; Osorio, J.C. y Arias, D. (2010). Formulación de un modelo para priorización de despacho de producto terminado en empresas manufactureras usando QFD - FUZZY. En: XVI International Conference On Industrial Engineering And Operations Management.

Saaty, T. (1990). How to make a decision: the analytic hierarchy process. European Journal of Operational Research, 48(1), 9-26.

Shen, S.Y. y Honda, M. (2009). Incorporating lateral transfers of vehicles and inventory into an integrated replenishment and routing plan for a three-echelon supply chain. Computers & Industrial Engineering, 56, 754-775.

Vinodh, S.; Prasanna, M. y Prakash, N.H. (2014). Integrated Fuzzy AHP-TOPSIS for selecting the best plastic recycling method: A case study. Applied Mathematical Modeling, 38, 4662-4672.

Villareal, E. y Arango, D.A. (2014). Estrategias para el entrenamiento de redes neuronales de números difusos. Revista Tecnura, 18(40), 36-47.