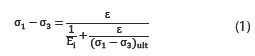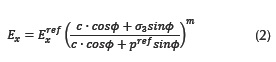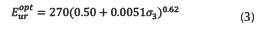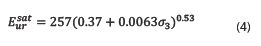Stiffness of a granular base under optimum and saturated water contents

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.3.a05

Stiffness of a granular base under optimum and saturated water contents

Rigidez de una base granular bajo humedad óptima y saturada

Fausto Andrés Molina-Gómez¹, Javier Fernando Camacho-Tauta², Oscar Javier Reyes-Ortiz³

¹ Civil Engineer, MSc in Civil Engineering (c), Assistant Professor: Military University Nueva Granada, Colombia, Bogotá, Contact: fausto.molina@unimilitar.edu.co
² Civil Engineer, MSc in Civil Engineering, PhD in Civil Engineering, Associate Professor: Nueva Granada Military University, Colombia, Bogotá, Contact: javier.camacho@unimilitar.edu.co
³ Civil Engineer, MSc of Civil Engineering, PhD in Civil Engineering, Full Professor: Nueva Granada Military University, Colombia, Bogotá, Contact: oscar.reyes@unimilitar.edu.co

Fecha de recepción: 13 de febrero de 2015 Fecha de aceptación: 15 de mayo de 2016

Cómo citar: Molina Gómez, F. A., Camacho Tauta, J. F., & Reyes Ortiz, O. J. (2016). Stiffness of a granular base under optimum and saturated water contents. Revista Tecnura, 20(49), 75-85. doi: 10.14483/udistrital.jour.tecnura.2016.3.a05

Abstract

Objective: This research work addressed the comparison of the stiffness of a granular base under optimum water content and total saturation conditions.

Methodology: The methodology focused in the development of an experimental program and the computation of a function, which permits to assess the elastic moduli of the material. A triaxial cell equipped by local LVDT transducers, capable of managing different stress paths, was used to measure the small-strain stiffness of a granular base under two different conditions of moisture. The material was compacted with optimum water content and subjected to a series of loading-unloading cycles under isotropic conditions. In addition, identical specimens were prepared to be saturated and the experimental procedure was repeated to obtain the moduli in these new circumstances. The moduli were assessed by a hyperbolic model, and its relationship with the confining pressure was computed.

Results: The results indicated that numerical model was adjusted to the experimental results. In addition, it was found that the elastic moduli decrease 3% to 8% in conditions of total saturation versus the condition of optimum water contents.

Conclusions: The small-strain stiffness in the granular base depends on the water content, and the moisture can affect the deformation in the pavement structures.

Keywords: granular bases, hyperbolic model, local transducers, small-strain stiffness, unload-reload moduli.

Resumen

Objetivo: Este trabajo de investigación aborda la comparación de la rigidez de una base granular con contenido de agua óptimo y condiciones de completa saturación.

Metodología: La metodología de trabajo se centró en el desarrollo de un plan experimental y el cálculo de una función que permite evaluar los módulos elásticos del material. Se utilizó una cámara triaxial para medir la rigidez del suelo, a pequeñas deformaciones, bajo dos condiciones diferentes de humedad. El equipo utilizado es capaz de generar trayectorias de esfuerzos y fue equipado con transductores locales tipo LVDT. El material se compactó con contenido óptimo de agua y se sometió a una serie de ciclos de carga-descarga en condiciones isótropas. Por otro lado, se prepararon las muestras idénticas para ser saturadas y repetir el mismo el procedimiento experimental bajo estas nuevas circunstancias. Los módulos fueron evaluados mediante un modelo hiperbólico y se calculó su relación con la presión de confinamiento.

Resultados: Los resultados indicaron que el modelo numérico se ajustó a los resultados experimentales. Además, se encontró que los módulos de elasticidad disminuyen de 3% a 8% en condiciones de completa saturación frente a la condición de humedad óptima.

Conclusiones: La rigidez a pequeñas deformaciones de la base granular depende de la humedad y que el contenido de agua puede inducir deformaciones en las estructuras de pavimento.

Palabras Clave: bases granulares, modelo hiperbólico, módulos de descarga-recarga, rigidez a pequeñas deformaciones, sensores locales.

INTRODUCTION

Density criterion for granular layers is the most common practice in quality control and quality assurance for pavement construction (Chen, Chang, & Fu, 2011). Granular bases are compacted under optimal water content to achieve a maximum dry unit weight. These controlling variables are obtained by the laboratory compaction test (ASTM International, 2014a). However, during construction the water content is not a fully controlled variable. Likewise, after construction water content may change due to climate effects, damage or absence of the asphaltic layer or drainage difficulties.

In regions with seasons, the spring thaw modifies the water content of the pavement structure due to the water flow through fissures, cracks and pores on the asphalt layer. In tropical regions, the weather changes and the rain variability produces the same effect. Usually, the damage in the asphalt layer which induced the seepage to granular bases is caused by the fatigue phenomenon (Paredes, Reyes-Ortiz, & Camacho-Tauta, 2014). The water flow generates a reduction of shear strength in granular bases, because water content directly governs the stability of the pavement system (Perera, Zapata, Houston, & Houston, 2004). In saturated granular bases, water deteriorates the quality of material and reduces the bearing capacity of a pavement structure (Zhang, Ishikawa, Tokoro, & Nishimura, 2014). The variation in the moisture content changes the strength parameters due to changes of the matric suction, as it is studied in the unsaturated soil mechanics (Fredlund & Rahardjo, 1993).

Authors as Colesanti, Ferretti, Novali, Prati, & Rocca (2003) and Li, Saboundjian, Liu, & Xiong (2013) measured the pavement deformation during seasonal change through monitoring systems installed directly on the road. Other authors like Ishikawa, Zhang, Tokoro, & Miura (2014) and Inam, Ishikawa, & Miura (2012), developed experimental programs to measure the stiffness variation in granular bases with triaxial cells for unsaturated soils. Furthermore, it is possible to estimate the permanent strain in granular materials by numerical experiments based on constitutive models created from laboratory and in-situ test Lekarp & Dawson (1998) and Hicher & Chang (2008).

Jafarzadeh and Sadeghi, Jafarzadeh & Sadeghi (2012) studied the variation of dynamic properties of sands depending on the degree of saturation. They showed that the shear modulus is almost constant for a wide range of saturation, but it reduces considerably as the full saturation is reached. Similar results were found by Lu & Kaya (2014). To Boscardin, Selig, Lin, & Yang (1990) and Zhang, Li, & Chen (2013) the hyperbolic model is useful to compute elastic moduli and strains during loading process.

In this research, it was used several specimens of a material used for the road construction in Bogotá (Colombia). After that the specimens were compacted with optimum water content by the standard effort (ASTM International, 2014a) and consolidated under different isotropic stresses (p₀') in a stress path triaxial cell. This cell was equipped with LVDT local transducers. The procedure was aimed to assess the influence of two key water contents (optimum and saturated) on the stiffness of a granular base. The stiffness measured during loading, unloading and reloading stages and the elastic moduli were computed through the hyperbolic model.

STIFFNESS OF SOIL

Stiffness is a key property in the behaviour of soil materials under loading and unloading cycles. The initial stiffness is characterized by the initial shear modulus (G₀) (Ortiz-Pulido, Gaitán-Serrano, & Camacho-Tauta, 2014). This parameter can be measured in laboratory mainly by resonant column, bender element, or cyclic triaxial tests. The shear modulus is affected principally by the effective stress (p'₀) and the void ratio (e) (Camacho-Tauta, Jiménez Álvarez, & Reyes-Ortiz, 2012). According to Ramos Cañón (2015) p'₀ has the main influence in the stiffness of granular materials.

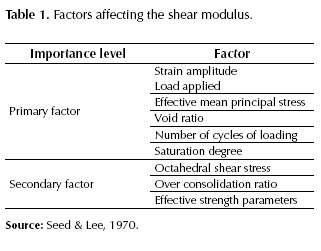
However, a number of factors can affect the initial shear modulus. Hardin & Black, (1968) found that the soil stiffness could be affected by a number of factors as: effective octahedral normal stress (s₀), octahedral shear stress (τ₀), void ratio (e), saturation degree (Sr), amplitude of vibration (A), frequency of vibration (f), and temperature (T), among others.

From this wide range of influencing factors, Seed & Lee (1970) selected and classified the most significant in two groups of importance level, as shown in Table 1. In their work, they studied the effect of the load applied, strain amplitude and saturation degree in the stiffness of granular base.

Any elastic moduli can be assessed by knowing two elastic parameters (Timoshenko & Goodier, 1986), as the elastic modulus (E) and the Poisson's ratio (n). The stiffness of granular materials also can be measured through loading and unloading process with sensors installed directly on the specimen.

PERMANENT DEFORMATION IN GRANULAR MATERIALS

Traditionally, in pavement engineering the two most important factors to evaluate the performance of a structure are: fatigue in cemented layers and rutting in non-cemented layers. Both damages are products of repetitive loads due to traffic action. In granular bases, each load application produces a permanent deformation on the structure. The gradual accumulation of many plastic deformations reduces the serviceability or increases the possibility of collapse due to excessive rutting of the road (Lekarp & Dawson, 1998).

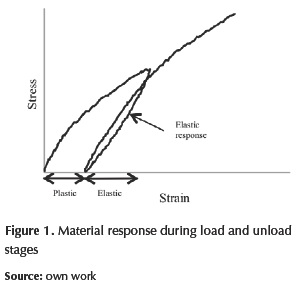
At small-strain, the granular material has an elastic behaviour. Beyond this range, the material experiments energy dissipation by plasticity with permanent deformations. Figure 1 shows the deformation process during loading and unloading stages without reach the failure.

This is the typical response of a granular base in a pavement structure. After unloading, the irrecoverable or permanent deformation is the plastic strain and it could be considered as a new reference state, where the elastic response can be measured since the failure is not achieved (Wood, 1991).

HYPERBOLIC MODEL

The hyperbolic model represents the non-linearity and the dependency of the stress level in the stress-strain behaviour of granular soils, where each increment consider the soil as elastic linear material (Boscardin et al., 1990). Hyperbolic equations are useful tools to describe the non-linear elastic behaviour before achieving the failure (Duncan & Chang, 1970). The curve representing this model was proposed by Kondner (1963), and its equation (1).

Where (σ₁-σ₃) is the deviatoric stress; (σ₁-σ₃)_ult is the deviatoric stress at failure and the asymptotic value of the model; ε is the axial deformation; and E_i is the initial tangent modulus. Generally, the values of strain and deviatoric stress are obtained through triaxial tests under different confining pressures. From the shear strength parameters and the reference elastic modulus is possible to establish the stress-stiffness as a function of the confining pressure (equation (2)).

The stress-stiffness dependency normalizes elastic modulus respect to a reference pressure. Where E_ref is the elastic modulus of reference obtained by numerical adjust; c and Φ are the shear strength parameters; p_ref is a reference pressure which usually is the atmospheric pressure (100 kPa); and finally m is an amount of stress dependency represented by a power, which has values between 0.5 and 1. It is necessary to note that the σ₃ is the confining pressure corresponding a compression stress (thus, insert as negative value).

METODOLOGY

Materials

This study was carried out with a granular base from Soacha, near Bogota (Colombia). Geologically, the high plateau of Bogota is composed by almost 600 m of lacustrine and fluvial sediments (Coronado, Caicedo, Taibi, Correia, & Fleureau, 2011). Granular base material of this area corresponds to sandstones from adjacent slopes to the plateau. These sandstones are constituted principally by orthoquarcites composed by: undulose quartz, semi-composite quartz, composite quartz and stretched quartz (Aalto, 1972).

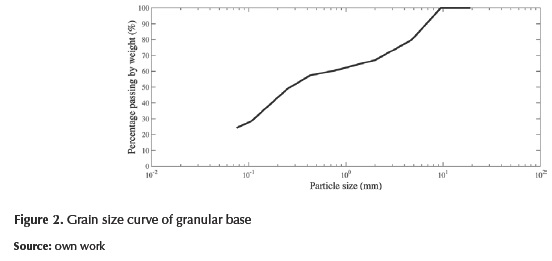
Figure 2 shows the grain size curve, which was obtained according to the procedure stabilised in the standard ASTM D422 (ASTM International, 2007b).

Plasticity limits were found by the standard procedure of ASTM D4318 (ASTM International, 2010) and the specific gravity of soils for particles with size less than 4.75 mm was estimated through the method of ASTM D854 (ASTM International, 2014b). The values obtained are shown in Table 2.

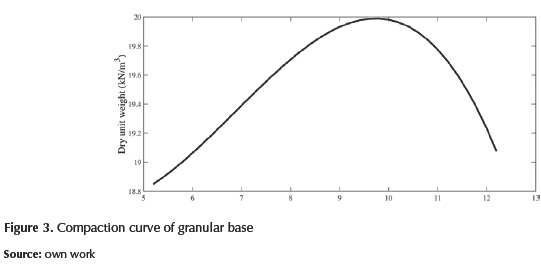
The parameters of optimum water content and maximum dry unit weight are 9.6% and 1.96 g/cm³, respectively. The curve of compaction is presented in Figure 3.

Equipment

A GDS triaxial equipment, able to generate stress path automatically, was used to estimate the stress-strain behaviour of the granular base during load-unload-reload stages. The device is equipped with an 8 kN submersible load cell, three pressure/volume controllers of 0.1 kPa and 1 mm³ of precision, and LVDT type local transducers (Figure 4) capable to measure axial and radial strains of the specimen directly.

Test procedure

Twelve different specimens of granular base were compacted at optimal water content and maximum dry unit weight according to the Standard Effort Method, which is provided in the standard ASTM D698 (ASTM International, 2014a). Three of these specimens were subjected to the procedure regulated by the standard ASTM D2850 (ASTM International, 2007a) in order to assess the shear strength parameters in conditions unconsolidated undrained (UU) under confining pressures of 50, 100 and 150 kPa. Additionally, other three specimens were first saturated and then subjected to consolidation and shear stages to evaluate the strength parameters in consolidated undrained (CU) conditions, according to the standard D2850 (ASTM International, 2007a), with the consolidation stress of 50, 100 and 200 kPa. Finally, the remaining six specimens were subjected to load and unload stages, in two groups of three, with the aim of assessing and comparing the elastic moduli in conditions of optimum water content and total saturation. The stress path tests were performed with the same confining pressure than UU triaxial tests.

RESULTS

Triaxial tests

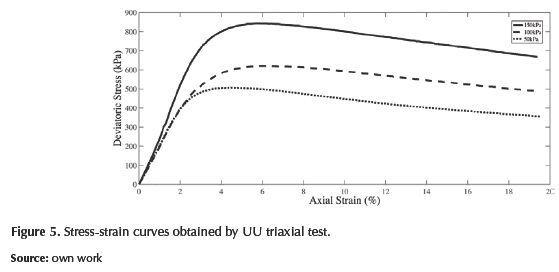
Figure 5 shows the experimental results of stress-strain behaviour for each confining pressure in the granular base with maximum axial strain of 20% obtained by an Unconsolidated Undrained triaxial test.

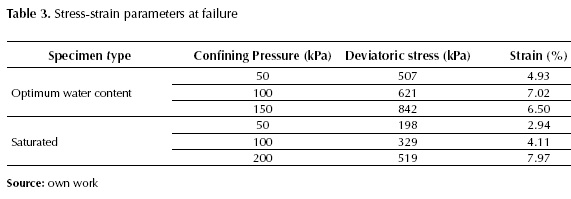
Results show that strength of the granular bases increases and the strains decreases due to the non-linear behaviour of this type of material, according to Atkinson (2007). Table 3 presents the maximum values at failure obtained from triaxial tests.

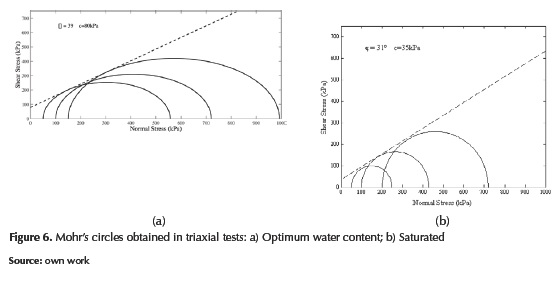
Figure 6 shows the results of shear strength through Mohr's circles for the specimens at the both moisture content.

The shear strength parameters show that the values of friction and cohesion are lower for the total saturation condition compared to the optimal water content. Results indicate that the stability of any geotechnical structure built with this granular base can be affected by moisture variations.

Hyperbolic model

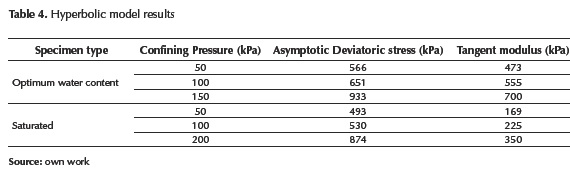
Taken the data of Table 3 and the information from all triaxial tests, it was used the hyperbolic model to obtain the parameters in equation 1. By this way, it was possible to evaluate the hyperbolic model of this granular base under different confining pressure and obtain the elastic moduli during load-unload-reload cycles.

Since maximum deformation before the failure is less than 8%, according to Stark, Ebeling, & Vettel (1994) the hyperbolic model is valid to describe the stress-strain behaviour in this type of material. Table 4 presents the parameters of the hyperbolic model evaluated by means of linear adjustment.

The experimental information indicates that the numerical curves adjust in the elastic range with the experimental results. For this reason, is valid to estimate the initial tangent modulus of the material studied through this model.

Loading and unloading test

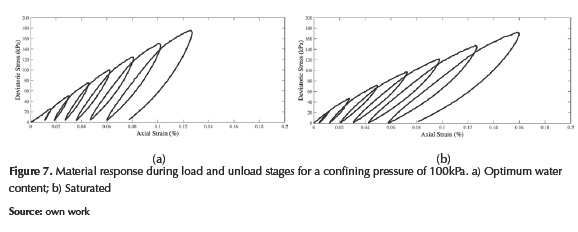
The elastic moduli during unload-reload stages were computed directly by mean of vertical and radial measurements through the local transducers and the internal load cell. This information was obtained for each confining pressure at conditions of optimum water content and total saturation.

Results exhibit that the unload-reload moduli for the saturated specimen are lower than the specimen with optimum moisture. Table 5 presents the average moduli obtained by hyperbolic model in the stress path test.

Figure 7 shows the results obtained during the application of stress path, which include deviatoric stress of 25, 50, 75, 100, 125, 150 and 175 kPa.

The moduli were evaluated in each cycle, and the differences among them show variations between 3-8% for both water conditions. The relative low variability of this parameter suggests that the moduli do not depend on the load level for the strain range imposed in the tests. Equation 2 was used to describe and represent the effect of confinement on the granular base for the atmospheric pressure and the values of shear strength parameters (optimum water content: c=80 kPa ϕ=39º, and saturated: c=35 kPa ϕ=31º) obtained by the triaxial tests. Equation 3 gives unload-reload elastic moduli and the power parameter to optimum water content condition. In addition, equation 4 presents the same parameters in total saturation conditions.

Replacing σ₃ in equations 3 and 4 for the value of atmospheric pressure, was found that E_ur has a variation of 1% and 4% comparing with the results showed in Table 5 for a confining pressure of 100 kPa in both water conditions. Figure 8 presents the numerical adjust between experimental data with model results.

The small changes between the experimental and numerical results validate the unload-reload moduli stress-stiffness dependency model is a good approximation to describe the stress-strain behaviour of this material. Yang & Han, (2012); Mazari et al., (2014); and Salour & Erlingsson, (2015) evaluated the moduli in similar materials to the Soacha granular base. Their calculation results do not present significant differences with the values found in equations 3 and 4 under a confining pressure of 100 kPa.

CONCLUSIONS

The stress-stain behaviour of a granular base was evaluated by an experimental program during loading, unloading and reloading stages. The material was compacted and tested under two different water contents, optimum and saturated. The program included tests with a triaxial device capable to generate different stress paths and equipped with local transducers to measure local strains.

The elastic moduli of the granular base were assessed under different stress level through a hyperbolic model. Furthermore, from these values and shear strength parameters, it was proposed an equation which permits estimate the elastic moduli as a function of the confining pressure. The numerical model presented a suitable correlation to the experimental measures.

Results obtained from the experimental data show that the shear strength change is a function of the saturation degree. This effect is due to the suction inside the soil. Hence, the strength for unsaturated samples is greater than for saturated samples. Also, the soil suction increases the stiffness of unsaturated specimens.

According to the compared results, of both moisture conditions, it was found that the stiffness of this granular base depends on the water content. The model calculation presents a parallel trend between the two moistures. Therefore, it is possible to affirm based on results, the material presents lowest modulus values at saturation total state.

ACKNOWLEDGEMENTS

This work is part of the Research Project INV-ING-1765 (2015) supported by the Research Direction of the Nueva Granada Military University. The first author acknowledges to COLCIENCIAS, Call 617/2013.

REFERENCES

Aalto, K. R. (1972). Diagenesis of Orthoquartzites Near Bogota Colombia. Journal of Sedimentary Research, 42(2). http://doi.org/10.1306/74D72540-2B21-11D7-8648000102C1865D.

ASTM International. D2850-Standard Test Method for Unconsolidated-Undrained Triaxial Compression Test on Cohesive Soils (2007).

ASTM International. D422-Standard Test Method for Particle-Size Analysis of Soils, 63 Annual Book of ASTM Standards 1-8 (2007).

ASTM International. D4318-Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils (2010). http://doi.org/10.1520/D4318-10.

ASTM International. D698-Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Standard Effort (12 400 ft-lbf /ft3 (600 kN-m /m3)) (2014).

ASTM International. D854-Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer (2014).

Atkinson, J. (2007). The Mechanics of Soils and Foundations, Second Edition-(2nd ed.). CRC Press Book.

Boscardin, M. D., Selig, E. T., Lin, R., & Yang, G. (1990). Hyperbolic Parameters for Compacted Soils. Journal of Geotechnical Engineering, 116(1), 88-104. http://doi.org/10.1061/(ASCE)0733-9410(1990)116:1(88).

Camacho-Tauta, J. F., Jiménez Álvarez, J. D., & Reyes-Ortiz, O. J. (2012). A Procedure to Calibrate and Performance The Bender Element Test. DYNA, 79(176), 10-18. Retrieved from http://www.revistas.unal.edu.co/index.php/dyna/article/view/26165/43542.

Chen, D.-H., Chang, G., & Fu, H. (2011). Limiting Base Moduli to Prevent Premature Pavement Failure. Journal of Performance of Constructed Facilities, 25(6), 587-597.

Colesanti, C., Ferretti, A., Novali, F., Prati, C., & Rocca, F. (2003). SAR monitoring of progressive and seasonal ground deformation using the permanent scatterers technique. In IEEE Transactions on Geoscience and Remote Sensing (Vol. 41, pp. 1685-1701). http://doi.org/10.1109/TGRS.2003.813278.

Coronado, O., Caicedo, B., Taibi, S., Correia, A. G., & Fleureau, J.-M. (2011). A macro geomechanical approach to rank non-standard unbound granular materials for pavements. Engineering Geology, 119(1-2), 64-73. http://doi.org/10.1016/j.enggeo.2011.02.003.

Duncan, J. M., & Chang, C. Y. (1970). Nonlinear Analysis of Stress and Strain in Soils. ASCE Journal of the Soil Mechanics and Foundations Division, 95(5), 1629-1653.

Fredlund, D. G., & Rahardjo, R. (1993). Soil Mechanics for Unsaturated Soils. John Wiley & Sons INC.

Hardin, B. O., & Black, W. L. (1968). Vibration Modulus of Normally Consolidated Clay. Journal of the Soil Mechanics and Foundations Division, 94(2), 353-370.

Hicher, P. Y., & Chang, C. S. (2008). Elastic model for partially saturated granular materials. Journal of Engineering Mechanics, 134(6), 505-513. http://doi.org/10.1061/(ASCE)0733-9399(2008)134:6(505).

Inam, A., Ishikawa, T., & Miura, S. (2012). Effect of principal stress axis rotation on cyclic plastic deformation characteristics of unsaturated base course material. Soils and Foundations, 52(3), 465-480. http://doi.org/10.1016/j.sandf.2012.05.006.

Ishikawa, T., Zhang, Y., Tokoro, T., & Miura, S. (2014). Medium-size triaxial apparatus for unsaturated granular subbase course materials. Soils and Foundations, 54(1), 67-80. http://doi.org/10.1016/j.sandf.2013.12.007.

Jafarzadeh, F., & Sadeghi, H. (2012). Experimental study on dynamic properties of sand with emphasis on the degree of saturation. Soil Dynamics and Earthquake Engineering, 32(1), 26-41. http://doi.org/10.1016/j.soildyn.2011.08.003.

Kondner, R. L. (1963). A hyperbolic stress-strain formulation for sands. In 2nd Pan-Am Conf. on Soil Mech. and Found. Engrg (p. 289). Sao Paulo: Northwestern University.

Lekarp, F., & Dawson, A. (1998). Modelling permanent deformation behaviour of unbound granular materials. Construction and Building Materials. http://doi.org/10.1016/S0950-0618(97)00078-0.

Li, L., Saboundjian, S., Liu, J., & Xiong, Z. (2013). Permanent Deformation Behavior of Alaskan Granular Base Materials. Planning for Sustainable Cold Regions © ASCE 2013 ISCORD 2013: Planning for Sustainable Cold Regions © ASCE, (1955), 428-435.

Lu, N., & Kaya, M. (2014). Power Law for Elastic Moduli of Unsaturated Soil. Journal of Geotechnical and Geoenvironmental Engineering, 140(1), 46-56. http://doi.org/10.1061/(ASCE)GT.1943-5606.0000990.

Mazari, M., Navarro, E., Abdallah, I., & Nazarian, S. (2014). Comparison of numerical and experimental responses of pavement systems using various resilient modulus models. Soils and Foundations, 54(1), 36-44. http://doi.org/10.1016/j.sandf.2013.12.004.

Ortiz-Pulido, M. del P., Gaitán-Serrano, J. F., & Camacho-Tauta, J. F. (2014). Modelo unificado de curvas de degradación del módulo cortante en arenas del río Guayuriba. DYNA, 81(184), 77-84. http://doi.org/10.15446/dyna.v81n184.36603.

Paredes, L. A., Reyes-Ortiz, Ó. J., & Camacho-Tauta, J. F. (2014). Comportamiento de mezclas asfálticas densas a partir del ensayo de viga semicircular simplemente apoyada. Revista Tecnura, 18(41), 103. http://doi.org/10.14483/udistrital.jour.tecnura.2014.3.a08.

Perera, Y., Zapata, C., Houston, W., & Houston, S. (2004). Long-Term Moisture Conditions under Highway Pavements (ASCE). In M. K. Y. and E. Kavazanjian (Ed.), Geotechnical Engineering for Transportation Projects (pp. 1132-1143). Los Angeles: ASCE. http://doi.org/10.1061/40744(154)102.

Ramos Cañón, A. M. (2015). Influence of the void ratio and the confining on the static liquefaction in slopes in changi sand. Revista Tecnura, 19(43), 63. http://doi.org/10.14483/udistrital.jour.tecnura.2015.1.a04.

Salour, F., & Erlingsson, S. (2015). Resilient modulus modelling of unsaturated subgrade soils: laboratory investigation of silty sand subgrade. Road Materials and Pavement Design, 16(3), 553-568. http://doi.org/10.1080/14680629.2015.1021107.

Seed, H. B., & Lee, K. L. (1970). Liquefaction of Saturated Sands During Cyclic Loading. Journal of the Soil Mechanics and Foundations Division, 92(6), 105-134.

Stark, T. D., Ebeling, R. M., & Vettel, J. J. (1994). Hyperbolic Stress‐Strain Parameters for Silts. Journal of Geotechnical Engineering, 120(2), 420-441. http://doi.org/10.1061/(ASCE)0733-9410(1994)120:2(420).

Timoshenko, S., & Goodier, J. N. (1986). Theory of Elasticity (3rd ed., Vol. 49). Mc Graw Hill.

Wood, D. M. (1991). Soil Behaviour and Critical State Soil Mechanics (1st ed.). Cambridge University Press.

Yang, X., & Han, J. (2012). Analytical Model for Resilient Modulus and Permanent Deformation of Geosynthetic-Reinforced Unbound Granular Material. http://dx.doi.org/10.1061/(ASCE)GT.1943-5606.0000879, 139(9), 1443-1453. http://doi.org/10.1061/(ASCE)GT.1943-5606.0000879.

Zhang, Q., Li, L., & Chen, Y. (2013). Analysis of Compression Pile Response Using a Softening Model, a Hyperbolic Model of Skin Friction, and a Bilinear Model of End Resistance. http://dx.doi.org/10.1061/(ASCE)EM.1943-7889.0000640.

Zhang, Y., Ishikawa, T., Tokoro, T., & Nishimura, T. (2014). Influences of degree of saturation and strain rate on strength characteristics of unsaturated granular subbase course material. Transportation Geotechnics, 1(2), 74-89. http://doi.org/10.1016/j.trgeo.2014.04.001.