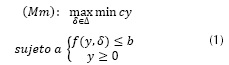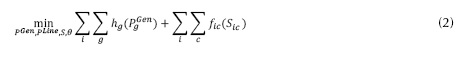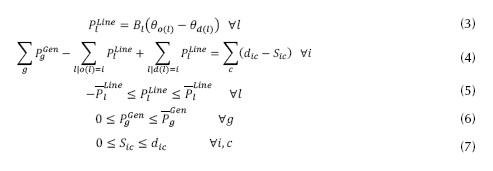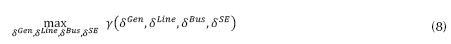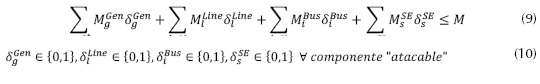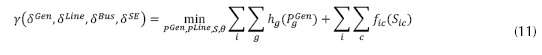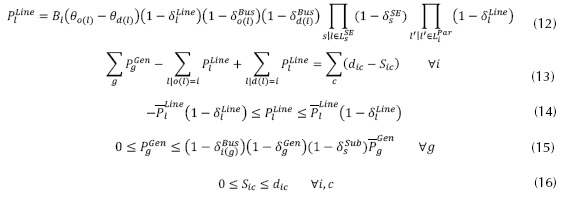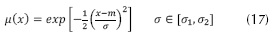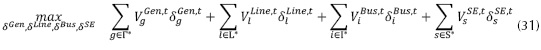Análisis de vulnerabilidad de sistemas de potencia incluyendo incertidumbre en las variables con lógica difusa tipo 2

DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.3.a07

Análisis de vulnerabilidad de sistemas de potencia incluyendo incertidumbre en las variables con lógica difusa tipo 2

Analysis of power system vulnerability considering uncertainty in variables using fuzzy logic type 2

Julián Alexánder Melo Rodríguez¹, Camilo Andrés Cortés²

¹ Ingeniero Electricista, magíster en Ingeniería Eléctrica. Profesional especializado Banco de la República. Bogotá, Colombia. Contacto: jamelor@unal.edu.co
² Ingeniero Electricista, doctor en Ingeniería Eléctrica. Profesor asociado de la Universidad Nacional de Colombia. Bogotá, Colombia. Contacto: caacortesgu@unal.edu.co

Fecha de recepción: 4 de febrero de 2016 Fecha de aceptación: 15 de mayo de 2016

Cómo citar: Melo Rodríguez, J. A., & Cortés, C. A. (2016). Análisis de vulnerabilidad de sistemas de potencia incluyendo incertidumbre en las variables con lógica difusa tipo 2. Revista Tecnura, 20(49), 100-119 doi: 10.14483/udistrital.jour.tecnura.2016.3.a07

Resumen

Objetivo: En este trabajo se propone una nueva metodología de análisis de vulnerabilidad de sistemas de potencia incluyendo incertidumbre en algunas variables.

Método: La metodología implementa un modelo de optimización binivel entera-mixta. En el nivel inferior se minimizan los costos asociados a la generación de energía y a la penalidad por deslastre de carga, mientras que en el nivel superior se maximiza el daño en el sistema de potencia representado por el deslastre de carga. Se utiliza la Lógica Difusa tipo 2 para modelar la incertidumbre tanto en variables lingüísticas como en variables numéricas. Las variables lingüísticas modelan los factores del entorno geográfico mientras que las variables numéricas modelan los parámetros del sistema de potencia.

Resultados: La metodología se validó en un sistema de prueba IEEE RTS-96 modificado. Los resultados muestran que al incluir particularidades del entorno geográfico se detectan distintas vulnerabilidades en el sistema de potencia. Además, se logró identificar que el componente más crítico del sistema es la línea 112-123, ya que es atacada 16 veces en 18 escenarios contemplados, y que el máximo deslastre de carga en el sistema varía desde 145 a 1258 MW.

Conclusiones: Esta metodología puede ser usada para coordinar y afinar los planes de seguridad de la infraestructura eléctrica del sistema.

Financiamiento: Grupo de investigación EMC-UN

Palabras clave: Vulnerabilidad, Sistemas de potencia, Lógica difusa tipo 2.

Abstract

Objectives: This paper presents a new methodology for analyzing the vulnerability of power systems including uncertainty in some variables.

Method: The methodology optimizes a Bi-level mixed integer model. Costs associated with power generation and load shedding are minimized at the lowest level whereas at the higher level the damage in the power system, represented by the load shedding, is maximized. Fuzzy logic type 2 is used to model the uncertainty in both linguistic variables and numeric variables. The linguistic variables model the factors of the geographical environment while numeric variables model parameters of the power system.

Results: The methodology was validated by using a modified IEEE RTS-96 test system. The results show that by including particularities of the geographical environment different vulnerabilities are detected in the power system. Moreover, it was possible to identify that the most critical component is the line 112-123 because it had 16 attacks in 18 scenarios, and that the maximum load shedding of the system varies from 145 to 1258 MW.

Conclusions: This methodology can be used to coordinate and refine protection plans of the power system infrastructure.

Funding: EMC-UN research group.

Keywords: Vulnerability, Power systems, Fuzzy logic type 2.

Introducción

Un sistema de potencia es un conjunto de redes e instalaciones que ofrecen un servicio público de suministro de energía eléctrica esencial para la sociedad y su economía. Este sistema se considera una infraestructura crítica, ya que una falla parcial o total de uno o más de sus componentes puede tener una incidencia negativa de orden económico, ambiental, político o social. De hecho, es necesario que los sistemas de potencia tengan altos índices de calidad, seguridad y eficiencia (Bolaños y Correa, 2014). Sin embargo, los incrementos en la demanda y en las restricciones ambientales así como la liberalización de los mercados de electricidad han ocasionado que los sistemas de potencia estén operando cada vez más cerca de sus límites de estabilidad (Perdomo Fontalvo, 2015). Por este motivo es importante determinar la vulnerabilidad de estos sistemas ante cualquier eventualidad, ya sea natural o intencional, mediante la implementación de diferentes metodologías.

Vulnerabilidad de sistemas de potencia ante ataques

La importancia de determinar la vulnerabilidad de los sistemas eléctricos adquiere cada día mayor trascendencia, por tanto, mediante la implementación de metodologías para su análisis, es posible estudiar las consecuencias de diferentes eventos. Son escazas las investigaciones en el campo de la vulnerabilidad de sistemas de potencia con anterioridad a los atentados terroristas del 11 de septiembre del 2001 en Estados Unidos. Sin embargo, luego de esta fecha ha aumentado la necesidad de proteger los sistemas eléctricos ante cualquier eventualidad, ya sea natural o intencional. Por esta razón, actualmente en diferentes países se están estudiando nuevos métodos para el análisis de la vulnerabilidad de los sistemas de potencia.

Las metodologías actuales, que abordan el tema del análisis de vulnerabilidad de sistemas de potencia, tienen en su mayoría el mismo punto de partida: la metodología VEGA (Salmeron, Wood, y Baldick, 2003) que implementa optimización binivel, donde se describen nuevas técnicas analíticas que ayudan a mitigar disrupciones en sistemas de potencia causadas por ataques intencionales. Modelos matemáticos binivel identifican componentes críticos del sistema (líneas de transmisión, generadores, transformadores y subestaciones), con lo se crean planes de ataque máximamente disruptivos para el atacante que, se asume, posee recursos de ataque limitados. El modelo matemático binivel se compone de dos problemas de optimización: la minimización interna busca suministrar la energía en el sistema a menor costo y penalidad por energía no suministrada, mientras que la maximización exterior busca el plan de ataque que maximice la energía no suministrada.

La metodología VEGA fue punto de partida para varias propuestas posteriores. En Arroyo y Galiana (2005), la formulación binivel se investiga a través de una función en el cual el objetivo del atacante es minimizar el número de componentes del sistema que deben ser destruidos con el fin de causar un deslastre de carga mayor o igual a un nivel específico, convirtiendo las no-linealidades en equivalentes lineales. En Motto, Arroyo y Galiana (2005) se presenta un procedimiento de solución para el modelo de programación lineal binivel entera-mixta obtenido del análisis de vulnerabilidad. A partir de resultados de la teoría de programación lineal y de linealización de productos entre variable, se propone modelo estándar de programación lineal entera-mixta (de un nivel). En Delgadillo, Arroyo y Alguacil (2010), la metodología se formula como un problema de programación no lineal binivel entera-mixta. En el nivel superior de optimización, el agente atacante maximiza el daño causado en el sistema de potencia, el cual es medido en términos del deslastre de carga. Por otro lado, en el nivel inferior de optimización, el operador del sistema minimiza el daño por medio de una operación óptima del sistema de potencia por medio de acciones correctivas, modificando su topología. Dado que es un problema no-convexo y no-lineal, el problema de programación binivel resultante no puede ser transformado en un problema de optimización estándar de un nivel. En Alguacil, Delgadillo y Arroyo (2014) se aborda el problema de vulnerabilidad de sistemas de potencia con un enfoque de programación trinivel: en el primero, el operador del sistema identifica los componentes a ser reforzados con el fin de reducir el daño asociado a posibles apagones; en el segundo, el atacante determina el conjunto de componentes a atacar con el fin de maximizar el daño en el sistema, y en el tercero, el operador del sistema minimiza en daño causado por el ataque ejecutado por medio de una operación óptima del sistema de potencia. Incluso, recientemente se propuso una metodología de análisis de vulnerabilidad binivel basada en flujo de potencia AC para incluir los efectos de la potencia reactiva y los niveles de tensión en los nodos del sistema (Agudelo, López-Lezama y Muñoz, 2014).

Desde otra perspectiva, Tranchita (2008) y Tranchita, Hadjsaid y Torres (2006) presentan un método basado en la evaluación del riesgo, el cual les permite a los operadores y planeadores evaluar la seguridad del sistema de potencia con respecto a posibles ataques. Mediante la implementación de inferencia probabilística y teoría de la posibilidad, se considera tanto la incertidumbre asociada con el comportamiento dinámico del atacante, como también la asociada con la predicción de las potencias generada y demandada.

En el presente trabajo se propone una metodología de optimización binivel entera-mixta que permite analizar la vulnerabilidad de sistemas de potencia teniendo en cuenta las variables del entorno geográfico con sus respectivos grados de incertidumbre. De esta forma, los operadores de sistemas de potencia pueden determinar cuáles componentes del sistema se encuentran en mayor grado de vulnerabilidad y, con base en esto, tomar medidas con el fin de proteger los componentes críticos para la operación del sistema.

METODOLOGÍA

El análisis de vulnerabilidad de sistemas de potencia consiste en examinar un conjunto de contingencias factibles y su efecto en la operación del sistema. Es importante destacar que cuando se busca en qué puntos atacar el sistema para maximizar el deslastre de carga (o función de costos), en últimas se está determinando cómo proteger al sistema ante ataques intencionales.

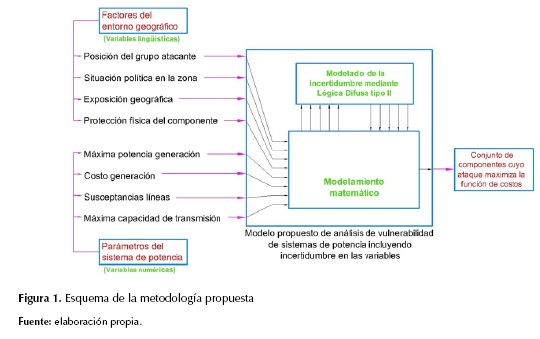
En la figura 1 se muestran las principales etapas de la metodología propuesta. En primer lugar se presentan las variables de entrada que se dividen en dos grupos, el primero se relaciona con los factores del entorno geográfico (variables lingüísticas) y el segundo con los parámetros del sistema de potencia (variables numéricas). En segundo lugar se muestra el cuerpo de la metodología en el cual el modelo matemático de vulnerabilidad de sistemas de potencia recurre al modelado de la incertidumbre en algunas de las variables. Por último, el resultado obtenido de la metodología propuesta es un conjunto de componentes que cuando son atacados de manera coordinada, hacen que se maximice el deslastre de carga (o función de costos) en el sistema.

Así, el modelo propuesto de análisis de vulnerabilidad de sistemas de potencia que incluye incertidumbre en algunas de sus variables. Partiendo de la metodología propuesta en Salmeron, Wood y Baldick (2004), se desarrolla un modelo de interdicción y un algoritmo para resolver el problema de análisis de vulnerabilidad de manera aproximada. El modelo de interdicción es un problema max-min (Mm) de optimización como se muestra en la ecuación (1).

Para un plan de interdicción dado δ, el problema interior es un flujo de potencia que minimiza los costos de generación más la penalización por carga no suministrada, denotado por cy, en donde y representa las potencias generadas, los ángulos de los fasores, los flujos de potencia por las líneas y la potencia no suministrada (deslastre de carga). La maximización exterior selecciona el plan de ataque (interdicción) δ ∈ Δ que conlleva al mayor deslastre de carga posible. En la metodología propuesta en este trabajo se modela la afectación que los factores del entorno geográfico tienen sobre el sistema de potencia, esto se tiene en cuenta en la expresión ƒ (y, δ) de la ecuación (1).

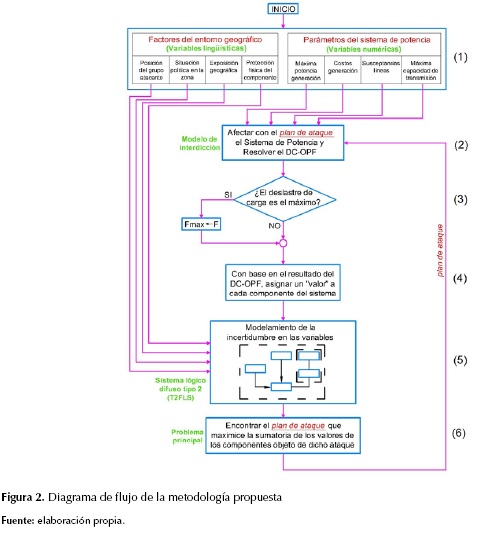
La figura 2 muestra el diagrama de flujo de la metodología. Las variables de entrada (paso 1) se dividen en dos grupos: las lingüísticas, relacionadas con los factores del entorno geográfico, y las numéricas, relacionadas con los parámetros del sistema de potencia.

En el paso 2 se muestra el modelo de interdicción en el cual se resuelve el DC-OPF (flujo de potencia óptimo DC) para el sistema de potencia. Dicho DC-OPF se lleva a cabo retirando del sistema los componentes afectados por el plan de ataque proveniente del problema principal (paso 6). En el paso 3 se evalúa si el deslastre de carga provocado por el plan de ataque es máximo; de ser así, dicho plan de ataque sería el mejor para el atacante. En el paso 4 se asigna un valor a cada componente del sistema, dicho valor se basa en la cantidad de potencia que pasa a través del componente. En el paso 5 se lleva a cabo el modelado de la incertidumbre de los factores del entorno geográfico mediante lógica difusa tipo 2. Por último, en el paso 6 se soluciona el problema principal en el cual se busca el plan de ataque de mayor valor.

Solución del flujo de potencia óptimo

Como se propone en Salmeron, Wood y Baldick (2004) el modelo de flujo de carga se simplifica mediante la implementación del modelo DC. Esta simplificación es válida en el contexto de los análisis de seguridad. El objetivo del flujo de carga DC es generar y distribuir energía a mínimo costo. El flujo de potencia óptimo DC se formula en la ecuación (2).

Sujeto a las siguientes restricciones:

El modelo DC-OPF minimiza generación más costos de deslastre (penalidades). La restricción (3) aproxima el flujo de potencia activa en las líneas. La restricción (4) representa el balance de potencia en los nodos. Las restricciones (5) y (6) establecen las capacidades máximas de transmisión y generación respectivamente. La restricción (7) establece que el deslastre de carga en los nodos no debe ser mayor a su respectiva demanda.

Modelo de interdicción

En el modelo de interdicción de la metodología VEGA (paso 2, figura 1) mediante el flujo óptimo de carga DC se minimizan los costos de generación más la demanda no satisfecha en el sistema de potencia (Salmeron, Wood y Baldick, 2003). En dicho sistema se retiran los componentes que han sido afectados por el atacante de acuerdo con el plan de ataque δ que se obtiene del problema principal (paso 6, figura 1). Las interdicciones δ llevadas a cabo por los atacantes son variables binarias que toman el valor de 1 cuando hay ataque y 0 en caso contrario. El modelo de interdicción I-DC-OPF se muestra en la ecuación (8).

Sujeto a las restricciones de las ecuaciones (9) y (10):

Donde:

Sujeto a las restricciones (13) a (16):

En la ecuación (15), mediante la adición del factor (1-δ_s^sub), se considera el caso de sistemas de potencia que contemplan generadores conectados directamente a uno de los nodos de una subestación (Leal, Sandoval y Cortés, 2007). Es decir, en el momento de ser atacada una subestación, los generadores que estén entregando su potencia a los nodos de ella deben ser desconectados como consecuencia del ataque. De acuerdo con Salmeron, Wood y Baldick (2004), la solución del I-DC-OPF maximiza la disrupción. La disrupción se evalúa a través del problema de minimización interno que consiste en un modelo de flujo de potencia óptimo DC-OPF del cual de antemano se retiran los componentes atacados. En el nivel superior, (9) refleja las opciones del atacante para ejecutar las diferentes combinaciones de ataque limitadas por el recurso total de ataque M. La expresión (10) define las opciones del atacante como variables binarias. Las ecuaciones (12) a (16) son análogas a (3) a (7), con la diferencia de que los componentes de sistema atacados (directa o indirectamente) han sido removidos de las ecuaciones a través de las variables binarias.

Modelado de los factores del entorno

Se decidió utilizar para este propósito un sistema lógico difuso tipo 2 (T2FLS, Type 2 Fuzzy Logic System) ya que es capaz de modelar eficientemente las incertidumbres acerca del significado de las palabras utilizadas en los factores del entorno geográfico; es decir, las palabras significan diferentes cosas para diferentes personas (Mendel, 2001). La naturaleza de esta incertidumbre concuerda con la definición de vaguedad, es decir, incertidumbre resultado de la imprecisión lingüística (Romero, 2005). Una descripción completa de los fundamentos matemáticos, metodologías de cálculo y aplicaciones de los conjuntos y sistemas de lógica difusa tipo 2 es presentada en Mendel (2001).

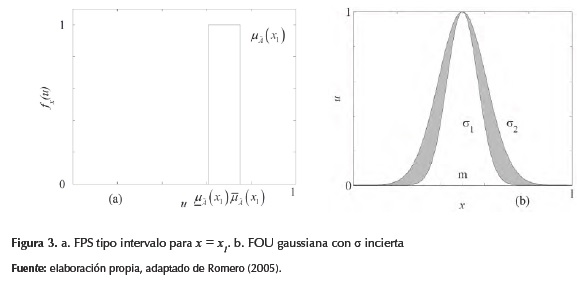
Para implementar los T2FLS, en este trabajo se utilizan funciones de pertenencia secundaria (FPS) de intervalo (figura 3a), dado que computacionalmente son menos complejas. Para determinar la huella de incertidumbre (FOU Footprint Of Uncertainty) de las funciones gaussianas con desviación estándar σ incierta que toma los valores entre [σ₁,σ₂] (figura 3b) se tiene la siguiente ecuación (17).

En los vectores, (18) y (19) muestran los valores de desviación estándar σ para implementar el T2FLS de la metodología propuesta; estos vectores contienen los cinco valores de desviación estándar σ₁ y σ₂ que se utilizan para las variables de entrada al T2FLS.

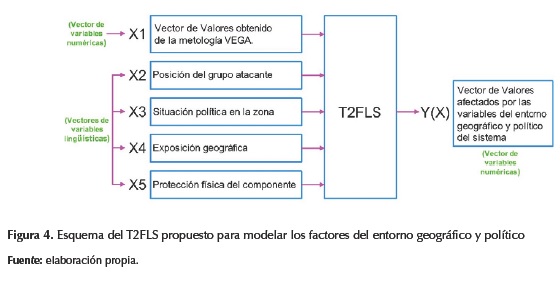
En la figura 4 se muestra el esquema del T2FLS que es propuesto para modelar los calificadores lingüísticos del entorno geográfico y político. La entrada X a este sistema se compone del vector de valores entregado por la metodología VEGA y de los calificadores lingüísticos del entorno geográfico, mientras que la salida Y(X) es el vector de valores con afectación del entorno geográfico y político.

Las entradas y salidas del T2FLS son vectores de n elementos, donde n es el número total de elementos del sistema de potencia (generadores, líneas, nodos y subestaciones). El vector de entrada X1 es el vector de valores obtenido de la metodología VEGA, el dominio de esta variable es el intervalo [0,1], cuanto más cercano a 1, mayor es la importancia del componente en el sistema de potencia. Los vectores X2, X3, X4 y X5 son de variables lingüísticas que toman los calificadores según la tabla 1. El vector de salida Y(X) es el vector de valores afectado por las variables del entorno geográfico y político del sistema. Al igual que el vector X1, el dominio de esta variable es el intervalo [0,1] y cuanto más cercano a 1, mayor es la importancia del componente en el sistema de potencia.

Los factores del entorno se definen de la siguiente forma:

• Predominio del grupo atacante: la presencia o predominio de un grupo atacante en un área determinada se entiende como el grado de influencia y control que este ejerce. Se relaciona con el grado de poder que el grupo posee en dicha zona.
• Situación política en la zona: mediante los ataques terroristas, los grupos insurgentes buscan un impacto político para alcanzar sus objetivos de intimidación en la población civil.
• Exposición geográfica de los componentes: Dado que los sistemas de potencia abarcan regiones extensas en las cuales la mayoría de los componentes se encuentran en zonas apartadas, los componentes del sistema que se encuentran más expuestos geográficamente son más vulnerables a ataques.
• Protección física de los componentes: Al encontrarse los sistemas de potencia localizados en vastas regiones, en la práctica es imposible proteger con la fuerza pública todos los componentes del sistema. Por ejemplo, las unidades de generación se encuentran más protegidas que las líneas de transmisión de energía.

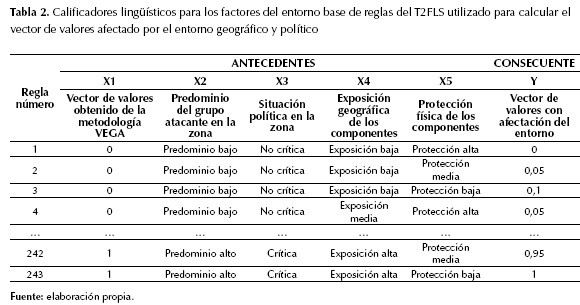
El T2FLS propuesto para calcular el vector de valores afectado por el entorno Y(X) utiliza la base de reglas mostrada en la Tabla 2. Cada regla tiene cinco antecedentes 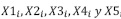y un consecuente Yi (Para la regla i). La regla número 1 representa la condición menos atractiva para el atacante ya que el valor del componente es 0, el predominio del grupo atacante en la zona es bajo, la situación política en la zona no es crítica, el componente del sistema de potencia no está expuesto y la protección física del componente es alta. Por otro lado, la regla número 243 presenta la condición más atractiva para el atacante, ya que el valor del componente es 1, el predominio del grupo atacante es alto, la situación política en la zona es crítica, el componente del sistema de potencia está expuesto y la protección física del componente es baja. El número de reglas es 3⁵=243, ya que son cinco antecedentes, cada uno de los cuales tiene tres estados. Se puede observar que el vector de valores con afectación del entorno Y, es una función de X1, X2, X3, X4 y X5. El T2FLS realiza un mapeo del espacio de entrada al espacio de salida utilizando la base de reglas de la tabla 2 (la tabla completa se puede descargar de http://tinyurl.com/zmesusp).

Algoritmo de interdicción

El algoritmo inicia solucionando el DC-OPF asumiendo que no hay ataques. El resultado es un flujo de potencia óptimo para operación normal, un flujo típico en el cual se minimizan los costos de generación sin deslastrar carga. El patrón de dicho flujo de potencia es utilizado para asignar valores relativos a todos los componentes del sistema: generadores, líneas, nodos y subestaciones. A continuación, en el problema principal se maximiza la sumatoria de los valores de los componentes, teniendo en cuenta que el recurso de ataque es limitado. Con este plan de ataque, se modifica el lado derecho de las ecuaciones del DC-OPF (12)-(16) y se obtiene su solución. El resultado es un flujo de potencia que otra vez minimiza costos de generación más la penalización asociada al deslastre de carga: es posible que en este caso algunas demandas hayan sido deslastradas ya que componentes valiosos han sido removidos del sistema. El proceso continúa mediante la identificación de diferentes conjuntos de componentes valiosos para atacar (planes de ataque) que no han sido encontrados en iteraciones anteriores, ecuación (28), así como mediante la evaluación del deslastre de carga asociado a cada plan de ataque.

Subproblema: DC-OPF para un plan de interdicción específico

Se asume que en la iteración t del algoritmo, un plan de ataque (interdicción) específico 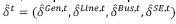es dado; el superíndice t es el contador de las iteraciones. El flujo de potencia DC-OPF 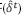asociado a la interdicción, junto a las ecuaciones (11)-(16) es lo que se conoce como el subproblema cuya solución conlleva al valor: 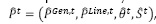, junto con las potencias generadas, flujos de potencia, ángulos de los fasores de tensión y potencias deslastradas; representados por 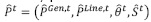. Este vector está representado por y en la ecuación (1).

Vector de valores

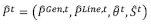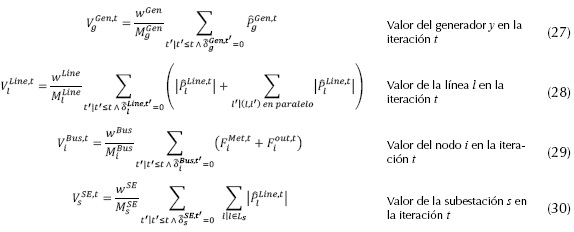
El vector solución que se obtiene como resultado del subproblema I-DC-OPF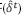 sirve para construir una lista de componentes del sistema no atacados que se ordena respecto a su atractividad para las siguientes interdicciones. Para determinar la importancia (valor) de cada uno de los componentes del sistema, Salmeron, Wood y Baldick (2003) definen las ecuaciones (20) a (26):

En las expresiones (20) a (26), las ponderaciones 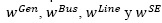son dadas como datos de entrada para representar los estimativos preliminares de los valores para cada tipo de componente del sistema. En los resultados mostrados en la sección 5 se usan los mismos valores de Salmeron, Wood y Baldick (2003), es decir, 2, 5, 1 y 5, respectivamente.

Desde el punto de vista del atacante, sus recursos de ataque son limitados y, por tanto, es conveniente atacar los componentes que requieran menos recursos. Los recursos requeridos para atacar un generador, línea, nodo o subestación son 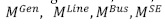respectivamente. Este hecho se tiene en cuenta mediante la inclusión del recurso de ataque en el denominador de cada una de las ecuaciones (27) a (30). Al ser mayor el recurso M requerido, se reduce el valor V del componente haciéndolo menos atractivo.

Cada vez que un componente es atacado, el flujo a través de este es nulo, por tanto, en la siguiente iteración no es atractivo para atacar. Para solucionar esto se define el valor acumulativo como el promedio de los valores de las iteraciones anteriores cuando el componente no ha sido atacado. Las ecuaciones (27) a (30) definen los valores de los componentes del sistema de potencia:

Problema principal

Como resultado del modelo de interdicción del punto anterior, se obtiene un vector de valores de todos los componentes del sistema 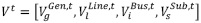. Con base en este se plantea el problema principal de maximización de tipo binario {0,1} para la variable δ, cuya función objetivo es definida en la ecuación (31):

Sujeto a las restricciones (32) a (39):

Las ecuaciones (33) a (37) tienen respectivamente los siguientes propósitos: atacar un generador o el nodo al cual está conectado, pero no ambos; atacar una línea o el nodo al cual está conectada, pero no ambos; si las líneas están en paralelo, atacar una, no ambas; atacar un nodo o su subestación, no ambos; atacar una línea o la subestación a la cual está conectada, no ambos. Dado que en la nueva metodología se considera el caso de generadores conectados directamente a las subestaciones, se adicionó la restricción (38), en la cual se ataca la subestación o el generador, pero no ambos. La solución del problema principal se expresa como 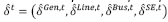y se utiliza en el subproblema para iniciar una nueva iteración del algoritmo.

Resultados

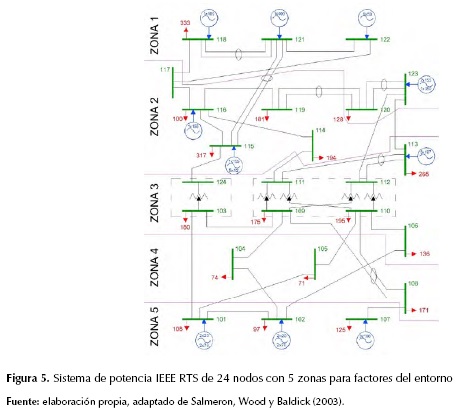
La metodología propuesta fue analizada en el mismo sistema de prueba de la metodología VEGA, es decir el sistema de prueba IEEE-RTS-1996 de 24 nodos (RTS Task Force, 1999). No obstante, para establecer diferentes condiciones del entorno se definieron 5 zonas geográficas, como lo muestra la figura 5.

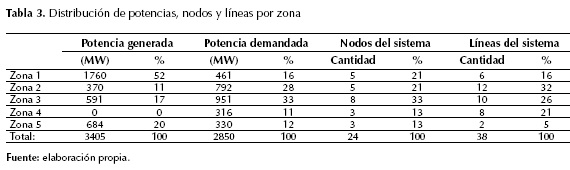
En la tabla 3 se resumen los datos del sistema de potencia de prueba, mostrando la distribución de potencia generada, la potencia demandada, la cantidad de nodos del sistema y la cantidad de líneas de transmisión del sistema, por cada zona.

La tabla 3 muestra que la zona que presenta la mayor potencia generada es la zona 1 con el 52 % del total de la generación del sistema, siguen en su orden las zonas 5, 3 y 2 con el 20 %, 17 % y 11 %, respectivamente. En la zona 4 no existe generación. Se observa además que la mayor potencia demandada se da en la zona 3 con el 33 % de la demanda total del sistema. Siguen en su orden las zonas 2, 1, 5 y 4 con el 28 %, 16 %, 12 % y 11 %, respectivamente.

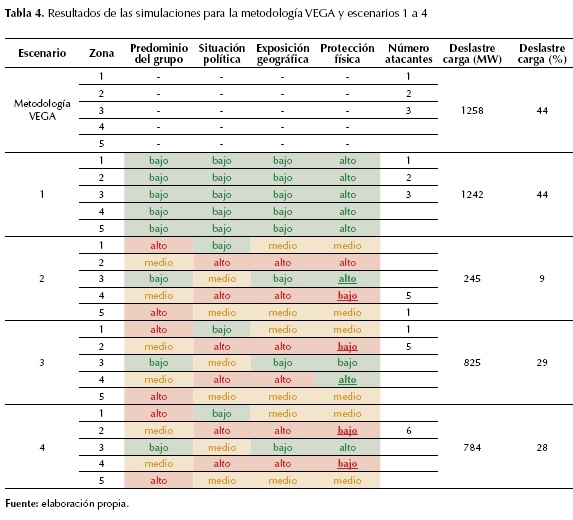
En la tabla 4 se muestran los resultados de cuatro escenarios iniciales propuestos para probar la metodología, junto con los resultados de originales de la metodología VEGA. Entre la información mostrada en las tablas se encuentra el número de atacantes en cada zona resultado de la aplicación de la metodología, así como el deslastre de carga en MW y en valor porcentual. En primer lugar se presenta el resultado correspondiente a la metodología VEGA el cual no contempla la influencia de factores del entorno geográfico, es decir, el predominio del grupo, la situación política, la exposición geográfica y la protección física de los componentes del sistema. Cuando un calificador lingüístico es mostrado con color verde significa que es la condición menos atractiva para el atacante, dado que los calificadores lingüísticos del entorno (predominio del grupo atacante, situación política en la zona y exposición geográfica del componente) son bajos y la protección física de los componentes es alta. Por otro lado, cuando un calificador lingüístico se muestra con color rojo significa que es la condición más atractiva para el atacante, dado que los calificadores lingüísticos del entorno son altos y la protección física de los componentes es baja. El color amarillo representa el valor medio entre los dos anteriores.

La combinación de factores del entorno utilizado en la metodología propuesta, que arroja el mismo ataque que el proyecto VEGA original, es aquella en la cual la combinación de factores del entorno es la menos atractiva para el atacante (los calificadores lingüísticos se muestran en color verde). Dicha combinación se muestra en el escenario 1 de la tabla 5. En los escenarios 2 a 4 se asumió una combinación de calificadores lingüísticos para la operación del sistema de potencia de prueba. Entre estos tres escenarios únicamente varía el calificador lingüístico correspondiente a la protección física para las zonas 2 y 4. En el escenario 2, esta se deja en alto para la zona 2 y en bajo para la zona 4. En consecuencia, la mayoría del ataque (cinco atacantes) se dirigen a la zona 4 ya que se encuentra con la protección física en bajo. En el escenario 3, la protección física se deja en bajo para la zona 2 y en alto para la zona 4. Como consecuencia de esto la mayoría del ataque (cinco atacantes) se dirigen a la zona 2 ya que se encuentra con la protección física en bajo. En el escenario 4, la protección física se deja en bajo tanto para la zona 2 como para la zona 4. En este caso la metodología podría dirigir el ataque a cualquiera de las dos zonas ya que ambas tienen la protección en bajo. En este caso, la metodología encuentra más atractivo dirigir el ataque a la zona 2 (seis atacantes) ya que allí se provoca el mayor deslastre de carga que es 784 MW.

Las simulaciones en los escenarios señalan que con la metodología propuesta, al incluir información sobre el entorno geográfico de cada zona del sistema de potencia, se obtienen distintos puntos de ataque y, por tanto, distintos valores de deslastre de carga. Esta metodología puede ser usada entonces para coordinar y afinar los planes de seguridad de la infraestructura eléctrica del sistema, teniendo en cuenta que siempre se cuenta con recursos limitados para su protección. Por ejemplo, con la configuración de protección física del escenario 2 tendría solamente 9 % de deslastre de carga, a diferencia del 28 % y 29 % de los escenarios 3 y 4.

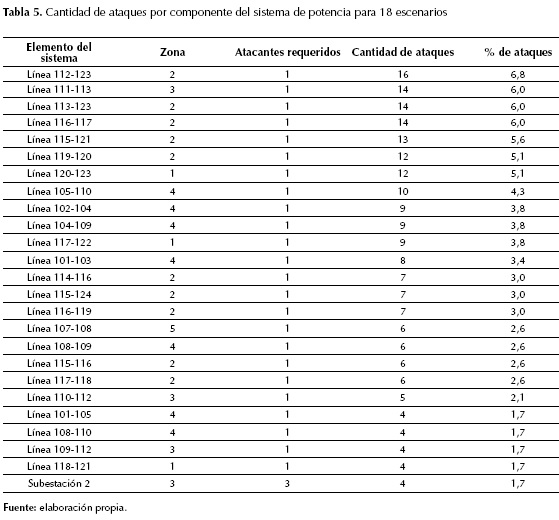
Por otra parte, la metodología propuesta puede ser usada para determinar los elementos más críticos del sistema, independientemente del entorno geográfico de cada una de las zonas del sistema de potencia. Es decir, algunos calificadores lingüísticos pueden variar con el tiempo, como por ejemplo, el predominio del grupo atacante en la zona puede variar, así como la situación política en la zona o la protección física de los componentes. Se puede entonces correr varios escenarios para establecer cuáles son los elementos que más presentan ataques sin importar la variación de los calificadores lingüísticos. En la tabla 5 se detalla la cantidad de ataques en cada componente del sistema de potencia para el sistema de prueba usado, considerando 18 escenarios. Allí se observa que el elemento más atacado es la línea de transmisión que se encuentra entre los nodos 112 y 123. Esta línea es estratégica para el sistema ya que conecta un nodo con alta potencia generada y la subestación 2 que se encuentra en la zona 3. Los siguientes elementos en importancia son las líneas 111-113, 113-123 y 116-117. De esta forma, se puede planear mayor protección para estos elementos identificados como críticos en por recibir más ataques en los escenarios estudiados.

De igual forma, se puede establecer cuáles son las zonas más críticas del sistema. La figura 5 muestra la distribución de ataques en las distintas zonas del sistema para los 18 escenarios contemplados. Se observa que la zona a la cual van dirigidos la mayor cantidad de recursos de ataque es la zona 2 con un 45 %. Una explicación de este fenómeno se debe a que la zona 2 es el punto intermedio entre la zona 1, que presenta la mayor potencia generada (52 %), y la zona 3 que posee la mayor potencia demandada (33 %). Otra explicación de este fenómeno es que la zona 2 posee la mayor cantidad de líneas de transmisión (las cuales requieren de un (1) solo atacante para su interdicción), y dicha zona posee 12 líneas que corresponden al 32 % del total de líneas

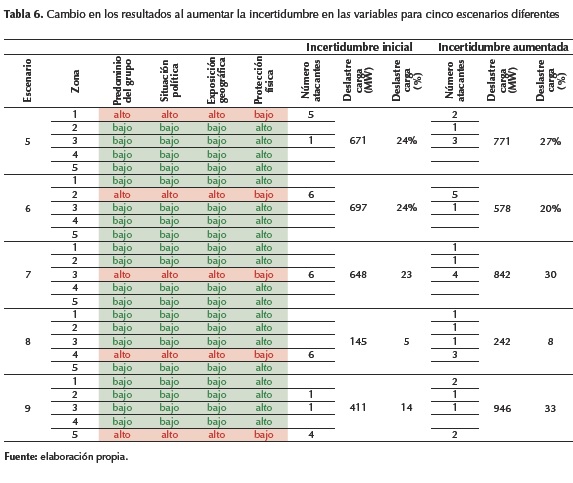
Por otra parte, es de interés conocer la influencia en los resultados del cambio de la incertidumbre en las variables, la cual es modelada con los conjuntos difusos tipo 2. La tabla 6 muestra cinco escenarios donde se calculan los cambios en los resultados al aumentar la incertidumbre sobre los valores de las variables. Nótese que al aumentar la incertidumbre, los ataques óptimos cambian, es decir, se puede tener distintos ataques. No obstante, los valores del deslastre de carga en los casos de incertidumbre aumentada son cercanos (entre 3 % y 19 %) del valor obtenido con los casos de baja incertidumbre.

Por último, en las pruebas realizadas en el sistema de prueba, la metodología no tuvo problemas de convergencia en todos los escenarios planteados, al igual que la metodología original planteada por Salmeron, Wood y Baldick (2004). No obstante, es necesario hacer pruebas de convergencia para sistemas de mayor tamaño (en número de nodos y elementos) para establecer las limitaciones de la metodología planteada.

Conclusiones

La metodología propuesta permite incorporar factores del entorno geográfico en el análisis de vulnerabilidad de sistemas de potencia, donde se integran en un mismo análisis información de tipo cualitativo como los factores del entorno (predominio del atacante, situación política, exposición geográfica y protección de componentes) y de tipo cuantitativo como los parámetros del sistema de potencia (potencias generadas, demandadas, capacidades, entre otros). Esto hace posible incorporar en el análisis de vulnerabilidad el conocimiento de los expertos en un determinado sistema de potencia. Se propone modelar la incertidumbre asociada con sistemas lógicos difusos tipo 2, debido a que los factores del entorno geográfico provienen de estudios y estimativos de diferente profundidad y detalle.

La metodología se validó usando el sistema de prueba de IEEE RTS-96, al que se le definieron cinco zonas geográficas. En dicho sistema se mostró que al incluir calificadores lingüísticos para las variables de predominio del grupo atacante, la situación política de la zona, la exposición geográfica de los elementos en la zona, y la protección física de los elementos, el máximo deslastre de carga varía desde 1258 MW en el caso más extremo a 145 MW. Además, la metodología permitió encontrar el componente más crítico del sistema (la línea 112-123), ya que es el elemento que es más veces atacado (16 veces) en los 18 escenarios estudiados. De igual forma, se puede establecer que la zona más crítica del sistema es la zona 2, en la cual se tienen el 45 % de los ataques en los 18 escenarios planteados.

La nueva metodología puede ser implementada en sistemas de potencia reales gracias a la definición de los factores del entorno geográfico y a su flexibilidad para definirlos. Gracias al modelado matemático de la incertidumbre no se requieren estudios detallados y extensos para obtener los datos necesarios para la implementación de la metodología. Para ello, se deben considerar: el conocimiento de los expertos en temas de seguridad y topografía en el sistema en estudio, y la experiencia de los operadores del sistema de potencia.

Financiamiento

Grupo de investigación EMC-UN de la Universidad Nacional de Colombia.

Referencias

Agudelo, L.; López-Lezama, J. y Muñoz, N. (2014). Análisis de vulnerabilidad de sistemas de potencia mediante programación binivel. Información Tecnológica, 24(3), 103-114.

Alguacil, N.; Delgadillo, A. y Arroyo, J.M. (2014). A trilevel programming approach for electric grid defense planning. Computer & Operations Research, 41, 282-290.

Arroyo, J. y Galiana, F. (2005). On the solution of the Bilevel Programming Formulation of the Terrorist Threat Problem. IEEE Transactions on Power Systems, 20(2), 789-797.

Bolaños, R. y Correa, C. (2014). Planeamiento de la transmisión considerando seguridad e incertidumbre en la demanda empleando programación no lineal y técnicas evolutivas. Tecnura, 18 (39), 62-76.

Delgadillo, A.; Arroyo, J. y Alguacil, N. (2010). Analysis of Electric Grid Interdiction With Line Switching. IEEE Transactions on Power Systems, 25(2), 633-641.

Leal, A.; Sandoval, D. y Cortes, C.A. (2007). Análisis de la metodología VEGA para estudiar la vulnerabilidad del sistema eléctrico de potencia colombiano. En: Encuentro Regional Iberoamericano del CIGRE-XII ERIAC (pp. 1-6). Foz de Iguazú: Cigre.

Mendel, J. (2001). Uncertain rule-based fuzzy logic system: introduction and new directions. Upper Saddle River: Prentice Hall PTR.

Motto, A.; Arroyo, J. y Galiana, F. (2005). A mixed-integer LP procedure for the analysis of electric grid security under disruptive threat. IEEE Transactions on Power Systems, 20(3), 1357-1365.

Perdomo F., D. (2015). Implicaciones del agotamiento de la reserva de potencia reactiva dinámica de las unidades de generación en la red de potencia. Tecnura, 19, 170-175.

Romero, J. (2005). Inferencia dinámica de la configuración operativa de la red de distribución de media tensión utilizando información de tiempo real, tiempo real extendido, histórica y conocimiento experto. Tesis de doctorado. San Juan, Argentina: Universidad Nacional de San Juan.

RTS Task Force. (1999). The IEEE reliability test system-1996. IEEE Trans. Power Systems, 14(3), 1010-1020.

Salmeron, J.; Wood, K. y Baldick, R. (2003). Optimizing Electric Grid Design Under Asymmetric Threat. Monterrey, California: Naval Postgraduate School.

Salmeron, J.; Wood, K. y Baldick, R. (2004). Analysis of electric grid security under terrorist threat. IEEE Transactions on Power Systems, 19(2), 905-912.

Tranchita, C. (30 de abril de 2008). Risk assessment for power system security with regard to intentional events. Tesis de doctorado. Bogotá, Colombia: Universidad de los Andes.

Tranchita, C.; Hadjsaid, N. y Torres, A. (2006). Ranking contingency resulting from terrorism by utilization of Bayesian networks. IEEE Mediterranean Electrotechnical Conference, MELECON (págs. 964-967). IEEE.