DOI:
https://doi.org/10.14483/22487638.11578Published:
2018-01-01Issue:
Vol. 22 No. 55 (2018): January - MarchSection:
ResearchVigencia del método de Roth para la determinación de fuerzas de cortocircuito en devanados de transformadores
Roth method validity for the determination of short-circuit forces in transformer windings
Keywords:
electrodynamic forces, short circuit, windings, analytical methods, mechanical stress (en).Keywords:
fuerzas electrodinámicas, cortocircuito, devanados, métodos analíticos, esfuerzo mecánico (es).Downloads
References
Ahn, H.-M., Oh, Y.-H., Kim, J.-K., Song, J.-S. y Hahn, S.-C. (2012). Experimental Verification and Finite Element Analysis of Short-Circuit Electromagnetic Force for Dry-Type Transformer. IEEE Transactions on Magnetics, 48(2), 819-822. http://doi.org/10.1109/TMAG.2011.2174212
Aslam M., M.S. (2007). Dynamic Behaviour of Transformer Winding under Short-Circuits. Johannesburg: University of the Witwatersrand.
Bertagnolli, G. (2006). The ABB Approach to Short-circuit duty of power Transformers. 3a. ed. Zúrich: ABB Management Services.
Bharat Heavy Electricals Limited (2003). Transformers. 2a. ed. Nueva Delhi: Tata McGraw-Hill Education Pvt. Ltd.
Bueno, M. y Pérez, L. (2007). Utilización de un método algorítmico y un sistema neurodifuso para localización de fallas en sistemas de distribución radiales. Tecnura, 20(10), 65-77.
Correa, W. (2014). Análisis de los esfuerzos dinámicos generados en un transformador de hasta 10 MVA durante una condición de cortocircuito franco. Cali: Universidad del Valle.
Deaconu, I., Chirilă, A., Ghiţă, C., Năvrăpescu, V. y Chicco, G. (2009). Analytical computation method for electrodynamic forces acting over electrical transformer windings. UPB - Scientific Bulletin, 71(series C), 143-154.
Díaz, G. (2013). Nueva metodología para el modelado magnético de transformadores con devanados en conductor laminado. Buenos Aires: Universidad Nacional de San Juan.
Estrada, N., Mora, J. y Pérez, S. (2008). Análisis y selección de los parámetros de configuración para un localizador de fallas monofásicas aplicado a sistemas de distribución. Tecnura, 11(22), 73-83.
Kurita, K., Kuriyama, T., Hiraishi, K., Kusumoto, S., Shida, S., & Hori, Y. (1969). Mechanical Strength of Transformer Windings under Short-Circuit Conditions. IEEE Transactions on Power Apparatus and Systems, PAS-88(3), 222–230. http://doi.org/10.1109/TPAS.1969.292310
Institute of Electrical and Electronics Engineers (2016). IEEE Std C57.12.00-2015 Standard for General Requirements for Liquid-Immersed Distribution, Power, and Regulating Transformers. Nueva York.
International Electrotechnical Commission (2006a). IEC 60076-5 Annex B Calculation method for the demostration of the ability to withstand the dynamic effects of Shortcircuit. Ginebra.
International Electrotechnical Commission (2006b). IEC 60076-5 Power transformers - Part 5: Ability to withstand short circuit. 3a. ed. Ginebra.
Kulkarni, S.V. y Khaparde, S.A. (2004). Transformer Engineering: Design and Practice. 4a. ed. Mumbai, India: Taylor & Francis.
Lurie, A., Zenova, V., Panibratets, A., Leviskaya, E., Drovishevskij, A., Milman, L. y Cadavid, H. (2005). Elektrodinamicheskaya stoikost’ transformatorov i reaktorov pri korotkikh zamykaniyakh (Electrodynamical Resistance of Transformers and Reactors under Short Circuits). Moscú: Znak.
Patel, M. (1973). Dynamic Response of Power Transformers Under Axial Short Circuit Forces Part I - Winding and Clamp as Individual Components. IEEE Transactions on Power Apparatus and Systems, PAS-92(5), 1558-1566. http://doi.org/10.1109/TPAS.1973.293702
Rosentino P., A.J. (2010). Estimativa dos esforços eletromecânicos em transformadores submetidos a um curto-circuito trifásico. Uberlândia: Universidade Federal de Uberlândia.
Saffari, S., Faiz, J., Fereidunian, A. y Ebrahimi, B.M. (2014). Analytical estimation of short circuit axial and radial forces on power transformers windings. IET Generation, Transmission & Distribution, 8(2), 250-260. http://doi.org/10.1049/iet-gtd.2013.0268
Saravolac, M. P., Vertigen, P. A., Sumner, C. A., & Siew, W. H. (2000). Design Verfication Criteria for Evaluating the Short Circuit Withstand Capability of Transformer Inner Winding. En CIGRE Session.
Smeets, R. y Paske, L. (2009). 13 Years Of Test Experiences with Short-Circuit Withstand Capability of Large Power Transformers. EnergoEkspert, 15(4), 1-84.
Solanilla, A.M., Hincapié, R.A. y Gallego, R.A. (2015). Planeación óptima de sistemas de distribución considerando múltiples objetivos: costo de inversión, confiabilidad y pérdidas técnicas. Tecnura, 19(43), 106-118.
Tournier, Y., Ebersohl, G., Ciniero, A., Yakov, S., Madin, A. B., & Whitaker, J. D. (1962). A study of the dynamic behaviour of transformer windings under short-circuit conditions. En Cigré Conférence Internationale des Grands Réseaux Electriquesa Haute Tension.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 3 de febrero de 2017; Aceptado: 28 de noviembre de 2017
RESUMEN
Contexto:
Debido a la dificultad para realizar la prueba de aptitud al cortocircuito en transformadores de gran potencia, la norma IEC 60076-5 2006 de la Comisión Electrotécnica Internacional acepta como método alternativo la estimación de las fuerzas y esfuerzos a través de cálculo y consideraciones de diseño.
Método:
En este artículo se presenta la implementación del método analítico de Roth para el cálculo de las fuerzas axiales y radiales de cortocircuito en un transformador trifásico con núcleo tipo columnas de 630kVA.
Resultados:
Las fuerzas máximas obtenidas con el método de Roth son comparables con las calculadas a través de métodos modernos para el diseño de transformadores como el método de elementos finitos, las diferencias entre los cálculos fueron mínimas a excepción de la fuerza axial máxima del devanado de baja tensión.
Conclusiones:
Aunque el método de Roth es una herramienta tradicional para solución de problemas de electromagnetismo, este es adecuado para hacer una estimación rápida y sencilla de parámetros magnéticos y fuerzas de cortocircuito en transformadores.
Palabras clave:
fuerzas electrodinámicas, cortocircuito, devanados, métodos analíticos, esfuerzo mecánico.ABSTRACT
Context:
Due to the difficulty of testing large power transformers, the International Electrotechnical Commission standard IEC 60076-5 2006 accepts as an alternative method to validate the short-circuit withstand ability, the forces and dynamic stresses estimation by means of calculation and design considerations.
Method:
In this paper, the Roth analytical method was used to calculate the axial and radial short-circuit forces in a three-phase 630kVA core type transformer.
Results:
The calculated forces provided by the Roth method are comparable to the values obtained through modern methods used for electrical transformers design as the finite element method, the difference among calculated values were minimum except the maximum axial force
Conclusions:
Although the Roth method is a traditional tool to solve electromagnetism problems, it is still suitable to compute magnetic parameters and transformers short-circuit forces in a fast and simple way.
Keywords:
electrodynamic forces, short circuit, windings, analytical methods, mechanical stress.INTRODUCCIÓN
Durante la operación de los transformadores se pueden presentar fallas de cortocircuito que conducen a un aumento excesivo en la corriente de los devanados; esta condición origina un incremento súbito en las fuerzas electrodinámicas que pueden generar afectaciones mecánicas sobre las bobinas y las estructuras de sujeción (Rosentino, 2010).
Las fallas en los transformadores generan interrupciones del suministro y problemas en los sistemas eléctricos; por tal razón, se ha despertado el interés de fabricantes, usuarios y operadores de red por mejorar el diseño de estos equipos y validar su comportamiento ante condiciones de falla (Bueno y Pérez, 2007; Estrada, Mora y Pérez, 2008).
La capacidad que tiene un transformador para soportar los esfuerzos de cortocircuito se puede determinar a través de la prueba de aptitud al cortocircuito definida en las normas IEC 60076-5 de 2006 e IEEE C57.12.00 de 2016 (International Electrotechnical Commission, 2006b; Institute of Electrical and Electronics Engineers, 2016). El ensayo requiere de una fuente de alimentación de gran potencia con niveles variables de tensión, de tal forma que se garantice condiciones de voltaje nominal durante las pruebas. Debido a las exigencias normativas existen pocas instalaciones en el mundo aptas para realizar el ensayo en transformadores de gran potencia (Smeets y Paske, 2009). Considerando estas dificultades, la norma IEC 60076-5 en su actualización del año 2006 incluyó la posibilidad de validación teórica de la aptitud al cortocircuito en transformadores. El procedimiento de validación teórica tiene dos alternativas: la primera se basa en el cálculo de fuerzas y esfuerzos claves, estos valores se comparan con los obtenidos en un transformador de referencia sometido exitosamente al ensayo; la segunda consiste en calcular los valores de fuerzas y esfuerzos máximos del transformador y compararlos con los límites de diseño establecidos por el fabricante (International Electrotechnical Commission, 2006b).
En este trabajo se describen las fuerzas electrodinámicas generadas durante una condición de cortocircuito y los efectos mecánicos que producen; luego se presentan algunos métodos utilizados para el modelado magnético y cálculo de fuerzas de cortocircuito en transformadores, y finalmente, se aplica el método analítico de Roth para el cálculo de las fuerzas en un caso particular, comparando los resultados con los obtenidos por el método de elementos finitos (MEF); esto demuestra la validez de la aplicación. Este artículo es producto de un trabajo de grado desarrollado en la escuela de ingeniería eléctrica y electrónica de la Universidad del Valle (Correa, 2014).
Fuerzas electrodinámicas de cortocircuito
De acuerdo con la ley de Ampere, cada elemento rectilíneo de un conductor con longitud dl, transportando una corriente I, en un campo magnético de densidad de flujo B, perpendicular a la longitud dl, se somete a una fuerza df, como se indica en la ecuación (1). La fuerza es perpendicular al plano formado por el vector de densidad de flujo magnético y el diferencial de longitud dl, aunque las fuerzas de cortocircuito tienen un origen electromagnético son conocidas como fuerzas electrodinámicas debido al efecto producido sobre los devanados y las estructuras de soporte del transformador (Aslam, 2007).

Si el análisis de fuerzas es hecho en dos dimensiones con la densidad de corriente en el eje Z, la densidad de flujo magnético en cualquier punto puede ser resuelta en dos componentes: uno en la dirección radial (B X ) y otro en la dirección axial (B Y ). Las fuerzas radiales (F X ) se originan por la interacción entre la corriente y la densidad de flujo magnético axial y las fuerzas axiales (F Y ) por la interacción entre la corriente y la densidad de flujo magnético radial.
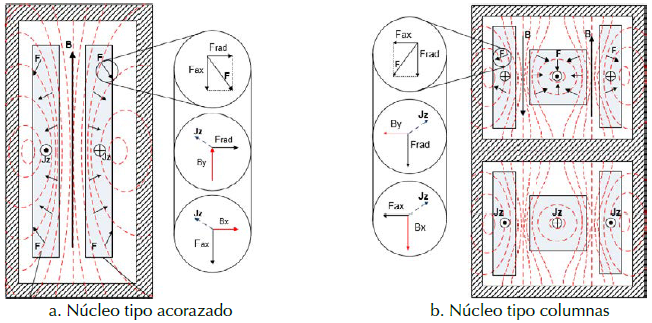
En transformadores con núcleo tipo columna, las fuerzas más significativas son las radiales, mientras que en transformadores con núcleo tipo acorazado las fuerzas axiales son predominantes (International Electrotechnical Commission, 2006a). En la figura 1 se observa el sentido de las fuerzas y la distribución de las líneas de campo magnético para diferentes tipos de transformadores.
Figura 1: Líneas de campo magnético y fuerzas en transformadores
Fuerzas de cortocircuito en transformadores con núcleo tipo columnas
Las fuerzas radiales tienden a comprimir el devanado interior hacia el centro del núcleo y expandir el devanado exterior; estas fuerzas producen esfuerzos mecánicos de tensión en los conductores del devanado exterior y de compresión en los conductores del devanado interior (Ahn et al., 2012).
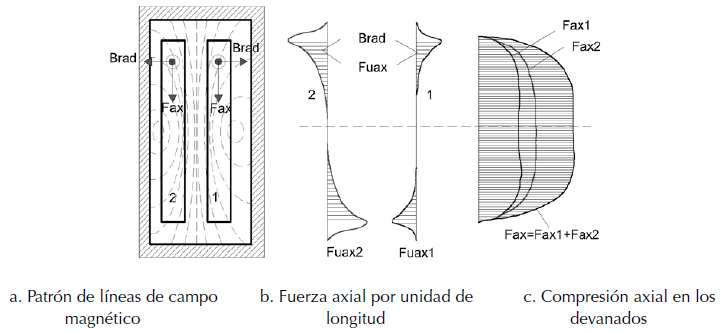
Las fuerzas axiales aparecen como consecuencia del establecimiento de líneas de campo magnético en la dirección radial, esta variación tiene lugar en la parte superior e inferior de las bobinas. En un transformador de dos devanados concéntricos, si las bobinas tienen alturas geométricas iguales, están alineadas radialmente y presentan una distribución uniforme de la fuerza magneto-motriz, las fuerzas axiales por unidad de longitud del conductor serán máximas en las espiras ubicadas en los extremos de los devanados; sin embargo, la fuerza de compresión axial total (acumulativa) será máxima en el centro de cada devanado, la distribución de las fuerzas axiales en transformadores con núcleo tipo columna se muestra en la figura 2.
Figura 2: Fuerzas axiales en transformadores con núcleo tipo columna
Cuando los centros magnéticos de los devanados no están alineados o existe un desequilibrio de la fuerza magneto-motriz, la densidad de flujo magnético radial aumenta y las fuerzas axiales tienden a desplazar los devanados e incrementar el desbalance de los centros magnéticos (Kulkarni y Khaparde, 2004).
Las fuerzas de cortocircuito tienen un carácter oscilatorio en el tiempo y actúan sobre un sistema mecánico compuesto por los conductores, el aislamiento y las estructuras de sujeción. Las fuerzas dinámicas transmitidas a varias partes del transformador pueden ser muy diferentes a las fuerzas de origen electromagnético generadas en los conductores, esto depende de las frecuencias naturales del sistema mecánico (Patel, 1973). En la dirección radial las frecuencias naturales son mayores a 100 y 120 Hz; por tanto, las probabilidades de que se produzca un fenómeno de resonancia mecánica son mínimas. En la dirección axial la cantidad de aislamiento es significativa, principalmente en transformadores de mediana y gran potencia, conllevando a que las frecuencias naturales mecánicas estén cerca de las frecuencias de oscilación de las fuerzas axiales, incrementando la probabilidad de aparición de resonancia mecánica; este fenómeno produce grandes desplazamientos de las bobinas y colapso de las estructuras de soporte (Kulkarni y Khaparde, 2004).
En transformadores con núcleo tipo columnas las fuerzas radiales producen esfuerzos de tensión circunferencial que tratan de estirar los conductores del devanado externo, si la tensión ejercida supera la tensión máxima del material la falla se manifiesta como ruptura del conductor. En el devanado interno las fuerzas radiales de compresión producen flexión del conductor entre soportes o pandeo, por su parte, las fuerzas axiales generan dos modos de falla los cuales son flexión entre separadores radiales e inclinación de los conductores (Bertagnolli, 2006).
La severidad de un cortocircuito en un transformador depende de las características del sistema donde está instalado, por tanto, dentro de la planeación de los sistemas eléctricos se deben considerar estrategias de protección que minimicen el tiempo de duración de las fallas, de esta manera se asegura la confiabilidad del suministro de energía eléctrica y la integridad del transformador (Solanilla, Hincapié y Gallego, 2015).
ESTUDIO DE LAS FUERZAS Y ESFUERZOS DE CORTOCIRCUITO
La determinación precisa de los esfuerzos mecánicos asociados a la condición de cortocircuito en transformadores implica que el problema se enfoque desde el punto de vista dinámico, sin embargo, estos cálculos son complejos y requieren información específica de los materiales constructivos utilizados por los fabricantes (International Electrotechnical Commission, 2006a).
Desde 1950 se han desarrollado estudios para analizar el comportamiento dinámico de los devanados de los transformadores. Inicialmente, estos se limitaron al modelamiento del comportamiento axial ya que se asumía que los devanados eran capaces de soportar los esfuerzos radiales, los modelos de análisis dinámico propuestos fueron simplificados para reducir tiempos de cálculo (Aslam, 2007).
Dentro de los estudios llevados a cabo desde el punto de vista dinámico se pueden destacar los propuestos por Tournier et al. en 1962, quienes desarrollaron un modelo para estimar el movimiento axial considerando los espaciadores radiales como resortes lineales; Patel en 1972 evaluó el comportamiento de los devanados y su sistema de sujeción ante fuerzas axiales de cortocircuito; Kurita et al. en 1971 llevaron a cabo un estudio experimental para investigar el comportamiento radial y axial de los devanados; Saravolac et al. en 2000 estudiaron la deformación radial de diferentes tipos de bobinas sometidas a fuerzas radiales uniformes (Aslam, 2007). En el año 2005, el Instituto de Investigaciones Eléctricas de Rusia publica un libro recopilatorio de los trabajos realizados sobre fuerzas electrodinámicas de cortocircuito, los estudios abarcaron transformadores de distribución y potencia implementando sistemas de medida, análisis numérico y ensayos sobre unidades completas (Lurie et al., 2005).
Los cálculos dinámicos pueden contribuir al entendimiento del fenómeno; sin embargo, definir un método general para demostrar la habilidad de los transformadores para soportar los esfuerzos dinámicos de cortocircuito aplicable a todas las prácticas de diseño resulta ser una tarea desafiante, por esta razón el enfoque dado por el procedimiento de validación teórica de la norma IEC 60076-5 de 2006 está limitado al cálculo estático de fuerzas radiales y axiales máximas y la evaluación de esfuerzos mecánicos claves según la forma constructiva del transformador (International Electrotechnical Commission, 2006b).
Métodos para el cálculo de fuerzas
El cálculo de las fuerzas de cortocircuito requiere la estimación del flujo magnético de dispersión en la región ocupada por los devanados, producido por el valor instantáneo de las corrientes de cortocircuito, para este propósito se pueden utilizar métodos analíticos que permiten modelar geometrías sencillas, requieren poca información y menor tiempo de cálculo comparado con métodos numéricos. Por otra parte, el estudio de transformadores elaborados con bobinas en conductores laminados se debe realizar utilizando metodologías que consideren la variación de la distribución de la corriente por el efecto de la densidad de flujo magnético radial, en este caso los métodos analíticos tradicionales resultan imprecisos. En la tabla 1 se muestran algunos métodos utilizados para el modelado magnético y cálculo de fuerzas de cortocircuito en transformadores (Díaz, 2013).
Fuente: elaboración propia.
Tabla 1: Métodos para el modelado magnético de transformadores y cálculo de fuerzas de cortocircuito

Los métodos de Roth y Rabins tienen similitud en cuanto al procedimiento utilizado para la solución del flujo magnético de dispersión en la ventana del núcleo; sin embargo, el método de Rabins requiere de funciones especiales de Bessel y Struve haciendo más compleja su implementación. Con el método de Roth para el cálculo de fuerzas máximas, se han reportado errores de hasta el 9 % comparado con la solución a través del método de elementos finitos (Saffari, Faiz, Fereidunian y Ebrahimi, 2014).
Método de Roth
Entre 1927 y 1938 el ingeniero francés Edouard Roth desarrolló un método para la solución de problemas de ingeniería eléctrica con condiciones de potencial vectorial magnético igual a cero en la frontera, para su aplicación a problemas de campos magnéticos en máquinas eléctricas. El método consiste en resolver la ecuación de Laplace-Poisson que relaciona el potencial vectorial magnético en cualquier punto con la densidad de fuerza magneto-motriz (FMM), asumiendo una geometría plana en coordenadas cartesianas en 2D (Bharat Heavy Electricals Limited, 2003).
Para determinar la fuerza es necesario conocer el valor pico de la corriente de cortocircuito asimétrica i, la cual se calcula a través de la ecuación (2). I sc es el valor eficaz de la corriente de cortocircuito simétrica, U es el voltaje de línea y Z es la impedancia equivalente en el punto de conexión del transformador, k es el factor de asimetría de la corriente y depende de la resistencia R y reactancia X del circuito (International Electrotechnical Commission, 2006b).
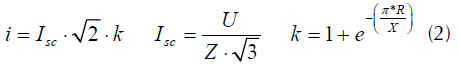
El potencial vectorial magnético A en la región de la ventana del núcleo se describe a través de las ecuaciones diferenciales de Laplace y Poisson (3), µ 0 es la permeabilidad magnética del espacio libre y J es la densidad de corriente, a partir de estas expresiones se obtienen las condiciones de contorno que se muestran en la ecuación (4).
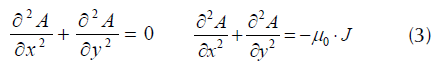
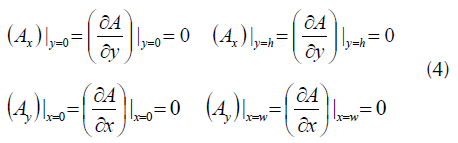
La densidad de corriente se calcula a partir de la ecuación (5), Nj es el número de espiras de la bobina j, mientras que wj, hj, w’j y h’j representan las coordenadas del devanado j-ésimo.
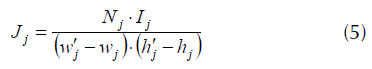
La solución para el potencial vectorial magnético A en la ventana del núcleo puede expresarse como una doble serie de Fourier como se observa en la ecuación (6), m y n corresponden a los términos de la serie. Los factores Mm y Nn se determinan a partir de la ecuación (7).
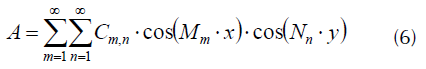
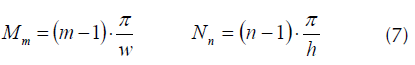
La ecuación (6) será una solución para el potencial vectorial magnético si cumple con (3), teniendo en cuenta esto se calculan los coeficientes C m,n para diferentes valores de m y n, tal como se muestra en las ecuaciones (8), (9) y (10).
Para m≠1 y n≠1.
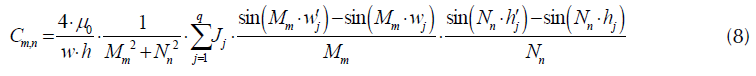
Para m=1 y n≠1
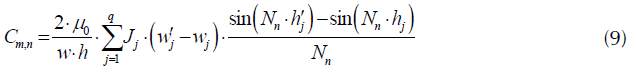
Para m≠1 y n=1.
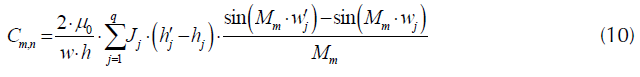
Una vez definido el potencial vectorial magnético se calculan los componentes de la densidad de flujo magnético en la dirección radial (B X ) y axial (B Y ) a través de la ecuación (11).
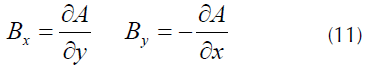
Las fuerzas radiales Frj y axiales Faj para un filamento de área d X *d Y se calculan según las ecuaciones integrales (12) y (13).
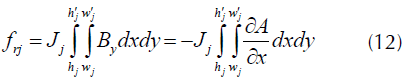
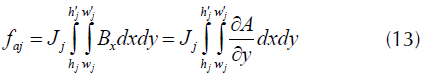
Finalmente, las fuerzas radiales y axiales por unidad de longitud del devanado quedan definidas por las ecuaciones (14) y (15) respectivamente (Saffari et al., 2014).
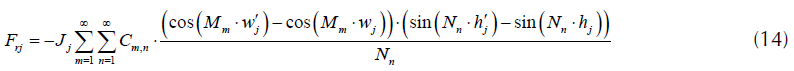
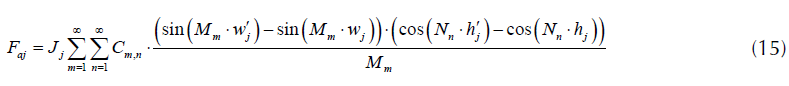
El método de Roth para el cálculo de la densidad de flujo magnético y fuerzas de cortocircuito en transformadores se implementó en el software Matlab®.
METODOLOGÍA
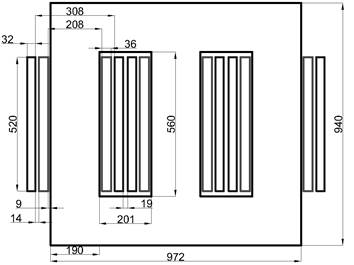
Se calcularon las fuerzas de cortocircuito en un transformador trifásico de dos devanados con núcleo tipo columnas de 630kVA (Deaconu et al., 2009). En la tabla 2 se muestran las características nominales del transformador utilizado para el análisis y en la figura 3 se incluyen las dimensiones. En este trabajo se evaluaron varios casos de estudio para analizar el efecto del número de armónicos sobre el cálculo de las fuerzas; los resultados fueron comparados con los obtenidos a través del método de elementos finitos (MEF) tomados de Deaconu et al. (2009).
Fuente: tomado de Deaconu et al. (2009).
Tabla 2: Especificaciones técnicas del transformador de estudio
Especificación
Valor
Potencia nominal [kVA]
630
Tensión nominal del primario [kV]
10
Tensión nominal del secundario [kV]
0,4
Impedancia de cortocircuito [%]
5,58
Espiras del primario/espiras del secundario
1082/25
Grupo de conexión
Dy5
Factor de asimetría (k)
1,8
Corriente de cortocircuito simétrica alta tensión (kA)
0,65
Corriente de cortocircuito simétrica baja tensión (kA)
16,29
Figura 3: Dimensiones en milímetros del transformador utilizado para el caso de estudio
RESULTADOS
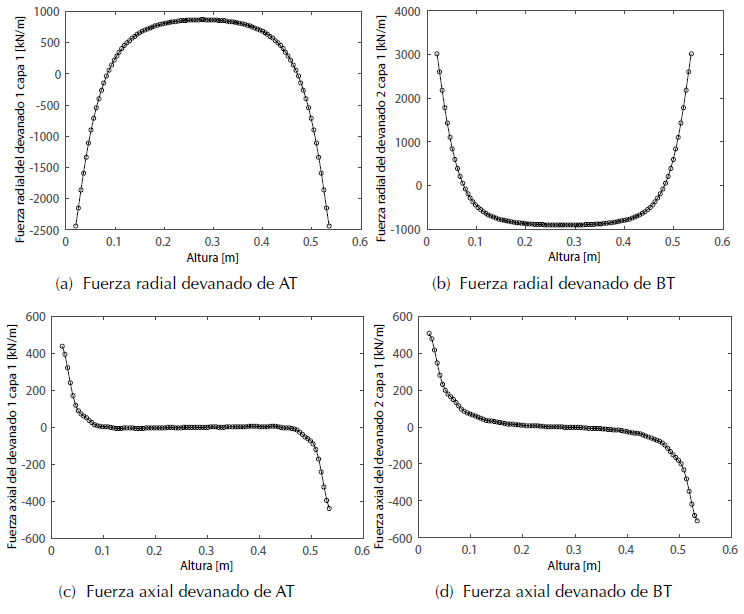
Se calcularon las fuerzas con el método de Roth evaluando el efecto del número de armónicos de la serie de Fourier, para este análisis se asumió que el devanado de alta tensión es el exterior (devanado 1), y el devanado de baja tensión es el interior (devanado 2).
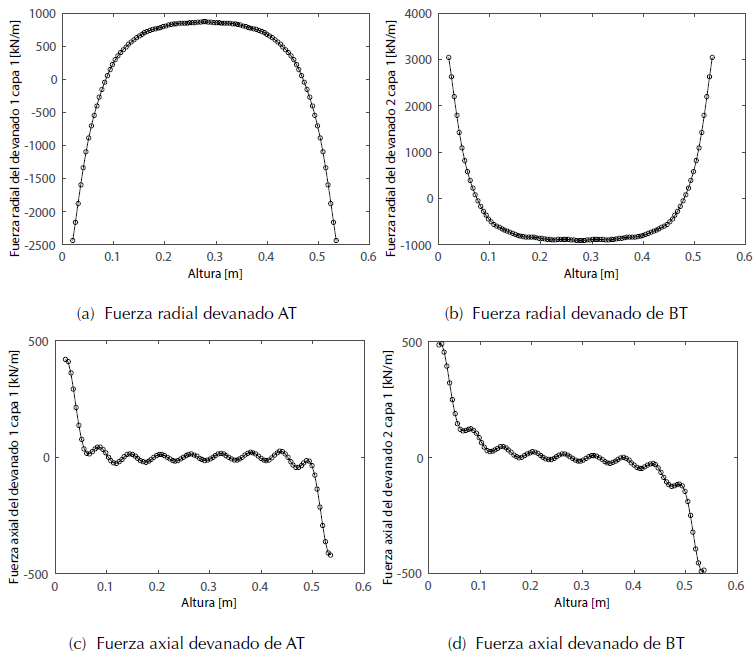
En la figura 4 se muestran las fuerzas radiales y axiales obtenidas con 20 armónicos y 100 divisiones sobre la altura de los devanados, con estos armónicos las gráficas de las fuerzas axiales presentan ondulaciones que alteran el valor de la fuerza en cada división de la altura.
Figura 4: Fuerzas calculadas con 20 armónicos y 100 divisiones en la altura
En la figura 5 se ilustran las fuerzas radiales y axiales calculadas con 30 armónicos y 100 divisiones sobre la altura de los devanados, la gráfica de fuerzas axiales presenta menos ondulaciones que las obtenidas con 20 armónicos; por tanto, se considera que 30 armónicos son suficientes para obtener una curva más suave que permite estimar el valor de la fuerza axial a lo largo de la longitud del devanado.
Figura 5: Fuerzas calculadas con 30 armónicos y 100 divisiones en la altura
El patrón de las curvas es el típico para las fuerzas tanto axiales como radiales, sin embargo, las curvas de fuerzas radiales muestran un desplazamiento sobre el eje de las ordenadas, teóricamente las fuerzas radiales en los devanados son unidireccionales, el devanado externo se somete a fuerzas de tensión y el devanado interno a fuerzas de compresión, aunque se presentó este desplazamiento de las curvas los valores máximos de las fuerzas no se afectaron.
En la tabla 3 se resumen las fuerzas máximas obtenidas para los diferentes casos de estudio; los valores calculados a través del MEF fueron tomados de Deaconu et al. (2009). Las fuerzas radiales máximas calculadas con 20, 30 y 60 armónicos presentan diferencias mínimas con respecto a los resultados del MEF, igual comportamiento se obtuvo con la fuerza axial máxima del devanado 1; sin embargo, en la fuerza axial máxima del devanado 2 se encontró una diferencia mayor, esto puede producirse debido a que la bobina de baja tensión es elaborada con conductores laminados y el método de Roth en este caso no proporciona los mejores resultados, este tema se continuará investigando en futuros trabajos.
Fuente: elaboración propia, resultados MEF (Deaconu et al., 2009).
Tabla 3: Comparación de resultados obtenidos con el método de Roth para diferentes casos de estudio
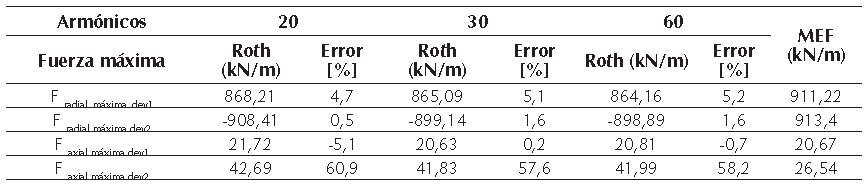
Utilizar un número mayor a 30 armónicos para el cálculo de fuerzas axiales o radiales no representa un cambio significativo en los errores promedio comparando el método de Roth con MEF.
Debido a las diferencias encontradas en la distribución grafica de las fuerzas radiales y el valor máximo de la fuerza axial del devanado 2 (devanado de baja tensión), se programó el método de Roth en el software Mathematica®, encontrándose las mismas diferencias evidenciadas en Matlab®, con esto se descarta algún inconveniente en el algoritmo programación del método de Roth.
CONCLUSIONES
En este artículo se presentó una aplicación del método de Roth para el cálculo de la densidad de flujo magnético y fuerzas de cortocircuito en transformadores con núcleo tipo columnas y devanados concéntricos circulares; a través de los resultados se demuestra la vigencia del método para el cálculo magnético de transformadores, por lo que es una alternativa frente a métodos modernos los cuales requieren herramientas de software especializadas y tiempos de modelado y cálculo prolongados.
De acuerdo a los resultados, se puede afirmar que la aplicación del método de Roth es adecuada cuando se desean conocer las fuerzas máximas de cortocircuito; la distribución de las fuerzas radiales a lo largo del devanado presenta ciertas diferencias, las cuales se podrían revisar evaluando las ecuaciones originales propuestas en la metodología de Roth o implementando el método analítico de Rabins para efectos de comparación.
El cálculo de las fuerzas máximas de cortocircuito a través del método de Roth representa la etapa inicial del procedimiento de validación teórica de la aptitud para soportar cortocircuitos en transformadores; a partir de estas se estiman esfuerzos en los conductores y estructuras de soporte del devanado, posteriormente estos valores son comparados con los límites definidos en la norma para demostrar teóricamente la aptitud al cortocircuito del equipo.
El método de Roth es una de las primeras herramientas para el cálculo magnético de transformadores con núcleo tipo columnas y devanados circulares concéntricos, a pesar de su antigüedad aún está vigente y sus resultados pueden compararse con técnicas modernas de diseño como el método de elementos finitos. La ventaja de este radica en su facilidad de implementación y en la velocidad de cálculo, lo que facilita realizar análisis en la etapa de diseño de transformadores.
REFERENCIAS
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.