DOI:
https://doi.org/10.14483/22487638.11708Publicado:
2017-10-01Número:
Vol. 21 Núm. 54 (2017): Octubre - DiciembreSección:
InvestigaciónModelación estadística de la textura del clutter marino en Matlab
Statistical modeling of the texture of sea clutter in Matlab
Palabras clave:
Statistical modeling, sea clutter, texture of the clutter, gamma distribution, inverse gamma distribution, inverse gaussian distribution, root-gamma distribution (en).Palabras clave:
Modelación estadística, clutter marino, textura del clutter, distribución gamma, distribución inversa gamma, distribución inversa gaussiana, distribución raíz gamma (es).Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 2 de marzo de 2015; Aceptado: 28 de agosto de 2017
Resumen
Contexto:
La modelación estadística de la señal interferente conocida como clutter marino se efectúa a través de dos componentes: uno de capilaridad y otro de textura. La distribución más utilizada para la textura es la gamma. No obstante, varios autores han defendido el uso alternativo de la inversa gamma y la inversa gaussiana.
Método:
Con el objetivo de brindar un acceso fácil a la manipulación de los modelos y a la realización de comparaciones entre ellos, los autores del presente artículo simularon en Matlab las características principales de estas tres distribuciones. Adicionalmente, se agregó la distribución raíz gamma que sustituye a la gamma cuando se trabaja con muestras de amplitud. El método aplicado consistió en la revisión bibliográfica para encontrar las expresiones de cada uno de los parámetros modelados, y la posterior simulación computacional que permitió detectar errores ocasionales que surgen al consultar diferentes estudios.
Resultados:
Se creó una pequeña librería de simulación estocástica que incluye funciones de densidad y distribución, generación de variables aleatorias, estimación de parámetros y cálculo de momentos estadísticos, entre otros. Además, se elaboraron funciones informáticas complementarias que permitieron la validación por comparación con resultados dados por terceros y mediante la interacción de los diferentes componentes de la librería.
Conclusiones:
La librería creada habilita el uso de múltiples distribuciones, para la modelación del eco electromagnético de la superficie marina. Esto permitirá generar nuevos detectores de radar que se adapten a condiciones heterogéneas como las encontradas en las costas cubanas, donde alternan distintos niveles de profundidad, manglares, aguas salobres, islotes, vegetación acuática prominente, entre otras.
Palabras clave:
modelación estadística, clutter marino, textura del clutter, distribución gamma, distribución inversa gamma, distribución inversa gaussiana, distribución raíz gamma.Abstract
Context:
The statistical modeling of the interference signal known as sea clutter is achieved assuming the input results from the combination of two components: one for the speckle and another for the texture. The Gamma distribution is the more widely applied for the texture component. Nevertheless, several authors have defended the idea of using the Inverse Gamma and Inverse Gaussian instead.
Method:
In order to provide an easy access to the handling of the models and the execution of comparisons between them, the authors of the current paper simulated in MATLAB the main characteristics of these distributions. In addition, the Root-Gamma model was also included because it replaces the Gamma distribution when samples are processed in the amplitude domain. The applied method consisted in a deep bibliography review for finding the corresponding expressions for each simulated model; the method also included additional computational simulations that allowed to identify occasional errors that were committed by different authors when characterizing the models.
Results:
A small framework was created for stochastic simulation containing density and distribution functions, mechanisms for random variable generation, parameter estimation methods and statistical moment closed expressions, among others. Besides, complementary functions were prepared for guaranteeing the validation by comparison with results provided by third parties and through the interaction between the different components of the library.
Conclusions:
The created library enables the use of multiple distributions for the modeling of the electromagnetic echo received from the sea surface. This will certainly motivate the creation of new radar detectors adapted to heterogeneous conditions such as the ones existing in Cuban coastal regions, where one may find different depth levels, mangrove swamps, brackish water, islets, prominent aquatic vegetation, among others.
Keywords:
statistical modeling, sea clutter, texture of the clutter, Gamma distribution, Inverse Gamma distribution, Inverse Gaussian distribution, Root-Gamma distribution.INTRODUCCIÓN
El clutter marino es la principal señal interferente que es necesario procesar en sistemas de radar. Cuando el haz del radar explora un medio marino, la señal de sondeo, además de reflejarse sobre los barcos o aviones que vuelan a baja altitud, interactúa con la superficie del mar, provocando un eco que se recibe de vuelta por la propia antena transmisora. Dada la variabilidad introducida por el oleaje, esta señal de eco, o clutter, toma amplitudes cambiantes con valores elevados (spikes) que pueden confundirse con blancos (Skolnik, 2008).
La supresión del clutter se realiza comúnmente con procesadores de razón de falsa alarma constante (CFAR, constant false alarm rate) de ventana deslizante, que requieren de la suposición de un modelo para el clutter, de forma que pueda ajustarse el umbral de detección de manera eficiente (Rohling, 1983). Esta necesidad ha motivado el estudio de la estadística del clutter, caracterizándose el fondo con distribuciones estadísticas variadas.
Aunque distribuciones más sencillas matemáticamente, como la weibull (Ishii, Sayama y Mizutani, 2011; Palama, Greco, Stinco y Gini, 2013), y la log-normal (Chen, Liu, Wu y Wang, 2013; Sayama e Ishii, 2013), han encontrado aplicación en la representación del clutter marino, generalmente se reconoce a la distribución K como la que mejor modela el fenómeno. Con una enorme cantidad de desarrollos vinculados (Meng, Feng, Xue y He, 2013; Tanriverdi, 2012; Yunlong, Chao, Hongzhong y Qiang, 2012; Zhijian, Ruilai, Yong y Jian, 2011; Zhou y Wang, 2009), la distribución K debe su popularidad al hecho de que se relaciona con las características físicas del mar.
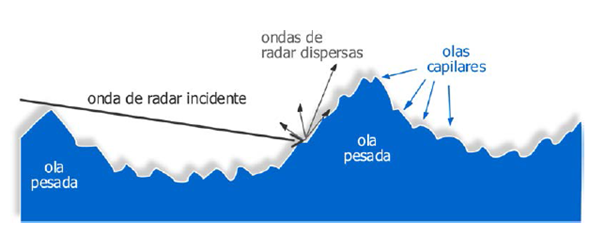
El modelo K surge de combinar las distribuciones exponencial y gamma, asumidas para la capilaridad (speckle) y la textura respectivamente (Chan, 1990). La textura representa las olas gravitatorias, u olas pesadas, que no se rigen por las variaciones del viento, y tienen mayores longitudes de onda, con un ritmo lento de cambio.
Como se aprecia en la figura 1, las olas capilares tienen menores dimensiones y son moduladas por las gravitatorias. Las olas capilares suman un número elevado y son generadas por la influencia del viento, expresando la tensión superficial del agua. La velocidad de cambio es mucho mayor en este caso, lo cual justifica la aplicación de dos distribuciones independientes (Totir, Rador y Anton, 2008). En efecto, gracias a su definición compuesta, el modelo K tiene ventajas en la representación de las propiedades de correlación de la señal de clutter (Yunlong et al., 2012).
Figura 1: Dinámica del mar: olas capilares moduladas por olas pesadas o gravitatorias
La distribución exponencial usada para la capilaridad ha sido aceptada por la mayoría de los autores, sin que se ofrezcan argumentos sólidos en su contra. Por el contrario, modificaciones han sido presentadas en diversos artículos para el cambio de la distribución de la textura hacia los modelos inversa gamma (Rosenberg y Bocquet, 2013, 2015; Stinco, Greco y Gini, 2011) e inverso gaussiano (Chen, Cui, Kong y Yang, 2014; Mezache, Soltani, Sahed y Chalabi, 2015; Ollila, Tayler, Koivumen y Poor, 2012), con lo que se demuestra que estos pueden proporcionar mejores ajustes a los datos de clutter marino.
A pesar del éxito de las nuevas distribuciones, la K continúa siendo la opción preferencial en la mayoría de las investigaciones actuales (Jiang et al., 2015; Schoenecker, Willett y Bar Shalom, 2016; Wang et al., 2015). Igualmente, muchos de los estudios realizados sobre datos de clutter no consideran las texturas inversa gamma e inversa gaussiana, sino que aplican invariablemente una textura gamma (Fioranelli et al., 2016; Johnsen, 2015; Preston y Abraham, 2015; Ritchie, Stove, Woodbridge y Griffiths, 2016). Una de las principales limitantes en este sentido es la reducida difusión de las distribuciones entre la comunidad de radar.
Para solucionar este problema, los autores se dieron a la tarea de recopilar en un solo documento las definiciones matemáticas fundamentales relacionadas a las distribuciones gamma, inversa gamma e inversa gaussiana. Además, se implementó una pequeña librería de código abierto en Matlab donde se pueden simular las funciones de densidad y distribución, la generación de muestras aleatorias, el cálculo de los momentos y la estimación de los parámetros de las distribuciones, entre otros. También se agregaron funciones adicionales para validar el código por comparación con resultados dados por terceros y mediante la interacción de las propias funciones. La distribución raíz gamma fue incluida como un cuarto componente de la librería, ya que ella se obtiene cuando se procesa en el dominio de la amplitud, mientras que la gamma corresponde al dominio de la potencia.
Se espera que el presente artículo contribuya a fomentar el uso de diferentes alternativas para la textura del clutter marino, y que facilite la realización de comparaciones fiables, así como el diseño de detectores adaptados a diferentes condiciones electromagnéticas. La implementación realizada es de código abierto y contiene varias funciones no presentes en el Toolbox estadístico de Matlab 2016.
El artículo se desarrolla como sigue. La “Metodología” introduce las definiciones matemáticas de las cuatro distribuciones modeladas en Matlab y describe las funciones informáticas que fueron creadas. “Resultados” ofrece ejemplos de utilización del código creado, además muestra la validación de este. Luego, en “Valoración del estudio”, se analizan los principales aportes y aplicaciones de la investigación. “Conclusiones” resalta los puntos fundamentales de la labor realizada y ofrece pautas para el desarrollo ulterior.
METODOLOGÍA
En esta sección se presentan los fundamentos matemáticos de las distribuciones gamma, raíz gamma, inversa gamma e inversa gaussiana. Posteriormente, se describen las funciones informáticas implementadas en Matlab.
Distribución gamma
La distribución gamma es asumida comúnmente para la textura del clutter marino, como parte de la formulación compuesta de la distribución K cuando se trabaja con muestras de intensidad (Fioranelli et al., 2016; Ritchie et al., 2016; Schoenecker, Willett y Bar Shalom, 2016). La función de probabilidad de densidad (PDF, probability density function) (Watts, 2012) y la función de distribución acumulada (CDF, cumulative distribution function) (O’Connor, 2011) gamma, se muestran en las ecuaciones (1) y (2), respectivamente.
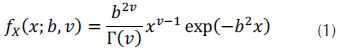
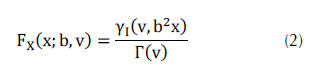
Donde b es el parámetro de escala, v es el parámetro de forma y Γ(.) es la función gamma, o función gamma completa, definida (O’Connor, 2011) según la ecuación (3).
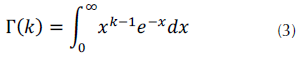
Además, γ1(.) es la función gamma incompleta, o función gamma incompleta inferior, que obedece a la ecuación (4) (O’Connor, 2011).
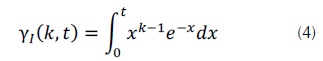
La media (E[x]), la varianza (V[x]), y el tercero (μ3) y cuarto (μ4) momentos centrados se calculan como (Krishnamoorthy, 2016) se indica en las ecuaciones descritas en (5) (Krishnamoorthy, 2016).
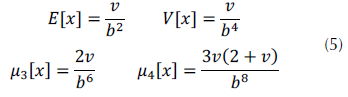
Mientras que la asimetría (S[x]) y la curtosis (K[x]) se ofrecen en la ecuación (6) (Walck, 2007).
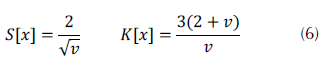
Los momentos con respecto al origen se pueden calcular como se aprecia en la ecuación (7) (Krishnamoorthy, 2016).
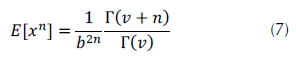
La ecuación (8) muestra cómo puede realizarse la estimación de los parámetros gamma a través del método de los momentos según Forbes, Evans, Hastings y Peacok (2011).
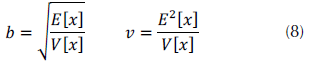
Para la generación de muestras gamma se han presentado una buena cantidad de algoritmos. La variante de Marsaglia y Tsang (2000) aplica un método de aceptación/rechazo que ha probado ser muy eficiente, manteniendo a la vez una secuencia simple de pasos. La propuesta es válida para v ≥ 1.
Paso 0: (Preparación) Calcular 
Paso 1: Generar V = (1+CN)3 donde N es una variable estándar normal. Repetir si V ≤ 0
Paso 2: Generar U distribuida estándar uniforme.
Paso 3: Si U <1 - 0,0331N 4 devolver D * V
Paso 4: Si ln (U)<0,5N 2 +D(1-v + in (V))devolver D * V
VPaso 5: Ir al paso 1
Para generar muestras gamma ( γv ) con v < 1 se implementó el algoritmo de Best (1993) que fue recomendado por Gentle (2003).
Paso 0: (Preparación) Calcular 
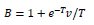
Paso 1: Generar dos variables U 1 y U 2 distribuidas uniformemente.
Calcular V = BU 1
Paso 2: Si V ≤ 1 S = TV 1/V
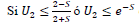entonces devolver 5
De lo contradio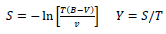 
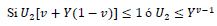entonces devolver 5
Paso 3: Volver al paso 1.
Luego de ejecutar cualquiera de los dos algoritmos anteriores, se obtiene un número aleatorio distribuido gamma con el parámetro de forma (v) especificado y con parámetro de escala igual a la unidad (b = 1). Si se multiplica a la variable generada por 1/ b2 , el parámetro de escala pasará a ser b en lugar de 1.
Distribución raíz gamma
La distribución raíz gamma (root-gamma), también conocida como generalizada chi-cuadrado (generalized-chi-squared), se aplica en la modelación de la textura del modelo K compuesto para el tratamiento de señales de amplitud (Fiche, Angelliaume, Rosenberg y Khenchaf, 2015; Marhaban, 2008; Santos Ugarte, De Miguel Vela y Besada Portas, 2008). Ella surge a partir de hallar la raíz cuadrada a una variable distribuida gamma, de ahí la similitud entre las definiciones de ambos modelos.
La PDF raíz gamma fue dada en Tanriverdi (2012), como se indica en la ecuación (9).
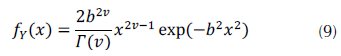
La CDF de la distribución puede calcularse a partir de la ecuación (9), dando lugar a la ecuación (10).
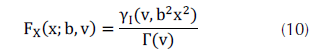
La generación de muestras raíz gamma se realiza utilizando los mismos algoritmos que para el caso gamma, y luego aplicando la raíz cuadrada al resultado.
La ecuación (11) muestra la manera en que se calculan los momentos algebraicos de este modelo de acuerdo con Cetin (2008).
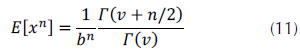
Las expresiones de los momentos centrales, junto a la asimetría y la curtosis, pueden calcularse usando las siguientes expresiones de transformación a partir de los momentos algebraicos (Walck, 1991), dadas en la ecuación (12).
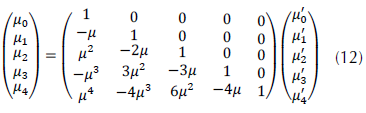
Donde μ'n son los momentos algebraicos de orden n, μ es la media y μn los momentos centrados de orden n.
Por último, dado que no se encontró ningún método de estimación de la distribución raíz gamma en la literatura revisada, los autores dedujeron un mecanismo de estimación a través del método de los momentos. Luego de calcular los dos primeros momentos algebraicos de un grupo de muestras, se puede encontrar el parámetro de forma usando la ecuación (13).
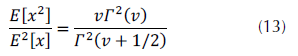
La ecuación (13) anterior debe resolverse aplicando una búsqueda binaria ante la imposibilidad de despejar la v dentro de la función gamma. Luego, el parámetro de escala se halla aplicando la ecuación (14).
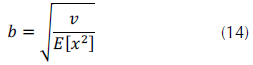
Distribución inversa gamma
La distribución inversa gamma, también conocida como Pearson tipo V, o gamma invertida (inverted gamma), está siendo utilizada con una frecuencia cada vez mayor en la modulación de la componente de textura del clutter marino (Palama, Greco, Stinco y Gini, 2015; Turlapaty y Jin, 2016), como parte del modelo compuesto gaussiano (compound Gaussian). Igualmente, se aplica cuando se trata la modelación de la distribución Pareto asumiendo que se está en presencia de un modelo compuesto por una distribución exponencial modulada por una distribución inversa gamma (Rosenberg y Bocquet, 2015; Wang y Xu, 2014, 2015). Además, el modelo se ha extendido para datos de radar de apertura sintética (SAR, synthetic aperture radar) (Ku Mahapatra y Prosad Roy, 2015).
La ecuación (15) ofrece la fórmula de la PDF de la distribución inversa gamma (Bocquet y Rosenberg, 2014).
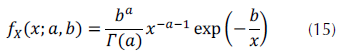
Donde a es el parámetro de forma, b es el parámetro de escala y Γ(.) es la Función Gamma, o Función Gamma Completa, definida de acuerdo a la ecuación (3) (O’Connor, 2011).
Por su parte, la CDF, dada por McLaughlin (2014), se muestra en la ecuación (16).
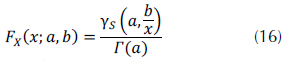
Donde Ys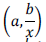 
hace referencia a la función gamma incompleta superior (upper incomplete gamma function) definida por (O’Connor, 2011), como se observa en la ecuación (17).
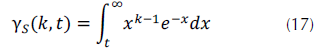
La media y la varianza, dadas en la ecuación (18), fueron tomadas de Fayard y Field (2009).
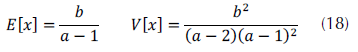
Por su parte, la ecuación (19) muestra cómo puede hallarse la asimetría y la curtosis (Carolynne, 2013).
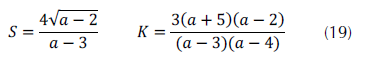
Según fue planteado en Llera y Beckmann (2016), la estimación de los parámetros de la inversa gamma puede hacerse a través del método de los momentos que resulta en la ecuación (20).
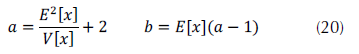
Los momentos algebraicos, o momentos con respecto al origen, de la distribución Inversa Gamma fueron dados por Carolynne (2013), y se ofrecen en la ecuación (21).
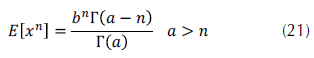
La distribución inversa gamma debe su nombre a que si X es una variable distribuida gamma, entonces se distribuye inversa gamma. Para generar valores de la distribución inversa gamma, una solución fácil es generar muestras de la distribución gamma y hallarle el inverso (Gentle, 2013). El parámetro de forma de la distribución gamma coincidirá con el de la inversa gamma, mientras que el parámetro de escala de la gamma será el cuadrado del de la gamma (McLaughlin, 2014). Lo anterior es cierto si se asume que la PDF gamma es la dada en la ecuación (1).
Un análisis similar es también aplicable para la distribución inversa Wishart que resulta del inverso de una variable distribuida Wishart. En cambio, el procedimiento no es aplicable a la inversa gaussiana donde el término inversa no significa que la distribución se obtenga mediante el inverso de la distribución normal o gaussiana.
Distribución inversa gaussiana
La distribución inversa gaussiana fue utilizada por primera vez para representar la textura del clutter marino por Olilla et al. (2012), donde se probó que proporcionaba un mejor ajuste que sus competidores gamma e inversa gamma, para un conjunto de datos tomados por el radar IPIX de la Universidad de McMaster. La inversa gaussiana aplicada contó con un único parámetro de escala, dando lugar al modelo global de la amplitud denominado inverso gaussiano-compuesto gaussiano (inverse Gaussian compound Gaussian, IG-CG).
Posteriormente, en Mezache, Soltani, Sahed y Chalabi (2013, 2015), se introdujo una distribución inversa gaussiana más general con un parámetro de escala y otro de localización, produciéndose el modelo global de la envolvente denominado compuesto inverso gaussiano (CIG, compound inverse Gaussian). El nuevo modelo fue hallado superior al previo IG-CG, al K y a otros cinco modelos para un grupo de datos específicos.
Si bien algunos artículos han comenzado a aplicar la textura inversa gaussiana en diversos desarrollos (Chen et al., 2014; Gao, Zhan y Wan, 2014; Mezache et al., 2016; Yi, Yan y Han, 2014), la distribución no ha adquirido aún un alto grado de aceptación en la comunidad de modelación de clutter de radar. Este hecho se justifica, en parte, por el corto tiempo que ha transcurrido desde su aplicación inicial. Dado que los pocos estudios relacionados a ella han brindado resultados excelentes, los autores del presente artículo la recomiendan para la evaluación de la textura del clutter.
La PDF de la distribución inversa gaussiana, también conocida como Wald (Forbes et al., 2011), se ofrecen en la ecuación (22) (tomada de Mezache et al., 2013, 2015).
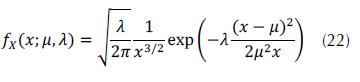
Donde μ es el parámetro de localización y λ es el parámetro de escala.
La CDF de la inversa gaussiana fue dada por Krishnamoorthy (2016), y obedece a la ecuación (23).
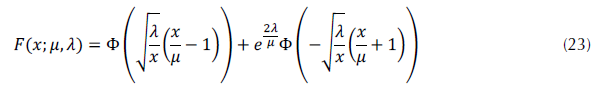
Donde es el CDF de la distribución estándar gaussiana.
La ecuación (24) muestra la forma en que se calculan los momentos algebraicos (Mezache et al., 2015).
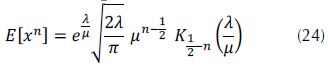
Donde es la función modificada de Bessel de segundo tipo y orden .
Alternativamente, de acuerdo con (Mezache et al., 2015), los tres primeros momentos algebraicos pueden calcularse usando la ecuación (25).
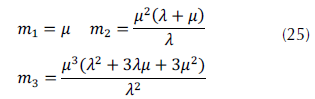
La ecuación (26) contiene la fórmula de los momentos con respecto a la media (Forbes et al., 2011).
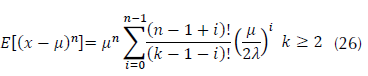
Conjuntamente, la varianza, la asimetría y la kurtosis pueden calcularse aplicando la ecuación (27) dada por Forbes et al. (2011) .
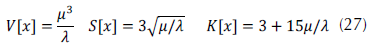
La estimación de los parámetros se puede realizar por máxima verosimilitud según lo explicado por Johnson, Kotz y Balakrishnan (1995), que ofrece la ecuación (28).
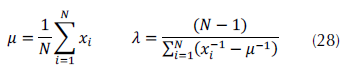
Donde N es la cantidad de muestras de un conjunto dado.
La generación de variables aleatorias se puede ejecutar con el siguiente algoritmo (Krishnamoorthy, 2016):
Funciones implementadas
La tabla 1 muestra las funciones que fueron implementadas en Matlab para la modelación de la distribución gamma, junto a una breve descripción de cada una. Las funciones comienzan todas con el prefijo gam- que indica se corresponden a la distribución gamma. Funciones semejantes fueron implementadas para la raíz gamma, la inversa gamma y la inversa gaussiana aplicando los prefijos gamr-, igm- e ig- respectivamente.
Fuente: elaboración propia
Tabla 1: Función de modelación de la distribución gamma implementadas en matlab
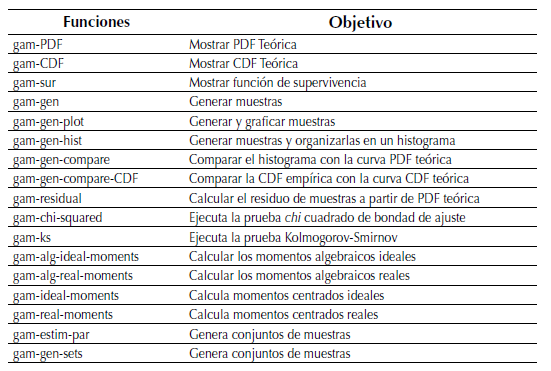
En comparación con una implementación previa de la distribución gamma realizada por Machado Fernández (2016a), ahora se agregaron tres nuevas funciones. La primera de ellas muestra la función de supervivencia que es frecuentemente aplicada para estudiar las diferencias en la cola de las distribuciones (Dong, 2006). La segunda realiza una comparación entre las CDF teóricas y empíricas que complementa la comparación antes disponible para las PDF. La tercera ejecuta la prueba de ajuste Kolmogorov-Smirnov que es muy popular en radares y tiende a reemplazar a la chi cuadrado (Makhoul et al., 2014; Mandal y Bhattacharya, 2013).
RESULTADOS
La presente sección está dedicada a mostrar las salidas de las principales funciones implementadas. La validación de las mismas partió de la comparación de las curvas de la PDF con gráficas dadas por distintos autores. Así, las curvas de la PDF gamma fueron comparadas con éxito con las de Forbes et al. (2011) y O’Connor (2011), las curvas inversas gamma con las de McLaughlin (2014) y Roth (2013), y las curvas inversa gaussiana con las de Johnson, Kotz y Balakrishnan (1995). Luego, se procedió a validar el resto de las funciones mediante su interacción con la PDF y la aplicación de diferentes mecanismos, siendo los más importantes las pruebas de bondad de ajuste.
En el caso de la raíz gamma, no se encontró ningún documento que ofreciera gráficas detalladas de la PDF. Aun así, la distribución pudo ser validada mediante la interacción de sus componentes con los de la gamma, gracias a la estrecha relación que existe entre las dos distribuciones.
Funciones de densidad de probabilidad (PDF) y distribución acumulativa (CDF)
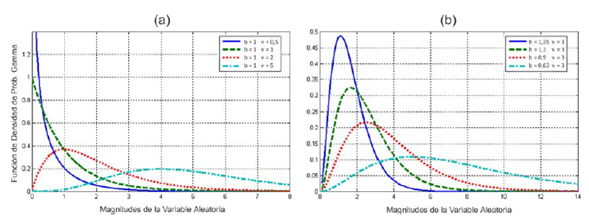
Las funciones de densidad de probabilidad y de distribución acumulada son la clave de la modelación matemática de una distribución; de ahí que la implementación informática comenzara por ellas. La figura 2 muestra cómo los parámetros de la distribución gamma modifican el trazo de las curvas de la PDF de la distribución. El parámetro de forma (υ) es el que tiene un mayor impacto sobre el trazo ya que es capaz de alterar la relación de proporcionalidad entre las magnitudes de la variable aleatoria.
Figura 2: Influencia de la variación de los parámetros gamma sobre las curvas de la PDF
Obsérvese cómo, en la figura 2a, las curvas con v = 0,5 y v = 1 tienen un máximo al comienzo del eje de coordenadas. Este comportamiento cambia para v = 2 y v = 5 donde el máximo comienza a aparecer más hacia el centro de la distribución, lo cual reduce la asimetría que se calcula a través del tercer momento centrado. En cambio, el parámetro de escala (b) introduce un efecto multiplicativo inverso sobre las muestras, modificando su dispersión. Como se puede ver en la figura 2b , ahora la posición del máximo no varía dentro de las curvas, sino que estas comienzan a ser más alargadas.
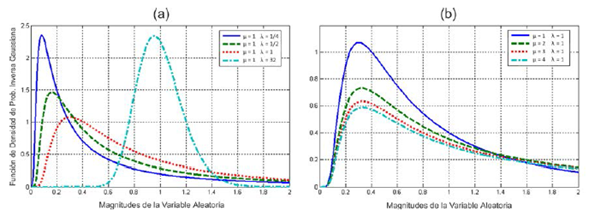
La figura 3 grafica también la PDF pero en este caso para la distribución inversa gaussiana que tiene un parámetro de escala (λ) y otro de localización (μ). El efecto del parámetro de escala (figura 3a) continúa siendo el mismo que en el caso anterior. Mientras tanto, el parámetro de localización varía fundamentalmente la posición del gráfico, con una clara influencia sobre la media de los conjuntos.
Figura 3: Influencia de la variación de los parámetros de la distribución inversa gaussiana sobre la curva de la PDF
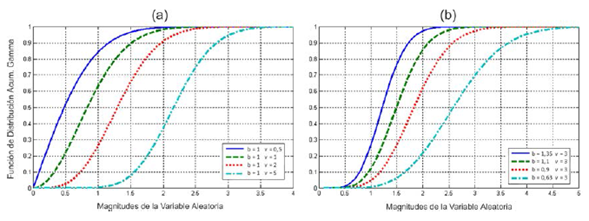
La figura 4 se enfoca en la influencia de los parámetros raíz gamma sobre las curvas de la distribución acumulativa, en la que el parámetro de forma (v) continúa introduciendo cambios más significativos. Lo anterior se aprecia en la figura 4a donde los trazos experimentan cambios de concavidad al hacer fluctuar υ. Por el contrario, la modificación del parámetro de escala (b) se limita a un efecto de estiramiento de la curva hacia la derecha, lo que se traduce en un aumento de la dispersión de las muestras hacia magnitudes superiores.
Figura 4: Influencia de la variación de los parámetros de la distribución Raíz Gamma sobre la curva de la CDF
Comparación entre datos empíricos y teóricos
Además de comprobar que las curvas siguen las formas dadas en diversas publicaciones, un elemento esencial en la validación es verificar que los métodos de generación de variables aleatorias aplicados sigan fielmente el comportamiento teórico esperado. En este sentido, se encontraron ligeras imprecisiones en algoritmos descritos por algunas fuentes, pero una revisión profunda de la literatura, unida a pequeños ensayos de prueba y error, permitió encontrar mecanismos fiables que pasaron las pruebas de validación.
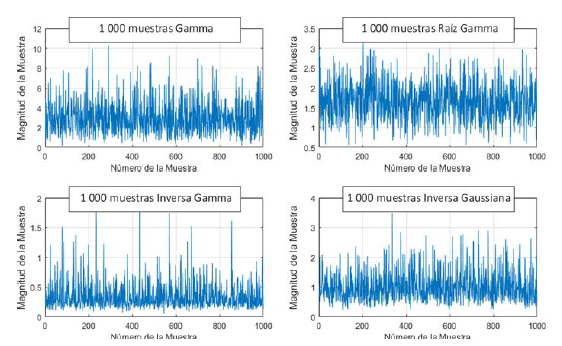
Cuando se genera una variable aleatoria se está produciendo una secuencia de números según se ilustra en la figura 5. Las propiedades estadísticas de un conjunto son difícilmente deducibles a partir del estudio de una secuencia de valores.
Figura 5: Secuencias de muestras de diferentes distribuciones
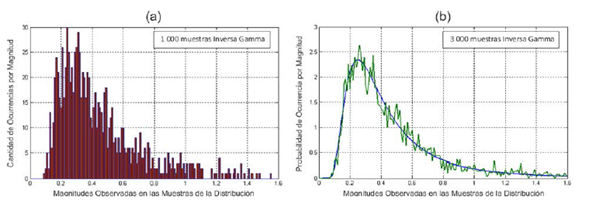
Para su mejor análisis, las secuencias se transforman en histogramas, que agrupan los valores observados para cada magnitud posible de las muestras. La figura 6a presenta un histograma conformado a partir de 1000 muestras de la distribución inversa gamma. Para comparar el histograma con la curva PDF teórica, el eje de las ordenadas se debe convertir de cantidad de ocurrencias a probabilidad de ocurrencia. Luego, pueden producirse gráficos como el de la figura 6b donde se comparan las formas de la PDF empírica (también conocida como histograma de frecuencias relativas) y la teórica. Como resultado, se verifica la correcta correspondencia de las muestras generadas a la distribución estadística en cuestión.
Figura 6: Comparacion entre un pictograma empiricoy la curva PDF teorica esperada de la inversa gamma
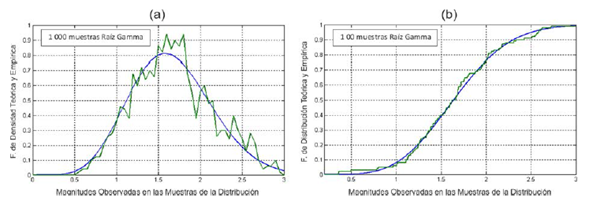
Para lograr una verificación mayor se pueden realizar también comparaciones con respecto a las curvas de la CDF. La figura 7 ofrece un ejemplo de comparaciones tanto de la PDF (figura 7a) como de la CDF (figura 7b) para la distribución raíz gamma. Una característica importante es que la convergencia para el caso de la CDF es siempre más rápida. En la figura 7b se observa una mayor cercanía entre los gráficos teóricos y empíricos que en la figura 7a, aun cuando se usan menos muestras. Esto se debe a que la CDF resulta de la integración de la PDF hasta cada valor del eje de las abscisas, lo cual contribuye a reducir el error.
Figura 7: Comparacion entre la PDF y la CDF empírica con las curvas teóricas esperadas
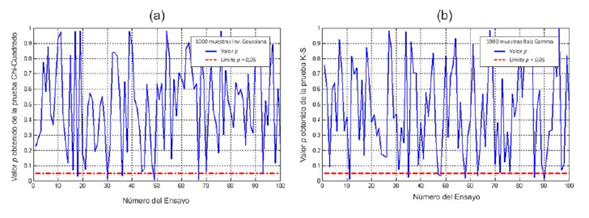
Las pruebas de bondad de ajuste proporcionan otro método de verificación de la correspondencia entre las distribuciones empíricas y teóricas. Específicamente en radares, se utilizan las pruebas chi cuadrado y Kolmogorov-Smirnov (K-S) que fueron incluidas en la implementación realizada. La figura 8 muestra un ejemplo de la salida de estas pruebas. Se observa que el valor p obtenido es mayor a 0,05 en la mayoría de los casos. Por tanto, se reafirma la pertenencia de las muestras generadas al modelo raíz gamma. Resultados similares se obtuvieron para el resto de los modelos.
Figura 8: Resultados de la aplicación de las pruebas chi cuadrado y K-S
Cálculo de los momentos y estimación paramétrica
El cálculo de los momentos y la estimación paramétrica complementan la modelación realizada. Se implementaron las expresiones teóricas de los primeros cuatro momentos centrados y algebraicos, junto a la asimetría y la curtosis para las cuatro distribuciones. En este punto también se encontraron algunas imprecisiones en la literatura que fueron corregidas mediante múltiples consultas a diferentes fuentes y ensayos de prueba y error.
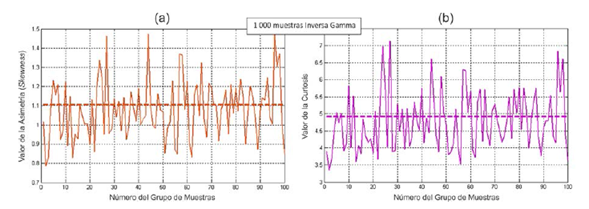
Evidencia del correcto funcionamiento del código se brinda en la figura 9 donde se representa el cálculo de la asimetría y la curtosis sobre grupos de 1000 muestras inversa gamma cada uno. Como puede apreciarse, los valores obtenidos oscilan alrededor de la cifra teórica esperada.
Figura 9: Oscilación de la asimetría y la curtosis empíricas, de grupos de 1000 muestras inversa gamma al rededor del valor teórico esperado.
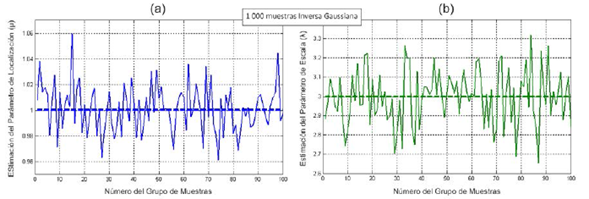
Por último, la figura 10 ofrece un ejemplo de la estimación de los parámetros de las distribuciones. Específicamente, se grafica la estimación de los parámetros de la inversa gaussiana, considerando 100 grupos de 1000 muestras cada uno. La estimación realizada se mantiene cercana al valor teórico con el que fueron generados los grupos de muestras. En general, todos los métodos de estimación descritos en la sección “Materiales y métodos” mostraron un comportamiento favorable, incluido el método propuesto para la distribución raíz gamma.
Figura 10: Variación de la estimación de los parámetros de la distribución inversa gaussiniana alrededor de los valores con que fueron generadas las muestras
VALORACIÓN DEL ESTUDIO
En la presente investigación se realizó una recopilación bibliográfica importante relativa a la modelación de cuatro distribuciones estadísticas que han sido aplicadas en la representación de la textura del clutter marino de radar. Las expresiones matemáticas que modelan a las distribuciones gamma, raíz gamma, inversa gamma e inversa gaussiana fueron programadas en una pequeña librería informática en el lenguaje M de Matlab. La implementación incluyó funciones de densidad y distribución, algoritmos de generación de variables aleatorias, métodos de estimación de parámetros, y cálculo de momentos centrados y algebraicos, entre otros. También se agregaron mecanismos adicionales para la validación por diferentes métodos, garantizándose la correcta pertenencia de cada distribución implementada al modelo teórico.
La pequeña librería creada brinda una herramienta alternativa de código abierto al Toolbox Estadístico que ofrece Matlab, ya que solo se utilizaron rutinas disponibles en el core de este asistente matemático. De hecho, las funciones informáticas de las distribuciones inversa gamma y raíz gamma no tienen par en la versión 2016, lo cual agrega aún más novedad a la implementación.
Los resultados obtenidos dan continuidad a lo previamente logrado para las distribuciones weibull, log-Normal, rayleigh, exponencial, K de la amplitud, K de la intensidad y pareto (Machado Fernández, 2016b; Machado Fernández y Bacallao Vidal, 2016c). Ellas también se utilizan para representar el fondo de radar adquirido bajo diferentes condiciones. Conjuntamente, la implementación actual mejora la propuesta de Machado Fernández (2016a), quien presentó una modelación menos completa de la distribución gamma, ignorando al resto de las variantes disponibles para la textura. Todos estos desarrollos siguen el mapa trazado en (Machado Fernández, 2017b), donde se señalaron las distribuciones más relevantes relacionadas al clutter marino.
Las cuatro distribuciones simuladas viabilizan la realización de estudios sobre el eco electromagnético producido en la superficie marina. Así, se resuelve uno de los problemas principales que se encontraron en la literatura: la mayoría de los análisis conducidos no evalúan las distintas variantes disponibles para la representación de la textura del clutter de mar. Precisamente, los modelos que consideran una distribución para la textura son los más adecuados para simulación del fenómeno, pues cuentan con una fundamentación física del motivo por el cual son aplicables. Otras alternativas, como la weibull y la log-normal, si bien son ampliamente usadas, se sustentan en una correspondencia empírica con las muestras extraídas.
Esta investigación también contribuye al desarrollo de detectores adaptados a fondos heterogéneos como los que aparecen en las costas cubanas, donde alternan diferentes niveles de profundidad, manglares, aguas salobres, islotes, vegetación acuática prominente y bandadas de pájaros, entre otros entes que afectan el modo común de operación. El parque de radares con que cuenta Cuba no está, generalmente, adaptado al medio que le rodea, sino que los modelos son estándares. Por tanto, la simulación de un medio con condiciones variables a través de cuatro distribuciones cambiantes permitirá diseñar detectores más eficientes que podrán combinarse con la técnica existente, realizándose un procesamiento mejorado de la señal. De hecho, las modelaciones de distribuciones realizadas previamente por Machado Fernández (2016b) y Machado Fernández y Bacallao Vidal (2016c) permitieron el desarrollo de mecanismos novedosos de estimación paramétrica (Machado Fernández y Bacallao Vidal, 2016a, 2016b; Machado Fernández, Bacallao Vidal y Chávez Ferry, 2015), usando inteligencia artificial, que a la postre posibilitaron el diseño de detectores adaptativos (Machado Fernández, 2015; Machado Fernández y Bacallao Vidal, 2016d, 2017a, 2017c; Machado Fernández, Torres Martínez y Bacallao Vidal, 2017).
Como proyecciones futuras, los autores esperan que la labor realizada dé paso a la modelación de distribuciones más intrincadas pertenecientes a la familia compuesta gaussiana (Compound Gaussian) como la Rician inversa gaussiana (Eltoft, 2005), y la compuesta inversa gaussiana (Mezahe et al., 2013, 2015). Estas distribuciones asumen un componente para la textura y otro para la capilaridad, lo cual les ofrece ventajas en la representación de las propiedades de correlación del clutter. El objetivo global del desarrollo es contribuir a la creación de la librería MATE-CFAR 2, para la simulación de clutter y detectores de radar, que será una progresión del MATE-CFAR original presentado por Machado Fernández y Bacallao Vidal, 2014) y pretende traducirse a otros lenguajes como Python. Adicionalmente, se anima a investigadores hispanos a incorporarse a esta línea de investigación, ya que se considera que el presente documento es uno de los principales textos en idioma español sobre la temática abordada.
CONCLUSIONES
La presente investigación recopiló e implementó en Matlab las expresiones matemáticas más importantes relacionadas a las distribuciones gamma, raíz gamma, inversa gamma e inversa gaussiana. De esta forma, se completó la modelación informática y validación de las diferentes alternativas que han sido propuestas para representar la textura del eco electromagnético recibido de la superficie del mar. Los resultados alcanzados permiten la realización de comparaciones fiables sobre la pertenencia del clutter marino a una distribución específica, así como la creación de nuevas variantes de detección adaptadas a entornos heterogéneos como los encontrados en las costas cubanas, donde las irregularidades del relieve pueden resultar en cambios constantes de la distribución del eco. El código creado se une a estudios previos para contribuir a la formación de la librería MATE-CFAR 2, dedicada a la simulación de la respuesta de detectores CFAR de ventana deslizante frente a múltiples escenarios. Además, la modelación de la textura en Matlab abre el camino hacia la simulación de varias distribuciones compuestas que representan fielmente las propiedades de correlación del clutter de mar.
REFERENCIAS
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.
