DOI:
https://doi.org/10.14483/22487638.12961Published:
2018-04-01Issue:
Vol. 22 No. 56 (2018): April - JuneSection:
ResearchAdsorción de rojo 40 sobre cascarilla de arroz: determinación del equilibrio, cinética y termodinámica
Adsorption of red 40 dye on rice husk: determination of the equilibrium, kinetic and thermodynamic of the process
Keywords:
kinetic, azo dye, design of experiments, isotherm, removal, agricultural by-product. (en).Keywords:
cinética, colorante azo, diseño de experimentos, isotermas, remoción, residuo agrícola (es).Downloads
References
Aksu, Z. y Akpinar, D. (2001). Competitive biosorption of phenol and chromium(VI) from binary mixtures onto dried anaerobic activated sludge. Biochemical Engineering Journal, 7(3), 183–193. DOI: https://doi.org/10.1016/S1369-703X(00)00126-1
Aksu, Z., Ertuğrul, S. y Dönmez, G. (2009). Single and binary chromium(VI) and Remazol Black B biosorption properties of Phormidium sp. Journal of Hazardous Materials, 168(1), 310–8.
Allen, S.J., Gan, Q., Matthews, R. y Johnson, P.A. (2005). Kinetic modeling of the adsorption of basic dyes by kudzu. Journal of Colloid and Interface Science, 286(1), 101–9.
Azizian, S. (2004). Kinetic models of sorption: a theoretical analysis. Journal of Colloid and Interface Science, 276(1), 47–52. DOI: https://doi.org/10.1016/j.jcis.2004.03.048
Balakrishnan, V.K., Shirin, S., Aman, A.M., De Solla, S.R., Mathieu-Denoncourt, J. y Langlois, V.S. (2016). Genotoxic and carcinogenic products arising from reductive transformations of the azo dye, Disperse Yellow 7. Chemosphere, 146, 206–215. DOI: https://doi.org/10.1016/j.chemosphere.2015.11.119
Bingol, D., Tekin, N. y Alkan, M. (2010). Brilliant Yellow dye adsorption onto sepiolite using a full factorial design. Applied Clay Science, 50(3), 315–321. DOI: https://doi.org/10.1016/j.clay.2010.08.015
Carneiro, P.A., Umbuzeiro, G.A., Oliveira, D.P. y Zanoni, M.V.B. (2010). Assessment of water contamination caused by a mutagenic textile effluent/dyehouse effluent bearing disperse dyes. Journal of Hazardous Materials, 174(1–3), 694–699. DOI: https://doi.org/10.1016/j.jhazmat.2009.09.106
Cestari, A.R., Vieira, E.F.S., Tavares, A.M.G. y Bruns, R.E. (2008). The removal of the indigo carmine dye from aqueous solutions using cross-linked chitosan: evaluation of adsorption thermodynamics using a full factorial design. Journal of Hazardous Materials, 153(1–2), 566–74. DOI: https://doi.org/10.1016/j.jhazmat.2007.08.092
Chong, K.H. y Volesky, B. (1996). Metal biosorption equilibria in a ternary system. Biotechnology and Bioengineering, 49(6), 629–38.
De Aragão Umbuzeiro, G., Freeman, H.S., Warren, S.H., De Oliveira, D.P., Terao, Y., Watanabe, T. y Claxton, L.D. (2005). The contribution of azo dyes to the mutagenic activity of the Cristais River. Chemosphere, 60(1), 55–64.
Deng, L., Su, Y., Su, H., Wang, X. y Zhu, X. (2007). Sorption and desorption of lead (II) from wastewater by green algae Cladophora fascicularis. Journal of Hazardous Materials, 143(1–2), 220–225.
Dotto, G.L., Vieira, M.L.G., Esquerdo, V.M. y Pinto, L.A.A. (2013). Equilibrium and thermodynamics of azo dyes biosorption onto Spirulina platensis. Brazilian Journal of Chemical Engineering, 30(1), 13–21.
Elkady, M.F., Ibrahim, A.M. y El-Latif, M.M.A. (2011). Assessment of the adsorption kinetics, equilibrium and thermodynamic for the potential removal of reactive red dye using eggshell biocomposite beads. Desalination, 278(1–3), 412–423.
Faria, P.C.C., Orfão, J.J.M. y Pereira, M.F.R. (2004). Adsorption of anionic and cationic dyes on activated carbons with different surface chemistries. Water Research, 38(8), 2043–52.
Fedearroz (2006). Índice mensual de producción de arroz. Revista Arroz, 54(461), 27.
Figueroa, M.L.H. y Rodríguez, B.L. (2008). Cinética e isotermas de adsorción de Pb ( II ) en suelo de Monterrey. Ingenierías,. XI(41), 24–31.
García, M.C., García, C.A. y De Plaza, J.S. (2016). Estudio exploratorio del tratamiento de agua de tintas por método de electrocoagulación/electroflotación. Tecnura, 20(47), 107–117.
Halbus, A.F., Athab, Z.H. y Hussein, F.H. (2013). Adsorption of disperse blue dye on iraqi date palm seeds activated carbon. International Journal of Chemistry Science, 11(3), 1219–1233.
Ho, Y.S. (2006). Review of second-order models for adsorption systems. Journal of Hazardous Materials, 136(3), 681–9.
Ho, Y. y McKay, G. (1999). Pseudo-second order model for sorption processes. Process Biochemistry, 34(5), 451–465.
Hormaza, A., Moreno, A. y Figueroa, D. (2013). Diseño estadístico para la remoción eficiente del colorante rojo 40 sobre tusa de maíz. Producción Más Limpia, 7(2), 9–19. Recuperado de http://repository.lasallista.edu.co:8080/ojs/index.php/pl/article/view/259
Howell, J. y Buckius, R. (1990). Principios de termodinámica para ingenieros. 1a. ed. México D.F.: McGraw-Hill.
Jabeen, H.S., Ur Rahman, S., Mahmood, S. y Anwer, S. (2013). Genotoxicity assessment of amaranth and allura red using saccharomyces cerevisiae. Bulletin of Environmental Contamination and Toxicology, 90(1), 22-26. DOI: https://doi.org/10.1007/s00128-012-0870-x
Konicki, W., Pełech, I., Mijowska, E. y Jasińska, I. (2012). Adsorption of anionic dye Direct Red 23 onto magnetic multi-walled carbon nanotubes-Fe3C nanocomposite: Kinetics, equilibrium and thermodynamics. Chemical Engineering Journal, 210, 87–95.
Kuo, C.Y., Wu, C.H. y Wu, J.Y. (2008). Adsorption of direct dyes from aqueous solutions by carbon nanotubes: determination of equilibrium, kinetics and thermodynamics parameters. Journal of Colloid and Interface Science, 327(2), 308–15.
McCann, D. et al. (2007). Food additives and hyperactive behaviour in 3-year-old and 8/9-year-old children in the community: a randomised, double-blinded, placebo controlled trial. Lancet, 370, 1560–1567.
Mittal, A. (2006). Adsorption kinetics of removal of a toxic dye, Malachite Green, from wastewater by using hen feathers. Journal of Hazardous Materials, 133(1–3), 196–202. DOI: https://doi.org/10.1016/j.jhazmat.2005.10.017
Nollet, H., Roels, M., Lutgen, P., Van der Meeren, P. y Verstraete, W. (2003). Removal of PCBs from wastewater using fly ash. Chemosphere, 53(6), 655–65.
Núñez, D. (2012). Uso de residuos agrícolas para la producción de biocombustibles en el departamento del Meta. Tecnura, 16(34), 142–156.
O’Neill, C., Hawkes, F.R., Hawkes, D.L., Esteves, S. y Wilcox, S.J. (2000). Anaerobic-aerobic biotreatment of simulated textile effluent containing varied ratios of starch and azo dye. Water Research, 34(8), 2355-2361.
O’Neill, C., Hawkes, F.R., Hawkes, D.L. y Lourenc, N.D. (1999). Review Colour in textile effluents – sources, measurement, discharge consents and simulation: A review. Journal of Chemical Technology and Biotechnology, 74, 1009–1018. DOI: https://doi.org/0.1002/(SICI)1097-4660(199911)74.
Piccin, J.S., Dotto, G.L., Vieira, M.L.G. y Pinto, L.A.A. (2011). Kinetics and Mechanism of the Food Dye FD & C Red 40 Adsorption onto Chitosan. Journal of Chemical & Engineering Data, 56, 3759–3765.
Rodríguez, J.P., García, C.A. y Pardo, J. (2015). Selección de tecnologías para el tratamiento de aguas residuales municipales. Revista Tecnura, 19(46), 149. DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2015.4.a12
Sánchez, T. (2002). Utilización de la cascarilla de arroz como fuente energética en ladrilleras. Soluciones Prácticas, 82, 13-22.
Sánchez-Duarte, R.G., Sánchez-Machado, D.I., López-Cervantes, J. y Correa-Murrieta, M.A. (2012). Adsorption of allura red dye by cross-linked chitosan from shrimp waste. Water Science and Technology, 65(4), 618–623. DOI: https://doi.org/10.2166/wst.2012.900
Santos, S.C.R. y Boaventura, R.A.R. (2008). Adsorption modelling of textile dyes by sepiolite. Applied Clay Science, 42(1–2), 137–145.
Tehrani-Bagha, A.R., Nikkar, H., Mahmoodi, N.M., Markazi, M. y Menger, F.M. (2011). The sorption of cationic dyes onto kaolin: Kinetic, isotherm and thermodynamic studies. Desalination, 266(1–3), 274–280.
Volesky, B. (2003). Sorption and biosorption. Canadá: BV Sorbex, Inc.
Volmajer, J., Majcen Le Marechal, A. y Vajnhandl, S. (2011). Water in the textile industry. Treatise on Water Science, 4, 685–706.
Wu, C.H. (2007). Adsorption of reactive dye onto carbon nanotubes: equilibrium, kinetics and thermodynamics. Journal of Hazardous Materials, 144(1–2), 93–100.
Wu, F.C., Tseng, R.L. y Juang, R.S. (2009). Characteristics of Elovich equation used for the analysis of adsorption kinetics in dye-chitosan systems. Chemical Engineering Journal, 150(2–3), 366–373.
Yagub, M.T., Sen, T.K., Afroze, S. y Ang, H.M. (2014). Dye and its removal from aqueous solution by adsorption: A review. Advances in Colloid and Interface Science, 209C, 172–184.
Yeddou, N. y Bensmaili, A. (2005). Kinetic models for the sorption of dye from aqueous solution by clay-wood sawdust mixture. Desalination, 185(1–3), 499–508.
Yeddou, N. y Bensmaili, A. (2007). Equilibrium and kinetic modelling of iron adsorption by eggshells in a batch system: effect of temperature. Desalination, 206(1–3), 127–134.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Recibido: 23 de noviembre de 2017; Aceptado: 23 de febrero de 2018
Resumen
Contexto:
Los residuos agrícolas se han convertido en adsorbentes no convencionales de gran interés debido a su amplia disponibilidad, mínimo costo y alta eficiencia. En este trabajo se evaluó la capacidad adsorbente del subproducto cascarilla de arroz (CA) en la remoción del colorante aniónico rojo 40 (R40), bajo un sistema discontinuo.
Método:
Para determinar las mejores condiciones de remoción de este colorante, se implementó un diseño factorial 23, que permite alcanzar una remoción del 75,6 % a pH=2,0, concentración inicial de 15 mg/L, dosificación de 8,0 g/L y tiempo de contacto de 18 horas.
Resultados:
Se evaluó el equilibrio del proceso y se encontró que el modelo Langmuir es el que mejor representa los resultados experimentales con q máx de 2,74 mg/g y un coeficiente de ajuste de R2 = 0,987. En cuanto a la cinética, el modelo de pseudosegundo orden con q t de 1,09 mg/g presentó el mejor ajuste (R2 = 0.970). Con respecto a las propiedades termodinámicas, la energía libre de Gibbs (con ΔG = -1,11 kJ/mol) y la entropía (con ΔS = 23,9 J/mol*K), señalan un proceso espontáneo, en tanto que la entalpía mostró que la remoción de R40 constituye un proceso endotérmico, con un de ΔH = 6,71 kJ/mol. Adicionalmente, la energía de activación con valor de 14,1 kJ/mol sugiere que el mecanismo de adsorción del R40 transcurre a través de una fisi-adsorción.
Conclusiones:
Estos resultados señalan que la cascarilla de arroz ofrece una adecuada capacidad adsorbente para la retención de colorantes azo de efluentes contaminados y que el escalado de dicho proceso es factible dadas sus características termodinámicas.
Palabras clave:
cinética, colorante azo, diseño de experimentos, isotermas, remoción, residuo agrícola.Abstract
Context:
Agricultural residues have become unconventional adsorbents of great interest due to their wide availability, minimum cost, and high efficiency. In this work, the adsorbent capacity of rice husk by-product (RH) in the Red 40 (R40) anionic dye removal was evaluated under a discontinuous system.
Method:
For determining the best conditions for the removal of this dye, a factorial design 23 was implemented, which allows to achieving a removal of 75.6% at pH = 2.0, an initial concentration of 15 mg/L, dosage of 8.0 g/L, and contact time of 18 hours.
Results:
The equilibrium, kinetics and thermodynamic properties of the process were evaluated. It was found that the Langmuir model best represents the experimental results with q max of 2.74 mg/g and an adjustment coefficient of R2=0.987. Regarding kinetics, the pseudosecond order model with qt of 1.09 mg/g presented the best fit (R2 = 0.970). Finally, Gibbs free energy (ΔG = -1.11 KJ/mol) and entropy (ΔS = 23.9 J/mol*K) indicate a spontaneous process, while enthalpy showed that the removal of R40 constitutes an endothermic process, with ΔH = 6.71 KJ/mol. Furthermore, the activation energy of 14.1 KJ/mol suggests that the mechanism of adsorption of the R40 takes place through a physi-adsorption.
Conclusions:
These results indicate that the rice husk offers a adequate adsorbent capacity for the retention of azo dye off contaminated effluents; besides, scaling up this process is feasible given its thermodynamic characteristics.
Keywords :
kinetic, azo dye, design of experiments, isotherm, removal, agricultural by-product.Introducción
Se estima que anualmente se producen en el mundo 10 millones de toneladas de colorantes, de las cuales, cerca de 70 % corresponde a los compuestos azo, que se utilizan principalmente en la industria textil y alimentaria (O’Neill et al., 2000). Dado que su fijación no es totalmente eficiente, se reporta que el 10 % de estos colorantes son vertidos en ríos y fuentes de agua, lo que constituye un serio problema ambiental para las autoridades sanitarias (Volmajer, Majcen Le Marechal y Vajnhandl, 2011).
La descarga de estos efluentes es indeseable no solo debido a un desfavorable impacto visual, sino también a los riesgos para la salud humana en razón de las características tóxicas o mutagénicas atribuidas a estos colorantes (De Aragão Umbuzeiro et al., 2005). Además, cabe señalar que la mayor afectación se relaciona con la disminución del paso de la radiación solar, reduciendo los procesos fotosintéticos y, con ello, la disponibilidad de oxígeno para la flora y fauna (Carneiro, Umbuzeiro, Oliveira y Zanoni, 2010). Sin tratamientos adecuados, estos tintes se estabilizan y pueden permanecer en el ambiente durante largos periodos de tiempo (O’Neill, Hawkes, Hawkes y Lourenc, 1999).
Varios estudios han demostrado mediante pruebas con animales que el grupo azo es un causante de cáncer, por tanto, se prevé su efecto carcinógeno en seres humanos (Balakrishnan et al., 2016). El colorante R40 es soluble en agua y se utiliza principalmente en los productos cárnicos y confitería, pero debido a su naturaleza azoica puede provocar intolerancia en aquellas personas que son afectadas por los salicilatos (McCann et al., 2007). Estudios recientes comprobaron el potencial genotóxico del R40 mediante ensayos cometas en células de levadura (Jabeen, Ur Rahman, Mahmood y Anwer, 2013).
La legislación ambiental es cada vez más estricta en cuanto al contenido de color en el vertimiento de efluentes coloreados, por lo cual su remoción se ha convertido en parámetro de cumplimiento. El color, aún en concentraciones mínimas de 1 ppm, es altamente visible y para su tratamiento se utilizan diferentes métodos químicos, físicos y biológicos (Yagub, Sen, Afroze y Ang, 2014). Dentro de los métodos químicos físicos se encuentran: adsorción con carbón activado, filtración con membrana, intercambio iónico y coagulación, que, aunque son factibles, presentan alta concentración de lodos (García, García y De Plaza, 2016). En cuanto a los métodos químicos, se destacan los procesos oxidativos, ozonización, fotoquímica y destrucción electroquímica que, a pesar de que tienen tiempos de vida cortos, pueden formar subproductos tóxicos además de tener velocidades de flujo cortas que ocasionan una baja remoción. Los métodos biológicos, como bioadsorción, decoloración con hongos y biorremedicación, han demostrado no ser eficientes para todos los colorantes, además de producir metano y sulfuro de hidrógeno (Rodríguez, García y Pardo, 2015). Por otro lado, solo recientemente el Gobierno nacional implementó controles para el vertimiento de efluentes coloreados en cuerpos de agua mediante la Resolución 0631 de 2015, en el que se especifican las concentraciones de colorantes máximas que pueden ser vertidas. No obstante, cabe señalar que la vigilancia y cumplimiento de esta norma son mínimos.
Dentro de los productos agrícolas destacados en Colombia por su alta producción, el arroz se posiciona como uno de los más importantes, con una producción estimada de 2,5 millones de toneladas de arroz paddy y 1,7 millones toneladas de arroz blanco por año que dan lugar a 400 mil toneladas de cascarilla de arroz (CA). Este subproducto agrícola no es utilizado en actividades alternas, de tal forma que su disposición representa una grave problemática ambiental para este gremio económico (Fedearroz, 2006). Actualmente, solo una pequeña parte de la cascarilla de arroz generada es utilizada, especialmente en galpones, cultivos de flores y secado de granos en hornos, el resto del volumen producido es quemado a cielo abierto. Recientemente, este residuo se está utilizando como combustible en ladrilleras para aprovechar así todo el calor que produce (Núñez, 2012; Sánchez, 2002).
A la fecha, los trabajos relacionados con la remoción de R40 son pocos; cabe señalar la investigación de Sánchez-Duarte, Sánchez-Machado, López-Cervantes y Correa-Murrieta (2012), quienes obtuvieron una remoción del 94 % a pH=3,0 y del 63 % a pH=11,0 sobre quitosán. Este material también ha sido utilizado por Piccin, Dotto, Vieira y Pinto (2011) alcanzando una capacidad máxima de adsorción de 300 mg/g. No obstante, dentro de los residuos agrícolas, solo se ha reportado la evaluación de la tusa de maíz para este propósito (Hormaza, Moreno y Figueroa, 2013). Así, con el ánimo de contribuir al diseño de alternativas eficientes, económicas y viables para el tratamiento de este colorante azo, en este trabajo se llevó a cabo la evaluación de la capacidad adsorbente del residuo agrícola CA. Un diseño factorial completo 23 fue implementado para determinar las condiciones más propicias del proceso de remoción. Así mismo, la evaluación del equilibrio, la cinética y la termodinámica permitieron describir el proceso. Las expresiones matemáticas de Langmuir y Freundlich fueron seleccionadas para el análisis de las isotermas, en tanto que la cinética fue evaluada a través de las ecuaciones de pseudoprimer orden, segundo orden y Elovich
MATERIALES Y METODOS
Colorante R40
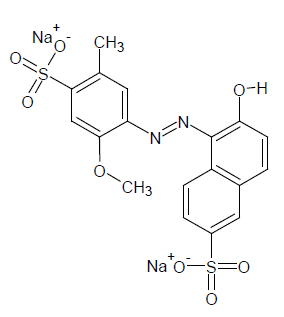
Este colorante, también conocido como FD&C Rojo No. 40, y ha sido designado por la Food and Drugs Administration (FDA) como rojo Allura o rojo alimenticio 17. Según el CI se encuentra clasificado con el número 16035, tiene un peso molecular de 496,42 g/mol, una fórmula molecular C18H14N2O8S2Na2, cuya estructura química se presenta en la figura 1. El colorante R40 de grado comercial fue suministrado, para este estudio, por Color Química S.A., con una pureza de 85 %.
Figura 1: Estructura química del rojo 40
Preparación del adsorbente
La cascarilla de arroz natural se obtuvo de las agroindustrias arroceras localizadas en el municipio de Planeta Rica, departamento de Córdoba, Colombia. El muestreo se realizó de forma aleatoria en cinco puntos de recolección durante el primer trimestre del año para evitar la humedad debido a que los sitios de almacenamiento se encuentran a cielo abierto. El tratamiento incluyó tres lavados utilizando agua tipo II, y un posterior secado a 80 °C durante un tiempo de 24 horas en un horno digital HDF-64 Marca A&E, molienda y tamizado para disponer de partículas con un tamaño en un intervalo específico. El adsorbente así preparado fue almacenado en recipientes herméticos. Se prepararon soluciones patrón del R40 a una concentración de 30 mg/L, a partir de las cuales se realizaron las correspondientes diluciones para las curvas de calibración, estas fueron medidas a la longitud de onda de máxima absorbancia, es decir, a λmáx = 505 nm.
Diseño estadístico de experimentos para la remoción de R40
En este trabajo se implementó un diseño factorial completo 23 para evaluar la importancia de los factores concentración inicial del colorante (A), dosificación de adsorbente (B), y tiempo de contacto (C) en la remoción del colorante. Los parámetros que permanecieron constantes fueron pH, tamaño de partícula, temperatura y velocidad de agitación. En la tabla 1 se detallan los factores y sus respectivos niveles.
Fuente: elaboración propia.
Tabla 1: Factores y niveles del diseño factorial 23 para R40
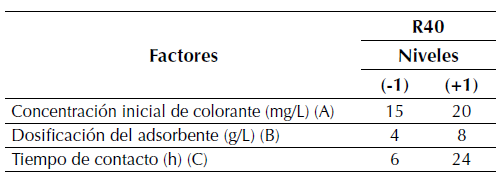
Todos los experimentos se llevaron a cabo por triplicado, utilizando 25 mL de la solución de colorante a pH = 2,0, adsorbente con partículas cuyo tamaño oscila entre 0,3 y 0,5 mm, a temperatura ambiente y una velocidad de agitación de 180 rpm.
El porcentaje de remoción del R40 (tabla 2) se calculó según la ecuación (1).
Fuente: elaboración propia.
Tabla 2: Análisis de varianza para % de remoción - R40

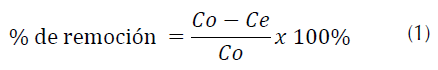
Donde, C 0 es la concentración inicial del colorante y C e es la concentración en el equilibrio.
Los efectos de la interacción para cada colorante mediante la ecuación (2).
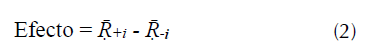
Donde, Ṝ +,i y Ṝ -,i son los promedios de los porcentajes de remoción para los niveles alto (+) y bajo (-) para cada factor. Los efectos principales se refieren a los promedios de los resultados (+) y (-) del factor cuyo efecto es calculado sin considerar los niveles de los otros factores. Para interacciones binarias, Ṝ +,i es el promedio de los resultados de ambos factores a sus niveles (+1) y (-1), mientras Ṝ -,i es el promedio de los resultados para los factores, cuando uno de ellos está en el nivel alto y el otro en el nivel bajo (Cestari, Vieira, Tavares y Bruns, 2008).
El análisis de varianza, anova (Bingol, Tekin y Alkan, 2010; Santos y Boaventura, 2010) (tabla 2), donde la importancia de los coeficientes de regresión fue determinada aplicando la prueba t Student, señala que la concentración del colorante, la dosificación del adsorbente y el tiempo de contacto fueron los factores que cumplen con el nivel de confianza del 95 % (P < 0,05)
Estudio de equilibrio del colorante R40
Las isotermas de adsorción son importantes para describir la interacción de los colorantes con el adsorbente y de gran utilidad para determinar la capacidad adsorbente de diferentes materiales. En este trabajo se emplearon en particular las expresiones de Langmuir y Freundlich.
Isoterma de Langmuir: este modelo se representa matemáticamente mediante la ecuación (3) (Faria, Orfão y Pereira, 2004).
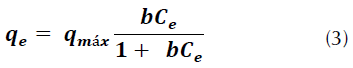
Donde, q máx es la capacidad máxima de adsorción del colorante bajo las condiciones dadas, en este caso el colorante [mg/g], b es la constante de Langmuir que indica la afinidad del adsorbato por el adsorbente, q e es la cantidad de adsorbato que se ha trasladado a la superficie del adsorbente y C e es la concentración de la solución en el equilibrio.
Isoterma de Freundlich: matemáticamente este modelo se describe mediante la ecuación (4) (Deng et al., 2007).

Donde, K F es la constante de Freundlich relacionada con la capacidad de adsorción, n es la constante de Freundlich relacionada con la intensidad de la adsorción, q e y C e son la cantidad de adsorbato que se ha trasladado a la superficie del adsorbente y concentración en el equilibrio.
Para evaluar las isotermas de adsorción se utilizó una solución madre de 30 mg/L en Erlenmeyers de 100 mL a pH=2,0, de la cual se prepararon nueve soluciones diluidas entre 3,0 y 27 mg/L, incrementando la concentración en 3 mg/L en cada solución. De cada solución se tomaron 20 mL en un Erlenmeyer, a los cuales se adicionó 120 mg de CA. Los Erlenmeyers se sellaron y se dispusieron en un agitador con incubadora con el fin de mantener constante la temperatura durante 24 horas a una velocidad de agitación de 180 rpm. Para la determinación del contaminante residual, se tomaron 2,0 mL de muestra y se midieron en el espectrofotómetro a 505 nm. Todos los análisis se realizaron por triplicado a las temperaturas de 298, 308, 318 y 328 K. Al analizar estas muestras se midió la concentración en equilibrio C e. Con este valor, se procedió a calcular la capacidad de adsorción mediante la ecuación (5).
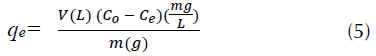
Luego, podemos graficar q e vs C e para evaluar las isotermas.
Cinética de adsorción de R40
La cinética de adsorción permite determinar la rapidez con la cual el colorante interacciona con la superficie adsorbente para su remoción; es una de las características importantes que definen la eficiencia de un adsorbente. Para la presente investigación, se implementaron tres ecuaciones cinéticas correspondientes al cinética de pseudoprimer orden, pseudosegundo orden y Elovich (Azizian, 2004; Ho y McKay, 1999).
Ecuación de pseudoprimer orden: es uno de los modelos cinéticos más ampliamente utilizados, puede ser expresado mediante la ecuación (6) (Allen, Gan, Matthews y Johnson, 2005; Yeddou y Bensmaili, 2005).
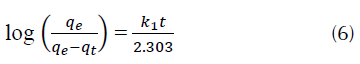
Donde, q e y q t son la cantidad de adsorbato que se ha trasladado a la superficie del adsorbente en el equilibrio y en el tiempo t, respectivamente. k1 es la constante de velocidad en min-1.
Ecuación de pseudosegundo orden: esta expresión matemática se basa en la capacidad de adsorción en equilibrio y asume que la velocidad de adsorción es directamente proporcional al cuadrado de sitios disponibles, como se muestra en la ecuación (7) (Ho y McKay, 1999; Ho, 2006; Halbus, Athab y Hussein, 2013).
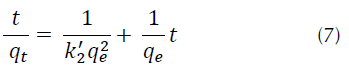
Donde, q t es la cantidad de colorante adsorbido sobre la superficie del adsorbente en el tiempo (mg/g), t: tiempo en (min), qe cantidad de adsorbato sobre la superficie del adsorbente en el equilibrio (mg/g), k’ 2: constante de velocidad (g/mg*min).
Modelo de Elovich: según este criterio se supone que los sitios activos del adsorbente son heterogéneos y por ello exhiben diferentes energías de activación que se representa mediante la ecuación (8) (Figueroa y Rodríguez, 2008; Yeddou y Bensmaili, 2005).
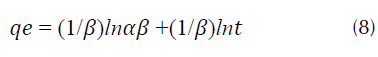
Donde, α es la velocidad inicial de adsorción (mg*g-1·min-1), β es la energía de activación por quimiadsorción (mg/g).
La solución de R40 se preparó a partir de la mejor condición de concentración obtenida del diseño estadístico, es decir, 15 mg/L. En Erlenmeyers de 100 mL, se tomaron 20 mL de cada solución, a los cuales se adicionaron 120 mg de CA. Los Erlenmeyers se sellaron y se dispusieron en un agitador con incubadora con el fin de mantener constante la temperatura durante el proceso a una velocidad de agitación de 180 rpm. Estas soluciones se evaluaron por 24 horas variando el tiempo de muestreo en 15, 30, 60, 120, 180, 360 y 1440 minutos. Estas muestras fueron medidas a la longitud de onda de máxima absorción para la concentración residual en la muestra. Todos los análisis se realizaron por triplicado a las temperaturas de 298, 308, 318 y 328 K.
Posteriormente, se utilizaron las ecuaciones 6, de la expresión de pseudoprimer orden; 7, correspondiente a la cinética de pseudosegundo orden, y 8, de Elovich, para determinar el modelo que mejor se ajusta a los resultados experimentales.
RESULTADOS
Diseño de experimentos para la remoción de R40
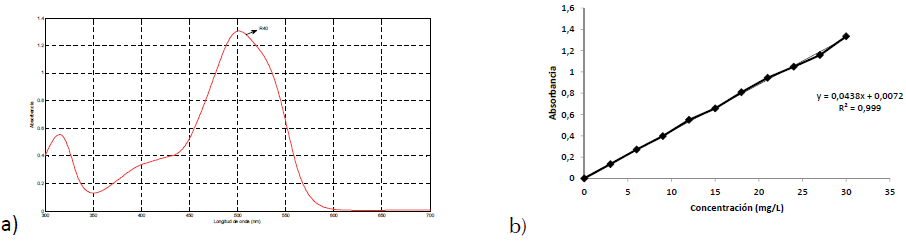
Inicialmente se llevaron a cabo las respectivas curvas de calibración, su análisis presentó coeficientes de correlación R2 de 0,999, señalando una adecuada linealidad. A partir de ellas, se estableció que el intervalo adecuado de estudio para el seguimiento por absorbancia de R40, es decir, dentro de la ley de Lambert-Beer, corresponde a 0-30 mg/L que son mostradas en las figuras 2a y 2b.
Figura 2: a) Espectro de R40 (concentración inicial 30 mg/L), b) Curva de calibración de R40
El análisis de varianza que se muestra en la tabla 2, determino que los factores concentración, dosificación y tiempo de contacto son los que cumplen con el nivel de confianza del 95% (p<0.05).
A partir de esta información se determinó la remoción de R40 usando la ecuación (9).
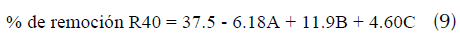
Donde, A, B, C pueden tomar los valores (±1) de la concentración, dosificación del adsorbente y tiempo de contacto respectivamente. Con esta ecuación fue posible predecir los porcentajes de remoción del R40 sobre CA. Al comparar los porcentajes de adsorción experimentales con los predichos de la tabla 3, se aprecia una gran similitud, permitiendo sugerir que el modelo matemático establecido es adecuado para la evaluación del proceso de adsorción.
DA = Dosificación del adsorbente C
O
= Concentración inicial del colorante TC = Tiempo de contacto Fuente: elaboración propia.
Tabla 3: Diseño factorial 23 de la remoción de R40 en CA experimentales y predichas
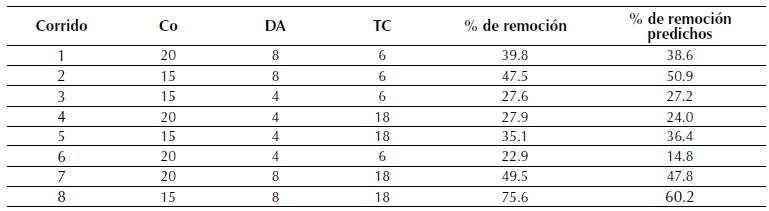
En el diseño de experimentos factorial 23 para la remoción de R40 en CA, se encontró que la mejor remoción se obtiene con 15 mg/L de concentración, 8 g/L de dosificación de adsorbente y 18 horas de tiempo de contacto para una remoción de 75,6 %.
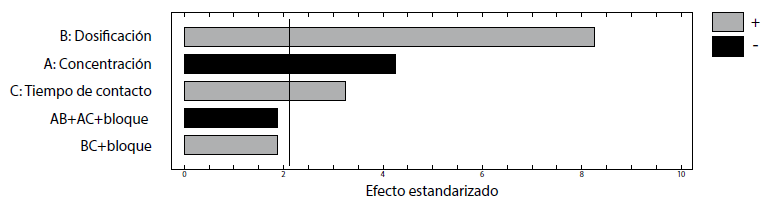
La importancia de los efectos principales de los factores y sus interacciones en la remoción del colorante R40 sobre CA son presentadas en el diagrama de Pareto de la figura 3. En este caso, la dosificación del adsorbente (B) y tiempo de contacto (C) son factores significativos con un efecto positivo, mientras que la concentración del colorante (A) también es significativa, pero con un efecto negativo sobre el porcentaje de remoción. Por otro lado, las interacciones binarias no superan la línea de referencia, indicando su menor significancia estadística, por lo cual no son considerados en el análisis (Bingol, Tekin y Alkan, 2010).
Figura 3: Diagrama de Pareto estandarizado de la remoción de R40 en CA
Evaluación del equilibrio de R40
Los resultados del equilibrio del proceso de remoción del R40 son mostrados en la tabla 4. Como es conocido, los coeficientes de correlación, R2, permiten determinar el modelo de equilibrio que mejor se ajuste con los datos experimentales. A partir de este criterio, los resultados de la tabla 4 señalan que la isoterma de Langmuir ofrece la mejor representación el proceso de remoción del R40 sobre CA con un valor R2=0,987. Las constantes de los modelos de equilibrio de Langmuir q máx y b, y de Freundlich K F y n señalan las propiedades de la superficie del adsorbente y la afinidad por ciertos adsorbatos, esto permite comparar las capacidades de adsorción de diferentes adsorbentes.
Fuente: elaboración propia.
Tabla 4: Isotermas de Langmuir y Freundlich para R40 a 298, 308, 318 y 328 K

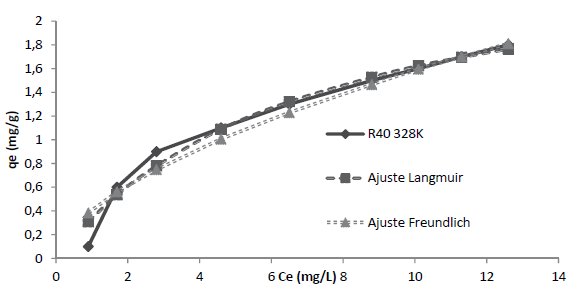
Los valores del parámetro de Langmuir, q máx describen la capacidad de saturación de la superficie del material adsorbente en el equilibrio. Así, de la tabla 4, se puede concluir que, en el equilibrio a 328 K, se obtiene la capacidad máxima de adsorción de la superficie R40 con un q máx de 2,74 mg/g. Es decir, con el incremento de la temperatura se ve favorecido el proceso de adsorción. Se aprecia que la temperatura ejerció una influencia debido a que q máx muestra un aumento, pasando de 1,55 a 2,74 mg/g al incrementar la temperatura de 298 a 328 K. Cabe señalar que b es definido en la ecuación (10) como un coeficiente relacionado con la afinidad entre el adsorbente y el adsorbato.

En donde, K es la constante de equilibrio que representa la afinidad del adsorbato por el sitio activo del adsorbente, tal como se muestra en la ecuación (11).

Por tanto, b representa el inverso de la afinidad (Volesky, 2003). Entonces, de la tabla 4 se puede concluir que, en el equilibrio a 328 K, se presenta la máxima afinidad entre adsorbato y el sitio activo del adsorbente con un K de 6,99. Estos resultados se explican debido al aumento de la temperatura, es decir, la afinidad se favorece con su incremento, y adicionalmente muestran concordancia con los valores descritos para q máx . Los valores de R2 de la expresión de Freundlich permiten establecer que este modelo no ofrece un ajuste satisfactorio ya que los coeficientes de correlación, entre 0,899 y 0,953, tienen un valor menor a los R2 obtenidos con la isoterma de Langmuir. Las constantes K F y n del modelo de Freundlich denotan la capacidad de adsorción y la intensidad de adsorción respectivamente; cabe señalar que para esta última, cuanto más cercano sea su valor a cero, mayor será la afinidad de la superficie por el colorante (Aksu y Akpinar, 2001). En ese sentido, de esta información se puede establecer que, en el equilibrio a 328 K, con un n de 2,30 se presenta la mayor afinidad de adsorción.
En cuanto a la capacidad de adsorción, se observa que el valor de K F del R40 aumenta de forma poco significativa con el cambio de temperatura de 298 K a 328 K, pasando de 0,501 a 0,516 respectivamente; es decir, la temperatura ejerce una influencia mínima en dicha capacidad.
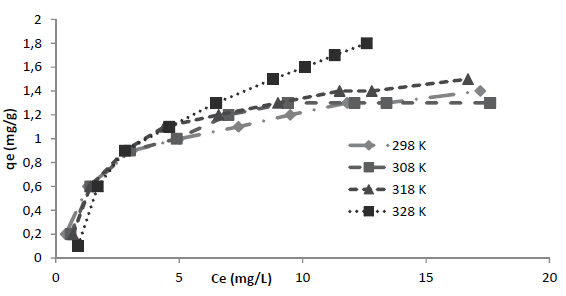
Los resultados experimentales de la capacidad de adsorción en equilibrio qe y concentración en equilibrio Ce a las temperaturas de 298, 308, 318 y 328 K, son mostrados en la figura 4. En la figura 5 se aprecia que a 328 K se alcanza la capacidad máxima de adsorción para este colorante, q máx (tabla 4), por lo cual dicha temperatura fue seleccionada para llevar a cabo el ajuste a las ecuaciones de equilibrio de Langmuir y Freundlich fue efectuado a dicha temperatura.
Figura 4: Ce(mg/L) frente a qe(mg/g) de R40 a diferentes temperaturas
Figura 5: Ce(mg/L) frente a qe(mg/g) de R40 a 328K con los ajustes de Langmuir y Freundlich
Evaluación de la cinética de R40
En cuanto a la cinética del proceso de remoción del R40 para los tres modelos evaluados, los valores de k 1, k 2, q e y R2 así como 𝛼 y β a diferentes temperaturas son presentados en la tabla 5.
Fuente: elaboración propia.
Tabla 5: Modelos cinéticos de pseudoprimer orden, pseudosegundo orden y Elovich para la adsorción de R40 sobre CA
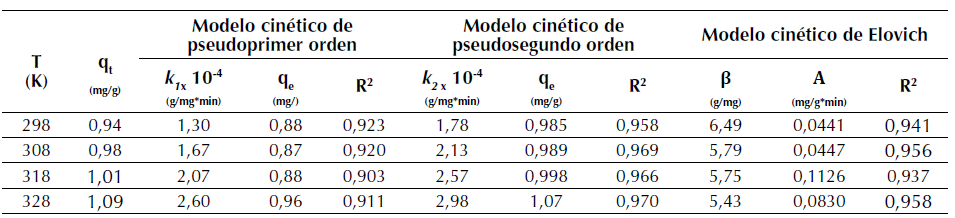
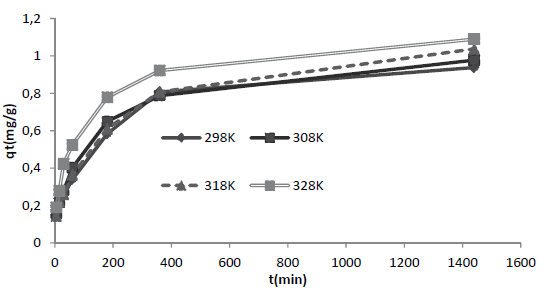
Los resultados experimentales de la cinética a las temperaturas de 298, 308, 318 y 328 K, son mostrados en la figura 6. Allí se aprecia que a 328 K se alcanza el mayor valor de la capacidad máxima de adsorción para este colorante, q t (tabla 5). La cinética de adsorción de R40 sobre CA señala que el proceso sigue satisfactoriamente el modelo cinético de pseudosegundo orden, con un coeficiente de correlación máximo R2 = 0,970 a la temperatura de 328 K, señalando, por consiguiente, que la ocurrencia del proceso es función de la concentración inicial del soluto y es representativo de soluciones de baja concentración.
Figura 6: t frente a qt de R40 a temperaturas de 298, 308, 318 y 328 K
Cabe señalar que estos resultados concuerdan con los reportados por investigadores como Azizian (2004), quien demuestra que concentraciones bajas de distintos colorantes como azul básico 169, azul ácido 25 y rojo ácido 114, presentan mejor ajuste a una cinética de pseudosegundo orden a una concentración inicial baja. Continuando con el modelo cinético de pseudosegundo orden, se puede observar que el parámetro experimental qt, a cada temperatura evaluada, tiene mayor similitud con el valor del parámetro teórico qe correspondiente al modelo cinético de pseudosegundo orden, confirmando que la adsorción de R40 sobre CA transcurre a través de dicho modelo. De forma general, para los tres modelos cinéticos evaluados se puede destacar en dichas tablas que las constantes de velocidad k 1, k 2 y q e de la adsorción del R40 sobre CA, incrementan su valor cuando la temperatura aumenta, debido al cambio en la concentración de la solución (Ho, 2006). Así, por ejemplo, la k 2 pasa de 1.78 × 10-4 (g/mg*min) a 298 K a 2.98 × 10-4(g/mg*min) a 328 K. El incremento en el valor de la constante de pseudosegundo orden con el aumento en la temperatura obedece a la ecuación de Arrhenius, donde la constante k 2 es expresada en función de la temperatura según la ecuación (12) (Yeddou y Bensmaili, 2007).
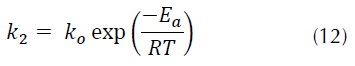
Donde, k o es un factor independiente de la temperatura (g/mg*min). E a es la energía de activación (kJ/mol). R es la constante de los gases (8.314 J/mol*K). T es la temperatura de la solución (K).
Para el modelo de Elovich, la constante 𝛼, que indica la velocidad de adsorción, aumenta con la temperatura como en los modelos anteriores y la constante β, que indica la energía de adsorción y es inversa a la capacidad de adsorción, muestra de acuerdo con lo previsto, una disminución con el aumento de la temperatura, tal como se reporta en estudios previos realizados con el adsorbente quitosano y el colorante rojo reactivo 222 como adsorbato (Wu, Tseng y Juang, 2009). Parte de la información anteriormente descrita, también puede apreciarse en la figura 7, donde se confirma que el mejor ajuste fue alcanzado a 328 K y que a esta temperatura, el modelo de Ho presentó la mejor correlación.
Figura 7: Cinética de adsorción de pseudoprimer orden, pseudosegundo y Elovich del R40 a 328 K
Parámetros termodinámicos
Los parámetros termodinámicos son de gran importancia dado que señalan las aplicaciones prácticas de un proceso. Así, por ejemplo, valores negativos para la energía libre de Gibbs, ΔG, se asocian con procesos que ocurren de forma espontánea (Dotto, Vieira, Esquerdo y Pinto, 2013; Elkady, Ibrahim y El-Latif, 2011). El cambio en la energía libre de Gibbs ΔG° de la adsorción fue calculado de acuerdo con la ecuación (13).
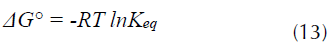
Donde, R es la constante universal de los gases (8.314 J mol-1 K-1) y T (K) la temperatura absoluta y Keq, es la constante de equilibrio, cuyo valor fue calculado a partir de la información de las isotermas de adsorción, mediante la ecuación (14).

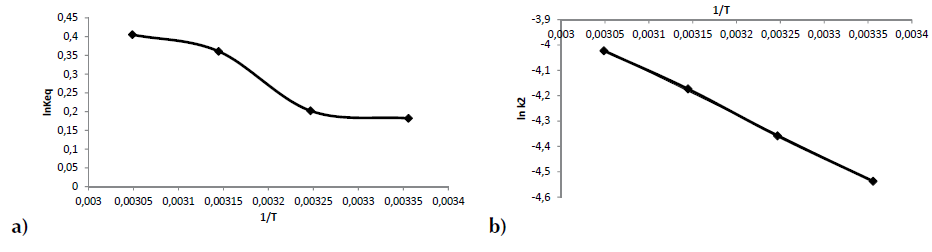
Donde, q e es la cantidad del colorante adsorbido sobre el adsorbente, y C e es la concentración del adsorbato en solución en el equilibrio considerando la dosificación de adsorbente en gL-1. De la tabla 6 se observa que la constante de equilibrio Keq aumenta al incrementar la temperatura, pasando de 1,20 a 298 K a 1,50 a 328 K. Es decir, el proceso de adsorción se ve favorecido a una mayor temperatura.
Fuente: elaboración propia.
Tabla 6: Parámetros termodinámicos de la adsorción de R40 sobre CA a temperaturas de 298, 308, 318 y 328 K

Como ya se mencionó, la factibilidad de la energía libre de Gibbs ΔG° donde valores más negativos señalan una mayor favorabilidad de la remoción, este parámetro está relacionado con la entalpía ΔH° (kJ/ mol) y la entropía ΔS° (J/mol*K), de acuerdo con la ecuación (15) (Tehrani-Bagha, Nikkar, Mahmoodi, Markazi y Menger, 2011).
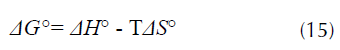
Reemplazando obtenemos la ecuación (16) a partir de la cual se calcula la pendiente - ΔH° y el intercepto ΔS°:
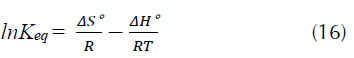
Valores positivos de ΔH° señalan que la remoción del proceso se ve favorecida cuando se incrementa la temperatura, de igual manera valores positivos de ΔS° indican una favorabilidad y ocurrencia espontánea del proceso (Howell y Buckius, 1990; Chong y Volesky, 1996). Los valores de ΔH° y ΔS° son calculados de la pendiente e intercepto respectivamente después de graficar ln K eq. frente a 1/T de la ecuación 15 (figura 8a), estos valores se presentan en la tabla 6. Los valores negativos de la energía libre de Gibbs (ΔG°) para el R40 indican que la adsorción de este colorante aniónico sobre CA es espontánea a estas temperaturas, y se favorece al aumentar la temperatura pasando de -0,451 kJ/mol a 298 K a -1,11 kJ/mol a 328 K, lo que indica una mayor espontaneidad a esta temperatura. Los valores pequeños de ΔG° en la tabla 6 indica que los valores de la constante de equilibrio K eq son pequeños. La entalpia ΔH° de 6,7 kJ/mol (tabla 6) señala que la adsorción de este colorante se ve favorecida a 328 K (Mittal, 2006). Por su parte, el valor positivo de ΔS° 23,9 kJ/mol*K (tabla 6), muestra que el proceso experimenta un aumento en la aleatoriedad en la interfase sólido-solución durante el proceso de adsorción (Aksu, Ertuğrul y Dönmez, 2009), y por consiguiente señala un proceso de naturaleza espontánea. Este valor positivo de entropía indica que existe una buena afinidad entre la cascarilla de arroz y el R40 (Mittal, 2006). La magnitud de la energía de activación proporciona una idea del tipo de adsorción. Los dos principales tipos de adsorción pueden ocurrir a través de fisiadsorción o quimiadsorción. El proceso de adsorción física, por lo general, tiene una energía de activación entre 5-40 kJ/mol, mientras que la adsorción química tiene energías de activación entre 40-800 kJ/mol (Nollet et al., 2003). Como ya se describió, la ecuación de pseudosegundo orden es la que ofrece la mejor descripción para la cinética de adsorción de R40. En consecuencia, la k 2 de pseudosegundo orden fue considerada en el cálculo de la energía de activación E a de la adsorción del colorante mediante la ecuación (17), la cual está expresada en función de la temperatura, proveniente de la ecuación (11) (Konicki, Pełech, Mijowska y Jasińska, 2012).
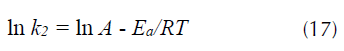
Figura 8: a) 1/T frente a lnKeq en la adsorción de R40 sobre CA b) 1/T frente a lnk2 en la adsorción de R40 sobre CA
Donde, E a es la energía de activación de la adsorción que representa la energía mínima que requieren los reactivos para que ocurra la reacción, A: factor de Arrhenius independiente de la temperatura, R: constante de los gases igual a 8,314 J/mol*K, T: temperatura absoluta de la solución (K). Así, cuando se gráfica lnk2 frente a 1/T, se encuentra que la pendiente es -E a /R (figura 8b). Como se observa en la tabla 6, la energía de activación de 14.1 kJ/mol, para la adsorción de R40 sobre CA, indica que este proceso ocurre a través de una adsorción física o fisiadsorción. Resultados similares en cuanto a la E a han sido reportados por diversos autores, quienes han encontrado que la adsorción de colorantes aniónicos tiene lugar a través de una fisiadsorción; así, por ejemplo, para el rojo directo 23 se reporta una Ea de 15,0 kJ/mol (Konicki, Pelech, Mijowska y Jasińska, 2012), de 33,35 kJ/mol para el rojo Procion® MX-5B (Wu, 2007), de 9,62 kJ/mol para el amarillo directo 86 y de 12,13 kJ/mol para el rojo directo 224 (Kuo, Wu y Wu, 2008).
Conclusiones
La evaluación de equilibrio, cinética y termodinámica en la adsorción del R40 sobre CA, señala que este residuo agrícola exhibe una considerable capacidad de adsorción y que el proceso ocurre en un tiempo adecuado y con liberación de energía; es decir, es espontáneo, y brinda condiciones apropiadas para un futuro escalado. El equilibrio de adsorción presentó mejor ajuste mediante el modelo de Langmuir, dado que muestra coeficientes de correlación cercanos a 1,0, con lo cual es posible establecer que la remoción tiene lugar mediante monocapas sobre la superficie del adsorbente. La cinética de adsorción de este colorante tuvo un mejor ajuste con el modelo cinético de pseudosegundo orden, con un coeficiente de correlación cercano a 1,0, indicando así que la ocurrencia del proceso es función de la concentración inicial del soluto y es representativo de soluciones de baja concentración.
La determinación de los parámetros termodinámicos señala que la remoción del R40 es un proceso espontáneo, ΔG = - 1.11 kJ/mol, en tanto que la entalpía mostró un proceso endotérmico, con valores de ΔH = 6,71 kJ/mol, por tanto se ve favorecido al incrementar la temperatura. La entropía positiva, ΔS = 23,9 J/mol*K, confirma la espontaneidad del proceso de remoción de este colorante. Por su parte, la energía de activación permite sugerir que el R40 sigue un mecanismo de adsorción a través de una fisiadsorción (14,1kJ/mol).
Acknowledgements
Agradecimientos
Los autores estamos agradecidos con el Departamento de Ciencia y Tecnología de Colombia, Colciencias, por el apoyo con la beca doctoral de la convocatoria 727 de 2015. Así mismo, a esta entidad por el respaldo financiero a través del Proyecto Código 111871250685.
Referencias
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.