DOI:
https://doi.org/10.14483/22487638.13387Publicado:
20-12-2018Número:
Vol. 22 Núm. 58 (2018): Octubre - DiciembreSección:
InvestigaciónEstimación del potencial de disipación de energía del oleaje de estructuras sumergidas y flotantes
Estimate of wave energy potential dissipation of submerged and floatable offshore structures
Palabras clave:
artificial reefs, coastal erosion, coastal protection, wave energy (en).Palabras clave:
arrecifes artificiales, energía del oleaje, erosión costera, protección costera (es).Descargas
Referencias
Alonso C., D.A., Sierra-Correa, P.C., Arias-Isaza, F.A. y Fontalvo, M.L. (2003). Conceptos y guía metodológica para el manejo integrado de zonas costeras en Colombia. Manual 1: preparación, caracterización y diagnóstico. Santa Marta, Colombia: Invemar.
Coastal Engineering Research Center (CERC) (1984). Shore Protection Manual. Vol. 2. Washington, D.C. DOI: http://doi.org/10.5962/bhl.title.47830
Chen, Z., Wang, Y., Dong, H. y Zheng, B. (2012). Time-Domain Hydrodynamic Analysis of Pontoon-Plate Floating Breakwater. Water Science and Engineering, 5(3), 291–303. DOI: http://doi.org/doi:10.3882/j.issn.1674-2370.2012.03.005
Correa, I.D., Alcántara-Carrió, J. y González R, D.A. (2005). Historical and Recent Shore Erosion along the Colombian Caribbean Coast. Journal of Coastal Research, 49, 52-57. DOI: http://doi.org/10.2112/014-NIS.1
Diamantoulaki, I. y Angelides, D.C. (2010). Analysis of performance of hinged floating breakwaters. Engineering Structures, 32(8), 2407–2423. DOI: http://doi.org/10.1016/j.engstruct.2010.04.015
Dorrel, D. E. (2004). EP 0 628 113 B1. Europe.
Invemar y Ministerio de Ambiente, Vivienda y Desarrollo Territorial (2003). Programa holandés de asistencia para estudios en Cambio Climático: Colombia. Definición de Vulnerabilidad de los sistemas bio-geofísicos y socioeconómicos debido a un cambio en el nivel del mar en la zona costera colombiana y medidas para su adaptación. Santa Marta.
Ji, C. Y., Chen, X., Cui, J., Gaidai, O. e Incecik, A. (2016). Experimental study on configuration optimization of floating breakwaters. Ocean Engineering, 117, 302–310. DOI: http://doi.org/10.1016/j.oceaneng.2016.03.002
Jiang, Z., Liang, Z., Zhu, L. y Liu, Y. (2016). Numerical simulation of effect of guide plate on flow field of artificial reef. Ocean Engineering, 116, 236–241. DOI: http://doi.org/10.1016/j.oceaneng.2016.03.005
Liu, H., Zhang, K., Li, Y. y Xie, L. (2013). Numerical study of the sensitivity of mangroves in reducing storm surge and flooding to hurricane characteristics in southern Florida. Continental Shelf Research, 64, 51–65. DOI: http://doi.org/10.1016/j.csr.2013.05.015
Lonin, S. y Escobar, C.A. (2009). Aspectos sobre modelación numérica de la evolución morfológica en el mar Caribe. En J. Alcántara-Carrió et al. (ed.), Métodos en teledetección aplicada a la prevención de riesgos naturales en el litoral (pp. 189–204). Madrid: Servicio de Publicaciones Programa Iberoamericano de Ciencia y Tecnología para el Desarrollo.
Mendonça, A., Fortes, C., Capitão, R., Neves, M., do Carmo, J. y Moura, T. (2011). Hydrodynamics around an artificial surfing reef at Leirosa, Portugal. Journal of Waterway, Port, Coastal, and Ocean Engineering, 138(3), 226–235. DOI: http://doi.org/10.1061/(ASCE)WW.1943-5460.0000128.
Michailides, C. y Angelides, D.C. (2012). Modeling of energy extraction and behavior of a Flexible Floating Breakwater. Applied Ocean Research, 35, 77–94. DOI: http://doi.org/10.1016/j.apor.2011.11.004
Peng, W., Lee, K.H., Shin, S.H. y Mizutani, N. (2013). Numerical simulation of interactions between water waves and inclined-moored submerged floating breakwaters. Coastal Engineering, 82, 76–87. DOI: http://doi.org/10.1016/j.coastaleng.2013.07.002
Posada, B.O. y Henao, W. (2008). Diagnóstico de la erosión en la zona costera del Caribe colombiano. Santa Marta: Invemar
Srisuwan, C. y Rattanamanee, P. (2015). Modeling of Seadome as artificial reefs for coastal wave attenuation. Ocean Engineering, 103, 198–210. DOI: http://doi.org/10.1016/j.oceaneng.2015.04.069
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 28 de mayo de 2018; Aceptado: 30 de agosto de 2018
RESUMEN
Contexto:
Los fenómenos erosivos en las playas del Caribe colombiano tienen repercusiones negativas sobre la población, razón por la cual se decidió evaluar diferentes propuestas de estructuras para la protección costera. Se realizó un análisis comparativo entre arrecifes artificiales y estructuras flotantes mediante modelación CFD para condiciones típicas del Caribe colombiano con el objetivo de establecer cuál estructura presenta mejor comportamiento.
Métodos:
Se utilizó el software Flow3D para evaluar cinco estructuras básicas sumergidas, configuraciones grupales de éstas y una placa flotante, en dos profundidades de lámina de agua y dos escenarios de altura de ola.
Resultados:
Se estableció el efecto de la profundidad y de la geometría en el flujo para las estructuras básicas y las grupales, así como los campos de velocidad y esfuerzos cortantes presentes en éstas. Para la estructura flotante sólo se analizó el efecto de la profundidad.
Conclusiones:
Se encontró que las estructuras que presentan el mejor comportamiento son el prisma triangular para las básicas y el grupo de cubos para las grupales. La estructura cónica es aquella con el peor comportamiento para ambas condiciones. La estructura flotante funciona mejor cuando está más cerca de la superficie y, para la misma profundidad, la configuración grupal de cubos tiene un mejor comportamiento que la estructura flotante.
Palabras clave:
arrecifes artificiales, energía del oleaje, erosión costera, protección costera.ABSTRACT
Context:
The erosive phenomenon on beaches of the Colombian Caribbean has negative repercussions over the people, which is why we decided to analyze different proposals for structures for coastal protection. In order to establish under which conditions each structure works best, a comparative analysis between artificial reefs and floatable structures was made with CFD modeling.
Method:
The Flow3D software was used to evaluate, in two depths of water sheet and two wave height scenarios, five submerged basic structures, group configurations of these basic structures, and a floating plate.
Results:
The effect of depth and geometry on the flow was established for the basic and group structures, as well as the velocity and shear stress fields present for each case. For the floating structure, only the effect of depth was analyzed.
Conclusions:
It was found that the structures that show the best behavior are the triangular prism (for the basic structures) and the cubes (for the group structures); while the conical structure presents the worst behavior in both conditions. Additionally, the floating structure works best when it is closer to the surface while, for the same depth, the group configuration of cubes has a better behavior than the floating structure.
Keywords:
Artificial reefs, Coastal erosion, Coastal protection, Wave energy.INTRODUCCIÓN
El Caribe colombiano ha experimentado fenómenos erosivos desde finales del siglo XVIII, y esta situación ha empeorado desde la década de 1970 debido a causas naturales y humanas (Correa, Alcántara-Carrió y González, 2005; Posada y Henao, 2008). Esta situación tiene un efecto negativo en la gente que vive en las áreas costeras, que es aproximadamente 12,5 % de la población del país, puesto que el retroceso de la línea de costa y de los arrecifes ocasiona pérdida de manglares, de tierra, y daños a las construcciones humanas (Alosnso, Sierra-Correa, Arias-Isaza y Fontalvo, 2003, Posada y Henao, 2008).
Entre los fenómenos naturales que ocasionan la erosión se encuentran: viento; mareas (que en el Caribe colombiano se caracterizan por ser mixtas tipo semidiurnas, con predominancia de los componentes diurnos, y micromareal con amplitudes menores a 0,5 m); aumento del nivel medio del mar y el oleaje, el cual tiene dirección principal oeste, periodos de entre 6 a 9 s, y alturas entre 1 m y hasta 3 m en condiciones de tormenta, y pueden producir escapamientos de 10 cm a 50 cm, en el sentido de las corrientes (Correa, Alcántara-Carrió y González, 2005; Posada y Henao, 2008; Invemar y Ministerio de Ambiente, Vivienda y Desarrollo Territorial, 2003; Lonin y Escobar, 2009).
Para proteger las zonas costeras de la erosión, alrededor del mundo se han realizado diferentes propuestas de estructuras tanto sumergidas como flotantes, las cuales se han analizado con modelos numéricos. Un ejemplo de esto se tiene en el estudio realizado por Dorrel (EP 0 628 113 B1, 2004), de un arrecife artificial formado por estructuras huecas, con el cual predijo la elevación de la superficie libre antes y después de la estructura. Por su parte, Jiang, Liang, Zhu y Liu (2016); Liu, Zhang, Li y Xie (2013); Mendonça et al. (2011); Srisuwan y Rattanamanee (2015), realizaron simulaciones numéricas de arrecifes artificiales y evaluaron su capacidad para atenuar el oleaje, para la protección costera. Chen, Wang, Dong y Zheng (2012) adelantaron una modelación hidrodinámica en 2D de un rompeolas flotante; Diamantoulaki y Angelides (2010) analizaron el efecto de la configuración sobre la efectividad de rompeolas flotantes; Ji et al. (2006) estudiaron diferentes estructuras flotantes en condiciones de oleaje regular; Michailides y Angelides (2012) usaron modelos tridimensionales para evaluar el comportamiento de estructuras flotantes; Peng, Lee, Shin y Mizutani (2013) compararon parámetros entre modelos físicos y numéricos.
El objetivo de este artículo es investigar el comportamiento hidrodinámico aproximado de dos tipos de estructuras de disipación de oleaje, sumergida y flotante. Para esto se seleccionaron cinco estructuras básicas sumergidas (prisma triangular, cubo, esfera, cono, y cilindro), configuraciones grupales de estas y una placa flotante como estructuras de protección costera. Su desempeño fue evaluado para la reducción de la altura del oleaje bajo condiciones típicas de oleaje del Caribe colombiano, a diferentes profundidades, para establecer cuál estructura presenta el mejor funcionamiento para las diferentes condiciones. Inicialmente se explica la metodología; es decir, se detallan las geometrías, configuración del modelo numérico y escenarios de simulación; posteriormente, se realiza el análisis de resultados considerando el efecto de la profundidad, geometría y los campos de velocidad en la reducción del oleaje transmitido por cada geometría; por último, se mencionan las conclusiones del trabajo.
METODOLOGÍA
Cinco estructuras básicas sumergidas, prisma triangular, cubo, esfera, cono y cilindro, configuraciones grupales de estas geometrías y una estructura flotante fueron analizadas en un modelo CFD, con el software Flow3D con el fin de lograr una primera aproximación a condiciones asociadas hacia estas diferentes geometrías mediante modelación CFD. En la figura 1 se muestran las estructuras a evaluar.
Figura 1: Configuraciones de estructuras a evaluar a) Geometrías básicas; b) Configuraciones grupales; c) Estructura flotante
El dominio computacional fue el siguiente:
-
Geometrías básicas: 40 m de largo, 3 m de ancho y alto de entre 5 m y 6 m.
-
Configuración grupal: 60 m de largo, 6,4 m de ancho y alto de entre 5 m y 6 m.
-
Estructura flotante: 60 m de largo, 6,4 m de ancho y alto de 8 m.
Debido a la extensión del dominio computacional y con la finalidad de reducir costos computacionales durante las simulaciones se usaron dos bloques de mallas: una malla gruesa de celdas de 0,10 m que abarca todo el dominio computacional, y una malla fina que se concentra en la geometría, para así obtener resultados con mayor precisión alrededor de esta, con celdas de 0,05 m. Para la estructura flotante, se usó un solo bloque de malla con celdas de 0,15 m teniendo en cuenta que por lo menos existan 4 celdas en la longitud más pequeña de la estructura para lograr un óptimo renderizado durante las simulaciones.
Figura 2: Malla computacional fina para configuración grupal de cubos
Se simuló un tren de olas lineal (basado en la teoría de Airy, la cual asume que el tren de olas proviene de un reservorio de fondo plano) como condición de frontera de entrada que se desplaza a lo largo del eje X, con una condición de frontera outflow en la salida del modelo, junto con condiciones de frontera laterales tipo simetría y una condición de frontera superior de tipo presión. Los módulos físicos usados para esta simulación fueron el renormalization group model (RGM) como modelo de turbulencia, y air entrainment.
Con respecto a las variables de simulación, para cada una de las estructuras se evaluaron dos profundidades (2 m y 3 m), de tal forma que estas se mantuvieran en condiciones sumergidas, y dos alturas de ola con su respectivo periodo asociado (altura de 0,88 m con un periodo de 13,58 s y altura de 2,71 m con un periodo de 7,91 s), las cuales son representativas de las condiciones del Caribe colombiano, específicamente en las playas de los departamentos de La Guajira y Magdalena, donde se ha evidenciado la problemática de erosión costera en los últimos años. Por lo que se obtienen 20 casos de simulación para las geometrías básicas (tabla 1).
Fuente: elaboración propia.
Tabla 1: Casos a evaluar para las geometrías básicas y configuraciones grupales, y flotantes

Para las configuraciones grupales se evaluaron los mismos 20 casos que se usaron para las geometrías básicas. Para la estructura flotante se evaluaron cuatro casos, con las mismas profundidades y alturas de ola analizadas para las geometrías básicas y las configuraciones grupales (tabla 2).
Fuente: elaboración propia.
Tabla 2: Casos a evaluar para la estructura flotante

Se tomaron dos puntos de medición, antes y después de la estructura, en donde se midió la elevación de la superficie libre. A partir de esto, se calcularon las alturas de ola antes y después de la estructura; con estos datos se obtuvo el coeficiente de transmisión por medio de la ecuación (1).

En donde Hi y Ht corresponden a las alturas de olas incidentes y transmitidas, respetivamente, por la estructura evaluada (CERC, 1984). Debido a que esta investigación es una primera aproximación, no se realizó una calibración con modelos físicos. Si bien una modelación física es necesaria para poder calibrar el modelo numérico, estas simulaciones se hacen como una primera aproximación con la cual es posible obtener tendencias, comportamientos generales y órdenes de magnitud para las estructuras evaluadas, y así facilitar una mejor planeación para pruebas físicas que se puedan llevar a cabo en el futuro.,
RESULTADOS
En el presente estudio se realizaron simulaciones numéricas con el fin de evaluar el efecto sobre el coeficiente de transmisión de las olas, producido por diversas geometrías de estructuras sumergidas y flotantes.
Geometrías básicas individuales
Se analizaron los resultados para establecer el efecto de la profundidad y geometría en el flujo.
Efecto de la profundidad
En general, para el prisma triangular, cubo, esfera y cilindro, los menores coeficientes de trasmisión se presentan en el caso 1, en donde se tienen la menor profundidad, y la menor altura de ola; los mayores coeficientes de trasmisión están en los casos 2 y 4, en los que se tiene la mayor altura de ola. Para una misma profundidad se encontró que a una mayor altura de ola, los valores para el coeficiente de trasmisión aumentan.
El cono presenta un comportamiento irregular con respecto a las demás estructuras. La gran mayoría de los puntos presentan un coeficiente de transmisión por arriba de 0,6, y los mínimos valores del coeficiente de transmisión se dan cuando la profundidad del agua es la mayor evaluada (figura 3). Se utilizaron gráficos de cajas y bigotes para ilustrar los resultados, en los cuales la línea central representa la mediana, los extremos de la caja los percentiles 25 y 75, y los bigotes llegan hasta los puntos que no son atípicos; es decir, aquellos que son mayores que el percentil 75 más 1,5 por la diferencia entre el percentil 75 y 25, o menores que el percentil 25 menos 1,5 por la diferencia entre el percentil 75 y 25.
Figura 3: Coeficiente de transmisión para geometrías básicas prisma triangular y cono
Efecto de la geometría
Para analizar el efecto de la geometría se realizó una comparación entre las cinco estructuras básicas, evaluándolas en las profundidades seleccionadas.
Los resultados para todas las estructuras en una profundidad de 2 m se muestran en la figura 4. En estos casos, las estructuras presentan comportamientos diferentes. El coeficiente de transmisión para el cono es el mayor en comparación con las demás estructuras. Esto es consistente con el hecho que la relación entre el área proyectada ocupada y el área total para el cono es la menor de todas las estructuras, con un valor de 0,5. Esto da lugar a que el agua se desplace entre los espacios laterales vacíos del cono, posiblemente generando estos resultados.
Figura 4: Coeficiente de transmisión para geometrías básicas para h=2,00 m
Las estructuras para las cuales el área proyectada ocupada es mayor presentan menores valores de coeficiente de transmisión, como el prisma triangular, cubo o cilindro, las cuales tienen un valor de 1 de área proyectada, mientras que la esfera tiene un valor de 0,78, con menores resultados.
La geometría que presenta los menores valores de coeficiente de transmisión es el prisma triangular, en la condición de menor altura de ola. En la figura 5 se pueden apreciar los resultados de todas las estructuras para una profundidad de 3 m.
Figura 5: Coeficiente de transmisión para geometrías básicas para h=3,00 m
En este caso, todas las estructuras se comparan a la misma profundidad de 3 m. El prisma triangular presenta los menores valores del coeficiente de transmisión. Adicionalmente, a medida que el área proyectada ocupada de las estructuras crece, los valores para el coeficiente de transmisión disminuyen.
En general, las estructuras básicas con las cuales hay una mayor disminución de la altura del oleaje transmitido, en orden descendente son: prisma triangular, cubo, cilindro, esfera y cono.
Campos de velocidad y esfuerzo cortante
Para la interacción fluido/estructura, se sabe que el comportamiento del fluido varía de acuerdo con la estructura en el medio. En la figura 6, se ilustran los campos de velocidad alrededor de la estructura, después del paso de la primera ola.
Figura 6: Vectores de velocidad parar t=12 s, y h=2 m
En dicha figura también se muestra el efecto que cada estructura tiene en el fluido; en el prisma triangular, el cubo y el cilindro, se crean vórtices al lado derecho, en la esfera se crea un pequeño vórtice en el lado de la estructura y en el cono no se crearon vórtices significativos. Estos vórtices representan los patrones de velocidad generados debido a la interacción del fluido con la estructura, y pueden indicar zonas en donde es posible que puedan presentarse en un futuro problemas de socavación. La diferencia entre los vórtices que se dan en cada estructura puede deberse a las características geométricas de las estructuras que producen cambios en el comportamiento del flujo alrededor de la estructura.
Relacionado con los vórtices está la velocidad del fluido alrededor de la estructura, la cual incrementa los esfuerzos cortantes en el lecho; de esta manera se ocasionarían problemas de erosión y socavación. En la figura 7 se ilustran los esfuerzos cortantes alrededor de la estructura después del paso de una ola, los cuales pueden asociarse con la velocidad. Las geometrías con un área proyectada de 1 (prisma triangular, cubo y cilindro) muestran los esfuerzos cortantes máximos al lado derecho de las estructuras, al nivel de la base, mientras que la esfera y el cono señalan los esfuerzos cortantes máximos a ambos lados de las estructuras.
Figura 7: Esfuerzo cortante para T=9 s
En la figura 8 se observan las líneas de flujo para el prisma triangular, cono y esfera, respectivamente. Para las geometrías que ocupan todo el espacio en la sección transversal, las líneas de flujo son rectas; el área que recibe el impacto del flujo es mayor, y puede asociarse a un menor coeficiente de transmisión. Para las geometrías que no ocupan todo el espacio en la sección transversal, las líneas de flujo rodean la estructura y los valores del coeficiente de transmisión tienden a ser mayores.
Figura 8: Streamlines para prisma triangular, cono y esfera
Configuraciones grupales
Se analizaron los resultados de los escenarios evaluados para las geometrías básicas en grupo. Se estudió el efecto del cambio en la profundidad y de la geometría de cada grupo.
Efecto de la profundidad
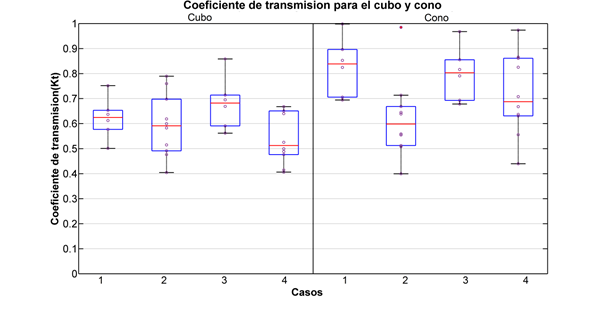
Entre los casos evaluados se tiene que la profundidad afecta el coeficiente de transmisión en los casos 1 y 3, es decir, en los que se evaluó la menor altura de ola y presentan menores valores en la menor profundidad. El cono, de igual manera que para las geometrías básicas individuales, muestra un comportamiento irregular en comparación con el resto de las geometrías (figura 9).
Figura 9: Coeficiente de transmisión para configuraciones grupales cubo y cono
Efecto de la geometría
Los valores obtenidos para los coeficientes de transmisión son similares para las diferentes configuraciones, tanto para la condición de profundidad de 2 m, como para la profundidad de 3 m. En promedio el grupo de estructuras cónicas muestra el menor desempeño, con valores promedio de coeficiente de transmisión de 0,83 en el caso de la profundidad de 2 m (figura 10), y valores promedio de 0,80 para el coeficiente de transmisión en la profundidad de 3 m.
Figura 10: Coeficiente de transmisión para configuraciones grupales para h=2,00 m
En general, de las configuraciones evaluadas, las que presentan los mayores porcentajes de reducción de flujo de energía medio local en orden descendente son: configuración de cubos, cilindros, prismas triangulares, esferas y conos, aunque los resultados obtenidos para el prisma triangular, el cilindro y la esfera son muy similares.
Campos de velocidad y líneas de flujo
El campo de flujo alrededor del grupo de estructuras se ve afectado debido a la interacción de las líneas de flujo con las caras de las estructuras. En la figura 11 se observan las líneas de flujo alrededor del grupo de cubos (lado izquierdo) y conos (lado derecho). El color de las líneas de flujo corresponde a la variable de velocidad.
Figura 11: Streamlines para configuración de cubos y conos
En el caso del grupo de cubos existe una mayor interacción y, por ende, una mayor afectación sobre las trayectorias de las líneas de flujo, en comparación con las trayectorias en el caso del grupo de conos. El grupo de cubos obtuvo los menores valores de coeficiente de transmisión, lo cual puede obedecer a la alta cantidad de colisiones y cambios de trayectorias que se dan entre los espacios del grupo de cubos. Por el contrario, el grupo de estructuras cónicas presentó altos valores del coeficiente de transmisión, lo cual se puede asociar a las pocas colisiones frontales de las líneas de flujo producto del cambio suave en la dirección de las líneas de flujo debido a la superficie redondeada de las caras de los conos.
Estructura flotante
La figura 12 muestra, a través de un diagrama de cajas, los resultados obtenidos en cuanto al coeficiente de transmisión para la estructura flotante.
Figura 12: Coeficiente de transmisión de placas flotantes
Los valores más bajos de reducción de energía del oleaje para la estructura flotante ocurrieron con una altura de ola de 0,88 m con una profundidad de 3,0 m, mientras que para la misma condición de profundidad, pero con una altura de ola mayor (2,71 m), se observó una gran variación en los valores del coeficiente de transmisión en cada una de las olas que se trasmitieron sobre la estructura flotante.
CONCLUSIONES
Se tienen las siguientes conclusiones, de acuerdo con los resultados obtenidos:
-
Entre las estructuras básicas, la que presenta un menor coeficiente de transmisión es el prisma triangular.
-
La estructura cónica es la que posee el mayor coeficiente de transmisión tanto para la estructura básica como para la configuración grupal.
-
Todas las estructuras para la configuración grupal, excepto el cono, tienen un comportamiento similar, aunque el menor coeficiente de transmisión se da con la configuración grupal de cubos.
-
La estructura flotante tiene menores coeficientes de transmisión cuando la estructura se encuentra más cerca de la superficie.
Para una misma profundidad, la configuración grupal cúbica tiene un mejor desempeño que la estructura flotante.
REFERENCIAS
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.