DOI:
https://doi.org/10.14483/22487638.16302Publicado:
2021-01-01Número:
Vol. 25 Núm. 67 (2021): Enero - MarzoSección:
InvestigaciónLocalización de múltiples fuentes basada en información de dirección de llegada mediante el uso de la teoría de sensado comprimido de la posición basado en información de dirección de llegada aplicando sensado comprimido a la matriz de covarianza
Location Estimation of Multiple Sources Based on Direction of Arrival Applying Compressed Sensing Theory
Palabras clave:
direction of arrival, sparse reconstruction, compressive sensing, radio localization systems (en).Palabras clave:
dirección de llegada, reconstrucción dispersa, sensado comprimido, sistemas de radiolocalización (es).Descargas
Referencias
Asghar-Sayed, Z. y Ng, B. P. (2019). Aperiodic geometry design for DOA estimation of broadband sources using compressive sensing. Signal Processing, 155, 96-107. DOI: https://doi.org/10.1016/j.sigpro.2018.09.026 DOI: https://doi.org/10.1016/j.sigpro.2018.09.026
Baron, D., Duarte, M. F., Wakin, M. B., Sarvotham, S. y Baraniuk, R. G. (2009). Distributed compressive sensing. Recuperado de http://arxiv.org/abs/0901.3403 DOI: https://doi.org/10.21236/ADA521228
Becerra-Mora, Y. A. (2020). Una revisión de plataformas robóticas para el sector de la construcción. Tecnura, 24, 115-132. DOI: https://doi.org/10.14483/22487638.15384 DOI: https://doi.org/10.14483/22487638.15384
Bougher, B. (2015). Introduction to compressed sensing. Leading Edge, 34(10), 1256-1257. DOI: https://doi.org/10.1190/tle34101256.1 DOI: https://doi.org/10.1190/tle34101256.1
Candès, E. J. y Romberg, J. (2006). Quantitative robust uncertainty principles and optimally sparse decompositions. Foundations of Computational Mathematics, 6(2), 227-254. DOI: https://doi.org/10.1007/s10208-004-0162-x DOI: https://doi.org/10.1007/s10208-004-0162-x
Candès, E. J., Romberg, J. K. y Tao, T. (2006a). Stable signal recovery from incomplete and inaccurate measurements. Communications on Pure and Applied Mathematics, 59(8), 1207-1223. DOI: https://doi.org/10.1002/cpa.20124 DOI: https://doi.org/10.1002/cpa.20124
Candès, E. J., Romberg, J. y Tao, T. (2006b). Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 52(2), 489-509. DOI: https://doi.org/10.1109/TIT.2005.862083 DOI: https://doi.org/10.1109/TIT.2005.862083
Cotter, S. F. (2007). Multiple snapshot matching pursuit for direction of arrival (DOA) estimation. En 2007 15th European Signal Processing Conference (pp. 247-251). Poznán, Polonia.
Donoho, D. L. (2006). Compressed sensing. IEEE Transactions on Information Theory, 52(4), 1289-1306. DOI: https://doi.org/10.1109/TIT.2006.871582 DOI: https://doi.org/10.1109/TIT.2006.871582
Duarte, M. F., Sarvotham, S., Baron, D., Wakin, M. B. y Baraniuk, R. G. (2005a). Distributed compressed sensing of jointly sparse signals. En Conference Record - Asilomar Conference on Signals, Systems and Computers, 1537-1541. DOI: https://doi.org/10.1109/acssc.2005.1600024 DOI: https://doi.org/10.1109/ACSSC.2005.1600024
Duarte, M., Sarvotham, S., Wakin, M., Baron, D. y Baraniuk, R. (2005b). Joint sparsity models for distributed compressed sensing. En Online Proceedings of the Workshop on Signal Processing with Adaptive Sparse Structured Representations (SPARS).
Eldar, Y. C., Kuppinger, P. y Bölcskei, H. (2010). Block-sparse signals: uncertainty relations and efficient recovery. IEEE Transactions on Signal Processing, 58(6), 3042-3054. DOI: https://doi.org/10.1109/TSP.2010.2044837 DOI: https://doi.org/10.1109/TSP.2010.2044837
Foucart, S. y Rauhut, H. (2013). A mathematical introduction to compressive sensing. Nueva York: Birkhäuser Basel. DOI: https://doi.org/10.1007/978-0-8176-4948-7 DOI: https://doi.org/10.1007/978-0-8176-4948-7
Gross, F. (2005). Smart Antennas for wireless communications. McGraw-Hill. https://doi.org/10.1036/007144789X
ross, F. (2005). Smart Antennas for wireless communications. Nueva York: McGraw-Hill. DOI: https://doi.org/10.1036/007144789X
Gu, J. F., Zhu, W. P. y Swamy, M. N. S. (2011). Compressed sensing for DOA estimation with fewer receivers than sensors. En Proceedings - IEEE International Symposium on Circuits and Systems, 1752-1755. DOI: https://doi.org/10.1109/ISCAS.2011.5937922 DOI: https://doi.org/10.1109/ISCAS.2011.5937922
Gürbüz, A. C., McClellan, J. H. y Cevher, V. (2008). A compressive beamforming method. En ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing - Proceedings, 2617-2620. DOI: https://doi.org/10.1109/ICASSP.2008.4518185 DOI: https://doi.org/10.1109/ICASSP.2008.4518185
Hincapié, R., Gómez, C., Betancur, L., Lavrenko, A. y Schmitz, J. (2018). Sparse framework for hybrid TDoA/DoA multiple emitter localization. En 2017 IEEE International Symposium on Signal Processing and Information Technology, ISSPIT, 174-179. DOI: https://doi.org/10.1109/ISSPIT.2017.8388637 DOI: https://doi.org/10.1109/ISSPIT.2017.8388637
Jouny, I. (2011). Music DOA estimation with compressive sensing and/or compressive arrays. En IEEE Antennas and Propagation Society, AP-S International Symposium (Digest). DOI: https://doi.org/10.1109/APS.2011.5996902 DOI: https://doi.org/10.1109/APS.2011.5996902
Lagunas, E., Sharma, S. K., Chatzinotas, S. y Ottersten, B. (2016). Compressive sensing based target counting and localization exploiting joint sparsity. En ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing - Proceedings, 3231-3235. DOI: https://doi.org/10.1109/ICASSP.2016.7472274 DOI: https://doi.org/10.1109/ICASSP.2016.7472274
Li, G. y Huang, G. (2014). DOA estimation based on compressive sampling array with novel beamforming. En 2014 31th URSI General Assembly and Scientific Symposium, URSI GASS. DOI: https://doi.org/10.1109/URSIGASS.2014.6929037 DOI: https://doi.org/10.1109/URSIGASS.2014.6929037
Malioutov, D., Çetin, M. y Willsky, A. S. (2005). A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Transactions on Signal Processing, 53(8), 3010-3022. DOI: https://doi.org/10.1109/TSP.2005.850882 DOI: https://doi.org/10.1109/TSP.2005.850882
Marín-Alfonso, J., Betancur-Agudelo, L. y Alguello-Fuentes, H. (2017). Further compressio of focal plane array in compressive spectral imaging architectures. Tecnura, 21(52), 45-52. DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a03 DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2017.2.a03
Martínez-Sarmiento, F. H. y Giral-Ramírez, D. A. (2016). OpenRRArch: una arquitectura abierta, robusta y confiable para el control de robots autónomos. Tecnura, 21(51), 96-104. DOI: Retrieved from https://www.redalyc.org/pdf/2570/257050668007.pdf DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2017.1.a07
Nikitaki, S. y Tsakalides, P. (2011). Localization in wireless networks based on jointly compressed sensing. En 2011 19th European Signal Processing Conference (pp. 1809-1813). Barcelona, España.
Pahlavan, K., Krishnamurthy, P. y Geng, Y. (2015). Localization challenges for the emergence of the smart world. IEEE Access, 3, 3058-3067. DOI: https://doi.org/10.1109/ACCESS.2015.2508648 DOI: https://doi.org/10.1109/ACCESS.2015.2508648
Paul, A. y Sato, T. (2017). Localization in wireless sensor networks: a survey on algorithms, measurement techniques, applications and challenges. Journal of Sensor and Actuator Networks, 6(4), 24. DOI: https://doi.org/10.3390/jsan6040024 DOI: https://doi.org/10.3390/jsan6040024
Pazos, S., Hurtado, M. y Muravchik, C. (2014). DOA estimation using random linear arrays via compressive sensing. IEEE Latin America Transactions, 12(5), 859-863. DOI: https://doi.org/10.1109/TLA.2014.6872896 DOI: https://doi.org/10.1109/TLA.2014.6872896
Rappaport, T. S. (2001). Wireless communications. Recuperado de https://www.pearson.ch/HigherEducation/ElectricalEngineering/Communications/EAN/9780130422323/Wireless-Communications
Schmitz, J., Mathar, R. y Dorsch, D. (2015). Compressed time difference of arrival based emitter localization. En 2015 3rd International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar, and Remote Sensing, CoSeRa 2015, 263-267. DOI: https://doi.org/10.1109/CoSeRa.2015.7330305 DOI: https://doi.org/10.1109/CoSeRa.2015.7330305
Wang, Y., Leus, G. y Pandharipande, A. (2009). Direction estimation using compressive sampling array processing. En IEEE Workshop on Statistical Signal Processing Proceedings, 626-629. DOI: https://doi.org/10.1109/SSP.2009.5278497 DOI: https://doi.org/10.1109/SSP.2009.5278497
Xenaki, A., Gerstoft, P. y Mosegaard, K. (2014). Compressive beamforming. The Journal of the Acoustical Society of America, 136(1), 260-271. DOI: https://doi.org/10.1121/1.4883360 DOI: https://doi.org/10.1121/1.4883360
Zhao, H., Irshad, M. J., Shi, H. y Xu, W. (2019). Passive source localization using compressive sensing. Sensors, 19(20), 4522. DOI: https://doi.org/10.3390/s19204522 DOI: https://doi.org/10.3390/s19204522
Zhu, W. y Chen, B. X. (2013). Novel methods of DOA estimation based on compressed sensing. Multidimensional Systems and Signal Processing, 26(1), 113-123. DOI: https://doi.org/10.1007/s11045-013-0239-2 DOI: https://doi.org/10.1007/s11045-013-0239-2
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 2 de junio de 2020; Aceptado: 3 de noviembre de 2020
Resumen
Contexto:
Los algoritmos de dirección de llegada han sido ampliamente utilizados en los sistemas de posicionamiento; sin embargo, tienen restricciones importantes con respecto a la estacionariedad espacial y temporal de las fuentes, y la correlación entre estas y el ruido. Ahora bien, el problema de la localización, por su naturaleza, se puede considerar como disperso, razón por la cual es posible aplicar la teoría de sensado comprimido y reconstrucción dispersa para estimar la posición de fuentes no colaborativas.
Método:
En este trabajo se simula un sistema compuesto por varios nodos de referencia (RN, por su sigla en inglés) que comparten información con una entidad central denominada centro de fusión (FC, por su sigla en inglés), en la cual se llevará a cabo la estimación final de posición de varias fuentes no colaborativas. El proceso se divide en dos etapas: offline y online. En la primera, cada RN construye un diccionario que contiene la matriz de covarianza del factor de arreglo de antenas para cada una de las posibles posiciones de transmisión. Por su parte, en la etapa online se realiza la estimación de la posición, en la cual cada RN recibe la señal de las fuentes activas y calcula una versión comprimida de la matriz de covarianza de la señal recibida. Luego se realiza la estimación de la posición de las fuentes dentro del área de interés mediante el algoritmo OMP para la reconstrucción dispersa.
Resultados:
Los resultados muestran el desempeño del sistema en términos de precisión en la estimación de la posición, cuando se varían parámetros como la cantidad de sensores activos, el ruido del sistema y la tasa de compresión empleada en la matriz de sensado. El peor resultado se da cuando hay dos fuentes en el sistema y se obtiene un error cercano a los 4,5 metros; mientras que cuando solo existe una fuente, el error promedio del sistema es cercano a los 0,14 metros. Finalmente, el costo computacional del sistema disminuye cuando se incrementa la tasa de compresión empleada, debido a que el tamaño de las matrices empleadas disminuye.
Conclusiones:
El método propuesto proporciona alta precisión en la estimación, sin tener problemas con las restricciones en los requerimientos de estacionariedad espacial y temporal presentes en los algoritmos tradicionales de dirección de llegada, además de las condiciones de correlación entre las fuentes y el ruido.
Financiamiento:
MinCiencias Colombia y Universidad Pontificia Bolivariana.
Palabras clave:
dirección de llegada, reconstrucción dispersa, sensado comprimido, sistemas de radiolocalización.Abstract
Objective:
Diction of arrival algorithms have been widely used in positioning systems. However, they have important restrictions to take into account in terms of spatial and temporal stationary requirements between the sources and correlation proprieties between them and the noise. Nevertheless, due to its nature the localization problem could be posed like a sparse reconstruction problem, and is possible to apply the compressive sensing and sparse reconstruction theory to estimate the position of several non-collaborative sources. Besides, considering a joint estimation system as we propose in this work, is possible to exploit both inter and intra-correlation signal aiming to improve the accuracy estimation.
Methodology:
In this work we simulate a localization system composed by several reference nodes (RN) which share information with a central entity named fusion center (FC) where the target estimation will take place. The process is divides in two stages: offline and online. In the first one we discretize the region of interest (ROI) in K candidates position where the sources could be located. Each RN builds its own dictionary that contains the covariance matrix of the steering vector for each cell into the grid. In the online stage, the target position estimation is performed. To do so, each RN receives the signal from the sources and calculates the compressed version of the covariance matrix, which is sent to the FC. In the FC the orthogonal matching pursuit (OMP) is performed to estimate the target coordinates inside the ROI.
Results:
The results show the system performance in terms of accuracy in the position estimation when parameters like number of sensors, system’s noise and compression rate in the measurement matrix are varied.
Conclusions:
The proposed method provides high accuracy in the estimation without restricting requirements on the spatial and temporal stationery and correlation properties of the sources and the noise, which are common in traditional direction of arrival algorithms.
Financing:
Miniciencias Colombia and Pontificia Bolivariana University.
Keywords:
direction of arrival, sparse reconstruction, compressive sensing, radio localization systems.INTRODUCCIÓN
La localización es una tarea importante que cada día toma más fuerza en diferentes áreas del conocimiento. Algunos autores coinciden en que uno de los componentes críticos de las aplicaciones actuales de internet de las cosas (IoT, por su sigla en inglés) y las redes de sensores es la localización o el tracking del sensor o de los nodos móviles (Pahlavan, Krishnamurthy y Geng, 2015; Paul y Sato, 2017). Actualmente, en diversas áreas del conocimiento se emplean robots autónomos para completar tareas que antes eran desarrolladas por seres humanos (Becerra-Mora, 2020; Martínez-Sarmiento y Giral-Ramírez, 2016); para ello, esos robots requieren sistemas de localización que les permitan conocer su posición exacta o la de otros objetos dentro de una región de interés.
En los sistemas de radiolocalización, el objetivo es determinar la posición de transmisores desconocidos mediante la explotación de parámetros de propagación de las señales emitidas (Hincapié et al., 2018). Para ello se emplean diferentes algoritmos, entre los cuales se encuentran aquellos basados en ángulos, denominados algoritmos de ángulo de llegada (AOA, por su sigla en inglés) o dirección de llegada (DOA, por su sigla en inglés).
Los sistemas de DOA han generado un considerable interés en las últimas tres décadas, debido a su importancia en múltiples campos de aplicación como radar, sonar, sismología, comunicaciones inalámbricas, entre otros (Gu, Zhu y Swamy, 2011). Este tipo de sistemas emplean arreglos de antenas para determinar la dirección de llegada de una señal, aplicando técnicas basadas en subespacios y estimación de parámetros (Gross, 2005; Zhu y Chen, 2013). Sin embargo, estos algoritmos presentan inconvenientes y bajo desempeño en los casos en los que la relación señal a ruido (SNR, por su sigla en inglés) es baja y las fuentes tienen alto grado de correlación, además de que requieren un alto número de mediciones (Xenaki, Gerstoft y Mosegaard, 2014). Cabe mencionar que los sistemas de DOA tienen altos requerimientos en cuanto al arreglo de antenas, y la separación entre los elementos no debe ser mayor a la mitad de la longitud de onda, con el fin de evitar la aparición de lóbulos fantasmas (grating lobes) que pueden resultar en la estimación de falsos positivos, limitando de esta manera la apertura del arreglo. Lo anterior implica que si se quiere tener un sistema con mayor apertura es necesario tener arreglos con muchos elementos de antena, lo cual es problemático porque se requiere un mayor número de circuitos de front-end, trayendo implicaciones de hardware y software, ya que el tamaño de las matrices usadas es muy grande y genera alta carga computacional (Wang, Leus y Pandharipande, 2009).
Recientemente, debido a la naturaleza de esparcidad existente en los sistemas de posicionamiento, se ha propuesto usar la teoría de sensado comprimido (CS, por su sigla en inglés) para formular la tarea de localización como un problema de reconstrucción dispersa (Malioutov, Çetin y Willsky, 2005).
El sensado comprimido es una técnica de muestreo, que ha surgido en los últimos años, que permite disminuir la tasa de muestreo de la señal sin perder información, siempre y cuando la señal posea una representación dispersa en alguna base o diccionario conocido (Donoho, 2006). Dicho esto, el CS es especialmente atractivo para los esquemas de localización donde debido al esquema centralizado de procesamiento en banda base, un alto volumen de datos debe ser transmitido y procesado. Ahora bien, para poder formular el problema de localización basado en la teoría de reconstrucción dispersa, es necesario encontrar una base de representación adecuada, la cual permita estimar la posición de una o múltiples fuentes mediante proyecciones adaptativas no lineales de las mediciones sobre dicha base.
Por otra parte, teniendo en cuenta que muchos de los sistemas de posicionamiento emplean varios receptores de manera simultánea, es posible aplicar los algoritmos de sensado comprimido conjunto distribuido (JDCS, por su sigla en inglés), los cuales buscan explotar la inter- e intracorrelación de la señal, lo que permite mejorar la precisión del sistema (Lagunas, Sharma, Chatzinotas y Ottersten, 2016).
A partir de lo anterior, muchos autores han propuesto trabajos que permiten estimar la dirección de llegada de una o múltiples señales, realizando una discretización del espacio angular para aplicar las técnicas de reconstrucción dispersa y sensado comprimido. Gran parte de los trabajos relacionados buscan reducir la complejidad tanto en hardware como en software que puede generar el uso de grandes arreglos de antenas. Es el caso de Li y Huang (2014), quienes proponen una matriz de compresión para aplicar al factor de arreglo de tal manera que sea posible estimar el DOA, empleando algunos elementos de antena elegidos de manera aleatoria. Trabajos similares son presentados por Gürbüz, McClellan y Cevher (2008); Jouny (2011); Wang, Leus y Pandharipande (2009), y Xenaki, Gerstoft y Mosegaard (2014). Por su parte, Cotter (s. f.) aprovecha las múltiples muestras de la señal como mediciones diferentes con el fin de expandir el alcance del algoritmo y mejorar la precisión en la estimación. De otro lado, Asghar-Sayed y Ng (2019), y Pazos, Hurtado y Muravchik (2014) evalúan el desempeño de sistemas DOA con arreglos de antena que no son lineales uniformes (ULA) a los cuales se les aplica matrices de sensado comprimido en el dominio angular para estimar la dirección de llegada. Finalmente, Hincapié et al. (2018) diseñan un sistema híbrido DOA/TDOA (time difference of arrival) para estimar la posición de múltiples fuentes transmisoras.
Ahora bien, este trabajo evalúa el desempeño de un sistema de DOA aplicando la teoría de sensado comprimido a la matriz de covarianza de la señal usada tradicionalmente en los algoritmos clásicos de DOA, tal y como lo proponen Zhu y Chen (2013).
Al elegir el sensado comprimido a la matriz de covarianza, se brinda mayor estabilidad al sistema, en especial en condiciones en las que el canal es altamente ruidoso. Después de múltiples pruebas por simulación con la matriz de compresión a la señal recibida, se observa que el sistema pierde precisión, pues arroja estimaciones imprecisas en varias ocasiones, mientras que al hacerlo con la matriz de covarianza la precisión del sistema se conserva cuando se varían los niveles de ruido del canal.
Sin embargo, el mayor aporte y elemento diferenciador con los demás trabajos expuestos radica en que el sistema propuesto estima las coordenadas dentro de la región de interés (ROI, por su sigla en inglés) de múltiples fuentes transmisoras; de esta manera se obtiene una posición exacta dentro de un área y no solo un ángulo de llegada como sucede en la mayoría de los casos. Para ello se considera un sistema compuesto por múltiples nodos de referencia (RN, por su sigla en inglés), cada uno equipado con un arreglo de antenas, los cuales toman mediciones de la señal recibida y las envían al centro de fusión (FC, por su sigla en inglés) donde se aplica un algoritmo de JDCS para estimar la posición de los transmisores dentro de la ROI. Cabe mencionar que durante el trabajo se varían parámetros como el número de sensores, el ruido del sistema y las tasas de compresión, con el fin de evaluar el impacto de esto sobre la precisión en la estimación.
MODELO DEL SISTEMA
El modelo propuesto considera un sistema compuesto por Q fuentes transmisoras denominadas nodos objetivo (TN, por su sigla en inglés) y R receptores llamados nodos de referencia (RN, por su sigla en inglés), cada uno de los cuales tiene un arreglo de antenas compuesto por M elementos. Tanto los RN como los TN se ubican aleatoriamente dentro de una ROI, la cual se discretiza en K celdas, cada una de las cuales tiene coordenadas bidimensionales (BSk x, BSk Y) Adicionalmente, se cuenta con una entidad central denominada centro de fusión (FC, por su sigla en inglés) en la cual se lleva a cabo la estimación final de la posición empleando información recolectada y enviada por los RN mediante una red de backbone que los conecta.
Cada uno de los RN tiene coordenadas (Xr, Yr) dentro de la grilla, mientras que los TN tienen coordenadas (Xq, Yq), las cuales son desconocidas y serán estimadas a través del método propuesto.
A partir de lo anterior, se define un modelo de señal en el que se considera un canal simple sin multitrayectoria, el cual solamente considera efectos de atenuación y retardo sobre la componente de línea de vista (LOS, por su sigla en inglés) de la señal transmitida. Por tanto, cada RN recibe una señal
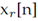dada por la ecuación (1), donde Sq es la señal transmitida por la fuente q-ésima; αq,r es el factor de atenuación, y Tq,r es el retardo en número de muestras que sufre la señal por la propagación entre el TNq y el RNr, y
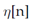es el vector de ruido blanco gaussiano (AWGN, por su sigla en inglés) con media cero y varianza σ2 :
Sin embargo, si consideramos que cada RN tiene un arreglo de antenas compuesto por 𝑀 elementos entonces, la señal recibida está dada por la ecuación (2):
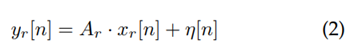
Donde:
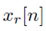es la señal recibida después de haber pasado por el canal, y Ar
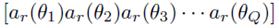es la matriz de los vectores de dirección propia del factor de arreglo. Cada uno de los elementos de Ar indica la dirección de llegada de cada una de las fuentes presentes en el sistema al RNr y está dada por la ecuación (3), donde λ = c/f es la longitud de onda de la señal recibida y dq es la distancia que hay entre el transmisor q-ésimo y cada elemento del arreglo de antenas del RNr:
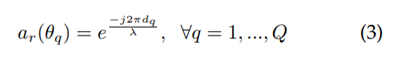
Representación dispersa y sensado comprimido
En la mayoría de casos prácticos de los sistemas de localización, el número de fuentes es mucho menor al de posiciones desde las cuales puede provenir una señal; es decir, al discretizar la región de interés, la cantidad de celdas que efectivamente contienen fuentes transmisoras es mucho menor al tamaño de la grilla como tal, razón por la cual es posible plantear el problema de localización como de reconstrucción dispersa (Zhao, Irshad, Shi y Xu, 2019). Además, basados en la teoría de sensado comprimido desarrollada por Candès y Romberg (2006); Candès, Romberg y Tao (2006a, 2006b), y Donoho (2006), la señal recibida
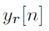se puede aproximar correctamente como una combinación lineal de algunos pocos elementos de una base de representación conocida o diccionario (Marín-Alfonso, Betancur-Agudelo y Alguello-Fuentes, 2017). Por consiguiente, es posible proponer un estimador
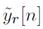para la señal recibida en cada RN dada por la ecuación (4), donde
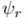es el diccionario conocido con dimensiones N x K , siendo K la cantidad de celdas dentro de la grilla y N la longitud de la señal, y br es el vector disperso, con dimensiones K X 1, que tiene tantos coeficientes diferentes de cero como número de fuentes existen en el sistema (Schmitz, Mathar y Dorsch, 2015):
La ecuación (4) se puede resolver mediante la minimización de la norma
buscando los valores diferentes de cero en el vector br; sin embargo, esto es un problema NP-hard, lo cual implica que el número de combinaciones posibles para encontrar una solución óptima tiende a infinito, por lo cual se busca simplificar el problema, mediante una relajación de la norma
. Esto se puede dar bajo condiciones adicionales que se asumen sobre la matriz
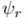, obteniendo de esta manera una posible solución mediante la minimización de la norma
(Schmitz, Mathar y Dorsch, 2015). En consecuencia, se plantea el problema de minimización siguiendo la ecuación (5), que puede ser resuelta mediante esquemas de optimización convexa o algoritmos codiciosos como orthogonal matching purtsuit (OMP):
Por su parte, la teoría de sensado comprimido permite incorporar una matriz φ
r
de dimensiones P X N con P N, que reduzca el tamaño del vector de mediciones
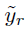. Además, bajo la teoría de sensado comprimido es posible reconstruir br usando un menor número de muestras mediante proyecciones lineales no adaptativas sobre una matriz de observaciones φ
r
que es incoherente con
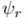(Bougher, 2015; Foucart y Rauhut, 2013). Por consiguiente, el vector de mediciones
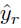está dado por la ecuación (6):
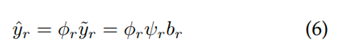
La matriz φ r se genera como una matriz de submuestreo, en la cual se toman P filas de una matriz identidad de N X N con el fin de tomar P muestras de la medición original. Ahora bien, reformulando la ecuación (5), se obtiene que el problema de optimización está dado por la ecuación (7), y se resuelve aplicando el mismo algoritmo OMP.
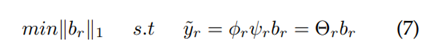
Sensado comprimido conjunto distribuido
Teniendo en cuenta que el sistema propuesto considera un esquema centralizado con múltiples nodos de referencia para estimar la posición, es posible aplicar la teoría de sensado comprimido conjunto distribuido (JDCS, por su sigla en inglés) y explotar tanto la inter- como la intracorrelación de la señal, como lo sugieren Duarte et al. (2005) a . JDCS considera la esparsidad conjunta de una señal para obtener una reconstrucción precisa de la señal (Nikitaki y Tsakalides, 2011).
En un escenario típico de DCS, cada sensor mide señales que son dispersas individualmente en alguna base de representación y a su vez están correlacionadas entre sí. Por eso, cada sensor de manera independiente codifica su señal mediante proyecciones incoherentes sobre su base de representación dispersa, y en las condiciones adecuadas un decodificador en el centro de fusión puede reconstruir de manera conjunta y precisa la señal, de lo que se obtienen las coordenadas (Xq, Yq) de los transmisores dentro de la región de interés (Duarte et al., 2005b).
METODOLOGÍA
El método propuesto para estimar la posición de varios transmisores, mediante sensado comprimido y reconstrucción dispersa a la matriz de covarianza usada en los algoritmos tradicionales de dirección de llegada, se realiza en dos etapas: offline y online.
En la primera etapa, offline, se construye el diccionario o base de representación dispersa
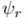para cada uno de los nodos de referencia del sistema. Mientras que en online se toman las mediciones que son enviadas al FC para realizar la estimación de la posición. A continuación se describen en detalle estas etapas.
Etapa offline: construcción de diccionarios
Cada RN construye su propio diccionario
, que contiene la versión vectorizada de la matriz de covarianza del factor de arreglo para cada una de las k posiciones dentro de la grilla. Cada elemento se calcula empleando la ecuación (8), donde α(θ) se calcula con la ecuación (3), y (.)H denota la hermitiana de un vector:
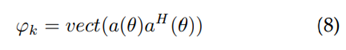
Para construir el diccionario, una vez se tenga discretizada la región de interés, se ubican los RN dentro de esta y se fijan en las coordenadas (Xr, Yr). Posteriormente se ubica una única fuente transmisora en la primera celda de la grilla cuyas coordenadas corresponden a (BS1 X,BS1 Y) y se aplica la ecuación (8). En este caso, la distancia dq de la ecuación (3) se reescribe como dr m,1, la cual corresponde a la distancia entre el elemento m del arreglo de antenas del r-ésimo receptor y la k=1 posición dentro de la grilla. Este proceso se repite para cada una de las posiciones dentro de la grilla hasta finalizar la construcción del diccionario. Por tanto, el tamaño de la base de representación es de M2 x K, donde M es el número de elementos de antena del arreglo y K es la cantidad de celdas de la grilla.
Etapa online: medición
En esta etapa se toman las mediciones de las fuentes reales, las cuales son enviadas al centro de fusión para aplicar el algoritmo OMP y estimar las coordenadas (Xq, Yq). Para realizar las mediciones, cada RN calcula la matriz de covarianza de la señal recibida dada por la ecuación (9) (Gross, 2005), donde N es la longitud de la señal recibida y Yr está definida por la ecuación (2).
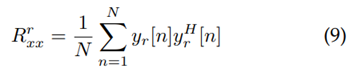
Una vez se tenga la matriz de covarianza se vectoriza y se comprime aplicando la ecuación (10), que es la medición que cada RN calcula y envía al FC. La versión vectorizada de la matriz de covarianza es de dimensiones M2X1, mientras que la versión comprimida es de PX1, donde P M2.
Estandarizando la notación de las variables, decimos que
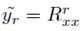es la medición sin comprimir, y que
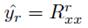es la medición comprimida.
Estimación de la posición
Para realizar la estimación se debe contar con los dos insumos recolectados en las etapas previas: los diccionarios y la medición, para proceder a aplicar el algoritmo OMP que nos permite obtener las coordenadas de los transmisores.
El algoritmo OMP construye de manera iterativa una estimación de un conjunto soporte desconocido. β Si β es estimado en la iteración (i _ 1), se usa el residual
de la aproximación por mínimos cuadrados de
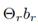, donde
, para elegir una actualización para β. Esto se logra seleccionando el índice donde el vector de la proyección definida por la ecuación (11) es máximo (Schmitz, Mathar y Dorsch, 2015).
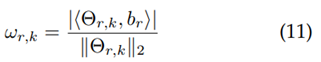
En el caso de JDCS, se hace una combinación no coherente de los valores máximos de correlación obtenidos para cada RN con el fin de medir que tanto un transmisor está presente en una determinada celda k. Lo anterior supone una modificación en el algoritmo OMP que ha sido ampliamente estudiado por diferentes autores (Baron et al., 2009; Eldar, Kuppinger y Bölcskei, 2010).
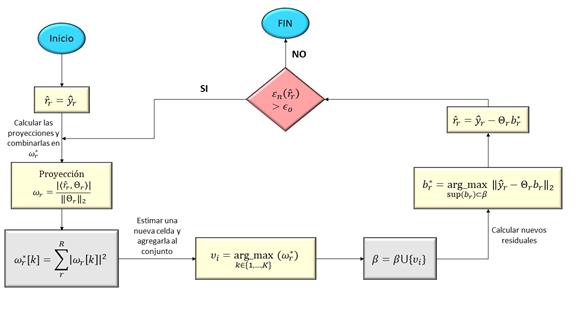
El algoritmo usado se detalla en la figura 1, el cual puede tener como criterio de parada un número de iteraciones igual al número de fuentes del sistema, siempre y cuando este sea conocido como en el caso de los ambientes colaborativos, o si se cumple una condición de parada usualmente relacionada con la energía del residual, la cual implica que la norma del residual actual es menor que un umbral definido, que usualmente es una función de la relación señal a ruido de la señal.
Figura 1: Algoritmo de localización
Ahora bien, con fin de confirmar las consideraciones teóricas y evaluar el desempeño del sistema propuesto, se realizan simulaciones numéricas de un ambiente de radio propagación en dos dimensiones, empleando un modelo de canal simple basado en la ecuación de Friis (Rappaport, 2001). A continuación, se describen los parámetros empleados y se explica en detalle el proceso desarrollado para la obtención de resultados.
Cada transmisor genera una señal banda base con una frecuencia de muestreo de 100 MHz, con modulación BPSK. Cada receptor recibe una señal dada por la ecuación (1), la cual corresponde a la suma de las señales transmitidas, las cuales están retrasadas en el tiempo y tienen una atenuación en potencia causada por los efectos de propagación entre cada par de transmisores y receptores. Además, esta ecuación incluye ruido blanco gaussiano
con media cero y matriz de covarianza
, el cual se asume idéntico en todos los RN.
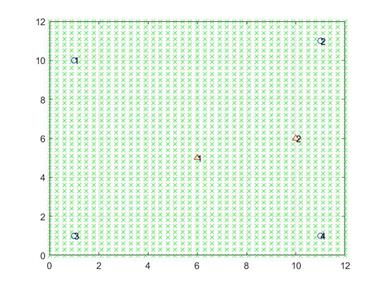
El escenario considera una ROI como la que se muestra en la figura 2, la cual tiene 4 RN (círculos azules) ubicados en posiciones fijas para todas las simulaciones, y 2 TN (triángulos rojos) los cuales se ubican de manera aleatoria dentro de la ROI en cada iteración del algoritmo. Esta figura muestra la ROI ya discretizada para llevar a cabo la construcción del diccionario. Cada una de las cruces verdes corresponde a la posición k-ésima con coordenadas
Figura 2.: Escenario de evaluación del sistema con 4 RN y 2 TN
Se plantean tres escenarios diferentes en los que se calcula el RMSE (root mean square error) de la estimación de la posición, a partir de 1000 simulaciones Monte-Carlo para cada caso. A continuación, se describen los escenarios propuestos.
Escenario 1: tasa de compresión vs. RMSE con 2 TN
Se establecen cuatro tasas de compresión diferentes, las cuales indican el porcentaje de muestras que se toman de la señal original para realizar la estimación de la posición, y se calcula el RMSE para diferentes valores de σ2. Esto implica más o menos ruido en la medición.
Los valores de la tasa de compresión empleados son:
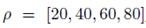, y los valores de varianza evaluados son:
.
Escenario 2: tasa de compresión vs. RMSE para 1 TN
Igual al caso anterior, se calcula el RMSE para cuatro tasas de compresión diferentes y cinco valores de σ2; sin embargo, aquí se estima la posición de una única fuente, con el fin de comparar los resultados con el caso en el que hay dos TN y determinar la influencia que tiene en el desempeño del sistema la presencia de múltiples fuentes transmisoras.
Los valores de la tasa de compresión empleados son:
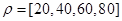, y los valores de varianza evaluados son:
.
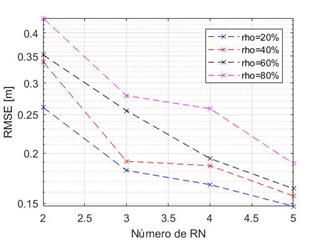
Escenario 3: número de RN vs. RMSE para 2 TN
Se varía el número de RN presentes en el sistema y se calcula el RMSE para diferentes tasas de compresión empleando un canal ideal, es decir, σ2 =0.
RESULTADOS
A continuación, se detallan los resultados para cada caso de estudio y se realiza una breve discusión al respecto.
Escenario 1
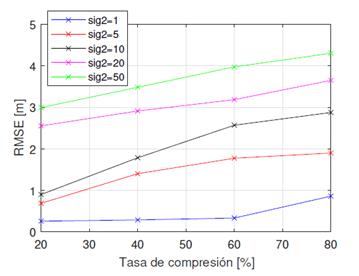
La figura 3 muestra cómo el RMSE aumenta gradualmente a medida que aumenta el porcentaje de la tasa de compresión. Como era de esperarse, entre menos muestras de la señal se tomen para hacer la estimación, mayor es el error en la estimación; sin embargo, cabe mencionar que las variaciones del error son poco significativas, aun cuando el ruido de la medición es alto. El peor escenario se obtiene cuando se tiene un σ2 =50 y un ρ=80, lo cual implica que solo con el 20 % de las muestras y un canal muy ruidoso se tiene un error inferior a 4,5 metros de la posición real; mientras que para el mismo valor de ρ pero en un canal casi ideal, el error del sistema es ligeramente inferior a 1 m.
Figura 3: Tasa de compresión vs. RMSE con 2 TN para diferentes valores de σ2
Es claro que, a medida que aumentan los valores de ρ y σ2, el desempeño del sistema disminuye. Sin embargo, en términos generales, la precisión del sistema es buena incluso cuando las condiciones del canal son desfavorables.
Cabe mencionar que tener menor cantidad de muestras en la medición disminuye el costo computacional del algoritmo, ya que el tamaño de las matrices disminuye.
Escenario 2
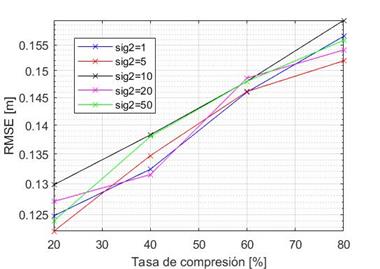
En este caso se evalúan los mismos parámetros que en el caso anterior, pero solamente se considera un transmisor activo en el sistema. La figura 4 muestra que, como era de esperarse, el error disminuye cuando solo se considera una fuente con respecto al caso anterior. Además, es posible observar que la diferencia entre cada uno de los casos es muy pequeña, casi despreciable, teniendo un promedio de error cercano a 0,14 metros en la estimación de la posición. A diferencia del primer caso el error de la posición no se acumula en el cálculo de los residuales del algoritmo OMP, ya que solo se precisa de una iteración para calcular las coordenadas del TN, lo cual impacta directamente en la precisión del sistema.
Figura 4: Tasa de compresión vs. RMSE con 1 TN para diferentes valores de σ2
Escenario 3
En este caso se considera un canal ideal, sin ruido, y los mismos valores de la tasa de compresión, sin embargo, se varía el número de RN que tiene el sistema con el fin de evaluar qué tanto afecta este parámetro la precisión del sistema.
La figura 5 muestra cómo, a medida que aumenta el número de RN en el sistema, el error disminuye para todos los valores propuestos de ρ. Además, a medida que aumenta la tasa de compresión el error es mayor, lo cual es lógico pues se están tomando menos muestras de la medición para hacer la estimación. Sin embargo, cabe mencionar que la diferencia de los errores calculados es muy baja, teniendo un error promedio de 0,34 metros cuando hay 2 RN y de 0,16 metros cuando hay 5 RN. Lo anterior implica que es necesario determinar el rango de precisión que requiere el sistema considerado, dado que aumentar la cantidad de RN aumenta de manera considerable el costo del sistema y adicionalmente la complejidad computacional también se incrementa, pero la ganancia en términos del error es muy baja.
Figura 5: Número de sensores vs. RMSE
CONCLUSIONES
Este trabajo presenta un novedoso sistema de localización, basado en algoritmos de dirección de llegada (DOA, por su sigla en inglés), que explota la esparsidad espacial propio del problema de localización para aplicar la teoría de sensado comprimido con el fin de estimar la posición de una o múltiples fuentes transmisoras. El método utiliza la matriz de covarianza de la señal recibida, usada típicamente en las técnicas clásicas de DOA para calcular con una alta precisión la posición de las fuentes. Sin embargo, en este trabajo, el tamaño de esta matriz se puede disminuir hasta en un 80 %, gracias a la teoría de sensado comprimido. Los resultados demuestran que la precisión del sistema es alta, incluso en los casos en los que las condiciones de ruido son altas, al igual que las tasas de compresión. Para dos fuentes, se obtiene un error máximo inferior a las 4,5 metros con respecto a la posición real, para el peor escenario, e inferior a los 0,5 metros, para el mejor caso. Por su parte, cuando solo hay un transmisor en el sistema, el desempeño del sistema es mucho mejor, ya que no hay acumulación del error en los residuales calculados en el algoritmo OMP, de lo que se obtiene un error promedio cercano a los 14 centímetros con respecto a la posición real del TN. Adicionalmente, se evalúa el caso en el que se vería el número de RN, observando que, para un canal ideal, la precisión no mejora de forma significativa en comparación con el aumento en la carga computacional.
Este trabajo permite entonces concluir que gracias a la esparcidad presente en la naturaleza del problema de localización es posible aplicar la teoría de sensado comprimido para estimar la posición de múltiples fuentes transmisoras con alta precisión.
FINANCIAMIENTO
Los resultados presentados en este documento forman parte del trabajo de investigación doctoral titulado “Evaluación de un sistema de radiolocalización híbrido mediante el uso de la teoría de reconstrucción dispersa y sensado comprimido conjunta para la localización de múltiples fuentes transmisoras”, realizado en la Universidad Pontificia Bolivariana, sede Medellín, y financiado por la Convocatoria 727 de MinCiencias.
Acknowledgements
AGRADECIMIENTOS
Gracias a MinCiencias por la financiación para el desarrollo de esta investigación doctoral, a la Universidad Pontificia Bolivariana y a los asesores de tesis y colegas, el PhD Roberto Hincapié y la PhD Cristina Gómez, por su apoyo constante durante el desarrollo de este trabajo.
Referencias
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.
