DOI:
https://doi.org/10.14483/22487638.18245Publicado:
01-07-2021Número:
Vol. 25 Núm. 69 (2021): Julio - SeptiembreSección:
InvestigaciónOptimal Power Flow through Artificial Intelligence Techniques
Flujo óptimo de potencia a través de técnicas de inteligencia artificial
Palabras clave:
optimización de colonia de hormigas, inteligencia artificial, algoritmo genético, optimización, sistema eléctrico (es).Palabras clave:
ant colony optimization, artificial, intelligence, genetic algorithm, optimization, power system (en).Descargas
Referencias
seidel power flow solver on a high performance reconfigurable computer. In IEEE (Eds.) Annual IEEE Symposium on Field-Programmable Custom Computing Machines (FCCM 2009). IEEE. DOI: https://doi.org/10.1109/FCCM.2009.23 DOI: https://doi.org/10.1109/FCCM.2009.23
CENTELSA (2011). Cables de Aluminio Desnudo. Recuperado de: https://www.centelsa.com/pdf/CablesdeAluminioDesnudo.pdf
CODENSA S. A. (2011). LA204 Circuito primario sencillo construcción tipo bandera con cruceta de 2,5 m. http://likinormas.micodensa.com/Norma/lineas_aereas_urbanas_distribucion/lineas_aereas_11_4_13_2_kv /la204_circuito_primario_sencillo_construccion_tipo_bandera_cruceta
Collado, A. L. & López-Sarmiento, J. A. (2010). Algoritmos para el flujo de carga en circuitos de distribución secundaria. Santa Clara. https://dspace.uclv.edu.cu/bitstream/handle/123456789/999/Ariel%20López%20Collado.pdf?sequence=1&isAllowed=y
Costa V. M., Martins M. & Preira L. R. (2001). An augmented Newton-Raphson power flow formulation based on current injections. Electrical Power and Energy Syst., 23(4), 305-312. https://doi.org/10.1016/S0142-0615(00)00045-4 DOI: https://doi.org/10.1016/S0142-0615(00)00045-4
Haghrah, A., Nazari-Heris, M., & Mohammadi-Ivatloo, B. (2016). Solving combined heat and power economic dispatch problem using real coded genetic algorithm with improved Mühlenbein mutation. Applied Thermal Engineering, 99, 465-475. DOI: https://doi.org/10.1016/j.applthermaleng.2015.12.136 DOI: https://doi.org/10.1016/j.applthermaleng.2015.12.136
Huertas, C. (2016). Preparadurías Sistemas de Potencia I : Flujos de Carga.
IEEE (2018). Estandar IEEE 1250: Guide for Identifying and Improving Power Quality in Power Systems. IEEE.
Vazquez, J. (2014). Aplicación del algoritmo de colonia de hormigas al problema de rutas de reparto con destinos móviles [Thesis, Universidad de Sevilla]. Recuperado de: http://bibing.us.es/proyectos/abreproy/5760/fichero/PFC_Jesus_Vazquez.pdf
Játiva-Ibarra, J., Constante-Flores, G., & Cabrera-Celi, G. (2014). Flujo de Potencia por Newton-Raphson con el Jacobiano Calculado en las Ecuaciones de Errores de Potencia. Revista Politécnica, 33(1), e157. https://revistapolitecnica.epn.edu.ec/ojs2/index.php/revista_politecnica2/article/view/157
Khanacademy. (2018). La terminología de los circuitos (artículo) | Khan Academy. https://es.khanacademy.org/science/electrical-engineering/ee-circuit-analysis-topic/circuit-elements/a/ee-circuit-terminology
Arito, F. L. A. (2010). Algoritmos de Optimización basados en Colonias de Hormigas aplicados al Problema de Asignación Cuadrática y otros problemas relacionados [Undergraduate thesis, Universidad Nacional de San Luis]. http://www0.unsl.edu.ar/~dmcc/files/tesis-f.pdf
Mora, J. C. S. T., Marín, J. M., & Romero, N. H. (2016). Introducción a los Algoritmos Genetícos con Matlab. Tecnologías avanzadas en ingeniería. Recuperado de: https://www.uaeh.edu.mx/docencia/P_Lectura/icbi/asignatura/introduccion_a_los_algoritmos_geneticos_con_matlab.pdf
Nazari-Heris, M., Mehdinejad, M., Mohammadi-Ivatloo, B., & Babamalek-Gharehpetian, G. (2019). Combined heat and power economic dispatch problem solution by implementation of whale optimization method. Neural Computing and Applications, 31(2), 421-436. DOI: https://doi.org/10.1007/s00521-017-3074-9 DOI: https://doi.org/10.1007/s00521-017-3074-9
Pranith, S., & Bhatti, T. S. (2015, March 12-13). Modeling and parameter extraction methods of PV modules-Review [Conference presentation]. 2015 International Conference on Recent Developments in Control, Automation and Power Engineering (RDCAPE 2015). DOI: https://doi.org/10.1109/RDCAPE.2015.7281372 DOI: https://doi.org/10.1109/RDCAPE.2015.7281372
Pravos García, L. (2017). Análisis de flujos de carga para el análisis de redes de distribución. Implementación del algoritmo "Fordward and Backward [Tesis, Universidad Politécnica de Madrid]. Recuperado de: http://oa.upm.es/47864/1/TFG_LETICIA_PRAVOS_GARCIA.pdf
Remolino, A. S. & Paredes, .H. F. R. (2009). Método Eficiente Para La Solución De Flujos De Potencia En Sistemas Eléctricos De Distribución. 1(1), 322.
Soifer, A. & Loiseau, I. (2015). Algoritmos de Colonia de Hormigas para el Problema del Viajante de Comercio por Familias y para el Problema de Ruteo de Vehículos por Familias [Conference presentation]. 13º Simposio Argentino de Investigación Operativa. http://sedici.unlp.edu.ar/bitstream/handle/10915/59301/Resumen.pdf-PDFA.pdf?sequence=1&isAllowed=y
Stevenson, W. D. (1996). Análisis de Sistemas de Potencia. McGraw-Hill.
Sánchez-Huertas, W., Gómez, V., & Hernández, C. (2018). Optimization Algorithms for Solving Microgrid and Smart Grid Integration Problems. International Journal of Applied Engineering Research, 13(21), 14886-14892. https://www.ripublication.com/ijaer18/ijaerv13n21_08.pdf
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 14 de diciembre de 2020; Aceptado: 1 de abril de 2021
ABSTRACT
Context:
The integration of optimization methods into the various processes carried out by an electric power system seeking energy efficiency have led to satisfying results in the reduction of consumption, as well as in terms of technical losses, security increase, and system reliability.
Objective:
The purpose of this article is to identify a method that provides the best optimization outcome for the power flow of an energy distribution system with 10 nodes at 13,2 kV.
Methodology:
The results obtained from the voltage profiles are presented for a 10-node energy distribution system using the Newton-Raphson method. Afterwards, the system was optimized using genetic and ant colony algorithms.
Results:
The implementation of these techniques determined that the sum of the potential differences of distribution lines is notably reduced with the genetic algorithm. However, the ant colony optimization code takes less time to run and has a lower number of iterations.
Conclusions:
The most efficient optimization is achieved with the genetic algorithm, given that the evolution of the population shows better optimization levels in comparison with the ant colony algorithm.
Financing:
Universidad Francisco José de Caldas and Colciencias
Keywords:
ant colony optimization, artificial intelligence, genetic algorithm, optimization, power system.RESUMEN
Contexto:
La integración de métodos de optimización en los diversos procesos llevados a cabo por un sistema de energía eléctrica que busca la eficiencia energética ha llevado a resultados satisfactorios en la reducción del consumo, así como en términos de pérdidas técnicas, aumento de seguridad y confiabilidad del sistema.
Objetivo:
El propósito de este artículo es identificar un método que ofrezca el mejor resultado de optimización para el flujo de energía de un sistema de distribución de energía con 10 nodos a 13,2 kV.
Metodología:
Los resultados obtenidos de los perfiles de voltaje se presentan para un sistema de distribución de energía de 10 nodos utilizando el método de Newton-Raphson. Posteriormente, el sistema se optimizó utilizando algoritmos genéticos y de colonias de hormigas.
Resultados:
La implementación de estas técnicas determinó que la suma de las posibles diferencias de las líneas de distribución se reduce notablemente con el algoritmo genético. Sin embargo, el código de optimización de la colonia de hormigas tarda menos tiempo en ejecutarse y tiene un número menor de iteraciones.
Conclusiones:
La optimización más eficiente se logra con el algoritmo genético, dado que la evolución de la población muestra mejores niveles de optimización en comparación con el algoritmo de colonias de hormigas.
Financiamiento:
Universidad Francisco José de Caldas y Colciencias
Palabras clave:
optimización de colonia de hormigas, inteligencia artificial, algoritmo genético, optimización, sistema eléctrico.INTRODUCTION
Currently, the study and calculation of load flows in power systems is becoming a highly relevant matter (Arito, 2010). The purpose of calculating power flow is to find the values of the nodal voltages and use these variables to determine the flows in the distribution lines. The data obtained are an important tool for the design, planning, operation, and control of electric systems (Costa et al., 2001).
In most cases, the calculation of voltage values requires solving a system of simultaneous non-linear equations. To this effect, the Newton-Raphson (NR) and Gauss-Siedel (GS) iterative methods are considered as an important basis for comparison with any artificial intelligence algorithm (Huertas, 2016). The NR method consists of an iterative procedure in which non-linear equations are used, involving variables such as voltage magnitude, voltage angle, active power, and reactive power. Since there are only two power equations, the remaining variables must be calculated (Játiva-Ibarra et al., 2014). In Pranith and Bhatti (2015), the NR method is used to calculate photovoltaic parameters and carry out the modeling process. The GS method is an iterative strategy in which the number of unknown variables is equal to the number of equations to be solved. It consists of designing a converging succession according to previously defined criteria (Collado et al., 2010). The convergence values are the solutions of the nodal voltages and powers of the electric system. In Byun et al. (2009), the GS method is chosen to accelerate the solution of power flows in a high-performance reconfigurable computer.
The NR method converges faster than GS. However, this swiftness is overshadowed by the large amount of memory and computational resources required for the execution of the algorithm (Pravos-García, 2017). Both methods can lead to convergence problems or incorrect solutions in special cases involving power systems or under low impedances (Remolino & Paredes, 2009). Therefore, it is appropriate to conduct research on other methods in order to solve these types of problems.
The continuous progress achieved in the field of artificial intelligence has enabled the use of different meta-heuristic methodologies to deliver approximations of the power flow algorithms described above. A clear example of this is shown in the work by Haghrah et al., (2016), where the authors studied a coded genetic algorithm with the improved mutation of Mühlenbein (RCGA-IMM). Thus, the optimization task is solved based on the cost function and the transmission-related losses, thus leading to satisfying results regarding load flow. Furthermore, Nazari-Heris et al. (2019) studied the optimization of co-generation based on whale optimization algorithms (WOA), which are inspired in the behavior of humpback whales, particularly in their hunting patterns for fish close to the surface. This technique mainly focuses on the creation of distinctive bubbles throughout a circle or path. The algorithm operates similarly, seeking the best solution for the target (prey) or the closest one. Hence, in this research, the optimal solution represents the efficiency and viability of WOA and its capacity to obtain better solutions for the load flow convergence in comparison with other optimization techniques regarding operational costs and robust power system implementation.
This article presents a 10-node distribution system, which can be solved through conventional numeric methods and artificial intelligence techniques. In this case, the NR method serves as a numeric strategy to solve the power flow problem. Furthermore, two artificial intelligence techniques are adopted - genetic algorithms (GA) and ant colony optimization (ACO) - in order to optimize the results of the power flow.
This document is organized as follows: first, the power distribution system to be optimized is presented; then, the applied methodology is described; the subsequent sections describe the GA and ACO algorithms, respectively; then, the obtained results are presented; and finally, a set of conclusions for the overall work is stated.
MATERIALS AND METHODS
The starting point for obtaining the necessary data to solve a power flow problem is the one-line diagram of the power system. The input data includes information regarding nodes, transmission lines, transformers, and generators. Their values are used to form the bar admittance matrix of the power system. To build this matrix, the equivalent circuit of the power system must be simplified, so that there is a single admittance between two nodes and a single admittance between each node and the ground.
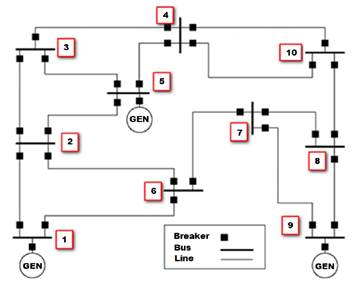
The one-line diagram used in this exercise is based on the IEEE 1250 standard (2018), given that it represents a general use power system in rural distribution networks of medium-level voltage in Colombia. This power system comprises 10 nodes, where 2 of them are generator nodes. Figure 1 shows the one-line diagram of the power system.
Figure 1: 10-node transmission system
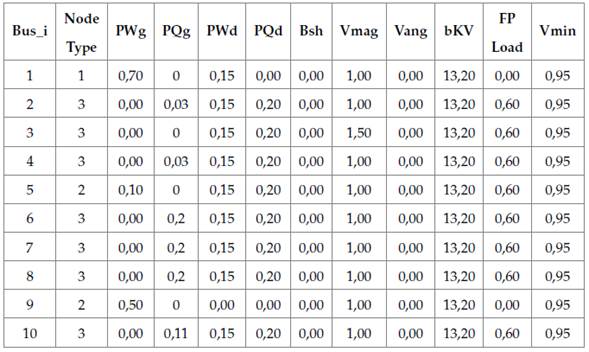
The nodes of the power system are those in which two or more elements are interconnected (Khanacademy, 2018) while maintaining the same voltage level. In Table 1, the types of nodes of the power system are defined.
Source: Authors
Table 1: Definition of the nodes of the distribution system
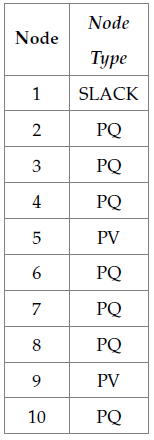
The load nodes or PQ nodes are those in which the net active and reactive powers are specified, whereas the voltage magnitude and phase angle are still unknown. The stable voltage nodes, or PV nodes, are the ones where the devices (such as synchronous generators) are located. These devices are capable of controlling the voltage magnitude in the terminals through the generation or absorption of the reactive power. In the compensation nodes or SLACK nodes, the known variables are the voltage magnitude in the bar and its phase angle, which serve as a reference for the phase angle in the other bars. In general, the phase angle is set at 0°.
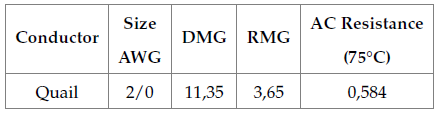
The distribution power lines are in charge of interconnecting the nodes, thus carrying the energy from the generation points up to the load connection points of for final use. The distribution lines in the medium-level voltage are often made of ACSR (Aluminum-Conductor Steel-Reinforced) cables, naked conductors with a steel structure designed for the power level of 13,2 kV. The conductor that meets the power distribution requirements that was chosen to be used for simulation purposes is Quail (CENTELSA, 2011). Table 2 shows its electric parameters.
Source: Authors
Table 2: Parameter table for the conductor
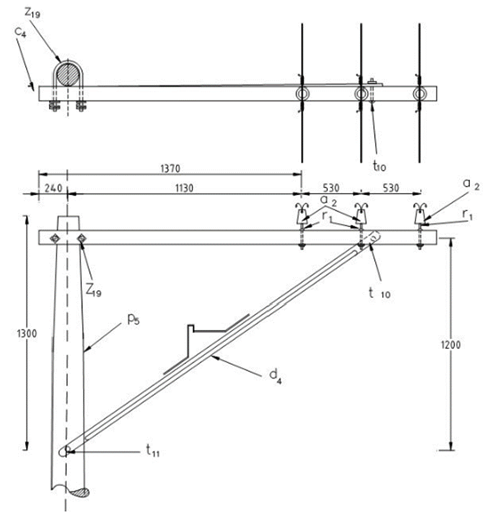
The structure that supports the distribution network is from Codensa’s LA 204 regulations (2011) (Figure 2). This structure is commonly used in rural distribution networks as a basis for modeling line calculations.
Figure 2: LA 204 Structure for the simple primary circuit
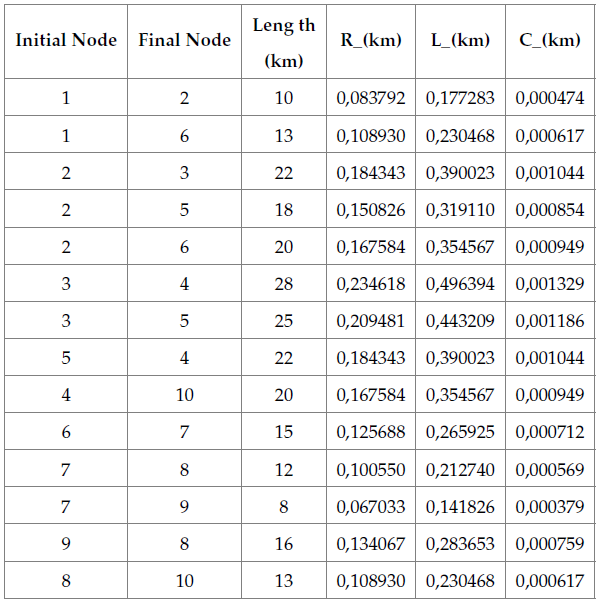
Table 3 includes the length and impedances of the lines that interconnect the nodes.
Source: Authors
Table 3: Distance between nodes and impedances of the lines
The loads are the elements of the system that consume energy for its designated end-use. All loads connected to the PQ nodes are modeled in the same way. For this power system, the loads are set with a lagging power factor of 0,6, an active power of 0,3, and a reactive power of 0,4. Traditional methods used to solve power system flows lead to obtaining the values in the nodal voltages that comprise them. Higher potential differences between nodes translate into higher energy losses within the power system. Equation (1) represents the sum of voltage differences between the nodes that are interconnected through a line:

where V Lf represents the voltage of the final node of line L, and V Li is the value of the voltage in the initial node of L, beginning from the first distribution line and up to the n th distribution line, where n is the number of lines interconnected in the power system.
The purpose of implementing genetic algorithms and ant colony optimization methods is to minimize the sum of potential differences of all system nodes and, hence, reduce the system losses.
GENETIC ALGORITHMS
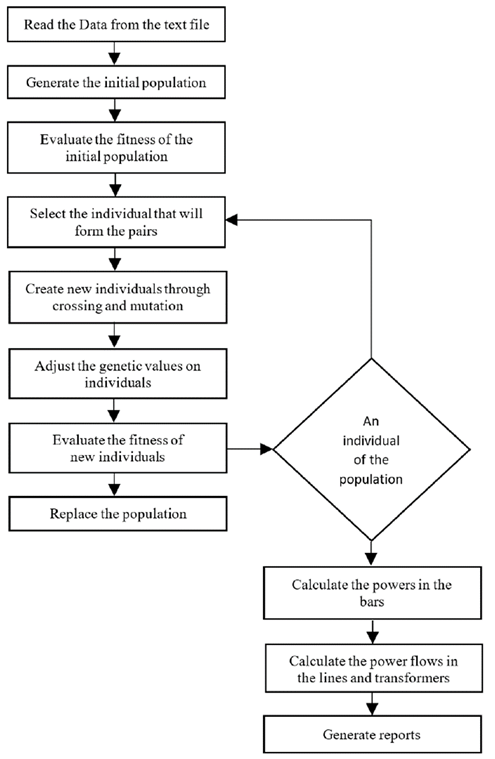
Genetic Algorithms are systematic methods used to solve search and optimization problems, which are based on biological evolution processes such as population-based selection, sexual reproduction, and mutation (Mora et al., 2016). Figure 3 shows a flow diagram of the genetic algorithm that explains the general operation of the code for the solution of the system in to solve and optimize the solution of the power flow. This is carried out for each individual within the population that begins or continues to live in the coded system, starting with random values of the voltage magnitude and phase angle in the bars to be optimized.
Figure 3: Flow diagram of the genetic algorithm
ANT COLONY OPTIMIZATION
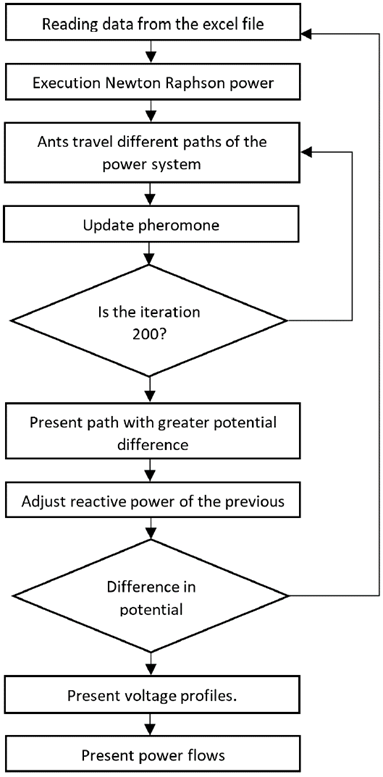
Solving computational problems by using ACO involves analyzing the behavior of ants and their pheromone-based communication. Pheromones lead ants to find the shortest paths between their nest and possible food sources (Soifer & Loiseau, 2015). Figure 4 shows the flow diagram of the algorithm.
Figure 4: ACO diagram
The iterative procedure of ACO is based on the probabilistic methods described below. The k th ant moves from state X to state Y with the probability shown in Equation (2).

where τ 𝑥𝑦 is the number of pheromones deposited in the transition from state x to y, α ≥ 0 is a parameter used to control the influence of 𝜏 𝑥?? , and 𝜂 𝑥𝑦 is the convenience of state xy (an a priori knowledge commonly defined as 1/dx, where d is the distance and β ≥ 1 is a parameter controlling the influence of η xy ).
The ACO method consists of three phases: 1) parameter initialization, 2) exploration phase, and 3) exploitation phase. This method was used to solve and optimize the 10-node power system.
RESULTS
This section presents the nodal voltages obtained after the execution of the NR algorithm, GAs and ACO. Then, the errors from GA and ACO are computed based on the data derived from NR.
Execution of the Newton-Raphson algorithm
In order to compare the results between GA and ACO, the power flow is computed for the NR method. These results are then used to establish a comparison. The voltage profiles derived from the simulation of the power system with this method are presented in Table 4, where nodes 3, 4, and 10 remain under the 95% threshold.
Source: Authors
Table 4: Nodal voltages with the Newton-Raphson method
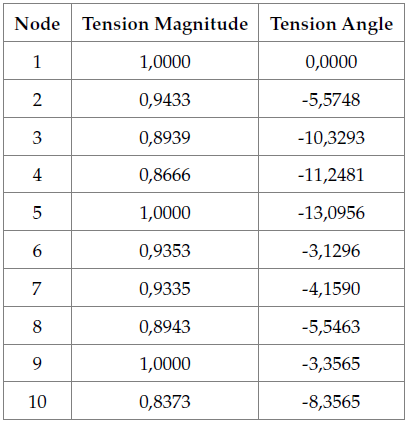
Execution of the GA
Table 5 shows the execution results of the GA. The voltage values in every node are significantly increased and, hence, optimize the power system. PG and PD are in MW, and QG and QD are in MVAR.
Source: Authors
Table 5: Results of the power flow with the GA
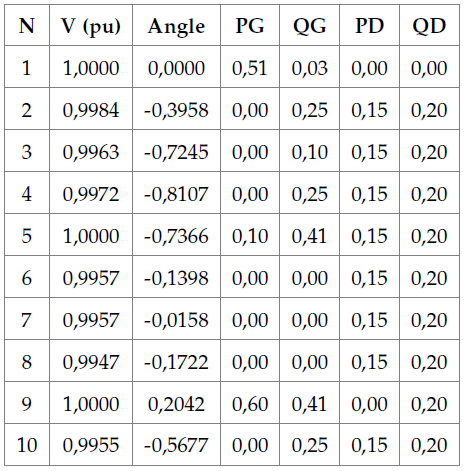
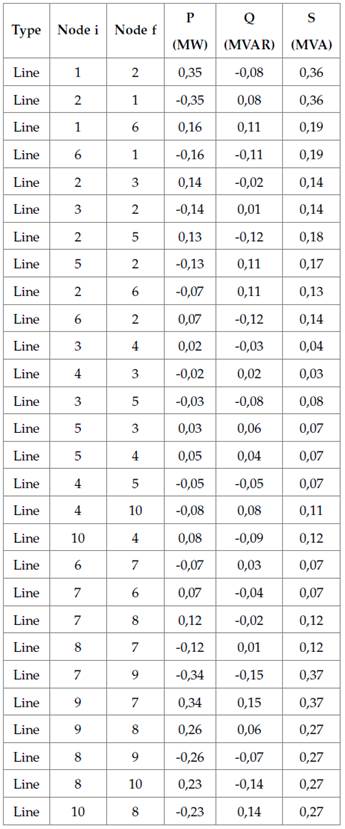
Table 6 shows that the GA can be used to calculate the system power flow and determine the energy distribution in the lines.
Source: Authors
Table 6: Power flow with GA
The result of the GA was solved within 106 generations, with a population of 300 individuals, and 150 crossing operations in every generation.
Execution of the Ant Colony Optimization
The ant colony algorithm was programmed so that the execution results of the NR method could serve as input parameters. To this effect, the possible paths that the ant could pass through were defined by stating an analogy between the distances and potential differences within transmission lines. Therefore, after the code was executed, the paths with the highest potential differences were found by both ants; they are shown in Tables 7 and 8. Table 9 shows the path with the largest pheromone trail in all nine iterations.
Source: Authors
Table 7: Paths found by ant 1
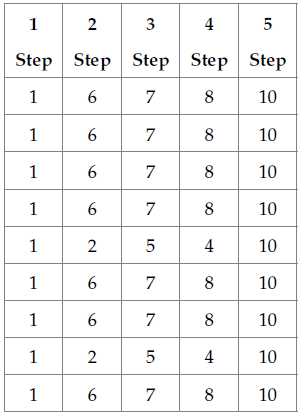
Source: Authors
Table 8: Paths found by ant 2
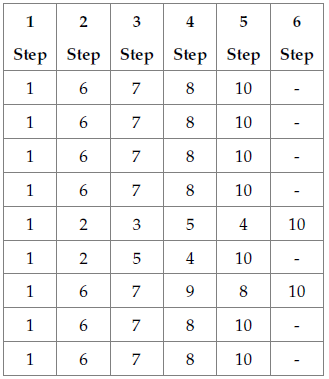
Source: Authors
Table 9: Paths with the largest pheromone trails
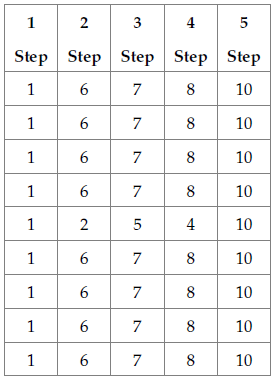
Table 10 shows the results obtained after five iterations of the algorithm. The voltage levels increase in nodes 2, 3, 4, 6, 7, 8, and 10, since there is a compensation in the reactive power generated in each node. Table 11 shows the corrections applied to the Q generated in the nodes after nine iterations of the algorithm.
Source: Authors
Table 10: Correction of the nodal voltages with the ACO method
Source: Authors
Table 11: Reactive compensation in the nodes
Comparison of results
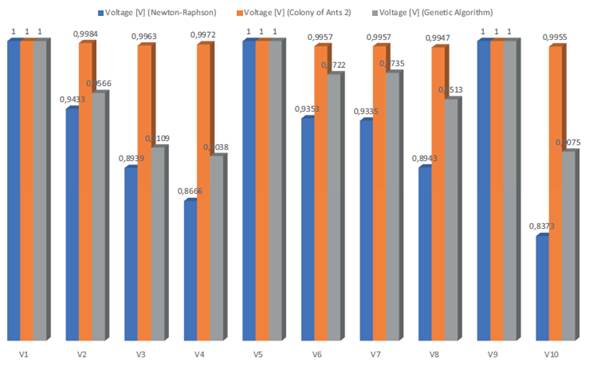
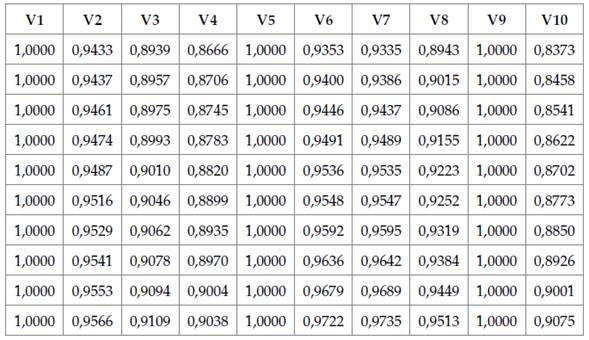
In order to compare which algorithm offers the best optimization, the voltage magnitudes derived from the algorithms are shown in Figure 5, which shows an increase in the voltage of every node within the power system with GA compared to NR and with ACO compared to NR. Genetic algorithms optimize the voltage profiles in the system nodes 2,46 times more than the ant colony optimization.
Figure 5: Nodal voltages for Newton-Raphson vs ACO vs GA
Table 12 shows the percentage of errors obtained after running the GA and ACO methods. The GA optimization is more effective, given that no node has a percentage error higher than 1%.
Source: Authors
Table 12: Percentage errors after the optimization of GA and ACO
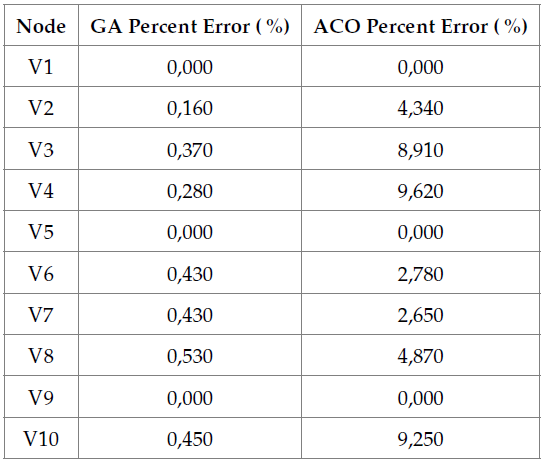
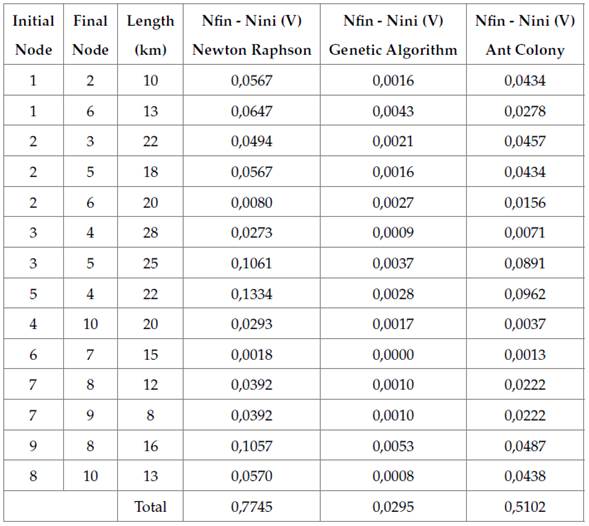
Table 13 shows the sum of the voltage differences between the system power lines for each algorithm used in the calculation of the power flow. It is evidenced that the sum in NR is 0,775, the sum in GA is 0,0295, and the sum in ACO is 0,5102. This indicates that the algorithm that offers the best results is GA since it reduces the voltage differences and, as a consequence, reduces the losses within transmission lines.
Source: Authors
Table 13: Potential difference between nodes
Execution times of the algorithms
Table 14 shows the execution times of the discussed algorithms. The ACO method runs in 21,02 s, while the GA takes 7501 s, (54 s faster than ACO).
Source: Authors
Table 14: Execution times of the algorithms

Number of iterations of the algorithms
Table 15 shows the number of iterations required by the program to converge. The GA converges in 106 iterations, whereas ACO converges in 9 iterations.
Source: Authors
Table 15: Number of iterations for each algorithm

Analysis of results
The GA was originally far from the solution and approached it exponentially as more generations were produced. It solved in 13 generations. The GA optimizes the system nodes outside of the defined range. In this example, it was evidenced that genetic algorithms are capable of solving power flow problems. Although only a few generations were necessary to find a solution with an acceptable tolerance, the solution can change depending on the initial population of the system.
GAs have the advantage of seeking a solution based on a population of ‘dots’ without the need for the derivatives of the power flow equations. Their disadvantage lies in the fact that they can be relatively slow in delivering a solution. Since the population size is proportional to the number of nodes that obey probabilistic rules, many generations could be required to find a solution.
The ant colony algorithm has various limitations, since the definition of the algorithm used to solve power system flows requires an adjustment of the initial simulation conditions for the results to be coherent. This algorithm rapidly identifies the most unbalanced nodes of the system, yet its optimization process is not effective.
CONCLUSIONS
After executing the algorithms, it was determined that the sum of the potential differences in the distribution lines drastically drops with the GA. Nonetheless, the code takes less time to run and has a lower number of iterations compared to the ant colony alternative. Hence, it is concluded that GA requires more memory usage and computational resources. The most efficient optimization is achieved with GAs since the evolution of the population shows better optimization levels in comparison to the ant colony algorithm. The latter presents a low level of optimization in the detection of the paths with a higher potential difference. Genetic algorithms can be used to solve power flow problems, as an alternative to iterative methods such as Newton-Raphson and Gauss-Seidel.
Acknowledgements
ACKNOWLEDGMENTS
The authors would like to thank the Center for Research and Scientific Development of Universidad Distrital Francisco José de Caldas, as well as Colciencias, for supporting and funding this research project.
REFERENCES
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.