DOI:
https://doi.org/10.14483/22487638.18617Publicado:
01-10-2021Número:
Vol. 25 Núm. 70 (2021): Octubre - DiciembreSección:
InvestigaciónDiseño óptimo de un resorte helicoidal usando un algoritmo genético continuo
Optimal Design of a Helical Spring by Using a Genetic Continuous Algorithm
Palabras clave:
mechanical design, metaheuristic optimization, helical springs, genetic algorithm (en).Palabras clave:
diseño mecánico, optimización metaheurística, resortes helicoidales, algoritmo genético (es).Descargas
Referencias
Azad, A. V., & Amidpour, M. (2011). Economic optimization of shell and tube heat exchanger based on constructal theory. Energy, 36(2), 1087–1096. https://doi.org/10.1016/j.energy.2010.11.041 DOI: https://doi.org/10.1016/j.energy.2010.11.041
Bidabadi, M., Sadaghiani, A. K., & Azad, A. V. (2013). Spiral heat exchanger optimization using genetic algorithm. Scientia Iranica, 20(5), 1445–1454. http://scientiairanica.sharif.edu/article_3402.html
Denkena, B., Abele, E., Brecher, C., Dittrich, M. A., Kara, S., & Mori, M. (2020). Energy efficient machine tools. CIRP Annals, 69, 646–667. https://doi.org/10.1016/j.cirp.2020.05.008 DOI: https://doi.org/10.1016/j.cirp.2020.05.008
Espitia Cüchango, H. E., & Sofrony Esmeral, J. I. (2014). Algoritmo de optimización basado en enjambres de partículas con comportamiento de vorticidad y búsqueda individual y grupal. Revista Tecnura, 18(42), 24. https://doi.org/10.14483/udistrital.jour.tecnura.2014.4.a02 DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2014.4.a02
Gaikwad, S. S., & Kachare, P. S. (2014). Static Analysis of Helical Compression Spring. International Journal of Research in Engineering and Technology, 03(15), 835–838. https://doi.org/10.15623/ijret.2014.0315158 DOI: https://doi.org/10.15623/ijret.2014.0315158
Giri, C., Tipparthi, D. K. R., & Chattopadhyay, S. (2008). A genetic algorithm based approach for system-on-chip test scheduling using dual speed TAM with power constraint. WSEAS Transactions on Circuits and Systems, 7(5), 416–427. http://www.wseas.us/e-library/transactions/circuits/2008/30-728.pdf
Jang, D., & Jang, S. (2014). Development of a lightweight CFRP coil spring. SAE Technical Papers, 1. https://doi.org/10.4271/2014-01-1057 DOI: https://doi.org/10.4271/2014-01-1057
Kar, D., Ghosh, M., Guha, R., Sarkar, R., Garcia-Hernandez, L., & Abraham, A. (2020). Fuzzy mutation embedded hybrids of gravitational search and Particle Swarm Optimization methods for engineering design problems. Engineering Applications of Artificial Intelligence, 95(June), 103847. https://doi.org/10.1016/j.engappai.2020.103847 DOI: https://doi.org/10.1016/j.engappai.2020.103847
Ke, J., Wu, Z. yu, Liu, Y. sheng, Xiang, Z., & Hu, X. dong. (2020). Design method, performance investigation and manufacturing process of composite helical springs: A review. Composite Structures, 252(928), 112747. https://doi.org/10.1016/j.compstruct.2020.112747 DOI: https://doi.org/10.1016/j.compstruct.2020.112747
Montoya, O. D., Gil-González, W., & Grisales-Noreña, L. F. (2018). Optimal power dispatch of DGS in DC power grids: A hybrid gauss-seidel-genetic-algorithm methodology for solving the OPF problem. WSEAS Transactions on Power Systems, 13, 335–346. https://www.wseas.org/multimedia/journals/power/2018/a665116-598.pdf
Moradi, M. H., & Abedini, M. (2012). A combination of genetic algorithm and particle swarm optimization for optimal distributed generation location and sizing in distribution systems with fuzzy optimal theory. International Journal of Green Energy, 9(7), 641–660. https://doi.org/10.1080/15435075.2011.625590 DOI: https://doi.org/10.1080/15435075.2011.625590
Mott, R. L. (2004). Machine elements in mechanical design.
Rodriguez Cabal, M. A., Grisales Noreña, L. F., Ardila Marín, J. G., & Montoya Giraldo, O. D. (2019). Optimal Design of Transmission Shafts: a Continuous Genetic Algorithm Approach. Statistics, Optimization & Information Computing, 7(4). https://doi.org/10.19139/soic-2310-5070-641 DOI: https://doi.org/10.19139/soic-2310-5070-641
Sealy, M. P., Liu, Z. Y., Zhang, D., Guo, Y. B., & Liu, Z. Q. (2016). Energy consumption and modeling in precision hard milling. Journal of Cleaner Production, 135, 1591–1601. https://doi.org/10.1016/j.jclepro.2015.10.094 DOI: https://doi.org/10.1016/j.jclepro.2015.10.094
Shevale, D. V, & Khaire, N. D. (2016). Analysis of Helical Compression Spring for Estimation of Fatigue Life. Imperial Journal of Interdisciplinary Research, 210), 2088-2093. http://www.onlinejournal.in/IJIRV2I10/272.pdf
Shi, W., Atlar, M., Norman, R., Aktas, B., & Turkmen, S. (2016). Numerical optimization and experimental validation for a tidal turbine blade with leading-edge tubercles. Renewable Energy, 96, 42–55. https://doi.org/10.1016/j.renene.2016.04.064 DOI: https://doi.org/10.1016/j.renene.2016.04.064
Solarte Martínez, G. R., Castillo Sanz, A. G., & Rodríguez Gahona, G. (2015). Optimización de un ruteo vehicular usando algoritmo genético simple chu-beasley. Revista Tecnura, 19(44), 93. https://doi.org/10.14483/udistrital.jour.tecnura.2015.2.a07 DOI: https://doi.org/10.14483/udistrital.jour.tecnura.2015.2.a07
Szabó, B., & Actis, R. (2012). Simulation governance: Technical requirements for mechanical design. Computer Methods in Applied Mechanics and Engineering, 249–252, 158–168. https://doi.org/10.1016/j.cma.2012.02.008 DOI: https://doi.org/10.1016/j.cma.2012.02.008
Thamaraikannan, B., & Thirunavukkarasu, V. (2014). Design optimization of mechanical components using an enhanced teaching-learning based optimization algorithm with differential operator. Mathematical Problems in Engineering, 2014. https://doi.org/10.1155/2014/309327 DOI: https://doi.org/10.1155/2014/309327
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Recibido: 2 de agosto de 2021; Aceptado: 12 de agosto de 2021
Abstract
Objective:
In this paper, a continuous genetic algorithm (CGA) for the optimal design of a closed-coil helical spring is proposed.
Methodology:
The solution methodology uses the minimization of the total spring volume as objective function, considering the wire diameter, mean diameter and number of active coils as main variables. As set of constraints, the technical and physical requirements for the correct and safe design of the aforementioned element are implemented. A CGA is employed as a solution method, and, as comparison methods, different optimization algorithms were used, which were employed in the specialized literature for solving the problem addressed in this study.
Results:
The results obtained show that the CGA achieved the minimum value of volume, 1.5% less than the best reported technique, with a processing time lower than 1 s, which proves that the proposed methodology obtains the best results in terms of solution quality and processing time.
Conclusions:
The simulation results show that the CGA obtains the best solution in comparison with the other techniques, at a low computational cost and providing a solution that meets the physical and technical constraints of the design.
Keywords:
mechanical design, metaheuristic optimization, helical springs, genetic algorithm.Resumen
Objetivo:
En este artículo de investigación se propone un algoritmo genético continuo (CGA) para realizar el diseño óptimo de un resorte helicoidal de bobina cerrada.
Metodología:
La metodología de solución emplea como función objetivo la minimización del volumen total de un resorte helicoidal, considerando como variables principales el diámetro del alambre, el diámetro promedio y el número de bobinas activas. Como conjunto de restricciones se implementan los requerimientos físicos y técnicos para el diseño seguro y adecuado del elemento mencionado. Como método de solución se emplea un CGA, y como métodos de comparación son usados diferentes algoritmos de optimización que han sido implementados en la literatura especializada para dar solución al problema abordado.
Resultados:
Los resultados obtenidos muestran que el CGA obtiene el mínimo valor de volumen, siendo menor en un 1,5% en comparación con la mejor técnica reportada, con un tiempo de procesamiento menor a 1 s, lo cual demuestra que la metodología propuesta obtiene los mejores resultados en términos de calidad de la solución y tiempo de procesamiento.
Conclusiones:
Los resultados de simulación muestran que el CGA obtiene la mejor solución en comparación con las demás técnicas, a un bajo costo computacional y entregando una solución que cumple con los requerimientos físicos y técnicos del diseño.
Palabras clave:
diseño mecánico, optimización metaheurística, resortes helicoidales, algoritmo genético.Introduction
Helical springs are elements that can be subjected to traction or compression. These are usually manufactured with metal alloys bent in a cylindrical way. The spring has a constant pitch, and its cross-section depends on the application of the spring, be it cylindrical or square (Bidabadi et al., 2013). The end of the coil spring can be an open or closed coil. The main difference lies in the angle formed between the coil and the vertical (Shevale & Khaire, 2016). Some of the most common applications for coil springs are absorbing shocks, applying forces to brakes and clutches, controlling movement by acting as a stabilizer, and for energy storage in toys and watches (Bidabadi et al., 2013). When designing a helical spring, the geometry, the loads it supports, and the deflection must be specified based on spatial limitations (Mott et al., 2004). The main variables for the design of a helical spring are the diameter of the wire, the internal diameter, and the number of turns. From these, the other factors associated with it are calculated, such as length and maximum performance, as well as the points where the design will withstand the stress to which it will be subjected.
The optimization of the design of a helical spring was performed in an article published by Thamaraikannan and Thirunavukkarasu (2014). The objective function was to minimize the volume of the spring. The main variables were the physical dimensions of the spring, and the set of constraints were constructive criteria associated with each variable, the maximum forces, and the deflections allowed. Optimization techniques play an important role, as they are widely used in the specialized literature to solve engineering problems such as minimizing weights, volume, size, costs, among others (Azad & Amidpour, 2011; Giri et al., 2008; Shi et al., 2016). Obtaining viable solutions at low computational costs is desirable, but it depends on each problem’s physical restrictions. One of the most important characteristics of these optimization methodologies is the fact that they can be implemented in free software such as Python, octave, or Scilab, which implies zero investment costs in terms of software and constitutes an important advantage over commercial optimization tools such as General Algebraic Models (GAMS).
In the field of mechanical design and the industry in general, focus has been given in recent years to improving efficiency in the construction processes of mechanical devices, optimizing production costs through weight and volume reduction and thus complying with the limits of mechanical forces. The reduction of the weight and size of the elements of the different mechanical devices leads to an improvement in the efficiency of industrial processes by achieving a reduction in the consumption of materials, and therefore in their processing and manufacturing times (Szabó & Actis, 2012). At the same time, this allows reducing energy consumption within its particular applications, given that less effort is required for movement (Jang & Jang, 2014; Ke et al., 2020). All this helps to reduce the carbon footprint from the perspective of the manufacturing industry (Denkena et al., 2020).
In terms of optimization techniques, in the specialized literature, there are works where metaheuristic optimization algorithms, such as genetic algorithms, have been used to reduce the weight of transmission shafts, improve the heat transfer coefficient of spiral plate heat exchangers, reduce the volume of a pressure vessel, among others, obtaining good results by resolving nonlinear, non-convex mathematical models with reduced computing times (Espitia-Cüchango & Sofrony-Esmeral, 2014; Gaikwad & Kachare, 2014; Kar et al., 2020; Sealy et al., 2016). In addition, coil springs have high applicability in the industry, thus making it necessary to establish methodologies that allow obtaining more efficient designs from a constructive point of view, complying with the conditions of maintainability, safety, and reliability, since these mechanical elements fulfill vital functions in machines and equipment, as the axis is in charge of transmitting power to the different elements and springs. This has applications in shock absorbers, clutches, and machines in which energy storage in the form of compression is necessary. This article proposes to reduce the weight and size of a coil spring by meeting its technical and operational constraints at all times through optimal design. To optimize the design of this type of geometry, it is necessary to carry out calculations and iterative processes in order to ensure that the dimensions are given so that each element meets the requirements of each particular case (economic and technical).
As mentioned above, genetic algorithms have certain advantages over the others, which is why they are used for this study, where a comparison is made with a similar work. The objective function is to minimize the volume of the spring and use restrictions such as length, maximum deflection, efforts, and other physical parameters. The first part of this article presents the mathematical approach with its restrictions and parameters. Then, the technique used to solve the problem is fully explained, and, finally, the results of the study are presented.
Mathematical formulation
Helical springs are made from a wire, whose cross-section can be circular, square, or triangular, and they are rolled onto a helical form. This type of spring is designed to support compression and traction loads, aiming to find the dimension that supports the loads with a minimum volume. For this reason, the design of helical springs employs the main geometrical variables to establish the volume, the wire diameter (d), the mean diameter (D), and the number of coils (Nc), as shown in Equation (1).

As mentioned above, geometrical parameters must support the applied load without exceeding the allowed stresses and the geometrical values associated with the available space according to the technical design conditions. These constraints are mentioned below.
Set of constraints
The first constraint represents the allowable stresses, where a relation between stress, the maximum load applied, and the geometrical parameters is established. Here, the stress exerted by the maximum force (F max ) cannot exceed the allowable stress (S). This is represented by Equation (2).

where C f is the geometrical parameter defined in Equation (3).
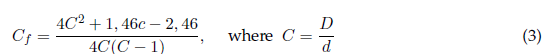
As for spring configuration, it is important to mention that the free length must be less that a specified value. To define it, it is necessary to know the spring constant k, which is defined in Equation (4), where G is the shear modulus.

The deflection under maximum working load can be expressed by Equation (5).

To define the free length (l f ), it is assumed that l f is α times the solid length, as shown in Equation (6).

This implies that the free length of the spring must not be less that the maximum value l max , which is a design parameter (Equation (7)).

The wire diameter must not exceed the minimum specified value, which is expressed in Equation (8).

Additionally, the outside diameter of the coil cannot exceed the maximum specified value, which is defined in Equation (9).

Based on the physical spring characteristics, the mean diameter must be at least β times the wire diameter to ensure the correct installation of the spring. This constraint is expressed in Equation (10).

Under load operation, spring deflection must be less than a specified value (Equation (11)).

This implies that:

Note that the combined deflection must be consistent with the free length, which can be formulated as Equation (13).

The deflection under preload conditions must be consistent with the design value. This is defined in Equation (14), where δ is a constant value.
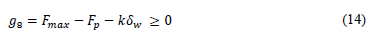
Finally, to solve the mathematical model, the variables are constrained in order to define a concrete solution space. The constraints are defined in Equations (15) to (17).

After knowing and interpreting each constraint, the set of penalties are presented. These are expressed in Equations (18) to (25), which are related to each previously mentioned constraint and defined by the maximum function, where px takes the maximum value, being 0 if the constraint is satisfied, and g if the constraint is violated.

The parameters considered for the design of the helical spring solved in this paper are reported in Table 1, and they are taken from Thamaraikannan and Thirunavukkarasu (2014).
Source: Authors
Table 1: Design parameters of the closed-coil helical spring
Parameter
Value
Unit
Parameter
Value
Unit
F
max
453,6
kgf
S
808543,6
kgf/cm2
G
808543,6
kgf/cm2
α
1,05
-
L
max
35,56
cm
β
3
-
δ
w
3,175
cm
dmax
1,016
cm
d
min
0,508
cm
Dmax
7,620
cm
D
min
1,270
cm
Nmax
25
-
N
cmin
15
-
-
-
-
Solution technique
The presented mathematical model is a non-convex, nonlinear problem with a single objective function and continuous variables. For this reason, it is necessary to determine solution techniques that allow dealing with the constraints by penalty factors which are added to the objective function. In order to solve this optimization problem, a continuous genetic algorithm (CGA) is proposed. CGAs are a classic optimization technique, which has been used in the specialized literature to solve continuous optimization problems, as well as for the optimization of nonlinear continuous functions with acceptable solutions (Giri et al., 2008; Montoya et al., 2018; Moradi & Abedini, 2012; Rodríguez-Cabal et al., 2019). Genetic algorithms work with five main characteristics, which are described below (Solarte-Martínez et al., 2015).
Initial population
As the CGA is an optimization technique based on population, the latter must be generated. It is proposed as a matrix with a rows and s columns, where a corresponds to the number of potential solutions and s to the number of variables of the problem. The matrix is represented in Table 2, where d, D, and N c are the three variables of the problem under study.
Source: Authors
Table 2: Population used for the problem under study
D11
d12
d13
d21
d22
d23
.
.
.
.
.
.
.
.
.
da1
da2
da3
axs
Fitness function
Before the population is generated, each individual has to be evaluated with the fitness function (FF). It is worth noting that the CGA turns a constrained problem into a conditional one; for this optimization problem, the FF is Equation (1), added with the sum of each evaluated constraint and multiplied by a penalty factor (θ). The FF is expressed in Equation (26) and the penalty factor in Equation (27).
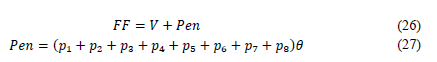
Descendant population
As CGAs imply an iterative process, the generation of new potential solutions is necessary at each iteration. This, with the purpose of replacing the bad solutions contained in the population. To achieve this, the mutation and recombination operators are adapted; a classic selection allows good solutions within the population and enables them to improve its position. The selection methods are explained below:
-
Selection: The descending population starts selecting, in a random way, a subgroup of individuals in the actual population. In this selection, a random number between r and 1 is chosen. Then, a new matrix is generated with a potential solution by employing the same strategy as the initial population. Finally, the total group of the selected individuals is formed through both strategies mentioned above.
-
Recombination: This process alters the descendant population as follows; if the probability of recombination r p is less than 50%, then two random individuals are averaged in order to create a new potential candidate. Note that this operation always generates feasible individuals, since the initial population, like the new candidates, is generated inside the solution space.
-
Mutation: At this point, the probability of mutation m p is explored, i.e., if m p is greater than 50%, a new random position of the potential solution is modified for a random value that ensures compliance. If m p is under 50%, the potential solution is not modified. This process is applied to each individual in the descendant population.
Once the descendant population is generated, the FF is evaluated once more.
New population
Once the new population has been evaluated, the group with the best solutions found by the CGA is saved. Then, a new population is generated by combining the group of descendant individuals, which produce a population with 2a following potential solutions. If two potential solutions are identical, one of them is removed from the list. This procedure is repeated until it is guaranteed that all potential solutions are different. Now, the list of resulting potential solutions is organized in an ascending form, the best solutions are selected as the new population, and they move on to the new iteration.
Stopping criterion
The proposed CGA ends the optimization process when one of the following conditions is satisfied:
-
The total iteration number has been reached.
-
The best potential solution does not improve its value after m continuous iterations.
Finally, Algorithm 1 shows the pseudo-code that describes the iterative process of the genetic algorithm.
Algorithm 1: Pseudocode used for the CGA
Results
The solution technique was programmed in MATLAB with a desktop computer (HPZ600, with 8GB RAM and 4 processor cores). In order to compare the numerical results, different optimization techniques were used, such as the conventional method, particle swarm optimization (PSO), and artificial bee colony (ABS), as published by Thamaraikannan and Thirunavukkarasu (2014).
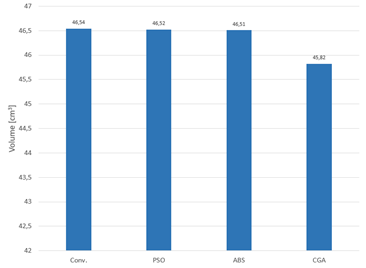
In Figure 1, it can be observed that the CGA obtained the lowest value compared with the other techniques; the best objective value went from 46,51 cm3, as obtained by the best reported technique, to 45,80 cm3, which represents an improvement of 1,5%. Compared to the reported techniques, CGA shows an improvement in the fitness function, with a feasible solution taking an average computing time of 1 s, which finds the following values of the decision variables: d = 0,6739 cm, D = 2,4048 cm, and N c = 15. When the set of constraints were evaluated, it was found that the values obtained by the purposed method were satisfied, which shows the feasibility of the design, not only with respect to the available space, determined by the free length, but also regarding the constraints related to the stresses and deflection under maximum load, which guarantees the quality of the solution.
Figure 1: Fitness function values found by the optimization techniques
Therefore, the CGA proves to be an efficient and fast technique for solving problems such as the one addressed in this study. The difference between the values of the techniques may be due to the tuning and programming of the algorithms, which not only affects the quality of the response, but also the processing times, which are not reported by Thamaraikannan and Thirunavukkarasu (2014).
Conclusions
In this paper, the optimization of a closed coil helical spring was carried out through a continuous genetic algorithm, where the objective function was the minimization of the volume of the spring by means of an adequate selection of the wire diameter, the mean diameter, and the number of coils; and, as a set of constraints, the technical and physical conditions that should be considered in this type of devices to ensure a reliable and safe design. For the sake of comparison, particle swarm optimization, artificial bee colonies, and the conventional method were employed, which have been proposed in the literature to solve the problem addressed in this research. Computational simulations showed that the CGA obtained the best results in terms of quality of the solution, with a volume 1,5% less that the best value reported by the comparison methods, while taking only 1 s to obtain the solution and meeting all the set of constraints. This proves that the proposed method can be used to solve not only the mathematical model employed, but also a problem with non-convex, nonlinear functions, at a low computational cost. This can be achieved by the way in which the algorithm explored and exploited the solution space.
Acknowledgements
Acknowledgments
This work was supported by Instituto Tecnológico Metropolitano de Medellín (Colombia), under the research groups of Advanced Computing and Digital Design (SeCADD) and mathematical modeling, programming, and optimization applied to engineering, which belongs to the research group of advanced materials and energy (MATyER).
References
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.