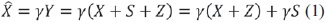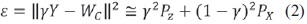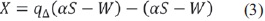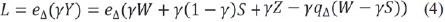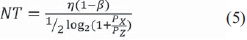Descripción y optimización de un esquema dirty paper coding

Descripción y optimización de un esquema dirty paper coding

Description and optimization of a dirty paper coding scheme

Diego Mauricio Camargo Casas¹

¹ Ingeniero Electrónico y de Telecomunicaciones. Investigador de la Universidad Católica de Colombia. Bogotá, Colombia. Contacto: dmcamargo38@ucatolica.edu.co

Fecha de recepción: 21 de noviembre de 2011 Fecha de aceptación: 16 de octubre de 2012

Resumen

En este artículo se expone una técnica de precodificación conocida como "Dirty Paper Coding" que permite transmitir con niveles de potencia acotados sobre canales donde la interferencia es conocida por el transmisor. Las interferencias consideradas poseen varianza finita, como es el caso de las comunicaciones MIMO (múltipleentrada múltiple-salida) que poseen ISI (interferencia intersimbólica), interferencias Intra-Cell e Inter-Cell, entre otras. Se describe el rol de los parámetros de dilatación apropiados en el transmisor y receptor utilizados para hacer uso de la estimación lineal que minimizan su error cuadrático medio de las señales involucradas. Además, se explica en detalle un esquema de cuantización equivalente a una operación módulo, para la precancelación de interferencia en el transmisor, demostrando que el conocimiento de la interferencia es utilizado tanto como sea posible por el codificador que se trata de adaptar al valor de la interferencia. Logrando, de esa manera, que la señal que se envía se decodifque de manera casi que original al volverse totalmente independiente de la interferencia.

Palabras clave: DPC, FDP, MIMO.

Abstract

This paper presents a pre-coding technique, known as "Dirty Paper Coding", which allows transmission with limited levels of power over channels where the interference level is known by the transmitter. The interference levels considered have finite variance-just like in MIMO (multiple-input and multiple-output) communications, where there is ISI (inter-symbol interference), Intra-Cell and Inter-Cell interference among other types of interference. The role of proper scaling parameters at the transmitter and receiver is described. Such parameters make use of a linear estimator that minimizes the mean square error of the signals involved. Moreover, a quantization scheme equivalent to a module operation is explained in detail. The purpose of this scheme is to pre-cancel the interference at the transmitter, showing that interference knowledge is used by the encoder as much as possible, namely the encoder attempts to adapt itself to the interference value. Thus, it is possible to decode the signal to make it look almost like the original signal since the new signal is now totally independent of interference.

Key words: DPC, FDP, MIMO.

1. Introducción

En las comunicaciones inalámbricas se requiere una alta eficiencia espectral y altas tasas de información pico a través de toda el área de cobertura; así mismo, son deseables bajos costos por bit de información y baja latencia. Para acercarse al cumplimiento de estas metas es prioridad minimizar la interferencia o ruido no correlacionado.

Tradicionalmente, se han empleado técnicas de cancelación de interferencia en el receptor, sin embargo, las nuevas tendencias sugieren que la mejor manera de realizar esto con las comunicaciones actuales MU-MIMO (multi-usuario multi-entrada multi-salida) es aplicar una técnica avanzada de tecnología de tipo evolutivo y revolucionario, que usa algoritmos como la precodificación en el transmisor. La precodificación es un conjunto de operaciones que, basado en el conocimiento de la interferencia, proponen un esquema que se acerque a la capacidad del canal. Dirty Paper Coding es un tipo de precodificación que realiza este proceso ofreciendo ventajas exquisitas para las comunicaciones 4G (cuarta generación).

2. Antecedentes y estado actual

Para mejorar el rendimiento de un sistema de comunicación inalámbrica que tiene presencia de interferencias conocidas por el transmisor, Max H Costa publicó en el año 1983 un artículo con el título "Writing on dirty paper" [1], explicando el funcionamiento de una técnica de precodificación aplicada sobre un canal gaussiano con la interferencia identificada por el transmisor. Esta técnica se expone como una estrategia para reducir los efectos generados por la presencia de interferencias en el sistema, o sea, una estrategia para mejorar el rendimiento del sistema.

Basado en el estudio ejecutado por Tomlinson y Harashima [2], [3]; Uri Erez y Stephan Brink [4] consiguieron que la precodificación propuesta por los dos primeros investigadores (una técnica no lineal de pre-ecualización) fuera usada para la transmisión a través de canales MIMO. Utilizando la precodificación en un canal MIMO, se logró una mayor eficiencia de potencia a un menor retraso de codificación que los otros esquemas de la competencia.

Por eso, una aplicación importante de DPC es sobre las comunicaciones MIMO, donde múltiples antenas están presentes en el transmisor y el receptor. Por ejemplo, la comunicación de una estación base con múltiples usuarios de una red de telefonía móvil se puede mejorar utilizando DPC, ya que la interferencia generada por las antenas del transmisor, de cierta manera, es conocida por el sistema de transmisión. Esto permite enviar información al mismo tiempo por parte de los usuarios, de modo que cada terminal no vea ninguna interferencia de otros usuarios.

Teóricamente, se ha demostrado que en un canal broadcast, DPC alcanza la capacidad total del canal de transmisión MIMO Gaussiano [5]. Sin embargo, en las comunicaciones reales DPC, no es una estrategia fácil de implementar debido a su complejidad en lo que respecta, por ejemplo, a la aplicación TDMA (acceso múltiple por división de tiempo).

Sin embargo, basado en un estudio realizado por Nihar Jindal y Andrea Goldsmith [6], del Departamento de Ingeniería Eléctrica de la Universidad de Stanford en junio del 2004, donde comparaban el rendimiento entre Dirty Paper Coding vs. TDMA para canales broadcast tipo MIMO; se concluyó que la capacidad "sum-rate" de un canal MIMO con M antenas transmisoras y K usuarios, que se alcanzó usando DPC, es por lo menos min (M, K) veces mayor que el máximo alcanzado usando TDMA. Esto aplicaba para cualquier tipo de SNR y para cualquier cantidad de antenas receptoras. Para canales "Rayleigh-fading" sucede lo mismo mientras exista una SNR alta. En el modo "uplink", en sistemas donde existen muchos usuarios que operen altas SNR, DPC, proporciona un desempeño de ganancia significante si se agregan antenas en la estación base (BTS) sin tener que aumentar el costo asociado a antenas adicionales en cada móvil.

En junio de 2008, Sae-Young Chung [7], miembros importantes del IEEE, propusieron una codificación multinivel y una decodificación iterativa para DPC, considerando una alta SNR, para ello dividieron la codificación en dos niveles: el nivel superior, que interactuaba con el código "shaping"; y el inferior, que se encargaba que no hubiera perdida de información, luego se evaluaron la capacidad de nivel y se diseñaron códigos para alcanzar la capacidad estimada. Demostraron en simulaciones que un buen desempeño se puede alcanzar al usar códigos LDPC (comprobación de paridad de baja densidad) en cada nivel. La mejor codificación estaba distanciada tan solo 0,45 dB en comparación con un caso en el que no se considera la interferencia para un modelo de capacidad gaussiana de una eficiencia espectral de 3 bisiHz.

A mediados del año 2010, en mayo, Anatoly Khina junto con Uri Erez [8], publicaron un estudio donde concluían que, cuando la varianza de la interferencia es finita o infinita, el esquema de codificación DPC de constelación extendida se puede mejorar al escoger un valor sensato para los parámetros de dilatación en el sistema, dando como resultado un aumento en la tasa de información.

3. Conceptos bases de dirty paper coding

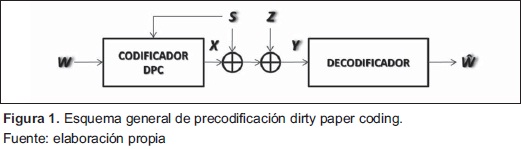
La Figura 1 muestra el esquema general donde W es la secuencia de símbolos de información, Z es la secuencia de ruido aditivo que posee distribución gaussiana Z~N(0,P_Z) y S es la secuencia de interferencia, la cual se asume que posee una distribución gaussiana Z~N(0,P_S). La señal transmitida X debe satisfacer la siguiente restricción en potencia: .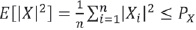

Si la interferencia S es conocida por el transmisor, es posible realizar una precancelación total o parcial de esta, transmitiendo la siguiente señal 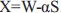, obteniendo la señal recibida como: 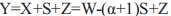. Si el factor de dilatación a es igual a uno, la interferencia se cancela totalmente y la señal recibida sería la ideal Y=W+Z. Sin embargo, si se desea una precancelación total de la interferencia la señal transmitida no debería estar acotada en potencia o la potencia debería ser demasiado grande, para ambas condiciones es algo inaceptable para un sistema de comunicación real.

Para ese caso, se puede emplear una solución diferente. Considérese la precodificación unidimensional, de modo que antes de transmitir la información original sea posible replicar infinitamente la constelación original sobre el eje real. Esto transformaría la constelación original de unos cuantos puntos, en una constelación extendida basada en el concepto de clases de equivalencia. Teniendo presente que, en los sistemas actuales, ese proceso de réplica se hace finitamente.

Una consecuencia directa de tener una constelación equivalente, es la posibilidad de identificar cada uno de los símbolos de la información original W por otros del conjunto de periódico de copias sobre el eje real. Permitiendo, de esta manera, cumplir con la restricción de potencia en el transmisor al seleccionar la copia idéntica de W, llamada W_C más cercana la valor de la interferencia y transmitiendo la diferencia entre W_C y la interferencia S.

Una operación módulo se implementa para ejecutar la operación de precodificación descrita antes. Esto se logra al considerar la clase equivalente de cualquier constelación PAM (Pulse Amplitude Modulation) como un cuantizador uniformemente espaciado q_W(.) sobre el eje real.

Fíjese que, en la siguiente figura, X=q_W(S)-S es el error de cuantizacion, donde q_W(S)=W_C representa la cuantizacion de la interferencia en un símbolo particular W_C (copia de un símbolo W de la constelación original) que minimiza la diferencia W-S dando como resultado llS-W_Cll.

Debido a que el receptor posee un conocimiento de la constelación extendida utilizada en el transmisor, le es posible identificar la réplica correcta de la constelación original, o sea, es capaz de encontrar la copia de W más cercana a Y.

Sin embargo, la regla de decodificación del punto más cercano puede conllevar a tomar malas decisiones cuando el vector de la señal Z es más grande que la señal transmitida, por lo que la señal recibida estaría definida por el ruido. Para evitar tales confusiones, decodificar al punto más cercano de Y en la constelación requiere que la constelación extendida tenga demasiados puntos espaciados sobre el eje real.

Se puede minimizar el MSE (error cuadrático medio) en el receptor al realizar una estimación lineal de la señal útil, esto se logra dilatando la señal recibida. La señal recibida corresponde a: Y=X+S+Z. El estimador lineal de X basado en la ecuación (1) es:

El estimador es igualado a yS con respecto a la métrica recibida ideal y(X+Z) (escenario que no posee interferencia). Debido a que el receptor no tiene conocimiento sobre S, esta igualación tan solo puede compensarse en el trasmisor. En este caso, es suficiente transmitir X=W_C-yS=q_W(yS)yS. Aplicando la ley de los grandes números el MSE se puede calcular así ecuación (2):

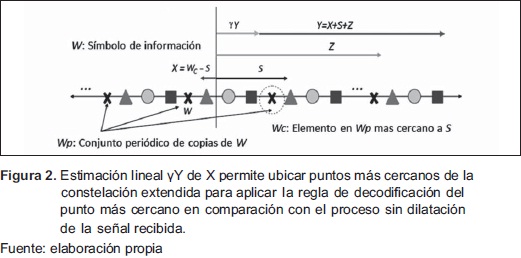
El vector error en el receptor es y Y-W_C=y(X+Z)W_C, el cual no es dependiente de S. El MSE es minimizado así: 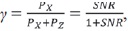donde SNR=P_X/P_Z. El factor de dilatación y tiende a uno si SNR (relación señal a ruido) incrementa, pero tiende a cero si SNR decrementa. La Figura 2 muestra la estrategia descrita antes, donde una constelación 4PAM se replica infinitamente para crear una constelación equivalente. La precodificación multidimensional se puede generalizar basada en la estrategia unidimensional explicada antes.

4. Metodología

4.1 Esquema simple DPC

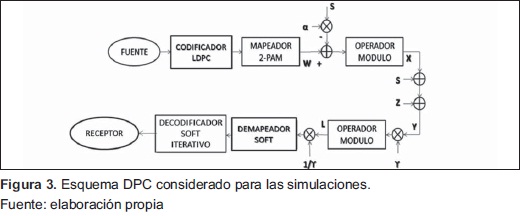
Se considera el siguiente esquema particular DPC (ver Figura 3):

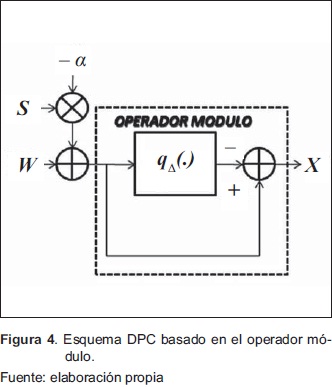
El bloque del operador módulo calcula el error de cuantización de W-aS (ver Figura 4). Se usa un cuantizador uniforme con el paso de cuantizacion Δ caracterizado por ser una función característica de entradaisalida e impar. La señal X se identifica así: 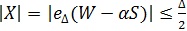; permitiendo relación esta restricción con la restricción original de la potencia en el transmisor. La cual queda satisfecha para ciertos pasos de cuantizacion.

Debido a que q_Δ(n)=-q_Δ(-n) la señal transmitida X se puede expresar mediante la ecuación (3) así:

Se iguala 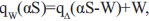permitiendo identificarla como la función que implementa la cuantizacion de aS basada en la información del símbolo W, esto es 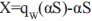. Lo cual demuestra que la operación módulo aplicada en la figura anterior sigue la idea general de precodificación DPC.

Después de aplicar el operador módulo a la señal recibida en el receptor esto es yY, la señal L está dada por la ecuación (4):

5. Resultados

5.1 Resultados de la simulación

El análisis y medida de la BLER (tasa de error por bloque) constituye un parámetro importante de calidad del servicio en un sistema de comunicación inalámbrica. Para tener una idea más clara del desempeño del sistema, el estudio se enfocó en cómo la BLER y el rendimiento normalizado cambiaban.

Para las simulaciones, se asume que el máximo rendimiento es la capacidad de Shannon; por lo que el rendimiento normalizado corresponde a la relación entre el rendimiento efectivo y la capacidad de Shannon, ver ecuación (5).

Donde P_X es la potencia de transmisión, P_Z es la potencia total del ruido, β es la BLER y η es la eficiencia espectral del sistema. Para sistemas constituidos por un codificador que tenga una tasa de código R_C y que la señal contenga una constelación de 2^m señales, la eficiencia espectral resultante es η=R_Cm. Para las simulaciones se usó una constelación BPSK y código irregular LDPC (800, 400).

5.2 Factores de dilatación adaptativos

Supóngase que se posee un conocimiento total del canal en el transmisor. Bajo esta suposición, el sistema puede ser capaz de implementar factores de dilatación dinámicos que cambian basados en la SNR del escenario, en este sentido, ambos factores de dilatación se pueden adaptar a las condiciones del canal, con los cuales se puede obtener el MMSE (mínimo MSE) en el receptor.

Teniendo en cuenta lo mencionado anteriormente, el problema se reduce a encontrar el paso de cuantización Δ óptimo que minimice la BLER y maximice el rendimiento normalizado, garantizando que el enlace de comunicación trabaje bajo diferentes niveles de potencia de interferencia.

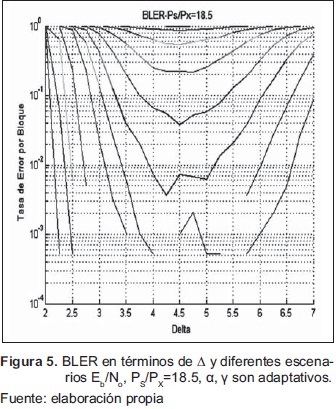
Considérese un caso donde la relación de potencia, entre la señal de la interferencia y la de la señal útil, sea grande, por ejemplo P_S=18.5P_X. En este caso Δ=4.5 optimiza la BLER independiente de la SNR del escenario como se muestra en la Figura 5, donde cada curva está asociada a un valor particular de la relación E_b/N_o (energía por bit de información/densidad espectral de la potencia de ruido).

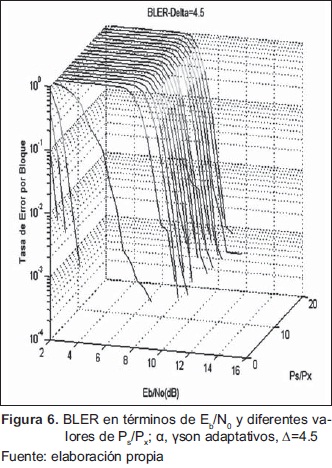
Sin embargo, se desea que el enlace trabaje independiente de la relación P_S/P_X. Al fijar Δ=4.5 (valor que minimiza BLER y maximiza NT en un escenario de relación grande de P_S/P_X) es una solución óptima, debido a que se alcanza una BLER=10^-2 para E_b/N_o≥10.1 dB independiente de la relación P_S/P_X como se muestra en la Figura 6.

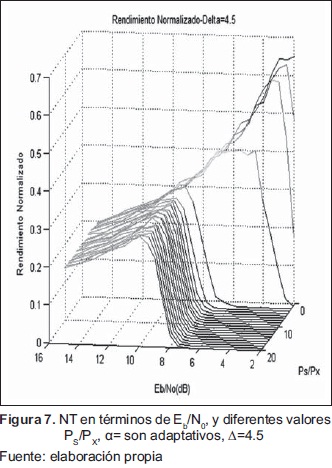
Adicionalmente, el sistema es capaz de alcanzar un rendimiento máximo normalizado NT≈0.65 para valores pequeños de la relación P_s/P_x y NT≈0.25 para valores grandes P_s/P_x. La figura que viene a continuación muestra el rendimiento normalizado en términos de E_b/N₀ y diferentes valores de la relación P_s/P_x para el valor Δ=4.5 (ver Figura 7).

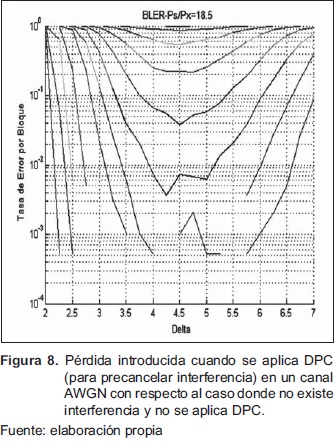
5.3 Desempeño del sistema con respecto al caso donde no se considera la interferencia y no se aplica DPC

En presencia de la interferencia, si se aplica DPC al usar el operador módulo de la Figura 7 y de los factores de dilatación adaptativos, el sistema es capaz de alcanzar un desempeño de 7.8 dB de diferencia con su correspondiente LDPCC (Low Density Parity Check Code) en un canal AWGN (Additive White Gaussian Noise) con respecto a un sistema que no considere la interferencia ni aplique DPC (ver Figura 8).

6. Conclusiones

Dirty Paper Coding representa un técnica efectiva que reduce los efectos de la interferencia al precancelarla en el transmisor, incluso si la potencia de transmisión es acotada.

El trabajo adecuado de dilatación en el transmisor y el receptor, y el uso de las operaciones módulo para la cancelación de la interferencia constituyen la base de la implementación DPC.

Resultados numéricos demostraron que el enlace de comunicación considerado en las simulaciones es capaz de alcanzar una BLER=10^-2 independiente de la cantidad de interferencia.

7. Trabajo futuro

Un estudio futuro tratará de implementar una cuantización multidimensional como una manera de alcanzar tasas cercanas a la capacidad del canal, lo mismo que el uso de diferentes codificaciones, debido a que el esquema es fácil de generalizar.

Referencias

[1] M. H. Costa, "Writing on Dirty paper", IEEE Trans. Inf. Theory, IT29, pp. 439-441, May, 1983.

[2] M. Tomlinson, "New automatic equalizer employing modulo arithmetic", Electron. Lett, Vol. 7, pp. 138-139, Mar., 1971.

[3] H. Harashima and H. Miyakawa, "Matchedtransmission technique for channels with inter-symbol interference", IEEE Trans. Commun., Vol. COM-20, pp. 774-780, August, 1972.

[4] U. Erez and S Brink, "A close-to-capacity Dirty Paper Coding scheme", submitted to IEEE trans. on informs. Theory, Abr. 4, 2004; Sep. 1, 2004.

[5] H. Weingarten, Y. Steinberg and S. Shamai, "The capacity region of the Gaussian MIMO broadcast channel", IEEE Trans. Information Theory. 174, Jun, 2004.

[6] N. Jindal and A. Goldsmith, "Dirty paper coding vs. TDMA for MIMO broadcast channels", Submitted to IEEE Trans. on Information Theory, Jun, 2004.

[7] S. Y. Chung, "Multi-level Dirty Paper Coding", IEEE communications letters, Vol. 12, No. 6, Jun, 2008.

[8] A. Khina and U. Erez, "On the robustness of Dirty Paper Coding", IEEE transactions on communications, Vol. 58, No. 5, May, 2010.