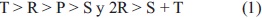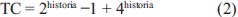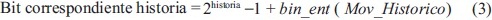Aprendizaje de estrategias de decisión en juegos repetitivos no cooperativos

Aprendizaje de estrategias de decisión en juegos repetitivos no cooperativos

Learning decision strategies in non-cooperative repetitive games

Fabián Andrés Giraldo Giraldo¹, Jonatan Gómez Perdomo²

¹ Ingeniero de Sistemas e Informática, candidato a magister en Ingeniería de Sistemas y Computación. Docente investigador de la Fundación Universitaria San Martin. Bogotá, Colombia. Contacto: fabian.giraldo@ingenieria.sanmartin.edu.co
² Ingeniero de Sistemas, doctor en Matemáticas. Docente de la Universidad Nacional de Colombia. Bogotá, Colombia. Contacto: jgomezpe@unal.edu.co

Fecha de recepción: 31 de agosto de 2011 Fecha de aceptación: 28 de agosto de 2012

Resumen

Este artículo tiene como objetivo presentar el diseño e implementación de diferentes mecanismos para realizar procesos de evolución de estrategias en juegos no cooperativos, específicamente en el dilema del prisionero iterado, ampliamente usado como modelo a estudiar en el ámbito de la economía evolutiva. Las estrategias desarrolladas para los mecanismos de evolución de estrategias de juego fueron Algoritmos Genéticos (GA) y Particle Swarm Optimization (PSO). El resultado final es un ambiente de simulación en el cual se puede verificar la emergencia de estrategias que pueden vencer a otras estrategias a través de un proceso de entrenamiento en el cual se pueden especificar los juegos utilizando un enfoque de programación por bloques ó a través de un lenguaje específico de dominio textual, facilitando notablemente las tareas de programación involucradas.

Palabras clave: algoritmos genéticos, lenguajes de programación, PSO, teoría de juegos.

Abstract

This article presents the design and implementation of different mechanisms applied to evolutionary processes within non-cooperative strategies, especially applied to the iterated prisoner's dilemma (a widely-used reference model in the feld of evolutionary economics). The strategies developed for the evolution mechanisms were Genetic Algorithms (GA), whereas Particle Swarm Optimization (PSO) was used for the evolution of game strategies. The result is a simulation environment that can be used to verify the emergence of strategies. Emergent strategies can defeat other strategies through a training process. In this environment games can be specifed using a block programming approach or a textual domain-specifc language, facilitating the programming tasks involved to a great extent.

Key words: genetic algorithms, programming languages, PSO, game theory.

1. Introducción

La teoría de juegos es una herramienta matemática con aplicaciones en economía, que permite analizar comportamientos estratégicos de jugadores cuando existe conficto de intereses.

La teoría de juegos clásica trata de analizar la dinámica de la toma de decisiones haciendo uso de supuestos poco realistas, como: homogeneidad, racionalidad perfecta y convergencia. Dichos modelos han sido desplazados por modelos evolutivos en los cuales se trata de estudiar las condiciones de cómo y porqué ciertos comportamientos, en un entorno complejo, puede ser aprendido por agentes con racionalidad limitada, a través de un proceso de adaptación guiado por planes estratégicos.

Diferentes estrategias de evolución han sido utilizadas para generar estrategias de juego, entre algunas se encuentran: estrategias evolutivas [1], algoritmos genéticos [2], programación genética [3], programación genética gramatical [4], técnicas de coevolución [5], [6]. Sin embargo, no es posible comparar dichos mecanismos, dado que no existe una metodología común sobre la cual fueran diseñados los experimentos, y no existe tampoco una plataforma de computación basada en agentes común sobre los cuales fueran modelados los diferentes casos de prueba especificados. Adicionalmente, no hay métricas de comparación comunes con el fin de determinar medidas de rendimiento de los algoritmos.

El presente artículo tiene como objetivo presentar el diseño e implementación de un ambiente de simulación en el cual se puedan especificar juegos no cooperativos iterativos, a través de lenguajes específicos de dominio gráfico y textual, que permitan configurar a los diferentes jugadores estrategias de juego. Adicionalmente, se estudian las diferentes técnicas de evolución de estrategias utilizadas, tales como GA y PSO para la evolución de estrategias en el dilema del prisionero iterado.

El artículo está organizado de la siguiente forma: en la segunda sección se realiza el planteamiento del problema; en la tercera, se presenta la especificación del dilema del prisionero. En la cuarta sección se especifican los métodos de solución propuestos. La sección quinta especifica la implementación de los métodos propuestos. En la sección sexta se indican pruebas y resultados obtenidos. Finalmente, en la séptima sección se presentan las conclusiones.

2. Planteamiento del problema

La teoría de juegos es una herramienta matemática con aplicaciones en economía, que permite analizar comportamientos estratégicos de jugadores cuando existe conficto de intereses. Existen varios tipos de juegos en la teoría de juegos, entre ellos, se encuentran los juegos no cooperativos, en los cuales los jugadores no se pueden comunicar, es decir, no se puede llegar a acuerdos previos, por lo tanto, cada jugador debe tener una estrategia de toma de decisiones con el fin de maximizar la recompensa esperada [7].

La teoría de juegos clásica trata de analizar la dinámica de la toma de decisiones haciendo uso de supuestos poco realistas, como: homogeneidad (todos los jugadores son idénticos y aprenden siguiendo el mismo proceso) y racionalidad perfecta (los jugadores ejecutan estrategias sin errores, los jugadores suponen que cambiar su estrategia no provoca desviaciones en las estrategias de los otros contrincantes y existe un conocimiento común tanto de las reglas como de los supuestos de racionalidad). En conclusión, se puede indicar que un juego en el enfoque clásico se interpreta como una descripción literal de una interacción idealizada en los que supuestos de racionalidad perfecta parecen bastante naturales, sin embargo, los modelos basados en racionalidad han sido desplazados en las últimas décadas por modelos evolutivos en los cuales se trata de estudiar las condiciones de cómo y porqué ciertos comportamientos en un entorno complejo puede ser aprendido por agentes con racionalidad limitada, a través de un proceso de adaptación guiado por planes estratégicos [8].

Como resultado de lo anterior, surge la economía evolutiva, la cual es un área del pensamiento económico que rechaza las asunciones tradicionales, las cuales indican que la economía es un sistema cerrado que eventualmente logra un estado de equilibrio, y en el cual, muchos supuestos poco realistas (racionalidad perfecta, inversiones homogéneas) deben hacerse para permitir la trazabilidad analítica. En su lugar, esta área del pensamiento ve a la economía como un sistema complejo adaptativo y dinámico, guiado por procesos de aprendizaje que trata de comprender el comportamiento emergente del sistema macroscópico a partir de la dinámica microscópica de agentes económicos (humanos, frmas, mercados, entre otros), con sus propias metas y objetivos, capaces de realizar interacciones entre sí y con su entorno [9]. El interés principal es encontrar las condiciones o reglas en las cuales el comportamiento del sistema se asemeja al comportamiento real.

Con el fin de comprender los comportamientos emergentes en los juegos no cooperativos, muchos trabajos de investigación han abordado el problema. Entre las estrategias propuestas está la economía computacional basada en agentes [10], la cual permite configurar agentes económicos utilizando diferentes estados, reglas, estrategias o conductas. Esto con el fin de experimentar variados escenarios del sistema y tratar de comprender comportamientos globales que surgen a nivel macro a través de interacciones locales repetidas de agentes egoístas. Sin embargo, estas aproximaciones requieren que las reglas y estrategias de los agentes sean preconfiguradas con anterioridad al proceso de simulación, un elemento que, en muchos sistemas, no se conoce y que en algunas circunstancias no se puede modelar dadas las características de complejidad, no linealidad e incertidumbre. Otras aproximaciones utilizan agentes integrados con redes neuronales, con el fin de modelar el comportamiento racional limitado de los agentes y así evolucionar sus comportamientos de tal forma que se adapten mejor al ambiente. La idea general es buscar mecanismos que permitan a los agentes originar, adaptar y retener estrategias que garanticen su adaptabilidad al entorno, a partir de variables económicas subyacentes a un sistema económico específico [11].

Diferentes estrategias de evolución han sido utilizadas, entre las cuales se encuentran: técnicas de neuroevolución [12], estrategias evolutivas [1], algoritmos genéticos [2], programación genética [3], programación genética gramatical [4], y técnicas de coevolución [5], [6].

A pesar que existen diversos mecanismos para la evolución de estrategias, no es posible comparar dichos mecanismos [13]. Adicionalmente, la ejecución de los procesos de simulación requiere un proceso adicional, comprender o construir una plataforma de modelamiento con el fin de configurar los diferentes sistemas que se quieren simular. Actualmente, existe una variedad de plataformas (StartLogo [14], NetLogo [15], MASON [16], entre otras), sin embargo, para la implementación de modelos, se deben conocer elementos sintácticos del lenguaje, lo cual complica un poco la tarea, y adicionalmente se deben proveer, a los agentes, mecanismos de adaptabilidad a partir de proceso de aprendizaje, mecanismos que no están en el núcleo central de dichas plataformas y si lo están, requieren de cierta experticia en programación de computadores y técnicas de aprendizaje particulares que se deseen aplicar.

3. Dilema del prisionero

El dilema del prisionero (PD) es un modelo clásico de la teoría de juegos denominado juego de suma no nula, formulado por el matemático Tucker con base en las ideas de Flood y Dresher en 1950. Desde entonces, ha sido discutido ampliamente por los teóricos de juegos, economistas, matemáticos, biólogos, flósofos, especialistas en política, especialistas en ética, sociólogos y científicos de la computación [17].

El juego es tradicionalmente descrito usando la metáfora de dos sospechosos que han sido arrestados y están siendo interrogados por separado. Sin ningún tipo de comunicación, cada jugador debe decidir si cooperar C (guardar silencio) o no cooperar D (traicionar a su pareja). Cada jugador recibe un pago individual dependiendo de las decisiones tomadas [18].

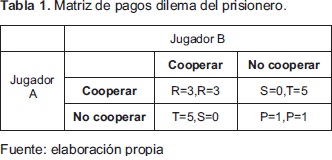
Existen cuatro posibles resultados: ambos jugadores deciden cooperar (Reward), ambos jugadores deciden no cooperar (Punishment), el Jugador A decide cooperar mientras que el jugador B no coopera (Sucker), y el jugador A decide no cooperar mientras que el jugador Bdecide cooperar (Temptation).

El juego constituye un dilema si se cumplen las siguientes desigualdades, ecuación (1):

Si existe una única oportunidad de jugar y basados en supuestos de racionalidad, la mejor decisión es siempre no-cooperar; por lo tanto, esta última es denominada una estrategia dominante en el juego(equilibrio de Nash).

Muchas variaciones del juego han sido propuestas; una de ellas es el dilema del prisionero iterado (IPD) presentada por Axelrod en 1984, en el cual dos contrincantes juegan repetidamente el dilema del prisionero. La clave del IPD es que ambos jugadores pueden jugar nuevamente, lo cual habilita a los jugadores a desarrollar estrategias de juego basados en interacciones de juegos previos, con el fin de maximizar los pagos recibidos. Teóricamente, el movimiento de un jugador puede influir en el comportamiento de su oponente en el futuro, afectando de esta manera futuros pagos. Esto remueve la estrategia dominante de la no-cooperación mutua [19].

4. Métodos de solución propuestos

4.1 Algoritmos genéticos

Los algoritmos genéticos constituyen una técnica de búsqueda y optimización inherentemente paralela, inspirada en el principio Darwiniano de selección natural y adaptación. Bajo el enfoque de algoritmos genéticos se han desarrollado una serie de trabajos orientados a realizar procesos de evolución de estrategias para el dilema del prisionero iterado. Axelrod, pionero en utilizar enfoques basados en computador, diseñó un entorno de simulación con el fin de estudiar la emergencia de la cooperación y el proceso de cambio de estrategias dentro de un marco de computación evolutiva, específicamente algoritmos genéticos [20]. Bajo este enfoque, cada cromosoma corresponde a una estrategia de juego a usardentro del dilema del prisionero iterado.

Dado que, convencionalmente, la solución candidata a un problema dentro del esquema de algoritmos genéticos es codificada en una cadena de longitud fija, el trabajo de Axelrod determinó que utilizar una memoria de tres juegos previos era suficiente para decidir el próximo movimiento a ejecutar. Para cada juego del dilema del prisionero hay cuatro posibilidades: CC, CD, DC, DD, así que para un dilema del prisionero, con una historia de tres, hay 64 (4³) posibles historias. Por lo tanto, una cadena de longitud 64 podría ser usada para representar la acción a tomar (C o D) basado en la historia de juegos previos.

Como no existe memoria para los tres primeros movimientos, se realizó una suposición de la historia de juego de cada jugador con seis bits adicionales para hacer frente a los tres primeros movimientos, por lo tanto, la longitud del cromosoma utilizado corresponde a setenta.

Dado que es necesario evaluar la estrategia generada, el dilema del prisionero provee un mecanismo natural para realizar la evaluación del fitness de cada solución y está directamente relacionada con la matriz de pagos.

Para tal fin, Axelrod utilizó estrategias de juegos enviadas por contrincantes humanos a dos torneos de dilema del prisionero iterado organizado por él. Cada solución o estrategia de juego era puesta a jugar en un torneo Round Robin con las demás estrategias, buscando maximizar el pago obtenido basado en la matriz de pagos provista en el juego. Los resultados obtenidos determinaron que el algoritmo genético converge a la estrategia que maximiza el pago obtenido cuando se compite con otras estrategias.

El esquema propuesto por Axelrod fue utilizado posteriormente por Errity A [19], sin embargo, este último realizó una modificación en la codificación de los tres primeros movimientos, con el fin de utilizar movimientos previos realizados. Bajo este enfoque, el primer bit del cromosoma corresponde a la primera jugada, los dos siguientes bits corresponden con la segunda jugada; basado en si el oponente cooperó o no cooperó en el primer movimiento. Los bits 4, 5, 6, 7 indican el tercer movimiento a ejecutar basado en los dos movimientos previos del oponente. Estos 7 Bits, adicionados a los 64 propuestos por Axelrod, determinan un cromosoma de longitud 71. El esquema utilizado por Errity A, es utilizado como mecanismos para el diseño del cromosoma en el presente artículo. Sin embargo, se generalizaron algunos aspectos con el fin de facilitar el diseño de la solución computacional. El tamaño del cromosoma es adaptado dinámicamente dependiendo de la historia definida para la estrategia, para tal fin se utiliza la ecuación (2).

Adicionalmente, la correspondencia entre los bits y los movimientos propuestos inicialmente fueron replanteados utilizando el siguiente esquema: Definida una historia de juego a considerar para tomar las decisiones de juego y bajo un esquema de representación binaria, se puede determinar para cada bit la historia que le corresponde usando la ecuación (3):

Donde: bin_ent corresponde a realizar la operación de convertir una representación binaria a número entero y Mov_Historico, corresponde a los juegos previos de los jugadores; considerando como cooperación (C) el número binario 1 y como No-cooperacion (D) el número cero.

De esta forma, se conoce el bit dentro del cromosoma de cada uno de los movimientos históricos y por ende el movimiento a ejecutar en la repetición respectiva.

4.2 PSO (Particle Swarm Optimization)

PSO es una técnica meta heurística evolutiva desarrollada por Kennedy y Eberhart en 1995, inspirada en el comportamiento social de los enjambres pájaros, cardumen de pescados, entre otros. En general, el trabajo con enjambres requiere de una representación del problema mediante un vector de fotantes; cada vector es una estructura de datos que representa una de las posibles soluciones del espacio de búsqueda del problema. Además, con el fin de evaluar cada partícula, se debe definir una función de evaluación, la cual asigna un valor a cada posible solución codificada indicando la bondad de la solución [20].

El esquema de codificación propuesto para representar el vector solución de cada partícula fue igual al propuesto bajo el esquema de algoritmos genéticos. Por lo tanto, se tendrá un cromosoma de igual longitud (71), sin embargo adaptable dinámicamente y se usará el mismo esquema de evaluación de la solución.

5. Metodología

5.1 Diseño del simulador dilema del prisionero iterado

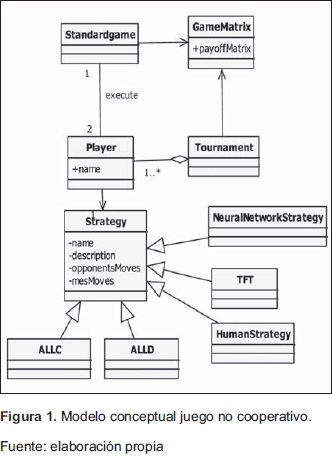
El diseño de un simulador que cumpla con las especificaciones definidas para la realización de un juego no cooperativo (dilema del prisionero) debe tener en cuenta los siguientes elementos: se debe poder configurar los jugadores, cada jugador debe poder seleccionar una estrategia de juego, se debe poder definir una matriz de pagos, con el fin que los jugadores reciban recompensas basadas en las decisiones tomadas a través de las estrategias. Dado la anterior, se definió el modelo conceptual presentado en la Figura 1, para realizar la especificación de un juego no cooperativo. Es importante indicar que el simulador desarrollado fue una adaptación del propuesto por [21].

Para realizar el proceso de configuración de una simulación se debe utilizar las siguientes clases: GameMatriz, clase que administra la matriz de pagos. Player, clase que permite configurar un jugador del dilema del prisionero. Strategy, clase que administra la información de las estrategias,almacena la información previa de los dos jugadores participantes. StandarGame, permite simular un juego de dilema del prisionero iterado. Tournament, permite simular un torneo Round Robin del dilema del prisionero iterado.

Definido lo anterior, se pueden crear configuraciones sencillas de juegos, usando estrategias preconfiguradas o generadas por entornos de programación evolutiva ó inteligencia colectiva.

5.2 Algoritmos genéticos

Definido el cromosoma y la función de adaptación (competencia), se procedió a implementar el algoritmo genético en el entorno de trabajo JGAP (Java Genetic Algorithms Package), el cual permite la solución de problemas utilizando algoritmos genéticos y programación genética. JGAP es un entorno de programación que tiene especificados operadores de selección, cruce, mutación y reemplazo, por lo tanto, facilita las tareas de implementación.

Los operadores de selección que tiene son: Best-ChromosomesSelector (Elitismo), WeightedRouletteSelector (Ruleta) y TournamentSelector (Torneo). Existen un operador de cruce por defecto, denominado CrossoverOperator (Operador de cruce monopunto) y un operador de mutación por defecto MutationOperator (Operación de mutación aleatoria bit a bit). Para el caso puntual del problema, el proceso de evolución de estrategias para el dilema del prisionero, se realizó el proceso de configuración del algoritmo genético utilizando el objeto DefaultConfiguration provisto por JGAP, en el cual se definieron las especificaciones de diseño del algoritmo; entre los cuales se pueden mencionar: el tipo de cromosoma a utilizar, en este caso se definió al objeto IChromosome la configuración BooleanGene de tamaño 71, con el fin que estuviera alineado con los elementos considerados en el métodos de solución planteado en sección anterior, sin embargo, se adapta dinámicamente basado en el tamaño de historia de juego a considerar en los proceso de decisión.

Para la definición del porcentaje de cruce y mutación, se utilizaron dos clasesprovistas por el Framework: CrossoverOperator, MutationOperator. El proceso de evaluación de la función objetivo, se realiza un juego del dilema del prisionero con la estrategia a la cual se quiere derrotar. Para el caso puntual se crearon dos Player; a cada jugador se le configura la respectiva estrategia; al contrincante se le configura una de las estrategias provistas por el simulador es decir: ALLC, ALLD, GRIM, HumanStrategy, NEG, RAND, STFT, TFT, TFTT, PLStrategy, NeuralNetwork-Strategy (Perceptrón multicapa) [22].

Al algoritmo genético se le especifica la estrategia AGStrategy, la cual recibe el cromosoma generado utilizando los elementos provistos por JGAP. Configurados ambos jugadores, se procede a crear un objeto de tipo GameMatrix, el cual define la matriz de pagos y por último se procede a desarrollar un StandardGame, con el fin de realizar el proceso de simulación. El fitness de cada cromosoma es determinado usando los resultados entregados por el simulador.

Es importante indicar, adicionalmente, que la estrategia resultante es enviada a un objeto generador de código que tiene la funcionalidad de traducir el mejor individuo de la población a un programa especificado en PROLOG, con el fin de ser utilizado posteriormente.

5.3 PSO (Particle Swarm Optimization)

Definido el vector solución y la función de adaptación, se procedió a implementar el algoritmo en el entorno de trabajo jSwarm-PSO (Java Swarm PSO), el cual permite la solución de problemas basado en el enfoque de enjambres de partículas.

Para la configuración del entorno de programación se debió definir los elementos de configuración en un objeto Swarm al cual se debe especificar: valor máximo del vector solución (tamaño para configurar la estrategia), velocidad máxima de las partículas (permite explorar zonas de búsqueda, velocidad pequeña corresponde realizar explotación sobre una zona local y una velocidad alta corresponde a realizar un proceso de exploración) usando el método swarm.setMaxMinVelocity, factor de inercia (regula el cambio de velocidad y por lo tanto regula el vuelo de cada partícula) usando el método swarm.setInertia, número de partículas y, por último, el tamaño del vecindario (permite conocer cantidad de partículas con las cuales va comunicarse con el fin de compartir soluciones parciales encontradas durante el proceso de vuelo) usando el objeto swarm.setNeighborhood, swarm.setNeighborhoodIncrement.

Es importante indicar, adicionalmente, que la estrategia resultante es enviada a un objeto generador de código que tiene la funcionalidad de traducir el mejor individuo de la población a un programa especificado en PROLOG.

5.4 Lenguaje específico

5.4.1 Lenguaje gráfio

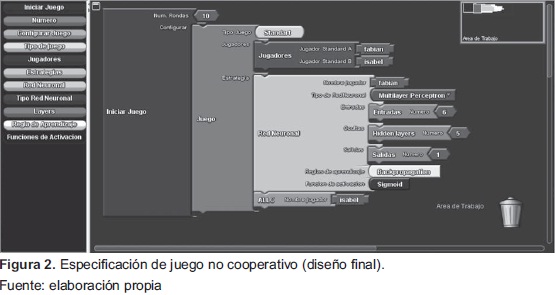
Como se especifcó en la definición de la problemática, para una persona con pocos conocimientos en programación, especificar un juego garantizando el cumplimiento de los requerimientos especificados es complicado, por tal motivo, se diseñó un esquema de especificación de simulaciones bajo el paradigma del modelo de programación por bloques [23]. Este se presenta en la Figura 2. Como se puede observar se proveen los siguientes elementos:

Iniciar juego: permite la configuración del juego no cooperativo, se debe especificar el número de repeticiones y la configuración general del juego (jugadores, estrategias).

Corfigurar juego: este bloque permite la configuración general del juego. Se debe indicar: a) Tipo de juego, existen dos posibilidades: juego estándar, en el cual se enfrentan dos jugadores; o torneo, en el cual se enfrentan todos contra todos múltiples jugadores; b) Jugadores: se debe indicar la lista de jugadores que van a participar en el juego no cooperativo; c) Estrategias: se deben indicar las estrategias de juego a utilizar por cada uno de los jugadores; entre las opciones se encuentran: ALLC (siempre cooperar), ALLD (nunca cooperar), NEG (coopera si el contrincante en la repetición anterior no cooperó y viceversa), TFT (primera repetición coopera y las siguientes decisiones se basa en la decisión tomada por el contrincante en la jugada anterior; si el contrincante cooperó se coopera si no cooperó no se coopera), HumanStrategy (en cada repetición un ser humano tiene que tomar la decisión) y NeuralNetwork-Strategy (la decisión a tomar, está basada en la respuesta entregada por un perceptrón multicapa, luego de un proceso de entrenamiento). Actualmente, bajo este enfoque, las simulaciones se generan bajo el enfoque de programación basado en sistemas multiagentes; específicamente se utiliza la plataforma de sistemas multiagentes JADE. El lenguaje gráfico no soporta la evolución de estrategias.

5.4.2 Lenguaje textual

Con el fin de integrar el esquema de simulación del dilema del prisionero con las técnicas de metaheurísticas que permiten la evolución de estrategias, se desarrolló un lenguaje específico de dominio; para su construcción es necesario comprender los elementos conceptuales de desarrollo de un compilador.

Un compilador se compone internamente de varias etapas, o fases, que realizan distintas operaciones lógicas, entre ellas se pueden encontrar: analizador léxico, analizador sintáctico, analizador semántico, generador de código, entre otros, [24].

Para el caso del dilema del prisionero se definieron expresiones regulares para las siguientes categorías léxicas: palabras reservadas de alto nivel, palabras reservadas que identifican las estrategias de decisión, palabras reservadas para la especificación de algoritmos genéticos, palabras reservadas para la especificación de PSO.

La especificación gramatical es LL (1) soportado por el metacompilador JAVACC (Java Compiler Compiler), a continuación se presenta un fragmento de la gramática, en la Figura 3.

Por su parte, el analizador semántico, se encarga de que los tipos que intervienen en las expresiones sean compatibles o que los parámetros reales de una función sean coherentes con los parámetros formales. Generador de código, es la parte final de un compilador, en esta fase se define la estructura del lenguaje objeto y se realiza la generación. Dicha fase es utilizada para la generación de programas especificados en PROLOG para ser utilizados posteriormente en posibles enfrentamientos.

6. Resultados

Los resultados a presentar están dividos en dos partes: una, relacionada con el desarrollo del simulador, usando esquema de programación por bloques, el cual permite la configuración de juegos; sin embargo, actualmente no soporta procesos de evolución.

Por otra parte, el simulador, usando el lenguaje específico de dominio, el cual soporta la especificación completa; es decir, especificación de juegos utilizando estrategias predefinidas y los procesos de evolución usando algoritmos genéticos, PSO y programas especificados en PROLOG, es importante anotar adicionalmente que la matriz de pago utilizada para los juegos corresponde a la presentada en la Tabla 1.

6.1 Esquema de simulación por bloques

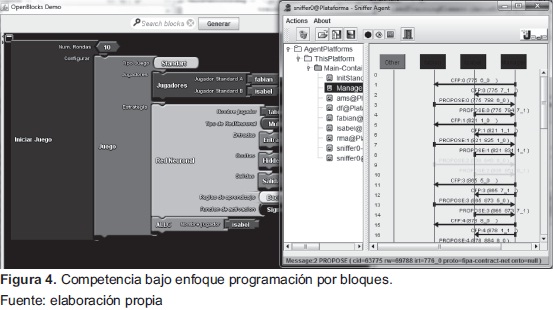
El proceso de implementación del simulador fue desarrollado utilizando el lenguaje de programación JAVA. En la Figura 4, se puede visualizar una competencia entre dos jugadores, uno utilizando como estrategia una red neuronal con una arquitectura preconfigurada y el otro usando la estrategia ALLC.

Como se puede observar en la Figura 4, provisto por JADE, el fujo de mensajes intercambiados entre jugadores (Fabian, Manager, y demás) garantiza que los jugadores en cada iteración toman una decisión basada en la estrategia propuesta.

6.2 Esquema de simulación usando lenguaje específico de dominio

Para este caso, se plantearon varios escenarios de prueba, a saber:

6.2.1 Adaptación de estrategias utilizando algoritmos genéticos

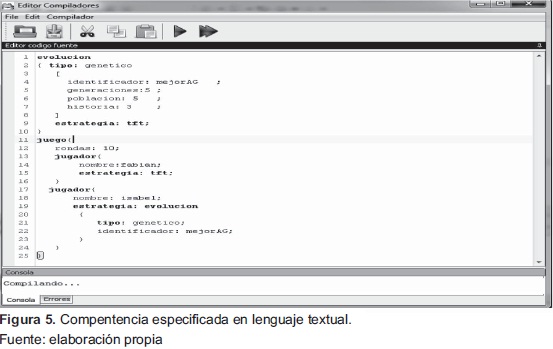
El escenario base consiste en realizar el programa que permite ejecutar el escenario de simulación: como se puede observar en la Figura 5, se plantea desarrollar la evolución de estrategias usando algoritmos genéticos, para tal fin compite con la estrategia TFT.

El pago final obtenido es 30 (cooperación mutua, máximo pago posible) y corresponde ala estrategia: 110110001101001001001000010101111010 01100100000101100100 001010100010011, donde 1, corresponde a cooperar y 0 no cooperar.

La interpretación de la estrategia puede ser consultada en el apartado de métodos utilizados del presente artículo. Adicionalmente, como se indicó en fases anteriores, luego de realizar el aprendizaje de las reglas, se genera automáticamente un programa especificado en PROLOG que posteriormente puede ser utilizado para competir. A continuación se presenta un aparte del programa generado, en la Figura 6.

Posteriormente, con el archivo generado, se realiza un juego del dilema del prisionero compitiendo con la misma estrategia aprendida por el algoritmo genético obteniendo resultado similares.

Rordas: l0
% mejorAG.pl compiled 0.00 sec, 124 bytes
consult('mejorAG.pl') succeeded
*** Game Results (nrRounds = 10):
player=tft strategy=TFT (Tit-for-Tat) points=30
player=xxx strategy=PLAG (AG) points=30

Lo que garantiza el correcto funcionamiento del aprendizaje de reglas dado que la mejor decisión compitiendo con la estrategia TFT es cooperar; dado que ambos maximizan el pago obtenido (emergencia de la cooperación).

6.2.2 Adaptación de estrategias utilizando PSO

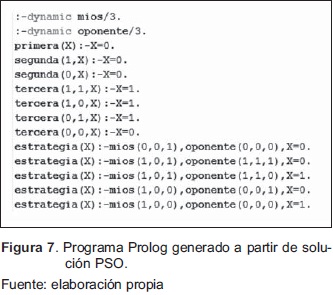
El escenario base consiste en realizar el programa que permite ejecutar el escenario de simulación: como se puede observar en la Figura 7, se plantea desarrollar la evolución de estrategias usando PSO, para tal fin compite con la estrategia ALLD.

El pago final obtenidoes 10 (no cooperación mutua) y corresponde a la estrategia: 000101000001 0000011001011100011111101000010100100001 1000100110111110000

La interpretación de la estrategia puede ser consultada en el apartado de métodos utilizados del presente artículo. Adicionalmente, como se indicó en fases anteriores, luego de realizar el aprendizaje de las reglas, se genera automáticamente un programa especificado en PROLOG que posteriormente puede ser utilizado para competir.

Posteriormente, con el archivo generado se realiza un juego del dilema del prisionero compitiendo con la misma estrategia aprendida usando PSO obteniendo resultados similares.

Rordas: l0
% mejorPSO.pl compiled 0.00 sec, 124 bytes
consult('mejorPSO.pl') succeeded
*** Game Results (nrRounds = 10):
player=tft strategy=ALLD (ALLD) points=10
player=xxx strategy=PLPSO (PSO) points=10

7. Conclusiones

Luego de realizar elproceso de evolución de estrategias se pueden extraer las siguientes conclusiones: los resultados obtenidos confrman que es posible ver los sistemas económicos como procesos de conocimiento que evolucionan en el tiempo y que pueden ser simulados en ambientes computaciones, en los cuales, los agentes tienen la capacidad de adaptarse a través de proceso de aprendizaje basados en computación evolutiva (algoritmos genéticos) e inteligencia colectiva. Esto se demuestra con la emergencia de estrategias cuando se compiten contra estrategias predefinidas en dilema del prisionero iterado.

Los resultados experimentales garantizan que la evolución de estrategias, usando técnicas meta-heurísticas (AG, PSO), garantizan la maximización de pagos, por lo tanto, los juegos evolutivos pueden ser utilizadosparaestudiar las condiciones de cómo y porqué ciertos comportamientos en un entorno complejo puede ser aprendido por agentes con racionalidad limitada, a través de un proceso de adaptación guiado por planes estratégicos.

Las pruebas realizadas en personas con pocos conocimientos en programación garantizan que el esquema de programación por bloques y textual es prometedor para realizar procesos de simulación, dado que no se debe pensar en detalles de implementación sino en la lógica de lo que se quiere lograr con la simulación. Por lo tanto, es necesario desarrollar mecanismos de extensibilidad sobre la propuesta inicial, con el fin que se puedan integrar otras estrategias de decisión y otros juegos no cooperativos repetitivos.

8. Financiamiento

Grupo de Investigación ALIFE, Línea de investigación Ecología, Sociedad y Cultura Artificial, Universidad Nacional de Colombia, Bogotá, Colombia.

9. Agradecimientos

Integrantes del Grupo de Investigación ALIFE, por los aportes realizados durante el desarrollo de la investigación.

Referencias

[1] K. Chellapilla and D. Fogel, "Evolution, Neural Networks, Games, and Intelligence", Proceedings of the IEEE, Vol. 87, pp. 1471-1496, 1999.

[2] X. Jin, D. Jang, T. Kim and C. Univ. "Evolving Game Agents Based on Adaptive Constraint of Evolution", International Conference on Convergence Information Technology, 2007.

[3] D. Rivero, J. Dorado, J. Rabunal and A. Pazos, "Generation and simplification of Artificial Neural Networks by means of Genetic Programming", Neurocomputing, Brazilian Symposium on Neural Networks (SBRN2008), Vol. 73, Issues 16-18, pp. 3200-3223, 2010.

[4] I. Tsoulos, D. Gavrilis and E. Glavas, "Neural network construction and training using grammatical evolution", Neurocomputing, Machine Learning for Signal Processing (MLSP 2006) / Lije System Modellirg, Simulation, and Bio-inspired Computing (LSMS 2007), Vol 72, Issues 1-3, pp. 269-277, 2008.

[5] S. Yew and C. Xin Yao, "Multiple Choices and Reputation in Multiagent Interactions", in Evolutionary Computation, IEEE Transactions, 2007.

[6] Y. Yau and J. Teo "An Empirical Comparison of Non-Adaptive, Adaptive and Self-Adaptive Co-evolution for Evolving Artificial Neural Network Game Players", IEEE International Conference on Cyber retics ard Irtelligert Systems (CIS 2006), pp 405-410, Bangkok, Thailand, 2006.

[7] H. Sally and R. Muhammad, "A survey of Game Theory using Evolutionary Algorithms", Information Technology. International Symposium, Vol. 3, pp. 1319-1325, 2010.

[8] L. Samuelson, "Evolution and Game Theory", Journal of Economic Perspectives, American Economic Association, Vol. 16, No. 2, pp. 47-66, 2002.

[9] M. Fontana, "Can Neoclassical Economics Handle Complexity? The Fallacy of the Oil Spot Dynamic", Journal of Economic Behavior & Organization, 2010.

[10] L. Tesfatsion, "Agent-Based Computational Economics: A Constructive Approach to Economic Theory", Handbook of Computational Economics, 2006.

[11] K. Dopfer, J. Foster and J. Potts, "Micromeso-macro", Journal of Evolutionary Economics, 2004.

[12] D. Sgroi and D. Zizzo, "Neural networks and bounded rationality", Physica A: Statistical Mechanics and its Applications, Vol. 375, Issue 2, 1, pp. 717-725, 2007.

[13] L. Asher, "Empirically evaluating multiagent reinforcement learning algorithms in repeated games", Electronic Thesis or Dissertation, University of British Columbia, 2005.

[14] M. Resnick, "StarLogo: an environment for decentralized modeling and decentralized thinking", Conference companion on Human factors in computing systems, 1996.

[15] S. Tisue, and U. Wilensky, "NetLogo: A Simple Environment for Modeling Complexity", 2004.

[16] S. Luke, C. Cioff-Revilla, L. Panait, K. Sullivan and G. Balan. "MASON: A Multiagent Simulation Environment", Journal Simulation, 2005.

[17] R. Brunauer, A. Löcker and A. Hemut, "Evolution of iterated prisoner's dilemma strategies with different history lengths in static and cultural environments", ACM Symposium on Applied Computing, 2007.

[18] R. Chiong, "Applying genetic algorithms to economy market using iterated prisoner's dilemma", in Proceedirgs oj the 22rd Arnual ACM Symposium on Applied Computing, pp. 733-737, 2007.

[19] A. Errity, "Evolving Strategies for the Prisoner's Dilemma", in Technical Manual, Faculty of Computing and Mathematical Sciences, Dublin City University.

[20] E. Ocampo, Y. Restrepo y M. Granada, "Adaptación de la técnica de particle swarm al problema de secuenciamiento de tareas", Scientia et Technica Año XII, No. 32, diciembre de 2006. UTP. ISSN 01221701.

[21] D. Goldenberg, Genetic algorithms in search, optimization and machine learning. Reading, MA. Addison-Wesley, 1989.

[22] S. Chong, J. Humble, G. Kendall, J. Li and X. Yao, "Iterated Prisoner's Dilemma and Evolutionary Game Theory", World Scientifc Publishirg Co. 2011.

[23] I. K. Cho, "Bounded Rationality, Neural Network and Folk Theorem in Repeated Games with Discounting", Economic Theory, 1994.

[23] R. Roque, "OpenBlocks: an extendable framework for graphical block programming systems", in Massachusetts Institute of Technology, 2007.

[24] M. Mitchell, An Introduction to Genetic Algorithms, MIT Press, 1998.