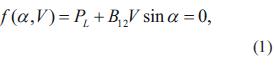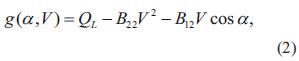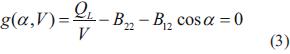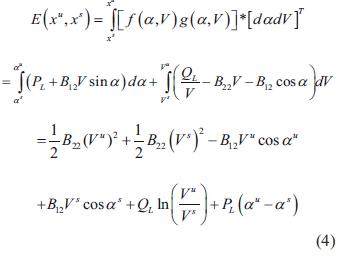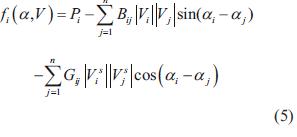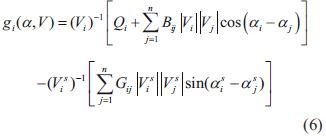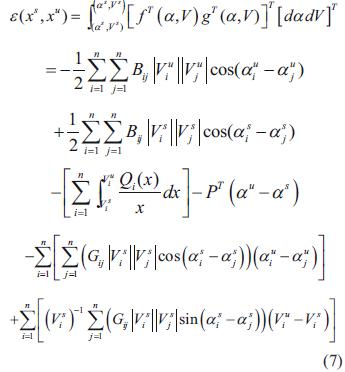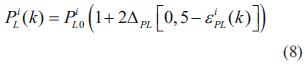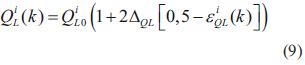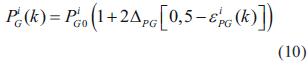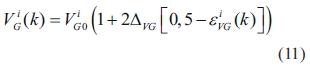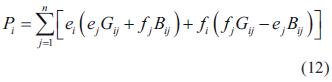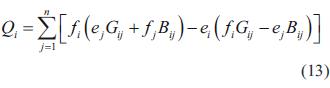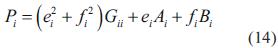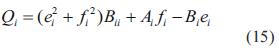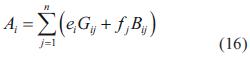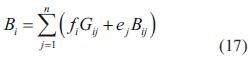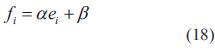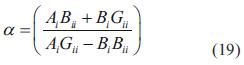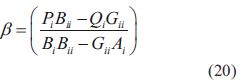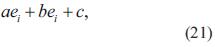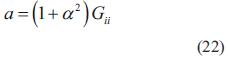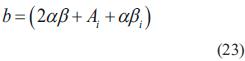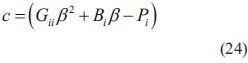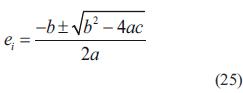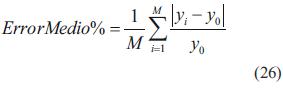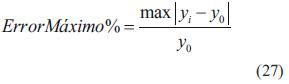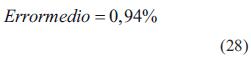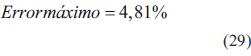DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2013.3.a02Published:
2013-07-01Issue:
Vol. 17 No. 37 (2013): July - SeptemberSection:
ResearchEstimación de los márgenes de estabilidad de tensión en un sistema de potencia usando redes neuronales artificiales
Keywords:
estabilidad de tensión, flujo de carga, margen de energía, redes neuronales. (es).Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Estimación de los márgenes de estabilidad de tensión en un sistema de potencia usando redes neuronales artificiales
Voltage stability margin estimation in a power system using artificial neural networks
Gloria Patricia López Sepúlveda1 , Christian David Sepúlveda Londoño2, Alexander Molina Cabrera3
1Ingeniera en Sistemas y Computación, Estudiante de Maestría en Ingeniería Eléctrica.
Investigadora de la Universida de Estadual Paulista "Julio Mesquita Filho". Sao Paulo,
Brasil. Contacto: pattylla@gmail.com
2Ingeniero Electricista, Estudiante de Maestría en Ingeniería Eléctrica. Investigador de la Universidad Tecnológica
de Pereira. Pereira, Colombia. Contacto:
chrisdavid1205@utp.edu.co
3Ingeniero Electricista, Magíster en Ingeniería Eléctrica. Docente de la Universidad Tecnológica
de Pereira. Pereira, Colombia. Contacto: almo@utp.edu.co
Fecha de recepción: 31 de marzo de 2012 Fecha de aceptación: 12 de febrero de 2013
Resumen
Debido al aumento de la carga y al creciente uso de energías alternativas en el sistema de potencia, este se ha vuelto más sensible a problemas de estabilidad de tensión. Si se considera que los métodos de análisis estático como el flujo de carga no evalúan de manera correcta la estabilidad de tensión, debido a que usan modelos simples para describir las componentes del sistema, y que los modelos dinámicos para el análisis de estabilidad de tensión son complejos y tienen un alto costo computacional, se evidencia la necesidad de desarrollar una metodología más precisa y eficiente.
Se presenta un modelo basado en Redes Neurona-les Artificiales (ANN, del inglés Artificial Neural Networks); estas tienen la capacidad de aprender y extraer las principales características de un conjunto de datos. Pueden ofrecer respuestas correctas para aquellas entradas que presentan variaciones causadas por los efectos del ruido o por las distorsiones del medio. Debido a que las ANN tienen habilidad para cambiar su estructura interna durante el entrenamiento han sido utilizadas para el desarrollo de este trabajo como máquinas de estimación del margen de estabilidad de tensión del sistema de potencia a partir su estado. Los datos de entrenamiento se obtienen por medio de un flujo de carga que entrega las condiciones iníciales o las también conocidas variables de entrada a la red y luego, mediante funciones de energía, se obtienen los márgenes de estabilidad que para este caso son las salidas deseadas. Se muestran resultados para un sistema de prueba de cuatro nodos, donde la RN estima de forma cercana las estimaciones efectuadas mediante el uso de márgenes de estabilidad determinísticos.
Palabras clave: estabilidad de tensión, flujo de carga, margen de energía, redes neuronales.
Abstract
Power systems have become more sensitive to voltage stability problems due to load growth and the increasing utilization of alternative energy. Voltage stability appears not to be properly evaluated by methods of static analysis, such as load flux, because these methods use simple models to describe the system's components. Moreover, dynamic models for voltage stability analysis require high computational cost. Considering this, there is a need of developing more efficient and accurate methodologies. This article shows a model based on Artificial Neural Networks (ANN). ANN is a technique of artificial intelligence inspired in the biological neural networks of the human brain. An ANN is capable of learning through experience and takes the main characteristics of a dataset. Additionally, such networks may offer correct answers for inputs that present variations due to noise effects or distortions in the environment. ANNs provide a switching behavior as a function of the environment, that is, they get an input dataset and transform it into a consistent output set. This represents the rationale behind using ANNs for the development of this work; in other words, ANNs allow the prediction of a voltage-stability margin in power systems using information about their state variables. The training datasets are obtained from the load flux method, which delivers the initial conditions (i.e. the network input variables). Results are obtained through an estimating NN based methodology and compared to the results obtained when using estimating margin deterministic methods in a 4-node tests system.
Key words: voltage stability, load flow, energy barrier, neural networks.
1. Introducción
El problema de estabilidad de tensión en sistemas eléctricos de potencia ha aumentado conforme el sistema ha crecido en infraestructura, número y tipo de usuarios, aumento de centrales generadoras y diferentes formas de generación [1]. Este crecimiento disminuye la robustez y la confiabilidad del sistema, lo que puede producir caídas de tensión, o en el peor de los casos colapsos de tensión (apagones). El fenómeno asociado a este tipo de eventos indeseables en la red es conocido como inestabilidad de tensión.
Un sistema de potencia en un punto de operación dado se considera estable si, después de una perturbación, la tensión de los diferentes nodos permanece cerca a valores de equilibrio, es decir, tiende a regresar a valores nominales. Si, por el contrario, después de la perturbación, la tensión se aleja del punto de operación por debajo de límites aceptables, se considera que el sistema es inestable [2].
Debido a los aspectos ya mencionados y a que el sistema se encuentra operando cerca de sus límites [3], el problema de estabilidad de tensión es estudiado por los operadores de red a la hora del planeamiento y la operación del sistema [4].
Con el objetivo de entender y resolver el problema de estabilidad de tensión se han propuesto diferentes metodologías, la mayoría de las cuales tienen un alto costo computacional [4], [5]. El análisis de la estabilidad de tensión en un sistema comprende tanto aspectos estáticos como dinámicos. El análisis estático determina la cercanía del sistema con los límites de estabilidad, mientras que el enfoque dinámico analiza la trayectoria recorrida por los estados del sistema eléctrico y las posibilidades de llegar a la inestabilidad [6]. Las técnicas analíticas estáticas y dinámicas para la solución del problema de estabilidad de tensión consumen mucho tiempo, lo que las hace inadecuadas para aplicaciones en línea e impide a los operadores de red implementar acciones preventivas o correctivas a su debido tiempo [7].
En la actualidad, uno de los principales objetivos en el estudio de la estabilidad de tensión consiste en desarrollar un método computacional, que pueda evaluar los límites de estabilidad de tensión en línea. Se plantea entonces un modelo para determinar los márgenes de estabilidad basado en redes neuronales artificiales, las cuales en la actualidad se emplean con frecuencia para tratar de resolver problemas altamente no lineales como el mencionado. Para el entrenamiento de la red neuronal se emplean como entradas las variables obtenidas en los flujos de carga, y como salidas los resultados obtenidos por medio del cálculo del margen de energía [1], [6], [8].
2. Estabilidad de tensión y Margende energía
Una manera de establecer un criterio de estabilidad de voltaje se basa en verificar que los niveles de tensión en cada nodo del sistema sean aceptables, antes y después de ocurrida una perturbación. Se deben, por tanto, establecer márgenes o distancias que permitan predecir la verdadera condición de operación.
Con el fin de monitorear los rangos de tensión sobre los cuales está operando el sistema, se han planteado diversos métodos para generar índices que predigan la proximidad que guarda el sistema con respecto al punto de operación crítico. En particular, en este artículo se utiliza el método de funciones de energía para encontrar dichos índices, conocidos como índices de estabilidad de tensión, los cuales son las salidas deseadas de la red neuronal [6].
2.1 Margen de energía como indicador de estabilidad de tensión
El método de funciones de energía está basado en el uso del método directo de Lyapunov, el cual provee un medio para asegurar la estabilidad de un sistema descrito a través de ecuaciones diferenciales no lineales, similar al modelo que representa el sistema de potencia para el análisis de estabilidad de tensión.
La expresión del margen de energía en función del sistema se deriva de un sistema radial simple y se puede generalizar para un sistema de n nodos.
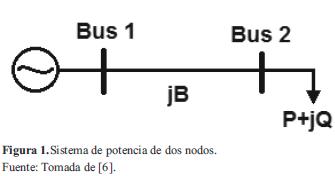
Considerando el sistema de dos nodos de la figura 1, donde el nodo 1 se toma como nodo slack de tensión 1 p.u., mientras que el nodo 2 se encuentra conectado a una carga constante del tipo PQ [6]. Las ecuaciones algebraicas que muestran el flujo de potencia del sistema están dadas por las ecuaciones (1) y (2):
donde,
V : es la magnitud de la tensión en la barra 2.
α= δ2-δ1: es la diferencia entre los ángulos de fase entre el nodo 2 y el nodo 1.
Multiplicando a ambos lados de la ecuación (2) por V-1, se obtiene la ecuación (3):
El margen de estabilidad basado en funciones de energía que indica la vulnerabilidad del sistema ante una perturbación de tensión, se obtiene integrando la función compuesta de las ecuaciones (1) y (3), es decir, f (α,V) y g (α,V), tomando como límite inferior el punto de operación en estado estable xs= (αs, Vs), y como límite superior una solución particular de bajo voltaje del flujo de carga xu(αu, Vu) como se muestra en la ecuación (4) [6].
A medida que la carga en el sistema aumenta, las dos soluciones xsy xuse acercan, y por tanto el margen de energía E disminuye en forma constante. El límite del nivel de carga en el cual xsy xuse unen y el margen de energía se reduce a cero representa el punto de inestabilidad de tensión.
Al extender estas expresiones a un sistema de n nodos se tiene que:
A partir de la ecuación (5) y la ecuación (6), la función de energía para n nodos se define como:
La función de energía, ecuación (7), muestra los pesos de la barrera de potencial entre la solución operable y la solución de bajo voltaje. Cuando los parámetros del sistema (cargas y generación) se mueven hacia el punto de inestabilidad de tensión, se disminuyen las soluciones de bajo voltaje [6].
investigación
3. Predicción del margen de Estabilidad usando redes Neuronales artificiales
El método de margen de energía puede establecer los márgenes de estabilidad, sin embargo este se encuentra limitado por el tiempo computacional. Debido a esto se deben considerar otras alternativas para el cálculo de los márgenes de estabilidad, entre las cuales se encuentran las tecnologías basadas en inteligencia artificial. Las ANN son una de las técnicas inteligentes más utilizadas actualmente.
La solución del flujo de carga del sistema entrega magnitudes de tensión, ángulo de la tensión, potencia real y potencia reactiva en el punto de operación inicial en todos los nodos del sistema. Se puede utilizar cualquier combinación de datos como entradas; para este caso, se utilizaron las potencias activas y reactivas inyectadas en todos los nodos del sistema para una condición particular de carga. La salida de la red es el margen de energía.
La red se entrenó bajo diferentes condiciones de carga, obteniendo así diferentes márgenes de energía. Después del entrenamiento la red debe ser capaz de determinar el margen de energía para cualquier condición de carga del sistema, esto servirá como un indicador para establecer la proximidad del sistema al límite de estabilidad de tensión.
3.1 Preparación de datos de entrenamiento
Se generan puntos de operación aleatorios sobre el sistema en estado estable, por medio de perturbaciones en la potencia activa y reactiva de cargas y generadores [8]. Se usa el siguiente modelo para generar los datos de entrada aleatorios para el flujo de carga:
Para nodos de carga
Para nodos de generación
Para los incrementos ΔPL , ΔQL , ΔQL , ΔPG , se establece en ±30% y ΔVG de todos los generadores y nodos de carga se establece en ±3%. ε es una variable uniformemente distribuida entre 0 y 1 [8].
El conjunto de puntos de operación iníciales generado usando las ecuaciones (8), (9), (10) y (11), se debe verificar mediante un flujo de carga, para garantizar que cada caso se encuentra en una zona factible de operación. Los casos que resulten aptos después del proceso de verificación se almacenan y se usan como vectores de entrada para el entrenamiento de la red. Las salidas objetivo de la red neuronal, serán los valores correspondientes al margen de estabilidad de tensión para cada caso, los cuales se generan usando la función de energía de la ecuación (7), en donde las soluciones de baja tensión se hallan usando la metodología mostrada en la siguiente sección [8].
3.2 Cálculo de soluciones de bajo voltaje Viu
Las ecuaciones del flujo de carga en el nodo i en un sistema de n nodos pueden ser expresadas en coordenadas rectangulares así [6]:
donde
Yij =(Gij -jBij ): son los ij elementos de la YBUS
Si =(Pi + jQi ): es la potencia compleja en la barra i
Vi =(ei + jf i ): es la tensión en la barra i
Las ecuaciones (12) y (13) se pueden reescribir como:
donde
De las ecuaciones (14) y (15) se remplaza por:
donde
Sustituyendo la ecuación (18) en la ecuación (14), se tiene que:
donde
La solución de ecuación (21) se encuentra en la ecuación (25):
Reemplazando las ecuaciones (16), (17), (19) y (20) en las ecuaciones (22), (23) y (24), se puede resolver la ecuación (25), la cual tiene dos soluciones, una para la raíz positiva y otra para la raíz negativa. fi puede ser obtenido sustituyendo ei en la ecuación (14). Así, se tienen dos soluciones Vsi =(esi, fsi ) y Vui =(eui, fui ) .
3.3 Diseño de la red neuronal
La red neuronal propuesta debe relacionar la condición de operación del sistema de potencia con el margen de estabilidad de tensión. La red neuronal diseñada consta de una capa de entrada, dos capas ocultas y una capa de salida. Se probó la topología de la red para diferente número de neuronas, esto con el fin de que las neuronas en las capas ocultas se eligieran de tal forma que el error de validación fuese bajo. Para el entrenamiento de la red se utilizó el algoritmo de gradiente descendente [9], [10].
Como entradas de la red para este caso se utilizaron las potencias activas y reactivas, la salida de la red es el margen de estabilidad calculado; la red neuronal se implementó usando el toolbox Neural Networks de Matlab [3], [11].
3.4 Medidas de desempeño
Se pueden usar dos formas para evaluar el rendimiento de la red sobre los datos de validación, uno es el error medio absoluto, el otro es el error máximo [1]:
y0
donde
yi
: es el margen de estabilidad objetivo obtenido por medio del margen de energía.
M: es el margen de estabilidad de tensión estimado por medio de las ANN
: es el número de casos probados
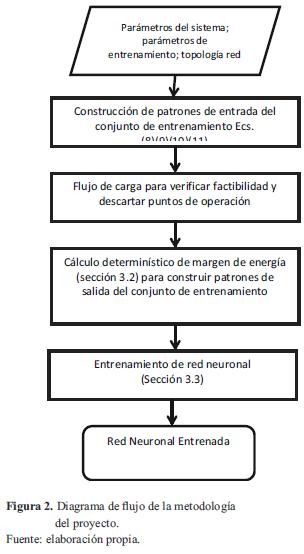
4. Metodología
El sistema analizado es el que se muestra en la figura 1, su estudio de estabilidad se realizó como se describe a continuación:
- Se simuló el sistema de la figura 2 para varios casos, aumentando y disminuyendo la carga y la generación, tal y como se describe en la sección 3.1 y mediante las ecuaciones (8), (9), (10) y (11).
- Se construyó una base de datos que contiene la potencia activa y reactiva del sistema para cuando se encuentra en estado estable y para cuando se encuentra en estado inestable desde el punto de vista de la tensión.
- Luego se aplicó el procedimiento para hallar el margen de energía que se muestra en la sección 3.2.
- Se estableció una red neuronal con un número de capas y neuronas determinado según la sección 3.3. Esta tiene como fin estimar el margen de energía del punto 3 teniendo como datos la potencias activas y reactivas del punto 2.
- Se tomó un conjunto de datos para validación y otro para entrenamiento de la red neuronal.
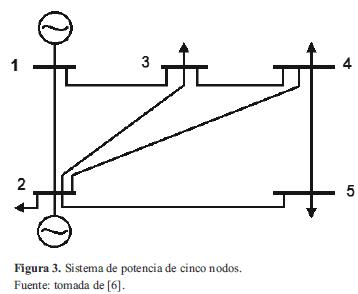
5. Resultados
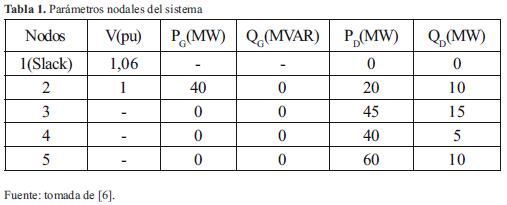
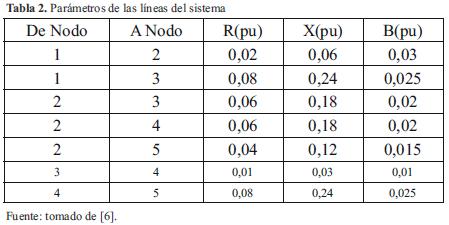
En esta sección se presentan los resultados obtenidos en simulación probados en el sistema de 5 nodos de [6], el sistema simulado se presenta en la figura 3. Para entrenar la red se tomaron las potencias activas y reactivas inyectadas en todos los nodos, la tabla 1 muestra los parámetros nodales del sistema y la tabla 2 muetsra los parámetros de las líneas del sistema.
Se entrenó una red neuronal de dos capas ocultas, para las cuales se tomó una neurona para cada capa, luego se aumentó el número de neuronas en cada capa oculta de uno en uno hasta llegar a diez, este aumento se realizó de manera independiente para cada capa. Se consideró un alto número de épocas debido a la variabilidad de los datos del margen en energía. Se tomó 50 % de los datos para entrenamiento y el otro 50 % para validación.
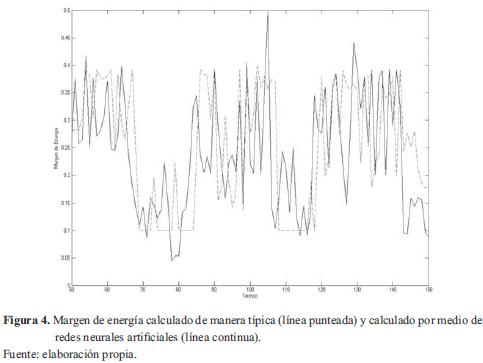
La figura 4 muestra el margen de energía calculado por medio del método habitual y calculado por medio de redes neuronales. Se puede ver cómo el error entre ambos márgenes es pequeño, a pesar de que las variaciones son altas.
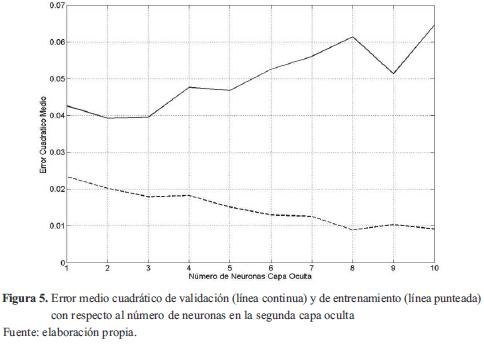
En la figura 5 se puede observar cómo el mínimo error de validación se encuentra cuando hay dos neuronas en la segunda capa oculta, pero el error de entrenamiento allí puede lograr ser menor. Como al pasar de dos a tres neuronas el error de validación no se ve afectado visiblemente, la simulación se hace para tres neuronas debido a que se presenta una mejora en el error de entrenamiento. Después de tres neuronas, el error de validación empieza a aumentar a pesar de que la red sigue aprendiendo, pero pierde generalidad con respecto a los datos desconocidos.
Para calcular el error de estimación de la red neuronal con respecto a la base de datos, se utilizan la ecuación (26) y ecuación (27), y se tiene que:
El error máximo que presenta la red sobre los datos de validación es de 4,81 %, como muestra la ecuación (29), el cual es bajo, dada la variabilidad en los datos. El error medio dado en la ecuación (28) tampoco excede el 1 %.
6. Conclusiones
Se comprueba para este problema en específico que las redes neuronales con dos capas ocultas muestran un mejor desempeño que con una sola capa, esto debido a que el margen de energía es altamente no lineal.
El uso de esta metodología utilizando datos simulados muestra eficiencia. Si se usara a partir de datos reales sería de mayor utilidad para la industria del sector eléctrico.
Otras técnicas de aprendizaje más poderosas pueden llegar a entregar una mejor estimación.
7. Financiamiento
Agradecimientos especiales a CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico de Brasil), y a Colciencias con su programa jóvenes investigadores e innovadores "Virginia Gutiérrez de Pineda", por el apoyo económico que permitió el desarrollo de esta investigación.
Referencias
[1] A. A. El-Keib, X. Ma, "Application of Artificial Neural Networks in Voltage Stability Assessment", IEEE Transactions on Power System, vol. 10, no.4, pp.1890-1896, Nov.1995.
[2] S. Kamalasadan, A.K. Sritvastava and D. Thurkaram, "Novel Algorithm for Online Voltage Stability Assessment Based on Feed Forward Neural Network", Power Engineering Society General Meeting, IEEE, pp.7-15. Montreal, 2006.
[3] B. Jesyasurya, "Artificial Neural Network for On-Line Voltage Stability Assessment", Power Engineering Society Summer Meeting, Seattle, vol.4, pp. 2014-2018, 2000.
[4] W. Nakawiro, and L. Erlich, "Online Voltage Stability Monitoring using Artificial Neural Network", DPRT Conference, Nanjing, China, Apr. 2008.
[5] M.B. Keskin, Continuation Power Flow and Voltage Stability in Power System, M.S. Thesis in Electrical and Electronics Engineering, Middle East Technical University, Ankara, Turkey, Sept. 2007.
[6] V.R. Dinvahai, and S.C. Srivastava, "ANN Based Voltage Stability Margin Prediction", Power Enginneering Society Summer meeting, Vancouver, Canada, vol. 2, pp. 1275-1280, Jul. 2001.
[7] M. La Scala, M. Trovato and F. Torelli, "A Neural Network-based for Voltage Security Monitoring", IEEE Transactions on Power System, vol. 11, no. 3, pp. 1332-1341, Aug. 1996.
[8] Q. D. Zhou, "Online Voltage Stablity Prediction and Control Using Computational Intelligence Technique", Ph.D. dissertation, Universidad de Manitoba, Winnipeg, Canada, 2010.
[9] Christopher M. Bishop, Pattern recognition and Machine Learning. Cambridge, U.K., Springer, 2006.
[10] P. J. Abrao, A.P. Alves da Silva and A.C. Zambroni de Souza, "Rule Extraction from Artificial Network for Voltage Security Analysis", Proceedings of the 2002 International Joint Conference on Neural Networks, 2002, IJCNN '02, Honolulu, Hawaii, vol. 3, pp. 2126-2131, May. 2002.
[11] J. A. Momoh, L.G. Dias and R. Adapa, "Investigation of Artificial Neural Networks for Voltage Stability Assessment", Intelligent Systems for the 21st Century, IEEE International Conference on IEEESystems, Man and Cybernetics, Washington, USA, vol.3, pp. 2188-2192, Oct. 1995.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.