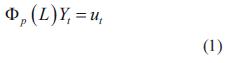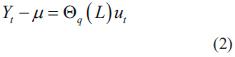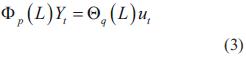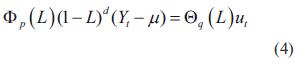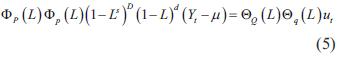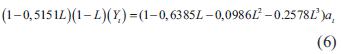DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2013.3.a05Publicado:
01-07-2013Número:
Vol. 17 Núm. 37 (2013): Julio - SeptiembreSección:
InvestigaciónModelado de pérdidas en una transmisión de video por medio de series de tiempo ARIMA y SARIMA
Palabras clave:
ARIMA, lenguaje R, modelos de tráfico, predicción, SARIMA. (es).Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Modelado de pérdidas en una transmisión de video por medio de series de tiempo ARIMA y SARIMA
Modeling video transmission losses using SARIMA and ARIMA models
Danilo Alfonso López Sarmiento1, Carlos Andrés Martínez Alayón2, Edward Johannes Uribe Sierra3, Nicolas Carlos Eduardo Torres Vallejo4
1Ingeniero Electrónico, Magíster en Teleinformática. Docente e investigador de la Universidad
Distrital Francisco José de Caldas. Bogotá, Colombia. Contacto:
dalopezs@udistrital.edu.co
2Ingeniero Electrónico. Estudiante de la Maestría en Ciencias de la Información y las
Comunicaciones de la Universidad Distrital Francisco José de Caldas. Bogotá, Colombia.
Contacto: camartineza@correo.udistrital.edu.co
Fecha de recepción: 26 de septiembre de 2012 Fecha de aceptación: 21 de mayo de 2013
Resumen
Este artículo presenta los resultados obtenidos al representar las pérdidas en una transmisión de video digital por medio de modelos ARIMA y SARIMA, siguiendo la metodología Box-Jenkins y haciendo uso del lenguaje de programación R para la estimación de los coeficientes. Se hizo una comparación de estos dos modelos con el fin de determinar cuál es el más apropiado para representar la serie original y estimar valores futuros, encontrando que el modelo SARIMA presenta un mejor ajuste y predice de mejor manera el comportamiento de la misma.
Palabras clave: ARIMA, lenguaje R, modelos de tráfico, predicción, SARIMA.
Abstract
This paper presents the results obtained by representing losses in a digital video transmission using ARIMA and SARIMA models. The experiments were conducted following the Box-Jenkins methodology and using programming language R for the estimation of coefficients. A comparison of these two models was conducted in order to determine what the most appropriate model was in order to represent the original series and estimate future values. The findings indicate that SARIMA provide better matching and better prediction of the original data set.
Key words: ARIMA, R language, traffic models, forecasting, SARIMA.
1. Introducción
En el auge que tienen actualmente las redes de datos, es de vital importancia el desarrollo de modelos que permitan entender y representar de mejor manera su funcionamiento. Entre las diferentes opciones que existen para modelar los distintos tipos de tráfico se destacan los modelos estadísticos, ya que representan de una mejor manera procesos estocásticos mediante herramientas probabilísticas y permiten tratar la no continuidad del tráfico de datos (paquetes, ráfagas y sesiones) [1]. Por esto las series de tiempo y los métodos para modelarlas han comenzado a utilizarse en el análisis de tráfico, dadas sus ventajas para representar y predecir procesos que fluctúan aleatoriamente con una referencia temporal conocida.
En el curso del desarrollo de una plataforma de servicios streaming dentro de la red RITA de la Universidad Distrital [2] y más puntualmente en el proceso de implementación de un segmento de red para el acceso a un repositorio digital de video [3], surgió la necesidad de realizar un análisis de las principales variables asociadas al tráfico de datos con el fin de modelar y caracterizar el desempeño del canal. Teniendo presente esta necesidad y sabiendo que para servicios de red basados en transmisiones multimedia en tiempo real los paquetes faltantes afectan directamente la experiencia de usuario, se propone la representación de las pérdidas en dicho canal mediante series de tiempo y su modelado por medio de procesos ARIMA y SARIMA, con el fin de realizar un análisis formal del tráfico generado durante una transmisión de video. Para la obtención de dichos modelos se hará uso del lenguaje y entorno de programación "R" y se seguirá la metodología Box-Jenkins.
De acuerdo a lo anterior, en las siguientes secciones se hará una breve exposición de los conceptos fundamentales para el análisis de las series de tiempo y los procesos ARIMA. Posteriormente se utilizará la metodología mencionada para el ajuste de los modelos expuestos a una muestra de las pérdidas en el canal y se realizarán predicciones de la serie con los parámetros obtenidos con el objetivo de comparar los resultados y determinar la idoneidad de cada uno de ellos para representar el comportamiento de la serie original. Por último, se elegirá el que presente mejores resultados como descripción formal de las pérdidas durante la transmisión.
2. Fundamentos
2.1 Series de tiempo
Las series de tiempo son secuencias de muestras de una variable tomadas típicamente en instantes sucesivos y espaciados uniformemente, que en el presente documento se utilizarán para la representación de las pérdidas en el canal, dada la dependencia temporal que presentan las ráfagas de datos en una transmisión de video. Estas series son herramientas estadísticas utilizadas para explicar (y en algunos casos predecir) el valor que toma en un momento de tiempo determinado la variable analizada.
2.2 Modelado de series de tiempo
Las series de tiempo por sí solas se reducen a una simple organización temporal de muestras que permiten la descripción de algunos parámetros básicos de un proceso estocástico. Lo que realmente representa un gran aporte en el estudio de este tipo de series son las metodologías y los modelos matemáticos que se han desarrollado en torno a la descripción y predicción de variables aleatorias, en especial los modelos autorregresivos, de medias móviles y todos los que han derivado de la combinación de estos dos. A continuación se hace una breve descripción de algunos de los estándares trabajados a lo largo de la investigación. La notación utilizada es la siguiente:
• Yt: serie de tiempo que será analizada.
• ut: función de blanco con promedio cero y varianza constante.
• dyD: grados de diferenciación normal y estacional.
• Φp(L): polinomio de orden p del componente autorregresivo.
• Φp(L): polinomio de orden P del componente estacional autorregresivo.
• θq: polinomio de orden q del componente de medias móviles.
• θQ(L): polinomio de orden Q del componente estacional de medias móviles.
• S: periodo de la función si presenta estacionalidad.
• µ promedio de la función original sin diferenciar.
2.2.1 Modelo Autorregresivo (AR)p
Con este modelo, descrito en la ecuación (1), se expresa el valor actual de la serie como una función de los valores que tomó la misma en las p muestras anteriores ponderados por un factor y de una perturbación aleatoria presente.
2.2.2 Modelo de medias móviles (MA)p
Considera que el valor de la serie estacionaria se desplaza alrededor de un valor medio µ. Además supone que el desplazamiento de µ en el tiempo presente t es ocasionado por infinitas perturbaciones ocurridas en el pasado, ponderadas por un factor que mide la influencia de cada una de ellas en el valor presente de la serie. Su descripción matemática se plasma en ecuación (2).
2.2.3 Modelo ARMA
Como se muestra en la ecuación (3), este modelo representa una serie de tiempo como una combinación de los dos modelos anteriores:
2.2.4 Modelo ARIMA
Algunas series deben ser diferenciadas para eliminar tendencias o varianzas cambiantes y así obtener series estacionarias. El modelo ARIMA hace referencia a un sistema ARMA que se ha aplicado a una serie diferenciada. Así, se tiene la representación mostrada en ecuación (4) para el modelo.
2.2.5 Modelo SARIMA
Es autorregresivo e integrado de promedio móvil estacional, se basa en ARIMA, con algunos de sus coeficientes en cero y componentes adicionales para integrar el comportamiento estacional de la serie. SARIMA tiene la siguiente notación:
3. Metodología
Para la elección de los modelos descritos anteriormente se hará uso de la metodología Box-Jenkins [4l, la cual puede resumirse en tres pasos:
- Identificación y selección del modelo (estacionariedad, estacionalidad, componentes autorregresivos y de medias móviles).
- Estimación de los coeficientes que mejor se ajustan a los parámetros escogidos por medio de algoritmos computacionales.
- Validación del modelo obtenido.
Dado que el análisis propuesto se enfoca en la pérdida de paquetes sin incluir índices adicionales de desempeño del canal como latencia, jitter u otros, se eligieron las series de tiempo univariadas para la representación de los datos teniendo en cuenta que permiten analizar el comportamiento de la variable en sí misma sin pretender explicar los factores que influyen en esta. A continuación se presentan detalladamente los pasos que se siguieron en la obtención de los modelos ARIMA y SARIMA.
3.1 Organización de los datos
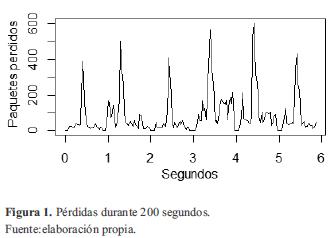
Para poder hacer una buena representación con series de tiempo se debe escoger un intervalo de tiempo que capture de alguna forma un comportamiento descriptivo para el patrón que se desea analizar. En econometría, por ejemplo, este problema depende generalmente de la periodicidad con la que se obtengan los datos (índices mensuales, anuales, trimestrales, etc.). En el tráfico de datos cada paquete transmitido porta encabezados que brindan información de manera casi continua, por lo cual se debe escoger un intervalo que arroje datos globales. En general, intervalos de tiempo muy cortos arrojarán comportamientos más puntuales, mientras que periodos muy largos harán énfasis en comportamientos más globales. Para el caso de estudio se analizaron las capturas obtenidas de una de las transmisiones de video generadas para el análisis de los parámetros de QoS del canal [3], y se tomaron las pérdidas por segundo durante 3,3 minutos (200 muestras), ya que al no tratarse de un canal congestionado no se tiene un tráfico constante y existen largos periodos de inactividad. Esto ayudará además a obtener una descripción matemática aproximada de las pérdidas como una variable de medición de la calidad de la transmisión de video.
Una vez organizados los datos, se almacenan en R como un objeto ts (time series) [6l, con una frecuencia de 34 muestras (frecuencia estacional de la serie obtenida al calcular el número promedio de muestras entre picos) y una referencia de inicio cualquiera, ya que no se sigue un índice diario, semanal, etc. (en este caso 0), y se procede a la representación gráfica de los mismos para observar la evolución de la variable a lo largo del tiempo. En la figura 1 se muestra la representación gráfica de la serie original.
Como se puede observar, a simple vista no es posible determinar la estacionariedad de la serie, ya que esta no presenta una tendencia clara ni una varianza definida, por lo cual se debe analizar más a profundidad las características de la misma.
3.2 Análisis de estacionariedad y estacionalidad
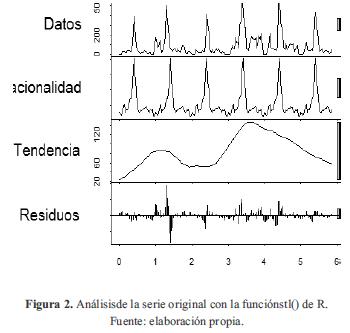
La figura 2 presenta el análisis de la serie creada con la función stl (serie, s.window="periodic") de R [7].
Esta función arroja cuatro gráficas en las que se plasman los datos, la componente estacional, la tendencia y los residuos entre las dos primeras. De la componente estacional -que se obtiene basándose en el número de promedio de retardos entre valores similares- se puede corroborar que la serie presenta un comportamiento cíclico cada 34 muestras. Sin embargo, como se puede observar en la tercera gráfica (obtenida mediante filtrado por promedios móviles para un N igual a la frecuencia indicada en el objeto "ts"), no es posible establecer si la serie es estacionaria o no, ya que no se obtiene una media constante a través del tiempo ni una tendencia creciente o decreciente. No obstante, adicionalmente al análisis de tendencia y de varianza, también es posible realizar diferenciaciones iteradas para observar cuál presenta una menor desviación estándar y así determinar el valor de "d" [9].
En la tabla 1 se presentan los valores de la varianza para diferentes grados de diferenciación de la serie original:
Como se puede observar, la varianza comienza a aumentar luego de la segunda diferenciación. Como se menciona en [8l, se debe evitar el sobre-diferenciar la serie original y eliminar información valiosa que se manifestaría en la función de autocorrelación, ya que en un caso de sobre diferenciación las autocorrelaciones se hacen aún más complicadas de analizar, el modelo pierde parsimonia, se incrementa la varianza y se pierden observaciones. Por lo anterior, se determina que la serie se debe diferenciar una vez.
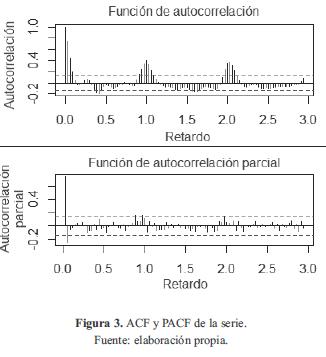
La estacionalidad de la serie puede comprobarse observando sus funciones ACF (Función de Auto-correlación) y PACF (Función de Autocorrelación Parcial), las cuales se muestran en la figura 3.
Como se puede observar, estas funciones arrojan valores significativos en los retardos cercanos a 34 y demás múltiplos de la frecuencia, lo cual muestra el comportamiento periódico de la serie. Además, como se describe en la siguiente sección, a partir de estas gráficas se establecerá el orden de los demás parámetros de cada modelo.
3.3 Determinación de los parámetros del modelo
De la figura 3 se observa también que dentro de los periodos de estacionalidad (entre los retardos múltiplos de la frecuencia) la autocorrelación más significativa se da con los retardos 1, 2, y con algunos valores adicionales en los retardos 3, 13 y 14, mientras que la autocorrelación parcial solo arrojó un valor considerable para el primer retardo. De las anteriores observaciones, se obtienen como candidatos los modelos AR(36) (tomando dos periodos y 3 retardos en el segundo ciclo), MA(34) (tomando dos periodos) y su combinación ARMA(36,34). Sin embargo, como se explica en [9l, el comportamiento observado en la gráfica también podría hacer referencia a una firma AR(1), ya que la ACF decae de forma relativamente lenta y la PACF presenta un corte abrupto en el primer retardo, lo cual podría indicar que la autocorrelación con el primer retardo se propaga a retardos superiores, por lo cual otro candidato a considerar es el AR(1). No obstante, no se espera que este modelo represente de buena forma el comportamiento de la serie, ya que por su simplicidad no captura la relación temporal del valor presente con valores anteriores.
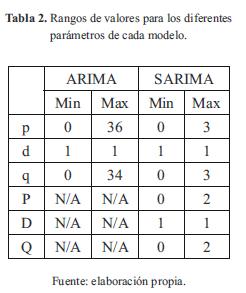
Para la componente estacional de las pérdidas, se realiza el análisis de la serie transformada por medio de una diferenciación de orden 34. Debido a esta diferenciación para incluir la estacionalidad en el modelo SARIMA, se tomará el valor 1 para D. Tanto la ACF como la PACF presentan valores significativos para los retardos estacionales 1 y 2. Del análisis descrito se obtienen modelos candidatos con parámetros SAR(2) y SMA(2), que adicionalmente (incluyendo el análisis hecho para los modelos ARIMA dentro de los periodos de estacionalidad) tienen componentes AR(3) y MA(3). Con lo anterior se tienen los siguientes valores o rangos para los parámetros especificados:
De las posibles combinaciones obtenidas al variar los parámetros descritos en la Tabla 2 se obtendrían 1224 modelos ARIMA y 144 SARIMA, muchos de los cuales arrojarían resultados similares a otros teniendo en cuenta que solo varían algunos coeficientes. Por lo anterior se limitó el rango de las variables p y q para tomar los valores 0 a 3 y 34 a 36 (valores importantes en la función de autocorrelación), con lo cual se obtienen 49 posibles modelos ARIMA a analizar.
3.4 Estimación de los coeficientes y validación de los modelos
Para la estimación de los coeficientes se utilizaron las funciones Arima() y auto.arima() del paquete forecast de R, las cuales realizan las iteraciones requeridas con base en los valores especificados de los parámetros p, d, q, P, D y Q para obtener los coeficientes de cada uno de los modelos [10l, además de arrojar los cálculos de la función AIC con la cual se puede validar la efectividad de cada uno para representar la serie especificada. La predicción de valores futuros conocidos se hizo por medio de la función forecast() del mismo paquete, que hace la predicción automática basado en el objeto Arima y el número de valores especificados.
4. Resultados
Para la evaluación de los modelos obtenidos se tuvieron en cuenta los factores de ajuste, predicción y complejidad. El ajuste se midió por medio del Criterio de Información de Akaike(o AIC por sus siglas en inglés) [12], el cual mide la bondad de ajuste de un modelo determinado a un conjunto de datos conocidos. Este índice se utilizará como criterio para determinar el mejor ajuste para la serie tratada [13]. La predicción se medirá por medio del error medio cuadrático (o RMSE por sus siglas en inglés) entre los datos originales y los obtenidos por el modelo. Con esta medida se podrá comparar qué tan alejadas están las predicciones de los datos reales. Finalmente, se evaluó la complejidad de los modelos teniendo en cuenta el número de coeficientes resultantes y los recursos computacionales que requirieron.
4.1 Ajuste
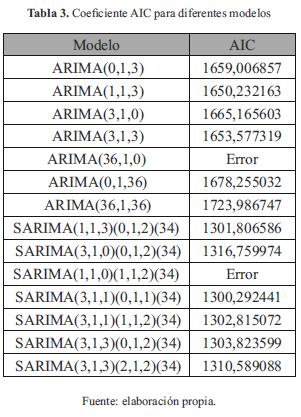
Se analizó un total de 193 modelos variando los parámetros p, q, P y Q. De los 49 modelos ARIMA que se procesaron, el 22 % (11 modelos) presentó errores de convergencia (no se pudieron obtener los coeficientes debido a que la función "optim" usada para su cálculo realiza iteraciones que en ocasiones generan valores catalogados como infinitos) mientras que el porcentaje de errores para los 144 modelos SARIMA analizados fue de 28 % (41 modelos). El lenguaje R calcula el índice AIC al generar cada modelo y este queda almacenado como una de las propiedades del mismo. En la tabla 3 se condensan los principales resultados obtenidos para los diferentes modelos.
Los modelos con un menor AIC presentan una mejor bondad de ajuste, y por tanto una mejor representación de los datos. El modelo ARIMA que presentó el mejor ajuste por AIC fue el ARIMA(1,1,3), cuya descripción matemática se plasma en la ecuación (6) (cabe anotar que estas ecuaciones siguen la notación descrita en el marco teórico):
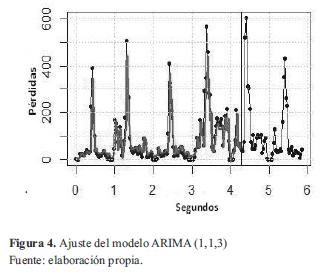
El ajuste hecho por R para este modelo se muestra en un color más claro dentro de la figura 4 junto a la serie original (en negro).
Como se puede observar, el ajuste se hace sobre una parte de la serie original (primeras 146 muestras) teniendo en cuenta que la parte restante se utilizará para hacer la predicción.
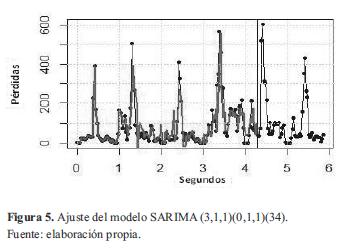
Por otro lado, el modelo SARIMA con mejor AIC fue el SARIMA(3,1,1)(0,1,1)(34), el cual queda descrito por la ecuación (7).
La figura 5 muestra el ajuste de este modelo en un tono más claro junto a la serie original (en negro).
Aunque gráficamente los dos modelos presentan similitudes, matemáticamente el modelo SARIMA presenta un mejor ajuste, ya que su AIC fue de 1300,29 frente al valor de 1650,23 obtenido para el modelo ARIMA. En general, todos los modelos SARIMA presentaron mejores índices AIC, con un valor promedio de 1318,22 frente a los modelos ARIMA, que presentaron un AIC promedio de 1675,03.
4.2 Predicción
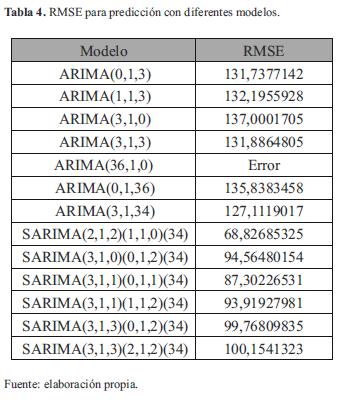
En la siguiente etapa se generó una predicción de un conjunto de datos y se comparó la capacidad de los modelos para estimar los datos reales. Como se mencionó anteriormente, se ajustaron los modelos sobre las primeras 146 muestras, luego de lo cual se hizo una predicción de las siguientes 74. En la tabla 4 se muestran algunos de los modelos y el error cuadrático medio que presentó su predicción frente a los valores reales de la serie original.
Como se puede observar, las predicciones realizadas con modelos SARIMA presentaron errores medios cuadráticos menores a los que se obtuvieron con ARIMA de orden superior.
Lo anterior se traduce en mejores predicciones de los datos reales, ya que los valores estimados están en promedio más cerca de la serie original.
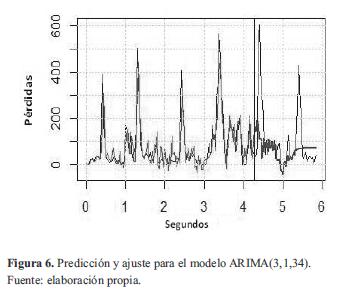
La predicción hecha por este modelo se muestra en la figura 6 (representado con el color más oscuro a partir de los 4,2 seg) junto a su ajuste y la serie original (en color más claro).
Aunque este modelo estimó de buena manera el comportamiento aleatorio de los valles de la función original hasta aproximadamente unas 50 muestras (luego de las cuales muestra una línea recta), no logró reproducir el comportamiento periódico de la serie original, que se traduce en los picos que se presentan cada 34 muestras.
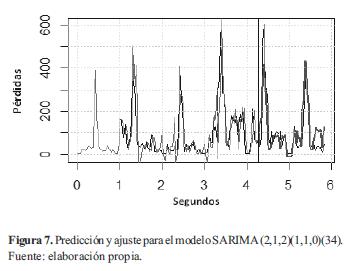
Por otro lado, el modelo SARIMA que realizó la mejor predicción fue el SARIMA(2,1,2)(1,1,0)(34) (con un RMSE de 68,82) que queda descrito por la ecuación (9).
La ecuación (8) describe el modelo ARIMA (3,1,34) que presento el mejor RMSE (127,11) entre los ARIMA.
En la figura 7 se muestra con el color más oscuro la predicción hecha a partir de los 4,2 seg; y el ajuste junto con la serie original en un tono más claro.
Este modelo predijo de mejor manera los valores conocidos de la serie original (su RMSE fue casi la mitad del obtenido con el mejor modelo ARIMA), ya que al tener componentes estacionales puede capturar el comportamiento periódico de la misma y por tanto, reproducir los picos que se presentan debido a las ráfagas en la transmisión.
4.3 Complejidad
Como se menciona en [8l, la parsimonia es también un factor a evaluar entre los modelos, ya que uno con demasiados parámetros no presenta facilidad en su tratamiento. Por el contrario, el hecho de obtener mejores resultados con modelos más simples, significa que se han capturado las propiedades intrínsecas de la serie de tiempo que se analiza. El cálculo de los coeficientes de los modelos ARIMA de orden superior requiere muchos más recursos computacionales que los SARIMA equivalentes. En una máquina con un procesador que opera a una frecuencia de 3.2GHz en cada uno de sus seis núcleos, el cálculo de los 37 coeficientes del modelo ARIMA(3,1,34) tomó 1 minuto y 40 segundos frente a los 3,94 segundos que tomó el cálculo de los cinco coeficientes del SARIMA(2,1,2)(1,1,0) (34), que como se mostró anteriormente realizó una mejor predicción. Lo anterior demuestra la idoneidad de los modelos SARIMA frente a los modelos ARIMA de orden superior en la representación de la serie original.
5. Conclusiones
Los modelos ARIMA, aun cuando consten de parámetros autorregresivos y de medias móviles relacionados a retardos alejados, no capturan el comportamiento periódico de las series de tiempo con frecuencias relativamente grandes.
Bajo ciertas condiciones de tráfico, como la que se presenta en la transmisión de un video autocorrelacionado y con ráfagas periódicas de datos, los modelos SARIMA permiten representar de manera óptima el comportamiento de las pérdidas y otras variables relacionadas.
Los modelos ARIMA de orden superior, aunque en teoría pueden capturar las características de una serie de tiempo de forma similar a los modelos SARIMA de orden estacional equivalente, requieren mayores recursos para su cálculo y mayor complejidad en su tratamiento, lo cual les resta parsimonia y por tanto, viabilidad como modelos de representación de tráfico de datos.
Referencias
[1] T. M. Chen, "Network Traffic Modeling", in The Handbook of Computer Networks, 1st ed. vol. 3, B. Hossein,Wiley: Ed.Berkeley, 2007.
[2] R. Ferro, D. López, y C. Martínez, "Desarrollo de una plataforma para servicios Streaming y repositorio digital multimedia mediante aplicaciones Multicast IPv6 para estructura de una Red de Investigaciones y Tecnología Avanzada en la Universidad Distrital empleando software libre y modelado ITU-TMN." Trabajo de pregrado, Facultad de Ingeniería, Universidad Distrital Francisco José de Caldas, Bogotá, 2012.
[3] N. Torres, y E. Uribe, "Diseño y análisis de conectividad de una plataforma multicast ipv6 basada en un entorno virtual 3d para un repositorio de video streaming sobre la red rita-ud mediante pruebas de QoS", Trabajo de pregrado, Facultad de Ingeniería, Universidad Distrital Francisco José de Caldas, Bogotá, 2012.
[4] E. Uribe, "Creación de un metaverso en OpenSim para la Universidad Distrital dentro de la red RITA-UD", Documento no publicado, 2012.
[5] G. Box, and G. Jenkins, Time series analysis: Forecasting and control. Revised Edition. Oakland, California: Editorial Holden-Day, 1976.
[6] B. Ripley, "Time Series in R 1.5.0", R. News, vol. 2. ED-1, pp. 2-5, Jun. 2002.
[7] R. Cleveland, W. Cleveland, J. McRae, and I. Terpenning. "STL: A Seasonal-Trend Decomposition Procedure Based on Loess", Journal ol Olficial Statistics, vol. 6,no. 1, pp. 3-73, Jun. 1990.
[8] O. Salcedo, C. Hernández, y A. Escobar, "Diseño de un modelo de tráfico a través de series de tiempo para pronosticar tráfico Wimax", Revista cientifica y tecnológica de la Facultad de Ingeniería UDFJC, vol.12, no.1, Jun. 2007.
[9] R. Nau, (2005, May 15), Decision 411 Forecasting (Curso de Duke University's Fuqua School of Business) [En línea], consultado en agosto 10 de 2012, disponible en: http:www.duke.edu∼rnau/411arim.htm.
[10] J. Carroll, C. Hernández y G. Puerta, "Comparación del modelo FARIMA y SFARIMA para obtener la mejor estimación del tráfico en una red Wi-Fi", Tecnura, vol. 16, no. 32, pp. 84-90, Jun.2012.
[11] P.S.P.Cowpertwait, and A.Metcalfe, Introductory Tim Series with R. Springer Series in Statistics, New York: Springer, 2009.
[12] A. Hirotugu, "A new look at the statistical model identification". IEEE Transactions on Automatic Control, vol. 19, no. 6, pp. 716-723, 1974.
[13] P. Brockwell, and R. Davis, Time Series: Theory and Methods, New York: Springer, 1986.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.