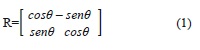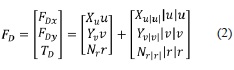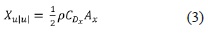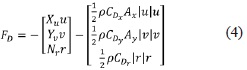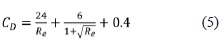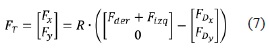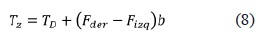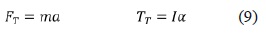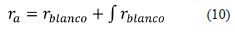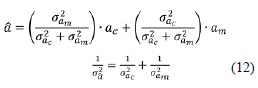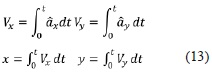Sistema de navegación para un robot limpiador de piscinas

Sistema de navegación para un robot limpiador de piscinas

Navigation system for a swimming-pool cleaner robot

Lorena Cardona Rendón¹, Paula Andrea Ortiz Valencia², Juan Sebastián Botero Valencia³

¹Ingeniera Mecánica, magíster en Ingeniería. Investigadora de la Universidad Nacional de Colombia. Medellín, Colombia. Contacto: lcardon0@unalmed.edu.co
²Ingeniera en Instrumentación y Control, magíster en Ingeniería. Docente e investigador del Instituto Tecnológico Metropolitano. Medellín, Colombia. Contacto: paulaortiz@itm.edu.co
³Ingeniero Electrónico. Investigador del Instituto Tecnológico Metropolitano. Medellín, Colombia. Contacto: juanbotero@itm.edu.co

Fecha de recepción: 1 de noviembre de 2012 Fecha de aceptación: 27 de agosto de 2013

Clasificación del artículo: investigación
Financiamiento: Instituto Tecnológico Metropolitano

Resumen

En este trabajo se desarrolló un sistema de navegación para estimar la posición, velocidad y orientación de un robot limpiador de piscinas que se quiere automatizar. Para el diseño del sistema de navegación se utilizó la técnica de mínimos cuadrados ponderados, que combina las medidas de un acelerómetro triaxial y un giróscopo, con la solución de las ecuaciones diferenciales que describen el comportamiento del robot. El sistema de navegación se probó sobre un modelo del robot elaborado en Simulink a partir de una reproducción tridimensional realizada en un software CAD (Autodesk Inventor). Al final se presentan los resultados concluyendo sobre la viabilidad del sistema de navegación para ser empleado en la tarea de automatización del robot limpiador de piscinas.

Palabras clave: estimación de estado, robot limpiador, SimMechanics, sistema de navegación.

Abstract

In this paper presents the development of a navigation system to estimate the position, velocity and orientation of a pool cleaner robot to be automated. We employ the weighted least-square technique for the design of the navigation system, which combines the noisy measurements of a triaxial accelerometer and a gyroscope with the solution to the differential equations that describe the robot's movement. The navigation system was tested using a (Simulink-based) model of the robot obtained from a tri-dimensional representation (built with CAD software – Autodesk Inventor). The final part of the paper presents the results and draws some conclusions about the feasibility of implementing the navigation system in the automation of a swimming-pool cleaner robot.

Keywords: State estimation, cleaning robot, SimMechanics, navigation system.

1. Introducción

La Liga de Natación de Antioquia (LNA) atiende 50000 usuarios anualmente en 12 piscinas del Complejo Deportivo Atanasio Girardot. Las labores de limpieza de estas piscinas son realizadas manualmente, lo que constituye una tarea tediosa, aburrida y poco eficiente para quienes la realizan, razón por la cual se busca su automatización.

Con el objetivo de automatizar la tarea de limpieza, la LNA adquirió recientemente un robot limpiador de piscinas, el cual no es efectivo, debido a que funciona de manera aleatoria, tipo de funcionamiento que constituye un factor común en el mercado de robots limpiadores de piscinas [1]. Efectuar una limpieza siguiendo una trayectoria aleatoria puede ser aceptable en una piscina pequeña, pero en una piscina de grandes dimensiones, como las que se tienen en la LNA, esta labor toma tiempos inmanejables sin garantías en la cobertura del área a limpiar. Por esto se propone, como solución al problema de la LNA, automatizar el robot limpiador adquirido por la institución para que realice las labores de limpieza en un tiempo óptimo, siguiendo una trayectoria predefinida. Como primer paso para la automatización de este robot, se busca diseñar un sistema de navegación que permita estimar el estado del robot en tiempo real, para realimentar un sistema de control.

Revisando el estado del arte en la navegación de vehículos subacuáticos, se encuentra que es un tema que está muy bien documentado para aplicaciones de exploración marina, operaciones de monitoreo en seguridad con aplicativos en tiempo real, y en la industria militar para patrullar zonas de alto riesgo y exploración en ambientes con condiciones especiales [2]. Pero estas labores son generalmente realizadas en amplias extensiones oceánicas o fluviales, de manera que los sensores usados para la navegación incluyen cámaras de exploración y GPS que son innecesarios en una labor de limpieza de piscinas. Por otra parte, si se hace una revisión del estado del arte de los robots limpiadores de piscinas, solo se encuentra un trabajo de aplicación directa de un sistema de control para un robo t [3]. La tarea de limpieza de piscinas es muy similar a la labor de limpieza de espacios terrestres, pero no se pueden aplicar los mismos sensores puesto que las condiciones subacuáticas son más exigentes y, en cuanto al desarrollo de un sistema de navegación, se deben tener en cuenta fuerzas hidrodinámicas, inexistentes en labores terrestres.

Lo que se pretende en este trabajo es desarrollar un sistema de navegación para el robot limpiador de piscinas adquirido por la LNA, para lo cual se asumirá la utilización de un acelerómetro triaxial y un giróscopo, y se aplicará la técnica de mínimos cuadrados ponderados. Aunque en los sistemas de navegación de robots subacuáticos es más común encontrar aplicaciones de filtros extendidos de Kalman [4], este algoritmo es muy sensible a las condiciones iniciales y su velocidad de convergencia puede ser más lenta [5], además de que la carga computacional es mayor debido a la necesidad de calcular la matriz jacobiana [6]. Por esto, la técnica de mínimos cuadrados recursivos es más simple y proporciona una alternativa más atractiva en este caso [7].

El diseño y prueba del sistema de navegación se realizará en un ambiente de simulación, con el propósito de probar su funcionamiento antes de realizar la compra y adaptación de los sensores al robot limpiador.

2. Metodología

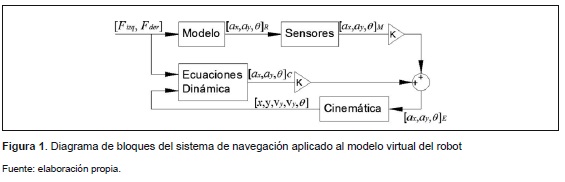
La forma como se pretende diseñar y probar el sistema de navegación se ilustra en la figura 1. Se construirá un modelo del robot con el objetivo de realizar pruebas en un ambiente de simulación. Paralelamente, se desarrollarán ecuaciones de la dinámica del robot, lo que permitirá predecir los valores de su aceleración y orientación. Esta predicción se combinará con la medida (simulada) de un acelerómetro triaxial y un giróscopo, usando la técnica de mínimos cuadrados ponderados. Con esto se logrará una estimación más precisa de los valores de estas variables, que luego se integrarán (cinemática) para obtener los valores de posición y velocidad del robot.

A continuación se explica la forma como se construyó cada una de las partes descritas en la figura 1.

2.1 Modelo del robot

El robot que se pretende automatizar es el Prowler 720 de Kreepy Krauly (figura 2). Este robot solo requiere una conexión eléctrica que se suministra con la fuente de alimentación de corriente directa de 130 W y su movimiento es aleatorio, impulsado a partir de un único motor que transmite su movimiento a una de las orugas del robot y que al mismo tiempo acciona un sistema de succión que remueve la suciedad del suelo.

Como primer paso para la automatización del robot, se vio la necesidad de incorporar otro motor para controlar de manera independiente la velocidad de las 2 orugas, y así lograr desplazamientos del robot en una trayectoria prediseñada. Aunque el robot no ha sido intervenido aún de manera física para integrar el otro motor, este sí se incorporó en el modelo.

Para obtener un modelo del robot, se recurrió a un software de modelado en 3D (Autodesk Inventor ® 2011), en el cual se construyeron los modelos tridimensionales de cada una de las partes que componen el robot, a partir de medidas realizadas sobre él, usando un flexómetro. Luego, las partes modeladas se unieron en un archivo de ensamble donde se generaron las relaciones entre ellas que determinan sus grados de libertad. El modelo en 3D se puede observa r en la figura 3.

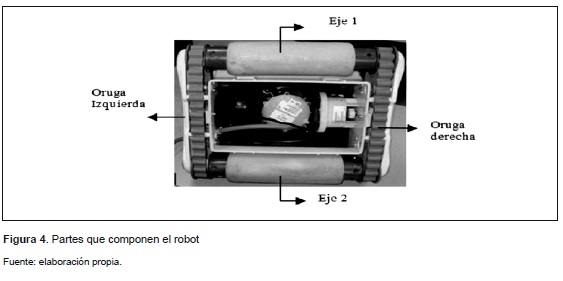
En la figura 4 se muestran las partes modeladas del robot. La oruga izquierda es accionada por un motor de corriente directa (DC) y la oruga derecha es accionada por otro motor con las mismas características.

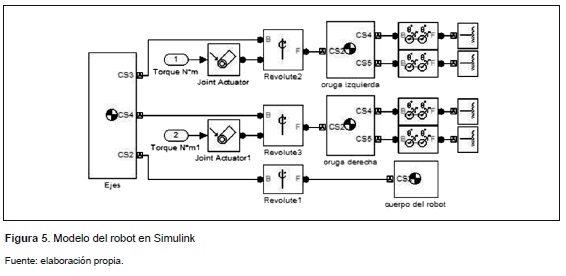
A partir de la representación en 3D fue posible crear un modelo del sistema en el software Simulink, usando un aplicativo de enlace entre los 2 programas llamado SimMechanics Link. Esto permitió exportar las propiedades físicas de los objetos modelados (masa, momentos de inercia, centros de gravedad), así como sus grados de libertad. El modelo exportado en Simulink se muestra en la figura 5.

En el modelo de la figura 5, los bloques que representan los cuerpos tienen puntos de conexión que están determinados por coordenadas espaciales [x, y, z]. Los cuerpos se conectan entre sí a través de uniones y restricciones. Estas uniones se crearon en el programa Autodesk Inventor y fueron exportadas automáticamente a Simulink por el software SimMechanics Link.

2.2 Dinámica del robot

Para el sistema de navegación se requiere formular las ecuaciones matemáticas que describen el comportamiento dinámico del robot, de tal forma que se puedan calcular los valores de aceleración y orientación del robot para combinarlos con las medidas de los sensores. Como primer paso para desarrollar estas ecuaciones, se definirán los marcos de referencia para la navegación.

2.2.1 Marcos de referencia

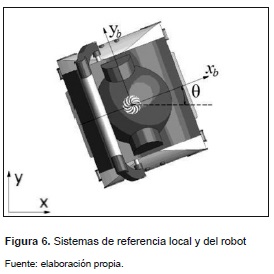
En este trabajo se consideran 2 marcos de referencia: un marco local, fijo a la piscina en la que se desplaza el robot (ejes x, y) y otro marco móvil, unido al robot (x_b, y_b), con origen en el centro de gravedad del robot. Estos marcos de referencia se mues tran en la figura 6. Asimismo, en la figura se muestra al marco del robot girado un ángulo θ con respecto al marco local.

Existe una matriz de rotación que permite pasar del marco B (unido al robot) al marco local (fijo a la piscina). Esta matriz de rotación tiene la propiedad que R^-1=R^T y está definida en la ecuación (1).

Al premultiplicar un vector expresado en el marco del robot por la matriz R se obtienen sus componentes en el marco local.

2.2.2 Fuerzas y momentos sobre el robot

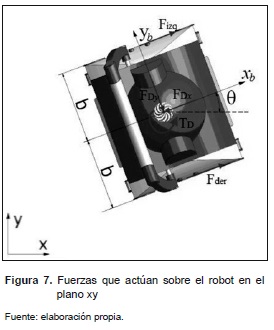
En la figura 7 se muestran las fuerzas que actúan sobre el robot limpiador de piscinas en el plano y los sistemas de referencia de la piscina (ejes x, y) y del robot (x_b, y_b). Las fuerzas F_der y F_izqson las fuerzas en las orugas derecha e izquierda del robot transmitidas por los motores, y las fuerzas F_DY , F_DX y el torque T_D, son fuerzas y momentos de arrastre (conocidas también como fuerzas de amortiguamiento hidrodinámico). No se muestran las fuerzas en el eje vertical (eje z) debido a que el robot no tiene movimiento en esta dirección.

Las fuerzas de amortiguamiento hidrodinámico, o fuerzas de arrastre, son las componentes de la fuerza que sufre un cuerpo al moverse a través del agua, en la dirección de la velocidad relativa entre el agua y el cuerpo. La resistencia es siempre de sentido opuesto a dicha velocidad, por lo que habitualmente se dice de ella que es la fuerza que se opone al avance de un cuerpo a través del agua.

2.2.3 Fuerzas de amortiguamiento hidrodinámico

Aunque, en general, el amortiguamiento de un vehículo subacuático es altamente no lineal y acoplado, muchos autores proponen una serie de simplificaciones [8]. La simplifi cación más común considera que la fuerza de amortiguamiento lineal cuadrática en cada eje depende únicamente de la componente correspondiente del vector de velocidad. Esto es similar a considerar que el robot realiza movimientos desacoplados. En este contexto, la fuerza de amortiguamiento se puede expresar como muestra la ecuación (2) [8].

Donde X_u y X_u│u│ son los coeficientes de viscosidad lineal y cuadrático, respectivamente, en la dirección de x_b. El coeficiente de viscosidad cuadrático se halla a partir de la ecuación (3) [9].

Donde ρ es la densidad del agua, C_Dx es el coeficiente de arrastre en la dirección de x_b y A_x es el área de la sección del cuerpo transversal a la dirección x_b.

De esta forma, la ecuación (2) se puede reescribir como la ecuación (4).

El coeficiente de arrastre C_D es una función que se encuentra relacionada directamente con el número de Reynolds y se calcula con la ecuación (5).

Donde R_e es el número de Reynolds. El número de Reynolds es un parámetro adimensional que se define como se ve en la ecuación (6).

Donde L es la longitud transversal al eje x, y o z, es la velocidad en el respectivo eje y μ es la viscosidad dinámica del agua.

2.2.4 Segunda ley de Newton aplicada sobre el robot

Para plantear las ecuaciones que rigen el movimiento del robot limpiador de piscinas, se aplica la segunda ley de Newton, utilizando como marco inercial de referencia el de la piscina. Inicialmente se suman las fuerzas para hallar la total en cada eje, ver ecuación (7).

donde R es la matriz de rotación.

También se suman los torques para hallar el torque total en el eje z, ver ecuación (8).

donde b es la distancia entre el punto de aplicación de las fuerzas F_der y F_izq al centro de gravedad del vehículo (figura 7).

A partir de las ecuaciones anteriores, se tiene la ecuación (9).

Donde m es la masa del vehículo, a es la aceleración del vehículo (en el marco local), I es el momento principal de inercia del vehículo (en el eje z) y α es la aceleración angular del vehículo (en el eje z).

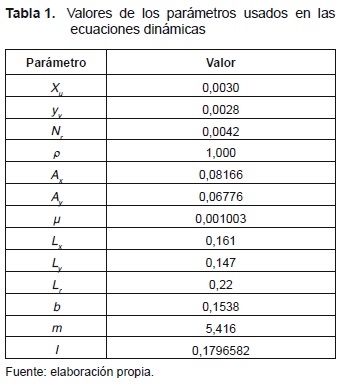
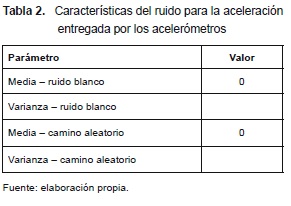
Los valores de los diferentes parámetros usados en las ecuaciones desarrolladas en esta sección se muestran en la tabla 1. Las áreas y longitudes transversales, así como la masa y el momento de inercia, son valores obtenidos con el software Autodesk Inventor.

2.3 Sensores y ruido

En el sistema de navegación para el robot subacuático se empleará un acelerómetro triaxial y un compás. A continuación se detallan las características de cada uno y se explica cómo fueron modelados.

2.3.1 Acelerómetro

El acelerómetro que se empleará es el MMA7260 de la compañía Freescale Semiconductor. Las especificaciones para este sensor se pueden encontrar en [10]. El acelerómetro triaxial se ubica en el centro de gravedad del robot, con sus ejes orientados en dirección a los ejes x_b, y_b y z_b. Este sensor mide por lo tanto las componentes de aceleración en el marco del robot [11].

Para simular el comportamiento del acelerómetro se agregó un sensor virtual de aceleración al modelo del robot construido en Simulink y se añadió una componente de ruido a esta medida de aceleración. En los acelerómetros reales existe una componente de desviación o bias que es aleatoria (un tipo de proceso estocástico, conocido como "camino aleatorio" o randomwalk), que puede modelarse como la integral de un ruido blanco gaussiano. De esta forma, el ruido del acelerómetro se modeló como la suma de un ruido blanco y un camino aleatorio, como se indica en la ecuación (10).

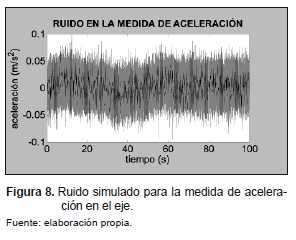
En l a figura 8 se muestra el ruido simulado para la aceleración medida por el acelerómetro en el eje x, con una duración de 100 segundos y los parámetros del ruido se presentan en la tabla 2. Se omite la gráfica para el eje y, debido a que se trata de un ruido con las mismas características.

2.3.2 Compás

El compás es un sensor que mide los cambios en la orientación del robot. El compás que se usará en el robot es el CMPS03 de la compañía Devantech Ltd. Las especificaciones del sensor se pueden consultar en [12].

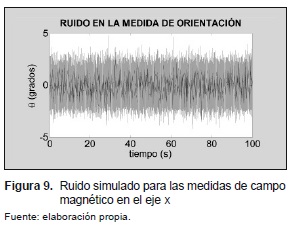
Para simular el comportamiento del compás, igual que con el acelerómetro, se agregó un sensor virtual de orientación (ángulo θ en la figura 6) al modelo del robot construido en Simulink, y se añadió una componente de ruido a la medida de orientación entregada por este sensor. El ruido se simuló como un ruido blanco gaussiano (figura 9). Las características de este ruido se presentan en l a tabla 3.

2.4 Estimación por mínimos cuadrados ponderados

A partir de las ecuaciones dinámicas desarrolladas en la sección 2.2.2, se pueden calcular las componentes de aceleración en los ejes x e y, y el ángulo θ. Construyendo la matriz de rotación, se pueden calcular las componentes de aceleración en el marco del robot, ver ecuación (11).

Los valores de aceleración y orientación se combinan con las medidas simuladas de los sensores para obtener una estimación más precisa de estas variables usando la técnica de mínimos cuadrados ponderados, expresada en la ecuación (12) [6]:

Donde â es la aceleración estimada, a_m σ² _am es la aceleración medida por el sensor y σ² _am es la varianza del error en dicha medida, a_c es la aceleración calculada con las ecuaciones desarrolladas en la sección 2.2.4 y σ² _ac es la varianza del error en dicho cálculo, σ_a ² es la varianza del error de la estimación â. La ecuación (12) se aplica para cada componente de la aceleración y para Ө.

2.5 Cinemática

A partir de los valores estimados de aceleración y orientación del robot, se puede calcular la velocidad y posición, integrando como lo expresa la ecuación (13):

Donde V_x y V_y son las componentes de velocidad del robot en el marco local, y x e y, son las coordenadas de posición del vehículo en el marco local.

2.6 Simulación

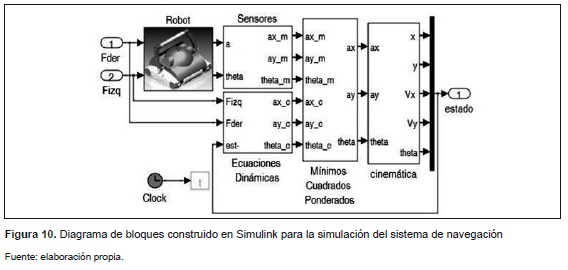
El modelo del robot, las ecuaciones de la dinámica de este, el modelo de los sensores, el estimador (por mínimos cuadrados ponderados) y la integración del resultado para obtener la posición y velocidad del robot, se implementaron en Simulink, como se muestra en la figura 10.

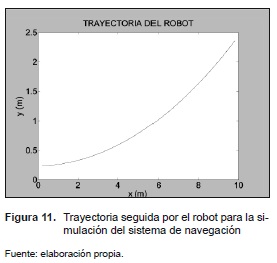
La simulación se realizó con un periodo de muestreo de 0,001 s y con una duración de 10 s. El tiempo de muestreo se seleccionó de acuerdo con la frecuencia de lectura de los sensores por utilizar. A partir de esta simulación se logró comprobar el funcionamiento del estimador y comparar los valores reales de las variables (que se pueden obtener directamente del modelo) con los valores estimados. La trayectoria del robot empleada para la simulación se ilustra en l a figura 11.

3. Resultados

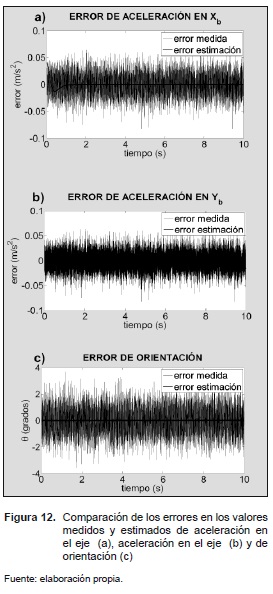
En la figura 12 se graficó el error en los valores medidos y estimados de aceleración y orientación del vehículo. Los errores se calcularon como la diferencia entre el valor (medido o estimado) y el valor real, tomado directamente del modelo. El valor estimado es el valor obtenido con la técnica de mínimos cuadrados ponderados.

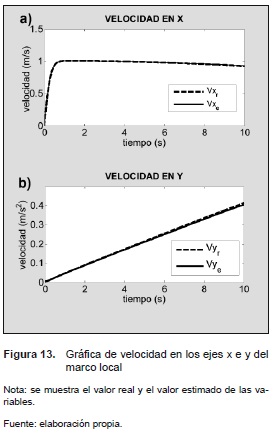
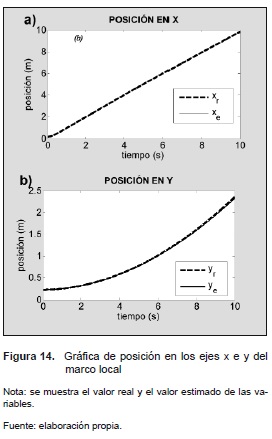
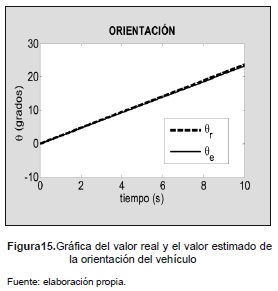
En las figuras 13, 14 y 15 se observan los valores estimados de posición, velocidad y orientación del vehículo, respectivamente, comparados con los valores reales de estas mismas variables.

4. Conclusiones

En este trabajo se diseñó un sistema de navegación para un robot limpiador de piscinas adquirido por la Liga de Natación de Antioquia, como primer paso para lograr su automatización. Con el trabajo realizado se buscaba comprobar si los sensores seleccionados junto con las ecuaciones que describen la dinámica del vehículo, combinados con la técnica de mínimos cuadrados ponderados, permitían lograr una estimación del estado del robot en tiempo real, con un grado de error aceptable.

5. Agradecimientos Y financiamiento

Este artículo se deriva del proyecto de investigación denominado "Vehículo no tripulado para la limpieza de la piscina de la Liga de Natación de Antioquia" del Instituto Tecnológico Metropolitano con código P10254. Los autores agradecen al grupo de investigación en Automática y Electrónica del Instituto Tecnológico Metropolitano y a la Liga de Natación de Antioquia sus aportes para la realización de este proyecto.

Referencias

[1] P. Fiorini and E. Prassler, "Cleaning and household robots: a technology survey", Autonomous Robots, vol. 9, no. 3, pp. 227-235, December 2000.

[2] Naval Command, Review of autonomous underwater vehicle (AUV) developments, United States General Books LLC, Washington, 2001.

[3] M. Simoncelli, G. Zunino, H. Christensen, and K. Lange, "Autonomous pool cleaning: self-localization and autonomous navigation for cleaning", Autonomous Robots, vol. 9, no. 3, pp. 261-2 70, December 2000.

[4] P. Vanicek and M. Omerbašic, "Does a navigation algorithm have to use Kalman filter?", Canadian Aeronautical and Space Institute Journal, vol. 45, no. 3, pp. 292-296, 1999.

[5] F. El-Hawary, "A comparison of recursive weighted least squares estimation and Kalman filtering for source dynamic motion evaluation", Canadian Journal of Electrical and Computer Engineering, vol. 17, no. 3, pp. 136-145, 1992.

[6] M. Gautieraand P. Poignet, "Extended Kalman filtering and weighted least squares dynamic identification of robot", Control Engineering Practice, vol. 9, no. 12, pp. 1361-1372, 2001.

[7] P. Ortíz-Valencia, J. Ramírez-Echavarría, y L. Cardona Rendón. Modelo Matemático y Control de Sistemas de Fluidos, Medellín: Instituto Tecnológico Metropolitano, 2011.

[8] T. Fossen, Guidance and Control of Ocean Vehicles, 1st. ed., Chichester: John Wiley & Sons, 1994.

[9] G . Conte and A.Serrani, "Modellingand simulation of underwater vehicles", in Proceedings of the IEEE International Symposium on Computer-Aided Control System Design, Dearborn, USA, pp. 62-67, 1996.

[10] Freescale-Semiconductor, "MMA7260QT Technical Data", 2008. [Online]. Available: http://cache.freescale.com/files/sensors/doc/data_sheet/MMA7260QT.pdf?pspll=1 [consultado el 10 de mayo de 2011].

[11] P. Savage, "What Do Accelerometers Measure?", Strapdown Associates, Inc., 2005. [Online]. Available:http://www.strapdow-nassociates.com/Accels%20Measure.pdf [consultado el 7 de abril de 2011].

[12] Hobby-Engineering, "CMPS03 -Robot Compass Module". [Online]. Available: http://www.hobbyengineering.com/specs/devantech-cmps03-tech.pdf [consultado el 10 de mayo de 2011].