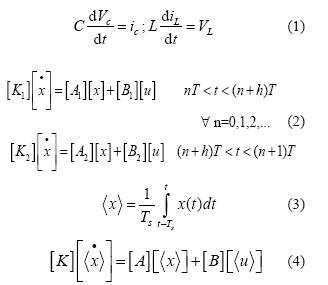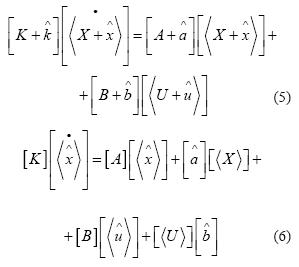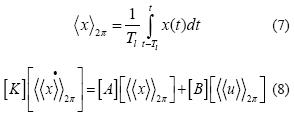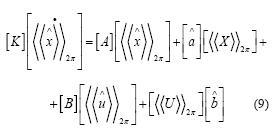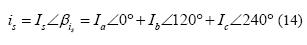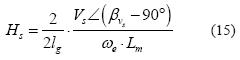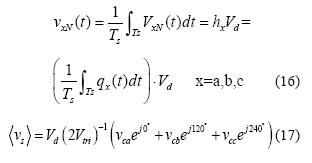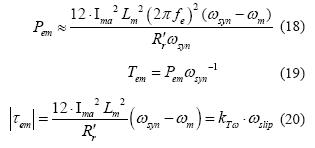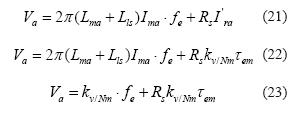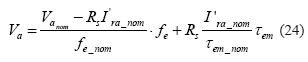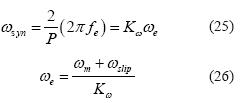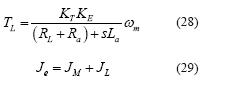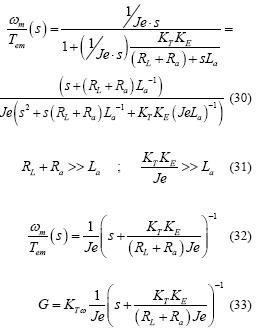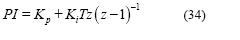DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2014.1.a07Published:
2013-12-20Issue:
Vol. 18 No. 39 (2014): January - MarchSection:
ResearchModelado e implementación de un manejador eléctrico para un motor de inducción trifásico
A three-phase induction motor electric driver - modeling and implementation
Keywords:
Variable speed drives, linear feedback control systems, power conversion, power system modeling (en).Keywords:
Accionamientos de velocidad variable, control retroalimentado de siste¬mas lineales, conversión de energía, modelado de sistemas de potencia. (es).Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Modelado e implementación de un manejador eléctrico para un motor de inducción trifásico
A three-phase induction motor electric driver – modeling and implementation
Arturo Fajardo Jaimes1, Fernando Ojeda Ruiz2, Abdel Karim Hay Harb3, Gabriel Perilla Galindo4
1Ingeniero Electrónico, magíster en Ingeniería Electrónica. Docente asistente de
la Pontificia Universidad Javeriana. Bogotá, Colombia.
Contacto: fajardoa@javeriana.edu.co
2Ingeniero Electrónico, magíster en Ingeniería Electrónica. Ingeniero de Investigación
y Desarrollo de U y G Ingeniería S.A. Bogotá, Colombia.
Contacto: fojeda@javeriana.edu.co
3Ingeniero Electrónico, magíster en Ingeniería Electrónica. Docente emérito de la
Pontificia Universidad Javeriana. Bogotá, Colombia.
Contacto: karim.hay@javeriana.edu.co
4Ingeniero Electrónico, magíster en Ingeniería Electrónica. Docente asistente de
la Pontificia Universidad Javeriana. Bogotá, Colombia.
Contacto: gabriel.perilla@javeriana.edu.co
Fecha de recepción: 23 de agosto de 2012 Fecha de aceptación: 21 de mayo de 2013
Clasificación del artículo: investigación
Financiamiento: Pontificia Universidad Javeriana
Resumen
En este artículo se presenta el desarrollo detallado del modelo lineal de un variador de velocidad no convencional para un motor de inducción trifásico. La arquitectura propuesta consiste en una etapa de factor de potencia unitario (PFC) monofásico seguido de un inversor trifásico, el cual alimenta el motor usando la técnica de control escalar. Todo el sistema es controlado de forma digital mediante un procesador digital de señales (DSP). Para obtener el modelo se propone el uso no convencional del operador promedio, en el cual el tiempo de cálculo del operador depende de las dinámicas de interés, este tipo de análisis simplifica el desarrollo de los modelos sin pérdidas significativas de la precisión del modelo. El proyecto se dividió en 3 etapas metodológicas, en la primera se definieron las dinámicas de interés para cada parte del manejador eléctrico, y se obtuvieron los modelos lineales con el operador promedio móvil definido adecuadamente para cada etapa. En la segunda etapa se validaron los modelos mediante simulación. Finalmente se diseñaron los controladores y se implementó el manejador para validar el proceso de diseño de forma experimental. El sistema implementado usando este modelamiento fue un variador de velocidad para un motor de inducción de 0,5 HP de tensión reducida (22 V), el sistema implementado se caracterizó por la corrección total del factor de potencia, una regulación de velocidad menor 5 % y una eficiencia de la unidad de procesamiento de potencia (PFC-Inversor) de 82 %.
Palabras clave: accionamientos de velocidad variable, control retroalimentado de sistemas lineales, conversión de energía, modelado de sistemas de potencia.
Abstract
This paper gives a detailed description of a nonconventional speed-variation linear model in-tended for a conventional three-phase induction motor. The proposed architecture consists in a single-phase unit-power-factor tap (PFC) followed by three-phase inverter, which feeds the motor by using the scalar-control technique. The whole system is digitally-controlled by a Digital Signal Processor (DSP). In order to obtain the model, non-conventional use of the average operator is suggested, which involves a calculation time span that depends on the target dynamics. This type of analysis simplifies the development of lossless models in terms of model precision. The project was divided into three methodological stages. Stage one established target dynamics for each of the electric-driver parts as well as providing linear models by means of a welldefined stage-specific mobile average operator. Stage two served to validate the models through simulation-based experiments. Finally, controllers were designed and the driver was implemented so as to validate the design process experimentally. The system that was implementing through this modeling process corresponds to a speed-variation unit for a 0,5-HP reduced-voltage (22V) induction motor. The implemented system was characterized in terms of the total power-factor correction, a speed regulation level lower than 5 %, and power-processing-unit efficiency (PFC-Inverter) of 82 %.
Keywords: variable speed drives, linear feedback control systems, power conversion, power system modeling.
1. Introducción
Inicialmente los motores eléctricos se usaron como fuentes de velocidad constante, el control de su velocidad apareció en medios de producción industriales [1]. Actualmente, las aplicaciones en las cuales los motores controlados están presentes, abarcan una amplia gama de aplicaciones entre las que se pueden contar: generación de energía, sistemas de calefacción y aire acondicionado, transporte de fluidos, sistemas de transporte, maquinaria para manufactura, entre otros [1] - [3]. Antes de 1980, los manejadores de velocidad de motores de corriente directa (CD) a diferencia de los de corriente alterna (CA) realizaban un control directo del torque desarrollado por el motor, generando dispositivos con una respuesta dinámica rápida y estable [3], [4]. Ya en la década de los noventa el desarrollo acelerado de los procesadores permitió la implementación de técnicas de control de motores de inducción muy robustas [2] como Control escalar [1], [4], [5], control vectorial [2], [6] - [8] y control vectorial sin sensores [9]. En esta década se introdujo el concepto del manejador eléctrico [1], [10] - [13], desde esta óptica existe un sistema unificado objeto del control, en el cual las variables controladas son tanto eléctricas como mecánicas.
En el resto del artículo se presenta el diseño e implementación de un manejador eléctrico, constituido por un motor de inducción trifásico con una carga acoplada y un variador de velocidad con factor de potencia unitario, que implementa la técnica de control escalar. Primero se expone la arquitectura del manejador implementado, posteriormente se presenta el desarrollo detallado del modelo lineal manejador. Finalmente, se presentan los principales resultados experimentales.
2. Metodología
Este proyecto parte de la base de que la topología del driver está preestablecida, por lo que la pregunta que intenta responder la investigación es: ¿Es posible obtener un modelo lineal de baja complejidad del sistema? Para responder esta pregunta, la investigación se dividió en 3 etapas metodológicas secuenciales. En las 2 primeras fases se realizó un proceso de apropiación científica y se propuso una utilización novedosa de las herramientas estudiadas, para obtener modelos lineales simplificados con un grado de precisión adecuado para orientar el diseño de los controladores, cuando hay disparidad en las dinámicas de interés en los circuitos (i.e control DC entrada vs control AC salida). En la primera etapa se analizó el impacto de las diferentes alternativas de linealización sobre los modelos presentes en la literatura estudiada. La segunda etapa consistió en aplicar las herramientas matemáticas de una forma novedosa para obtener los modelos lineales simplificados, junto con una validación de los modelos mediante simulación. Finalmente en la tercera etapa se diseñaron los controladores y se implementó el manejador para validar el proceso de diseño de forma experimental.
Cada una de las 2 últimas fases del proyecto consta de forma general de 4 etapas claramente diferenciables, a saber: diseño, simulación, implementación y evaluación. En la etapa de diseño se realiza el cálculo exhaustivo de los parámetros. En la etapa de simulación se trabajará el simulador para evaluar el sistema propuesto. En esta etapa se pretende evaluar si es necesario modificar el modelo teórico o si se debe realizar una optimización; de ser así, empieza de nuevo la fase desde la etapa de diseño. En la etapa de implementación se construirá el circuito impreso (PCB) o el archivo de simulación de sistema bajo las especificaciones de diseño. En la etapa de evaluación se medirán (con instrumentos o en el simulador), mediante un protocolo de pruebas claramente especificado, los parámetros de mérito del sistema. En este punto se analizan los resultados obtenidos, y se toma la decisión de pasar o no a una siguiente fase o si es necesario retornar a alguna etapa anterior de la presente fase como la de diseño, simulación o implementación.
3. Descripción del manejador Eléctrico
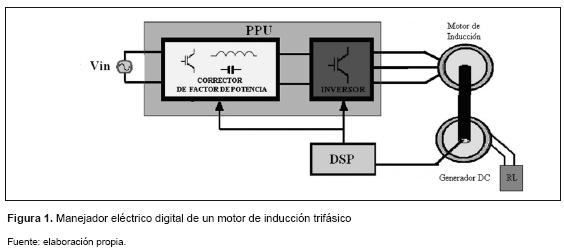
El manejador propuesto consiste en una unidad de procesamiento de potencia (PPU) y motor inducción trifásico al cual se le acopla un generador CD (Corriente Directa) para emular diferentes perfiles de carga. La PPU está conformada por un rectificador monofásico con corrector de potencia unitaria (PFC) y un inversor trifásico (VI). El control del sistema se implementó digitalmente en un DSP, adicionalmente para medir la velocidad del motor se usó un encoder. Un diagrama esquemático del manejador se ilustra en la figura 1.
4. Modelo lineal del manejador Eléctrico estudiado
Para modelar las dinámicas del PFC se parte de las ecuaciones dinámicas que rigen su comportamiento, obteniendo las ecuaciones de las variables de estado de la ecuación (1). Debido a la conmutación de los elementos activos, la representación canónica matricial de las ecuaciones de estado resultantes es de naturaleza discontinua. En la ecuación (2) se muestra por ejemplo un caso particular donde solo se tienen 2 posibles variables de estado, partiendo del supuesto de tener solo 2 posibles representaciones del circuito debido a la conmutación. Para eliminar la discontinuidad presente en la ecuación (2), se usa el operador promedio móvil definido por la ecuación (3), utilizando como tiempo de promediación un periodo de conmutación (Ts) del convertidor, con lo que se obtiene la ecuación (4). Cabe anotar que las ecuaciones continuas resultantes son válidas exclusivamente para frecuencias menores a 1/ (2Ts) [15]
Para obtener un modelo lineal del sistema descrito por la ecuación (4) se utiliza el método de excitación de señales [2], [14], [15], con lo que se obtiene la ecuación (5). Realizando la aproximación del análisis cuasiestacionario [1], [15], se obtiene la ecuación (6). Las ecuaciones (4) y (6) pueden ser representadas por circuitos, los cuales son utilizados para orientar el diseño del control.
La ecuación (4) origina los circuitos llamados de gran señal y la ecuación (6) los circuitos de pequeña señal.
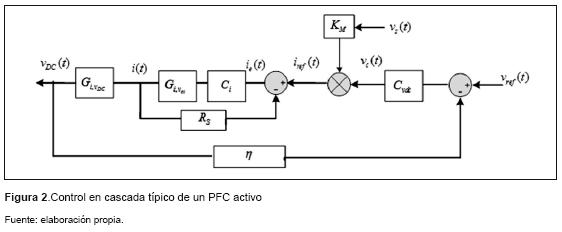
En el PFC es necesario controlar la corriente de alimentación para garantizar un factor de potencia unitario y mantener el voltaje a la salida regulado. Para realizar esta tarea, se propuso un control en cascada de 2 mallas [1], siendo la malla externa la malla de voltaje y la malla interna la de corriente. La malla de voltaje produce la referencia de la malla de corriente, que se implementa como la multiplicación entre un voltaje de control relacionado con la señal DC de salida y una muestra de la señal de entrada. Como existe una diferencia significativa entre las dinámicas de las mallas, se puede considerar que el lazo de corriente (interno), se encuentra estable cuando el externo empieza a responder, por lo que el problema del control se simplifica a un diseño de 2 mallas independientes. El esquema de control propuesto se muestra en la figura 2.
Bajo este esquema de control, es posible dividir el modelado del PFC. Para la malla de voltaje, dado que las dinámicas de interés son lentas comparadas con el límite de validez del modelo lineal obtenido en la ecuación (6), es posible hacer una simplificación adicional sin pérdida significativa en la precisión del modelo, que consiste en aplicar nuevamente el operador promedio móvil sobre un tiempo del periodo de la línea de alimentación Tl, como se presenta en la ecuación (7). Aplicando este operador a la ecuación (4) se obtiene la ecuación (8). Finalmente se aplica nuevamente el método de excitación de señales a la ecuación (8), con lo que se obtiene el modelo lineal del sistema en la ecuación (9).
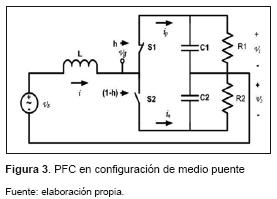
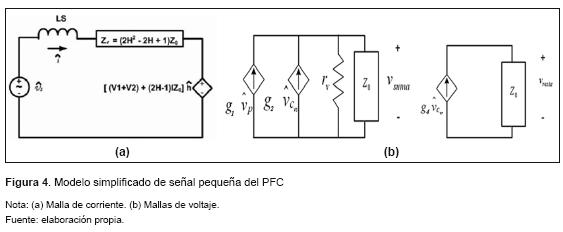
Al aplicar esta técnica de modelado al PFC (figura 3), se obtienen los circuitos de pequeña señal mostrados en la figura 4, el desarrollo detallado de este procedimiento se encuentra en [14], [16].
Para la malla de corriente se obtuvo la función de transferencia desde el voltaje de control hasta la corriente i como la ecuación (10). Este resultado se obtuvo asumiendo una modulación por ancho de pulso (PWM) con una amplitud de la portadora Vt, donde esta modulación es producto de comparar un voltaje de control con la portadora [1], [2], [15]. Posteriormente se calcula la función de transferencia por medio de la ecuación (11) desde la variable controlada (ciclo útil h), hasta la variable objeto del control (la corriente de entrada i).
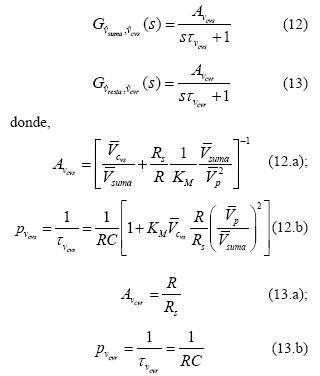
A partir del circuito de señal pequeña de la malla de voltaje se encuentran las funciones de transferencia de las variables de control (vcvs y vcvr ) a las variables reguladas (vsuma y vresta), estas funciones son (12) y (13):
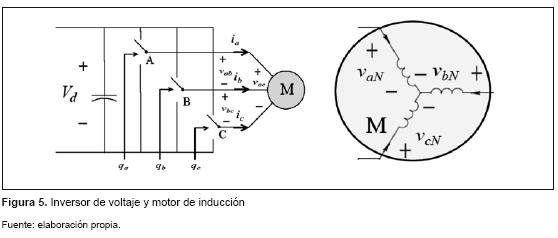
Para encontrar el modelo lineal del inversor-motor (figura 5) se parte del uso de una modulación basada en vectores espaciales [2]. En esta modulación una determinada combinación de las posiciones de las fases se traduce en una interacción de campos en el interior del motor, que para el caso de un motor de 2 polos se puede explicar a partir de un vector espacial de corriente definido por la ecuación (14), donde el ángulo asociado a cada fasor espacial de corriente está relacionado con la forma en que están distribuidos espacialmente los devanados en el estator del motor. Este vector se puede entender como un devanado virtual en una posición espacial βi, con una magnitud Is que produciría los mismos campos en el entrehierro que la superposición de los campos individuales producidos por cada devanado.
Como se muestra en [1], el campo en el entrehierro del motor está determinado por la ecuación (15), donde β vs es la posición espacial del vector de voltaje, we la frecuencia eléctrica del voltaje de alimentación de las fases, lg la longitud del entre-hierro, is la corriente de magnetización de la máquina y vs el voltaje que alimenta la inductancia de magnetización. Para obtener este resultado se asume que el motor se puede modelar como una inductancia de magnetización (Lm) por fase y que está operando en estado estacionario sinusoidal.
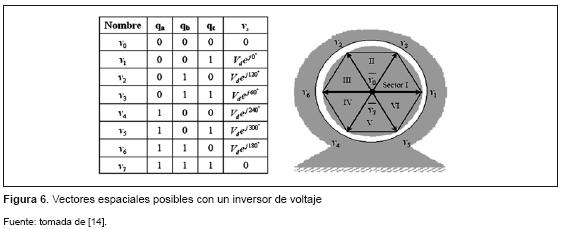
A partir de la ecuación (15) se deduce que la alimentación debe generar un vector espacial de voltaje vs =Vs ∠ wsynt si se desea generar un campo giratorio a una velocidad angular wsyn (velocidad sincronismo). Como se explica en [14], este voltaje se puede producir con la modulación por espacio de vectores. Con esta técnica, a partir de 8 vectores básicos que se resumen en la figura 6, es posible generar cualquier vector espacial deseado, si la frecuencia de conmutación es muy alta comparada con el ancho de banda del motor. Así, un vector espacial arbitrario se puede generar por medio de una combinación temporal de vectores espaciales básicos que produzcan la misma señal promedio en un intervalo de conmutación que la señal del vector espacial a sintetizar.
Al aplicar el operador promedio móvil (3) en cada rama del VI, los voltajes de alimentación del motor por fase están determinados por la ecuación (16), suponiendo que cada rama es controlada a partir de un voltaje de control (vcx), que a través de una modulación PWM (Pulse Wide Modulation) produce la señal que controla los interruptores. Adicionalmente, suponiendo que esta modulación se construye a partir de la comparación entre una señal portadora triangular de amplitud Vtri y con periodo Ts, se obtiene que el modelo del VI es simplemente un amplificador cuyas entradas son 3 voltajes de control y como salida un vector espacial de voltaje vs definido por la ecuación (17). Esta aproximación no significa una pérdida significativa en la precisión del modelo del sistema inversor-motor-carga, en gran medida porque el motor filtra gran parte de las dinámicas que se desprecian con este tipo de modelado, es decir, las dinámicas superiores a 0,5 fs.
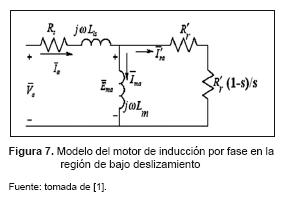
Finalmente, para modelar el sistema motor-generador, se parte del modelo tradicional de un motor de inducción trifásico por fase [3]. Considerando que el motor trabajará en la región de bajo deslizamiento, los efectos de la inductancia de dispersión del rotor son despreciables [1], por lo que el circuito equivalente por fase usado es el ilustrado en la figura 7, donde Rs y Ls modelan la resistencia y la inductancia de los devanados por fase del estator, Lm es inductancia de magnetización por fase, fe es la frecuencia de la línea de alimentación, Rr modela la disipación de potencia producto de las pérdidas en los conductores del rotor y Rr'(1 s)s-1 modela la energía transformada en energía mecánica siendo s el deslizamiento del motor.
De acuerdo con el modelo por fase y suponiendo operación en bajo deslizamiento, la potencia electromagnética entregada por el motor está determinada por la ecuación (18). A partir de las ecuaciones (18) y (19), se calcula el torque electromagnético producido por el motor, el cual queda determinado por la ecuación (20).
De la ecuación (20) se observa que el torque producido por el motor depende de la magnitud de la corriente de magnetización por fase (Ima) y de la velocidad de deslizamiento (ωslip). La técnica de control escalar propone desacoplar estas 2 variables, alimentando de forma adecuada el VI para que la corriente Ima sea contante por lo cual el torque dependería exclusivamente de ωslip. Como se presenta en [1], la magnitud del voltaje de alimentación por fase está determinada por la ecuación (21). Por otra parte, como la magnitud de corriente del rotor (Ira) depende de forma proporcional del torque impuesto por la carga, suponiendo equilibrio dinámico del sistema mecánico, la ecuación (21) se puede reescribir como la ecuación (22). Finalmente, si suponemos que la corriente de magnetización se mantiene constante, la ecuación (22) se puede reescribir como la ecuación (23).
Para definir el perfil V/Hz del VI usado en este proyecto, se utilizó la aproximación lineal al problema, en el cual las constantes presentes en la ecuación se pueden calcular a partir de los puntos de operación suministrados por el fabricante. Utilizando esta aproximación, la ecuación (23) se simplifica a la ecuación (24).
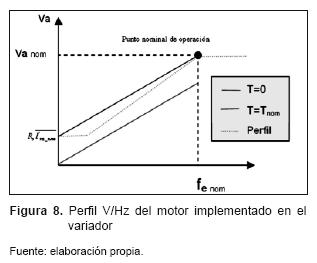
Con base en la ecuación (24) se definió el perfil a usar en el motor, el cual se caracterizó por tener una pendiente constante hasta que la amplitud de alimentación alcance el valor crítico RsI'ra _ nom , si la frecuencia de alimentación sigue disminuyendo se mantiene la amplitud constante. En el caso en que se necesite aumentar la frecuencia eléctrica a un valor mayor al nominal, se deja constante la amplitud nominal de alimentación del motor, para evitar daños por sobre voltaje. Este perfil se muestra en la figura 8.
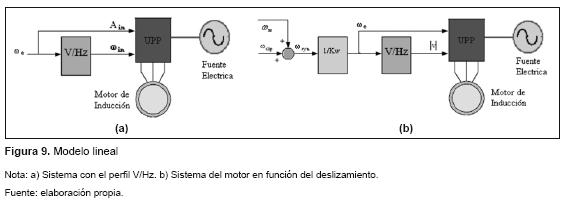
Bajo este contexto, la PPU se modela con una sola entrada, donde la frecuencia eléctrica del VI define también la amplitud de la señal generada por el VI (figura 9a). Por otra parte, como la ω synen un motor de P polos está dada por la ecuación (25) [1], se obtiene de la ecuación (20) la relación entre f e, ωeslip y ωm, la cual está determinada por la ecuación (26). Por lo cual, se propone un modelo
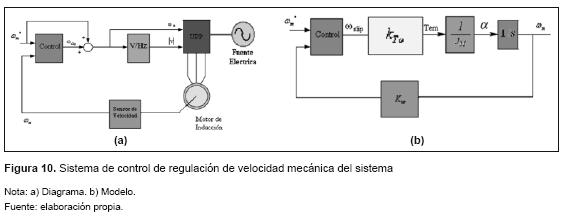
Para implementar el control de velocidad se usó un encoder incremental, en este dispositivo la frecuencia eléctrica de salida y su velocidad mecánica están relacionadas por la ecuación (27). En la figura 10 se muestra el sistema de control propuesto sin carga mecánica acoplada y despreciando el efecto de la fricción sobre el eje.
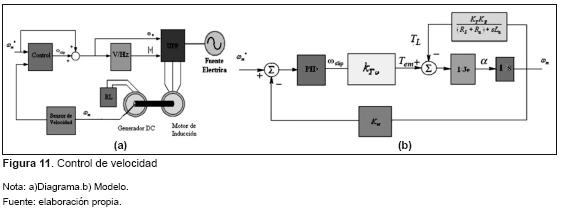
Para cambiar con facilidad el torque de carga, se acopló al motor trifásico de inducción un generador DC tipo PMDC con una resistencia variable (RL) conectada entre sus bornes. A partir del modelo del generador DC se puede encontrar una expresión para el torque electromagnético de carga del generador dado por la ecuación (28), como función de RL y los parámetros del circuito equivalente. Suponiendo un acople perfecto entre los ejes la inercia total del sistema está determinada por la ecuación ( 29). Finalmente, a partir delas ecuaciones (25), (26), (27), (28) y (29), se puede obtener el modelo lineal del sistema despreciando el torque por rozamiento. El modelo junto con un diagrama esquemático se ilustra en la figura 11.
A partir del modelo encontrado, se puede calcular la función de transferencia entre el torque electromagnético y la velocidad mecánica, por lo que se obtiene la ecuación (30). Para el caso particular del proyecto implementado en [14] cumple con la ecuación (31), por lo que la ecuación (30) se simplifica como se describe en la ecuación (32). Entonces la ecuación (30) se puede simplificar en la ecuación (32). A partir de la ecuación (32) y el esquema descrito por la figura 11 se puede encontrar la función de transferencia descrita por la ecuación (33). Esta función permite orientar el diseño del controlador:
En este proyecto se implementó el control de la PPU en un procesador digital de señales (DSP), todos los controladores son tipo PI discretos, caracterizados por la ecuación (34) diseñados por compensación.
Es necesario contemplar 2 diferencias importantes de este tipo de control con respecto al caso analógico. En primer lugar, como la señal moduladora varía cada ciclo de reloj, el ciclo útil permanece constante durante todo el ciclo produciendo un retenedor de orden cero adicional. En segundo lugar, como el tiempo que consumen los cálculos del algoritmo de control impide que el resultado sea utilizado dentro del mismo ciclo en que se muestrea, produce un retardo adicional de un ciclo. Tanto el retenedor de orden cero del muestreo de la señal como el producido por la implementación digital del PWM deben ser incluidos, posteriormente a la transformación de la planta análoga del entorno continuo al entorno discreto. En [14] se desarrolla en detalle del diseño de los controladores digitales y la discretización del sistema.
5. Resultados y Discusión
Para evaluar el variador de velocidad se implementó un banco de pruebas (figura 12) que permite modificar la referencia y algunos disturbios del lazo de control de velocidad tales como el voltaje de línea y el torque de carga del motor. Se diseñaron 3 pruebas en las que se modificaron los valores estáticos, tanto de la referencia como de los disturbios presentes en el lazo de control de velocidad. La primera prueba consistió en variar únicamente el disturbio de torque mientras que los demás parámetros permanecían fijos, en la segunda prueba se varió en forma simultánea tanto la referencia del lazo de control de velocidad como el torque de carga. Finalmente, en la tercera se modificó el voltaje de línea manteniendo las otras variables constantes.
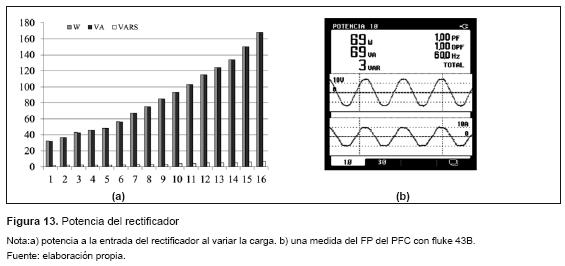
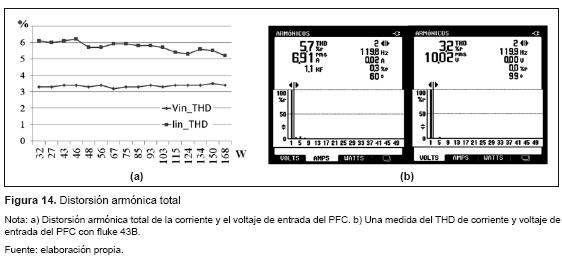
El PFC produjo un factor de potencia unitario en todo el rango de operación del sistema. En la figura 13 se presenta la relación entre potencia real, aparente y reactiva de entrad a al PFC junto con un ejemplo de la medida que entrega el fluke 43B. En la figura 14 se observa cómo la distorsión armónica total de la corriente disminuye a medida que la potencia de entrada aumenta, mientras que la distorsión armónica tot al del voltaje permanece casi constante en todo el rango de operación. En la figura 15 se presentan las medidas de voltaje de salida del PFC junto con una fotografía que ilustra el proceso de medida con un fluke 45, en estos resultados se encontró que el voltaje rms permanecía constante y su rizado siempre se caracterizó por tener un valor menor 1 % del valor rms.
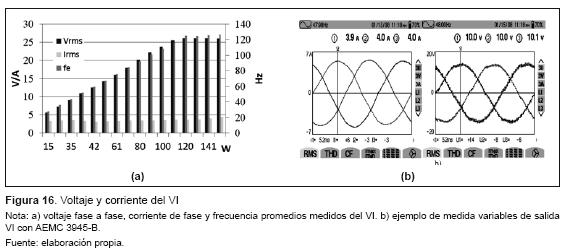
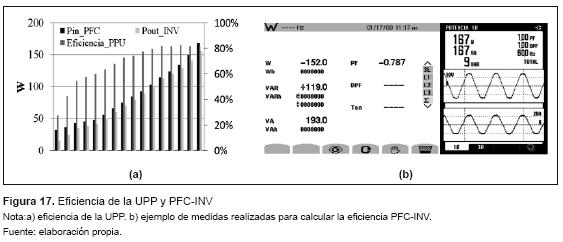
El VI produjo la señal trifásica con amplitud y frecuencia variable apropiada para accionar el motor, que en el caso de las medidas mostradas en la figura 16, eran producto de la acción de control para mantener una velocidad mecánica particular regulada, a cambios en la referencia de velocidad y cambios de torque de la carga. Para el análisis global de la UPP, se analizó la eficiencia del sistema. En la figura 17 se muestra un ejemplo de las medidas de la potencia a la entrada y a la salida de la PPU, junto con la eficiencia del sistema. Como se evidencia en esta gráfica, la eficiencia de la PPU es superior al 50 % desde la mitad de su rango de funcionamiento nominal hasta un valor máximo del 82 %. Este cálculo involucra el consumo de una fuente de alimentación adicional usada.
Para el análisis desde el punto de vista global del desempeño del variador de velocidad el principal indicador es la regulación de velocidad, esta se midió a través de la medida directa de la velocidad en el eje mecánico, variando la carga mecánica del motor desde 0,14 Nm hasta 0,35 Nm, manteniendo constante la referencia. Con la referencia en su valor nominal (3600 rpm), fue menor al 1,2 %, a velocidades más bajas este porcentaje aumenta hasta ser aproximadamente el 5 % en 360 rpm.
6. Conclusiones
En este proyecto se exploró el diseño y la implementación de un variador con factor de potencia unitario y bajo contenido armónico, controlado por DSP concordantes con las normas de regulación de calidad de energía. Con los resultados obtenidos se puede afirmar que es posible su manufactura en Colombia con diseño colombiano. Adicionalmente, las mediciones realizadas sobre el variador implementado llevan a interpretar que el modelo lineal encontrado es adecuado para el diseño de los controladores digitales, sin embargo, no se tiene certeza sobre el rango exacto de validez del modelo y sus posibles consecuencias en la estabilidad del sistema. Por otra parte, dados los resultados obtenidos en la regulación de velocidad con una regulación menor al 5 %, se puede afirmar que el modelo del manejador basado en control escalar permite predecir de forma apropiada sus dinámicas lentas y diseñar de igual manera los controladores para su correcto funcionamiento y desempeño.
7. Trabajos futuros
La herramienta de desarrollo de convertidores de potencia creada en [14] permite implementar, evaluar y optimizar con facilidad, unidades de procesamiento de potencia controladas digitalmente por DSP. El grupo pretende realizar varios proyectos adicionales sobre técnicas avanzadas de control de motores de inducción, como control directo de torque o control sin sensores, usando esta plataforma.
8. Agradecimientos
Al Ing. Carlos Iván Páez, M.Sc., por las discusiones sostenidas durante el desarrollo del presente artículo, las cuales fueron de gran importancia en su desarrollo. Al Departamento de Ingeniería Electrónica de la Pontificia Universidad Javeriana que otorgó los recursos necesarios para el desarrollo del proyecto de investigación.
Referencias
[1] N. Mohan, Electric Drives an Integrative Approach, Minneapolis y MNPERE, 2003.
[2] N. Mohan, Advanced Electric Drives, Minneapolis, MNPERE,2003.
[3] N. Mohan, T. Undeland and W. Robbins, Power Electronics: Converters, Applications and Design, 2nd. Ed, Estados Unidos, Wiley, 1995.
[4] N. Mohan, "Improvement in Energy Efficiency of Induction Motors by Means of Voltage Control", Power Apparatus and Systems, IEEE Transactions on, vol. PAS99, pp. 1466-1471, 1980.
[5] K. Suzuki, S. Saito, T. Kudor, A. Tanaka and Y. Andoh, "Stability Improvement of V/F Controlled Large Capacity Voltage-Source Inverter Fed Induction Motor", Industry Applications Conference, 2006. 41st IAS Annual Meeting. Conference Record of the 2006 IEEE, vol. 1, pp. 90-95, 2006.
[6] R. Bojoi, F. Farina, G. Griva, F. Profumo and A. Tenconi, "Direct torque control for dual three-phase induction motor drives", Industry Applications, IEEE Transactions on, vol. 41, pp. 1627-1636, 2005.
[7] A. M. Khambadkone and J. Holtz, "Vector-controlled induction motor drive with a self-commissioning scheme", Industrial Electronics, IEEE Transactions on, vol. 38, pp. 322-327, 1991.
[8] D. Telford, M.W. Dunnigan and B. W. Williams, "Online identification of induction machine electrical parameters for vector control loop tuning", Industrial Electronics, IEEE Transactions on, vol. 50, pp. 253-261, 2003.
[9] G. Pellegrino, R. Bojoi and P. Guglielmi, "Performance Comparison of Sensorless Field Oriented Control Techniques for Low Cost Three-Phase Induction Motor Drives", Industry Applications Conference, 2007. 42nd IAS Annual Meeting. Conference Record of the 2007 IEEE, pp. 281-288, 2007.
[10] N. Mohan, A. K. Jain, P. Jose and R. Ayyanar, "Teaching utility applications of power electronics in a first course on power systems", Power Systems, IEEE Transactions on, vol. 19, pp. 40-47, 2004.
[11] N. Mohan, W. P. Robbins, P. Imbertson, T. M. Undeland, R. C. Panaitescu, A. K. Jain, P. Jose and T. Begalke, "Restructuring of first courses in power electronics and electric drives that integrates digital control", Power Electronics, IEEE Transactions on, vol. 18, pp. 429-437, 2003.
[12] A. Boglietti, R. Bojoi, A. Cavagnino and A. Tenconi, "Efficiency Analysis of PWM Inverter Fed Three-Phase and Dual Three-Phase High Frequency Induction Machines for Low/Medium Power Applications", Industrial Electronics, IEEE Transactions on, vol. 55, pp. 2015-2023, 2008.
[13] V. G. Agelidis, "The future of power electronics/power engineering education: challenges and opportunities", Power Electronics Education, 2005. IEEE Workshop, pp. 1-8, 2005.
[14] A. Fajardo and F. Ojeda, "Implementación de un Controlador Digital para un Motor de Inducción Trifásico", Ingeniería y Universidad, vol. 13, no. 1. 2008.
[15] R. Erickson and D. Maksimovic, Fundamentals of Power Electronics Second Edition, Massachusetts, Kluwer Academic Publishers, 2001.
[16] A. Fajardo, F. Ojeda, A. Hay and G. Perilla, "Modelamiento de un rectificador en Configuración de Medio Puente con Factor de Potencia Unitario", Ingeniería y Universidad, vol. 13, Segundo Semestre 2009.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.