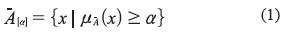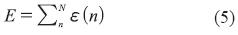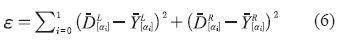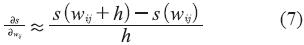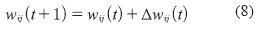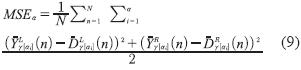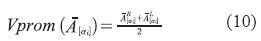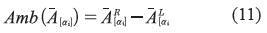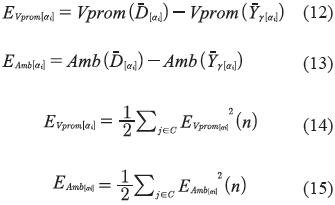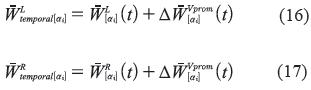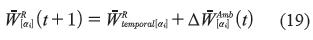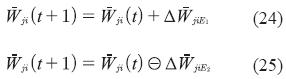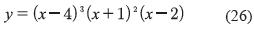Estrategias para el entrenamiento de redes neuronales de números difusos

Estrategias para el entrenamiento de redes neuronales de números difusos

Training strategies for fuzzy number neural networks

Edwin Villarreal López¹, Daniel Alejandro Arango²

¹Magíster en Automatización Industrial de la Universidad Nacional de Colombia.
Docente investigador del programa de Ingeniería Electrónica de la Universidad Manuela Beltrán. BogotÁ, Colombia, Contacto: edvillal@gmail.com
²Magíster en Ingeniería Electrónica de la Pontificia Universidad Javeriana. Docente investigador del programa de Ingeniería Electrónica de la Universidad Manuela Beltrán. BogotÁ, Colombia, Contacto: darangop@gmail.com

Fecha de recepción: 19 de noviembre de 2012 Fecha de aceptación: 27 de Agosto de 2013

Clasificación del artículo: investigación
Financiamiento: Universidad Manuela Beltrán

Resumen

El propósito de este artículo es presentar estrategias generales de entrenamiento para redes neuronales de números difusos utilizadas en el aprendizaje de sistemas a partir de información lingüística. Se exponen brevemente las principales tendencias en el entrenamiento de este tipo de sistemas y con base en ellas se proponen nuevas estrategias. La primera de ellas se basa en la retropropagación del error cuadrático medio en todos los α-cortes para pesos crisp. La segunda hace uso de un algoritmo genético con codificación real para redes con pesos crisp. La tercera consiste en la retropropagación del error en el valor promedio y la ambigüedad en todos los α-cortes para pesos difusos. Por último, se presenta una basada en la retropropagación de una medida difusa del error para redes con pesos difusos. Se realiza una etapa experimental en la que se implementan los algoritmos desarrollados junto con algunos de los más representativos reportados en el estado del arte, permitiendo identificar para qué conjuntos de datos particulares resulta útil cada una de las estrategias. Finalmente, se aplican dichas estrategias para la implementación de un sistema de evaluación de impacto ambiental en vertederos.

Palabras clave: algoritmos genéticos, redes neuronales difusas, retropropagación.

Abstract

The purpose of this article is to present general training strategies for training fuzzy number neural networks used in the learning of systems from linguistic data. We shortly analyze the main trends in the training of this kind of systems and from that point, we propose new strategies. The first of them is based on the backpropagation of the mean square error in all the α-cuts for crisp weights. The second strategy uses a real codification genetic algorithm for crisp weights networks. The third is based in the backpropagation of the mean error value and the ambiguity of all the α-cuts for fuzzy weights, and the last one uses the backpropagation of a fuzzy error measure for a fuzzy weighted network. An experimental stage is performed implementing the developed algorithms together with one of the most representative reported, allowing identifying the best suited data set for each of them. Finally the strategies are applied for an environmental impact assessment system for landfills.

Key words: Backpropagation, Fuzzy Neural Networks, Genetic Algorithms.

Introducción

La mayor parte de los sistemas para el manejo y tratamiento de la información que existen en la actualidad se basan en una arquitectura de procesamiento digital, esquema que, aunque ha demostrado ser de gran utilidad, se encuentra limitado por su incapacidad de representar de manera eficaz la información procedente del mundo real en una forma legible para las máquinas, información que por lo general, se encuentra contaminada con imprecisiones y distorsiones.

La lógica difusa, y en general la teoría de los conjuntos difusos (Zadeh, 1975), es un área de la inteligencia artificial que se ha enfocado en desarrollar herramientas que permitan representar y realizar operaciones con cantidades inexactas e imprecisas.

Uno de los principales conceptos manejados dentro de esta teoría es el número difuso, que facilita la tarea de modelar la imprecisión del mundo real, lo que permite a los sistemas operar a partir de mediciones y percepciones no muy exactas del medio. Con el objetivo de aprovechar esta cualidad y combinarla con las ventajas de otros tipos de sistemas de información, se han desarrollado múltiples técnicas híbridas, y entre estas se destacan las redes neuronales difusas.

Una red neuronal difusa de este tipo puede verse como la generalización de una red neuronal feedforward convencional, en la que, tanto las cantidades manipuladas -entradas, salidas y pesos de las conexiones-, como las operaciones necesarias para realizar la propagación -adición, multiplicación, función sigmoide- son extendidas al dominio de los números difusos mediante el principio de extensión formulado por Zadeh (1975), el cual ha sido reformulado de distintas formas (Klimke, 2006), resulta sencillo llevar estas operaciones a los números difusos. Sin embargo, dicha extensión no puede realizarse a los métodos de entrenamiento.

Diversos grupos de investigadores han venido desarrollando estrategias de entrenamiento para estas redes, las cuales, en su mayoría, simplifican las formas de las funciones de pertenencia de los números difusos propagados por la red, o desarrollan algoritmos aplicables únicamente a ciertas topologías.

En este artículo se presentan nuevas estrategias de entrenamiento más generales con respecto a la geometría de los pesos difusos y la arquitectura de la red. Se utiliza la notación barra 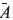para denotar un número difuso. Además, se define un α-corte de un número difuso 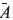como el conjunto de todos los x que pertenecen al conjunto difuso 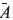con al menos un grado de pertenencia α. (ver la ecuación 1)

Trabajos Previos

La salida de una red neuronal que propaga números difusos está dada por las ecuaciones (2) y (3), en donde 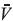se obtiene al realizar la combinación lineal de las entradas por medio de la extensión de la suma y la multiplicación al dominio de los números difusos y φ(�) es la función sigmoide 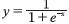extendida a los números difusos, como se muestra en las ecuaciones (2) y (3) (Duarte, 2005)

El problema del entrenamiento es encontrar un conjunto de pesos 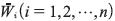que permitan el ajuste de la salida de la neurona a un conjunto de patrones de entrenamiento.

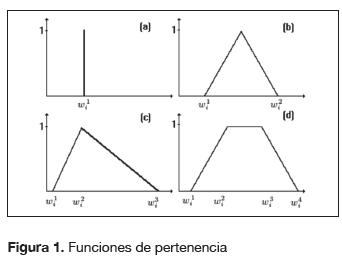
En Sevastjanov, Dymova y Bartosiewicz (2012) y Kimura, Nii, Yamaguchi, Takahashi y Yumoto (2011) estos definen distintos métodos de entrenamiento que tienen en común el limitar la forma de la función de pertenencia, tanto de los patrones de entrenamiento 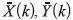-siendo {k) el índice del patrón- como de los pesos 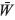a una geometría específica, como número crisp figura 1(a), triángulos simétricos 1(b), t. Asimétricos 1(c) o trapecios 1(d). Una vez que se tiene esta geometría se calcula el valor de la corrección necesaria en cada uno de los vértices característicos, por ejemplo, para el caso de pesos trapezoidales se tiene (ecuación 4):

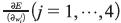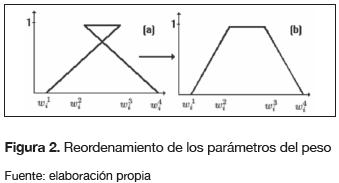
Cada uno de los valores es culado de manera similar como se realizaría para cuatro redes neuronales independientes, una por vértice. Este enfoque presenta principalmente dos desventajas, por un lado, puesto que se tienen correcciones independientes, es posible que el nuevo peso 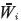obtenido no sea un número difuso (ver figura 2a), por lo tanto, es necesario reordenar los vértices como en la figura 2b. Se han planteado diversas alternativas para abordar este inconveniente, una de ellas desarrollada en Saad y Wunsch (2007) y en Huang y Wu (2011), quienes proponen una transformación que convierte el entrenamiento de la red neuronal difusa en un problema de optimización sin restricciones geométricas en los parámetros de los pesos difusos (Bede, Rudas y Benscsik, 2007).

Por otro lado, cuando se tiene una red con una o más capas ocultas, los gradientes 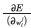dependen de los signos de los pesos de las capas siguientes.

Para afrontar este problema, se plantean algunas heurísticas que tienen en cuenta estos signos a la hora de obtener los gradientes. Dichas heurísticas solo se formulan para redes con una capa oculta, lo que limita la aplicación de este método de entrenamiento a redes con esta arquitectura.

Buckley, Czogala y Hayashi (2003) y Buckley, Czogala y Hayashi (2008) desarrollan también varias estrategias que se limitan a números difusos t. asimétricos como los de la figura 1c. El entrenamiento para el vértice w_i² se realiza mediante el algoritmo de retropropagación convencional, mientras que la corrección de la ambigüedad de los pesos se realiza por medio de algunas heurísticas. En Buckley et al. (2008) se propone otro método válido únicamente para entradas, salidas y pesos positivos, lo que elimina la discontinuidad en el gradiente del error que es ocasionada por los cambios de signo. En otro de estos trabajos (Krishnamraju, Buckley, Hayashi y Reilly, 2004) se plantea un entrenamiento a partir de algoritmos genéticos para pesos triangulares simétricos (figura 1b) donde los parámetros a ajustar son los extremos del soporte de cada peso (w_i¹, w_i³).

Metodología

Entre los principales inconvenientes que se aprecian en las estrategias discutidas en la sección anterior, se destacan las limitaciones impuestas tanto a la topología de la red, como a la geometría de los números difusos utilizados como pesos. Por esta razón, en este trabajo se formulan estrategias más generales respecto a las funciones de pertenencia de las entradas, salidas y pesos, así como a la arquitectura de la red.

Retropropagación del error cuadrático medio para todos los α-cortes para pesos crisp

Función de error

La función de error a minimizar es la mostrada en la ecuación (5).

Donde N es el conjunto de casos de entrenamiento y ε es, como se muestra en la ecuación (6), donde 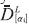representa el extremo izquierdo del i-ésimo α-corte de la salida deseada, 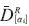representa su extremo derecho, 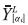es el extremo izquierdo del i-ésimo α-corte de la salida de la red neuronal y 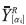es su extremo derecho.

Gradiente del error N

Como sucede en las redes neuronales convencionales, el valor del error, en este caso ε es función de todos los pesos w_ij, y para hallar la dirección de la corrección que debe ser aplicada a un peso w_ij es necesario obtener la derivada de ε con respecto a cada peso .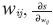

Para evitar las restricciones descritas en Villarreal (2008) para la obtención analítica de dicho gradiente, originadas por la dependencia de este valor de los signos de los pesos, se propone calcular una aproximación de forma numérica (ecuación 7).

Haciendo el valor de h cercano a cero para mejorar la calidad de la aproximación.

Algoritmo de entrenamiento

Puesto que el enfoque propuesto para el cálculo del gradiente es ineficiente desde el punto de vista del costo computacional, se implementó la heurística Rprop (Riedmiller, 1994). Este método tiene en cuenta únicamente el signo de la derivada para calcular el tamaño de la corrección de un peso y mejora considerablemente la velocidad de convergencia del algoritmo.

Las etapas necesarias para realizar el entrenamiento de la red propuesta mediante esta técnica son:

1. Propagar todos los casos hacia adelante y calcular el error total
2. Calcular el gradiente 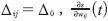mediante la ecuación (7).
3. Hallar el valor de la corrección necesaria para un peso w_ij, Δw_ij mediante la heurística Rprop (Riedmiller, 1994).
4. Actualizar el valor del peso mediante la ecuación (8).



5. Ir al paso 1 mientras Eumbral

Algoritmo genético para una red de números difusos con pesos crisp (AGCrisp)

Función objetivo

La ecuación (9) muestra la función de desempeño es el error cuadrático medio en todos los a-cortes(MSE^a

Siendo N el conjunto total de datos de entrenamiento. Por medio de la ecuación (9) se obtiene un índice que muestra qué tan semejantes son dos números difusos. Dicho índice puede ser utilizado como función de desempeño, que indique qué tan cerca se encuentra el algoritmo de la solución.

Codificación del individuo

La implementación del algoritmo genético se ha realizado bajo UN Genético 2.0 (Delgadillo, Madrid y Velez, 2004), una librería en C++ para la implementación de algoritmos genéticos. Gracias a la capacidad de esta herramienta de manejar individuos con genes de distintos tipos, la codificación del individuo se realizó asignando directamente a cada gen el valor de un peso sináptico de la red neuronal.

El problema de optimización ha sido limitado a tres funciones de razonamiento aproximado: combinación lineal, función sigmoide y polinomio.

Tanto la función combinación lineal como la logística toman la misma cantidad de parámetros. Por lo tanto, cada peso es asignado a un gen, indistintamente. Por otro lado, la función polinomio -que es válida solo para argumentos positivos- tiene algunos parámetros adicionales por optimizar -dependiendo del número de entradas a la neurona-, que representan los exponentes asignados a cada una de las entradas. Estos parámetros son representados por un arreglo de genes de tipo entero.

Retropropagación del error en el valor promedio y ancho de cada α-corte (BaPuzzy)

El enfoque sugerido aquí consiste en plantear dos funciones de error locales para cada α-corte, una correspondiente al valor promedio y otra a la ambigüedad. Luego, se calcula un gradiente independiente para cada una de ellas y se realizan correcciones simultaneas para cada iteración.

Definición 1: Sea 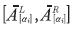un α-corte i de un número difuso 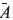el valor promedio de 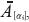, Vprom (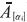) está dado por la ecuación (10).

Y la ambigüedad de 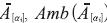se calcula mediante la ecuación (11).

Funciones de error

Las funciones de error por minimizar son entonces, para un α-corte i (ecuaciones 12 a 15).

Siendo C el conjunto de neuronas ubicadas en la capa de salida.

Actualización de los pesos

Debido a las funciones de error propuestas, para cada α-corte de un peso 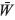_ij son necesarias dos correcciones, una para el valor promedio y otra para la ambigüedad. Para corregir el valor promedio es necesario desplazar todo el α-corte hacia la dirección deseada, como se muestra en las ecuaciones (16) y (17).

Mientras que para corregir la ambigüedad, es necesario modificar la separación entre los extremos, izquierdo y derecho de un α-corte (ecuaciones 18 y 19).

Para obtener los valores 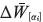se utiliza el algoritmo de retropropagación para redes crisp (Ru-melhart, Hinton y Willimas, 1986), de manera similar a la metodología utilizada en Lippe, Feuring y Mischke (1995).

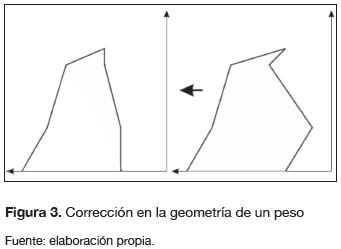
En el momento de realizar la actualización es necesario establecer ciertas restricciones a los nuevos extremos de los α-cortes de un peso 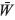_ij (figura 3), con el objetivo de que este continúe siendo un número difuso válido. Dichas restricciones son:

• Todo α-corte debe estar contenido en el α-corte inmediatamente anterior, esto es (ecuación 20)



Para ai < a₂

• No se permiten ambigüedades negativas, es decir, como se muestra en la ecuación (21)

Para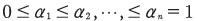

Retropropagación de un error difuso (BEFuzzy)

Definición de la función de error para una neurona difusa

La ecuación (22) muestra la función de error para una neurona difusa.

Seguida de la ecuación (23).

Donde el operador θ es conocido como la operación resta necesaria, definida como el inverso de la suma aritmética, así:

Definición 2: sean 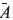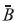dos números difusos, si existe un número difuso 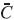tal que 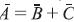entonces 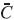se conoce como la resta necesaria entre 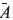y 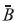y se denota por 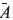Θ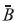

Para algunas formas particulares de 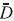y 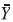_j es posible que no exista 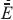₁ ni 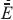₂ para estos casos se utiliza como medida de error una aproximación al número difuso más cercano a una posible solución.

Corrección de los pesos

En general, el error 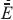₁ existe cuando se requiere un aumento en la ambigüedad de la salida 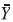_j y de forma complementaria, 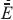₂ existe cuando debe reducirse la ambigüedad de 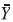_j. Por lo tanto, las correcciones en cada peso 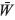_ji debido a cada uno de los errores deben tener efectos opuestos en la ambigüedad de 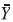_j. De esto se desprenden las ecuaciones (24) y (25) para la actualización de los pesos.

Algoritmo de entrenamiento

1. Realizar la propagación hacia adelante utilizando aritmética difusa.
2. Calcular el error 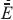₁ por medio de la ecuación (22).
3. Hallar Δ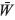_jie1
4. Corregir los pesos 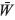_ji de acuerdo con la ecuación (22).
5. Propagar nuevamente hacia adelante.
6. ^Calcular 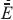₂ con la ecuación (23).
7. Hallar 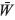_jie2.
8. Corregir los pesos 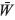_ji por medio de la ecuación (25).
9. Si no se satisface alguno de los criterios de parada definidos, ir al paso 1.

Resultados

Software implementado

FNetT (FuzzyNet Training) es una programa implementado en lenguaje C++ bajo el entorno de desarrollo wxWindows que permite el entrenamiento de redes neuronales que propagan números difusos implementadas en Fuzzynet 1.0.

FNetT además cuenta con las herramientas básicas para cargar y guardar los modelos de las redes, visualizar los casos de entrenamiento, visualizar y modificar los pesos de la red y exportar e importar los α-cortes de dichos pesos.

Estrategias implementadas

En FNetT se encuentran implementadas las siguientes estrategias de entrenamiento:

• Retropropagación del error cuadrático medio para todos los α-cortes para pesos crisp(BCrisp).
• Algoritmo genético para una red de números difusos con pesos crisp (AGCrisp).
• Retropropagación del error en el valor promedio y ancho de cada α-corte. sección (BαFuzzy).
• Retropropagación de un error difuso. (BE-Fuzzy).
• Con el objetivo de poder comparar el desempeño de las estrategias planteadas en este trabajo, con los trabajos previamente realizados acerca del entrenamiento de redes análogas a las tratadas aquí, fue necesario implementar una aproximación de una de las estrategias más representativas de las citadas en la sección correspondiente al estado del arte.
• Por último, FNetT cuenta con la implementa-ción de un algoritmo genético para la inversión de este tipo de redes, que permite el cálculo de las entradas a partir de una salida dada.

Experimentos realizados

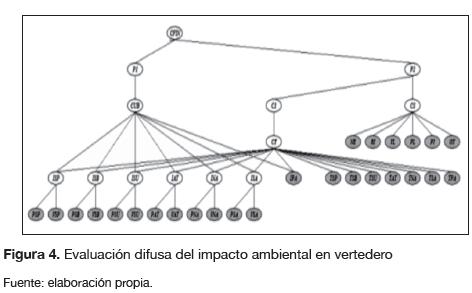
Evaluación Difusa del Impacto Ambiental en Vertederos (EDIAV). En una investigación previa, los parámetros de las distintas funciones presentes en la red de la figura 4 habían sido exitosamente sintonizados a partir de información proveniente de expertos en el tema. Para validar dicho sistema se calcularon los coeficientes de evaluación final para 34 vertederos ubicados en la provincia de Granada en España con resultados satisfactorios.

Con el objetivo de probar el desempeño de las estrategias de entrenamiento desarrolladas en la sección anterior, se implementó una nueva red de sistemas de computación con palabras que aproxime el mismo conjunto de casos utilizado para validar el sistema EDIAV. Dicha red debe tener 34 nodos de entrada, un bias y una salida CFIN. Los conjuntos difusos de las variables de entrada y de salida fueron normalizados, y se construyó -o función de activación- la extensión de la función sigmoide.

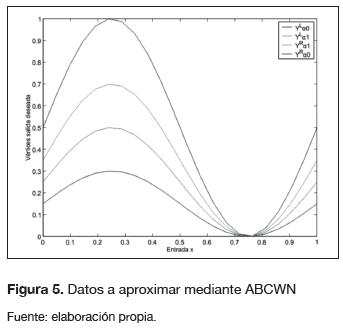
Modelamiento de un conjunto de datos de entrada crisp y salidas difusas. Los datos de entrada para este experimento son considerados números crisp, mientras que la salida es descrita de manera más adecuada mediante una variable lingüística cuyas etiquetas toman por valor números difusos con forma de campana. La figura 5 muestra los vértices de la salidad deseada 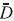para este conjunto de datos.

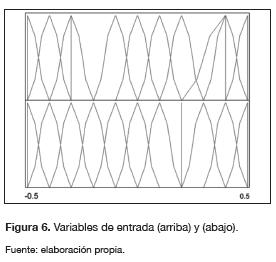
Modelamiento de un conjunto de datos de entrada difusos y salidas difusas. La función a aproximar es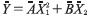

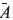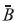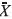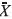Con = Campana(0.6, 0.8, 0.8, 1), = Trape-cio(0.4, 0.5, 0.6, 0.7). La figura 6 muestra los posibles valores que pueden tomar las variables ₁, ₂.

Realización de una base de reglas. Se construyó una ABCWN equivalente a la base de reglas de la tabla 1.

Aproximación de un polinomio que evalúa números difusos. La función crisp que ha sido extendida es la de la ecuación (26).

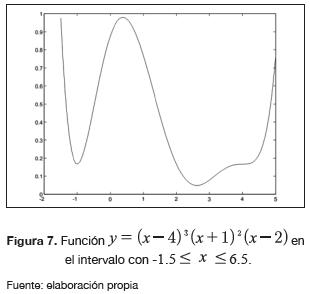
La figura 7 muestra el comportamiento de dicha función en el intervalo -1.5 ≤ x ≤ 6.5.

La forma extendida de y es idéntica a la ecuación (26) con la diferencia de que la variable x ha sido sustituida por la variable lingüística 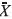. El espacio de entrada ha sido dividido en 40 etiquetas con forma triangular.

Discusión de los experimentos

Las conclusiones más significativas encontradas después de realizar este conjunto de experimentos son:

• Las dos estrategias que utilizan pesos crisp (AGCrisp y BCrisp) presentaron desempeños similares en cuanto a la calidad del modelo obtenido, dado que utilizan la misma función de desempeño. Sin embargo, el costo computacional de la estrategia basada en algoritmos genéticos presenta una gran desventaja, sobre todo en problemas de gran cantidad de parámetros por ajustar, como el descrito en el ejemplo EDIAV. Esto permite recomendar su utilización únicamente con problemas con un número reducido de variables y casos.
• En general, las estrategias de entrenamiento de pesos difusos, bien se trate de las desarrolladas en este trabajo (BαFuzzy y BEFuzzy) o de la implementación que se realizó de los planteamientos encontrados en la consulta de referencias, demostraron ser mejores, en términos de la calidad de ajuste, que los planteamientos que hacen uso de pesos crisp, en especial cuando se trata de modelar un conjunto de datos donde las entradas son crisp y las salidas son difusas.
• Se consideró la aproximación de un conjunto de datos proveniente de una función difusa, en el que, además de la incertidumbre propia del modelo, se tiene incertidumbre en las entradas. En el ejemplo planteado se encontró que una red con pesos crisp entrenada mediante BCrisp no presentó grandes desventajas en el aprendizaje de este conjunto de datos, en comparación de las estrategias que utilizan pesos difusos.
• En los problemas de aproximación de funciones, no se encontraron grandes diferencias a favor de ninguna de las estrategias de entrenamiento con pesos difusos; sin embargo, en la mayoría de los ejemplos, sí hay una ligera diferencia en favor de la estrategia de retro-propagación de un error difuso BEFuzzy, y en contra de la implementación de la estrategia propuesta por otros autores.
• En el ejemplo del sistema EDIAV se evidenció que, mientras las estrategias de pesos difusos planteadas aquí (BαFuzzy y BEFuzzy) convergen también a pesos crisp, los pesos calculados con la estrategia realizada por otros autores eran cada vez más ambiguos. Este hecho se reflejó en el pobre desempeño de la estrategia a la hora de evaluar la consistencia entre el conjunto difuso obtenido y las etiquetas predefinidas para la variable lingüística CFIN, en donde, generalmente se encontraron aproximaciones lingüísticas de la forma: muy posiblemente Bajo(1.0)-muy posiblemente Medio(1.0)-muy posiblemente Alto(1.0)-muy posiblemente Muy Alto(1.0).
• La retropropagación con pesos crisp presentó los mejores resultados a la hora de aproximar conjuntos de datos provenientes de funciones crisp extendidas -regresión de reglas y funciones extendidas-, así como en el modelamiento del sistema EDIAV, que mostró, por un amplio margen, ser la mejor estrategia.
• Una red de este tipo puede ser entrenada tanto a partir de información cuantitativa como cualitativa; además, permite modelar la incertidumbre presente, tanto en las entradas y las salidas, como en el modelo mismo.
• Gracias a que la información se almacena en los pesos de las conexiones, es decir, en los parámetros de las funciones de razonamiento aproximado, se evita el problema de la explosión del tamaño de la base de reglas, el cual siempre está presente cuando se manejan sistemas de lógica difusa para problemas con un número considerable de entradas, y etiquetas asociadas a cada entrada y con relaciones no muy evidentes entre entradas y salidas.
• El costo computacional de entrenar y propagar datos a través de una red de sistemas de computación con palabras es mucho mayor que en una red neuronal convencional y es proporcional a la cantidad de α-cortes utilizada para la representación discreta de un número difuso. En aplicaciones en las que no se deban considerar las formas de la salida, resulta sensato utilizar únicamente 2 α-cortes. Además, es importante tener en cuenta que el uso de cualquier tipo de sistema de computación con palabras se justifica únicamente cuando la información disponible es demasiado imprecisa para ser representada por números crisp.

Conclusiones

El uso de pesos crisp es una alternativa que debe ser tenida en cuenta a la hora de modelar la relación presente en un conjunto de datos difusos. El desempeño de esta estrategia se destacó en el problema del sistema de evaluación difusa del impacto ambiental en vertederos.

La totalidad de las estrategias de entrenamiento planteadas en este proyecto son válidas para redes con cualquier número de capas ocultas.

El entrenamiento de una ABCWN con pesos crisp mediante algoritmos genéticos con codificación real, puede arrojar resultados similares a los encontrados con BCrisp, en cuanto a la calidad de la aproximación. Sin embargo, el elevado tiempo de cálculo, debido a la gran cantidad de parámetros por ajustar limita la aplicación de esta estrategia a problemas relativamente pequeños. Este hecho hace dudar de la viabilidad del empleo de alguna técnica similar que considere pesos difusos, puesto que se tendría una cantidad aún mayor de parámetros por ajustar.

Ninguna de las dos estrategias para pesos difusos formuladas (BαFuzzy, BEFuzzy) presentan limitaciones en cuanto a la geometría de los pesos difusos -siempre que sean números difusos.

A pesar de que la estrategia BαFuzzy no maneja una función de error global, sino múltiples funciones de error independientes, mostró tener un comportamiento aceptable en los experimentos realizados, con excepción del problema EDIAV.

La estrategia fundamentada en la retropropagación de un error difuso (BEFuzzy) se obtuvo al extender algunos conceptos del cálculo crisp al dominio de los números difusos.

Las redes con pesos difusos mostraron ser el mecanismo más adecuado para representar la incertidumbre propia de un sistema. Los resultados de este enfoque se destacaron especialmente a la hora de aproximar conjuntos de datos con entradas crisp y salidas difusas.

Las estrategias para redes con pesos crisp mostraron los mejores desempeños a la hora de aproximar conjuntos de datos provenientes de funciones extendidas a los números difusos.

Financiamiento

El presente trabajo fue financiado por los autores e hizo parte del desarrollo de un trabajo de conclusión de Maestría en Automatización Industrial en la Universidad Nacional de Colombia.

Referencias

Duarte, O. (2005). Fuzzynet 1.0 software para el diseño e implementación de redes de sistemas de computación con palabras. Programa de Ingeniería Eléctrica, Universidad Nacional de Colombia.

Bede, B., Rudas, I. & Benscsik, A., (2007). First order linear fuzzy differential equations under generalized differentiability. Information Sciences, 177, 1648-1662.

Buckley, J., Czogala, E. & Hayashi, Y., (2003). Fuzzy neural networks with fuzzy signals and fuzzy weights. International Journal on Intelligent Systems, 8, 527-537.

Buckley, J., Czogala, E. & Hayashi, Y. (2008). Adjusting fuzzy weights in fuzzy neural nets. Second International Conference on Knowledge-Based Intelligent Electronic Systems.

Delgadillo, A., Madrid, J. y Vélez, J., (2004). Ampliación de UNgenético: una Librería en C++ de Algoritmos genéticos con Codificación Híbrida. (Tesis de Pregrado en Ingeniería Eléctrica). Universidad Nacional de Colombia.

Huang, H, & Wu, C., (2011). Approximation of fuzzy functions by regular fuzzy neural networks. Fuzzy Sets and Systems, 177, 60-79.

Kimura, D., Nii, M., Yamaguchi, T., Takahashi, Y., & Yumoto, T., (2011). Fuzzy Nonlinear Regression Analysis Using Fuzzified Neural Networks for Fault Diagnosis of Chemical Plants. J. Ref J. Adv. Comput. Intell. Intell. Informatics, 15 (3), 336-344.

Klimke, A. (2006). Uncertainty Modeling using Fuzzy Arithmetic and Sparse Grids. (PhD Tesis). Universitát Stuttgart, Alemania.

Krishnamraju, P., Buckley, J., Hayashi, J. & Reilly, K., (2004). Genetic learning algorithms for fuzzy neural nets. IEEE World Congress on Computational Intelligence 26-29.

Lippe, W., Feuring, T. & Mischke, L., (1995). Supervised Learning in Fuzzy Neural Networks. Department of Computer Science, University of Munster.

Riedmiller, M. (1994). Rprop-Description and Implementation Details. Technical Report. Inst. f. Logik, Komplexitát u. Deduktions-systeme.

Rumelhart, D., Hinton, G. & Willimas, R., (1986). Learning representations by back-propagating errors. Nature, 323, 533-536.

Saad, E. & Wunsch, D., (2007). Neural network explanation using inversion. International Journal on Neural Networks, 20, 78-93.

Sevastjanov, P., Dymova, L. & Bartosiewicz, P., (2012). A new approach to normalization of interval and fuzzy weights. Fuzzy Sets Syst, 198, pp.34-45.

Villarreal, E. (2008). Estrategias de Entrenamiento para un Red Neuronal Difusa. (Tesis de Maestría en Ingeniería. Automatización Industrial). Universidad Nacional de Colombia.

Zadeh, L. (1975). The Concept of a Linguistic Variable and its Application to Approximate Reasoning. IEEE Trans. Systems, Man, and Cybernet.