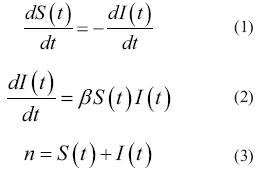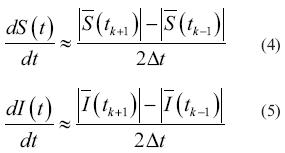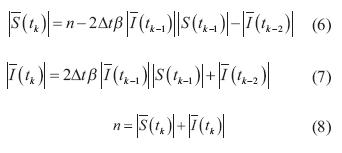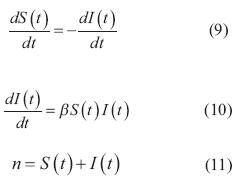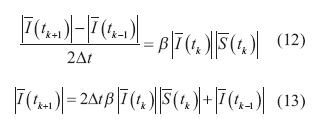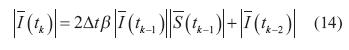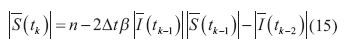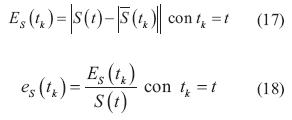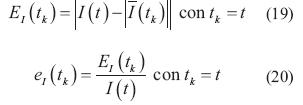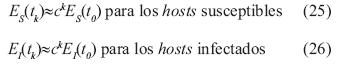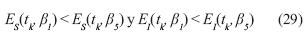DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2014.4.a01Publicado:
01-10-2014Número:
Vol. 18 Núm. 42 (2014): Octubre - DiciembreSección:
InvestigaciónAproximación numérica del modelo epidemiológico SI para la propagación de gusanos informáticos, simulación y análisis de su error
Numerical Approaching of Si Epidemic Model for Spreading of Computer Worms, Simulation and Error Analysis
Descargas
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Aproximación numérica del modelo epidemiológico S/ para la propagación de gusanos informáticos, simulación y análisis de su error
Numerical Approaching of Si Epidemic Model for Spreading of Computer Worms, Simulation and Error Analysis
Pedro Guevara López1, Jorge Salvador Valdez Martínez2, Jesús Audelo González3, Gustavo Delgado Reyes4
1Ingeniero electricista, maestro en Ciencias de la Computación, doctor en Ciencias de la Computación, doctor en Filosofía de la Educación Iberoamericana, profesor investigador de la Escuela Superior de Ingeniería Mecánica y Eléctrica, Distrito Federal, México. Contacto: pguevara@ipn.mx
2Ingeniero en Comunicaciones y Electrónica con especialidad en Acústica, maestro en Tecnología Avanzada, candidato a doctor en Ciencias en Ingeniería en Comunicaciones y Electrónica, profesor de la Universidad Tecnológica Emiliano Zapata, Morelos, México. Contacto: jorgevaldez@utez.edu.mx
3Ingeniero en Computación, maestro en Ciencias de Ingeniería en Microelectrónica, doctor en Ciencias en Ingeniería en Comunicaciones y Electrónica, Distrito Federal, México. Contacto: jaudelo@ipn.mx
4Ingeniero en Comunicaciones y Electrónica, maestro en Ciencias de Ingeniería en Microelectrónica, candidato a Doctor en Ciencias en Ingeniería en Comunicaciones y Electrónicam Distrito Federal, México. Contacto: gdelgador1200@alumno.ipn.mx
Fecha de recepción: 31 de agosto de 2013 Fecha de aceptación: 16 de mayo de 2014
Clasificación del artículo: Investigación
Financiamiento: Instituto Politécnico Nacional de México
Resumen
En el entorno biológico se han creado modelos epidemiológicos que tratan de explicar la dinámica de propagación de una epidemia en una población de individuos, para predecir el comportamiento de posibles epidemias que afecten a la humanidad. Esto ha servido de inspiración para estudiar las epidemias por gusanos informáticos, debido a que estos tienen la propiedad de propagarse por sí solos, a partir de un host infectado, hacia toda la red de hosts susceptibles. En este trabajo se analizó el modelo Susceptible-Infec-tado (SI) que asume que en una comunidad con n individuos, el número de individuos en estado susceptible S{t) entran en contacto directo con el número de individuos en estado infectado I(t). Estos últimos pueden contagiar o cambiar a estado infeccioso con una velocidad de infección ß. Este modelo, al estar basado en ecuaciones diferenciales, no es posible implementarlo directamente en un programa de computadora, debido a la complejidad que esto representa por la infinidad de cálculos implícitos. Por esta razón se propuso un modelo aproximado basado en ecuaciones en diferencias finitas para obtener un método numérico iterativo con operaciones aritméticas elementales y lograr una simulación de la epidemia mediante teoría de conjuntos y cardinalidades. Adicionalmente, al tratarse de un modelo aproximado, se tendrá presente un error de aproximación debido a truncamiento o redondeo, el cual es analizado a partir de un caso de estudio desarrollado en Si-mulink de Matlab, comparándose los resultados del modelo basado en ecuaciones en diferencias con el modelo aproximado por diferencias finitas.
Palabras clave: algoritmo, bioinspirado, epidemia, gusano informático, simulación.
Abstract
In the biological environment, there has been created epidemiological models that attempt to explain the spread dynamics of an epidemic in a population to predict the behavior of possible epidemics that can affect humanity. Based on that, this paper focused on the study of epidemics worms because they can spread by themselves from one infected host to the entire network of susceptible hosts. In this paper we analyzed the susceptible-infected {SI) model which assumes that in a community with n individuals, the number of individuals in the susceptible state S{t) are in direct contact with the number of individuals that are in infected state I(t). These last individuals can spread the infection or switch to an infectious state with the factor ß as a speed of infection. This model is based on differential equations so it cannot be implemented directly on a computer. Due to the complexity of this model, it is proposed an approximate model based on finite different equations to achieve a simulation of the epidemic using a set theory and cardinality obtaining an iterative numerical method which consists on basics arithmetic operations. Additionally, having in mind this is an approximate model, it will be presented an error due to truncation or rounding. At the end of this paper it will be presented a case of study developed in Simulink of Matlab software, and the results of the model based on difference equations is compared with the finite-difference approximate model including the analysis of approximation errors.
Keywords: algorithm, bio-inspired, computer worm, epidemic, simulation.
Introducción
En la historia de la humanidad, debido a la aparición de epidemias como la peste negra en el siglo XIV, la epidemia de gripe de 1918 a 1919 y hoy la pandemia del Síndrome de Inmunodeficiencia Adquirida (SIDA) o la gripe A (H1N1) -la cual causo la muerte de 18 000 personas en el mundo del 2009 al 2010-, se han creado modelos epidemiológicos que tratan de explicar la dinámica de propagación de una epidemia en una población de individuos, tomando en consideración varios factores como la velocidad de diseminación, la inmunidad hacia la enfermedad, el número de individuos, etcétera, para predecir el comportamiento de posibles epidemias que pueden afectar a la humanidad. Pero esto no ha sucedido solamente en el ámbito biológico, sino también en el ámbito tecnológico debido a la aparición de gusanos informáticos. De acuerdo con Audelo et al. (2012) y Erbschloe (2005), un gusano informático es un código malicioso (malware) con la propiedad de propagarse por sí solo mediante el uso de los procesos del sistema operativo, que generalmente son invisibles al usuario. Desde que apareció el primero en 1979, los gusanos informáticos han causado grandes daños a instituciones gubernamentales, universidades y empresas, generando numerosas pérdidas económicas (Au-delo et al., 2012), situación esta que es un anticipo de las repercusiones económicas y sociales que pueden causar en el futuro. El avance tecnológico actual ha permitido el desarrollo de este tipo de programas, en forma tal que cada vez es más difícil protegerse de ellos. De ahí la importancia de usar modelos epidemiológicos biológicos para modelar matemáticamente la dinámica de propagación de epidemias de gusanos informáticos, de tal manera que permitan el desarrollo de herramientas para contraatacarlos rápida y efectivamente (Nazario, 2004). Cabe señalar que la representación mediante modelos matemáticos no siempre es fácil de resolver a partir de métodos analiticos. En algunos casos es imposible obtener una solución exacta y en otros implica análisis y procesos complejos que consumen una cantidad considerable de tiempo; además, debe considerarse la dificultad de emulación del fenómeno computacionalmente.
Hoy en día se usan diversos métodos numéricos para la solución de este tipo de problemas. Estos métodos constituyen una serie de técnicas basadas en procesos cíclicos o iterativos, partiendo de la aplicación de ecuaciones expresadas en forma recursiva que relacionan dos o más elementos consecutivos de una sucesión de números, funciones, matrices, etc., lo cual permite formular problemas matemáticos que pueden resolverse con operaciones aritméticas realizadas por equipos de cómputo, obteniéndose aproximaciones numéricas que permiten acercarse a la solución con un cierto grado de aproximación (Iriarte, 2007). A este grado de aproximación o desviación del valor real se le llama error, el cual es acrecentado por los resultados de las operaciones aritméticas hechas por el equipo de cómputo, habida cuenta de que los valores obtenidos son truncados o redondeados y ello ocasiona que el error obtenido de la aproximación hecha con respecto a la desviación del valor real inicial (error inicial) permanezca constante o que vaya incrementándose conforme va evolucionando el sistema.
Por ello, en este trabajo se propone una aproximación numérica basada en la teoría de conjuntos y en el método numérico de diferencias finitas centrales, del modelo general epidemiológico Susceptible-Infectado (SI) que describe el comportamiento dinámico de uno de los modelos de propagación de enfermedades biológicas. Dicha aproximación es validada mediante el uso de medidas descriptivas basadas en el estudio del comportamiento de la desviación del valor real (error) conforme la evolución del tiempo. Lo que permite sugerir su uso para otros modelos epidemiológicos biológicos como el Modelo Susceptible-Infectado-Recuperado (SIR) o el Modelo Susceptible-Infectado-Recuperado-Susceptible (SIRS).
Metodología
Los modelos matemáticos basados en el modelo general de Kermack-McKendrick (Kermack y McKendrick, 1927), que se utilizan para describir el comportamiento dinámico de la propagación de enfermedades biológicas, se definen como sistemas dinámicos, pues al ser razones de cambio con respecto al tiempo de tres niveles de estado posibles: el estado Susceptible (S), el estado Infeccioso (I) y el estado Recuperado (R), pueden ser representados con ecuaciones diferenciales. Análogamente, estos sistemas dinámicos biológicos pueden ser utilizados para tratar de describir el comportamiento de la propagación de los gusanos informáticos, debido a que estos tienen la capacidad de propagarse sin necesidad de ninguna intervención del usuario.
Modelo epidemiológico Susceptible-Infectado (SI)
Para el caso de estudio, el modelo Susceptible-Infectado (SI), de acuerdo con Hincapié y Ospina (2007), este asume que en una comunidad con n individuos, el número de individuos en estado susceptible S(t) entra en contacto directo con el número de individuos en estado infectado I(t), quienes pueden contagiar o cambiar a estado infeccioso con una velocidad de infección ß a los individuos en estado susceptible. El número total de individuos n será igual a la suma del número de individuos en estado susceptible S(t), más el número de individuos en estado infectado I(t). En la ecuación (1) se describe la dinámica del número de individuos susceptibles, en la ecuación (2) el número de individuos infectados y en la ecuación (3) el número total de individuos:
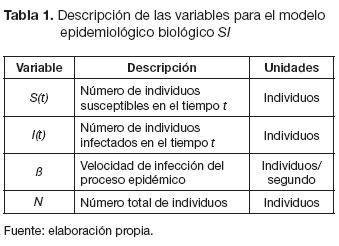
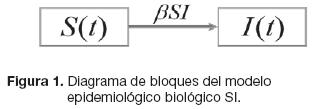
En la tabla 1 se presenta la descripción de variables, en tanto que el diagrama a bloques se aprecia en la figura 1.
El modelo epidemiológico biológico SI ha sido considerado por varios autores (Chang Chun et al., 2002; Yang y Chenxi, 2003; Tao et al., 2007; Onwubico et al., 2005; Juan et al., 2010) para modelar virus y gusanos informáticos en forma continua como un sistema dinámico basado en ecuaciones diferenciales, lo que dificulta la obtención y la programación de los algoritmos computacionales que hagan posible emular su dinámica en una computadora. Para ello es necesario contar con sus modelos aproximados. Sin embargo, en la literatura es complicado encontrar trabajos que basen su investigación en los modelos en forma discreta. Entre los encontrados está el presentado por Cohen (1992), que es uno de los principales trabajos en donde se puede observar un lenguaje formal para la descripción de los conceptos sobre gusanos informáticos. Además de Tassier (2005), en donde se trabaja con las bases matemáticas del modelo clásico SI de manera discreta, para modelar el comportamiento de gusanos informáticos. Esta problemática sirvió de motivación para el desarrollo de la siguiente sección.
Modelo SI expresado en aproximaciones por ecuaciones en diferencias
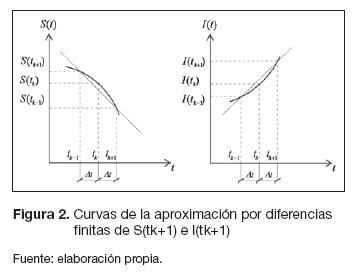
El método numérico de diferencias finitas consiste en una aproximación de las derivadas que aparecen en un problema de ecuaciones diferenciales ordinarias, de forma que se reduzca a resolver un sistema lineal en un número limitado de puntos seleccionados. Como resultado de la aproximación, la ecuación diferencial es reemplazada por un número finito de ecuaciones algebraicas en términos de los valores de la variable dependiente en puntos seleccionados (Hernández, 2010). Para el modelo epidemiológico SI usado para describir el comportamiento de propagación del gusano informático se consideran los instantes de tiempo 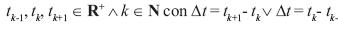 ; entonces, por diferencias finitas se consideraron las ecuaciones (4) y (5).
; entonces, por diferencias finitas se consideraron las ecuaciones (4) y (5).
Con base en la figura 2 y considerando el concepto de diferencia finita como aproximación a la derivada de las ecuaciones (4) y (5), se propone el siguiente teorema para la solución numérica del modelo SI.
Teorema 1. El modelo epidemiológico SI usado para describir la dinámica de propagación del gusano informático expresado en ecuaciones en diferencias está descrito por las ecuaciones (6), (7) y (8).
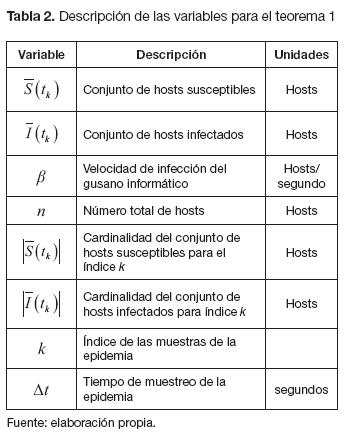
Cuya descripción de variables se puede apreciar en la tabla 2:
Demostración. Partiendo del trabajo de Hincapié y Ospina (2007), se presenta una analogía de la dinámica del comportamiento del gusano informático con el modelo clásico epidemiológico SI expresado en ecuaciones diferenciales por (9),
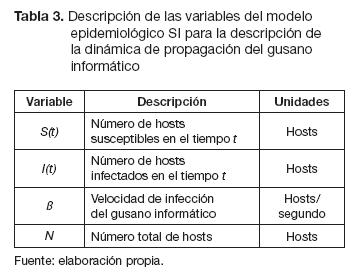
En este caso la descripción de variables se presenta en la tabla 3.
Considerando las ecuaciones (5) y (10) se obtienen las ecuaciones (12) y (13):
Reescribiendo la ecuación (13) y considerando un intervalo de tiempo anterior se obtiene la ecuación (14).
De las ecuaciones (11) y (14) se obtiene la ecuación (15).
Finalmente, de la ecuaciones (11), (14) y (15) se obtiene la ecuación (16).
Error y estabilidad numérica en la simulación por aproximaciones del modelo SI
El modelo aproximado SI, al obtenerse por diferencias finitas, proporciona un método numérico iterativo basado en operaciones aritméticas elementales (Nakamura, 1992). Al efectuar una serie de operaciones aritméticas para resolver un problema, se presentan algunas variaciones con respecto al valor real o a los errores que pueden clasificarse, de acuerdo con su origen, en tres tipos: errores inherentes, errores por truncamiento, errores por redondeo, los cuales se incrementan a lo largo de la evolución del sistema al efectuarse operaciones aritméticas elementales (Nakamura, 1992). Es bien sabido que los métodos iterativos no siempre proporcionan aproximaciones aceptables (Chapra, 2012), y en la mayoría de los casos el error que se obtiene al aplicarlos aumenta a medida que se incrementa el número de iteraciones. Por esa razón, es importante calcular el error generado por la aproximación, comparado con el modelo original, por lo que para el modelo de S(tk) se calculan el error absoluto ES(tk) y el error relativo eS(tk), mientras que para el modelo I(tk) se calculan el error absoluto EI(tk) y el error relativo eI(tk), definidos por las siguientes ecuaciones, basadas en Iriarte (2007) y representadas en las ecuaciones (17) y (18), donde S(tk) es la cardina-lidad del conjunto de hosts susceptibles para el índice k y S(t) es el número de hosts susceptibles en el tiempo t:
Las ecuaciones (19) y (20) corresponden al error absoluto y al error relativo del conjunto de hosts infectados, donde I(tk) es la cardina-lidad del conjunto de hosts infectados para el índice k e I(t) es el número de hosts infectados en el tiempo t:
Otra herramienta descriptiva que permite validar la aproximación numérica obtenida del método de aproximación es el estudio de la estabilidad numérica, la cual consiste en asegurarse de que tanto las aproximaciones numéricas como los sistemas reales, en su evolución temporal, no amplifiquen los errores iniciales, o que al menos no lo hagan de manera creciente y descontrolada (Zuazua, 2007).
Entonces, si por alguna razón el error absoluto de los modelos obtenidos Es(tk) y E(tk) se incrementa en forma lineal, o aproximadamente lineal conforme k aumenta, entonces se dice que el método de aproximación es numéricamente estable, de acuerdo con las ecuaciones (21) y (22) (Suárez, 1997).
Expresando las ecuaciones (21) y (22) en forma de cocientes se obtienen las ecuaciones (23) y (24).
Para alguna constante c < 1 que no depende de k.
En caso de que el error absoluto de los modelos obtenidos Es(tk) y EI(tk) se incremente en forma exponencial, o aproximadamente exponencial conforme k aumenta, entonces se dice que el método de aproximación es numéricamente inestable. Esto se expresa en las ecuaciones (25) y (26) para los hosts susceptibles e infectados respectivamente (Suárez, 1997).
La cual se reescribe en forma de cocientes en las ecuaciones (27) y (28) de la siguiente manera:
Para alguna constante c > 1.
Entonces, al usar el error absoluto así como su estabilidad numérica como medidas descriptivas, se asegura que del método numérico usado se obtiene una aproximación numérica aceptable.
Resultados
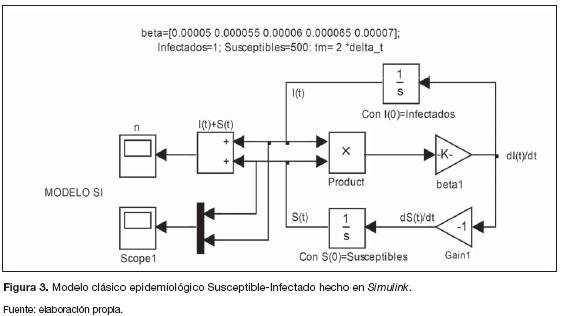
Como una demostración experimental de lo expuesto en la sección anterior, en este apartado se plantea hacer una comparación de los modelos expresados en forma continua, basados en ecuaciones diferenciales, y los modelos obtenidos a partir de las aproximaciones por ecuaciones en diferencias. A partir del modelo clásico de Susceptible-Infectado expresado en ecuaciones diferenciales, obtenido de Hincapié y Ospina (2007), las ecuaciones (9), (10) y (11) se simulan utilizando el entorno de diagramas de bloques para la simulación de sistemas continuos y discretos llamado Simulink de Matlab. Entonces, la representación por bloques para las ecuaciones del modelo SI en Simulink es la que se muestra en la figura 3.
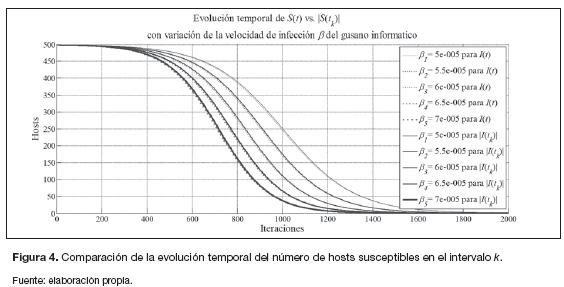
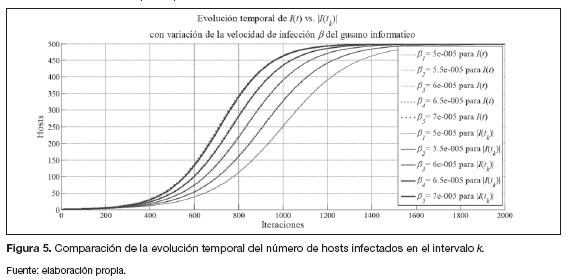
Tomando como referencia este modelo, así como sus valores propuestos, se pretende hacer una comparación del modelo de propagación del gusano informático SI, expresado en ecuaciones diferenciales, y la aproximación numérica obtenida a partir del método de diferencias finitas, variando la velocidad de infección ß del gusano informático. Como resultado se obtienen las gráficas que se presentan en las figuras 4 y 5.
En la figura 4 se puede apreciar que la aproximación numérica obtenida para el número de hosts en estado susceptible en el tiempo 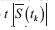 , utilizando el método de las diferencias finitas, tiende a un valor cercano de S(t) del modelo de propagación del gusano informático basado en Hincapié y Ospina (2007) y evoluciona siguiendo la misma trayectoria para cuando se varía la velocidad de infección ß del gusano informático en ambos modelos. Lo mismo se puede apreciar en la figura 5 para el caso de la evolución temporal de la aproximación numérica a partir del método de las diferencias finitas del número de hosts en estado infeccioso en el tiempo
, utilizando el método de las diferencias finitas, tiende a un valor cercano de S(t) del modelo de propagación del gusano informático basado en Hincapié y Ospina (2007) y evoluciona siguiendo la misma trayectoria para cuando se varía la velocidad de infección ß del gusano informático en ambos modelos. Lo mismo se puede apreciar en la figura 5 para el caso de la evolución temporal de la aproximación numérica a partir del método de las diferencias finitas del número de hosts en estado infeccioso en el tiempo 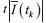 .
.
En este sentido, aunque gráficamente la aproximación numérica de 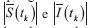 parece estar cerca de una región de valores reales de S(t) y de I(t), respectivamente, cuando tk = t, no es suficiente decir que es una buena aproximación. Entonces, para validar los resultados de estas aproximaciones se plantea utilizar medidas descriptivas como el error absoluto a partir de las ecuaciones (17) y (19) de la aproximación numérica, así como su estabilidad numérica, considerando a las ecuaciones (23), (24), (27) y (28).
parece estar cerca de una región de valores reales de S(t) y de I(t), respectivamente, cuando tk = t, no es suficiente decir que es una buena aproximación. Entonces, para validar los resultados de estas aproximaciones se plantea utilizar medidas descriptivas como el error absoluto a partir de las ecuaciones (17) y (19) de la aproximación numérica, así como su estabilidad numérica, considerando a las ecuaciones (23), (24), (27) y (28).
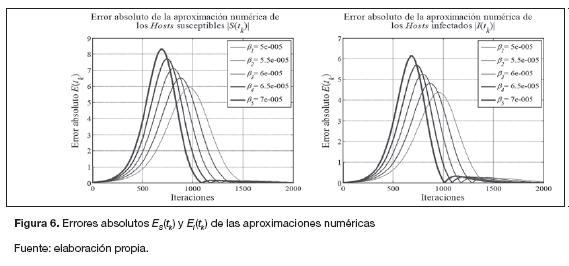
Para los errores absolutos ES(tk) y EI(tk) se obtienen las gráficas de la figura 6:
Considerando la figura 6, se observa que el error absoluto de la aproximación numérica del número de hosts susceptibles es ES(tk) = 8297 hosts para ß5 y de 5919 hosts para ß1 en donde ß5> ß1 para cuando n = 500. Por otra parte, el error absoluto de la aproximación numérica del número de hosts infectados es EI = 6131 hosts para ß5, y EI(tk) =4373 hosts para ß1 donde ß5 > ß1cuando n = 500. Al realizar la simulación de los modelos SI utilizando un muestreo Δt2 < Δt1 se destaca el hecho de que los errores absolutos ES(tk) y EI(tk) reducen su magnitud; sin embargo, considerando que ß5 > ß1 prevalece la ecuación (29).
Con esto se puede concluir que el error absoluto de la aproximación numérica del modelo SI uti-fizando el método de las diferencias finitas, además de ser afectado por el periodo de muestreo, también lo es por la velocidad de infección ß del gusano informático y aunque la reducción del error absoluto se suscita a medida que se utilizan tiempos de muestreo At cada vez menores, la condición que prevalece es que las magnitudes de los errores absolutos obtenidos para velocidades de infección grandes son mayores en comparación con los errores absolutos logrados a través de velocidades de infección pequeñas. Lo que permite concluir que el modelo de aproximación basado en diferencias finitas tiene, en general, un error mínimo comparado con el número total de hosts en la red computacional, que para este caso es de 500.
Para obtener la estabilidad numérica de la aproximación del modelo de propagación del gusano informático SI se parte del análisis de las gráficas mostradas en la figura 6.
A partir de la gráfica del error absoluto ES(tk) para el caso de la aproximación numérica del número de_ hosts en estado susceptible en el tiempo 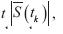 , se puede observar que para las velocidades de propagación propuestas, al principio de la simulación la estabilidad numérica tiene un comportamiento de tipo exponencial positivo, definido por la ecuación (27), llegando a un máximo de 8297 (en el caso de la velocidad de propagación ß5), para después tener un comportamiento exponencial negativo que va aproximándose hasta un valor cercano a cero, permaneciendo constante a lo largo de la evolución del sistema, lo que concuerda con lo mostrado en la ecuación (23). Lo mismo se puede decir de la estabilidad numérica para el caso de la aproximación numérica del número de hosts en estado infeccioso en el tiempo
, se puede observar que para las velocidades de propagación propuestas, al principio de la simulación la estabilidad numérica tiene un comportamiento de tipo exponencial positivo, definido por la ecuación (27), llegando a un máximo de 8297 (en el caso de la velocidad de propagación ß5), para después tener un comportamiento exponencial negativo que va aproximándose hasta un valor cercano a cero, permaneciendo constante a lo largo de la evolución del sistema, lo que concuerda con lo mostrado en la ecuación (23). Lo mismo se puede decir de la estabilidad numérica para el caso de la aproximación numérica del número de hosts en estado infeccioso en el tiempo 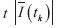 , a diversas velocidades de propagación del gusano informático ß. Lo que permite concluir que, en general, el modelo de aproximación basado en diferencias finitas tiene un comportamiento numérico estable a lo largo de la evolución del sistema.
, a diversas velocidades de propagación del gusano informático ß. Lo que permite concluir que, en general, el modelo de aproximación basado en diferencias finitas tiene un comportamiento numérico estable a lo largo de la evolución del sistema.
Conclusiones
La aproximación numérica basada en teoría de conjuntos, combinada con el método de las diferencias finitas centrales del modelo de propagación SI utilizado para la descripción de la propagación de gusanos informáticos, es eficaz y puede ser usada para aproximar otros modelos de propagación de gusanos informáticos de mayor complejidad basados en los modelos epidemiológicos biológicos SIR y SIRS.
En la validación de la aproximación basada en diferencias finitas centrales, el error absoluto permite observar la desviación del valor obtenido con respecto al valor real obtenido del modelo basado en ecuaciones diferenciales, pues la trayectoria que sigue el valor del error absoluto ES(tk) y EI(tk) es aceptable en comparación con el número total n de hosts en la red computacional, ya que el valor máximo no se repite a lo largo de la evolución del sistema, pues permanece dentro de una región cercana a cero. También se observa la razón de cambio con respecto al tiempo de la misma trayectoria del valor del error absoluto ES(tk) y EI(tk). La pendiente obtenida se dice que es pequeña, lo que permite afirmar que los valores de la aproximación numérica del modelo SI utilizando el método de las diferencias finitas son numéricamente estables, ya que en la curva mencionada no hay pendientes cercanas a uno.
Financiamiento
Este trabajo se deriva del proyecto de investigación con título Estimación de los Tiempos de Ejecución y de Transporte para Sistemas en Tiempo Real a Distancia Basados en TCP/IP, con registro 20131795 de la Secretaría de Investigación y Posgrado del Instituto Politécnico Nacional de México (enero de 2013 - diciembre de 2013).
Referencias
Audelo, J., Castañeda, A. y Guevara, P., "Gusanos informáticos: de los inicios a su primer impacto en los gobiernos", Revista Aleph Zero, Año 17, No. 64, 2012, pp. 22-25. Recuperado el 5 de junio de 2013, de http://www.comprendamos.org/az/alephzero/aleph64.pdf.
Chang Chun, C., Gong, W. y Towsley, D., "Code Red Worm Propagation Modeling and Analysis", CCS'02, Washington DC, USA, 2002, pp. 1-10, Recuperado el 5 de junio de 2013, de http://www-unix.ecs.umass.edu/~gong/papers/codered.pdf.
Chapra, S. C., Applied Numerical Methods with Matlab for Engineers and Scientists (3rd Ed.), McGraw-Hill, 2012.
Cohen, F., "A Formal Definition of Computer Worms and Some Related Results", Computers & Security, Vol. 11, No. 7, 1992, pp. 641-52. Recuperado el 5 de junio de 2013, de http://game.all.net/.books/tech/wormdef.pdf.
Erbschloe M., Trojans, Worms, and Spyware: A Computer Security Professional's Guide to Malicious Code, Massachusetts, USA, Butterworth-Heinemann (Elsevier), 2005. Recuperado el 5 de junio de 2013, de http://edc.tversu.ru/elib/inf/0110.pdf.
Hernández G., El método de diferencias finitas, Distrito Federal, México, Grupo de Geofísica Computacional, Universidad Nacional Autónoma de México, 2010. Recuperado el 5 de junio de 2013, de http://mmc2.geofisica.unam.mx/ghdez/hidrogeologia/NO-TAS_MDF-06.pdf.
Hincapié, D. y Ospina, J., "Bases para la modelación de epidemias: el caso del síndrome respiratorio agudo severo en Canadá", Journal of Public Health, Vol. 9, No. 1, 2007, pp. 117-128. Recuperado el 5 de junio de 2013, de http://redalyc.uaemex.mx/pdf/422/42290111.pdf.
Iriarte, R., "Capítulo 1: Aproximación numérica y errores", en Métodos numéricos (2a ed.), Distrito Federal, México, Trillas, 2007, pp. 11-22.
Juan, W., Chen Gyi, X. y Qifeng, L., "A Novel Model for the Internet Worm Propagation", VI ICNC 2010, Shandong, China, 2010, pp. 2885-88. Recuperado el 5 de junio de 2013, de http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5584495.
Kermack, W. O. y Mckendrick, A. G., "A Contribution to the Mathematical Theory of Epidemics", Proceedings of the Royal Society of London, Series A, Vol. 115, No. 772, 1927, pp. 700-21. Recuperado el 5 de junio del 2013, de www.math.utah.edu/~bkohler/Journal-club/kermack1927.pdf.
Nakamura S., Métodos numéricos aplicados con software, Estado de México, México, Prentice Hall Hispanoamericana, 1998.
Nazario, J., Defense and Detection Strategies against Internet Worms, Massachusetts, USA, Editorial Artech House, 2004. Recuperado el 5 de junio del 2013, de http://es.scribd.com/doc/59508754/Defense-and-Detection-Strategies-Against-Internet-Worms-2004#download.
Onwubiko, C., Lenaghan, A. P. y Hebbes, L., "An Improved Worm Mitigation Model for Evaluating the Spread of Aggressive Network Worms", EUROCON 2005, Belgrado, Serbia y Montenegro, 2005, pp. 1710-13. Recuperado el 5 de junio del 2013, de http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1630303.
Suárez, M., Matemática numérica, Distrito Federal, México, Ed. Del Instituto Politécnico Nacional, 1997.
Tao L., Zhi-Hong, G., Zhen Ping, W. y Xian Young, W., "Stability Analysis of A Delayed Model of the Spread of Worms", 2007 IEEE International Conference on Control and Automation, Guangzhou, China, 2007, p. 3188-90. Recuperado el 5 de junio del 2013, de http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=5234704.
Tassier, T., SIR Model of Epidemics, Nueva York, USA, Department of Economics, Fordham University, 2005. Recuperado el 5 de junio del 2013, de http://www.fordham.edu/images/Undergraduate/economics/faculty/SIR.pdf.
Yang, W. y Chenxi, W., "Modeling the Effects of Timing Parameters on Virus Propagation", WORM'03, Washington DC, USA, 2003, pp. 1-6. Recuperado el 5 de junio de 2013, de http://www.thehackademy.net/madchat/vxdevl/pa-pers/avers/worm.pdf.
Zuazua, E., Métodos numéricos de resolución de ecuaciones en derivadas parciales, Bilbao España, Basque Center for Applied Mathematics (BCAM), 2009.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.