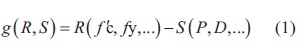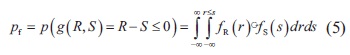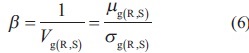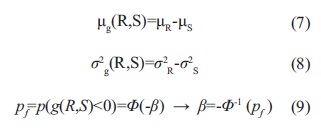Estimación del índice de confiabilidad B de las vigas de un puente usando conteos de tráfico real (TPDS) mediante simulación.

Estimación del índice de confiabilidad ß de las vigas de un puente usando conteos de tráfico real (TPDS) mediante simulación

Reliability Index ß Evaluation of the Girders of a Bridge Using Counts of Real Traffic (TPDS) by Simulation

Sergio Andrés Vanegas Herrera¹, Gustavo Chio Cho²

¹Ingeniero civil, magíster en Ingeniería Civil, docente de la Universidad Industrial de Santander (UIS), Bucaramanga, Colombia. Contacto: sergio.vanegas@correo.uis.edu.co
²Ingeniero civil, doctor ingeniero de caminos, canales y puertos, docente de la Universidad Industrial de Santander (UIS), Bucaramanga, Colombia. Contacto: gchioch@uis.edu.co

Fecha de recepción: 27 de agosto de 2013 Fecha de aceptación: 14 de marzo de 2014

Clasificación del artículo: Investigación
Financiamiento: Universidad Industrial de Santander

Resumen

El índice de confiabilidad ß es un parámetro utilizado para estimar la seguridad de una estructura o un elemento de esta durante su etapa de diseño o servicio. Este parámetro, definido en otros códigos del mundo (European Committee for Standardisation (Eurocode), EN 1990:2002; American Association of State Highway and Transportation Officials (AASHTO), 2012), no se especifica en el Código Colombiano de Diseño Sísmico de Puentes (CCDSP-95) (1995). En este artículo se presenta un trabajo sobre la estimación de los índices de confiabilidad ß de las vigas interiores y exteriores de un tablero de un puente de viga y losa, en concreto reforzado, de 30 m de longitud, simplemente apoyado y diseñado según el CCDSP-95. En la evaluación de los momentos resistentes se consideraron las propiedades de los materiales usando una distribución normal. Además, se utilizó una simulación de Monte Carlo para estimar la solicitación del momento en centro de luz de los efectos de la carga viva.

Palabras clave: distribución normal, métodos de Monte Carlo, puentes, teoría de confiabilidad.

Abstract

The reliability index ß is a parameter used to estimate the safety of a structure or an element during the design stage or service. This parameter defined in other codes in the world (European Committee for Standardisation (Eurocode), EN 1990:2002; American Association of State Highway and Transportation Officials (AASHTO), 2012), is not specified in the Colombian Code of Bridges Seismic Design (CCDSP-95) (1995). In this paper, it will be presented a study on the estimation of the reliability index ß of the interior and exterior girders of a beam and slab bridge with reinforced concrete, 30 m in length, simply supported and designed according to the CCDSP-95. In the evaluation of the resistant moments, there were considered properties of materials using a normal distribution, and moreover, a Monte Carlo simulation was used to estimate load effect of moment at mid-span of the live load.

Keywords: bridges, Monte Carlo methods, normal distribution, reliability theory.

Introducción

Una estructura debe ser segura. Por lógica siempre esperamos que nos lleven a mejorar nuestra calidad de vida y que tengan un largo periodo de funcionamiento. Todas las estructuras se diseñan buscando un punto óptimo estructural y económico. Si no fuese así, esto nos llevaría a tener dimensionamientos antieconómicos para la sociedad. Por ello, no se pueden construir edificios ni puentes que duren toda la vida, sino que siempre existirá una probabilidad al fracaso. Pero este fracaso debe ser muy pequeño para que el diseño sea confiable. La confiabilidad de una estructura se define como la probabilidad de que un sistema llevará acabo la función requerida en condiciones de servicio especificadas durante un periodo de tiempo determinado (Lemaire, 2009).

La probabilidad de falla está estrechamente ligada al índice de confiabilidad, que es el parámetro más usado para medir el nivel de seguridad de un sistema (Sánchez Silva, 2005). Este índice es usado en otras ramas de la ingeniería, como la ingeniería electrónica, en donde se construyen cientos de estructuras iguales, de las cuales un porcentaje muy pequeño presenta falla. Pero en la ingeniería civil no pasa eso, dado que solo se tiene una estructura (y no cientos de ellas), a la cual se le debe medir su seguridad ante eventos, como por ejemplo las cargas vivas o el sismo.

La teoría de confiabilidad es un método basado en la matemática estadística, donde las propiedades de los materiales y el proceso de carga -que varía con el tiempo y modelos inciertos- se pueden describir como variables aleatorias ajustadas a cualquier curva estadística.

Metodología

El margen de seguridad o función de estado límite es la forma matemática de describir la relación entre la resistencia (R) y la solicitación (S) en un sistema, o en este caso en una estructura. Tanto R como S pueden describirse por variables que pueden ser aleatorias o determinísticas, como por ejemplo fc y fy, por el lado de la resistencia, y por el lado de la solicitación las cargas de los camiones que pasan sobre el puente (representado por la letra P) o la carga muerta (representado por la letra D). Una manera común de representar la función de estado límite es mediante la ecuación (1) (James, 2003; Moses, 2001).

Donde:

R: representa las variables de resistencia del sistema.

S: representa las variables de resistencia del sistema.

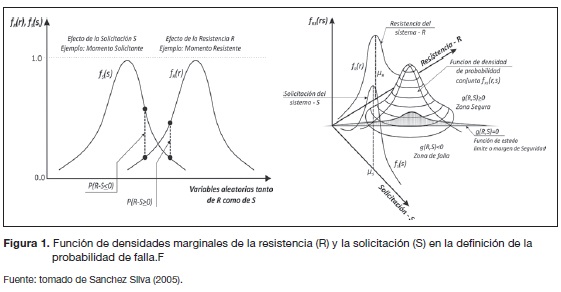
La función de estado límite divide el espacio x en dos espacios, uno llamado la zona segura (ZS), cuando g(R,S)>0, y el otro es la zona de falla (ZF), cuando g(R,S)<0. El sector que divide estos dos conjuntos se llama superficie de estado limite o superficie de falla, donde la función de estado limite g(R,S)=0. En las ecuaciones (2), (3) y (4) se muestra el resultado del anterior planteamiento.

El problema básico de la confiabilidad es encontrar la probabilidad de falla. En otras palabras, que p(g(R,S)<0). Entonces, matemáticamente se calcula mediante la función de densidades marginales de la resistencia (R) y la solicitación (S), usando la ecuación (5).

Donde se puede notar que los límites de la solicitación en la integral va desde -∞ hasta +∞, mientras que la resistencia se evalúa desde -∞ hasta cuando los valores de la resistencia son menores que los de la solicitación r<s, que es la condición de que ocurra falla. La ecuación (5) está expresada mediante funciones de densidad de probabilidad marginal f_R(r) y f_S(s). Lo anterior se puede entender mejor en la figura 1.

El índice de confiabilidad ß es el parámetro más usado para medir el nivel de seguridad de un sistema. Cuando las variables tanto de resistencia (R) como de solicitación (S) están distribuidas normalmente, el índice de confiabilidad se puede calcular como se muestra en la ecuación (6).

Donde:

μ_g(R,S): Valor medio del margen de seguridad (Ecuación (7)

σ_g(R, S): Desviación estándar del margen de seguridad (ecuación (8)

V_g(R,S): coeficiente de variación del margen de seguridad.

Otra definición de este índice, y de nuevo considerando que las variables tanto de resistencia (R) como de solicitación (S) se distribuyen normalmente, es por medio de la probabilidad de falla. Las ecuaciones (7), (8) y (9) muestran el planteamiento anterior.

Donde:

µ_R: valor medio de la resistencia (R)

µ_S: valor medio de la solicitación (S)

σ²_R: desviación estándar al cuadrado de la resistencia (R)

σ²_S: desviación estándar al cuadrado de la solicitación (S)

Φ(-ß): función de distribución de probabilidad normal estándar con media 0 y desviación 1 del valor negativo del índice de confiabilidad ß.

-Φ¹ (p_f): función inversa de la distribución de probabilidad normal estándar, con media 0 y desviación 1, de la probabilidad de falla.

Obtención de los datos

Obtención de los momentos resistentes MR

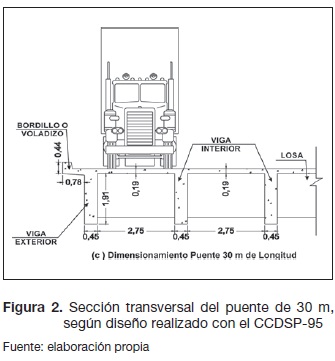
Para la realización de este estudio, primero se hizo un diseño de un puente recto de 30 m de longitud, en concreto reforzado, de viga y losa, según el Código Colombiano de Diseño Sísmico de Puentes (CCDSP-95), con la metodología descrita por Vallecilla Bahena (2004). Las dimensiones de la sección transversal se muestran en la figura 2.

Con el diseño se obtuvo el momento debido a las cargas muertas M_D y el momento debido a las cargas vivas M_L de las vigas internas y de las vigas externas, que según el CCDSP-95 se deben calcular siguiendo las cargas vivas mostradas en la figura 3, en donde por la longitud de 30 m ya no se usa el camión de diseño C40-95, sino la línea de carga, que es una carga distribuida más una carga puntual.

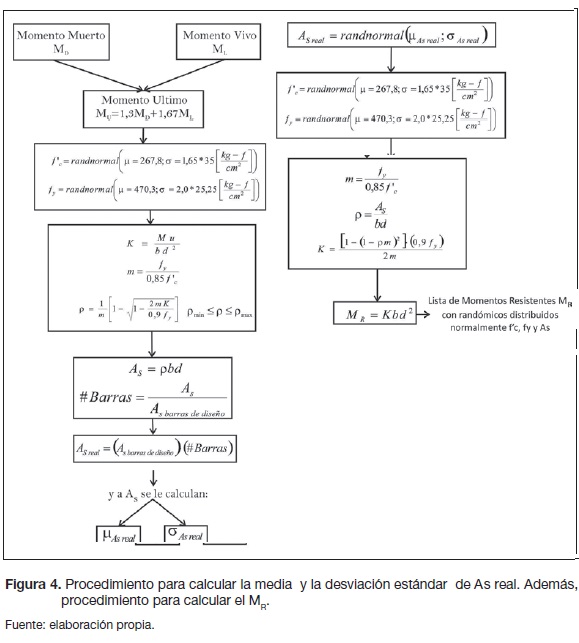
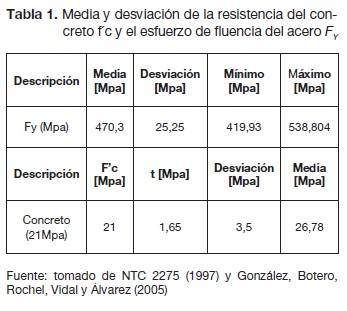
Con el fin de obtener el momento resistente M_R tanto para las vigas interiores como para las vigas exteriores, se realizó el procedimiento que se muestra en las figura 4. Además, se generaron valores aleatorios para la resistencia la compresión del concreto fc y la fluencia del acero fy, que se muestran en la tabla 1.

Obtención de los momentos solicitantes M_S

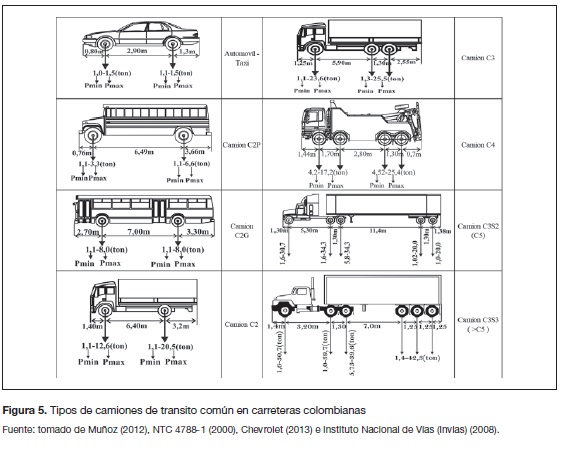
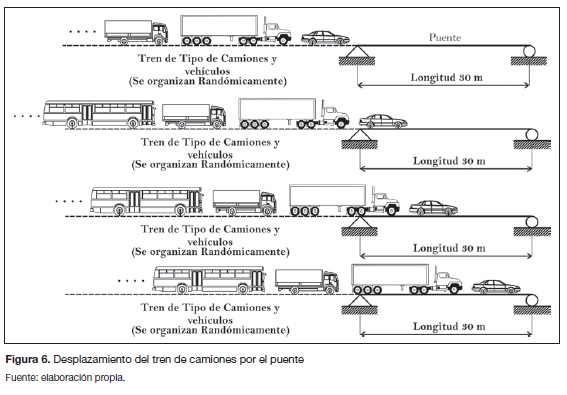
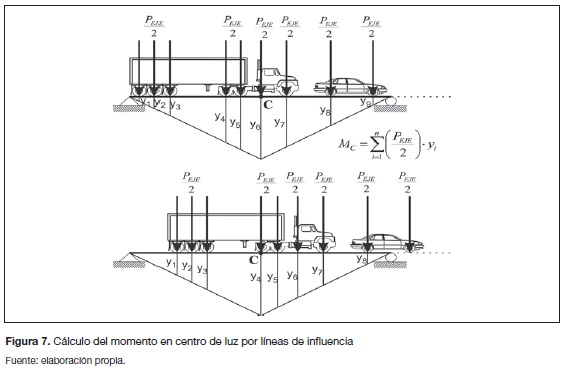
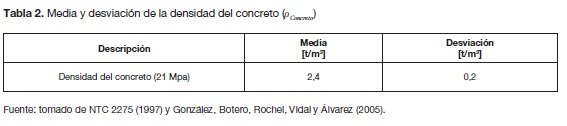
Para el cálculo de los momentos solicitantes se realizó una simulación de Monte Carlo, en donde el tráfico de los distintos tipos de carros (figura 5) se distribuyó aleatoriamente (figura 6) en el puente. Las cargas de los ejes de cada tipo de camión oscilan dentro de un intervalo, el cual se ajustó a una distribución normal. El desplazamiento del tren de vehículos y camiones se da en intervalos de 0,1 m, a una velocidad de 10 km/h. En cada intervalo de desplazamiento del tren se calculan los momentos producidos en centro de luz M_c, usando la metodología de las líneas de influencia (figura 7). En este análisis se generaron valores aleatorios de la densidad del concreto (tabla 2).

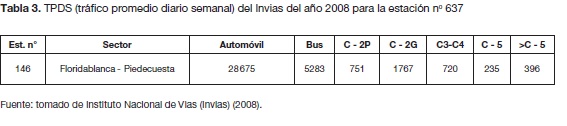
Los datos de tráfico fueron tomados de la cartilla del Invias del 2008, de la estación 146, entre Floridablanca-Piedecuesta, que se pueden ver en la tabla 3. Se tomó este conteo ya que es el que presenta mayor cantidad de camiones pesados en el sector de Bucaramanga y su área metropolitana. Se implementó un programa en Matlab©© que desarrolla el planteamiento de este artículo y que, de manera general, puede analizar cualquier tipo de TPDS para puentes cortos simplemente apoyados de concreto reforzado. Además, como simplificación del problema, el programa evalúa solo un carril, que sería el carril de diseño (carril crítico), por donde pasa la mayor probabilidad de vehículos de la simulación.

Para correr todo un TPDS, se dividió el tráfico diario semanal escogido en intervalos de 15 minutos, lo cual da un total de 96 intervalos de tráfico por día. Con esto simplificábamos, por partes, la cantidad de datos que serían evaluados; además de que se tiene una mejor precisión, ya que la evaluación se hace en intervalos de tiempo más cortos.

Resultados

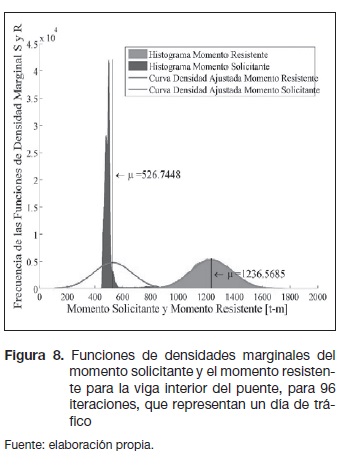
En el análisis de resultados se desarrollaron los histogramas o diagramas de frecuencia de los momentos solicitantes y momentos resistentes para las vigas internas y externas, como se puede apreciar en las figuras 8 y 9.

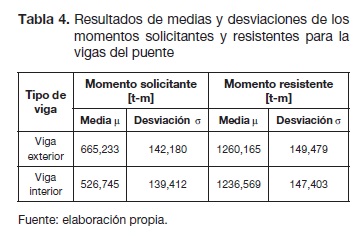
Las frecuencias mostradas anteriormente se ajustaron a una distribución normal, en donde para la viga interior la media del momento solicitante es de 526,7448 t-m y la media para el momento resistente medio es de 1236,5685 t-m. Para la viga exterior del puente la media del momento solicitante es de 665,2333 t-m y la media del momento resistente es de 1260,1647 t-m. Los resultados de las figuras 8 y 9 se pueden detallar mejor en la tabla 4.

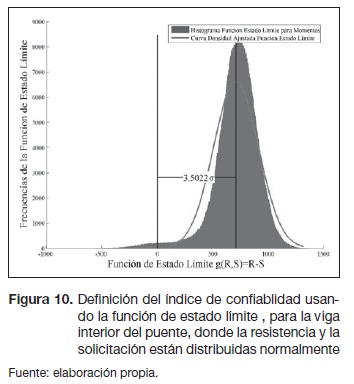
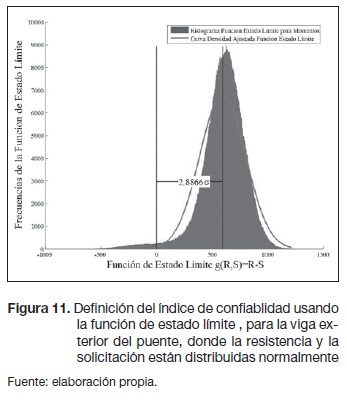
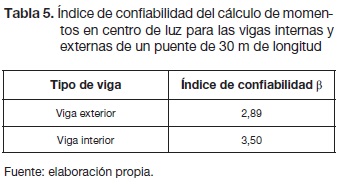
Los resultados de los índices de confiabilidad ß se desarrollaron usando la ecuación (6), en donde las frecuencias del margen de seguridad o ecuación de estado límite se representan en las figuras 10 y 11. Las frecuencias mostradas en estas figuras se ajustaron a curvas de distribución normal, donde la prueba de bondad de ajuste de Kolmogorov-Smirnov aceptó la hipótesis nula de los momentos resistentes, en donde la distribución de los datos sigue una curva normal, pero en los momentos solicitantes esto no es tan cierto, debido a la variabilidad de los datos ocasionada por las cantidades discontinuas entre vehículos y camiones, (ver tabla 3). Los valores obtenidos de índices de confiabilidad para este puente, en cada una de las vigas, se encuentran en la tabla 5.

El valor promedio calculado de beta, tomado de varias fuentes bibliográficas que se basan en muestras de diseños de puentes actuales, es de 3,5 (Muñoz, 2012). El Eurocódigo 0 específica para una construcción normal un índice de confiabilidad igual a 3,5 (European Committee for Standardisation (Eurocode), EN 1990:2002). Las especificaciones de diseño AASHTO LRFD Bridge (American Association of State Highway and Transportation Officials (AASHTO), 2012) sugieren a su vez un índice de confiabilidad de 3,5. Como indican las referencias anteriores, un valor referencia del índice de confiabilidad es 3,5. Además, hay que saber que en el diseño, cuando el índice de confiabilidad es mayor, mayor será también la seguridad del puente y menor la probabilidad de falla. Con esto podemos decir que la viga exterior del puente, con un índice de confiabilidad de 2,89 (tabla 5), está por debajo de 3,50, por lo cual no se encuentra dentro del criterio anterior. La viga interior, con un índice de confiablidad de 3,50 (tabla 5), está en el margen del valor de 3,5.

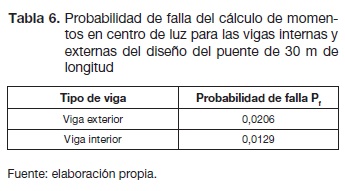
En el estudio de este trabajo también se calculó la probabilidad de falla para cada tipo de viga del puente diseñado, como se especifica en la tabla 6.

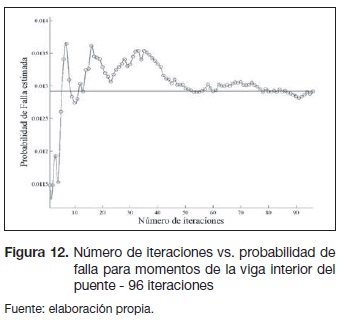
Las figuras 12 y 13 demuestran la convergencia de los resultados con el paso de las iteraciones.

Conclusiones

Los histogramas mostrados en las figura 8 y 9 se ajustaron a distribuciones normales, en donde se puede apreciar que el momento solicitante tiene una dispersión más notoria que la del momento resistente, debido a la variabilidad de los vehículos en el TPDS utilizado. Además, se puede notar que las frecuencias en el momento solicitante son mucho más altas que las del momento resistente, debido a que varios valores de los momentos solicitantes resultan muy similares, dando como resultado esfuerzos parecidos, producidos por las cargas de los ejes al pasar en cada instante sobre el puente.

En el desarrollo de este trabajo se calcularon los índices de confiabilidad para las vigas de un puente con un tablero de viga y losa de 30 m de longitud, en donde la viga interior, con un índice de confiabilidad de 3,5, se encuentra dentro de los márgenes internacionales y es una viga segura, desde el diseño, para el caso más crítico de carga de la simulación de trafico real. Mientras que la viga exterior, con un índice de confiabilidad de 2,89, no está dentro de los límites últimos de las normas internacionales, y se puede considerar como una viga con baja seguridad, desde el diseño, en las condiciones más críticas del paso real de vehículos.

Sabiendo que los valores típicos de probabilidad de falla para el diseño están entre 110² y 110^-3 (Sanchez Silva, 2005), En la tabla 6 se puede apreciar que la probabilidad de falla de la viga exterior no entraría en este intervalo, mientras que la viga interior alcanzaría a entrar en el intervalo. Con esto corroboramos la conclusión anterior.

Financiamiento

El financiamiento es realizado por la Universidad Industrial de Santander, mediante beca de sostenimiento.

Referencias

American Association of State Highway and Transportation Officials (AASHTO), AASHTO LRFD Brides: Design Especifications, Estados Unidos de América, 2012.

CCDSP-95, Código Colombiano de Diseño Sísmico de Puentes, Bogotá: Asociación Colombiana de Ingeniería Sísmica (ACIS), 1995.

Chevrolet, Chevrolet Colombia, 2013. Recuperado de http://www.chevrolet.com.co/vehiculos/buses-camiones/showroom_camiones.html.

European Committee for Standardisation (Eurocode) (EN 1990:2002), Basis of Structural Desing. Load of Bridge (Vol. 3).

González, V., Botero, J., Rochel, R., Vidal, J. y Alvarez , M., "Propiedades mecánicas del acero de refuerzo utilizado en Colombia", Ingeniería y Ciencia, Vol. 1, No. 1, 2005, pp. 67-76.

Instituto Nacional de Vías (Invias), Manual de Diseño Geometrico INV-2008, Bogotá, 2008.

Instituto Nacional de Vías (Invias), Volúmenes de tránsito, 2008. Recuperado el 15 de marzo de 2013, de http://www.invias.gov.co/index.php/documentos-tecnicos-izq.

James, G., Analysis of Traffic Load Effects on Railway Bridges (Doctoral Tesis), Structural Engineering Division, Royal Institute of Technology, Estocolmo, Suecia, 2003.

Lemaire, M., Structural Reliability. New Jersey, Estados Unidos: Wiley-ISTE, 2009.

Moses, F., NCHRP. Report 454: Calibration of Load Factors for LRFD Bridge Evaluation, Washington D. C: Portersville, Estados Unidos de America: National Cooperative Highway Research Program (NCHRP), 2001.

Muñoz, E., Ingeniería de puentes (Vol. 3), Bogotá: Gente Nueva, 2012.

NTC 2275, Ingeniería Civil y Arquitectura. Procedimiento recomendado para la evaluación de los resultados de los ensayos de resistencia de concreto, Bogotá: Icontec, 1997.

NTC 4788-1, Tipología de vehículos de transporte terrestre, Bogotá: Icontec, Mnisterio de Transporte, 2000.

Sanchez Silva, M., Introducción a la confiabilidad y evaluación de riesgos, Bogotá: Ediciones Uniandes, 2005.

Vallecilla Bahena, C., Curso de puentes en concreto, Bogotá: Bauen, 2004.