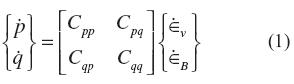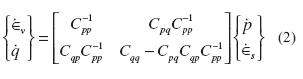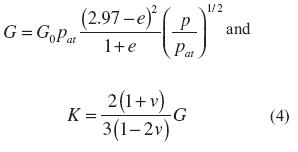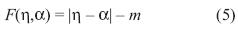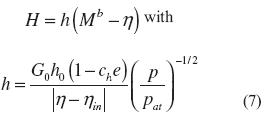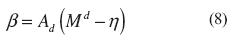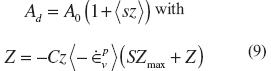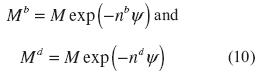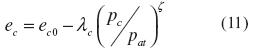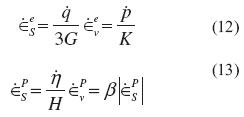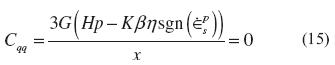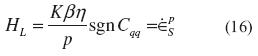DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2015.1.a04Publicado:
01-01-2015Número:
Vol. 19 Núm. 43 (2015): Enero - MarzoSección:
InvestigaciónInfluence of the void ratio and the confining on the static liquefaction in slopes in shangi sand
Influencia de la relación de vacíos y el confinamiento en la licuación estática en taludes de arena de Changi
Descargas
Referencias
Andrade, J. E., Ramos, A., & Lizcano, A. (2013). Criterion for Flow Liquefaction Instability. Acta Geotechnica, 8(5), 525-535.
Been, K.& Jefferies, M. (1985). State Parameter for sands. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 22(6), 198.
Chu, J., & Wanatowski, D. (2008). Instability Conditions of Loose Sand in Plane Strain. Journal of Geotechnical and Geoenvironmental Engineering, 134(1), 136-142.
Chu, J., Leroueil, S.& Leong, W. (2003). Unstable Behaviour of Sand and its Implications for Slope Instability. Canadian Geotechnical Journal, 40, 873-885.
Dafalias, Y., & Manzari, M. (2004). Simple Plasticity SandModel Accounting for Fabric Change Effects. Journal of Engineering Mechanics, 130(6), 622-633.
Darve, F.& Laouafa, F. (2000). Instabilities in Granular Materials and Application to Landslides. Mechanics of Cohesive-Frictional Materials, 5(8), 627-652.
Hyodo, M., Tanimizu, H., Yasufuku, N.& Murata, H. (1994). Undrained Cyclic and Monotonic Triaxial Behaviour of Saturated Loose Sand. Soils and Foundations, 34(1), 19-32.
Lade, P. (1994). Instability and Liquefaction of Granular Materials.Computers and Geotechnics, 16(2), 123-151.
Leong, W., Chu, J., & Teh, I. (2000). Liquefaction and Instability of a Granular Fill.Geotechnical Testing Journal, 23(2), 178-192.
Manzari, M.,& Dafalias, Y. (1997). A Critical State Two-Surface PlasticityModel for Sands. Géotechnique, 47(2), 255-272.
Nova, R. (1994). Controllability of the Incremental Response of Soil Specimens Subjected to Arbitrary Loading Programs. Journal of the Mechanical Behavior of Materials, 5(2), 193-201.
Ramos, A., Andrade, J. E., & Lizcano, A. (2011). Numerical Simulations of the Instability Line.DYNA, 78(2), 24-30.
Schofield, C. (1968). Critical State Soil Mechanics.NuevaYork: McGraw-Hill.
Vaid, Y., & Chern, J. (1985). Cyclic and Monotonic Undrained Response of Saturated Sands.Advances in the Art of Testing Soils under Cyclic Conditions. ASCE, 120-147.
Wanatowski, D., & Chu, J. (2007). Static Liquefaction of Sand in Plane Strain. Canadian Geotechnical Journal, 44(3), 299-313.
Wood, M. (1994). Strain Softening and State Parameter for Sand Modelling. Géotechnique, 44(2), 335-339.
Youd, T., Idriss, I., Andrus, R., Arango, I., Castro, G., Stokoe, K.et al. (2001). Liquefaction Resistance of Soils: Summary Report from the NCEER and 1998 NCEER/NSF Workshop on Evaluation of Liquefaction Resistance of Soils. Journal of Geotechnical and Geoenvironmental Engineering, 127(10), 817-833.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Influence of the void ratio and the confining on the static liquefaction in slopes in changi sand
Influencia de la relación de vacíos y el confinamiento en la licuación estática en taludes de arena de Changi
Alfonso Mariano Ramos Cañon1
1Ingeniero civil, magíster en Geotecnia, doctor en Ingeniería, profesor asociado de la Pontificia Universidad Javeriana, Bogotá, Colombia. Contacto: a-ramos@javeriana.edu.co
Fecha de recepción: 21 de febrero del 2014-Fecha de aceptación: 15 de agosto del 2014
Clasificación del artículo: InvestigaciónFinanciamiento: Pontificia Universidad Javeriana
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.1.a04
Abstract
A numerical study on the onset of static liquefaction in slopes under undrained conditions of loading was developed based on a general liquefaction flow instability criterion for elastoplastic soils based on the concept of loss of controllability. The criterion is applied to the case of axisym-metric loading to detect the onset of static liquefaction. The criterion is used in conjunction with an elastoplastic model for sands and is tested by means of numerical simulations of element tests. The numerical results are compared with experimental evidence obtaining good agreement. A quantitative study of the influence of the mean pressure, void ratio and the anisotropy of stress on the onset of static liquefaction is presented for the Changi sand. From the analysis of the numerical results, it can be concluded that: a. the mobilized friction angle at the onset of liquefaction is not an intrinsic property of the material, but is a state variable b. Despite of the multiple variables involved in the process of generation of und-rained instability, the state of stresses at the onset of static liquefaction can be conveniently represented by a linear relation between Δq/p0and η0. This graphical representation can be used in the practice of geotechnical engineering to quantify the margin of security against the static liquefaction of a sandy slope.
Keywords: instabilities in sands, static liquefaction, stress anisotropy.
Resumen
Se presenta un estudio numérico del inicio de la licuación estática en taludes, bajo condiciones no drenadas de carga, basado en un criterio de inestabilidad general para suelos elastoplásticos, fundamentado en el concepto de pérdida de controlabilidad. Se aplica el criterio al caso de carga axisimétrica, para detectar el punto de inicio de licuación con un modelo elastoplástico para arenas. Se comparan los resultados numéricos con evidencia experimental, encontrando un buen nivel de concordancia. Se presenta un estudio cuantitativo de la influencia de la presión media, relación de vacíos y la anisotropía inicial de esfuerzos sobre el inicio de la licuación en la arena de Changi. Se concluye que: a) el ángulo de fricción movilizado al inicio de la licuación no es una propiedad del material, sino que es una variable de estado; b) a pesar de las múltiples variables involucradas en el proceso de generación de inestabilidad no drenada, el estado de esfuerzos en el inicio de la licuación estática se puede representar convenientemente por una relación lineal entre Δq/p0y η0. Esta representación gráfica se puede usar en la práctica de la ingeniería geotécnica para cuantificar un margen de seguridad contra licuación estática de un talud arenoso.
Palabras clave: anisotropía de esfuerzos, inestabilidades en arenas, licuación estática.
Introduction
Failure of slopes under monotonic undrained conditions of loading is an instability process which occurs in loose sands. It is well known that the behavior of sands is greatly influenced by their initial conditions, such as the initial density and confining pressure (Hyodo, Tanimizu, Yasufuku, & Murata, 1994). A common approach used to tackle issues associated with liquefaction is based on phenomenology. Moreover, the most used methodologies for evaluating the potential of liquefaction are based on field test such as SPT and CPT (Youd et al., 2001). These methodologies disregard important aspects like the anisotropy of stresses in the evaluation of susceptibility of liquefaction. An alternative and more rational way to understand the static liquefaction is based on sets of laboratory tests, and based on these results it's proposed a generalization of the behaviour. For example Wanatowski and Chu (2007) depict a relation between the stress ratio ηL= qL/pL and void ratio for undrained triaxial tests iso-tropically and anisotropically compressed (qL and pLare the main pressure and the deviatoric stress in the onset of static liquefaction, respectively). On other hand, Chu and Wanatowski (2008) propose a mathematical equation between ηL and the Been-Jefferies critical state parameter ( ψ = e - ec). This equation is obtained by assuming that the increase of plastic volumetrics train is equal to the increase of total volumetric strain and both of them are equal to zero in the peak of deviatoric stress. It means that the dilatancy is zero in the peak of undrained effective stress path. However, Lade (1994) demonstrates that sands subjected to undrained loading show a behavior that must be modelled by a flow rule highly non associative. A similar approximation for detecting the onset of static liquefaction is to characterize the instability line for a specific type of sand. The instability line can be defined as the boundary in which large strains are rapidly generated due to the inability of a soil element to sustain a given stress or load (Chu, Leroueil, & Leong, 2003). The instability line was firstly proposed by Vaid and Chern (1985) defining it as the locus of points at which flow liquefaction is initiated for the same initial void ratio under monotonic undrained triaxial tests. Many researchers have analysed the instability line (Lade, 1994; Chu & Wanatowski, 2008; Chu, Leroueil, & Leong, 2003; Wanatows-ki & Chu, 2007; Hyodo, Tanimizu, Yasufuku, & Murata, 1994; Andrade, 2009; Andrade, Ramos, & Lizcano, 2013). Andrade (2009) and Ramos, Andradeand Lizcano (2011) using two different elastoplastic constitutive models concluded that the slope of the instability line is not a constant of the material but it is a state parameter.
In this work, a criterion for detecting the onset of static liquefaction derived by Andrade, Ramosand Lizcano (2013) and Ramos, Andradeand Lizcano (2011) was extended to an isotropic elastoplastic constitutive model with kinematic hardening and bounding surface theory (Manzari-Dafalias model). The application of this criterion matches very well with experiments reported in the literature, allowing to generate numerical simulation for different conditions with a high level of confidence. By making use of numerical simulations previously validated with experiments, it is possible to supply the deficiency of the experimental approximation and to have a greater spectrum of the behavior of the sandy slopes subjected to static liquefaction. As result, the influence of void ratio, mean pressure and initial anisotropy on the onset of static liquefaction is investigated. Finally, despite of the multiple variables involved in the process of generation of static liquefaction, the behavior of the sand can be condensed in a linear relation between Δq/p0and η0. This kind of relation can be used in the practice of geotechnical engineering to quantify the degree of security of a slope given the initial conditions of stress and void ratio.
The paper is organized as follow. The first section of this paper shows the instability criterion for detecting the onset of static liquefaction using the Manzari-Dafalias elastoplastic constitutive model. The 'Validation' section presents numerical simulations for prediction of static liquefaction and compares them with laboratory experiments. Finally, the influence of the void ratio, mean pressure and the initial stress anisotropy on the onset of static liquefaction is presented based on several simulations conducted with the constitutive model and the instability criterion. Findings from the application of the criterion are highlighted in the 'Conclusions' section.
Static liquefaction criterions and constitutive model
For the sake of simplicity, we limit the following derivation to infinitesimal strains and axisymmetric undrained conditions. Assuming a rate form for the constitutive model equation (1), the relation among the effective stress rate and the total strain rate can be written as
where 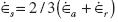 is the volumetric strain rate, and
is the volumetric strain rate, and 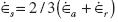 is the deviatoric component of the strain rate. Also,
is the deviatoric component of the strain rate. Also, 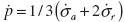 is the effective pressure rate and
is the effective pressure rate and 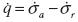 is the deviatoric stress rate. We note the usage of Cambridge p - q stress invariants to describe triaxial conditions. Finally, σais the axial total stress rate and σris its radial counterpart.
is the deviatoric stress rate. We note the usage of Cambridge p - q stress invariants to describe triaxial conditions. Finally, σais the axial total stress rate and σris its radial counterpart.
Following the concept of loss of controllability for elemental test conditions (Nova, 1994), the volumetric strain rate and the deviatoric stress rate under triaxial conditions can be controlled giving pressure increments and shear strain increments, equation (2), such that
Here, we look for the vanishing of the determinant of the matrix relating the controlled variables on the left to the emerging or responding variables on the right. The requirement of singularity implies Cqq/Cqq= 0 whichrequires
This condition, equation (3), will furnish a general criterion for detecting static liquefaction instability in terms of loss of controllability. Andrade et al (2012) demonstrated the similarity of the loss of controllability with the concept of loss of uniqueness and the second order work (Darve & Laouafa, 2000). We will adapt this general criterion to the case of the Dafalias and Manzari (2004) constitutive model. Now, the Dafalias and Manzari (2004) model will be briefly described. For a complete description of the model, interested readers are referred (Manzari & Dafalias, 1997; Dafalias & Manzari, 2004). The constitutive model is framed in the critical state soil mechanics concept (Schofield, 1968), and the elastic response is hypoelastic. The shear and bulk moduli are given by equation (4).
where G0is a constant, v is Poisson's ratio, e is the current void ratio, and patis the atmospheric pressure. The elastic region is enclosed by a yield surface in effective stress space which defines a wedge, equation (5).
with η = q/p as the stress ratio, á as the back stress, and m as a constant defining the width of the wedge so that in p - q space, the wedge has an opening of 2 mp at any value p. The inclination of the wedge defining the elastic region is given by the back stress, equation (6) whose evolution is governed by a kinematic hardening law
where H is the hardening modulus. To complete the description of the constitutive model, evolution of the hardening modulus H and dilatancy β must still be explained. The hardening modulus, equation (7), is a function of the state of the material whose sign is controlled by its relative distance to the bounding stress, i.e.,
where h is a positive function, Mb is the bounding stress ratio, and h0 and chare positive constants. The evolution of the dilatancy, equation (8), is given by a function similar to that of the hardening modulus, with the sign of the function dictated by its distance to the dilatancy stress so that
with Mdas the dilatancy stress ratio. When the value of h is less than the value of Md, response is contractive. For all other cases the model predicts dilation. The positive scaling function for dilatancy A, equation (9), is affected by changes in fabric such that
where A0 is a positive constant and s = ± 1 according to η = á ± m. The brackets < > are Macaulay brackets representing as <value> = value if value >0 or <value> = 0 if value < = 0. In addition, Zmax represents the maximum possible value of the state parameter z. The model is made to comply with critical state soil mechanics by postulating exponential evolution equations for the bounding and dilatancy stress ratios, equation (10). They are respectively,
with nband ndas positive constants. Conceptually, the evolution equations shown above require M and Mdto coincide with M as y ® 0, requiring its state to tend to critical state. The state parameter ψ= e - ecwas defined by Been and Jefferies (1985) and measures the distance to the critical state from the current state in void ratio space. Finally, the critical state line is defined in void ratio space according to the relationship proposed by Li and Wang (1998), equation (11)
with ec0 as the void ratio at pc= 0 and λc and ς as constants.
In order to present a self-content paper, the derivation of the static liquefaction criterion will be summarized. However its original development was proposed by the same authors of this paper in Andrade, Ramos and Lizcano (2013).
The Dafalias and Manzari (2004) constitutive model can be seen in the matrix form of Equation (1) by resorting the additive decomposition of incremental stress-strain relation as follows, equation (12) and equation (13)
Superscripts e and p denote the elastic and plastic part of strains. The increment in stress ratio is calculated as η =η/pp+q/p, where η = q/p. Based on the rates of total volumetric and deviatoric strains, equation (1) especially adapted
to the Dafalias and Manzari (2004) constitutive model reads, equation (14)
where, χ= 3G + Hp - Kβsgn(εps). Equation (3), which indicates loss of controllability and the onset of static liquefaction, when especially adapted to the Dafalias and Manzari model is, equation (15)
which, to be true in general, requires the quantity inside the parenthesis to vanish. In elastoplastic models the hardening modulus H is an indicator of the soil state. Andrade (2009) deduced a critical hardening modulus as a predictor of static liquefaction for an elastoplastic constitutive model with two invariants. From equation (15) a closed form of the hardening modulus that is able to detect the onset of static liquefaction can be derived (Andrade, Ramos, & Lizcano, 2013), equation (16).
At the moment when the hardening modulus equals the critical hardening modulus (H - HL= 0) instability occurs in the form of static liquefaction.
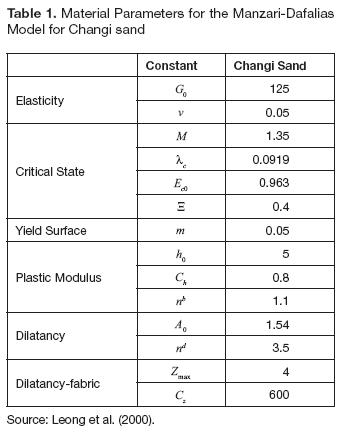
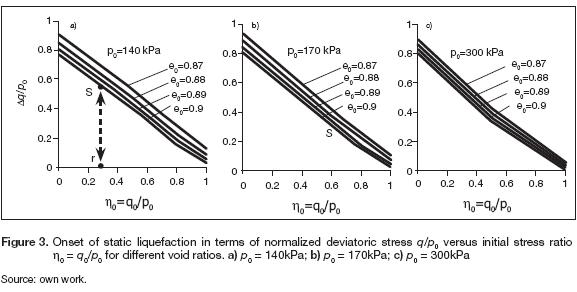
Validation of the criterion for detecting static liquefaction under anisotropic initial conditions of stress was given in Ramos, Andradeand Lizcano (2011). Ramos, Andradeand Lizcano (2011) developed numerical simulations using the generalized static liquefaction criterion introduced in equation (3) and adapted to the Manzari-Dafalias model utilizing the limiting hardening modulus encapsulated in equation (16). The anisotropic initial conditions of stress is representative of the conditions of stress in a slope which can be represented in the q - p space of stress by mean of q # 0 and p # 0. Wanatowski and Chu (2007) report a comprehensive set of triaxial and biaxial tests in Changi sand under both, isotropically and anisotropically compressed, and sheared under undrained conditions of loading. These sets of experiments generated a great opportunity to check the performance of the criterion (Eq.16) to detect the onset of static liquefaction. Parameters for the elastoplastic constitutive model were calibrated based on the sets of experiments reported byLeong, Chu and the (2000) (table 1).
(Ramos, Andrade and Lizcano (2011) simulated two isotropically compressed triaxial tests CU (p0 = 150kPa, q0 = 0 kPa, ec= 0.916); (p0= 150kPa, q0 = 0 kPa, ec= 0.888) and three triaxial compression test anisotropically compressed under a k0stress path K0U (p0 = 191.22 kPa, q0 = 152.83 kPa, ec= 0.899; (p0 = 199.57 kPa, q0 = 147.78 kPa, ec= 0.922); (p0 = 199.93 kPa, q0 = 183.28 kPa, ec= 0.88) using the elastoplastic constitutive model and the parameters of the table 1. Onset of liquefaction is obtained by mean of the application of the critical hardening modulus. Reasonable agreement between the experiment and the simulation was reported by Ramos, Andrade and Lizcano (2011).
Results
Once verified the performance of elastoplastic constitutive model as well as the criterion for detecting the onset of static liquefaction under both, isotropic and anisotropic initial conditions by mean of comparisons with experiments under triaxial conditions of loading (Ramos, Andrade, & Lizcano, 2011), a number of simulations were carried out in order to study the influence of the void ratio, the confining pressure, and the initial stress ratio η0 = q0/p0on the onsetof static liquefaction. Figure 1a depicts the stress ratio in the onset of static liquefaction ηL= qL/pLversus the void ratiofor six different mean pressures and the same initial stress ratio η0 = q0/p0.
From figures 1a and 1b it is possible to observe that for a given η0, the higher the mean pressure, the lower the stress ratio at the onset of static liquefaction hL. However, it was observed that the deviatoric stress qLis larger for larger mean pressure. If the mean pressure is kept constant, the looser the sand, the lower hL. Also, it is observed that for the same void ratio, the stress ratio at the onset of static liquefaction ηLis different. This means that ηLis not a constant of the material, what was originally proposed by Vaid and Chern, (1985) in terms of a constant mobilized friction angle. Using an elastoplastic constitutive model with kinematichardening, Andrade (2009) and Ramos, Andrade and Lizcano (2011) demonstrated that ηLisnot constant but state variable.
Also, an upper boundary in the figure 1a is found for η0 = 0. A similar upper limit can bederived for different values of η0. It is not possible toun-limitedly diminish the mean pressure in order to get a higher value of η0keeping constant the void ratio. Points above the upper boundary will show a strain hardening behavior. This upper boundary is given by the lower mean pressure that a sample can support in order to develop static liquefaction for a given void ratio. The curve for p0= 15 kPa - η0 = 0 is also a boundarywhich separates the behavior between the static liquefaction andstrain hardening.
An explanation for the upper boundary can be given by resorting to the critical state parameter ψ = e - ecproposed by Been and Jefferies (1985). The state parameter is a measurement of the distance between the current void ratio and the void ratio in the critical state for a given value of mean pressure. Negative values of ψ are expected for strain hardening materials, and positive values are for strain softening. Materials with the ability to suffering static liquefaction have always ψ > 0. Lets suppose amaterial with a given initial void ratio and a confining pressuresuch that ψ is larger than zero. As the mean pressure decreases, the state variable ψ also reduces. If the confining pressure is enoughly low, ψ can become negative, i.e. when the mean pressure diminishes, the material can change of having a contractive behavior to dilative one, and the material will not tend to undergo static liquefaction.
The upper boundary has values near to 1.35 for η0, which isthe slope of the critical state line in the qp space of stress.This means that for low values of mean pressure p, the onset of static liquefaction η0is located very near to the criticalstate line. The critical state line departs from the origin the qp space of stress. The aspects previously mentioned could indicate that the instability line across the origin of coordinates. However, the strain softening behavior is limited by a certain value of mean pressure larger than zero for a given void ratio. In this case, the sample changes its behavior and it begins to build up negative pore pressures, indicating that the material has strain hardening behavior. Therefore, the instability line could be projected onto the origin of coordinates in the qp space of stress for small values of mean pressure, although it will not have a geometric place in the origin in the qp space of stress.
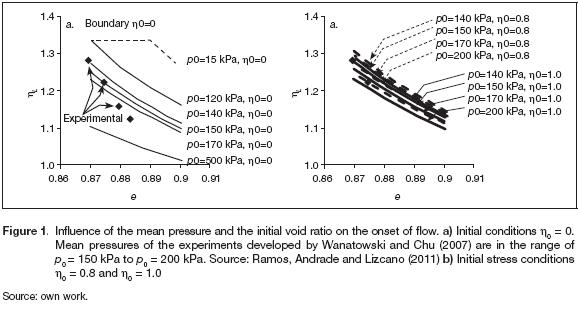
Wanatowski and Chu (2007) presented a line connecting the experimental points of figure 2a which relates the void ratios and the stress ratio at the onset of static liquefaction ηLin triaxial test for mean pressures ranging between p0= 150 - 200kPa. They argue in favour of that linear relation because of the narrow range of mean pressures used for the experiments. Each experiment corresponds to a different mean pressure. This means that a curve joining the experimental points would be crossed by curves of constant p0, as shown in 2a. Consequently, there is not only one line in the ηL- e space, but, a family of curves for different mean pressures for each initial conditions of stress η0. This hypothesis was confirmed with the experiments performed by Wanatowski and Chu (2007). On the other hand, the instability line can be easily constructed with the data from figure 1 by drawing a vertical cross section at a given void ratio (i.e. e = 0.89). It is possible to observe that the instability line is not a straight line, as it was proposed by Vaid and Chern (1985), but it is a curve, i.e. the mobilized friction angle at the onset of static liquefaction is not a constant. This clearly means that the instability line is not an intrinsic property of the material. Andrade (2009) and Ramos, Andrade and Lizcano (2011) demonstrated that the ratio of stress at the onset of liquefaction ηLis not a constant for two different elastoplastic constitutive models. Figure 2 shows a plot of the ratio of deviatoric stress Aq normalized with initial mean pressure p0versus initial void ratio for different initial stress ratios η0. Aq is defined
One might assimilate that the larger η0, the steeper the slope for a given depth i.e., constant mean pressure p0. Different values of η0 are representative of the anisotropyof the initial stress. By comparison of different η0 for a given void ratio and mean pressure in the figure 2, it is observed that the larger η0, the lower normalized increment of deviatoric stress Aq/p0. This means that a steeper slope will have the chance of experimenting static liquefaction with a lower increment of deviatoric stress. It is easier that a steeper slope static liquefied experiments static liquefaction than a smooth slope. Therefore, the anisotropy of stress η0 plays an important role in the stability of sandy slopes. In addition, concordantly with the trend observed in the figure 1, one can see that for a given η0 and an initial void ratio, the larger the mean pressure, the lower the ratio of normalized deviatoric stress. This means that for an homogeneous slope (both void ratio and slope constant), the deeper, the lower the ratio of normalized deviatoric stress Δq/p0. However, the deviatoric stresses qLneeded to produce static liquefaction are higher.
Conversely, the higher the initial stress η0, the lower the influence of the mean pressure. This means that a slope with high inclination will suffer static liquefaction under similar values of normalized ratio of deviatoric stress Δq/p0independently of the mean pressure. (Note that the curves for η0 = 1 are closer to each other than the curves for η0 = 0).
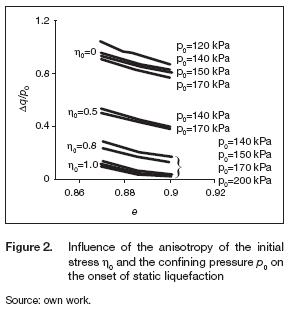
By definition, Δq/p0 cannot reach negative values because qL> q0 and p0 > 0. When Δq/p0 = 0, it means that the material is intrinsically unstable: no additional deviatoric stress needs to be applied to unleash static liquefaction. In this case, the initial stresses are located inside the zone of potential instability proposed by Lade (1994). This zone is called "potential" because the state of the material can be inside this zone under drained conditions, i.e. the formation process of the slope can lead to an in situ stress state that may lie within the potential instability zone. However, if external forces area applied fast enough and cause an und-rained loading process, the material will undergo instability in the form of static liquefaction. Also, it is worth noting that due to the negative slope in the curves of figure 3, a material is intrinsically unstable if it has high values of η0 (slopes with high inclinations) andif it is in a very loose state. When the void ratio is increased, a lower value of normalized ratio of deviatoric stress Δq/p0 is necessary in order to produce static liquefaction under constant mean pressure and initial stress ratio. This would mean that it is necessary to develop lower deviatoric stresses in softer material than in a denser material under the same conditions of both inclination of the slope and depth. Results of figure 2 previouslyanalyzed show a general panorama of the behavior of sandy slopes with possible static liquefaction. An alternative way to represent the afore mentioned analyzed data is shown in figure 3.
Figure 3 shows the normalized deviatoric stress ratio Δq/p0 versus the initial stress ratio η0 = q0/p0 for different void ratios and mean pressures p0. Additional to theremarks previously made, some additional observations can be proposed. Through comparison between figures 3a and 3c, it can be seen that the higher the mean pressure, the lower the influence of the void ratio. The separation between the curves for a given void ratio is narrower in figure 3c than in figure 3a. A more important aspect can be derived from figure 3. All the variables studied in this work are included in figure 3 (anisotropy of stresses, void ratio and mean pressure) and despite the somehow intricate behavior of the samples at the onset of static liquefaction, the results might be condensed in a straight line. For this range of mean pressures and void ratios, the possibility of static liquefaction does not show great variability, because the influence of the mean pressure is hidden when both, the abscissas and the ordinates are normalized. These types of graphs can be used as an indicator of the degree of safety of the slope because the abscissas are the initial conditions of stresses and the ordinates give the stresses needed to cause the instability by means of static liquefaction. Based on the know ledge of some basic characteristics of the slope, for example inclination, unit weight, ground water level and depth of the layer that one would like to analyse, it is possible to estimate the initial stress state h0. For example, we assume that for a given slope and a given layer for analysis, a point r in the abscissa of figure 3a can be located. Then, the distance Δq/p0measured along the vertical line linking the point r and the ordinate of the correspondenting void ratio curve (point s) would help to estimate the maximum over burden pressure that can be quickly and monotonically applied to the slope before reaching instability in the form of static liquefaction. Then, Δq/p0could be used as an indicator of the slope's margin of safety.
Conclusions
Once, both the constitutive model and the liquefaction criterion have been successfully tested, the following remarks can be stated:
There is no a unique relationship between the stress ratio at the onset of static liquefaction ηL= qLpLand the void ratio. This relationship depends not only on the mean pressure but also on the initial ani-sotropy of stresses.
Numerical and experimental evidence show that the well known instability line proposed by Vaid and Chern (1985) and Lade (1994) is not a straight line, but a curve in the p - q stress space which can be projected from the origin for Changi sand. This means that ηLis not an intrinsic property of the material. Therefore, it is not possible to assume that the mobilized friction angle at theonset of static of liquefaction is constant.
A quantification of the influence of the void ratio, mean pressure and anisotropy of stresses on the onset of static liquefaction for Changis and is presented. A similar procedure can be used for any sandy material. This methodology, based on the loss of controllability, takes into account more aspects that influence the undrained response, than simplified methods based only on phenomenology.
The most important novel aspect tackled in this paper is that despite many factors that influence the onset of static liquefaction, the behavior of the analysed sand might be condensed and described approximately by a straight line in a normalized graph of Δq/p0 versus η0. This type of plot canbe used in the practice of geotechnical engineering as an indicator of slope margin of safety against static liquefaction.
Acknowledgments
The first author acknowledges the financial support given to this work by Pontificia Universidad Javeriana- Colombia. Grant number 004709 "Instabilities in granular matter".
References
Andrade, J. (2009). A Predictive Framework for Liquefaction Instability. Geotechnique, 59 (8), 673-682.
Andrade, J. E., Ramos, A., & Lizcano, A. (2013). Criterion for Flow Liquefaction Instability. Acta Geotechnica, 8 (5), 525-535.
Been, K. & Jefferies, M. (1985). State Parameter for Sands. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 22 (6).
Chu, J., & Wanatowski, D. (2008). Instability Conditions of Loose Sand in Plane Strain. Journal of Geotechnical and Geoenvironmental Engineering, 134 (1), 136-142.
Chu, J., Leroueil, S. & Leong, W. (2003). Unstable Behaviour of Sand and its Implications for Slope Instability. Canadian Geotechnical Journal, 40, 873-885.
Dafalias, Y., & Manzari, M. (2004). Simple Plasticity Sand Model Accounting for Fabric Change Effects. Journal of Engineering Mechanics, 130 (6), 622-633.
Darve, F. & Laouafa, F. (2000). Instabilities in Granular Materials and Application to Landslides. Mechanics of Cohesive-Frictional Materials, 5 (8), 627-652.
Hyodo, M., Tanimizu, H., Yasufuku, N. & Murata, H. (1994). Undrained Cyclic and Mo-notonic Triaxial Behaviour of Saturated Loose Sand. Soils and Foundations, 34 (1), 19-32.
Lade, P. (1994). Instability and Liquefaction of Granular Materials. Computers and Geotechnics, 16 (2), 123-151.
Leong, W., Chu, J., & Teh, I. (2000). Liquefaction and Instability of a Granular Fill. Geotechnical Testing Journal, 23 (2), 178-192.
Manzari, M. & Dafalias, Y. (1997). A Critical State Two-Surface Plasticity Model for Sands. Géotechnique, 47 (2), 255-272.
Nova, R. (1994). Controllability of the Incremental Response of Soil Specimens Subjected to Arbitrary Loading Programs. Journal of the Mechanical Behavior of Materials, 5(2), 193-201.
Ramos, A., Andrade, J. E., & Lizcano, A. (2011). Numerical Simulations of the Instability Line. DYNA, 78 (2), 24-30.
Schofield, C. (1968). Critical State Soil Mechanics. Nueva York: McGraw-Hill.
Vaid, Y., & Chern, J. (1985). Cyclic and Mono-tonic Undrained Response of Saturated Sands. Advances in the Art of Testing Soils under Cyclic Conditions. ASCE, 120-147.
Wanatowski, D., & Chu, J. (2007). Static Liquefaction of Sand in Plane Strain. Canadian Geotechnical Journal, 44 (3), 299-313.
Wood, M. (1994). Strain Softening and State Parameter for Sand Modelling. Géotechnique, 44 (2), 335-339.
Youd, T., Idriss, I., Andrus, R., Arango, I., Castro, G., Stokoe, K. et al. (2001). Liquefaction Resistance of Soils: Summary Report from the NCEER and 1998 NCEER/NSF Workshop on Evaluation of Liquefaction Resistance of Soils. Journal of Geotechnical and Geoenvironmental Engineering, 127 (10), 817-833.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.