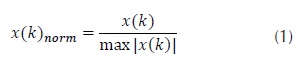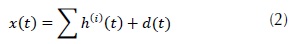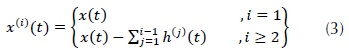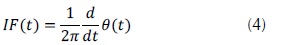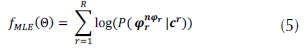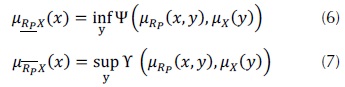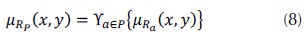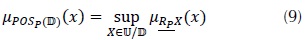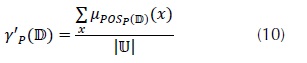DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2015.2.a06Publicado:
01-04-2015Número:
Vol. 19 Núm. 44 (2015): Abril - JunioSección:
InvestigaciónAnálisis estocástico de señales vibratorias de motores de inducción para la detección de fallas usando descomposición de modo empírico
Vibration signals stochastic analysis of induction motors for fault detection using empirical mode decomposition
Descargas
Referencias
Askari, M. R. (2010). Broken Bars Detection in Squirrel Cage Induction Motors Using Wavelet Theory. Journal of Applied Sciences, 10(6), 477-478.
Bulla, J. (2011). Hidden Markov Models with t Components, Increased Persistence and other Aspects. Quantitative Finance, 11(3), 459-475.
Cabal-Yepez, E. O.-R.-T.-H.-G. (2009). FPGA-Based Online Induction Motor Multiple-Fault Detection with Fused FFT and Wavelet Analysis. In International Conference on Reconfigurable Computing and FPGAs, 2009. ReConFig ’09, 101-106.
Fulufhelo V. U.; Nelwamondo, M., & Marwala, T. (2006). Early classifications of bearing faults using hidden Markov models, gaussian mixture models, mel-frequency cepstral coefficients and fractals. University of the Witwatersrand, Volume 2(6), 1281-1299.
Geramifard, O.; Xu, J., & Chen, W. (2012). An HMM-based semi-nonparametric approach for fault diagnostics in rotary electric motors. In 2012 IEEE International Symposium on Industrial Electronics (ISIE), 1218-1223.
Guo-liang, Z.; Yun-bing, W., & Gang, C. (212). Rotor Break-Bar Fault Diagnosis of Asynchronous Motor Based on Empirical Mode Decomposition. In Power and Energy Engineering Conference (APPEEC), 2012 Asia-Pacific.
Hernández, P. L.; Carro, M.; de Oca, J. M.; García, L., & Fernández, S. J. (2008). Optimización del mantenimiento preventivo utilizando las técnicas de diagnóstico integral. Resultados finales y evaluación económica. (Spanish. Optimization of the Preventive Maintenance Using the Techniques of Integral Diagnosis. Final Results and Economic Evaluation. (English), 29(2), 35-45.
Ho Soon, L.; Chong, K. T., & Su, H. (2006). Motor fault detection method for vibration signal using FFT residuals. International Journal of Applied Electromagnetics & Mechanics, 24(3/4), 209-223.
Jensen, R., & Shen, Q. (s.f.) Computational intelligence and feature selection: rough and fuzzy approaches. Wiley.
MacParthalain, N., & Jensen, R. (2009). Measures for Unsupervised Fuzzy-Rough Feature Selection. In Ninth International Conference on Intelligent Systems Design and Applications, 2009. ISDA ’09, 560-565.
Ocak, H., & Loparo, K. A. (2001). A new bearing fault detection and diagnosis scheme based on hidden Markov modeling of vibration signals. In 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2001. Proceedings. (ICASSP ’01 (05), 3141-3144.
Orrego, D. A.; Becerra, M. A., & Delgado-Trejos, E. (2012). Dimensionality reduction based on fuzzy rough sets oriented to ischemia detection. In 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 5282-5285.
Oweis, R. J., & Abdulhay, E. W. (2011). Seizure classification in EEG signals utilizing Hilbert-Huang transform. BioMedical Engineering OnLine, 10(1), 38-52.
Patel, R. K.; Agrawal, S., & Joshi, N. C. (2012). Induction motor bearing fault identification using vibration measurement. In 2012 Students Conference on Engineering and Systems (SCES), 1-5.
Patil, S. S., & Gaikwad, J. A. (2013). Vibration analysis of electrical rotating machines using FFT: A method of predictive maintenance. In 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), 1-6.
Qiang, S., & Changjian, F. (2012). Hybrid SVM-HMM Diagnosis Method for Rotor- Gear-Bearing Transmission System. Journal of Computers, 7(9), 2324-2329.
Qiwei-Xie, Bo-Xuan, Silong-Peng, Jianping-Li, Weixuan-Xu, & HAN, H. (2008). Bandwidth empirical mode decomposition and its application. International Journal of Wavelets, Multiresolution & Information Processing, 6(6), 777-798.
Radzikowska, A. M., & Kerre, E. E. (2002). A comparative study of fuzzy rough sets. Fuzzy Sets and Systems, 126(2), 137-155.
Ramírez-Castro, R. I., & Montejo, L. A. (2011). Transformada de Hilbert, descomposición modal empírica y sus aplicaciones en el análisis de vibraciones libres. Hilbert transform, empirical mode decomposition and its applications to free vibration analysis. (English), 11(2), 121-132.
Santana, D., & Madiedo, R. (2007). Valoración de métodos para la determinación de la eficiencia de motores de inducción que accionan cargas en régimen de trabajo continuo variables en el tiempo. (Spanish). Valoration or Methods to Determine the Induction Engines Efficiency That Carry Loods in a Continuous Work Regime Variables in Time. (English), 28(3), 25-29.
Shrivastava, A., & Wadhwani, S. (2014). An approach for fault detection and diagnosis of rotating electrical machine using vibration signal analysis. In Recent Advances and Innovations in Engineering (ICRAIE), 1-6.
Soualhi, A.; Medjaher, K., & Zerhouni, N. (2015). Bearing Health Monitoring Based on Hilbert; Huang Transform, Support Vector Machine, and Regression. IEEE Transactions on Instrumentation and Measurement, 64(1), 52-62.
XinGuang-Li, MinFeng-Yao, & JiaNeng-Yang. (2012). Speech Recognition Approach Based on Speech Feature Clustering and HMM. Journal of Computers, 7(9), 2269-2275.
Xinmin, T.; Baoxiang, D., & Yong, X. (2007). Bearings Fault Diagnosis Based on HMM and Fractal Dimensions Spectrum. In International Conference on Mechatronics and Automation, 2007. ICMA 2007, 1671-1676.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a06
Análisis estocástico de señales vibratorias de motores de inducción para la detección de fallas usando descomposición de modo empírico
Vibration signals stochastic analysis of induction motors for fault detection using empirical mode decomposition
Alejandro Rivera Roldán*,
Miguel Alberto Becerra Botero**,
Jaime Alberto Guzmán Luna***
* Ingeniero electrónico, Institución Universitaria Salazar y Herrera, Medellín, Colombia. Contacto: alejandroriveraroldan@gmail.com
** Ingeniero electrónico, magíster en Automatización y Control Industrial, Institución Universitaria Salazar y Herrera, Medellín, Colombia. Contacto: migb2b@gmail.com
*** Ingeniero civil, especialista en Comunicación educativa, magíster en Ingeniería de Sistemas, doctor en Ingeniería (énfasis Sistemas e Informática), Universidad Nacional de Colombia, Medellín, Colombia. Contacto: jaguzman@unal.edu.co
Fecha de recepción: 4 de febrero de 2014 Fecha de aceptación: 5 de diciembre de 2014
Citation / Para citar este artículo: Rivera Roldán, A., Becerra Botero, M. A., & Guzmán Luna, J. A. (2015). Análisis estocástico de señales vibratorias de motores de inducción para la detección de fallas usando descomposición de modo empírico. Revista Tecnura, 19(44), 83-91. doi: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.2.a06
Resumen
En este artículo se presenta un análisis de vibraciones en motores de inducción por medio de Modelos Ocultos de Markov (Hidden Markov Model–HMM) aplicado a características obtenidas de la Descomposición de Modo Empírico (Empirical Mode Decomposition–EMD) y transformada de Hilbert-Huang de señales de vibración obtenidas en las coordenadas x y y, con el fin de detectar fallas de funcionamiento en rodamientos y barras. Además se presenta un análisis comparativo de la capacidad de las señales de vibración en dirección x y en dirección y, para aportar información en la detección de fallas. Así, un HMM ergódico inicializado y entrenado por medio del algoritmo de máxima esperanza, con convergencia en 10e-7 y un máximo de iteraciones de 100, se aplicó sobre el espacio de características y su desempeño fue determinado mediante validación cruzada 80-20 con 30 fold, obteniendo un alto desempeño para la detección de fallas en términos de exactitud.
Palabras clave: descomposición de modo empírico, detección de fallas, Modelos Ocultos de Markov, motores de inducción, procesamiento de señales.
Abstract
This paper presents a vibration analysis on induction motors using Hidden Markov Models (HMM) applied to features obtained from the Empirical Mode Decomposition (EMD) and Hilbert-Huang transform to vibration signals obtained in the coordinates x and y, in order to detect malfunctions in bearings and bars. Additionally, a comparative analysis of the ability of the vibration signals in the x and y directions to provide information for failures detection is presented. Thus, an ergodic HMM initialized and trained by expectation maximization algorithm with convergence at 10e-7 and maximum iterations of 100 was applied to the feature space and its performance was determined by cross-validation with 80-20 with 30 fold for obtaining high performance fault detection in terms of accuracy.
Keywords: empirical mode decomposition, fault detection, Hidden Markov Models, induction motors, signal processing.
Introducción
La confiabilidad es un factor clave de competitividad en los procesos productivos del mercado actual; sin embargo, la maquinaria utilizada en dichos procesos, como los motores, sufren desgastes y averías que pueden llevar a una interrupción inesperada en las líneas de producción. Estos motores tienen una vida útil y un desgaste por el uso a través del tiempo, lo que lleva a que su eficiencia sea cada vez menor (Santana & Madiedo, 2007)(Ho Soon, Chong, & Su, 2006); de ahí la necesidad de implementar sistemas de mantenimiento preventivo y correctivo, mediante sistemas eficientes de detección de fallas que eviten largas paradas en las líneas de producción (Fulufhelo V., Nelwamondo, & Marwala, 2006), (Hernández, Carro, de Oca, García, & Fernández, 2008).
El movimiento irregular de los motores puede caracterizarse por medio del análisis de señales vibratorias, las cuales son complejas y no determinísticas, por lo que no resulta adecuado su análisis usando métodos tradicionales como la transformada de Fourier (Ramírez-Castro & Montejo, 2011). A pesar de esto, en estudios recientes se han efectuado análisis de señales de vibración de máquinas rotativas en el dominio de la frecuencia usando la transformada rápida de Fourier para el monitoreo de desalineación, problemas de engranaje y desbalanceo (Patil & Gaikwad, 2013) y en el dominio del tiempo para el análisis de fallas en rodamientos (Shrivastava & Wadhwani, 2014), demostrando resultados satisfactorios. Sin embargo, este tipo de características son afectadas significativamente en condiciones de ruido y son muy dependientes de los sistemas de inferencia cuando se emplean en detección automática. Debido a esto, su análisis se hace comúnmente aplicando la transformada wavelet que permite una codificación, eliminación de ruido, compresión y descomposición de las señales, para la detección de condiciones anormales (Askari, 2010)(Patel, Agrawal, & Joshi, 2012), pero debido a que este tipo de señales no tienen características particulares en la fase y frecuencia, no resulta suficientemente adecuado para su análisis. Por lo anterior, la descomposición de modo empírico (EMD) ha ido tomando fuerza para el análisis de este tipo de señales, el cual de manera sistemática y sin mayores bases matemáticas permite una descomposición de la señal, a partir de la cual se obtienen características representativas usando la transformada de Hilbert Huang que describe la dinámica del motor aplicando técnicas de caracterización (Oweis & Abdulhay, 2011)(Qiwei-Xie, y otros, 2008)(Soualhi, Medjaher, & Zerhouni, 2015). Adicionalmente, los clasificadores estocásticos basados en los modelos ocultos de Markov (HMM) han demostrado que pueden usarse en la identificación de series de tiempo no estacionarias y que tienen buen desempeño en el aprendizaje de modelos estadísticos, y aunque se conocen como técnica para el reconocimiento del habla, se han utilizado en el diagnóstico de sistemas de rotor, engranajes y rodamientos a través del análisis de señales de vibración en combinación con otras técnicas; sin embargo, gran cantidad de estudios hacen uso de señales en una sola dirección (x o y) y las consideraciones del ruido varían dependiendo de los datos a estudiar, los cuales generan un alto grado de afección en los resultados de la detección (Ocak & Loparo, 2001)(Qiang & Changjian, 2012).
En este estudio, se presenta un enfoque de análisis estocástico basado en HHT-HMM aplicado sobre la combinación de diferentes IMF de señales vibratorias del eje x y del eje y, junto con un análisis de relevancia basado en Fuzzy Rough Set (FRS) para reducir el número de características, con el fin de proporcionar un sistema eficiente para la detección de fallas en rodamientos y en barras en motores de inducción en forma más confiable.
Materiales y métodos
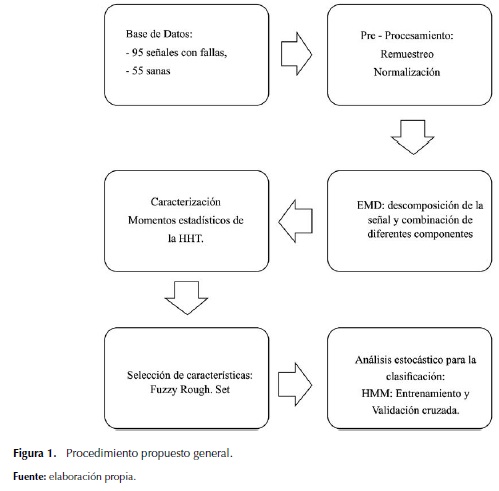
De acuerdo con el diagrama esquemático de la figura 1, la metodología desarrollada consta de 6 pasos: 1) base de datos, 2) preprocesamiento de la señal, 3) descomposición de la señal, 4) caracterización, 5) selección de características y 6) clasificación.
La base de datos es descrita por (Cabal-Yepez, 2009), pertenece a la Universidad de Guanajuato (México) y con ella se hicieron las pruebas en este trabajo usando las señales de vibración correspondientes a las direcciones x y y. En la etapa de preprocesamiento se remuestreó la señal a 150 Hz con un filtrado antialiasing y una normalización en la escala [-1, 1] usando la ecuación (1).
donde x(k)norm es x(k) normalizada.
Posteriormente se realizó la descomposición de la señal preprocesada en n IMF, donde 4≤n ≤6 aplicando EMD con una resolución de 40 dB, energía residual de 40 dB y gradiente de 0.1, con el fin de obtener dos constructos, los cuales resultan de reconstruir la señal realzando las características vibratorias del motor y atenuando el ruido. De cada constructo se obtienen 9 características para un total de 18 características por señal, basadas en los momentos estadísticos aplicados a la fase instantánea y amplitud instantánea calculadas mediante la transformada de Hilbert Huang, como se ilustra en la tabla 1, en donde a es la amplitud instantánea, w es la frecuencia angular instantánea, cte indica que una variable se asume como constante para el cálculo de la varianza (var) o de la desviación estándar (std) de la transformada de Hilbert (H).
Posteriormente las características son normalizadas en el rango [0,1] con el fin de mejorar el comportamiento del clasificador y de hacer la selección de características. Con el objetivo de obtener el reducto del espacio de representación, se aplicó el algoritmo Fuzzy Rough Sets con entropía descrito en (Orrego, Becerra, & Delgado-Trejos, 2012) sintonizando el parámetro de vecindad en 0,03 y el de inclusión en 0,6. El análisis estocástico del espacio de representación reducido se efectuó mediante un clasificador HMM ergódico de 2 estados y 3 gaussianas inicializado con un vector de parámetros aleatorios y su entrenamiento se hizo aplicando el algoritmo de máxima esperanza con una convergencia de 10 e-7 y un máximo número de iteraciones de 100. Finalmente se aplica validación cruzada 80/20 con 30 repeticiones, para determinar la consistencia y la capacidad de representación del espacio de características.
A continuación se detalla la base de datos de señales de vibración y las técnicas utilizadas.
Base de datos de señales de vibración de motores de inducción
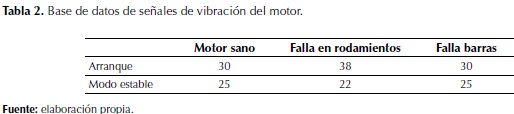
Las señales de vibración fueron adquiridas en el arranque y en el estado estable de tres motores con las mismas características pero con particularidades individuales, así: el primero con fallas en los rodamientos, el segundo con problema en las barras y el tercero no presentaba ningún tipo de fallos. En total se cuenta con 170 señales en las dirección x y y de motores sanos y con fallos, como se describe en la tabla 2. Las señales de vibración fueron adquiridas a una frecuencia de muestro de 1500 Hz, 12 bits utilizando un acelerómetro MEMS (Microelectromechanical Systems) de tres ejes cartesianos (x, y, z) ubicado en el cuerpo del motor.
Descomposición de modo empírico (EMD) para las señales de vibración
Esta descomposición se hace mediante un proceso iterativo adaptativo denominado tamizaje, el cual se emplea para descomponer las señales originales en funciones de modo intrínseco (Intrinsic Mode Function, IMF) que son componentes oscilatorios más sencillos que pueden ser o no lineales y/o estacionarios (Qiwei-Xie, y otros, 2008) (Ramírez-Castro & Montejo, 2011). Así, la descomposición de una señal multicomponente x(t) en L IMF h(i)(k) donde 1 ≤ i ≤ L, está dada por la ecuación (2).
Donde d(t) es un residuo cuya media es diferente de cero y h(i)(t), es cada una de las IMF estimadas de manera iterativa con el algoritmo denominado sifting, aplicado a la señal multicomponente residual y se expresa por medio de la ecuación (3).
De acuerdo con esto, durante la (n+1) enésima iteración el algoritmo sifting mejora el IMF  estimado temporalmente aplicando los siguientes pasos: 1) Determina el máximo y el mínimo de
estimado temporalmente aplicando los siguientes pasos: 1) Determina el máximo y el mínimo de  ; 2) realiza una interpolación usando spline cúbico, entre los puntos de
; 2) realiza una interpolación usando spline cúbico, entre los puntos de  previamente estimados con el fin de formar una envolvente superior e inferior; 3) computa las medias de todas las envolventes; 4) obtiene el refinado del estimado
previamente estimados con el fin de formar una envolvente superior e inferior; 3) computa las medias de todas las envolventes; 4) obtiene el refinado del estimado  ; 5) vuelve al paso 1 a menos que el criterio de parada haya sido alcanzado por completo. Es importante tener en cuenta que para la primera iteración h(i)(t) se usa h1(t) como estimación temporal del IMF.
; 5) vuelve al paso 1 a menos que el criterio de parada haya sido alcanzado por completo. Es importante tener en cuenta que para la primera iteración h(i)(t) se usa h1(t) como estimación temporal del IMF.
Transformada de Hilbert Huang (HHT) para la obtención de características
La amplitud instantánea a(t) y la fase instantánea θ(t) de la señal de vibración puede extraerse por medio de la HHT, la cual se usa para descomponer adaptativamente señales no estacionarias y no lineales. Con esta información puede hallarse la frecuencia instantánea (IF) mediante la ecuación (4) obteniendo resultados para cada instante de tiempo, si hay exclusivamente una frecuencia presente en la señal. Además, con la información de la HHT puede construirse el espectro de Hilbert Huang, el cual proporciona información de tiempo-frecuencia-energía utilizado en el análisis de señales (Guo-liang, Yun-bing, & Gang, 2012).
Modelos ocultos de Markov (HMM) para la clasificación de señales de vibración
Los modelos ocultos de Markov tienen un adecuado desempeño con señales de serie de tiempo por su doble proceso estocástico, aunque la aplicación en la cual se ejecuta con mayor frecuencia es en el reconocimiento del habla (XinGuang-Li, MinFeng-Yao, & JiaNeng-Yang, 2012). Estos son una extensión de las cadenas de Markov, donde cada estado está conectado por medio de un conjunto de distribuciones de probabilidad y cada estado no corresponde a un evento observable. Existen tres tipos de HMM que dependen del tipo de distribución de probabilidad de emisión, así: HMM discretos, continuos y semicontinuos. De igual forma, para el entrenamiento de los HMM existen varios criterios de entrenamiento: algoritmo de estimación de máxima verosimilitud (MLE), máxima información mutua (MMI), entre otros. Este estudio se enfoca en un modelo HMM continuo y MLE para el entrenamiento, dado su buen desempeño en otros estudios.
Tomando  un conjunto de entrenamiento de R muestras con categorías
un conjunto de entrenamiento de R muestras con categorías  para M clases diferentes, i.e.,
para M clases diferentes, i.e.,  Tambien, cada muestra
Tambien, cada muestra  es representada por una secuencia de vectores de características de longitud
es representada por una secuencia de vectores de características de longitud  , así,
, así,  El conjunto total de parámetros de los HMM se denota por Θ y está compuesto de M modelos, es decir,
El conjunto total de parámetros de los HMM se denota por Θ y está compuesto de M modelos, es decir,  , donde Λm denota el conjunto de parámetros de los HMM correspondiente a la clase cm. El entrenamiento basado en MLE se lleva a cabo teniendo en cuenta la función objetivo expresada en la ecuación (5).
, donde Λm denota el conjunto de parámetros de los HMM correspondiente a la clase cm. El entrenamiento basado en MLE se lleva a cabo teniendo en cuenta la función objetivo expresada en la ecuación (5).
La optimización de esta función se logra a partir del ajuste de parámetros para cada modelo separadamente, basado en la observación en el entrenamiento para obtener el máximo valor. Este procedimiento incluye el algoritmo de máxima esperanza (EM), el cual estima la máxima verosimilitud de los parámetros de distribución subyacente a partir de un conjunto de datos cuando los datos son incompletos o tienen parámetros ocultos (Fink, 2007).
Selección de características Fuzzy-Rough Set (FRS) para la reducción del espacio de representación
Los conjuntos difusos rough (FRS) representan la incertidumbre del conocimiento haciendo uso de los conceptos de vaguedad e indiscernibilidad en conjuntos rough, lo cual puede utilizarse de manera efectiva para la reducción del ruido en la información. Esta técnica brinda un medio que permite que los valores ruidosos de los datos reales o discretos (o una mezcla de ambos) puedan ser reducidos eficazmente, aun cuando no se cuente con información suministrada por el usuario, y como tal pueden ser aplicados para la regresión así como la clasificación de bases de datos (Jensen & Shen, 2008). Las ecuación (6) y la (7) expresan la aproximación inferior y superior, respectivamente, usando una relación de similaridad difusa transitiva ϒ para aproximar una clase equivalente difusa X (Radzikowska & Kerre, 2002).
Donde Ψ es una implicación difusa, Υ una t-norma y Rxp es la relación de similaridad difusa inducida por el subconjunto de características P expresada por medio de la ecuación (8).
µRa es el grado en que los objetos x e y son similares para la característica a. La función de membrecía de un objeto  , perteneciente a la región positiva difusa, puede definirse mediante la ecuación (9) (MacParthalain & Jensen, 2009).
, perteneciente a la región positiva difusa, puede definirse mediante la ecuación (9) (MacParthalain & Jensen, 2009).
Donde  es un conjunto de características de decisiones y el grado de dependencia de
es un conjunto de características de decisiones y el grado de dependencia de  sobre P es definido por la ecuación (10).
sobre P es definido por la ecuación (10).
Resultados
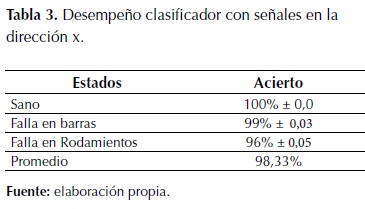
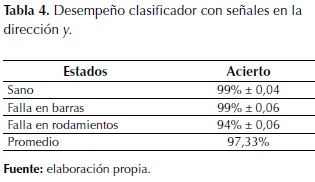
Con el fin de evaluar el sistema de detección de fallas en motores de inducción propuesto, se realizaron pruebas con señales de vibración del eje x y del eje y obteniendo una exactitud de 98,5% y 97%, respectivamente. En la tabla 3 se presentan los resultados en términos de exactitud obteniendo el mejor desempeño 100% en la detección de un motor sano y el más bajo rendimiento, 96% en la detección de fallas en los rodamientos. De igual forma, en la tabla 4 se presentan los resultados obtenidos del análisis estocástico con las señales de vibración en el eje y alcanzando el mejor desempeño en la detección de motores sanos 99% y en detección de falla en las barras, 99% y el más bajo desempeño 94% en fallas en los rodamientos.
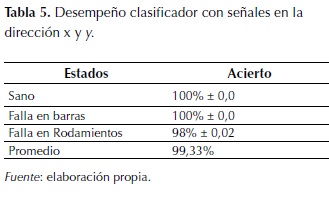
En la tabla 5 se presenta el desempeño del sistema propuesto en términos de precisión usando las señales de vibración del eje x y del eje y en conjunto, para la generación del espacio de representación, lo que permitió obtener un mayor número de características con alta capacidad discriminante y una precisión de 99,33% correspondiente a 1% más alto respecto a los resultados obtenidos con las señales en la dirección x y 2% superior respecto a las señales en la dirección y.
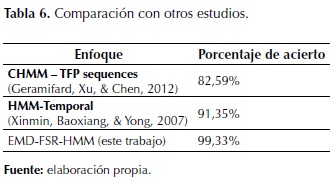
Finalmente en la tabla 6 se compara el sistema de detección de fallas propuesto con otros enfoques basados en HMM pero con diferentes tipos de características, donde el más alto desempeño es evidenciado.
Conclusiones
Se obtuvo un objetivo y exacto mecanismo de clasificación de señales de vibración en motores de inducción para una detección confiable de fallas. La capacidad de representación de la técnica EMD aplicada a señales de vibración y un análisis estocástico por medio de HMM ergódico de características derivadas de momentos estadísticos de la HHT presentan un alto comportamiento en la detección de fallas en barras y rodamientos en motores de inducción. Sin embargo, EMD demanda un costo computacional muy elevado, lo cual lo hace complejo de implementar en un sistema de detección en tiempo real. Aunque este clasificador demostró una alta dependencia con el espacio de representación y los parámetros de inicialización del modelo, la combinación de diferentes IMF disminuyó el ruido y, a pesar de que la información aportada por las señales de vibración en x y en y utilizadas en forma independiente permiten un adecuado desempeño del clasificador, el uso de ambas permitieron mejorar significativamente la exactitud del clasificador.
La reconstrucción de las señales de vibración denominadas constructos a partir de los IMF obtenidos al aplicar la EMD permitieron realzar significativamente factores diferenciadores de las señales de vibración de motores con fallas. Sin embargo, la selección de las IMF para formar el constructo fue experimental, lo que podría afectar negativamente los resultados con señales de vibración de otros motores. Adicionalmente, EMD presenta el problema de entregar diferentes números de IMF entre señales, denominado problema de mezcla, lo cual afecta el resultado del constructo y, por ende, a las características.
Trabajo futuro
Como trabajo futuro se propone un análisis de vibración de las señales basado en la descomposición de vibraciones de Hilbert (HVD) con el fin de disminuir el costo computacional y mejorar la calidad de la representación. Además se propone un análisis de correlación entre las señales de los ejes x, y y z.
Financiamiento
Este trabajo está soportado por el proyecto "Sistemas Inteligentes Web–SINTELWEB" con código Dime 20201009532 de la “Convocatoria Nacional de Apoyo para el Fortalecimiento de Grupos de Investigación o Creación Artística que Soporten Programas de Posgrado” de la Universidad Nacional de Colombia – Sede Medellín, 2012.
Referencias
Askari, M. R. (2010). Broken Bars Detection in Squirrel Cage Induction Motors Using Wavelet Theory. Journal of Applied Sciences, 10(6), 477-478.
Bulla, J. (2011). Hidden Markov Models with t Components, Increased Persistence and other Aspects. Quantitative Finance, 11(3), 459-475.
Cabal-Yepez, E. O.-R.-T.-H.-G. (2009). FPGA-Based Online Induction Motor Multiple-Fault Detection with Fused FFT and Wavelet Analysis. In International Conference on Reconfigurable Computing and FPGAs, 2009. ReConFig '09, 101-106.
Fulufhelo V. U.; Nelwamondo, M., & Marwala, T. (2006). Early classifications of bearing faults using hidden Markov models, gaussian mixture models, mel-frequency cepstral coefficients and fractals. University of the Witwatersrand, Volume 2(6), 1281-1299.
Geramifard, O.; Xu, J., & Chen, W. (2012). An HMM-based semi-nonparametric approach for fault diagnostics in rotary electric motors. In 2012 IEEE International Symposium on Industrial Electronics (ISIE), 1218-1223.
Guo-liang, Z.; Yun-bing, W., & Gang, C. (212). Rotor Break-Bar Fault Diagnosis of Asynchronous Motor Based on Empirical Mode Decomposition. In Power and Energy Engineering Conference (APPEEC), 2012 Asia-Pacific.
Hernández, P. L.; Carro, M.; de Oca, J. M.; García, L., & Fernández, S. J. (2008). Optimización del mantenimiento preventivo utilizando las técnicas de diagnóstico integral. Resultados finales y evaluación económica. (Spanish. Optimization of the Preventive Maintenance Using the Techniques of Integral Diagnosis. Final Results and Economic Evaluation. (English), 29(2), 35-45.
Ho Soon, L.; Chong, K. T., & Su, H. (2006). Motor fault detection method for vibration signal using FFT residuals. International Journal of Applied Electromagnetics & Mechanics, 24(3/4), 209-223.
Jensen, R., & Shen, Q. (s.f.) Computational intelligence and feature selection: rough and fuzzy approaches. Wiley.
MacParthalain, N., & Jensen, R. (2009). Measures for Unsupervised Fuzzy-Rough Feature Selection. In Ninth International Conference on Intelligent Systems Design and Applications, 2009. ISDA '09, 560-565.
Ocak, H., & Loparo, K. A. (2001). A new bearing fault detection and diagnosis scheme based on hidden Markov modeling of vibration signals. In 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2001. Proceedings. (ICASSP '01 (05), 3141-3144.
Orrego, D. A.; Becerra, M. A., & Delgado-Trejos, E. (2012). Dimensionality reduction based on fuzzy rough sets oriented to ischemia detection. In 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 5282-5285.
Oweis, R. J., & Abdulhay, E. W. (2011). Seizure classification in EEG signals utilizing Hilbert-Huang transform. BioMedical Engineering OnLine, 10(1), 38-52.
Patel, R. K.; Agrawal, S., & Joshi, N. C. (2012). Induction motor bearing fault identification using vibration measurement. In 2012 Students Conference on Engineering and Systems (SCES), 1-5.
Patil, S. S., & Gaikwad, J. A. (2013). Vibration analysis of electrical rotating machines using FFT: A method of predictive maintenance. In 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), 1-6.
Qiang, S., & Changjian, F. (2012). Hybrid SVM-HMM Diagnosis Method for Rotor- Gear-Bearing Transmission System. Journal of Computers, 7(9), 2324-2329.
Qiwei-Xie, Bo-Xuan, Silong-Peng, Jianping-Li, Weixuan-Xu, & HAN, H. (2008). Bandwidth empirical mode decomposition and its application. International Journal of Wavelets, Multiresolution & Information Processing, 6(6), 777-798.
Radzikowska, A. M., & Kerre, E. E. (2002). A comparative study of fuzzy rough sets. Fuzzy Sets and Systems, 126(2), 137-155.
Ramírez-Castro, R. I., & Montejo, L. A. (2011). Transformada de Hilbert, descomposición modal empírica y sus aplicaciones en el análisis de vibraciones libres. Hilbert transform, empirical mode decomposition and its applications to free vibration analysis. (English), 11(2), 121-132.
Santana, D., & Madiedo, R. (2007). Valoración de métodos para la determinación de la eficiencia de motores de inducción que accionan cargas en régimen de trabajo continuo variables en el tiempo. (Spanish). Valoration or Methods to Determine the Induction Engines Efficiency That Carry Loods in a Continuous Work Regime Variables in Time. (English), 28(3), 25-29.
Shrivastava, A., & Wadhwani, S. (2014). An approach for fault detection and diagnosis of rotating electrical machine using vibration signal analysis. In Recent Advances and Innovations in Engineering (ICRAIE), 1-6.
Soualhi, A.; Medjaher, K., & Zerhouni, N. (2015). Bearing Health Monitoring Based on Hilbert; Huang Transform, Support Vector Machine, and Regression. IEEE Transactions on Instrumentation and Measurement, 64(1), 52-62.
XinGuang-Li, MinFeng-Yao, & JiaNeng-Yang. (2012). Speech Recognition Approach Based on Speech Feature Clustering and HMM. Journal of Computers, 7(9), 2269-2275.
Xinmin, T.; Baoxiang, D., & Yong, X. (2007). Bearings Fault Diagnosis Based on HMM and Fractal Dimensions Spectrum. In International Conference on Mechatronics and Automation, 2007. ICMA 2007, 1671-1676.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.