DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2015.3.a01Publicado:
01-07-2015Número:
Vol. 19 Núm. 45 (2015): Julio - SeptiembreSección:
InvestigaciónRepresentación óptima de señales MER aplicada a la identificación de estructuras cerebrales durante la estimulación cerebral profunda
Optimal Representation of MER Signals Applied to the Identification of Brain Structures During Deep Brain Stimulation
Palabras clave:
deep brain stimulation, digital signal processing, machine learning, MER signals, Parkinson’s disease (en).Palabras clave:
aprendizaje de máquina, enfermedad de Parkinson, estimulación cerebral profunda, procesamiento digital de señales, señales MER (es).Descargas
Referencias
Bishop, C. (2006). Pattern Recognition and Machine Learning. New York: Springer.
Braunwald, E., Fauci, A., Kasper, D., Hauser, S., Longo, D., & Jameson, L. (2001). Principios de medicina interna. México D.F: McGraww-Hill interamericana.
Breit, S., Schulz, J. B., & Benabid, A. L. (2004). Deep Brain Stimulation. Cell Tissue Res, 318, 275-288.
Bustamante, J. (2007). Neuroanatomía funcional (4 ed.). Bogotá: Celsus.
Castellanos, G., Pinzon, R., Orozco, A., & Carmona, H. (2010). Feature selection using an ensemble of optimal wavelet packet and learning machine: Application to MER signals. CSNDSP, (pp. 25-30). Newcastle (UK).
Chan, H., Wu, T., Lee, S., Lin, M. A., He, S. M., Chao, P. K., & Tsai, S. T. (2010). Unsupervised wavelet spike sorting with dynamic codebook searching and replenishment. Neurocomputing, 73(7), 1513-1527.
Chen, S. S., Donoho, D. L., & Saunders, M. A. (2001). Atomic Decomposition by Basis Pursuit. SIAM, 43(1), 129-159.
Daubechies, I. (1998). Time-frequency localization operators. A geometric phase space approach. IEEE Trans. Inform Theory, 34, 605-612.
Gemmar, P., Gronz, O., Henrichsand, T., & Hertel, F. (2008). Advanced methods for target navigation using microelectrode recordings in stereotactic neurosurgery for deep brain stimulation. CBMS, (pp. 99-104). Jyvaskyla (Finland).
Giraldo, E., Castellanos, G., & Orozco, A. (2008). Feature extraction for MER signals using adaptive filter banks. Electronics, Robotics and Automotive Mechanics Conference, (pp. 582-585). Cuernavaca (México).
Guillén, P., Martínez, P., Sánchez, R., Argáez, M., & Velásquez, L. (2011). Characterization of subcortical structures during deep brain stimulation utilizing support vector machines. EMBC, (pp. 7949-7952). Boston (USA).
Guridi, J., Rodríguez, M., & Manrique, M. (2004). Tratamiento quirúrgico de la enfermedad de Parkinson. Neurocirugía, 15, 5-16.
Hernández, G. A., & Pedroza, A. (2002). Compendio de neurocirugía. Bogotá : Fundación pro-neurocirugía.
Huggins, P. S., & Zucker, S. W. (2007). Greedy Basis Pursuit. IEEE Transactions on Signal Processing, 55(7), 3760-3772.
Jensen, A., & La Cour-Harbo, A. (2001). Ripples in Mathematics-The Discrete Wavelet. Berlín: Springer.
Mallat, S. A. (1999). Wavelet tour of signal processing. Waltham: Academic Press-Elsevier.
Moore, S. K., Mahurin, M., & Christie, B. (2006). Psychiatry's shocking new tools. IEEE spectrum, 43, 19-25.
Novak, P., Daniluk, S., Elias, S., & Nazzaro, J. (2007). Detection of the subthalamic nucleus in microelectrographic recordings in Parkinson's disease using the high frequency (500 hz) neuronal background. Neurosurgery, 106, 175-179.
Nowinski, W. L., Belov, D., Pollak, P., & Benabid, A. L. (2005). Statistical analysis of 168 bilateral subthalamic nucleus implantations by means of the probabilistic functional atlas. Neurosurgery, 57, 319-330.
Orozco , A. A., Guarnizo, C., Alvarez, M. A., Castellanos, G., & Guijarro, E. (2005). Spike source identification using artificial intelligence techniques. 3rd IEE International Seminar on Medical Applications of Signal Processing, (pp. 105 - 109). London.
Orozco, A. A., Álvarez, M., & Guijarro, E. (2006). Identification of spike sources using proximity analysis through hidden Markov models. EMBC, (pp. 5555-5558). New York (USA).
Ortoft-Endelt, L., & La Cour-Harbo, A. (2005). Comparison of Methods for Sparse Representation of Musical Signals. ICASSP, (pp. 13-16). Philadelphia (USA).
Padilla, J. B., Vargas Cardona, H. D., Arango, A., Carmona, H., Álvarez, M., Guijarro, E., & Orozco, A. (2012). NEUROZONE: On-line recognition of brain structures in stereotactic surgery - Application to Parkinson's disease surgery. EMBC (pp. 2219-2222). Chicago (USA): IEEE.
Pinzon, R., Garcés, M., Orozco, A., & Nazzaro, J. (2009). Automatic identification of various nuclei in the basal ganglia for Parkinson's disease neurosurgery. EMBC, (pp. 99-104). Minneapolis (USA).
Pinzon, R., Orozco, R., Carmona, H., & Castellanos, G. (2010). Towards high accuracy classification of MER signals for target localization in Parkinson's disease. EMBC, (pp. 4040-4043). Buenos Aires (Argentina).
Pizarro, J., Guerrero, J., & Galindo, L. (2002). Multiple comparison procedures applied to model selection. Neurocomputing, 48, 755-173.
Polikar, R., Greer, M. H., Udpa, L., & Keinert, F. (1997). Multiresolution Wavelet Analysis of ERPs for the detection of Alzheimer's disease. EMBC, (pp. 1301-1304). Chicago.
Pouzat, C., Delescluse, M., Viot, P., & Diebolt, J. (2004). Improved spike-sorting by modeling firing statistics and burst-dependent spike amplitude attenuation: a markov chain Montecarlo approach. J Neurophysiol, 91, 2910-2928.
Ropper, A. H. (2002). Principios de Neurología de Adams y Victor (7 ed.). New York: McGraw-Hill Interamericana.
Snider, R., & Bonds, A. (1998). Classification of non-stationary neural signals. Journal of Neuroscience Methods, 84, 155-166.
Tahgva, A. (2011). Hidden semi-Markov models in the computerized decoding of microelectrode recording data for deep brain stimulator placement. World neurosurgery , 75, 758-764.
Vargas, H. D., Orozco, A. A., & Álvarez, A. A. (2012). Multi-patient learning increases accuracy for Subthalamic nucleus identification in deep brain stimulation. EMBC, (pp. 4341-4344). San Diego (USA).
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.3.a01
Investigación
Representación óptima de señales MER aplicada a la identificación de estructuras cerebrales durante la estimulación cerebral profunda
Optimal Representation of MER Signals Applied to the Identification of Brain StructuresDuring Deep Brain Stimulation
Hernán Darío Vargas Cardona*,
Mauricio A. Álvarez**,
Álvaro Orozco Gutiérrez***
** Ingeniero electrónico, doctor en Ciencias de la Computación, Universidad Tecnológica de Pereira, Pereira, Colombia. Contacto: malvarez@utp.edu.co
*** Ingeniero electricista, doctor en Bioingeniería, Universidad Tecnológica de Pereira, Pereira, Colombia. Contacto: aaog@utp.edu.co
Fecha de recepción: 25 de septiembre de 2014 Fecha de aceptación: 6 de abril de 2015
Como citar: Vargas Cardona, H. D., Álvarez, M.A., & Orozco Gutiérrez, Á. (2015). Representación óptima de señales MER aplicada a la identificación de estructuras cerebrales durante la estimulación cerebral profunda. Revista Tecnura, 19(45), 15-27. doi: 10.14483/udistrital.jour.tecnura.2015.3.a01
RESUMEN
La identificación de señales cerebrales provenientes de microelectrodos de registro (MER) es un procedimiento clave en la estimulación cerebral profunda (DBS en inglés) aplicada en pacientes con enfermedad de Parkinson (EP). El propósito de esta investigación es identificar con alta precisión una estructura cerebral llamada núcleo subtalámico (STN), ya que es la estructura objetivo donde se logran los mejores resultados terapéuticos de la DBS. Para ello, se presenta un enfoque de representación óptima de señales MER mediante el método de Frames (MOF por sus siglas en inglés), con el cual se obtienen coeficientes que minimizan la norma Euclidiana de orden 2. A partir de los coeficientes óptimos se realiza una extracción de características de las señales combinando diccionarios wavelet packet y coseno. Para tener un marco de comparación con el estado del arte, también se caracterizan las señales utilizando la transformada wavelet discreta (DWT) con diferentes funciones madre. La metodología propuesta se valida en una base de datos real, y se emplean máquinas de aprendizaje supervisadas simples, como el clasificador K-Nearest Neighbors (K-NN), el clasificador lineal bayesiano (LDC) y el cuadrático (QDC). Los resultados de clasificación que se obtienen con el método propuesto mejoran significativamente el rendimiento alcanzado con la DWT, de manera que se logra una identificación positiva del STN superior al 97,6%. Los índices de identificación logrados por el MOF son muy precisos, ya que potencialmente se puede obtener una tasa de falsos positivos menores al 2% durante la DBS.
Palabras clave: aprendizaje de máquina, enfermedad de Parkinson, estimulación cerebral profunda, procesamiento digital de señales, señales MER.
ABSTRACT
Identification of brain signals from microelectrode recordings (MER) is a key procedure during deep brain stimulation (DBS) applied in Parkinson's disease patients. The main purpose of this research work is to identify with high accuracy a brain structure called subthalamic nucleus (STN), since it is the target structure where the DBS achieves the best therapeutic results. To do this, we present an approach for optimal representation of MER signals through method of frames (MOF). We obtain coefficients that minimize the Euclidean norm of order two. From optimal coefficients, we extract some features from signals combining the wavelet packet and cosine dictionaries. For a comparison frame with the state of the art, we also process the signals using the discrete wavelet transform (DWT) with several mother functions. We val idate the proposed methodology in a real data base. We employ simple supervised machine learning algorithms, such as the K-Nearest Neighbors classifier (K-NN), a linear Bayesian classifier (LDC) and a quadratic Bayesian classifier (QDC). Classification results obtained with the proposed method improve significantly the performance of the DWT. We achieve a positive identificaron of the STN superior to 97,6%. Identification outcomes achieved by the MOF are highly accurate, as we can potentially get a false positive rate of less than 2% during the DBS.
Keywords: deep brain stimulation, digital signal processing, machine learning, MER signals, Parkinson's disease.
INTRODUCCIÓN
La enfermedad de Parkinson (EP) se relaciona con la pérdida de células pigmentadas de la substantia nigra reticulata (SNr), la cual produce un déficit acelerado de un neurotransmisor llamado dopamina (Nowinski, Belov, Pollak, & Benabid, 2005). Debido a este fenómeno, la EP puede generar desórdenes de los movimientos motores: temblor en extremidades, parálisis, disquinesias, trastornos en la marcha, entre otros (Bustamante, 2007; Guridi, Rodríguez, & Manrique, 2004). La estimulación cerebral profunda (DBS) es el tratamiento más común y exitoso para los pacientes que padecen enfermedad de Parkinson avanzada. La DBS ha sido aplicada en distintas estructuras cerebrales, como el globus pallidus internus (GPI) y el núcleo subtalámico (STN), y se ha visto que los síntomas de la EP mejoran significativamente en el paciente (Breit, Schulz, & Benabid, 2004). El procedimiento quirúrgico comprende la planeación del objetivo (especialmente el STN), el ajuste de un marco estereotáxico, exposición de la corteza, aseguramiento del electrodo y estimulación de estructuras vecinas (Nowinski, Belov, Pollak, & Benabid, 2005). Durante la cirugía, la actividad cerebral de las estructuras cerebrales puede ser capturada mediante microelectrodos exploratorios a través de señales que se conocen como registros de microelectrodo (MER). Las señales MER están compuestas por la suma de descargas de la población neuronal de un pequeño volumen próximo a la punta del electrodo y presentan un comportamiento no estacionario debido a la contribución de varios factores, como la propia variación de las descargas, que no son exactamente iguales ni exactamente regulares en su ritmo. A esto se añaden otros como la pulsación cortical causada por la actividad cardiaca o respiratoria, la reducción sistemática de la amplitud de un potencial de acción cuando la célula se dispara con alta frecuencia, el movimiento sistemático del electrodo desde el sitio original de registro (Snider & Bonds, 1998) y el ruido neuronal de fondo (Pouzat, Delescluse, Viot, & Diebolt, 2004). La importancia del procesamiento y clasificación de señales MER durante la DBS en pacientes con EP radica en la necesidad de un soporte de decisión para localizar correctamente una zona cerebral objetivo y la respectiva implantación del microelectrodo estimulador. Es prioritario y crítico lograr los mejores resultados terapéuticos posibles en los pacientes y a la vez generar los mínimos efectos secundarios.
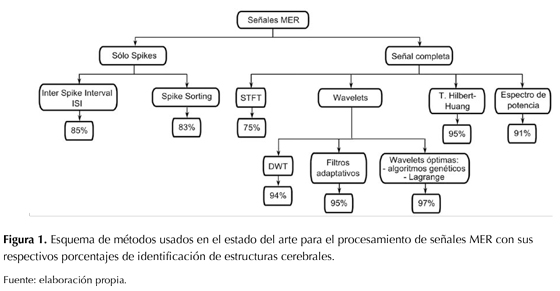
Previamente, se han abordado enfoques de procesamiento de señales MER basados en el análisis temporal de espigas (spikes) (Chan, et al., 2010; Orozco , Guarnizo, Alvarez, Castellanos, & Guijarro, 2005), pero el rendimiento de este análisis se reduce considerablemente, en zonas con baja actividad de spikes, como en la Zona Incerta (ZI). Otro enfoque muy común es el análisis tiempo-frecuencia, en el cual las señales MER se transforman a distintos espacios, por ejemplo, el espacio de la transformada corta de Fourier (STFT) (Novak, Daniluk, Elias, & Nazzaro, 2007), el espacio wavelet (WT) (Gemmar, Gronz, Henrichsand, & Hertel, 2008) y también con métodos empíricos como la transformada Hilbert-Huang (HHT) (Pinzon, Garcés, Orozco, & Nazzaro, 2009). Estas metodologías entregan resultados aceptables de clasificación, sin embargo no ofrecen buena generalización al momento de validar un sistema de identificación automática.
El procesamiento de señales no estacionarias y altamente oscilatorias, como las señales MER, requiere el uso de métodos especiales. El análisis por banco de filtros adaptativos es uno de los métodos de caracterización más potentes de las wavelet (Giraldo, Castellanos, & Orozco, 2008), donde los filtros adaptativos son un ensamble de descomposiciones wavelet adaptadas a las señales, construidos mediante esquemas lifting (LS), que a su vez se describen por operadores optimizados mediante algoritmos genéticos. En trabajos previos de investigación (Pinzon, Orozco, Carmona, & Castellanos, 2010; Castellanos, Pinzon, Orozco, & Carmona, 2010), esta metodología de caracterización combinada con clasificadores sencillos como el bayesiano lineal y bayesiano cuadrático demostró ser muy eficiente para extraer información discriminante de las señales MER, pues se obtuvieron excelentes resultados de identificación del STN cercanas al 97%. Así mismo, en Guillén, Martínez, Sánchez, Argáez y Velásquez (2011), Orozco, Álvarez y Guijarro (2006) y Tahgva (2011) se implementaron clasificadores más sofisticados, como máquinas de Soporte Vectorial con Kernel polinomial y también basados en modelos ocultos de Markov (HMM), con lo cual se lograron resultados de hasta 98% en la identificación de estructuras corticales profundas. No obstante, la enorme dificultad en la adaptación de este tipo de algoritmos en sistemas de identificación en tiempo real, debido al alto costo computacional que demandan, hace que no se recomiende implementar estos métodos en herramientas automáticas de identificación on-line. La figura 1 muestra un esquema de las metodologías usadas en el estado del arte para procesar señales MER y sus porcentajes de identificación del STN.
Debido a que los métodos tradicionales utilizados en el estado del arte se basan en transformadas tiempo-escala o tiempo-frecuencia que no ofrecen superresolución ni adaptabilidad, en este trabajo se propone una nueva metodología para representar y caracterizar las señales MER mediante una transformación optimizada basada en el método de Frames. La motivación de este trabajo es lograr simultáneamente una alta resolución y adaptabilidad en la representación de las señales MER, de modo que se puedan extraer características discriminantes que permitan identificar con alta precisión los registros provenientes del núcleo subtalámico durante la cirugía de la enfermedad de Parkinson. En este enfoque se busca representar las señales utilizando un conjunto de vectores redundantes llamados átomos (Ortoft-Endelt & La Cour-Harbo, 2005). Dichos átomos son obtenidos por medio de un conjunto de funciones base, que se conoce como diccionario (Huggins & Zucker, 2007). Hay varios diccionarios que se pueden implementar e incluso combinar: wavelets, wavelets segmentados, diccionario Gabor, diccionarios multiescala Gabor, wavelet packet (WP), coseno, chirplets y warplets (Chen, Donoho, & Saunders, 2001).
Se seleccionan los diccionarios WP y coseno debido a que, por validación cruzada, se encontró que estos se correlacionan mejor con las señales MER y logran los mejores índices de clasificación del STN. El método se valida en una base de datos real empleando máquinas de aprendizaje simples como el clasificador bayesiano lineal (LDC) y cuadrático (QDC), y el clasificador K-Nearest Neighbor (K-NN). Como marco de comparación se ejecutan los mismos experimentos de caracterización de las señales con la transformada wavelet discreta y con análisis multirresolución.
Los resultados de identificación positiva del STN obtenidos con la metodología propuesta son mayores al 97,6%, con lo cual se mejora ampliamente al análisis wavelet y también se iguala el rendimiento logrado con wavelets optimizada mediante algoritmos genéticos (Castellanos, Pinzon, Orozco, & Carmona, 2010), o realizando clasificación robusta con procesos gaussianos (Vargas, Orozco, & Álvarez, 2012), máquinas de soporte vectorial (Guillén, Martínez, Sánchez, Argáez, & Velásquez, 2011) y modelos ocultos de Markov (Orozco, Álvarez & Guijarro, 2006; Tahgva, 2011). Por el momento, esta metodología de procesamiento se está implementando en un sistema software, que ha sido probado por especialistas del Instituto de Epilepsia y Parkinson del Eje Cafetero.
MATERIALES Y METODOLOGÍAEnfermedad de Parkinson y señales MER
La enfermedad de Parkinson (EP) es un trastorno crónico y progresivo del sistema nervioso central que se inicia entre los 40 y 70 años de edad y es poco frecuente antes de los 30. La pérdida de células pigmentadas de la substantia nigra y otros núcleos (locus coeruleus, núcleo motor dorsal del vago) es el motivo más constante en la EP (Ropper, 2002). En condiciones normales las células nigrales disminuyen en cantidad con el paso del tiempo de 425.000 a 200.000 a los 80 años (Braunwald, et al., 2001). En la EP las células pigmentadas se reducen al 30% de las que tiene un individuo sano de la misma edad (Hernández & Pedroza, 2002). Las neuronas que conforman el tejido cerebral del organismo generan impulsos eléctricos, característicos de áreas, funciones y estados fenomenológicos en la sustancia blanca y gris de todo el encéfalo. Esta actividad, cuando es captada mediante microelectrodos de registro (MER), refleja la suma de descargas de la población neuronal de un pequeño volumen próximo a la punta del electrodo, por lo cual esta información sirve de soporte para localizar zonas cerebrales específicas, donde se requiere excitar, lesionar o implantar grupos de células madre, como en el caso de la enfermedad de Parkinson, en la localización de dianas para tratar desórdenes obsesivos compulsivos severos, entre otros (Moore, Mahurin, & Christie, 2006).
Base de datos (DB-UTP)
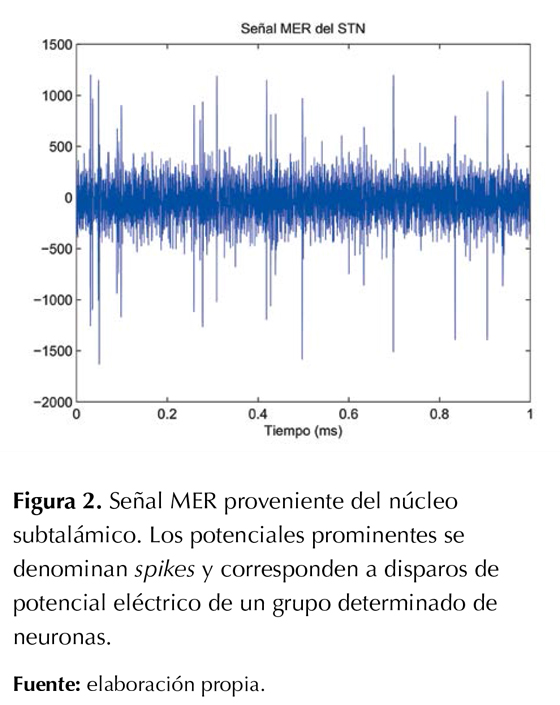
La base de datos MER de la Universidad Tecnológica de Pereira (DB-UTP) está compuesta por registros de varios procedimientos quirúrgicos en pacientes con enfermedad de Parkinson, cuyas edades están entre 55 y 56 años (4 hombres, 2 mujeres). Todos los pacientes firmaron un consentimiento informado. Los registros se adquirieron con el sistema ISIS MER (Innomed Medical GmbH). Las señales MER fueron etiquetadas por médicos neurofisiólogos y especialistas del Instituto de Epilepsia y Parkinson del Eje Cafetero, que se localiza en la ciudad de Pereira, Colombia. En total, hay 600 registros neuronales divididos en dos clases: 300 señales del núcleo subtalámico (STN) y 300 de otras estructuras del cerebro (Tálamo, Tal; Zona Incierta, ZI; Substantia Nigra Reticulata, SNr). Cada registro tiene una duración de 1 segundo y son muestreados a una frecuencia de 25 kHz y 16 bits de resolución. En la figura 2 se ilustra un registro MER proveniente del núcleo subtalámico perteneciente a la DB-UTP.
Método de Frames (MOF)
Dada una señal s y un diccionario de funciones base Φ, el MOF encuentra una solución donde los coeficientes de representación minimizan la norma euclidiana de orden 2 (ecuación (1)).
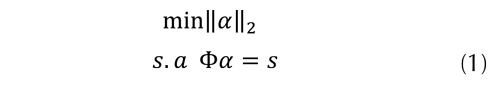
Este es un problema de programación cuadrática (QP), cuya solución es única y se denota como α*. El MOF genera pocos coeficientes cercanos a cero, debido a que el producto interno del diccionario con la señal es diferente de cero para la mayor parte de los coeficientes de representación. Este método obtiene los coeficientes αi. más cercanos al origen del subespacio Ep formado por todas las posibles soluciones de la ecuación (1). Los coeficientes óptimos α* pueden ser calculados utilizando un sistema de ecuaciones lineales, tal como se muestra en la ecuación (2).
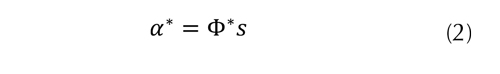
Donde la matriz Φ* es la inversa generalizada de Φ dada por la ecuación (3).
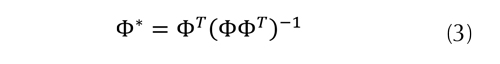
Se remite al lector a Daubechies (1998) para encontrar información más detallada del MOF.
Transformada wavelet discreta y análisis multi-rresolución
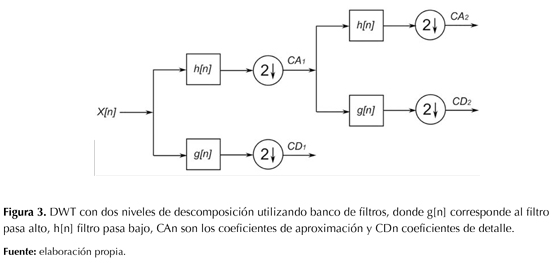
Como marco de comparación, en este trabajo se realiza el procesamiento de las señales MER similar al MOF mediante la DWT y el análisis multi-rresolución. La transformada wavelet discreta (DWT) utiliza bancos de filtros y submuestreo para realizar la descomposición de una señal. Dicha representación se puede observar en la figura 3.
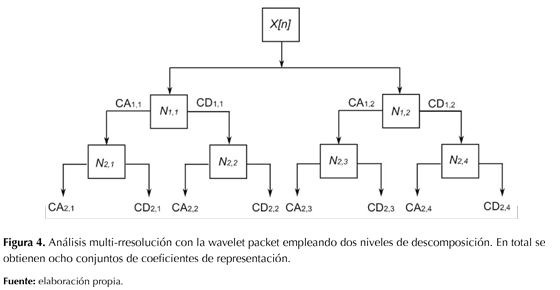
El análisis multi-rresolución se basa en aproximar una función f(t) en distintos niveles de resolución obtenidos con la wavelet { f1(t),f2(t),f3(t),…}, lo cual entrega una descomposición multiescala con redundancia, como se muestra en la figura 4. Para un entendimiento profundo de la transformada wavelet y el análisis multi-rresolución, el lector se puede remitir a Jensen y La Cour-Harbo (2001), Mallat (1999) y Polikar, Greer, Udpa y Keinert (1997).
Procedimiento metodológico
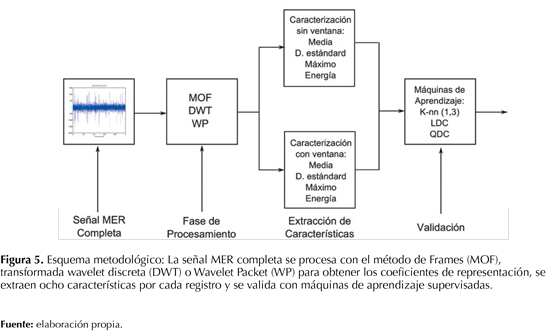
Los pasos metodológicos seguidos en este trabajo se detallan en los siguientes puntos. La figura 5 muestra un diagrama de flujo de la metodología empleada.
1. Se toman las señales MER con segmentos de 1 segundo de duración, debido a que trabajosanteriores (Giraldo, Castellanos, & Orozco, 2008; Pinzon, Orozco, Carmona, & Castellanos, 2010; Castellanos, Pinzon, Orozco, & Carmona, 2010) han demostrado que este segmento es suficiente para capturar el comportamiento dinámico de los registros, así como sus propiedades intrínsecas (spikes y ruido neuronal de fondo), además permite su implementación en sistemas en línea (Padilla, et al., 2012).
2. Se transforman los registros MER de 1 segundo de duración a un espacio vectorial tiempo-escala con el método de Frames, combinando los diccionarios wavelet packet y coseno. Se realizan dos niveles de descomposición, por lo que se obtienen dos conjuntos de coeficientes de representación óptimos αic, i= 1,…,n,c = 1,2 para cada registro, donde es el número de coeficientes de representación. El procedimiento es similar para la DWT: se aplica la transformada wavelet discreta y el análisis multi-rresolución a los registros usando dos niveles de descomposición y se obtienen los coeficientes wavelet para cada señal MER. Se prueban diferentes wavelet madre: Coiflets (coifl, coif5), Daubechies (db1, db3), Symlet (sym2, sym8), Meyer discreta (dmey).
3. Una vez se han obtenido los coeficientes, ya sea usando MOF, DWT o DWT con análisis multi-rresolución, se realizan dos tipos de caracterización, una sin enventanado de los coeficientes y la otra con enventanado de los coeficientes.
• Sin ventana: Se calcula directamente el valor máximo absoluto, la energía, el valor medio absoluto y la desviación estándar sobre los coeficientes de representación obtenidos en el paso metodológico número 2.
• Con ventana: Se aplican ventanas rectangulares de 80 milisegundos de duración con traslape del 50% a los coeficientes de representación. Luego a los coeficientes enventanados se aplican las mismas métricas estadísticas del caso sin ventana. Con este procedimiento se obtiene una matriz de características para cada señal MER. Finalmente se promedia la matriz sobre las columnas y se obtiene un vector de características, donde se captura de mejor manera el comportamiento dinámico de los registros.
4. Debido a que se realizan dos niveles de descomposición en todos los métodos de procesamiento, se obtienen ocho características por cada registro MER.
5. Máquinas de aprendizaje: Se evalúan clasificadores paramétricos y no-paramétricos. Dentro de la familia paramétrica, se emplea el clasificador de Bayes con matriz de covarianza compartida entre las clases, también conocido como el clasificador con discriminante lineal (LDC) y el clasificador de Bayes con matriz de covarianza diferente por clase, conocido como el clasificador con discriminante cuadrático (QDC). Dentro de la familia no-paramétrica, se emplea el algoritmo K-Nea-rest Neighbors (K-NN) con K=1 y K=3 (K-NN1 y K-NN3, respectivamente). La teoría de estos clasificadores se puede encontrar completamente en Bishop (2006). Todos los algoritmos son implementados en Matlab usando el toolbox PRTOOLS disponible en http://prtools.org/.
6. Validación: La validación de cada máquina KNN 1-3, LDC y QDC se realiza con el esquema Hold-Out repitiendo cincuenta veces cada experimento. Se toman permutaciones aleatorias de los datos. El conjunto completo de datos tiene dos clases y se divide en 50% para el entrenamiento y 50% para la validación. La clase 1 es el núcleo subtalámico (STN) y la clase 2 corresponde a otras zonas (Tálamo, Tal; Zona Incerta, ZI, y Substancia Nigra Reticulata, SNr).
RESULTADOS Y DISCUSIÓN
En esta sección se presentan y se discuten los resultados obtenidos en los experimentos, mostrando todas las combinaciones posibles de los métodos de procesamiento con los algoritmos de aprendizaje de máquina. Las wavelets madre corresponden a Coiflets (coifl, coif5), Daubechies (db1, db3), Symlet (sym2, sym8), Meyer discreta (dmey). K-NN1 y K-NN3 corresponden al clasificador K-Nearest Neighbors con 1 y 3 vecinos, respectivamente, LDC y QDC corresponden al clasificador bayesiano lineal y cuadrático, respectivamente.
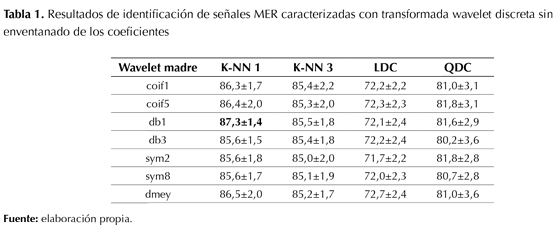
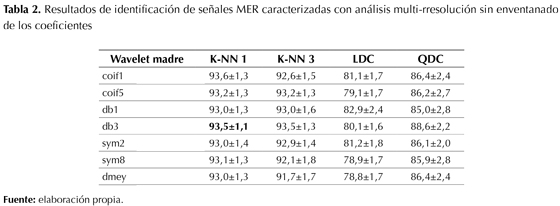
Resultados de clasificación para el procesamiento con la transformada wavelet discreta y el análisis multi-rresolución
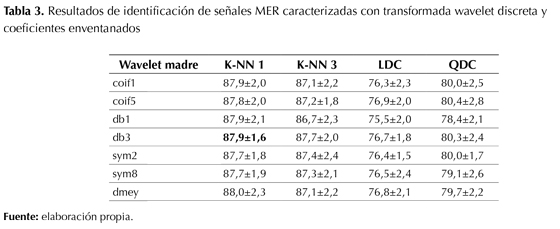
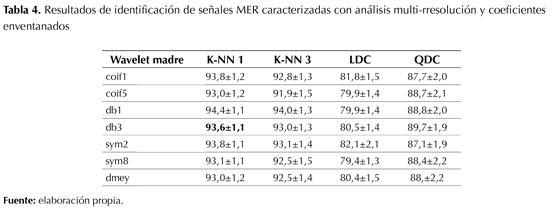
En la tabla 1 y la tabla 2 se puede observar fácilmente que el análisis multi-rresolución tiene un mejor rendimiento que la transformada wave-let discreta (DWT) básica. La tabla 3 y la tabla 4 reportan el porcentaje de acierto con enventanado de los coeficientes; en este caso la precisión en la identificación del STN mejora con respecto al caso donde no se realiza enventanado. Esto se explica porque las ventanas permiten capturar información de la dinámica temporal de los coeficientes de representación. Es aconsejable enventanar los coeficientes para realizar una caracterización localizada en el tiempo, debido a que la evolución temporal de las propiedades intrínsecas de las señales MER se conserva de mejor manera en un análisis con enventanado. En todos los casos el mejor clasificador es el K-NN 1 y la función madre que mejor se correlaciona con este tipo de señales es la Daubechies (db1 y db3). Igualmente, se puede establecer que el análisis multi-rresolución con transformada wavelet permite una representación aproximada y detallada de las señales en diferentes espacios de representación contenidos unos en otros, ya que genera redundancia en los coeficientes en comparación con la DWT simple. El punto débil de este método es que no presenta adaptabilidad a la no estacionariedad de las señales MER y por este motivo existen vacíos para diferenciar satisfactoriamente los registros que provienen del STN con los de las otras estructuras. Si bien los índices de acierto en la identificación de las señales MER alcanzan el 93,5% (sin enventanado) y 94,4% (con enventanado), estos resultados son inferiores a los que se han reportado en la literatura en este campo del conocimiento, donde se han utilizado máquinas de aprendizaje más potentes.
Resultados de clasificación para el procesamiento con el método de Frames (MOF)
Del experimento anterior con DWT y análisis multi-rresolución se establece que el enventanado de los coeficientes de representación permite una caracterización más discriminante de las distintas clases de señales MER, sobre todo para identificar el STN, que es la estructura objetivo en la cirugía de la enfermedad de Parkinson. En el análisis de las señales MER con el MOF se realiza el mismo enventanado de 80 ms con traslape del 50%, pero en este caso se obtuvieron coeficientes optimizados sobre la norma euclidiana de segundo orden.
Los resultados logrados con el método de Frames mejoran a la DWT y al análisis multi-rresolución. En la tabla 5 se observan los resultados de identificación del STN para diferentes combinaciones de diccionarios, donde el clasificador KNN-1 logra los mejores valores de precisión en la clasificación, llegando al 97,6%, además de que la dispersión es pequeña (± 0,9), lo cual indica que el método es robusto ante modificaciones en el conjunto de entrenamiento y validación. Otro aspecto importante es que la caracterización con MOF también genera un mejor rendimiento de las demás máquinas de aprendizaje, esto es muy importante porque demuestra que el método propuesto no depende de un clasificador robusto, o que el mejoramiento en la caracterización no se presenta en casos aislados. En cuanto a combinar diccionarios o solo emplear diccionarios WP, no se obtuvieron diferencias significativas en la identificación del STN. Esto se explica porque el MOF optimiza los coeficientes de representación y no el conjunto de funciones base (diccionario), entonces combinar dos o más diccionarios no modifica en gran medida la transformación que se hace a la señal MER.
Discusión general de los resultados
Es evidente que el método de Frames aplicado a las señales MER logra una extracción de características más discriminantes para identificar el núcleo subtalámico (STN). Al comparar los resultados consignados en todas las tablas se observa que MOF es el que exhibe el mejor rendimiento de todos, ya sea con el diccionario wavelet packet (WP) o combinando los diccionarios WP y coseno. En este trabajo se comparó MOF con métodos tradicionales como la DWT y el análisis multi-rresolución, y en todas las máquinas de aprendizaje MOF mejora a la DWT sin importar la función madre utilizada. Una diferencia clave entre MOF y la DWT (con o sin análisis multi-rresolución) es que MOF hace una representación de las señales con coeficientes optimizados, mientras que la única restricción que se tiene con la DWT es que la señal se pueda reconstruir perfectamente. La optimización de los coeficientes hace que la energía de la señal se concentre en un ancho de banda más pequeño, de modo que se hace más fácil extraer la información relevante para diferenciar las distintas clases de señales MER, sobre todo las que provienen del STN.
El mejor resultado de precisión en la identificación del STN fue del 97,6% con el clasificador KNN-1. Este resultado es muy satisfactorio porque esta máquina de aprendizaje es muy básica y de fácil implementación. Por esta razón, se puede asegurar que la fortaleza de la metodología propuesta radica en la representación óptima de las señales MER con MOF y no depende de clasificadores potentes.
En cuanto a la elección del diccionario dentro del MOF, se observa que las diferencias de los resultados no son estadísticamente significativas cuando se realiza una prueba de selección del modelo de Kruskal-Wallis (Pizarro, Guerrero, & Galindo, 2002). Esto es positivo porque la metodología no queda sujeta a la elección del diccionario. La tabla 5 muestra que la mejor combinación posible es el procesamiento con MOF usando dos diccionarios mezclados (coif5+coseno), sin embargo cuando se mezclan los diccionarios sym2+coseno y dmey+coseno los resultados son casi idénticos. Cuando no se utiliza el MOF, en casi todos los experimentos el procesamiento con la función madre db3 es la que entrega mejores resultados de clasificación. Una explicación de esto se fundamenta en que la db3 se correlaciona mejor con los registros MER, dada su forma de onda, pues esta tiene un comportamiento similar a un spike, de tal forma que permite concentrar grandes cantidades de energía en los coeficientes de representación.
Otro aspecto importante es que esta metodología se puede implementar sin mayores dificultades a sistemas software de reconocimiento automático de señales MER, como por ejemplo el trabajo desarrollado por Padilla et al. (2012). Este sistema actualmente se está validando en la clínica Neurocentro (Pereira, Colombia) como soporte médico durante la DBS aplicada en pacientes colombianos con enfermedad de Parkinson.
CONCLUSIONESEn este trabajo se desarrolló una metodología para caracterizar señales MER basada en el método de Frames con el fin de identificar registros provenientes del núcleo subtalámico. Los resultados demuestran que el método de Frames permite realizar una mejor generalización de cada una de las características intrínsecas en las series de tiempo. Además, en combinación con un clasificador común como es el KNN-1, es posible obtener una clasificación muy precisa del STN, incluso superior al 97,6%. Dado que los resultados preliminares son muy satisfactorios, se pretende implementar esta metodología en un sistema software aplicado al soporte clínico durante la DBS.
FINANCIAMIENTOEste trabajo forma parte del proyecto de investigación titulado: Desarrollo de un sistema efectivo y apropiado de estimación de volumen de tejido activo para el mejoramiento de los resultados terapéuticos en pacientes con enfermedad de Parkinson intervenidos quirúrgicamente, financiado por Colciencias mediante la Convocatoria 569 del año 2012 con código 111056934461. El autor H.D. Vargas está financiado por el programa de Colciencias para la formación de alto nivel para la ciencia, la tecnología y la innovación-Convocatoria 617 de 2013.
AGRADECIMIENTOSLos autores agradecen al Instituto de Epilepsia y Parkinson del Eje Cafetero-Neurocentro S. A. por la asesoría clínica y el etiquetado de la base de datos de señales MER.
REFERENCIAS
Bishop, C. (2006). Pattern Recognition and Machine Learning. New York: Springer.
Braunwald, E., Fauci, A., Kasper, D., Hauser, S., Longo, D., & Jameson, L. (2001). Principios de medicina interna. México D.F: McGraww-Hill interamericana.
Breit, S., Schulz, J. B., & Benabid, A. L. (2004). Deep Brain Stimulation. Cell Tissue Res, 318, 275-288.
Bustamante, J. (2007). Neuroanatomía funcional (4 ed.). Bogotá: Celsus.
Castellanos, G., Pinzon, R., Orozco, A., & Carmona, H. (2010). Feature selection using an ensemble of optimal wavelet packet and learning machine: Application to MER signals. CSNDSP, (pp. 25-30). Newcastle (UK).
Chan, H., Wu, T., Lee, S., Lin, M. A., He, S. M., Chao, P. K., & Tsai, S. T. (2010). Unsuper-vised wavelet spike sorting with dynamic codebook searching and replenishment. Neurocomputing, 73(7), 1513-1527.
Chen, S. S., Donoho, D. L., & Saunders, M. A. (2001). Atomic Decomposition by Basis Pursuit. SIAM, 43(1), 129-159.
Daubechies, I. (1998). Time-frequency localization operators. A geometric phase space approach. IEEE Trans. Inform Theory, 34, 605-612.
Gemmar, P., Gronz, O., Henrichsand, T., & Hertel, F. (2008). Advanced methods for target navigation using microelectrode recordings in stereotactic neurosurgery for deep brain stimulation. CBMS, (pp. 99-104). Jyvaskyla (Finland).
Giraldo, E., Castellanos, G., & Orozco, A. (2008). Feature extraction for MER signals using adaptive filter banks. Electronics, Robotics and Automotive Mechanics Conference, (pp. 582-585). Cuernavaca (México).
Guillén, P., Martínez, P., Sánchez, R., Argáez, M., & Velásquez, L. (2011). Characterization of subcortical structures during deep brain stimulation utilizing support vector machines. EMBC, (pp. 7949-7952). Boston (USA).
Guridi, J., Rodríguez, M., & Manrique, M. (2004). Tratamiento quirúrgico de la enfermedad de Parkinson. Neurocirugía, 15, 5-16.
Hernández, G. A., & Pedroza, A. (2002). Compendio de neurocirugía. Bogotá : Fundación pro-neurocirugía.
Huggins, P. S., & Zucker, S. W. (2007). Greedy Basis Pursuit. IEEE Transactions on Signal Processing, 55(7), 3760-3772.
Jensen, A., & La Cour-Harbo, A. (2001). Ripples in Mathematics-The Discrete Wavelet. Berlín: Springer.
Mallat, S. A. (1999). Wavelet tour of signal processing. Waltham: Academic Press-Elsevier.
Moore, S. K., Mahurin, M., & Christie, B. (2006). Psychiatry's shocking new tools. IEEE spectrum, 43, 19-25.
Novak, P., Daniluk, S., Elias, S., & Nazzaro, J. (2007). Detection of the subthalamic nucleus in microelectrographic recordings in Parkinson's disease using the high frequency (500 hz) neuronal background. Neurosurgery, 106, 175-179.
Nowinski, W. L., Belov, D., Pollak, P., & Benabid, A. L. (2005). Statistical analysis of 168 bilateral subthalamic nucleus implantations by means of the probabilistic functional atlas. Neurosurgery, 57, 319-330.
Orozco , A. A., Guarnizo, C., Alvarez, M. A., Castellanos, G., & Guijarro, E. (2005). Spike source identification using artificial intelligence techniques. 3rd IEE International Seminar on Medical Applications of Signal Processing, (pp. 105-109). London.
Orozco, A. A., Álvarez, M., & Guijarro, E. (2006). Identification of spike sources using proximity analysis through hidden Markov models. EMBC, (pp. 5555-5558). New York (USA).
Ortoft-Endelt, L., & La Cour-Harbo, A. (2005). Comparison of Methods for Sparse Representaron of Musical Signals. ICASSP, (pp. 13-16). Philadelphia (USA).
Padilla, J. B., Vargas Cardona, H. D., Arango, A., Carmona, H., Álvarez, M., Guijarro, E., & Orozco, A. (2012). NEUROZONE: On-line recognition of brain structures in stereotactic surgery-Application to Parkinson's disease surgery. EMBC (pp. 2219-2222). Chicago (USA): IEEE.
Pinzon, R., Garcés, M., Orozco, A., & Nazzaro, J. (2009). Automatic identification of various nuclei in the basal ganglia for Parkinson's disease neurosurgery. EMBC, (pp. 99-104). Minneapolis (USA).
Pinzon, R., Orozco, R., Carmona, H., & Castellanos, G. (2010). Towards high accuracy classification of MER signals for target localization in Parkinson's disease. EMBC, (pp. 4040-4043). Buenos Aires (Argentina).
Pizarro, J., Guerrero, J., & Galindo, L. (2002). Multiple comparison procedures applied to model selection. Neurocomputing, 48, 755-173.
Polikar, R., Greer, M. H., Udpa, L., & Keinert, F. (1997). Multiresolution Wavelet Analysis of ERPs for the detection of Alzheimer's disease. EMBC, (pp. 1301-1304). Chicago.
Pouzat, C., Delescluse, M., Viot, P., & Diebolt, J. (2004). Improved spike-sorting by modeling firing statistics and burst-dependent spike amplitude attenuation: a markov chain Montecarlo approach. J Neurophysiol, 91, 2910-2928.
Ropper, A. H. (2002). Principios de Neurología de Adams y Victor (7 ed.). New York: Mc-Graw-Hill Interamericana.
Snider, R., & Bonds, A. (1998). Classification of non-stationary neural signals. Journal of Neuroscience Methods, 84, 155-166.
Tahgva, A. (2011). Hidden semi-Markov models in the computerized decoding of microelectrode recording data for deep brain stimulator placement. World neurosurgery , 75, 758-764.
Vargas, H. D., Orozco, A. A., & Álvarez, A. A. (2012). Multi-patient learning increases accuracy for Subthalamic nucleus identification in deep brain stimulation. EMBC, (pp. 4341-4344). San Diego (USA).
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.