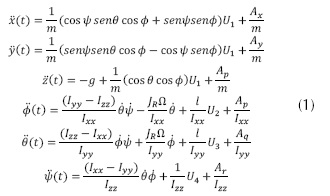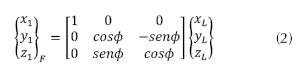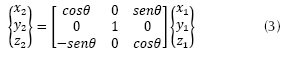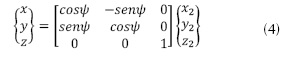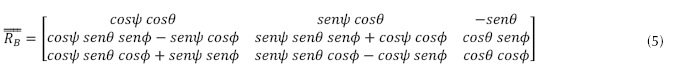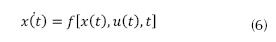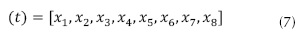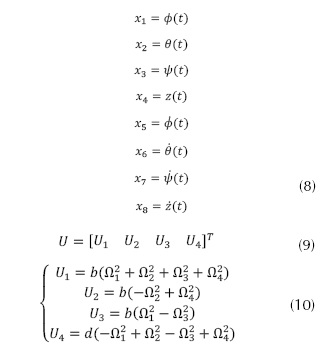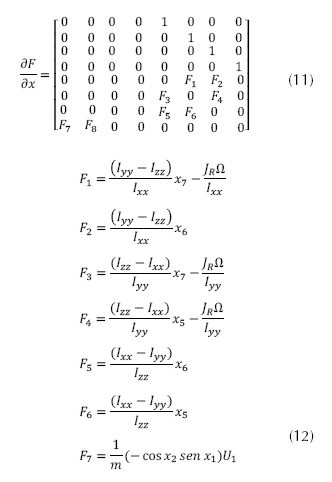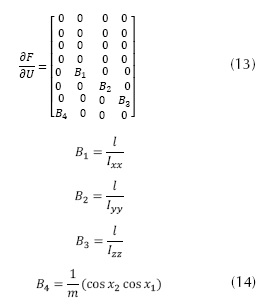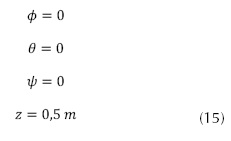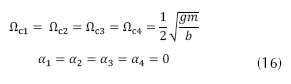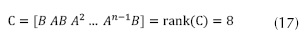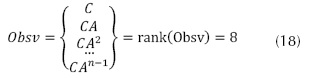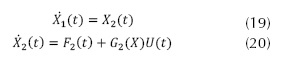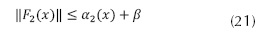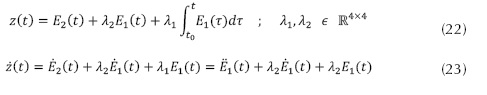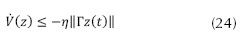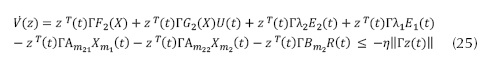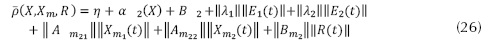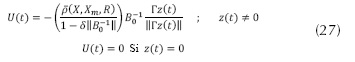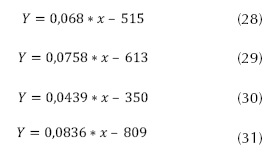DOI:
https://doi.org/10.14483/22487638.10256Published:
2017-07-01Issue:
Vol. 21 No. 53 (2017): July - SeptemberSection:
ResearchDiseño e implementación de un sistema de control de vuelo para un vehículo aéreo no tripulado tipo cuadricóptero
Design and implementation of control system for unmanned aerial vehicle quadrotor
Keywords:
control, modelo no lineal, modos deslizantes, vehículo no tripulado (es).Keywords:
control, non-lineal model, sliding mode, unmanned vehicle (en).References
Addati, G. y Lance, G. (2014). Introducción a los UAVs, drones o VANTs de uso Civil. Serie Documentos de Trabajo, 551. Buenos Aires: Universidad del CEMA. Recuperado de http://www.ucema.edu.ar/publicaciones/download/documentos/551.pdf
Barbashin, E., y Gerashchenko, E. (1965). Forced Sliding Regimes in Automatic Control Systems (Forced Sliding Regimes in Automatic Control Systems). Differential equations, 1, 16-20.
Bouabdallah, S. (2007). Design and Control of Quadrotors with Application to Autonomous Flying. [Doctoral dissertation], Lausanne: École Polytechnique federale de Lausanne.
Edwards, C., y Spurgeon, S. (1998). Sliding Mode Control: Theory and Applications. USA: CRC Press.
Salamanca, J. e Higuera, O. (2009). Control óptimo para el arranque en tiempo mínimo de un motor de inducción. Revista Tecnura, 13(25), 48-58.
Salamanca, J., e Higuera, O. (2015). Controlador robusto LMI para un helicóptero de dos grados de libertad. Revista Ingeniería, Investigación y Desarrollo, 15(2), 47-57. https://doi.org/10.19053/1900771X.4250
Young, K., Utkin, V. y Ozguner, U. (1999). A Control Engineer's Guide to Sliding Mode Control. IEEE Transactions on Control Systems Technology, 7(3), 328-342. https://doi.org/10.1109/87.761053
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: https://doi.org/10.14483/22487638.10256
Diseño e implementación de un sistema de control de vuelo para un vehículo aéreo no tripulado tipo cuadricóptero
Design and implementation of control system for unmanned aerial vehicle quadrotor
Brian Mauricio Lara Sosa,1 Elkin Yilmar Fagua Perez,2 Juan Mauricio Salamanca,3 Oscar Iván Higuera Martínez4
1 Ingeniero Electrónico. Miembro grupo de investigación DSP Universidad Pedagógica y Tecnológica de Colombia. Boyacá, Colombia. Contacto: brian.lara@uptc.edu.co
2 Ingeniero Electrónico. Miembro grupo de investigación DSP Universidad Pedagógica y Tecnológica de Colombia. Boyacá, Colombia. Contacto: elkin.fagua@uptc.edu.co
3 Ingeniero Electrónico, magister en Automatización Industrial, doctor en Ingeniería. Profesor Universidad Pedagógica y Tecnológica de Colombia. Boyacá, Colombia. Correo electrónico: juan.salamanca@uptc.edu.co
4 Ingeniero Electrónico, magister en Automatización Industrial. Profesor Universidad Pedagógica y Tecnológica de Colombia. Boyacá, Colombia. Contacto: oscar.higuera@uptc.edu.co
Fecha de recepción: 3 de abril de 2016 Fecha de aceptación: 17 de febrero de 2017
Cómo citar: Lara, B., Fagua, E., Salamanca, J., e Higuera, O. (2017). Diseño e implementación de un sistema de control de vuelo para un vehículo aéreo no tripulado tipo cuadricóptero. Revista Tecnura, 21(53), 32-46. doi: 10.14483/22487638.10256
Resumen
Contexto: La industria aeroespacial ha tenido bastante auge y así mismo el desarrollo y aplicación a los sistemas autónomos, propiciando desarrollos importantes en su implementación, y sistemas de control.
Método: En este trabajo se presenta el desarrollo y la implementación de un vehículo aéreo no tripulado, tipo quadricóptero, se inicia con el análisis matemático de los sistemas de vehículos aéreos encontrando el modelo dinámico; el modelado del prototipo se basa en las ecuaciones Euler LaGrange. Posteriormente, se realiza el diseño de la estructura y el desarrollo de los sistemas de control basado en modos deslizantes; se aplica la ley de control basada en modos deslizantes en el sistema implementado que utiliza solamente información de pitch, roll y elevación.
Resultados: Se implementó un prototipo de vehículo aéreo no tripulado tipo quadricóptero, y se implementó el sistema de control, donde se obtuvo un adecuado seguimiento de la referencia.
Conclusiones: La adecuada selección de los elementos para la implementación del prototipo permite poder implementar diferentes estrategias de control, para este caso demostrando el adecuado trabajo de los modos deslizantes para la estabilización en dos ejes del quadricóptero.
Palabras clave: control, modelo no lineal, modos deslizantes, vehículo no tripulado.
Abstract
Context: The aerospace industry had quite a rise and also the development and application to the autonomous systems, favoring important developments in its implementation, and control systems.
Method: This work presents the development and implementation of an Unmanned Aerial Vehicle, quad-rotor type. The process begins with the mathematical analysis of the aerial vehicle systems, and finding the dynamic model. The modeling of the prototype is based on the Euler LaGrange equations; the design of the structure and the development of control systems are based on sliding modes. Furthermore, the applied control law is also based on sliding modes in the implemented system, which uses only Pitch, Roll and Elevation information
Results: A prototype of unmanned aerial vehicle was implemented as a quadricopter, and the control system was implemented, where an adequate monitoring of the reference was obtained.
Conclusions: The proper selection of the elements for the implementation prototype allows to implement different control strategies, for this case demonstrating the adequate work of the sliding modes for the stabilization in quadricopter two axes.
Keywords: control, non-lineal model, sliding mode, unmanned vehicle.
INTRODUCCIÓN
En los últimos años, se han realizado avances en el desarrollo de diferentes tipos de vehículos aéreos no tripulados, especialmente en aplicaciones civiles (búsqueda y rescate, vigilancia comercial, exploración de edificios, entre otras). Estos vehículos poseen sensores de medición de inercia IMU (del inglés Inertial Measurement Unit) y un sistema de procesamiento, los cuales permiten realizar cálculos complejos para aplicar estrategias de control, con el fin de estabilizar la posición y lograr una trayectoria de vuelo del vehículo, estas dos características componen un sistema de control de vuelo.
Existen a su vez aeronaves que son propulsadas por múltiples rotores, el prototipo presentado en este trabajo corresponde a este tipo. Este vehículo consta de cuatro rotores, con sus correspondientes hélices dispuestas en un mismo plano, en una estructura con forma de cruz con ejes simétricos, denominado cuadricoptero (quadrotor en inglés). La comunidad universitaria ha volcado su mirada al desarrollo de este tipo de tecnologías, así como a herramientas que puedan ser empleadas en estos y otros desarrollos, tales como desarrollo de modelos de navegación colectiva multiagente (Jacinto, 2016), Aplicaciones para uso civil (Barrientos, 2007), de Modelos y control (Raffo, 2007), de control de estabilidad (Jaramillo, 2014), aplicación de Control difuso (Elso, (2012), de control óptimo (Salamanca, 2009), e incluso aplicaciones a helicópteros de dos grados de libertad (Salamanca, 2015).
Este trabajo presenta el modelado dinámico y el control no lineal de un vehículo aéreo no tripulado tipo quadrotor. En los helicópteros el tipo de ala es llamado “hélice”, esta gira alrededor de un eje o rotor (parte giratoria del vehículo), el cual está impulsado mediante un motor (Addati, 2014). Se desarrolla una estructura que cumpla con estos requisitos dinámicos para desempeñarse como un vehículo volador quadrotor desarrollada por el presente trabajo. Se destaca también el embebido del controlador de modo deslizante en un procesador digital y la aplicación de todo el proyecto a nivel de software y hardware abierto con respecto a licencia GPL.
En el presente artículo se concibe un modelo dinámico de vehículo tipo quadrotor, el cual se caracteriza por su despegue vertical; este sistema consta de cuatro rotores formados en cruz simétrica y en cada extremo se encuentra un conjunto de propulsión motor hélice, este tiene mayor libertad que un helicóptero convencional gracias a que no necesita cambiar el ángulo de ataque de sus hélices para generar sus correspondientes movimientos. Se presenta el procedimiento y análisis del desarrollo del proyecto desde su conformación del modelo dinámico, linealización, diseño del controlador, simulación e implementación en la estructura desarrollada.
METODOLOGÍA
Para el desarrollo de este proyecto se partió de un análisis de los diferentes modelos, estrategias de control e implementaciones realizadas en el control de los UAV, donde para este caso se describe el modelo empleado, el diseño de la estructura y el desarrollo del Sistema de Control basado en modos deslizantes.
Modelado del quadrotor
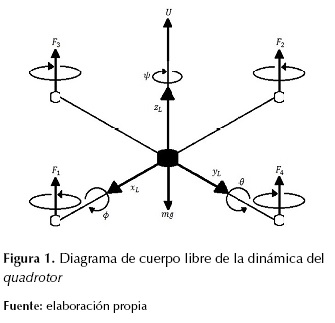
Para el estudio de esta dinámica del vehículo, es necesario incluir conceptos de mecánica de cuerpo rígidos, dinámica de vuelo, aerodinámica, sistemas dinámicos y control entre los más principales; se debe generar un modelo no lineal, inestable y complejo dado su naturaleza de diseño y su interacción con el medio en el cual se encuentre. Este sistema dinámico del quadrotor se muestra esquematizado en la figura 1, donde se puede ver al sistema quadrotor (B) con los respectivos vectores (asociados y directores) (x, y, z) (xL, yL, zL), fuerzas (F1, F2, F3, F4) y referencia inercial (I). Donde ζ es el vector de posición de centro de masa del quadrotor y f, θ, ψ son los angulos (roll, pitch y yaw).
El modelo dinámico que se presenta en la ecuación (1) se tomó por Bouabdallah (2007), el cual Euler Lagrange fue escogido por la simplificación de dinámicas no modelas e incertidumbres paramétricas, quien nos arroja las siguientes ecuaciones de movimiento para el sistema del quadrotor.
Donde:
M: Masa del quadrotor.
U4: Valor de entrada del i-ésimo motor.
Ωi: Velocidad Angular i-ésimo rotor.
x ̈(t), y ̈(t), z ̈(t): Aceleraciones lineales.
ϕ ̈(t), θ ̈(t), ψ ̈(t): Aceleraciones angulares.
Ax, Ay, Az, Ap, Aq, Ar: Fuerzas y pares aerodinámicos sobre el quadrotor.
Ixx, Iyy, Izz: Términos de la matriz inercial.
Además de obtener un modelo dinámico, se tiene en cuenta la orientación respecto de la referencia inercial de la base asociada al quadrotor; se obtendrá esta mediante los giros de Euler siguiendo la convención xyz, en la que se denominan como ángulos de Tait-Bryan, usados para describir una rotación general en el espacio euclídeo tridimensional. Así, la configuración de la rotación de un sólido rígido en el espacio se realizada a través de las matrices presentadas a continuación.
Rotación según 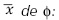 de f: en la ecuación (2) se presenta el primer giro realizado alrededor del eje x, correspondiente al ángulo de roll o de alabeo f.
de f: en la ecuación (2) se presenta el primer giro realizado alrededor del eje x, correspondiente al ángulo de roll o de alabeo f.
Rotación según 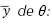 de θ: En la ecuación (3) se presenta el segundo giro en el eje y, y a partir del nuevo eje yL, con el ángulo de cabeceo (pitch), θ para dejar el eje yL en la posición final.
de θ: En la ecuación (3) se presenta el segundo giro en el eje y, y a partir del nuevo eje yL, con el ángulo de cabeceo (pitch), θ para dejar el eje yL en la posición final.
Rotación según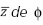 de f: en la ecuación (4) se presenta el tercer giro en el eje z, correspondiente al ángulo de guiñada (yaw) ψ, a partir del nuevo eje zL para llevar el helicóptero a su posición final.
de f: en la ecuación (4) se presenta el tercer giro en el eje z, correspondiente al ángulo de guiñada (yaw) ψ, a partir del nuevo eje zL para llevar el helicóptero a su posición final.
El inconveniente de esta rotación es que se puede generar una singularidad en 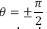 (Bouabdallah, 2007), no obstante, este ángulo de alabeo no puede ocurrir salvo en vuelos acrobáticos, por lo cual no se tendrá en cuenta; por otro lado, se permitió giros de 360 grados en f y ψ. La figura 2 representa tres rotaciones a partir de las cuales se definen las matrices de rotación que representan la orientación del solido rígido rotando alrededor de cada eje, esta matriz expresada en el sistema de coordenadas, B es la inversa de
(Bouabdallah, 2007), no obstante, este ángulo de alabeo no puede ocurrir salvo en vuelos acrobáticos, por lo cual no se tendrá en cuenta; por otro lado, se permitió giros de 360 grados en f y ψ. La figura 2 representa tres rotaciones a partir de las cuales se definen las matrices de rotación que representan la orientación del solido rígido rotando alrededor de cada eje, esta matriz expresada en el sistema de coordenadas, B es la inversa de R1, y por su propiedad de ortonormalidad equivale a su transpuesta y viene dada por la matriz de rotación total del sistema como se aprecia en la ecuación (5).
Ecuaciones de estado
Llegados a este punto, ya está modelado por completo el sistema físico, si bien para continuar el análisis conviene expresar las ecuaciones (1) a (5) en una única expresión; estas se conocen como las ecuaciones de estados, muy utilizadas en teoría de control, que son un conjunto de ecuaciones diferenciales de primer orden. En su forma general las ecuaciones de estado del espacio de estados de cualquier sistema no lineal como se expresa en la ecuación (6).
Ahora, luego de visualizar que el modelo no se comporta de una forma sólida con respecto a parámetros medibles en la implementación de la planta, se tendrá que reducir el modelo, donde el modelo original se tienen seis grados de libertad, en el modelo a implementar solo se tendrá en cuenta el control de cuatro grados de libertad.
Vector de estados
Considerando el vector de estados x(t) presente en la ecuación (7) con sus variables respectivas dadas por la ecuación (8), y el vector de entrada U, presentado en la ecuación (9), donde las entradas son mapeadas como se indica en la ecuación (10).
Donde:
La matriz de estado se presenta en la ecuación (11), con los términos de la misma son descritos por la ecuación (12).
La matriz de entrada está dada por la ecuación (13) y los términos de dicha ecuación, en este trabajo no se tendrá en cuenta la posición en x y y (posiciones traslacionales), pues se sale de la investigación.
Punto de equilibrio
Para calcular los puntos de equilibrio del sistema, se ha de buscar los valores de las variables de estado que hacen nulo el vector de estados; para lograr esto se iguala el vector de estado a cero y resolvemos el sistema de ecuaciones. Una vez hecho esto, se obtiene que las configuraciones del punto de equilibrio están dadas por los valores presentes en la ecuación (15), los tres ángulos se encuentran en posición inicial a cero grados y la altura corresponde a 0.5 m, y las velocidades y aceleraciones angulares de entrada que dan lugar a esta configuración del sistema se presentan en la ecuación (16).
Estabilidad
Las características de estabilidad del sistema se pueden analizar mediante la determinación de los valores propios de la matriz linealizada entorno al punto de equilibrio, se obtiene resolviendo la ecuación que resulta al igualar a cero el determinante de la matriz, es decir: det(λI–A) = 0, de lo anterior podemos afirmar que el λ1 = 0+0.5073i y λ2 = 0-0.5073i, λ3 = λ4 = λ5 = λ6 = λ7 = λ8 = 0 en donde, λ1 y λ2 son complejas conjugadas, asignan al sistema un comportamiento en espiral, en el cual fácilmente observamos que la matriz A no es simétrica produciendo que la planta sea inestable.
Controlabilidad
El sistema de control es completamente controlable, si es posible transferir al sistema del quadrotor desde un estado inicial arbitrario siempre y cuando este en la vecindad en torno al punto de equilibrio a cualquier estado deseado en un tiempo finito, en el cual aplicando la siguiente expresión que intervienen las matrices de estados, ecuaciones (11) y (13). Se puede observar gracias a la ecuación (17) que el índice de controlabilidad generado por el rango de la matriz C, corresponde al mismo orden del número de estados del sistema, que prácticamente informa que la planta a controlar es completamente controlable.
Observabilidad
El análisis de observabilidad del sistema a controlar es dual a la controlabilidad, e investiga la posibilidad de estimar el estado del sistema a partir del conocimiento de la entrada y salida del quadrotor; considerando el sistema linealizado estacionario de la ecuación (10), el cual es observable para cualquier estado inicial x(0) (desconocido), existe un tiempo T1, pues conociendo la entrada U y la salida Y sobre el intervalo [0,T1] es suficiente para determinar en forma única el estado inicial x(0), en el cual aplicando la ecuación (18), y la aplicación del rango de la matriz de observabilidad ecuación (8), corresponde al mismo número de estados del sistema a observar, el sistema es totalmente observable.
Estrategia de control
El control de modo deslizante (SMC, por sus siglas en inglés) es una estrategia de control robusto, debido a que el sistema es forzado a anular dinámicas no modeladas, adicionalmente no tiene en cuenta incertidumbre paramétricas, y presenta una alta insensibilidad a determinadas perturbaciones al sistema. Esta estrategia de control fue seleccionada para ser implementada en este proyecto debido a que la misma fue desarrollada y enfocada para ser aplicada a control de sistemas aéreos. Considerando el modelo no lineal descrito por las ecuaciones (19) y (20).
Donde ∆G2(x) representa una incertidumbre paramétrica acoplada, el objetivo de la ley de control es lograr un seguimiento del modelo a pesar de las incertidumbres paramétricas que pueden ocurrir en F2(x) y G2(x) y considerando que la ecuación (21) presenta lo que conocemos sobre F2(x).
Se define la superficie de error de seguimiento, ecuación (22) (Young, 1999). Y la dinámica en la superficie deslizante se define como se presenta en la ecuación (23).
Para inducir la condición de deslizamiento se debe cumplir la ecuación (24), por la teoría de estabilidad de Lyaponov (Barbashin, 1965).
Esto implica el cumplimiento de la ecuación (25).
Sea  , un parámetro importante de la ganancia del controlador definido por la ecuación (26).
, un parámetro importante de la ganancia del controlador definido por la ecuación (26).
La ley de control con modos deslizantes se define como se presenta en la ecuación (27).
Control embebido
Para implementar este tipo de estrategia de control en una tarjeta de desarrollo, se decide por la ChipkitMax32, de la compañía Digilent, la cual tiene un procesador principal de última generación de microcontroladores de microchip, el cual trabaja a 32 bits con emulación de punto flotante, su versatilidad y programación en c++. El controlador SMC es programado de forma matricial, dado que el tratamiento de señales multivariable se acomoda más fácilmente en este tipo de programación y el tratamiento de cada una de estas señales es sencillo. Por cuanto sus características principales son microcontrolador: PIC32MX795F512L, 512K de memoria de programa, RAM de 128K, voltaje de operación de 3.3V, Frecuencia de Operación de 80Mhz, 83 Pines I/O, 16 entradas analógicas, rango de voltaje analógico: 0V to 3.3V, banda de corrientes DC en pines: +/-18mA, periféricos avanzados: 10/100 ethernet MAC, controlador USB 2.0 full speed OTG, dos controladores CAN.
Diseño de la estructura de quadrotor
Se procede a la construcción del airframe (estructura), el cual fue enteramente diseñado y desarrollado por los autores del proyecto. En la figura 3, se pueden observar las principales etapas de diseño y construcción del esqueleto del UAV. En la figura 3a, se hace un primer periodo de diseño; inicialmente, la estructura tenía la capacidad de ser plegable para su fácil transporte por el usuario, pero cuando se instalaron los actuadores, ESC y demás componentes esta función se vio obstruida, además, previendo una posible fatiga de los cables y puntos de unión de los componentes dispuestos en este esqueleto y deteriorarse eléctricamente haciendo que el sistema no funcionara de manera adecuada. En la figura 3b, se inicia a realizar los cortes en los materiales seleccionados, esto para fabricar las diferentes piezas del quadrotor, que tenían en ese momento el aspecto mostrado en la figura 3c. Posteriormente, se procede a realizar agujeros a los brazos del quadrotor para reducir el peso total del mismo, el cual representaría un valor aproximado al 60% del total del sistema, lo anterior sin que el marco estructural pierda rigidez, figura 3d.
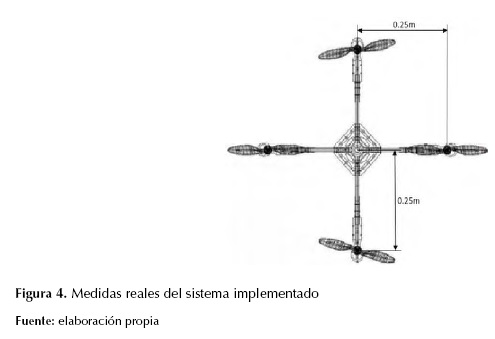
Posteriormente, se procede a establecer la medida más adecuada para la distancia entre el centro de gravedad del aparato y los respectivos motores, medida que se puede representar en la figura 4, a la cual se le asigna el valor de 0.50 m, que no difiere sustancialmente de las medidas de estructuras comerciales las cuales varían entre 0.45 y 0.55 m.
RESULTADOS
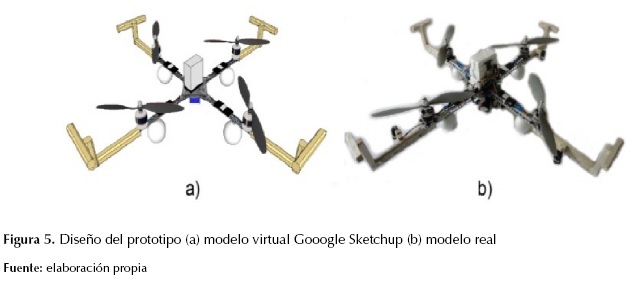
Se midieron los parámetros utilizados para realizar las simulaciones, en donde se obtuvo que la masa m = 1.075kg, y longitud del centro de masa al rotor, l = 0.21m el valor de gravedad que ya es conocido g = 9.81m/s. Los valores de las inercias del sistema fueron hallados utilizando un software con licencia GPL denominado Open Cascade, para desarrollo en 3D, en este software el modelo diseñado previamente en Google SketchUp es cargado y especificándole el tipo de materiales y el peso de cada una de las partes, genera las respectivas inercias en cada uno de los ejes, obteniendo así los valores correspondientes, en la figura 5 se observa el prototipo simulado e implementado.
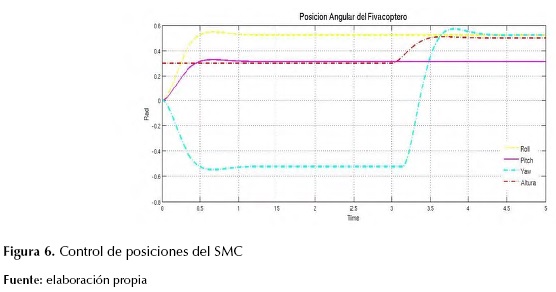
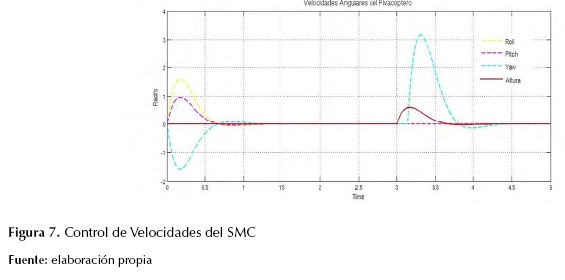
Tras tener implementado el modelo y determinadas las diferentes constantes, se procede a realizar la simulación del sistema de control descrito anteriormente, los resultados se pueden observar en la figura 6, el resultado del control de posiciones del SMC, y en la figura 7 el resultado del control de velocidades del SMC, esta simulación realizada en Matlab ® considera un sistema sin incertidumbres en los parámetros de inercia del modelo que no se tiene en cuenta perturbaciones externas, las inercias empleadas fueron: inercia en el eje x lxx = 5x10-3kg*m2, inercia en el eje y lyy = 5.3x10-3kg*m2, inercia en el eje z JRzz = 2.94x10-3kg*m, las señales deposición angular y de altura del sistema las cuales son producidas por el modelo de seguimiento, en base a las referencias dadas por los escalones como son: roll = pi/6, pitch = pi/10, yaw = 0.5 en radianes yz = 0.5 en metros.
Observando la figura 6 y la figura 7 se concluye que el modelo de seguimiento propuesto en las condiciones del diseño, se comporta de manera adecuada para los parámetros obtenidos que estabilizan el sistema en un tiempo finito. Luego de realizar las diferentes operaciones entre las posiciones y velocidades de dinámica de la planta y el modelo de seguimiento, en donde se generan errores y se operan junto con las matrices para definir la superficie deslizante z(t) y ρ, queda definido finalmente el SMC.
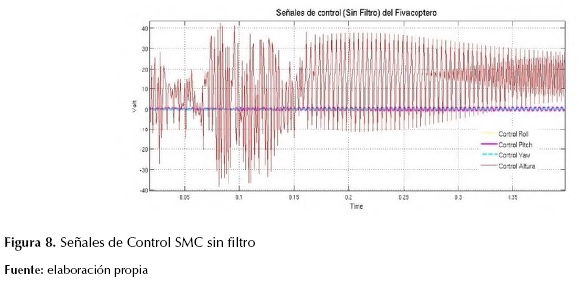
La implementación de esta estrategia de control en el sistema puede llegar a generar un fenómeno conocido como chattering, se debe a que la frecuencia de conmutación en la práctica y en la simulación no se puede hacer infinita (figura 8). Para reducir el fenómeno chattering, que puede generar problemas en los actuadores, se implementa un filtro Butterworth pasa bajas teniendo cuidado de no realizar un filtrado muy alto de la señal, el cual hace un compromiso al controlador ya que la alta conmutación en la ley de control es la que proporciona la robustez (Edwards, 1998).
RESULTADOS DE IMPLEMENTACIÓN
Dinámica del sistema
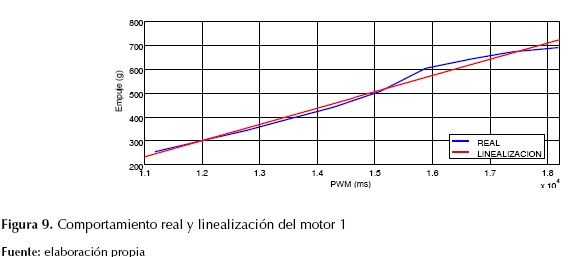
Para tener una plena dinámica de cada uno de los actuadores se procedió a medir y linealizar los empujes de cada motor gracias a una plataforma hecha en cursos anteriores de control de la Escuela de Ingeniería Electrónica de autoría de la ingeniera Sindy Amaya, la cual se adecúa perfectamente para la toma de datos, por su estructura muy similar a una balanza. Se tiene las siguientes linealizaciones de empuje versus PWM para cada actuador, en la figura 9 se observa el comportamiento real y la linealización del primer motor, en este caso no se muestran los demás comportamientos, debido a que tienen un comportamiento de forma similar en los cuatro motores.
Luego de adquirir los respectivos datos de cada uno de los actuadores del sistema, se realizó la respectiva linealización con un empuje mínimo de 250 gramos para que el sistema se sustente, esto en Matlab, por medio del Toolbox-Curve-Fitting, se obtuvieron las ecuaciones para cada uno de los actuadores, ítem muy importante a tener en cuenta en el momento de realizar la implementación en hardware como se puede apreciar en la ecuaciones (28) a (31), que describen el comportamiento linealizado de los motores.
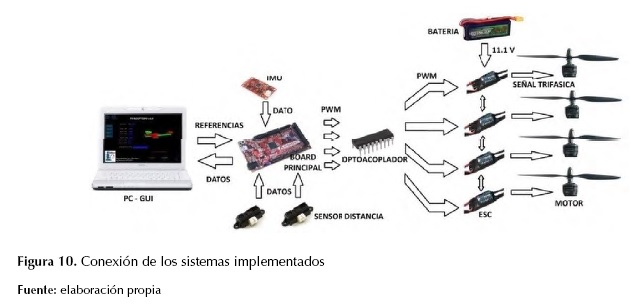
Los materiales elegidos para la implementación son los siguientes. Sensores angulares: IMU 9Dof Razor (nueve grados de libertad, posiciones y velocidades angulares); sensor altura (lineal): LV EZO (cero a seis metros) tecnología ultrasonido. Cuatro motores brushless Turnigy Park 480, cuatro ESC (variadores de velocidad) Turnigy 25ª, batería Turnigy 2200mAh, airframe (estructura): diseñada por los autores aluminio y valso, dos módulos Xbee Pro 900. En la figura 10 se detalla el diagrama de conexión empleado en la implementación del proyecto.
Interfaz gráfica
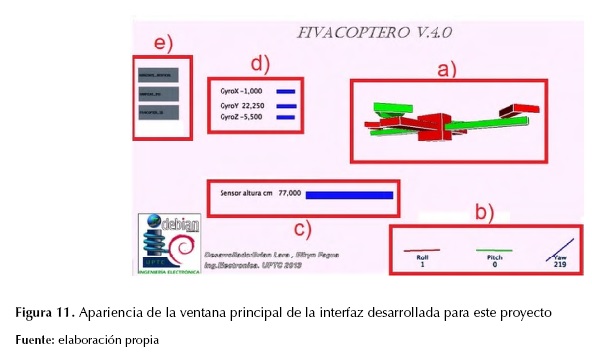
En esta etapa se procede a diseñar la GUI en processing, con base en el proyecto alemán de la universidad Técnica de Berlín, algo básico pero útil para iniciar el desarrollo de la interfaz deseada. Luego de realizar las adiciones y modificaciones respectivas al código original, se diseñó la GUI que finalmente se usaría para el uso del quadrotor, en donde la apariencia es la mostrada en la figura 11. En esta se muestran como lo son: en la figura 11a se representa mediante un modelo en 3D el comportamiento en tiempo real del sistema físico, en la figura 11b se muestra la rotación de la planta en cada uno de los ángulos Euler, en la figura 11c el dato de altura del sistema, en la figura 11d los datos censados por el giroscopio, y en la figura 11e los botones para cambiar de ventana en la interfaz.
Desempeño del sistema de control
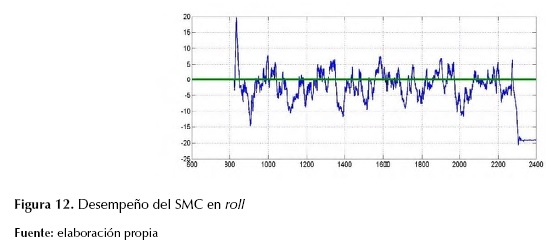
Para poder determinar el desempeño del SMC, se implementó la estructura desarrollada correspondiente, en donde fue asegurado el quadrotor a un soporte, el cual tiene como característica permitir al sistema realizar rotaciones en los tres ángulos Tayt-Bryan mencionados en la sección de modelado y linealización; sin embargo, en las diferentes graficas obtenidas se puede observar la alta velocidad de conmutación de los motores, esto en la señal de ruido existente en las mismas. Luego de adquirir los datos, se procede a determinar el comportamiento del sistema ante una perturbación de alrededor de quince grados realizada sobre el eje x, y posteriormente sobre el eje y, se puede observar en la figura 12 y figura 13 el desempeño del SMC en los ángulos de roll y pitch, en donde el sistema reacciona adecuadamente para lograr seguir la referencia.
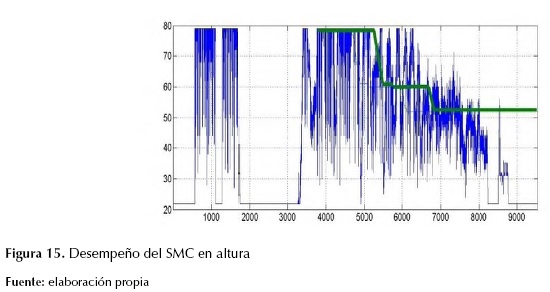
De igual forma, generando las gráficas para observar la reacción del sistema ante perturbaciones sobre el ángulo yaw (figura 14 y figura 15), se puede determinar que el seguimiento no es el deseado comparado con los obtenidos en los ángulos de pitch y roll, esto debido a que la fuerza ejercida sobre por perturbación, así como la generada por el controlador se realiza alrededor del eje z y no sobre este, como es el caso de los otros dos movimientos de rotación que aplican el torque sobre los ejes respectivos. Es por este motivo que se observa que el quadrotor reacciona de una manera más lenta cuando se requieren realizar movimientos sobre el eje z.
CONCLUSIONES
En el momento de diseñar una estrategia de control en modos deslizantes para un sistema determinado no lineal, es de vital importancia desarrollar un modelado matemático adecuado, el cual para este caso fue tomado de trabajos realizados por varios autores, donde en gran parte de estos realizan el modelado del sistema, utilizando ecuaciones Newton-Euler, así como Euler-Lagrange, siendo la última más adecuada para realizar el diseño de controladores. Debido a que se hacen algunas aproximaciones para describir algunas dinámicas que son bastante complejas para su medición, que dependen de la estrategia de control implementada la planta puede o no llegar a ser controlada, inconveniente solucionado por el SMC. Asimismo, en el momento de realizar la simulación del sistema con la implementación del controlador, se hace necesario tener definido las dinámicas del sistema, para lograr tener un gran desempeño del controlador.
Debido a que en estos trabajos no se están controlando los desplazamientos a través de los ejes x y y, se pueden presentar movimientos a través de estos, lo anterior se comprueba en simulación debido a las velocidades angulares tienden a cero, pero no llegan a este valor.
En la etapa de implementación del controlador y evitar accidentes sobre los individuos que hagan experimentos sobre la planta, lo anterior por las altas velocidades de rotación de las hélices, se hace necesario usar elementos de protección por parte de los investigadores, además se debe tener cuidado con la activación accidental de los motores por ruidos eléctricos introducidos al sistema lo cual es posible aunque no se envíen señales a los variadores de velocidad por parte de la procesador digital.
En la etapa de selección de componentes es de vital importancia tener algunos conocimientos básicos relacionados con el funcionamiento, compatibilidad de los mismos, así como de una característica importante como lo es el consumo de energía de cada uno de los módulos instalados en el vehículo, esto debido a que el tiempo de acceso a un voltaje de alimentación aceptable es limitado.
Es importante seleccionar un módulo que pueda generar una señal PWM con alta resolución, en los posible mayor a dieciséis bits, para no ingresar perturbaciones al sistema, requerimiento que es satisfecho por la tarjeta desarrollo.
REFERENCIAS
Addati, G. y Lance, G. (2014). Introducción a los UAVs, drones o VANTs de uso Civil. Serie Documentos de Trabajo, 551. Buenos Aires: Universidad del CEMA. Recuperado de http://www.ucema.edu.ar/publicaciones/download/documentos/551.pdf
Barbashin, E., y Gerashchenko, E. (1965). Forced Sliding Regimes in Automatic Control Systems (Forced Sliding Regimes in Automatic Control Systems). Differential equations, 1, 16-20.
Barrientos, A., del Cerro, J., Gutiérrez, P., San Martín, R., Martínez, A., & Rossi, C. (2007). Vehículos aéreos no tripulados para uso civil. Tecnología y aplicaciones. Universidad politécnica de Madrid, Madrid.
Bouabdallah, S. (2007). Design and Control of Quadrotors with Application to Autonomous Flying. [Doctoral dissertation], Lausanne: École Polytechnique federale de Lausanne.
Edwards, C., y Spurgeon, S. (1998). Sliding Mode Control: Theory and Applications. USA: CRC Press.
Elso Torralba, J., Esparza Martínez, C. M., & Pérez, M. J. (2012). Modelado, diseño, construcción y control borroso de un helicóptero quadrotor. Pamplona.
Salamanca, J. e Higuera, O. (2009). Control óptimo para el arranque en tiempo mínimo de un motor de inducción. Revista Tecnura, 13(25), 48-58.
Salamanca, J., e Higuera, O. (2015). Controlador robusto LMI para un helicóptero de dos grados de libertad. Revista Ingeniería, Investigación y Desarrollo, 15(2), 47-57. doi: https://doi.org/10.19053/1900771X.4250
Young, K., Utkin, V. y Ozguner, U. (1999). A Control Engineer’s Guide to Sliding Mode Control. IEEE Transactions on Control Systems Technology, 7(3), 328-342.
Recibido: 3 de abril de 2016; Aceptado: 17 de febrero de 2017
Resumen
Contexto:
La industria aeroespacial ha tenido bastante auge y así mismo el desarrollo y aplicación a los sistemas autónomos, propiciando desarrollos importantes en su implementación, y sistemas de control.
Método:
En este trabajo se presenta el desarrollo y la implementación de un vehículo aéreo no tripulado, tipo quadricóptero, se inicia con el análisis matemático de los sistemas de vehículos aéreos encontrando el modelo dinámico; el modelado del prototipo se basa en las ecuaciones Euler LaGrange. Posteriormente, se realiza el diseño de la estructura y el desarrollo de los sistemas de control basado en modos deslizantes; se aplica la ley de control basada en modos deslizantes en el sistema implementado que utiliza solamente información de pitch, roll y elevación.
Resultados:
Se implementó un prototipo de vehículo aéreo no tripulado tipo quadricóptero, y se implementó el sistema de control, donde se obtuvo un adecuado seguimiento de la referencia.
Conclusiones:
La adecuada selección de los elementos para la implementación del prototipo permite poder implementar diferentes estrategias de control, para este caso demostrando el adecuado trabajo de los modos deslizantes para la estabilización en dos ejes del quadricóptero.
Palabras clave:
control, modelo no lineal, modos deslizantes, vehículo no tripulado.Abstract
Context:
The aerospace industry had quite a rise and also the development and application to the autonomous systems, favoring important developments in its implementation, and control systems.
Method:
This work presents the development and implementation of an Unmanned Aerial Vehicle, quad-rotor type. The process begins with the mathematical analysis of the aerial vehicle systems, and finding the dynamic model. The modeling of the prototype is based on the Euler LaGrange equations; the design of the structure and the development of control systems are based on sliding modes. Furthermore, the applied control law is also based on sliding modes in the implemented system, which uses only Pitch, Roll and Elevation information
Results:
A prototype of unmanned aerial vehicle was implemented as a quadricopter, and the control system was implemented, where an adequate monitoring of the reference was obtained.
Conclusions:
The proper selection of the elements for the implementation prototype allows to implement different control strategies, for this case demonstrating the adequate work of the sliding modes for the stabilization in quadricopter two axes.
Keywords:
control, non-lineal model, sliding mode, unmanned vehicle.INTRODUCCIÓN
En los últimos años, se han realizado avances en el desarrollo de diferentes tipos de vehículos aéreos no tripulados, especialmente en aplicaciones civiles (búsqueda y rescate, vigilancia comercial, exploración de edificios, entre otras). Estos vehículos poseen sensores de medición de inercia IMU (del inglés Inertial Measurement Unit) y un sistema de procesamiento, los cuales permiten realizar cálculos complejos para aplicar estrategias de control, con el fin de estabilizar la posición y lograr una trayectoria de vuelo del vehículo, estas dos características componen un sistema de control de vuelo.
Existen a su vez aeronaves que son propulsadas por múltiples rotores, el prototipo presentado en este trabajo corresponde a este tipo. Este vehículo consta de cuatro rotores, con sus correspondientes hélices dispuestas en un mismo plano, en una estructura con forma de cruz con ejes simétricos, denominado cuadricoptero (quadrotor en inglés). La comunidad universitaria ha volcado su mirada al desarrollo de este tipo de tecnologías, así como a herramientas que puedan ser empleadas en estos y otros desarrollos, tales como desarrollo de modelos de navegación colectiva multiagente (Gómez, 2016), Aplicaciones para uso civil (Barrientos, 2007), de Modelos y control (Raffo, 2007), de control de estabilidad (Jaramillo, 2014), aplicación de Control difuso (Elso, (2012), de control óptimo (Salamanca, 2009), e incluso aplicaciones a helicópteros de dos grados de libertad (Salamanca, 2015).
Este trabajo presenta el modelado dinámico y el control no lineal de un vehículo aéreo no tripulado tipo quadrotor. En los helicópteros el tipo de ala es llamado “hélice”, esta gira alrededor de un eje o rotor (parte giratoria del vehículo), el cual está impulsado mediante un motor (Addati, 2014). Se desarrolla una estructura que cumpla con estos requisitos dinámicos para desempeñarse como un vehículo volador quadrotor desarrollada por el presente trabajo. Se destaca también el embebido del controlador de modo deslizante en un procesador digital y la aplicación de todo el proyecto a nivel de software y hardware abierto con respecto a licencia GPL.
En el presente artículo se concibe un modelo dinámico de vehículo tipo quadrotor, el cual se caracteriza por su despegue vertical; este sistema consta de cuatro rotores formados en cruz simétrica y en cada extremo se encuentra un conjunto de propulsión motor hélice, este tiene mayor libertad que un helicóptero convencional gracias a que no necesita cambiar el ángulo de ataque de sus hélices para generar sus correspondientes movimientos. Se presenta el procedimiento y análisis del desarrollo del proyecto desde su conformación del modelo dinámico, linealización, diseño del controlador, simulación e implementación en la estructura desarrollada.
METODOLOGÍA
Para el desarrollo de este proyecto se partió de un análisis de los diferentes modelos, estrategias de control e implementaciones realizadas en el control de los UAV, donde para este caso se describe el modelo empleado, el diseño de la estructura y el desarrollo del Sistema de Control basado en modos deslizantes.
Modelado del quadrotor
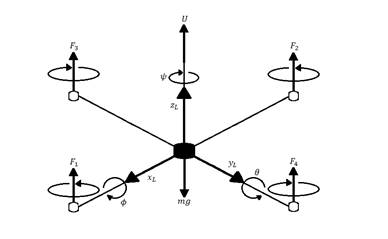
Para el estudio de esta dinámica del vehículo, es necesario incluir conceptos de mecánica de cuerpo rígidos, dinámica de vuelo, aerodinámica, sistemas dinámicos y control entre los más principales; se debe generar un modelo no lineal, inestable y complejo dado su naturaleza de diseño y su interacción con el medio en el cual se encuentre. Este sistema dinámico del quadrotor se muestra esquematizado en la Figura 1, donde se puede ver al sistema quadrotor (B) con los respectivos vectores (asociados y directores) (x, y, z) ( xL, yL, zL ), fuerzas ( F1, F2, F3, F4 ) y referencia inercial (I). Donde ζ es el vector de posición de centro de masa del quadrotor y (, θ, ψ son los angulos (roll, pitch y yaw).
El modelo dinámico que se presenta en la ecuación (1) se tomó por Bouabdallah (2007), el cual Euler Lagrange fue escogido por la simplificación de dinámicas no modelas e incertidumbres paramétricas, quien nos arroja las siguientes ecuaciones de movimiento para el sistema del quadrotor.
Figura 1: Diagrama de cuerpo libre de la dinámica del quadrotor
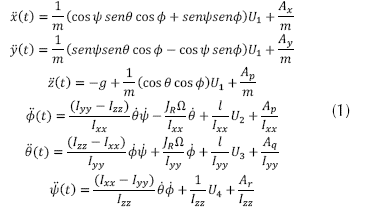
Donde:
M : Masa del quadrotor.
U4 : Valor de entrada del i-ésimo motor.
Ωi : Velocidad Angular i-ésimo rotor.
x ̈(t), y ̈(t), z ̈(t): Aceleraciones lineales.
ϕ ̈(t), θ ̈(t), ψ ̈(t): Aceleraciones angulares.
Ax, Ay, Az, Ap, Aq, Ar: Fuerzas y pares aerodinámicos sobre el quadrotor.
Ixx, Iyy, Izz: Términos de la matriz inercial.
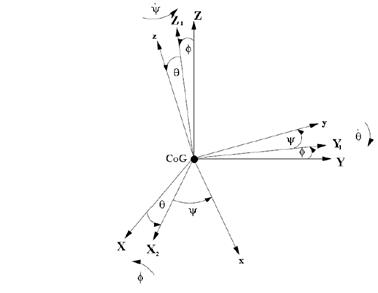
Además de obtener un modelo dinámico, se tiene en cuenta la orientación respecto de la referencia inercial de la base asociada al quadrotor; se obtendrá esta mediante los giros de Euler siguiendo la convención xyz, en la que se denominan como ángulos de Tait-Bryan, usados para describir una rotación general en el espacio euclídeo tridimensional. Así, la configuración de la rotación de un sólido rígido en el espacio se realizada a través de las matrices presentadas a continuación.
Rotación según de (: en la ecuación (2) se presenta el primer giro realizado alrededor del eje x, correspondiente al ángulo de roll o de alabeo (.
de (: en la ecuación (2) se presenta el primer giro realizado alrededor del eje x, correspondiente al ángulo de roll o de alabeo (.
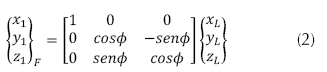
Rotación según de θ: En la ecuación (3) se presenta el segundo giro en el eje y, y a partir del nuevo eje y
L
, con el ángulo de cabeceo (pitch), θ para dejar el eje y
L
en la posición final.
de θ: En la ecuación (3) se presenta el segundo giro en el eje y, y a partir del nuevo eje y
L
, con el ángulo de cabeceo (pitch), θ para dejar el eje y
L
en la posición final.
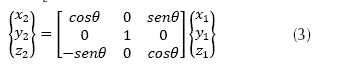
Rotación según 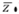 de (: en la ecuación (4) se presenta el tercer giro en el eje z, correspondiente al ángulo de guiñada (yaw) ψ, a partir del nuevo eje z
L
para llevar el helicóptero a su posición final.
de (: en la ecuación (4) se presenta el tercer giro en el eje z, correspondiente al ángulo de guiñada (yaw) ψ, a partir del nuevo eje z
L
para llevar el helicóptero a su posición final.
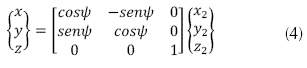
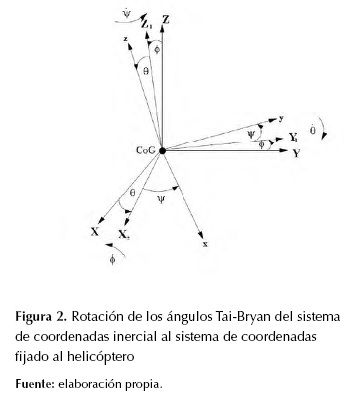
El inconveniente de esta rotación es que se puede generar una singularidad en 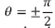 (Bouabdallah, 2007), no obstante, este ángulo de alabeo no puede ocurrir salvo en vuelos acrobáticos, por lo cual no se tendrá en cuenta; por otro lado, se permitió giros de 360 grados en ( y ψ. La Figura 2 representa tres rotaciones a partir de las cuales se definen las matrices de rotación que representan la orientación del solido rígido rotando alrededor de cada eje, esta matriz expresada en el sistema de coordenadas, B es la inversa de
(Bouabdallah, 2007), no obstante, este ángulo de alabeo no puede ocurrir salvo en vuelos acrobáticos, por lo cual no se tendrá en cuenta; por otro lado, se permitió giros de 360 grados en ( y ψ. La Figura 2 representa tres rotaciones a partir de las cuales se definen las matrices de rotación que representan la orientación del solido rígido rotando alrededor de cada eje, esta matriz expresada en el sistema de coordenadas, B es la inversa de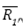 , y por su propiedad de ortonormalidad equivale a su transpuesta y viene dada por la matriz de rotación total del sistema como se aprecia en la ecuación (5).
, y por su propiedad de ortonormalidad equivale a su transpuesta y viene dada por la matriz de rotación total del sistema como se aprecia en la ecuación (5).
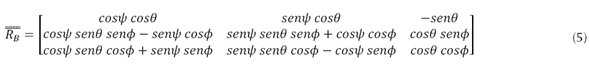
Figura 2: Rotación de los ángulos Tai-Bryan del sistema de coordenadas inercial al sistema de coordenadas fijado al helicóptero
Ecuaciones de estado
Llegados a este punto, ya está modelado por completo el sistema físico, si bien para continuar el análisis conviene expresar las ecuaciones (1) a (5) en una única expresión; estas se conocen como las ecuaciones de estados, muy utilizadas en teoría de control, que son un conjunto de ecuaciones diferenciales de primer orden. En su forma general las ecuaciones de estado del espacio de estados de cualquier sistema no lineal como se expresa en la ecuación (6).
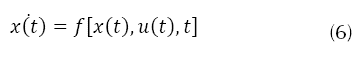
Ahora, luego de visualizar que el modelo no se comporta de una forma sólida con respecto a parámetros medibles en la implementación de la planta, se tendrá que reducir el modelo, donde el modelo original se tienen seis grados de libertad, en el modelo a implementar solo se tendrá en cuenta el control de cuatro grados de libertad.
Vector de estados
Considerando el vector de estados x(t) presente en la ecuación (7) con sus variables respectivas dadas por la ecuación (8), y el vector de entrada U, presentado en la ecuación (9), donde las entradas son mapeadas como se indica en la ecuación (10).
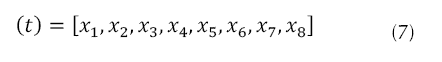
Donde:
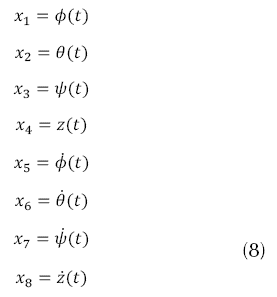
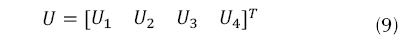
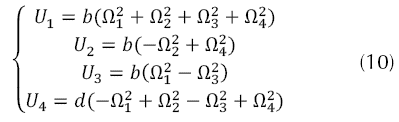
La matriz de estado se presenta en la ecuación (11), con los términos de la misma son descritos por la ecuación (12).
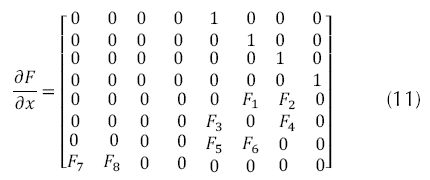
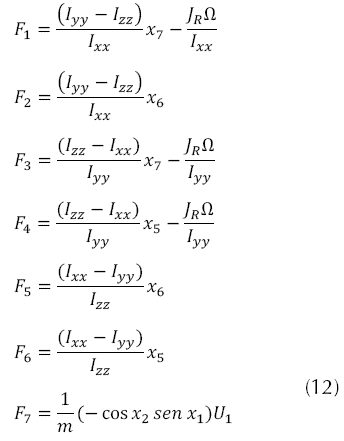
La matriz de entrada está dada por la ecuación (13) y los términos de dicha ecuación, en este trabajo no se tendrá en cuenta la posición en x y y (posiciones traslacionales), pues se sale de la investigación.
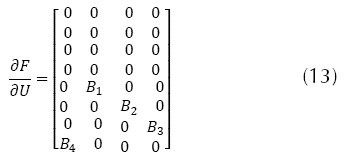
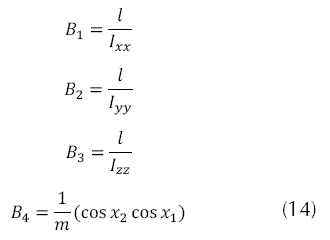
Punto de equilibrio
Para calcular los puntos de equilibrio del sistema, se ha de buscar los valores de las variables de estado que hacen nulo el vector de estados; para lograr esto se iguala el vector de estado a cero y resolvemos el sistema de ecuaciones. Una vez hecho esto, se obtiene que las configuraciones del punto de equilibrio están dadas por los valores presentes en la ecuación (15), los tres ángulos se encuentran en posición inicial a cero grados y la altura corresponde a 0.5 m, y las velocidades y aceleraciones angulares de entrada que dan lugar a esta configuración del sistema se presentan en la ecuación (16).

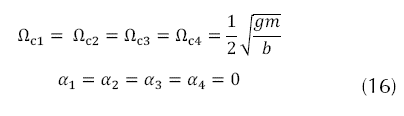
Estabilidad
Las características de estabilidad del sistema se pueden analizar mediante la determinación de los valores propios de la matriz linealizada entorno al punto de equilibrio, se obtiene resolviendo la ecuación que resulta al igualar a cero el determinante de la matriz, es decir: det(λI - A) = 0, de lo anterior podemos afirmar que el λ 1 = 0+0.5073i y λ 2 = 0-0.5073i, λ 3 = λ 4 = λ 5 = λ 6 = λ 7 = λ 8 = 0 en donde, λ 1 y λ 2 son complejas conjugadas, asignan al sistema un comportamiento en espiral, en el cual fácilmente observamos que la matriz A no es simétrica produciendo que la planta sea inestable.
Controlabilidad
El sistema de control es completamente controlable, si es posible transferir al sistema del quadrotor desde un estado inicial arbitrario siempre y cuando este en la vecindad en torno al punto de equilibrio a cualquier estado deseado en un tiempo finito, en el cual aplicando la siguiente expresión que intervienen las matrices de estados, ecuaciones (11) y (13). Se puede observar gracias a la ecuación (17) que el índice de controlabilidad generado por el rango de la matriz C, corresponde al mismo orden del número de estados del sistema, que prácticamente informa que la planta a controlar es completamente controlable.
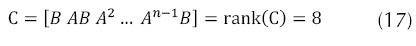
Observabilidad
El análisis de observabilidad del sistema a controlar es dual a la controlabilidad, e investiga la posibilidad de estimar el estado del sistema a partir del conocimiento de la entrada y salida del quadrotor; considerando el sistema linealizado estacionario de la ecuación (10), el cual es observable para cualquier estado inicial x(0) (desconocido), existe un tiempo T1, pues conociendo la entrada U y la salida Y sobre el intervalo [0,T1] es suficiente para determinar en forma única el estado inicial x(0), en el cual aplicando la ecuación (18), y la aplicación del rango de la matriz de observabilidad ecuación (8), corresponde al mismo número de estados del sistema a observar, el sistema es totalmente observable.
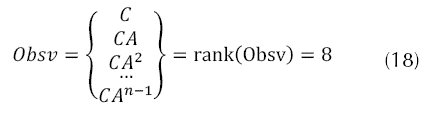
Estrategia de control
El control de modo deslizante (SMC, por sus siglas en inglés) es una estrategia de control robusto, debido a que el sistema es forzado a anular dinámicas no modeladas, adicionalmente no tiene en cuenta incertidumbre paramétricas, y presenta una alta insensibilidad a determinadas perturbaciones al sistema. Esta estrategia de control fue seleccionada para ser implementada en este proyecto debido a que la misma fue desarrollada y enfocada para ser aplicada a control de sistemas aéreos. Considerando el modelo no lineal descrito por las ecuaciones (19) y (20).

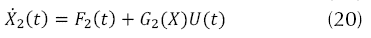
Donde ∆G 2 (x) representa una incertidumbre paramétrica acoplada, el objetivo de la ley de control es lograr un seguimiento del modelo a pesar de las incertidumbres paramétricas que pueden ocurrir en F 2 (x) y G 2 (x) y considerando que la ecuación (21) presenta lo que conocemos sobre F 2 (x).
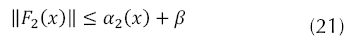
Se define la superficie de error de seguimiento, ecuación (22) (YOUNG, 1999). Y la dinámica en la superficie deslizante se define como se presenta en la ecuación (23).
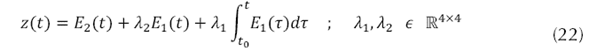
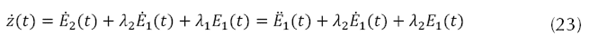
Para inducir la condición de deslizamiento se debe cumplir la ecuación (24), por la teoría de estabilidad de Lyaponov (Barbashin, 1965).
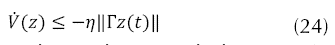
Esto implica el cumplimiento de la ecuación (25).
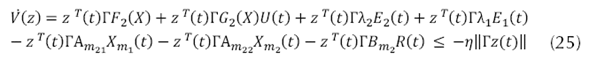
Sea 𝜌 , un parámetro importante de la ganancia del controlador definido por la ecuación (26).
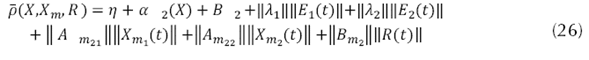
La ley de control con modos deslizantes se define como se presenta en la ecuación (27).
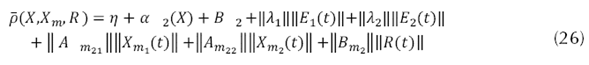
Control embebido
Para implementar este tipo de estrategia de control en una tarjeta de desarrollo, se decide por la ChipkitMax32, de la compañía Digilent, la cual tiene un procesador principal de última generación de microcontroladores de microchip, el cual trabaja a 32 bits con emulación de punto flotante, su versatilidad y programación en c++. El controlador SMC es programado de forma matricial, dado que el tratamiento de señales multivariable se acomoda más fácilmente en este tipo de programación y el tratamiento de cada una de estas señales es sencillo. Por cuanto sus características principales son microcontrolador: PIC32MX795F512L, 512K de memoria de programa, RAM de 128K, voltaje de operación de 3.3V, Frecuencia de Operación de 80Mhz, 83 Pines I/O, 16 entradas analógicas, rango de voltaje analógico: 0V to 3.3V, banda de corrientes DC en pines: +/-18mA, periféricos avanzados: 10/100 ethernet MAC, controlador USB 2.0 full speed OTG, dos controladores CAN.
Diseño de la estructura de quadrotor
Se procede a la construcción del airframe (estructura), el cual fue enteramente diseñado y desarrollado por los autores del proyecto. En la Figura 3, se pueden observar las principales etapas de diseño y construcción del esqueleto del UAV. En la Figura 3a, se hace un primer periodo de diseño; inicialmente, la estructura tenía la capacidad de ser plegable para su fácil transporte por el usuario, pero cuando se instalaron los actuadores, ESC y demás componentes esta función se vio obstruida, además, previendo una posible fatiga de los cables y puntos de unión de los componentes dispuestos en este esqueleto y deteriorarse eléctricamente haciendo que el sistema no funcionara de manera adecuada. En la Figura 3b, se inicia a realizar los cortes en los materiales seleccionados, esto para fabricar las diferentes piezas del quadrotor, que tenían en ese momento el aspecto mostrado en la Figura 3c. Posteriormente, se procede a realizar agujeros a los brazos del quadrotor para reducir el peso total del mismo, el cual representaría un valor aproximado al 60% del total del sistema, lo anterior sin que el marco estructural pierda rigidez, Figura 3d.
Figura 3: Etapas de construcción estructura quadrotor
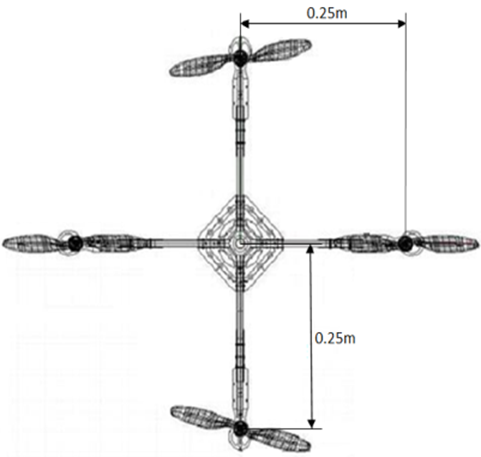
Posteriormente, se procede a establecer la medida más adecuada para la distancia entre el centro de gravedad del aparato y los respectivos motores, medida que se puede representar en la Figura 4, a la cual se le asigna el valor de 0.50 m, que no difiere sustancialmente de las medidas de estructuras comerciales las cuales varían entre 0.45 y 0.55 m.
Figura 4: Medidas reales del sistema implementado
RESULTADOS
Se midieron los parámetros utilizados para realizar las simulaciones, en donde se obtuvo que la masa m = 1.075kg, y longitud del centro de masa al rotor, l = 0.21m el valor de gravedad que ya es conocido g = 9.81m/s. Los valores de las inercias del sistema fueron hallados utilizando un software con licencia GPL denominado Open Cascade, para desarrollo en 3D, en este software el modelo diseñado previamente en Google SketchUp es cargado y especificándole el tipo de materiales y el peso de cada una de las partes, genera las respectivas inercias en cada uno de los ejes, obteniendo así los valores correspondientes, en la Figura 5 se observa el prototipo simulado e implementado.
Figura 5: Diseño del prototipo (a) modelo virtual Gooogle Sketchup (b) modelo real
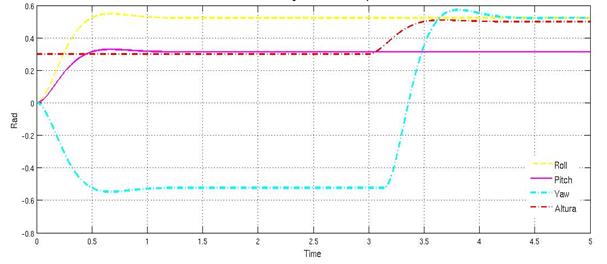
Tras tener implementado el modelo y determinadas las diferentes constantes, se procede a realizar la simulación del sistema de control descrito anteriormente, los resultados se pueden observar en la Figura 6, el resultado del control de posiciones del SMC, y en la Figura 7 el resultado del control de velocidades del SMC, esta simulación realizada en Matlab ® considera un sistema sin incertidumbres en los parámetros de inercia del modelo que no se tiene en cuenta perturbaciones externas, las inercias empleadas fueron: inercia en el eje x lxx = 5x10 -3 kg*m 2 , inercia en el eje y lyy = 5.3x10 -3 kg*m 2 , inercia en el eje z JRzz = 2.94x10 -3 kg*m, las señales deposición angular y de altura del sistema las cuales son producidas por el modelo de seguimiento, en base a las referencias dadas por los escalones como son: roll = pi/6, pitch = pi/10, yaw = 0.5 en radianes yz = 0.5 en metros.
Figura 6: Control de posiciones del SMC
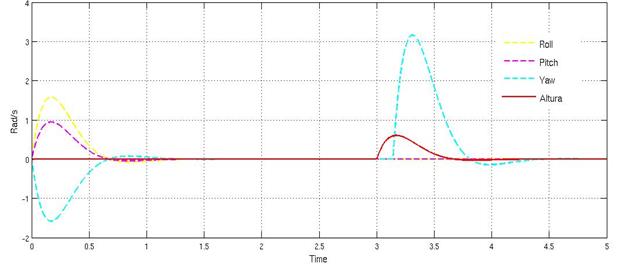
Figura 7: Control de Velocidades del SMC
Observando la Figuras 6 y la Figura 7 se concluye que el modelo de seguimiento propuesto en las condiciones del diseño, se comporta de manera adecuada para los parámetros obtenidos que estabilizan el sistema en un tiempo finito. Luego de realizar las diferentes operaciones entre las posiciones y velocidades de dinámica de la planta y el modelo de seguimiento, en donde se generan errores y se operan junto con las matrices para definir la superficie deslizante z(t) y ρ, queda definido finalmente el SMC.
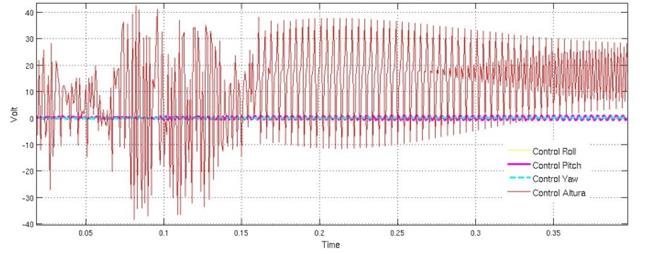
Figura 8: Señales de Control SMC sin filtro
La implementación de esta estrategia de control en el sistema puede llegar a generar un fenómeno conocido como chattering, se debe a que la frecuencia de conmutación en la práctica y en la simulación no se puede hacer infinita (Figura 8). Para reducir el fenómeno chattering, que puede generar problemas en los actuadores, se implementa un filtro Butterworth pasa bajas teniendo cuidado de no realizar un filtrado muy alto de la señal, el cual hace un compromiso al controlador ya que la alta conmutación en la ley de control es la que proporciona la robustez (Edwards, 1998).
RESULTADOS DE IMPLEMENTACIÓN
Dinámica del sistema
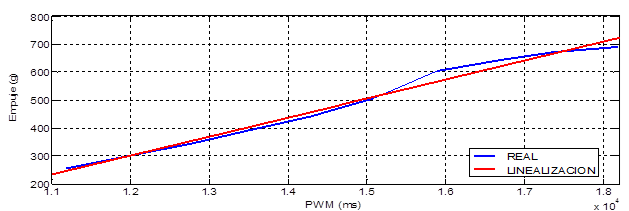
Para tener una plena dinámica de cada uno de los actuadores se procedió a medir y linealizar los empujes de cada motor gracias a una plataforma hecha en cursos anteriores de control de la Escuela de Ingeniería Electrónica de autoría de la ingeniera Sindy Amaya, la cual se adecúa perfectamente para la toma de datos, por su estructura muy similar a una balanza. Se tiene las siguientes linealizaciones de empuje versus PWM para cada actuador, en la Figura 9 se observa el comportamiento real y la linealización del primer motor, en este caso no se muestran los demás comportamientos, debido a que tienen un comportamiento de forma similar en los cuatro motores.
Figura 9: Comportamiento real y linealización del motor 1
Luego de adquirir los respectivos datos de cada uno de los actuadores del sistema, se realizó la respectiva linealización con un empuje mínimo de 250 gramos para que el sistema se sustente, esto en MATLAB, por medio del Toolbox-Curve-Fitting, se obtuvieron las ecuaciones para cada uno de los actuadores, ítem muy importante a tener en cuenta en el momento de realizar la implementación en hardware como se puede apreciar en la ecuaciones (28) a (31), que describen el comportamiento linealizado de los motores.
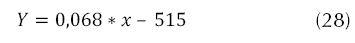
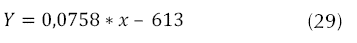
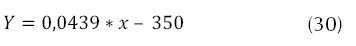

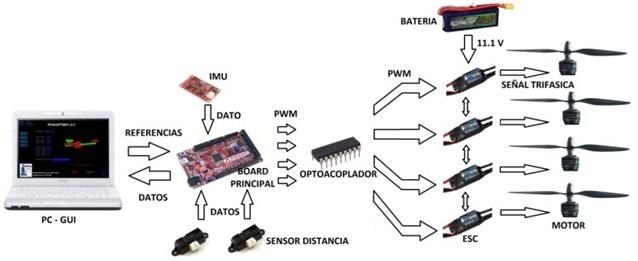
Los materiales elegidos para la implementación son los siguientes. Sensores angulares: IMU 9Dof Razor (nueve grados de libertad, posiciones y velocidades angulares); sensor altura (lineal): LV EZO (cero a seis metros) tecnología ultrasonido. Cuatro motores brushless Turnigy Park 480, cuatro ESC (variadores de velocidad) Turnigy 25ª, batería Turnigy 2200mAh, airframe (estructura): diseñada por los autores aluminio y valso, dos módulos Xbee Pro 900. En la Figura 10 se detalla el diagrama de conexión empleado en la implementación del proyecto.
Figura 10: Conexión de los sistemas implementados
Interfaz gráfica
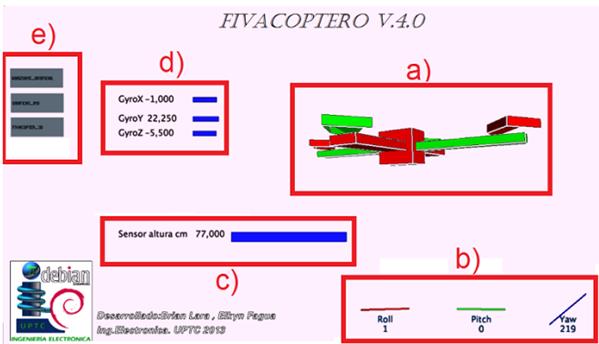
En esta etapa se procede a diseñar la GUI en processing, con base en el proyecto alemán de la universidad Técnica de Berlín, algo básico pero útil para iniciar el desarrollo de la interfaz deseada. Luego de realizar las adiciones y modificaciones respectivas al código original, se diseñó la GUI que finalmente se usaría para el uso del quadrotor, en donde la apariencia es la mostrada en la Figura 11. En esta se muestran como lo son: en la Figura 11a se representa mediante un modelo en 3D el comportamiento en tiempo real del sistema físico, en la Figura 11b se muestra la rotación de la planta en cada uno de los ángulos Euler, en la Figura 11c el dato de altura del sistema, en la Figura 11d los datos censados por el giroscopio, y en la Figura 11e los botones para cambiar de ventana en la interfaz.
Figura 11: Apariencia de la ventana principal de la interfaz desarrollada para este proyecto
Desempeño del sistema de control
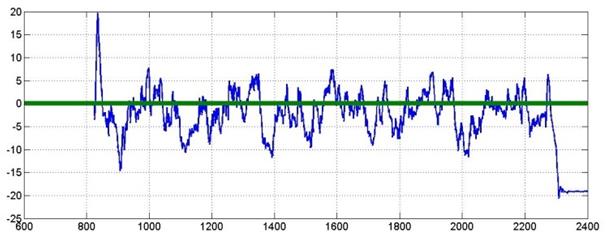
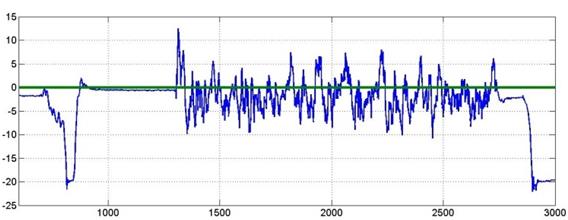
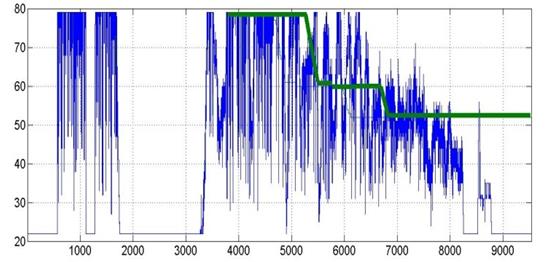
Para poder determinar el desempeño del SMC, se implementó la estructura desarrollada correspondiente, en donde fue asegurado el quadrotor a un soporte, el cual tiene como característica permitir al sistema realizar rotaciones en los tres ángulos Tayt-Bryan mencionados en la sección de modelado y linealización; sin embargo, en las diferentes graficas obtenidas se puede observar la alta velocidad de conmutación de los motores, esto en la señal de ruido existente en las mismas. Luego de adquirir los datos, se procede a determinar el comportamiento del sistema ante una perturbación de alrededor de quince grados realizada sobre el eje x, y posteriormente sobre el eje y, se puede observar en la Figura 12 y Figura 13 el desempeño del SMC en los ángulos de roll y pitch, en donde el sistema reacciona adecuadamente para lograr seguir la referencia.
Figura 12: Desempeño del SMC en roll
Figura 13: Desempeño del SMC en pitch
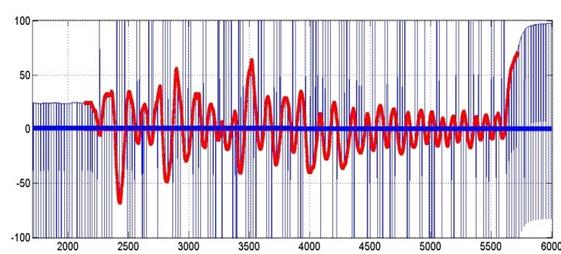
De igual forma, generando las gráficas para observar la reacción del sistema ante perturbaciones sobre el ángulo yaw (Figura 14 y Figura 15), se puede determinar que el seguimiento no es el deseado comparado con los obtenidos en los ángulos de pitch y roll, esto debido a que la fuerza ejercida sobre por perturbación, así como la generada por el controlador se realiza alrededor del eje z y no sobre este, como es el caso de los otros dos movimientos de rotación que aplican el torque sobre los ejes respectivos. Es por este motivo que se observa que el quadrotor reacciona de una manera más lenta cuando se requieren realizar movimientos sobre el eje z.
Figura 14: Desempeño del SMC en yaw
Figura 15: Desempeño del SMC en altura
CONCLUSIONES
En el momento de diseñar una estrategia de control en modos deslizantes para un sistema determinado no lineal, es de vital importancia desarrollar un modelado matemático adecuado, el cual para este caso fue tomado de trabajos realizados por varios autores, donde en gran parte de estos realizan el modelado del sistema, utilizando ecuaciones Newton-Euler, así como Euler-Lagrange, siendo la última más adecuada para realizar el diseño de controladores. Debido a que se hacen algunas aproximaciones para describir algunas dinámicas que son bastante complejas para su medición, que dependen de la estrategia de control implementada la planta puede o no llegar a ser controlada, inconveniente solucionado por el SMC. Asimismo, en el momento de realizar la simulación del sistema con la implementación del controlador, se hace necesario tener definido las dinámicas del sistema, para lograr tener un gran desempeño del controlador.
Debido a que en estos trabajos no se están controlando los desplazamientos a través de los ejes x y y, se pueden presentar movimientos a través de estos, lo anterior se comprueba en simulación debido a las velocidades angulares tienden a cero, pero no llegan a este valor.
En la etapa de implementación del controlador y evitar accidentes sobre los individuos que hagan experimentos sobre la planta, lo anterior por las altas velocidades de rotación de las hélices, se hace necesario usar elementos de protección por parte de los investigadores, además se debe tener cuidado con la activación accidental de los motores por ruidos eléctricos introducidos al sistema lo cual es posible aunque no se envíen señales a los variadores de velocidad por parte de la procesador digital.
En la etapa de selección de componentes es de vital importancia tener algunos conocimientos básicos relacionados con el funcionamiento, compatibilidad de los mismos, así como de una característica importante como lo es el consumo de energía de cada uno de los módulos instalados en el vehículo, esto debido a que el tiempo de acceso a un voltaje de alimentación aceptable es limitado.
Es importante seleccionar un módulo que pueda generar una señal PWM con alta resolución, en los posible mayor a dieciséis bits, para no ingresar perturbaciones al sistema, requerimiento que es satisfecho por la tarjeta desarrollo.
REFERENCIAS
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.