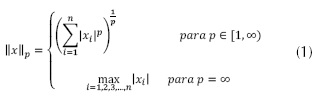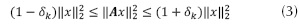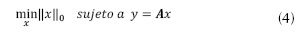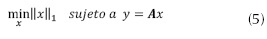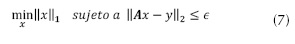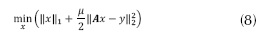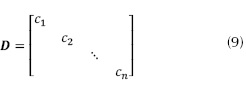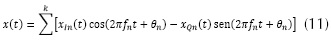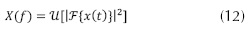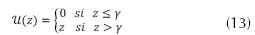DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2017.1.a03Published:
2017-01-01Issue:
Vol. 21 No. 51 (2017): January - MarchSection:
ResearchSondeo compresivo aplicado al sondeo de espectro de banda ancha eficiente en sistemas de radio cognitivo
Compressive sensing applied to efficient broadband spectrum sensing on cognitive radio systems
Keywords:
demodulador aleatorio, muestreo, relajación convexa, sondeo compresivo, sondeo de espectro. (es).Keywords:
Convex relaxation, Compressive sensing, Random demodulator, Sampling, Spectrum sensing (en).Downloads
References
Astaiza, E.; Jojoa, P.E. y Bermúdez, H.F. (2015). Compressive sensing: A methodological approach to an efficient signal processing. DYNA, 82(192), 203-210.
Candes, E.J. y Tao, T. (2005). Decoding by linear programming. IEEE Transactions on Information Theory, 51(12), 4203-4215. https://doi.org/10.1109/TIT.2005.858979
Candes, E.J.; Romberg, J. y Tao, T. (2006). Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 52(2), 489-509. https://doi.org/10.1109/TIT.2005.862083
Donoho, D.L. (2006). Compressed sensing. IEEE Transactions on Information Theory, 52(4), 1289-1306. https://doi.org/10.1109/TIT.2006.871582
Ghozzi, M.; Marx, F.; Dohler, M. y Palicot, J. (2006). Cyclostatilonarilty-Based Test for Detection of Vacant Frequency Bands. International Conference on Cognitive Radio Oriented Wireless Networks and Communications, IEEE (pp. 1-5). https://doi.org/10.1109/CROWNCOM.2006.363454
Gribonval, R. y Nielsen, M. (2007). Highly sparse representations from dictionaries are unique and independent of the sparseness measure. Applied and Computational Harmonic Analysis, 22(3), 335-355. https://doi.org/10.1016/j.acha.2006.09.003
Haque, T.; Yazicigil, R.T.; Pan, K.J.-L.; Wright, J. y Kinget, P.R. (2015). Theory and Design of a Quadrature Analog-to-Information Converter for Energy-Efficient Wideband Spectrum Sensing. IEEE Transactions on Circuits and Systems I. Regular Papers, 62(2), 527-535. https://doi.org/10.1109/TCSI.2014.2360756
Hernández, C.; Martínez, L.F.P. y Sarmiento, F.H.M. (2016). Algoritmos para asignación de espectro en redes de radio cognitiva. Revista Tecnura, 20(48), 69-88. https://doi.org/10.14483/udistrital.jour.tecnura.2016.2.a05
Hur, Y.; Park, J.; Kim, K.; Lee, J.; Lim, K.; Lee, C.; … Laskar, J. (2006). A Cognitive Radio (CR) Testbed System Employing a Wideband Multi-Resolution Spectrum Sensing (MRSS) Technique. IEEE Vehicular Technology Conference, IEEE (pp. 1-5). https://doi.org/10.1109/VTCF.2006.260
Kumar, P.; Taluja, S. y Lal, R. (2012). Performance analysis of Energy detection, Matched filter detection & Cyclostationary feature detection Spectrum Sensing Techniques. International Journal Of Computational Engineering Research, IJCER, 2(5), 1296-1301.
Lavanya, P.V.; Sindhu, R. y Saravanan, R. (2013). Wavelet and Energy Detection Based Spectrum Sensing Techniques in Cognitive Radio Technology. MIT International Journal of Electronics and Communication Engineering, 3(2), 53-58.
Mishali, M. y Eldar, Y.C. (2011). Wideband Spectrum Sensing at Sub-Nyquist Rates [Applications Corner]. IEEE Signal Processing Magazine, 28(4), 102-135. https://doi.org/10.1109/MSP.2011.941094
Natarajan, B.K. (2006). Sparse Approximate Solutions to Linear Systems. SIAM Journal on Computing, 24(2), 227–234. https://doi.org/10.1137/S0097539792240406
Olabiyi, O. y Annamalai, A. (2012a). Extending the capability of energy detector for sensing of heterogeneous wideband spectrum. IEEE Consumer Communications and Networking Conference (CCNC), IEEE (pp. 454-458). https://doi.org/10.1109/CCNC.2012.6181033
Olabiyi, O. y Annamalai, A. (2012b). Parallel multi-channel detection: A practical solution to energy detection of heterogeneous wideband spectrum. Sarnoff Symposium (SARNOFF), 2012 35th IEEE, IEEE (pp. 1-5). https://doi.org/10.1109/SARNOF.2012.6222719
Penagos, H.P.; Bohórquez, M.; Rodríguez, D.; Maldonado, D.; Sánchez, C. y Galarza, C. (2013). Tecnologia radiocognitiva en la banda ultra high frequency (UHF). Revista Tecnura, 18(39), 138-151. https://doi.org/10.14483/udistrital.jour.tecnura.2014.1.a10
Sahai, A.; Hoven, N. y Tandra, R. (2004). Some Fundamental Limits on Cognitive Radio. University of California. Recuperado de: http://people.eecs.berkeley.edu/~sahai/Papers/cognitive_radio_preliminary.pdf
Shobana, S.; Saravanan, R. y Muthaiah, R. (2013). Matched Filter Based Spectrum Sensing on Cognitive Radio for OFDM WLANs. International Journal of Engineering and Technology, 5(1), 142-146). Recuperado de: http://www.enggjournals.com/ijet/docs/IJET13-05-01-077.pdf
Sun, W.; Huang, Z.; Wang, F. y Wang, X. (2015). Compressive wideband spectrum sensing based on single channel. Electronics Letters, 51(9), 693-695. https://doi.org/10.1049/el.2014.4223
Sutton, P.D.; Nolan, K.E. y Doyle, L.E. (2008). Cyclostationary Signatures in Practical Cognitive Radio Applications. IEEE Journal on Selected Areas in Communications, 26(1), 13-24. https://doi.org/10.1109/JSAC.2008.080103
Tian, Z. y Giannakis, G.B. (2006). A Wavelet Approach to Wideband Spectrum Sensing for Cognitive Radios. International Conference on Cognitive Radio Oriented Wireless Networks and Communications, IEEE (pp. 1-5). https://doi.org/10.1109/CROWNCOM.2006.363459
Tropp, J.A.; Laska, J.N.; Duarte, M.F.; Romberg, J.K. y Baraniuk, R.G. (2010). Beyond Nyquist: Efficient Sampling of Sparse Bandlimited Signals. IEEE Transactions on Information Theory, 56(1), 520-544. https://doi.org/10.1109/TIT.2009.2034811
Urkowitz, H. (1967). Energy detection of unknown deterministic signals. Proceedings of the IEEE, 55(4), 523-531. https://doi.org/10.1109/PROC.1967.5573
Wang, Y.; Guo, C.; Sun, X. y Feng, C. (2015). Time-Efficient Wideband Spectrum Sensing Based on Compressive Sampling. IEEE 81st Vehicular Technology Conference (VTC Spring), IEEE (pp. 1-5). https://doi.org/10.1109/VTCSpring.2015.7146135
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2017.1.a03
Sondeo compresivo aplicado al sondeo de espectro de banda ancha eficiente en sistemas de radio cognitivo
Compressive sensing applied to efficient broadband spectrum sensing on cognitive radio systems
Evelio Astaiza Hoyos1, Héctor Fabio Bermúdez Orozco2, Luis Freddy Muñoz3
1 Ingeniero en Electrónica y Telecomunicaciones, magíster en Ingeniería área Electrónica y Telecomunicaciones, candidato a doctor en Ciencias de la Electrónica. Docente de la Universidad del Quindío, Armenia, Colombia. Contacto: eastaiza@uniquindio.edu.co
2 Ingeniero en Electrónica y Telecomunicaciones, magíster en Electrónica y Telecomunicaciones, candidato a doctor en Ingeniería Telemática. Docente de la Universidad del Quindío, Armenia, Colombia. Contacto: hfbermudez@uniquindio.edu.co
3 Ingeniero de Sistemas, candidato a doctor en Ciencias de la Electrónica. Docente de la Fundación Universitaria de Popayán (FUP), Popayán, Colombia. Contacto: freddy.munoz@docente.fup.edu.co
Fecha de recepción: 12 de marzo de 2016 Fecha de aceptación: 23 de noviembre de 2016
Cómo citar: Astaiza H., E.; Bermúdez O., H.F. y Muñoz, L.F. (2017). Sondeo compresivo aplicado al sondeo de espectro de banda ancha eficiente en sistemas de radio cognitivo. Revista Tecnura, 21(51), 42-56.
Resumen
Contexto: El sondeo de espectro es universalmente conocido como el principal habilitador de radio cognitivo (CR), dado que dota al dispositivo de CR de la capacidad de conocimiento del entorno de radio.
Objetivo: En este artículo se presenta un algoritmo diseñado para realizar el sondeo de espectro de banda ancha en sistemas de radio cognitivo (CR).
Método: El sondeo de espectro está basado en sondeo compresivo (CS), mediante el cual los usuarios cognitivos, sin necesidad de conocimiento a priori de características de la señal en el entorno de radio, minimizan la cantidad de muestras a procesar y, con ello, reducen de forma proporcional los tiempos de detección, consumos de energía y capacidades de procesamiento requeridas en los dispositivos de radio cognitivo (CRD).
Resultados: El desempeño del algoritmo propuesto se evalúa mediante la obtención de las curvas de probabilidad de detección, probabilidad de omisión de detección, probabilidad de falsa alarma y las características operativas del receptor (ROC) en comparación con otros algoritmos propuestos en el estado del arte.
Conclusión: Los resultados de simulación demuestran que el método propuesto permite realizar el sondeo de espectro de manera eficiente, mejorando el desempeño del sondeo en función de la probabilidad de detección y de las características operacionales del receptor con respecto a otros algoritmos propuestos basados en muestreo sub-Nyquist.
Palabras clave: demodulador aleatorio, muestreo, relajación convexa, sondeo compresivo, sondeo de espectro.
Abstract
Contex: Spectrum polling is universally known as the main Cognitive Radio (CR) enabler, since it provides the CR device with the ability to know the radio environment.
Objetive: This article presents an algorithm design to perform the broadband spectrum probing in Cognitive Radio systems.
Method: Spectrum polling is based on Compressive Sensing (CS), by which cognitive users minimize the amount of samples to be processed, without the need for a priori knowledge of signal characteristics in the radio environment. In this way, it is possible to proportionally reduce detection times, power consumption and processing capacity required in cognitive radio devices (CRD).
Results: The performance of the proposed algorithm is evaluated by obtaining the probability of detection, the probability of non-detection, the probability of false alarm, and the Receiver Operating Characteristics (ROC), and comparing it with other algorithms proposed in the state of the art.
Conclusion: The simulation results demonstrate that the proposed method allows the efficient sampling of the spectrum. This improves the probe performance based on the probability of detection and the Receiver Operating Characteristic ROC, and it is better than the other proposed algorithms based on sub-Nyquist sampling.
Keywords: Convex relaxation, Compressive sensing, Random demodulator, Sampling, Spectrum sensing.
INTRODUCCIÓN
En la actualidad, la demanda de servicios de comunicaciones inalámbricas ha crecido de manera exponencial, lo cual ha producido que se hable de una saturación del espectro, situación que no necesariamente es correcta, debido a que hay bandas de frecuencias subutilizadas, donde el ejemplo más evidente son las bandas asignadas para la prestación del servicio de televisión; por tanto, en general, existen huecos espectrales que en algunos casos son permanentes, y en otros, se producen en determinados momentos sobre algunas bandas de frecuencia; lo cual es un dilema, ya que, por un lado, los usuarios de algunos servicios como los móviles, no poseen suficiente cantidad de espectro para transmitir, por otro, algunas bandas espectrales no se encuentran completamente en uso. Para resolver este dilema surge radio cognitivo (RC), el cual es una tecnología propuesta para comunicaciones inalámbricas en la que, tanto los dispositivos de red y la red en sí misma, tienen la capacidad de cambiar sus parámetros de transmisión para establecer una comunicación en la cual se haga uso eficiente de los recursos de radio, sin interferir con los usuarios a quienes se les ha concedido el derecho legal de utilización de las bandas espectrales subutilizadas (usuarios licenciados o usuarios primarios). La alteración de parámetros de transmisión se basa en el monitoreo de ciertos factores en el entorno de radio, dentro de los cuales, uno de los más importantes es el estado del espectro, que se obtiene mediante la implementación de la función de sondeo de espectro, que a su vez permite realizar el proceso de acceso dinámico de espectro.
Sin embargo, realizar el sondeo de espectro es una tarea que implica grandes retos desde la perspectiva de los recursos computacionales requeridos, ya que implementar esta función con los métodos tradicionales, como: detector de energía (Urkowitz, 1967; Kumar, Taluja y Lal, 2012; Penagos et al., 2013; Hernández, Martínez y Sarmiento, 2016), sondeo por filtro adaptado (Kumar et al., 2012; Sahai, Hoven y Tandra, 2004; Shobana, Saravanan y Muthaiah, 2013), sondeo por características cicloestacionarias (Kumar et al., 2012; Ghozzi, Marx, Dohler y Palicot, 2006; Sutton, Nolan y Doyle, 2008) y detector wavelet (Tian y Giannakis, 2006; Hur et al., 2006; Lavanya, Sindhu y Saravanan, 2013), entre otros, implica realizar el muestreo del espectro de banda ancha a tasas por encima de la tasa de Nyquist; por ello, resulta atractivo implementar un nuevo paradigma denominado sondeo compresivo (SC) (Candes, Romberg y Tao, 2006; Donoho, 2006; Tropp et al., 2010), el cual proporciona una manera eficiente de procesar señales dispersas o señales que pueden ser aproximadas adecuadamente por señales dispersas, es decir, que pueden ser aproximadas por una expansión en términos de una base adecuada, que solo tiene algunos términos significativos; al ser SC una nueva herramienta, solo en Astaiza, Jojoa y Bermúdez (2015) se presenta una primera aproximación metodológica que permite abordar de manera formal problemas en el área del procesamiento de señales utilizando SC, aproximación que aún no se ha validado.
Con la motivación anterior, el presente trabajo se enfoca en proponer un algoritmo de sondeo de espectro de banda ancha basado en muestreo sub-Nyquist, que permita validar la metodología propuesta en Astaiza, Jojoa y Bermúdez (2015), reducir la complejidad computacional asociada al muestreo a tasas iguales o superiores a la tasa de Nyquist y que permita superar la limitación del detector de energía (energy detector, ED) con respecto a la necesidad de conocimiento a priori de la varianza del ruido y reducir los costos energéticos asociados al sondeo de espectro de banda ancha a la tasa de Nyquist.
Haciendo uso del hecho de que las señales inalámbricas en redes de espectro abierto son típicamente dispersas en el dominio de la frecuencia (Mishali y Eldar, 2011), se presenta un modelo de sondeo de espectro de banda ancha que permite reducir significativamente la tasa de muestreo; en el modelo, la banda de interés se divide en un número finito de bandas espectrales, en las cuales se examina la presencia o no de portadora mediante la reconstrucción del espectro muestreado; el proceso de muestreo se realiza a través del demodulador aleatorio propuesto en Tropp et al. (2010), y la reconstrucción del mismo para la identificación de ocupación o no a través de la identificación de presencia o ausencia de portadora, se realiza mediante el algoritmo de relajación convexa (Astaiza, Jojoa y Bermúdez, 2015).
El principal objetivo del presente artículo es validar la metodología propuesta en Astaiza, Jojoa y Bermúdez (2015) y evaluar el éxito del modelo propuesto basado en sondeo compresivo para el sondeo de espectro en sistemas de RC. La estructura del artículo se presenta a continuación: en el “Marco de referencia” se describen las generalidades de SC, el algoritmo de relajación convexa y el demodulador aleatorio; en la “Metodología y modelo del sistema” se ilustra el modelo del sistema y la metodología utilizada; en los “Resultados de simulación” se muestran y analizan los resultados de simulación, y por último se exponen las “Conclusiones”.
MARCO DE REFERENCIA
Sondeo compresivo
En el paradigma de sondeo compresivo, se asume que una señal z ε 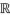 n se encuentra conformada por muestras tomadas a la tasa de Nyquist. Esta señal, a su vez, puede ser representada por una aproximación dispersa en un dominio transformado, donde se denota φ a la matriz de tamaño n x n que representa la transformación entre el dominio original de la señal y el dominio en el cual la señal es dispersa. Al asumir que en el dominio transformado, la señal x ε
n se encuentra conformada por muestras tomadas a la tasa de Nyquist. Esta señal, a su vez, puede ser representada por una aproximación dispersa en un dominio transformado, donde se denota φ a la matriz de tamaño n x n que representa la transformación entre el dominio original de la señal y el dominio en el cual la señal es dispersa. Al asumir que en el dominio transformado, la señal x ε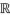 n, se describe como x =Φz, y tiene solamente k componentes significativas, donde k << n y las componentes restantes son aproximadamente cero (0). Se dice que la señal
n, se describe como x =Φz, y tiene solamente k componentes significativas, donde k << n y las componentes restantes son aproximadamente cero (0). Se dice que la señal 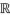 n es k dispersa, lo cual se representa como
n es k dispersa, lo cual se representa como 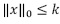 , donde el operador
, donde el operador 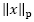 denota la norma
denota la norma 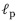 del vector x cuando p= 0. La norma definida en la ecuación (1) no cumple la desigualdad triangular, por tanto, por definición se tiene que
del vector x cuando p= 0. La norma definida en la ecuación (1) no cumple la desigualdad triangular, por tanto, por definición se tiene que 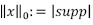 , donde supp indica el soporte de un vector y
, donde supp indica el soporte de un vector y 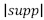 representa la cardinalidad del soporte del vector x, luego
representa la cardinalidad del soporte del vector x, luego 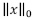 hace referencia al número de coeficientes diferentes de cero (0) que tiene el vector; la norma
hace referencia al número de coeficientes diferentes de cero (0) que tiene el vector; la norma 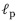 del vector x denotada por || ||p se define como se muestra en la ecuación (1).
del vector x denotada por || ||p se define como se muestra en la ecuación (1).
Se puede interpretar de una manera no muy precisa, pero muy ilustrativa, que el sondeo compresivo permite realizar un muestreo a la tasa de Nyquist seguido de un submuestreo realizado a través de una matriz A de tamaño n x n, donde m < n, por consiguiente, el proceso de tomar m medidas lineales mediante un sistema de adquisición, puede representarse matemáticamente como lo indica la ecuación (2).
Donde, y ε  m es el vector de mediciones.
m es el vector de mediciones.
Para garantizar la recuperación única de la señal original a partir de las medidas lineales y, la matriz de sondeo A debe cumplir en general con la propiedad de isometría restringida (RIP) (Candes y Tao, 2005), la cual se ilustra en la siguiente definición.
Definición 1: Una matriz A cumple la propiedad de isometría restringida de orden k, si existe un δk tal que
Para todo 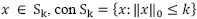
Si una matriz A satisface la propiedad de isometría restringida de orden 2k, de la ecuación (3) se puede interpretar que la matriz A conserva la distancia de cualquier par de vectores x dispersos.
El problema de reconstrucción de la señal x ε 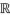 n a partir del vector de mediciones y ε
n a partir del vector de mediciones y ε 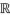 m, se puede realizar mediante algoritmos basados en relajación convexa; que expresan un enfoque fundamental de aproximación dispersa. Estos algoritmos reemplazan la función combinatoria l0 con la función convexa l1, trasladando el problema combinatorio a un problema de optimización convexa (Gribonval y Nielsen, 2007); la norma l1 es la función convexa más aproximada a la función l0. El enfoque natural, desde el cual se aborda el problema de aproximación dispersa, se basa en encontrar la solución dispersa de y =Ax, al resolver la ecuación (4).
m, se puede realizar mediante algoritmos basados en relajación convexa; que expresan un enfoque fundamental de aproximación dispersa. Estos algoritmos reemplazan la función combinatoria l0 con la función convexa l1, trasladando el problema combinatorio a un problema de optimización convexa (Gribonval y Nielsen, 2007); la norma l1 es la función convexa más aproximada a la función l0. El enfoque natural, desde el cual se aborda el problema de aproximación dispersa, se basa en encontrar la solución dispersa de y =Ax, al resolver la ecuación (4).
El problema planteado en la ecuación (4) es un problema combinatorio, el cual en general es NP-Hard (Natarajan, 2006), y el hecho de trabajar con todos los soportes de cardinalidad k se convierte en un problema computacional intratable, al reemplazar la norma l0 por la norma l1 el problema se convierte en el planteado en la ecuación (5).
Para el caso de mediciones imperfectamente dispersas (medidas contaminadas por ruido), se considera el modelo de sondeo presentado por la ecuación (6).
Donde A es la matriz de sondeo de tamaño m x n, y ε 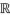 m es el vector de mediciones y w ε
m es el vector de mediciones y w ε 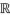 m es el vector de ruido, por tanto, las entradas de y son las medidas de x contaminadas por ruido, por ende el problema de optimización de la ecuación (5) se convierte en la ecuación (7).
m es el vector de ruido, por tanto, las entradas de y son las medidas de x contaminadas por ruido, por ende el problema de optimización de la ecuación (5) se convierte en la ecuación (7).
O, de manera equivalente
Los dos programas son equivalentes, ya que la solución de un problema es también la solución del otro, siempre que los parámetros ε y µ se establezcan adecuadamente; sin embargo, no se conoce a priori la correspondencia entre ε y µ. Dependiendo de la aplicación y la información disponible, alguno de ellos puede ser más fácil de obtener, lo que hace que uno de los dos problemas presentados en las ecuaciones (7) y (8) sea preferido sobre el otro. Es muy importante la selección adecuada en la práctica de o 0 ε 0 µ; como principios generales de selección se tienen: 1) realizar presunciones estadísticas, estimaciones de máximo a posteriori, sobre w y x e interpretar las ecuaciones (7) o (8). 2) Validación cruzada (reconstruir a partir de un subconjunto de medidas y hacer la validación de la recuperación sobre el otro subconjunto de medidas). 3) Determinar los mejores parámetros sobre un conjunto de datos de prueba y usarlos sobre los datos actuales con ajustes apropiados, para subsanar las diferencias en escala, rango dinámico, dispersión y nivel de ruido.
Demodulador aleatorio
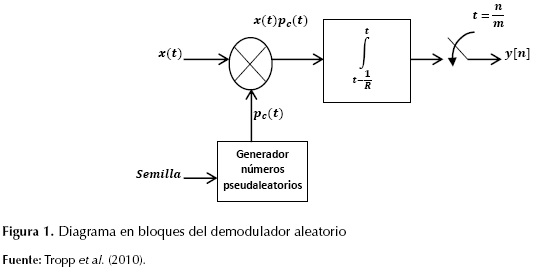
El demodulador aleatorio (random demodulator, RD) (Tropp et al., 2010) puede considerarse como un nuevo tipo de sistema de muestreo, el cual puede usarse para realizar la adquisición de señales dispersas limitadas en banda (señales con solo algunos tonos de frecuencia significativos), el diagrama en bloques de este sistema se muestra en la figura 1.
La figura 1 muestra que la señal de entrada al demodulador aleatorio se multiplica por una secuencia psudoaleatoria de alta tasa, la cual dispersa la energía de los tonos sobre el ancho de banda total ocupado por la secuencia; posteriormente, se aplica filtraje antialiasing de acuerdo con el límite superior del inverso de la tasa de información de la señal 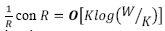 (Tropp et al., 2010), para finalmente muestrear la señal a una tasa inferior a la de Nyquist. El proceso de demodulación (multiplicación por la secuencia pseudoaleatoria) garantiza que cada tono presente en la señal de entrada presenta una firma diferente dentro de la banda pasante del filtro; dado que la señal de entrada al demodulador aleatorio se encuentra conformada solamente por algunos tonos, es posible identificar los tonos y sus amplitudes a partir de las muestras de baja tasa.
(Tropp et al., 2010), para finalmente muestrear la señal a una tasa inferior a la de Nyquist. El proceso de demodulación (multiplicación por la secuencia pseudoaleatoria) garantiza que cada tono presente en la señal de entrada presenta una firma diferente dentro de la banda pasante del filtro; dado que la señal de entrada al demodulador aleatorio se encuentra conformada solamente por algunos tonos, es posible identificar los tonos y sus amplitudes a partir de las muestras de baja tasa.
En el caso ideal, el demodulador aleatorio es un sistema lineal que mapea una señal de tiempo continuo a una secuencia discreta de muestras (Tropp et al., 2010), el cual actúa sobre la forma discreta de la señal de entrada x[n] de la señal de tiempo continuo x(t), cada muestra xn de la señal x[n], donde cada muestra es el promedio de la señal x(t) sobre el n-ésimo intervalo de tiempo, se multiplica por la señal aleatoria respectiva cn donde c1, c2 ...,cn es la secuencia de tiempo discreto de valores 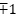 equiprobables, producida por el generador de números pseudoaleatorios, por consiguiente, el proceso de demodulación es equivalente a mapear x→ Dx donde D es una matriz diagonal de tamaño n x n como se aprecia en la ecuación (9).
equiprobables, producida por el generador de números pseudoaleatorios, por consiguiente, el proceso de demodulación es equivalente a mapear x→ Dx donde D es una matriz diagonal de tamaño n x n como se aprecia en la ecuación (9).
Por último, se considera la acción de muestreo conjunta con la integración (acumulación). Se asume que la tasa de muestreo es m y se supone que m divide exactamente a n; luego, cada muestra obtenida del demodulador aleatorio es la suma de n/m entradas consecutivas de la señal demodulada. Por tanto, la acción del muestreador en conjunto con la integración puede ser considerada como una matriz H de tamaño m x n cuya m-ésima fila tiene n/m entradas unitarias consecutivas, iniciando en la columna (Mn/m) + 1; para cada M = 1,2,3, ..., m, por ejemplo para m =3 y n =12 la matriz H tiene la forma que se muestra en la ecuación (10).
Por lo anterior, la matriz M =HD de tamaño m x n describe la acción del sistema hardware sobre la señal discreta x[n].
METODOLOGÍA Y MODELO DEL SISTEMA
Metodología
La metodología utilizada es la propuesta por Astaiza, Jojoa y Bermúdez (2015), en ella, se propone de manera inicial realizar la representación dispersa de la señal; proceso que inicia con la identificación de la base, en la cual la señal original es dispersa. Para este caso particular, se asume que la señal con la cual se trabaja es inalámbrica. La naturaleza de este tipo de señales hace que puedan considerarse dispersas en el dominio de la frecuencia (Mishali y Eldar, 2011). Posteriormente, se procede a realizar el proceso de umbralización, el cual se obtiene mediante la utilización de umbralización dura modificada. Debido a que el interés es identificar las sub-bandas de frecuencia ocupadas y libres, no es necesario efectuar una reconstrucción perfecta de la señal sensada, esto hace que el error de aproximación sea mayor que cuando se utiliza el método de umbralización sin modificaciones o la umbralización suave; sin embargo, para la aplicación requerida no es relevante minimizar el error, pero es de mayor importancia reducir la cantidad de muestras y, por consiguiente, reducir la complejidad computacional. En una segunda fase, de acuerdo con la metodología utilizada, se realiza la toma de medidas de la señal dispersa, para lo cual se emplea el demodulador aleatorio presentado en el “Marco de referencia” de este artículo, el cual utiliza una matriz pseudo aleatoria M de tamaño m x n para realizar el proceso de sondeo de la señal dispersa. La anterior matriz verifica el cumplimiento de la propiedad de isometría restringida de la definición 1 de acuerdo con Tropp et al. (2010). Finalmente, en la tercera y última fase de la metodología usada, se realiza la reconstrucción de la señal dispersa; en este caso, según Tropp et al. (2010), la reconstrucción se puede realizar tanto por métodos de optimización convexa como por algoritmos de búsqueda codiciosa, situación en la cual se evalúa la velocidad de caída de la distribución de la señal (Astaiza et al., 2015); dado que la función objetivo es la de energía (función de densidad espectral de energía) que presenta una caída rápida, se opta por utilizar relajación convexa para realizar la reconstrucción.
Modelo del sistema
Asumiendo que la banda licenciada a un operador primario se extiende sobre una banda de frecuencias con un ancho de banda total de B Hz, el cual se encuentra dividido en K sub-bandas no traslapadas de igual ancho de banda, dada por B/K Hz por canal. Adicionalmente, en la red, existen instantes de tiempo en los cuales no se encuentran en uso la totalidad de las sub-bandas disponibles. Por tanto, denotando por L el número de canales ocupados por los usuarios primarios que se encuentran activos en la red, luego se tienen K - L canales disponibles en la red que pueden ser aprovechados por usuarios secundarios de radio cognitivo.
El orden de la señal dispersa en la banda del operador primario en realidad es desconocido, pero ya que el problema de sondeo de espectro solo requiere identificar las portadoras activas dentro del ancho de banda licenciado, este orden de dispersión puede asumirse como el máximo posible, el cual equivale a tener los K canales del operador ocupados por los usuarios primarios; luego, la señal sensada en este caso es K -dispersa, con orden de dispersión k = K.
La función de sondeo de espectro realizada por el terminal cognitivo es determinar la ocupación de los K canales en la banda asignada al operador primario, donde los K - L canales disponibles en la red representan oportunidades de transmisión a los usuarios cognitivos siempre y cuando los terminales cognitivos se encuentren en capacidad de detectar correctamente los canales disponibles en la banda sensada.
En general, asumiendo que los usuarios primarios utilizan un esquema cualquiera de modulación digital, la señal presente en la banda licenciada se representa como se ilustra en la ecuación (11).
Donde, XIn(t) representa la componente en fase de la señal de la n-ésima portadora con frecuencia ƒn, xQn(t) representa la componente en cuadratura de la señal de la n-ésima portadora con frecuencia fn y θn representa la fase de la portadora.
Dado que la señal en el canal es dispersa en el dominio frecuencia, se realiza la transformada de Fourier de la señal x(t) y se umbraliza la magnitud cuadrática de la transformada, la cual permite llegar a la aproximación dispersa de la señal la cual se muestra en la ecuación (12).
Donde, U[z] representa la función de umbralización, la cual se define como se indica en la ecuación (13).
Con γ que denota la potencia de ruido en la banda de interés.
Una vez obtenida la representación dispersa de la señal 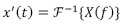 , se toman las medidas de x'(t) o medio del demodulador aleatorio, el cual entrega medidas y[m] de acuerdo a la ecuación (14).
, se toman las medidas de x'(t) o medio del demodulador aleatorio, el cual entrega medidas y[m] de acuerdo a la ecuación (14).
Donde M representa la matriz de sondeo de tamaño 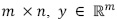 corresponde al vector de mediciones y
corresponde al vector de mediciones y 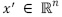 es el vector que representa la señal dispersa.
es el vector que representa la señal dispersa.
Con el vector de mediciones y ε 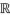 m se resuelve el problema de relajación convexa planteado en la ecuación (5), obteniendo el vector estimado de la señal
m se resuelve el problema de relajación convexa planteado en la ecuación (5), obteniendo el vector estimado de la señal 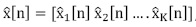 , donde
, donde 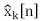 denota la k-ésima sub-banda de la banda licenciada, a las cuales se aplican las hipótesis de detección mostradas en la ecuación (15).
denota la k-ésima sub-banda de la banda licenciada, a las cuales se aplican las hipótesis de detección mostradas en la ecuación (15).
Las hipótesis de detección se plantean de esta manera, dado que el proceso de umbralización realizado para obtener la representación dispersa de la señal en la banda de interés considera el piso de ruido como umbral de decisión.
En el modelo propuesto en este artículo, la cantidad de mediciones m realizadas de la señal dispersa se aproxima a 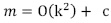 , donde c es el mínimo valor entero que permite garantizar que la relación n/m sea entera.
, donde c es el mínimo valor entero que permite garantizar que la relación n/m sea entera.
RESULTADOS DE SIMULACIÓN
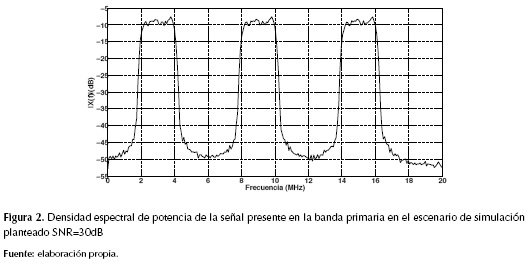
Por simplicidad, el escenario planteado de simulación considera una red que opera en una banda hipotética comprendida entre 1,5MHz y 19,5MHz, en la cual se definen 6 sub-bandas de frecuencia; cada usuario primario transmite a una tasa de 2Msps utilizando moduladores 16QAM con un factor de roll off de 0,5; asumiendo que, en un instante de tiempo cualquiera, en el sistema solo se tienen tres usuarios primarios activos, haciendo uso de las portadoras ubicadas en 3MHz, 9MHz y 15MHz, la señal presente en la banda del operador primario luce como se muestra en la figura 2.
En este escenario, se tiene que la cantidad de canales del sistema es K = 6, el número de canales ocupados por los usuarios primarios es L = 3, el número de canales disponibles para los usuarios cognitivos es K - L = 3, el ancho de banda licenciado al operador primario es 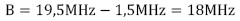 , por tanto cada canal cuenta con un ancho de banda de operación de
, por tanto cada canal cuenta con un ancho de banda de operación de 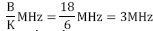 ; de igual forma se asume que todos los usuarios primarios transmiten con la misma potencia, y que la relación señal a ruido es de 30dB. Según lo planteado en “Metodología y modelo del sistema”, el orden de dispersión de la señal presente en la banda licenciada es desconocido, sin embargo, en general, se presenta un límite superior, el cual es igual a la cantidad de sub-bandas de frecuencias definidas en la banda de interés, motivo por el cual, el orden de dispersión con el cual se aborda el escenario es k = K = 6, sin desconocer que para el caso particular planteado en el escenario, el orden de dispersión se conoce de antemano el cual es igual a k = 3; se realiza la simulación con k = 6 con la intención de abordar el problema de realizar las mediciones y reconstrucción de la señal dispersa, en un escenario que se aproxime de mejor manera al escenario real, en el cual no se conoce con certeza el orden de dispersión.
; de igual forma se asume que todos los usuarios primarios transmiten con la misma potencia, y que la relación señal a ruido es de 30dB. Según lo planteado en “Metodología y modelo del sistema”, el orden de dispersión de la señal presente en la banda licenciada es desconocido, sin embargo, en general, se presenta un límite superior, el cual es igual a la cantidad de sub-bandas de frecuencias definidas en la banda de interés, motivo por el cual, el orden de dispersión con el cual se aborda el escenario es k = K = 6, sin desconocer que para el caso particular planteado en el escenario, el orden de dispersión se conoce de antemano el cual es igual a k = 3; se realiza la simulación con k = 6 con la intención de abordar el problema de realizar las mediciones y reconstrucción de la señal dispersa, en un escenario que se aproxime de mejor manera al escenario real, en el cual no se conoce con certeza el orden de dispersión.
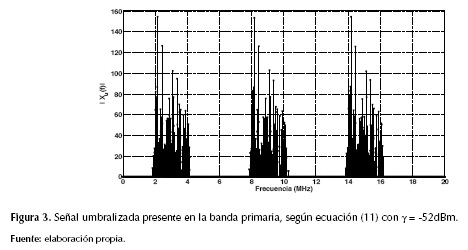
De acuerdo con la relación señal a ruido planteada de 30dB y con la ecuación (12), se realiza el proceso de umbralización de la señal, con lo que se obtiene la señal umbralizada que se muestra en la figura 3.
Sin embargo, el interés es identificar las sub-bandas de frecuencia ocupadas y libres, mas no se requiere efectuar una reconstrucción perfecta de la señal dispersa en la banda de interés. De acuerdo con el escenario de simulación, la mínima tasa de muestreo requerida en el sistema es 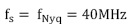 ya que se considera que la máxima frecuencia contenida en la banda a representar se aproxima a 20MHz, pero al representar la densidad espectral de potencia de la señal, se utiliza una transformada rápida de Fourier (FFT) de tamaño 512 (valor promedio que permite una representación espectral adecuada por carga computacional para la aplicación de sondeo de espectro). Esto implica que el espectro de un lado se encuentre representado de manera adecuada por 256 muestras espectrales, cantidad de muestras contenidas en las figuras 2, 3 y 4; por tanto, este es el valor que toma el parámetro n en la representación de la señal dispersa
ya que se considera que la máxima frecuencia contenida en la banda a representar se aproxima a 20MHz, pero al representar la densidad espectral de potencia de la señal, se utiliza una transformada rápida de Fourier (FFT) de tamaño 512 (valor promedio que permite una representación espectral adecuada por carga computacional para la aplicación de sondeo de espectro). Esto implica que el espectro de un lado se encuentre representado de manera adecuada por 256 muestras espectrales, cantidad de muestras contenidas en las figuras 2, 3 y 4; por tanto, este es el valor que toma el parámetro n en la representación de la señal dispersa 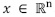 .
.
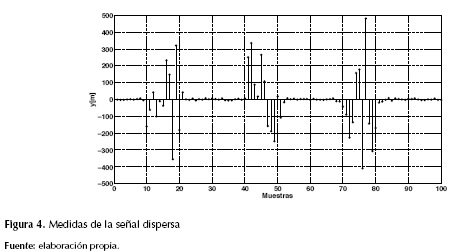
La toma de medidas y ε 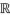 n se realiza con el demodulador aleatorio presentado en el “Marco de referencia”, en donde la cantidad de medidas se calcula según m = 0(k2)+ c como se indica en la mencionada sección, para realizar el cálculo del valor se tiene que, k2 =62=36, por tanto, 0(k2)=36, sin embargo, el cociente n/m debe ser entero; por esto, m solo puede tomar valores 2, 4, 8, 16, 32, 64, 128 o 256, lo cual implica en este caso que m = 64; identificado el valor de m, se procede a generar las matrices D y H. Adicionalmente, en el “Marco de referencia”, y dado que n = 256, m = 64 luego n/m = 4, la matriz H se estructura como se muestra en la ecuación (10), donde al realizar la operación de sondeo y Mx se obtienen las medidas ilustradas en la figura 4.
n se realiza con el demodulador aleatorio presentado en el “Marco de referencia”, en donde la cantidad de medidas se calcula según m = 0(k2)+ c como se indica en la mencionada sección, para realizar el cálculo del valor se tiene que, k2 =62=36, por tanto, 0(k2)=36, sin embargo, el cociente n/m debe ser entero; por esto, m solo puede tomar valores 2, 4, 8, 16, 32, 64, 128 o 256, lo cual implica en este caso que m = 64; identificado el valor de m, se procede a generar las matrices D y H. Adicionalmente, en el “Marco de referencia”, y dado que n = 256, m = 64 luego n/m = 4, la matriz H se estructura como se muestra en la ecuación (10), donde al realizar la operación de sondeo y Mx se obtienen las medidas ilustradas en la figura 4.
Al comparar, la cantidad de muestras presentes en la representación de la señal dispersa de la figura 3, con el número de muestras de las medidas tomadas en la figura 4, se evidencia la reducción de la tasa de muestreo requerida para realizar la operación de sondeo de espectro, la cual, en este caso, es de un factor de 4:1.
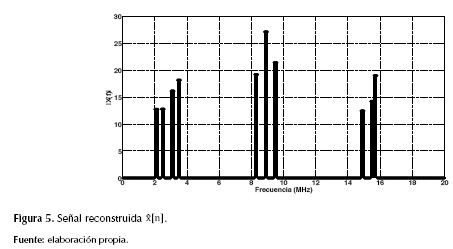
Finalmente, se realiza la detección de la señal mediante la solución del problema de optimización convexa de la ecuación (5), permitiendo obtener la señal estimada (reconstruida) 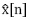 como se ilustra en la figura 5.
como se ilustra en la figura 5.
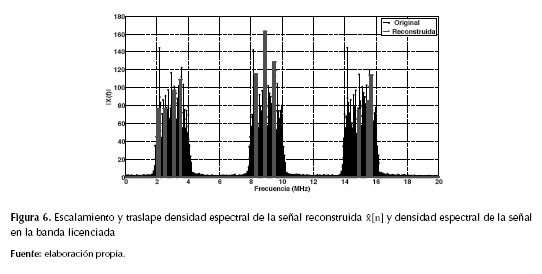
Para apreciar de mejor manera el proceso de detección planteado en la ecuación (14), se realiza un proceso de escalado y traslape de la señal reconstruida y la densidad espectral de potencia de la señal en la banda licenciada como se muestra en la figura 6, donde se evidencia, que al recuperar la señal dispersa de las m muestras tomadas con el demodulador aleatorio, se recuperan las frecuencias a las cuales existe presencia de portadora, y al conocer el ancho de banda utilizado por cada portadora en el sistema, es posible identificar que canales del sistema licenciado están disponibles para transmisiones de usuarios cognitivos; en este caso particular, se observa la disponibilidad de las portadoras ubicadas en 6MHz, 12MHz y 18MHz, con lo cual, un usuario cognitivo que requiera un ancho de banda menor o igual a 3MHz puede realizar su transmisión sobre cualquiera de estas portadoras, y de requerir un mayor ancho de banda para realizar la transmisión, puede reconfigurar su esquema de transmisión en un modo multiportadora de tal forma que aproveche la cantidad necesaria de canales disponibles.
Para evaluar el desempeño del algoritmo de sondeo de espectro propuesto, se realizan 20 corridas de simulación con 1000 réplicas por corrida generando aleatoriamente una señal por réplica para la obtención de las métricas de evaluación del desempeño. Se utilizan como métricas la probabilidad de falsa alarma, la probabilidad de omisión de detección y la probabilidad de detección, las cuales son analizadas en función de la cantidad de componentes recuperadas en la señal estimada mediante el algoritmo de reconstrucción propuesto y en función de la relación señal a ruido de la multibanda generada, adicionalmente se hace uso de las curvas de la característica operacional del receptor (ROC), comparadas con las métricas obtenidas del algoritmo de detección de energía secuencial (Olabiyi y Annamalai, 2012a, 2012b), y los algoritmos basados en sondeo compresivo propuestos por Haque et al. (2015), Sun, Huang, Wang y Wang (2015) y Wang, Guo, Sun y Feng (2015).
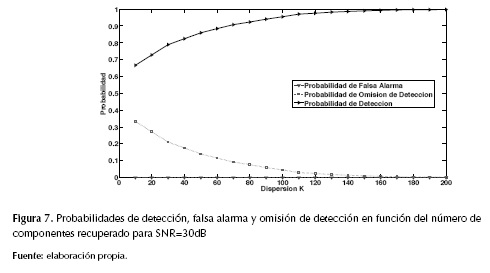
En la figura 7 puede observarse que el número de componentes significativas a recuperar de la señal multibanda (iteraciones del algoritmo de estimación) en el escenario de simulación descrito es de cerca de 180 para garantizar una probabilidad de detección aproximadamente igual a 1, donde se evidencia que la señal multibanda es una señal que no puede considerarse exactamente dispersa, ya que de ser dispersa, según la presunción bajo la cual se realiza el modelo de señal y del sistema, la cantidad de componentes significativas (iteraciones del algoritmo de estimación) que permitirían una recuperación cercana a la exacta de la señal sería de 6 componentes (iteraciones). En la figura 7 puede observarse que la probabilidad de falsa alarma permanece en cero, ya que las componentes recuperadas de la señal se encuentran en canales ocupados, pero no necesariamente en cada uno de ellos hay componentes recuperadas; por tanto, el algoritmo de sondeo propuesto siempre detectará de manera correcta los canales ocupados en los cuales el algoritmo detectó componente, pero aquellos ocupados en los cuales no se realizó detección de componente, el algoritmo propuesto lo estima como canal no ocupado, lo que deriva en una omisión de detección; de esta manera, en la medida que se ejecuta una mayor cantidad de iteraciones del algoritmo, mayor cantidad de componentes son recuperadas (una componente por iteración), y por consiguiente, mayor es la posibilidad de que en cada canal ocupado existan componentes recuperadas y con ello, mayor probabilidad de detección y menor probabilidad de omisión de detección.
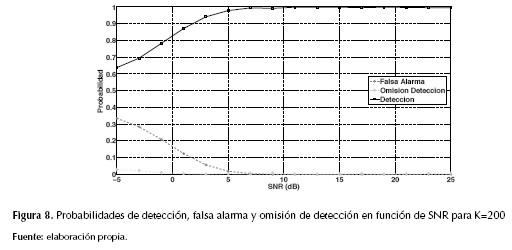
La figura 8 presenta el desempeño que alcanza el algoritmo, en el cual la probabilidad de detección es aproximadamente 1, para valores de SNR superiores a 5dB, para valores de SNR por debajo de 5dB, la probabilidad de omisión de detección es aproximadamente igual a 0, lo cual implica que en el escenario de Radio Cognitivo, en general, su desempeño será adecuado, evitando que un usuario cognitivo tome una banda ocupada por un usuario primario en condiciones de baja SNR, a pesar de desaprovechar oportunidades espectrales dados los altos valores de la probabilidad de falsa alarma.
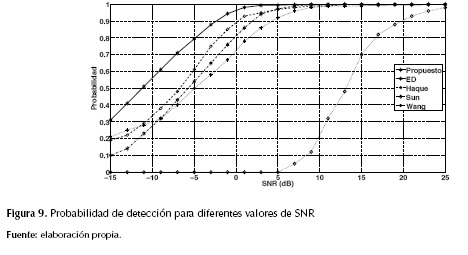
La figura 9 presenta, para el algoritmo propuesto, el desempeño en función de la probabilidad de detección contra el desempeño del detector de energía (Olabiyi y Annamalai, 2012a, 2012b) y contra el desempeño de los algoritmos basados en sondeo compresivo propuestos por Haque et al. (2015), Sun et al. (2015) y Wang et al. (2015); en la figura 9 también se puede apreciar las mejoras que el algoritmo propuesto induce sobre el desempeño de los otros algoritmos, sobre todo en condiciones de baja SNR (menores a 5dB) ya que la probabilidad de detección es mayor a la obtenida por los demás algoritmos con los cuales se hace el comparativo.
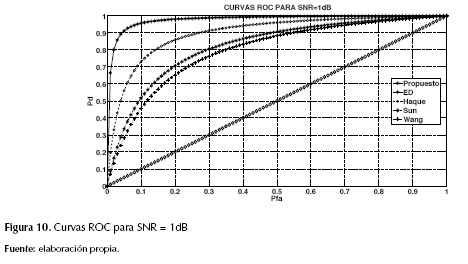
La figura 10, en términos de las curvas de ROC y en condiciones de baja SNR (1 dB), muestra que el mejor desempeño es para el algoritmo propuesto, ya que el área bajo la curva es la mayor, lo cual indica la capacidad de identificar acertadamente los WS. El algoritmo con peor desempeño es el propuesto por Sun [20], ya que la curva ROC indica una probabilidad de 0,5 de realizar una detección correcta de los WS.
CONCLUSIONES
En este artículo se presenta una validación de la metodología propuesta por Astaiza, Jojoa y Bermúdez (2015) para realizar el procesamiento de señales basado en sondeo compresivo, donde se evidencia la validez de la propuesta, aplicando la metodología al sondeo de espectro en sistemas de radio cognitivo.
De la misma manera, se evalúa el éxito del modelo propuesto basado en sondeo compresivo para el sondeo de espectro en sistemas de radio cognitivo, donde se pueden evidenciar que el modelo propuesto efectivamente permite realizar de manera exitosa la operación de sondeo de espectro, pero igualmente permite evidenciar como deficiencia presente en el mecanismo de muestreo compresivo denominado modulador aleatorio, la restricción referente a que el cociente n/m debe ser entero, esto hace que la cantidad de muestras a tomar de la señal dispersa sea mucho mayor a la teórica estimada, que para el escenario de simulación propuesto sería de 36.
Se evidencia que mediante la utilización del algoritmo propuesto, se puede realizar el sondeo de espectro de banda ancha con una cantidad de muestras 20 veces menor a las obtenidas a la tasa de Nyquist, lo cual permite obtener un mayor desempeño en condiciones de baja SNR comparado con los desempeños obtenidos por algoritmos propuestos por Olabiyi y Annamalai (2012a, 2012b) los cuales operan a la tasa de Nyquist, y Haque et al. (2015), Sun et al. (2015) y Wang et al. (2015), los cuales se fundamentan en sondeo compresivo y por consiguiente operan a tasas inferiores a la tasa de Nyquist.
Por último, se evidencia que SC es una tecnología prometedora, la cual contribuirá al mejoramiento significativo de la forma en que actualmente se realiza el procesamiento de señales, reduciendo los costos computacionales y con ello optimizando la utilización de otros recursos, como energía; esto soportado en el hecho de que para el escenario de simulación planteado se alcanza una reducción en un factor de 4 en la cantidad de muestras requeridas para realizar la operación de sondeo de espectro, factor en el cual se espera reducir, al menos, la cantidad de recursos computacionales requeridos para el desempeño de la función, esto, comparado con sistemas tradicionales de sondeo.
REFERENCIAS BIBLIOGRÁFICAS
Astaiza, E.; Jojoa, P.E. y Bermúdez, H.F. (2015). Compressive sensing: A methodological approach to an efficient signal processing. DYNA, 82(192), 203-210.
Candes, E.J. y Tao, T. (2005). Decoding by linear programming. IEEE Transactions on Information Theory, 51(12), 4203-4215. https://doi.org/10.1109/TIT.2005.858979
Candes, E.J.; Romberg, J. y Tao, T. (2006). Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 52(2), 489-509. https://doi.org/10.1109/TIT.2005.862083
Donoho, D.L. (2006). Compressed sensing. IEEE Transactions on Information Theory, 52(4), 1289-1306. https://doi.org/10.1109/TIT.2006.871582
Ghozzi, M.; Marx, F.; Dohler, M. y Palicot, J. (2006). Cyclostatilonarilty-Based Test for Detection of Vacant Frequency Bands. International Conference on Cognitive Radio Oriented Wireless Networks and Communications, IEEE (pp. 1-5). https://doi.org/10.1109/CROWNCOM.2006.363454
Gribonval, R. y Nielsen, M. (2007). Highly sparse representations from dictionaries are unique and independent of the sparseness measure. Applied and Computational Harmonic Analysis, 22(3), 335-355. https://doi.org/10.1016/j.acha.2006.09.003
Haque, T.; Yazicigil, R.T.; Pan, K.J.-L.; Wright, J. y Kinget, P.R. (2015). Theory and Design of a Quadrature Analog-to-Information Converter for Energy-Efficient Wideband Spectrum Sensing. IEEE Transactions on Circuits and Systems I. Regular Papers, 62(2), 527-535. https://doi.org/10.1109/TCSI.2014.2360756
Hernández, C.; Martínez, L.F.P. y Sarmiento, F.H.M. (2016). Algoritmos para asignación de espectro en redes de radio cognitiva. Revista Tecnura, 20(48), 69-88. https://doi.org/10.14483/udistrital.jour.tecnura.2016.2.a05
Hur, Y.; Park, J.; Kim, K.; Lee, J.; Lim, K.; Lee, C.; ... Laskar, J. (2006). A Cognitive Radio (CR) Testbed System Employing a Wideband Multi-Resolution Spectrum Sensing (MRSS) Technique. IEEE Vehicular Technology Conference, IEEE (pp. 1-5). https://doi.org/10.1109/VTCF.2006.260
Kumar, P.; Taluja, S. y Lal, R. (2012). Performance analysis of Energy detection, Matched filter detection & Cyclostationary feature detection Spectrum Sensing Techniques. International Journal Of Computational Engineering Research, IJCER, 2(5), 1296-1301.
Lavanya, P.V.; Sindhu, R. y Saravanan, R. (2013). Wavelet and Energy Detection Based Spectrum Sensing Techniques in Cognitive Radio Technology. MIT International Journal of Electronics and Communication Engineering, 3(2), 53-58.
Mishali, M. y Eldar, Y.C. (2011). Wideband Spectrum Sensing at Sub-Nyquist Rates [Applications Corner]. IEEE Signal Processing Magazine, 28(4), 102-135. https://doi.org/10.1109/MSP.2011.941094
Natarajan, B.K. (2006). Sparse Approximate Solutions to Linear Systems. SIAM Journal on Computing, 24(2), 227-234. https://doi.org/10.1137/S0097539792240406
Olabiyi, O. y Annamalai, A. (2012a). Extending the capability of energy detector for sensing of heterogeneous wideband spectrum. IEEE Consumer Communications and Networking Conference (CCNC), IEEE (pp. 454-458). https://doi.org/10.1109/CCNC.2012.6181033
Olabiyi, O. y Annamalai, A. (2012b). Parallel multi-channel detection: A practical solution to energy detection of heterogeneous wideband spectrum. Sarnoff Symposium (SARNOFF), 2012 35th IEEE, IEEE (pp. 1-5). https://doi.org/10.1109/SARNOF.2012.6222719
Penagos, H.P.; Bohórquez, M.; Rodríguez, D.; Maldonado, D.; Sánchez, C. y Galarza, C. (2013). Tecnologia radiocognitiva en la banda ultra high frequency (UHF). Revista Tecnura, 18(39), 138-151. https://doi.org/10.14483/udistrital.jour.tecnura.2014.1.a10
Sahai, A.; Hoven, N. y Tandra, R. (2004). Some Fundamental Limits on Cognitive Radio. University of California. Recuperado de: http://people.eecs.berkeley.edu/~sahai/Papers/cognitive_radio_preliminary.pdf
Shobana, S.; Saravanan, R. y Muthaiah, R. (2013). Matched Filter Based Spectrum Sensing on Cognitive Radio for OFDM WLANs. International Journal of Engineering and Technology, 5(1), 142-146). Recuperado de: http://www.enggjournals.com/ijet/docs/IJET13-05-01-077.pdf
Sun, W.; Huang, Z.; Wang, F. y Wang, X. (2015). Compressive wideband spectrum sensing based on single channel. Electronics Letters, 51(9), 693-695. https://doi.org/10.1049/el.2014.4223
Sutton, P.D.; Nolan, K.E. y Doyle, L.E. (2008). Cyclostationary Signatures in Practical Cognitive Radio Applications. IEEE Journal on Selected Areas in Communications, 26(1), 13-24. https://doi.org/10.1109/JSAC.2008.080103
Tian, Z. y Giannakis, G.B. (2006). A Wavelet Approach to Wideband Spectrum Sensing for Cognitive Radios. International Conference on Cognitive Radio Oriented Wireless Networks and Communications, IEEE (pp. 1-5). https://doi.org/10.1109/CROWNCOM.2006.363459
Tropp, J.A.; Laska, J.N.; Duarte, M.F.; Romberg, J.K. y Baraniuk, R.G. (2010). Beyond Nyquist: Efficient Sampling of Sparse Bandlimited Signals. IEEE Transactions on Information Theory, 56(1), 520-544. https://doi.org/10.1109/TIT.2009.2034811
Urkowitz, H. (1967). Energy detection of unknown deterministic signals. Proceedings of the IEEE, 55(4), 523-531. https://doi.org/10.1109/PROC.1967.5573
Wang, Y.; Guo, C.; Sun, X. y Feng, C. (2015). Time-Efficient Wideband Spectrum Sensing Based on Compressive Sampling. IEEE 81st Vehicular Technology Conference (VTC Spring), IEEE (pp. 1-5). https://doi.org/10.1109/VTCSpring.2015.7146135
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.