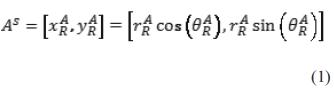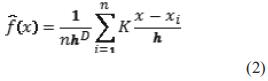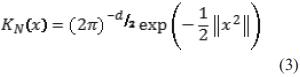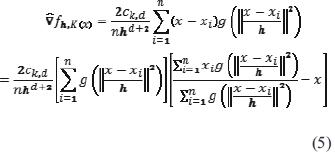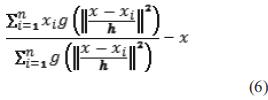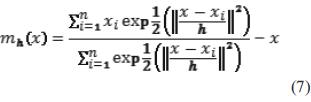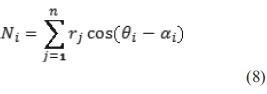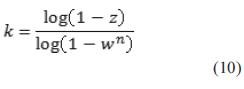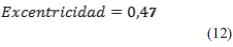DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2013.3.a08Published:
2013-07-01Issue:
Vol. 17 No. 37 (2013): July - SeptemberSection:
ResearchSegmentación y parametrización de líneas en datos láser 2D basado en agrupamiento por desplazamiento de media
Keywords:
análisis de componentes principales, análisis de regresión, medida por rayo láser, métodos de agrupación. (es).Downloads
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Segmentación y parametrización de líneas en datos láser 2D basado en agrupamiento por desplazamiento de media
Segmentation and parameterization of 2D lines based on mean shift clustering
Julie Stephany Berrío1, Lina María Paz2, Eduardo Caicedo Bravo3
1Ingeniera Mecatrónica, Magíster en Ingeniería con énfasis en Electrónica. Docente de la
Universidad Autónoma del Caribe. Barranquilla, Colombia.
Contacto: julie.berrio@uac.edu.co
2Doctora en Ingeniería Informática y Sistemas. Asistente de Docente en la Universidad
de Zaragoza. Zaragoza, España. Contacto: linapaz@unizar.es
3Ingeniero Electricista, Doctor en Informática Industrial. Docente Titular de la Universidad
del Valle. Cali, Colombia. Contacto: eduardo.caicedo@correounivalle.edu.co
Fecha de recepción: 28 de mayo de 2012 Fecha de aceptación: 12 de febrero de 2013
Resumen
El presente artículo realiza una exposición de un algoritmo robusto implementado para la segmentación y caracterización de lecturas obtenidas a través un barrido realizado por un sensor láser, obteniendo los parámetros polares que definen los segmentos de las líneas rectas que describen el ambiente escaneado. Se propone una estrategia de Mean Shift Clustering, que utiliza la media de los puntos del barrido láser, enmarcados en una elipse orientable, como estimación del gradiente de la densidad de puntos dentro de la ventana. El agrupamiento se alcanza deslizando dicha elipse hacia zonas del espacio donde la densidad de puntos es máxima, y reorientándola hacia la dirección de mayor dispersión de datos. Cada conjunto de puntos agrupados es procesado por un algoritmo RANSAC (Random Sample and Consensus) modificado, este método consiste en la construcción de hipótesis del modelo a partir de subconjuntos de datos mínimos escogidos al azar, y la evaluación de su validez con el apoyo de todos los datos, a medida que se actualizan las densidades de probabilidad asociadas. Los parámetros de los segmentos detectados son estimados por una regresión de TLS (Total Least Squares), que minimiza la suma de cuadrados de las diferencias entre la función y los datos. El algoritmo ha sido evaluado en entornos de interior usando como plataforma móvil un robot Pionner 3DX equipado con un sensor láser SICK, obteniendo resultados satisfactorios en cuanto a la compacidad y error de los parámetros de las rectas detectadas. De igual forma, se realizaron pruebas con datos simulados de densidad constante, donde el algoritmo clásico de MSC presenta fallas, logrando notables mejoras en la segmentación y parametrización de las rectas.
Palabras clave: análisis de componentes principales, análisis de regresión, medida por rayo láser, métodos de agrupación.
Abstract
This paper presents a robust algorithm that is implemented for segmentation and characterization of traces obtained through a sweep process performed by a laser sensor. The process yields polar parameters that define segments of straight lines, which describe the scanning environment. A Mean-Shift Clustering strategy that uses the average of laser scanning points set in an orient-able ellipse is proposed as an estimate of the density gradient of points within the window. Grouping is achieved by sliding this ellipse into areas of space where the density of points is high, and it is redirected towards the direction of greater data dispersion. Each grouped set of points is processed by a modified RANSAC (Random Sample and Consensus) algorithm. This method involves the construction of model assumptions from minimal data subsets chosen at random and evaluates their validity supported by the whole of data, while the associated probability densities are updated. The parameters of the detected segments are estimated by a TLS (Total Least Squares) regression, which minimizes the sum of squared differences between the function and the data. The algorithm is evaluated in indoor environments using mobile robot platform Pioneer 3DX (equipped with a SICK laser sensor), obtaining satisfactory results in terms of compactness and error parameters of the lines detected. Likewise, tests were conducted using simulated data with constant density (where the classic MSC algorithm performs poorly), achieving significant improvements in segmentation and line parameterization.
Key words: principal component analysis, regression analysis, measurement by laser beam, clustering methods.
1. Introducción
Para que un robot móvil sea totalmente autónomo debe interpretar primero el entorno en el que navega mediante sus sensores, a la vez que se localiza en el mismo, este es uno de los problemas fundamentales de la robótica que recibe actualmente el nombre de SLAM (Simultaneous Localization and Mapping) [1].
Una gran variedad de técnicas de localización y mapeo se basan en las representaciones del entorno de trabajo realizadas por un grupo de características detectadas por el sistema sensorial del robot (mapas basados en características) [2].
Para la representación de puntos de referencia, el robot hace uso de los datos muestreados por el sensor, algunos algoritmos simplemente los representan como puntos en el espacio de trabajo, otros corresponden a una descripción de cómo las lecturas se agrupan (características geométricas). Estos últimos son de los más utilizados, debido a la compacidad (menor capacidad de almacenamiento) sin pérdida significativa de información, esto incluye la extracción de líneas, curvas, esquinas, entre otros aspectos.
Entre las muchas formas geométricas, el segmento de línea es la más sencilla. Es fácil describir la mayoría de entornos semi-estructurados con segmentos de línea. Muchos algoritmos han sido propuestos para utilizar las características de las líneas extraídas de datos en 2D. En [3] Castellanos propone un método de segmentación de la línea inspirado en un algoritmo de visión por computador que luego es utilizado para obtener un mapa a priori para tareas de relocalización del robot. En [4] Vandorpe presenta un algoritmo para la construcción de mapas dinámicos basados en las características geométricas (líneas y círculos) utilizando un escáner láser. En [5] Arras utiliza un sensor 2D con un método de segmentación de regresión lineal basado en los mapas de ubicación. En [6] Jensfelt presenta una técnica para la adquisición y el seguimiento de la posición de un robot móvil con un escáner láser trazando líneas ortogonales (paredes) en un entorno de oficina. Por último, en [7] Pfster sugiere un algoritmo para la extracción de líneas de conexión ponderada para la construcción de mapas basados en líneas [8].
El artículo se organiza como sigue: en la sección 2 se presenta un estado del arte de métodos de segmentación, estimación de rectas y detección de espurios. En la sección 3 se define la metodología para la segmentación de rectas a través de medidas obtenidas con un sensor láser, en la sección 3.1 se introduce un método de clasificación Mean Shift Clustering con su respectiva modificación propuesta, en la 3.2 se describe un algoritmo básico de RANSAC para la detección robusta de espurios y una variación del mismo usando estimación basada en medianas. En el siguiente apartado se muestra el método de extracción de parámetros basado en TLS. En la sección 4 se muestran los resultados obtenidos para un experimento real llevado a cabo por un robot móvil Pionner 3DX equipado por un láser SICK LMS 200. Finalmente se concluye acerca del trabajo propuesto en el apartado 5.
2. Estado Del Arte
La segmentación de datos es un método de fraccionamiento basado en regiones, en el cual son ampliamente utilizadas áreas como las matemáticas y la estadística. Se usan centroides o prototipos para representar los numerosos componentes del grupo, logrando reducir el tiempo computacional y proveyendo una mejor condición de compresión de datos.
En general, la segmentación de información se puede clasificar en dos clases de sistemas, incluyendo agrupamiento no paramétrico y agrupamiento particional. En el agrupamiento no paramétrico se pueden cambiar los números de grupos durante el proceso. Sin embargo, en el agrupamiento particional, debemos decidir el número de grupo antes de procesarlos. El algoritmo de desplazamiento de media es una técnica de análisis no paramétrica del espacio de características que descompone los datos de referencia en regiones denominadas segmentos o clústeres. El desplazamiento de media fue primero propuesto en 1975 por Fukunaga y Hostetler [9], y extensamente olvidado, hasta que más tarde fue adaptado por Cheng [10] y más recientemente expandido por Comaniciu y Meer [11], [12], [13] para los problemas de visión, segmentación y rastreo. La utilización de esta técnica se basa en una aplicación iterativa del método para encontrar el máximo local o punto estacionario de la función de densidad más cercano a un punto del conjunto de datos. En este artículo hacemos uso de una técnica de análisis de componentes principales (PCA) para realizar la orientación de la ventana utilizada en el algoritmo propuesto. Debido a su simplicidad, el PCA es una herramienta estándar en el análisis de datos en diversos campos, desde la neurociencia hasta gráficos por ordenador, y corresponde a un método no paramétrico para extraer información relevante de los conjuntos de datos [14]. El objetivo del análisis de componentes principales es la identificación de una base significativa para volver a expresar un conjunto de datos, esta nueva base filtra el ruido y revela la estructura de datos.
El algoritmo RANSAC (Random Sample and Consensus) fue en primera instancia introducido por Fischler y Bolles [15] en 1981, como un método para estimar los parámetros de un modelo determinado a partir de un conjunto de datos contaminados por grandes cantidades de valores atípicos. El porcentaje de los valores outliers que pueden ser manejados por RANSAC puede ser mayor que el 50 % del conjunto de datos completo. Tal porcentaje, conocido también como el punto de ruptura, es comúnmente el límite práctico para muchas otras técnicas de uso común para la estimación de parámetros (como todos los métodos de regresión Least Squares o técnicas robustas al menos como Mean Squares) [16] - [21].
Difícilmente se podría nombrar a otro método que se utilice con tanta frecuencia como el método que se conoce como el Least Squares, aproximación que en estadística se considera como un estimador de máxima verosimilitud de un modelo de regresión lineal bajo criterios estándar (distribución normal residual de media cero y matriz de covarianza que es un múltiplo de la identidad). Del mismo modo, el TLS (Total Least Square) es un estimador de máxima verosimilitud en el modelo de errores invariantes. El TLS fue desarrollado por Golub y Van Loan [22] como una técnica de solución para un sistema sobredeterminado de ecuaciones y luego perfeccionado por Van Huffel [23]. Es una extensión del método usual de mínimos cuadrados, que permite manejar también ciertas inconsistencias en la matriz de datos. La popularidad del TLS se debe probablemente al hecho de que la minimización del residuo puede ser realizada de manera cercana a la analítica. Este método es lineal y es consistente con el principio de ortogonalidad de la aproximación óptima en sentido del error cuadrático medio.
El principal enfoque de este artículo es la segmentación de líneas a partir de puntos muestreados por un escáner láser SICK LMS-200 embarcado en un robot móvil Pionner 3-DX que brinda 360 datos en un rango de 180 0, ofreciendo una lectura cada 0,50. La segmentación solamente se realiza a partir de la información suministrada por los puntos, es por ello que se necesitan algoritmos que estimen algunas propiedades geométricas como la dirección privilegiada de los puntos y la detección de discontinuidades de la línea, sin necesidad de recurrir a estructuras globales. Esta investigación aporta una variación del algoritmo de desplazamiento de media para segmentar líneas en un recorrido con el sensor láser de un ambiente semi-estructurado, al mismo tiempo que proporciona una estimación de la ecuación de la recta que caracteriza cada clúster.
3. Metodología
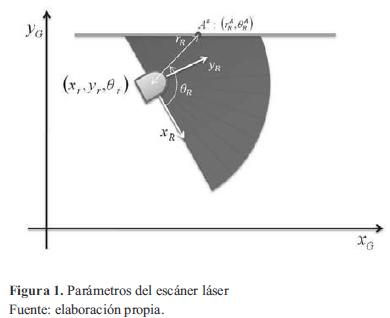
Un escáner láser describe un corte 2D del ambiente de trabajo del robot, a través de una serie de puntos específicos en el sistema de coordenadas polares (rR, θR) cuyo origen es la ubicación del sensor (figura 1). Se considera un robot navegando en un entorno 2D y denota que su ubicación es xk= [xr, yr, θr] (donde ( x1r, y1,(r)) y θr son la posición y orientación) en el instante, en un marco de referencia global (XG, YG). El espacio de trabajo es descrito por características estáticas rectilíneas (tales como partes de las paredes, puertas, estantes) detectadas por el sistema sensorial del robot. El robot está equipado con un sensor de proximidad (por ejemplo, los anillos de sonar o es cáner láser) que proporciona una serie de pasosS y medidas 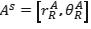 que son parametrizadas por su distancia rAR
desde el origen hasta el punto en la dirección de detección θAR.
que son parametrizadas por su distancia rAR
desde el origen hasta el punto en la dirección de detección θAR.
La pareja puede considerarse como las coordenadas polares de la lectura en un robot centrado en un sistema de referencia. Las coordenadas cartesianas se denotan por la ecuación (1).
3.1 Agrupamiento por desplazamiento de media
El agrupamiento por desplazamiento de media es uno de los métodos más conocidos de estimación de densidad de probabilidad basado en la utilización de un kernel de densidad. Dado un conjunto de datos xi, i=1,...,n de un espacio de dimensión d, Rd, la ecuación (2) presenta el estimador del kernel de densidad multivariable usando el Kernel K(x) con radio de ventana o ancho de banda h.
Uno de los kernels más utilizados es el kernel gaussiano o normal, que es un kernel radialmente simétrico y se define como se expresa en la ecuación (3).
Para todo kernel radialmente simétrico, como es el caso del kernel normal, ha de cumplirse: 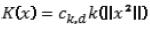 , siendo k(x) el perfil del kernel, para todo x ≥0, y Ck,d la constante de normalización que hace que la integral del kernel sea la unidad. En el caso del kernel gaussiano o normal, la ecuación (4) muestra su perfil.
, siendo k(x) el perfil del kernel, para todo x ≥0, y Ck,d la constante de normalización que hace que la integral del kernel sea la unidad. En el caso del kernel gaussiano o normal, la ecuación (4) muestra su perfil.
Se pueden usar otros kernels, como pueden ser el kernel uniforme o el Epanechnikov [24]. El primer paso en el análisis del espacio de características con densidad f(x) es encontrar las modas de esta densidad. Estas modas se encuentran en los puntos donde el gradiente de la función de densidad se anula, es decir, cuando 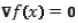 . El método de desplazamiento de media es una forma alternativa de encontrar estos puntos sin necesidad de estimar la función de densidad. La ecuación (5) define el gradiente del estimador de densidad.
. El método de desplazamiento de media es una forma alternativa de encontrar estos puntos sin necesidad de estimar la función de densidad. La ecuación (5) define el gradiente del estimador de densidad.
Donde 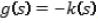 . El primer término es proporcional al estimador de densidad en calculado a partir del kernel
. El primer término es proporcional al estimador de densidad en calculado a partir del kernel  y el segundo término ecuación (6).
y el segundo término ecuación (6).
Es el mean shift vector o el vector de desplazamiento medio. Este vector apunta siempre a la dirección de máximo incremento de la densidad. El método de desplazamiento de media se obtiene a través de la sucesión de los siguientes pasos:
Cálculo del mean shift vector mh(xt).
Traslación de la ventana de desplazamiento  .
.
Este procedimiento garantiza la convergencia a un punto donde el gradiente de la función de densidad es cero, asegurando así la obtención de un punto estacionario de densidad máxima. La ecuación (7) presenta la expresión del mean shift vector en el caso de utilizar un kernel gaussiano.
La principal ventaja del kernel gaussiano es la suave trayectoria que se obtiene hasta llegar a la moda, es decir, el ángulo entre dos mean shift vectors consecutivos es siempre menor que 90° [11]. El algoritmo MSC concentra un conjunto de datos de dimensión relacionando a cada uno de ellos con la moda o la cúspide de la función de densidad de probabilidad del conjunto de datos. Para cada dato, el algoritmo calcula la moda correspondiente y la asocia a él. En primer lugar, se define un kernel radial centrado en el punto y con ancho de banda h y se calcula la media de los puntos que caen dentro del área definida bajo el kernel. Después, el algoritmo desplaza la ventana o el kernel hacia la media y se va repitiendo el proceso hasta que converge, es decir, hasta que el mh(x) calculado recursivamente se mantiene constante o hasta que su variación es inferior a un umbral determinado. En cada iteración, la ventana se desplazaría hacia zonas de mayor densidad de puntos hasta que se alcance el pico, donde los datos están distribuidos de la misma manera en la ventana. Al finalizar el algoritmo, todos los puntos asociados a una moda de valor similar son asignados a un mismo grupo [25].
Los grupos de puntos que describen una línea recta están formados por densidades constantes, así el algoritmo de desplazamiento de media no la reconoce como un grupo, sino que divide el grupo en distintos subgrupos. Esto sucede a causa de que el algoritmo de desplazamiento de media reconoce los grupos asociando cada uno de ellos con el punto (centroide) en la zona de mayor densidad. Es decir, supone que los grupos tienen una configuración con una parte más densa y otra menos densa, y cada punto del grupo es asociado con el centro de la zona de mayor densidad. Con el fin de subsanar este problema, se propone una variación del algoritmo. Para mayor comprensión de la modificación del método Mean Shift es importante conocer primero los conceptos de obtención de dirección dominante y ventana elipsoidal.
3.2 Obtención de dirección dominante
Si utilizamos un sistema de coordenadas cartesianas para representar la distribución bidimensional de la lectura de láser, obtendremos un conjunto de puntos similar a un diagrama de dispersión, cuyo análisis permite estudiar cualitativamente la relación entre ambas variables. La dirección dominante del conjunto de puntos es aquella donde la dispersión del grupo se hace mayor para todos los puntos, es decir, los datos se encuentran mayormente distribuidos a lo largo de esta orientación, lo que puede servir de indicador de la presencia de una posible línea detectada por el escáner láser.
Para obtener la dirección dominante del grupo de puntos, se crean bases a las que se asignan preferencialmente a una dirección radial α equidistante que varía en un rango desde 0 a π, donde se computa una ponderación [9] que se construye como la sumatoria de los cosenos de la diferencia angular entre dos direcciones distintas asociadas, una de las cuales es la establecida como preferencial para cada nodo i y la segunda corresponde al ángulo de θ del punto n coordenadas polares, además cada factor se multiplica por la magnitud rn [26], correspondiente a la distancia del punto n hasta el origen de coordenadas. Se reconoce que cada coeficiente obtenido es un producto punto entre la medida del láser y las bases; en otras palabras, es la proyección de la lectura en los vectores bases [27].
Para un conjunto dado de puntos, solo un nodo realizará el máximo de la suma de los factores dados en la ecuación (8). Esto es claro tras una operación de maximización de la ecuación (8) respecto a θj y es también evidente desde la inevitable cercanía de una de las direcciones asignadas a los nodos con la dirección de la sumatoria vectorial física o real. Luego se extrae entonces la posición angular αi del nodo donde la sumatoria vectorial es máxima, lo que corresponde físicamente a la dirección dominante Ω.
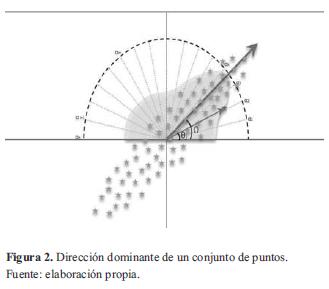
La figura 2 muestra gráficamente el proceso que se realiza para la obtención de la dirección dominante, donde se encuentran n puntos distribuidos semi-aleatoriamente en el espacio bidimensional, describiendo una forma elíptica rotada intencionalmente en un ángulo Ω para que sea detectada por el algoritmo.
La sumatoria de cosenos por nodo también se encuentra representada en la figura 2. Es claro notar que la sumatoria se hace mayor para aquellos valores de αi cercanos a la dirección dominante, ya que la diferencia θi- αi se acerca a cero, valor en el cual la función coseno obtiene su máximo valor.
3.3 Ventana elipsoidal
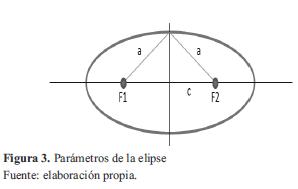
Se llama elipse al lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos F1 y F2, llamados focos es una constante que denominaremos 2a. La línea que une los dos focos se llama eje principal de la elipse y la mediatriz de los mismos eje secundario. Se llama vértices de la elipse a los puntos donde esta corta sus ejes. El punto medio de los dos focos se llama centro de la elipse y la distancia entre ellos se llama distancia focal designada 2c (figura 3).
La excentricidad de una elipse es su grado de achatamiento y su valor está determinado por la expresión de la ecuación (9).
Cuanto mayor es la excentricidad más achatada es la elipse. En una elipse α < c < 0 y por lo tanto es positiva y menor que uno.
3.4 Algoritmo Mean Shift modificado
El algoritmo modificado agrupa datos bidimensionales asociando a cada uno de los puntos con la cumbre de la función de densidad de probabilidad del agregado de datos. Para las lecturas del escaneo láser, el algoritmo calcula la moda correspondiente y la relaciona a él.
Para la segmentación, primero se define un kernel elipsoidal centrado en un punto aleatorio y con ancho de banda relacionado con la distancia focal de la ventana elíptica —que a su vez presenta dependencia con el tamaño del espacio de datos— y se calcula la media de las lecturas que se encuentran al interior del área delimitada por el kernel, para determinar si la lectura se encuentra dentro de la ventana elipsoidal, basta con obtener las distancias entre el punto y los focos, sumarlas y revisar si el resultado es menor que el valor constante definido por la excentricidad y distancia focal escogida.
A continuación, el algoritmo efectúa un desplazamiento de la ventana o el kernel hacia la media, al mismo tiempo que orienta el eje principal de la elipse hacia la dirección de mayor dispersión de puntos (figura 4) y se repite el proceso hasta que converge, es decir, hasta que el mean shift vector calculado recursivamente varíe muy poco, y sea inferior a un umbral determinado, momento en el cual se almacena el centroide y la dirección privilegiada de cada clúster identificado. La principal ventaja de la ventana elíptica es que al ser esta fácilmente orientable, una mayor cantidad de puntos de una posible recta podrán ser asociados al clúster en el momento de convergencia, disminuyendo el coste computacional, ya que todos aquellos puntos cuya distancia a la moda es menor que el ancho de banda del kernel se asume que van a converger a esa misma moda. Al converger siempre a una misma moda, pueden ser directamente asociados a dicho centroide sin tener que repetir el proceso para cada uno de ellos.
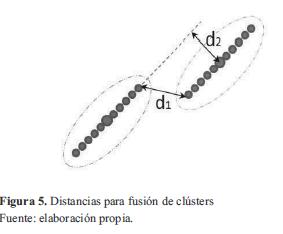
En cada ciclo, la ventana se trasladará hacia los lugares de mayor densidad de puntos y se orientará en dirección a la mayor dispersión hasta que se logre alcanzar la cima, donde los datos están repartidos de igual forma en la ventana. Al encontrar un centroide, el algoritmo realiza un chequeo donde verifica si los datos pueden estar relacionados a otro clúster y dado el caso, fusionarlos. Para tomar la decisión de fusionar datos de diferentes clústers, se toman dos medidas que son comparadas con umbrales (figura 5), la primera de ellas d1, corresponde a la distancia más cercana entre los puntos extremos de cada grupo, siendo esta parte del algoritmo una aplicación del método de segmentación secuencial denominado SEF (Successive Edge Following), que establece un segmento de recta a un punto si la distancia a el siguiente punto consecutivo es menor a un umbral.
La segunda distancia, se obtiene como la distancia más corta entre el centroide y la línea recta que pasa por el centro de un clúster diferente y que tiene la pendiente en dirección a la dispersión de los datos. Estas dos distancias son luego comparadas con umbrales que se encuentran en función del tamaño del espacio de datos. El algoritmo de la figura 6 muestra el pseudocódigo del agrupamiento por desplazamiento de media modificado. Al finalizar el algoritmo, cada centroide tendrá el conjunto de puntos asignados a dicho grupo y una dirección privilegiada (ángulo de dispersión). Con la ubicación del punto y la dirección de dispersión de puntos se logra obtener un estimado de la ecuación de la recta descrita por los datos correspondientes a cada clúster.
El algoritmo implementado es una variación del RANSAC que usa la mediana para estimar los datos espurios y actualizar las probabilidades y el número máximo de iteraciones adaptativamente. El algoritmo requiere una estimación inicial del porcentaje de los datos espurios que existen en la muestra, que servirá para hacer la primera estimación del número de iteraciones, también debe especificar un valor mínimo de datos que deben estar alineados para definir una línea, el umbral o el margen de error para que un punto pueda ser clasificado como perteneciente a una línea y un valor medio mínimo, que debe tener un valor inicial relativamente alto en función de los valores mínimo y máximo de los datos a segmentar.
3.5 Ransac
El objetivo general del método consiste en ajustar un modelo matemático para un conjunto de datos experimentales. El ajuste también es robusto, ya que reconoce la presencia de valores outliers en los datos. Algunos métodos de ajuste utilizan todos los datos disponibles para obtener una solución inicial y luego tratar de eliminar los puntos que no forman parte del modelo. El procedimiento RANSAC funciona de la manera opuesta, se compone de dos pasos que se repiten de forma iterativa (hipótesis y el marco de la prueba) [28]:
- Hipótesis: en primer lugar establece un mínimo de muestras (MSS) seleccionadas al azar del conjunto de datos de entrada y los parámetros del modelo se calculan utilizando solo los elementos del MSS. La cardinalidad de los MSS es la más pequeña para determinar los parámetros del modelo (a diferencia de otros enfoques, tales como los mínimos cuadrados, donde los parámetros se estiman utilizando todos los datos disponibles, posiblemente con un peso adecuado).
- Prueba: en el segundo paso del RANSAC se evalúa que los elementos del conjunto de datos sean coherentes con el modelo instanciado con los parámetros estimados en el primer paso. El conjunto de tales elementos se llama conjunto consenso.
- El algoritmo del RANSAC para la extracción de la línea se inicia con un conjunto de puntos, y se ajusta a una línea de dos puntos seleccionados al azar. Después se establece un conjunto de consenso, que forma parte de los puntos que se pueden considerar que están cerca de la línea o inliers. Si el número de puntos del conjunto de consenso Nc es mayor que un umbral, a continuación se vuelve a reajustar la línea para el conjunto de puntos de consenso (con los mínimos cuadrados, por ejemplo). De lo contrario el algoritmo se repite hasta que se alcanza un número máximo de iteraciones establecido de antemano.
El margen de error se puede determinar experimentalmente. Por ejemplo, puede hacer una estimación de datos erróneos, se calcula el error medio y luego se establece el margen de error a una o dos desviaciones estándar en comparación con el error medio.
Por otro lado, el número máximo de iteraciones se puede considerar como el número k datos pertenecientes al modelo correcto con una probabilidad de de ensayos que se llevarán a cabo con el fin de obtener un conjunto de n datos pertinentes al modelo correcto con una probabilidad de z. Si w se define como la probabilidad de que al menos un punto pertenezca al conjunto de datos erróneos, k se obtiene con la ecuación (10).
Para determinar el número de puntos del conjunto de consenso se puede hacer de la siguiente manera: sea y la probabilidad de que un punto está dentro del margen de error de un modelo incorrecto. Se pretende que sea muy pequeña. Aunque es muy difícil determinar con precisión y, es razonable suponer que será inferior w.
El algoritmo implementado es una variación del RANSAC, llamada Adaptive Scale Sample Consensus (ASSC), que usa la mediana para estimar los datos espurios y actualizar las probabilidades y el número máximo de iteraciones adaptativamente.
El algoritmo requiere una estimación inicial del porcentaje de los datos espurios que existen en la muestra, que servirá para hacer la primera estimación del número de iteraciones. También debe especificar un valor mínimo de datos que deben estar alineados para definir una línea, el umbral o el margen de error para que un punto pueda ser clasificado como perteneciente a una línea y un valor medio mínimo, que debe tener un valor inicial relativamente alto en función de los valores mínimo y máximo de los datos a segmentar.
Los dos primeros puntos son elegidos al azar de una lista ordenada, de tal forma que no se repita el mismo par de puntos en las siguientes iteraciones. Para no hacer un nuevo cálculo de una misma línea supuesta, entonces se calculan los parámetros de la línea con los puntos escogidos. A continuación, todas las distancias de los puntos a la línea son calculadas. Teniendo en cuenta los valores de las distancias, se separan aquellas que se encuentran por encima del 50 % de la distancia máxima de los de abajo (mediana), se calculan los datos espurios, para luego calcular el número de puntos que son clasificados como pertenecientes a la línea (inliers). Si el valor de la mediana es menor que el primer valor (muchos puntos con la pequeña distancia a la línea), la línea de datos se guarda y se procede a la actualización de las probabilidades y el número máximo de iteraciones realizadas. Cuando todas las iteraciones se terminan, se obtiene la línea con una regresión de los puntos clasificados como inliers con el TLS. En el algoritmo de la figura 7 se muestra un resumen del proceso.
3.6 Total Least Squares
TLS es un método de ajuste que se utiliza cuando hay errores tanto en el vector de observación como en la matriz de datos, por eso es una buena opción para obtener los parámetros apropiados de la línea final. El TLS minimiza la suma del cuadrado de las distancias de los puntos a la recta (medidas en perpendicular). En el caso del problema del TLS, se quieren tomar en cuenta las perturbaciones en la matriz de sensibilidad, para ello el TLS se define como la minimización sobre el rango y perturbaciones de la matriz de sensibilidad de tal forma que la distancia normal euclidiana entre la recta y los puntos que la componen sea la menor posible.
En el presente trabajo los puntos que han sido clasificados como inliers (puntos de consenso que pertenecen a la recta) se usan para calcular los parámetros de la recta siguiendo el algoritmo de la figura 8.
Cabe anotar que los parámetros de la recta obtenidos a través de la aplicación del TLS están dados en forma polar paramétrica, estos parámetros pueden ser utilizados en una etapa posterior para construir un mapa mediante algoritmos de SLAM.
4. Resultados
Para los resultados experimentales, un conjunto de datos ha sido obtenido mediante un láser SICK LMS-200 embarcado en un robot móvil PIONNER 3-DX que nos brinda 360 datos en un rango de 180 grados, ofreciendo una lectura cada 0,5 grados, proporciona 10 barridos por segundo, con una precisión de 2 grados y 2cm.
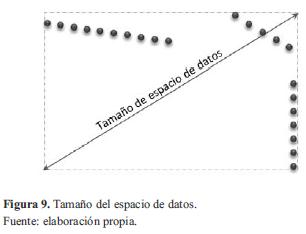
El algoritmo meanshift modificado fue calibrado mediante métodos heurísticos para obtener los parámetros de excentricidad y la distancia focal de la ventana elíptica en función del tamaño del espacio de datos. El tamaño del espacio de datos se obtiene como la diagonal del rectángulo límite creado por los puntos extremos de cada dimensión (figura 9).
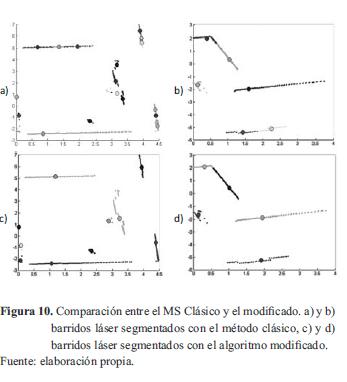
La prueba se hace en un solo barrido del escáner láser, el cual se segmenta mediante el algoritmo mean shift, con el fin de separar los diferentes segmentos de recta que componen el ambiente escaneado, luego cada clúster o grupo identificado es procesado por un algoritmo RANSAC modificado, para proceder con la parametrización de los fragmentos de líneas rectas. Algunos de los resultados obtenidos son contrastados con el método clásico en la figura 10.
La ecuación (11) y ecuación (12) enseñan los parámetros de la ventana elipsoidal asignados.
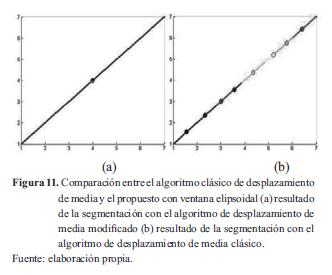
Un experimento que pone a prueba el algoritmo de segmentación corresponde a una línea recta de densidad constante, para lo cual se ingresan puntos alineados y distribuidos uniformemente en el espacio bidimensional al algoritmo propuesto, al igual que al algoritmo de desplazamiento de media clásico. Para realizar la comparación en ambos casos, los resultados de la prueba se muestran en la figura 11, donde se observa que el algoritmo propuesto segmenta toda la línea recta en un solo grupo, mientras que el clásico la fragmenta agrupándola en pequeños clústeres.
Luego de separar los diferentes segmentos de recta que componen el entorno escaneado, cada clúster o grupo identificado es procesado por el algoritmo RANSAC modificado, para proceder con la parametrización de los fragmentos de líneas rectas.
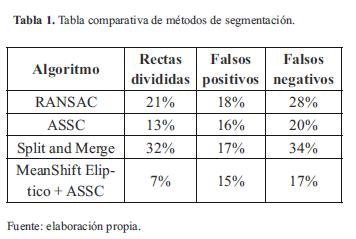
A continuación se muestra una tabla de resultados obtenidos con diferentes algoritmos que se realizó con el ánimo de obtener datos comparativos, con lo cual se observa que se obtuvieron resultados mejores con el algoritmo propuesto (MeanShift Eliptico + ASSC) respecto a el tratado con el MeanShift+ASSC, y bastante superiores en comparación con el Split and Merge. La tabla 1 muestra una comparación del número de rectas obtenidas con el algoritmo clásico y el modificado de MS, en relación a una segmentación manual.
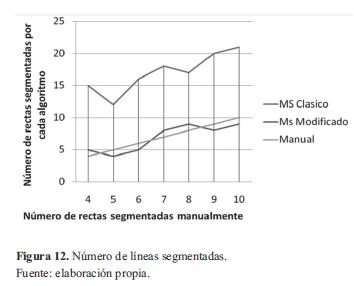
Se observa en la figura 12 que la cantidad de líneas extraídas con MS clásico es notablemente mayor a la segmentación manual, esto se debe al fraccionamiento que hace de las rectas; en cambio, con el MS modificado se obtiene un número de líneas muy cercano, sin redundancia de datos.
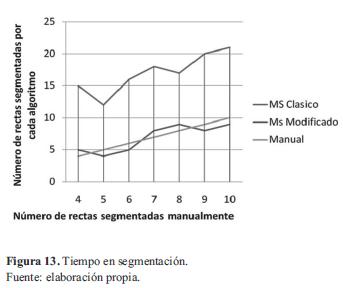
Si bien se realizaron algunas modificaciones (asociación directa al grupo de puntos cercanos al clúster) para disminuir el coste computacional, el procesamiento que acarrea los cálculos de dirección de la nube de puntos, el cambio de orientación y movimiento de la ventana elipsoidal hacen que el algoritmo sea mucho más lento que el utilizado clásicamente (figura 13), por lo que se podría utilizar en aplicaciones offine (por ejemplo, reconstrucción de mapas).
5. Conclusiones
Una parte del algoritmo implementado realiza una segmentación de un barrido láser, utilizando el método de agrupamiento por desplazamiento de media con una modificación del kernel y de asignación de puntos a clúster, la ventana elíptica aplicada como kernel en el presente documento es orientable para que la mayoría de los datos de la línea sean asociados directamente al grupo cuando el ciclo converja, reduciendo el tiempo de cómputo.
Por otra parte, el algoritmo también realiza una estimación robusta, aprovechandolas características del RANSAC, obteniendo resultados ya esperados en la mayoría de los datos experimentales, a pesar de que en las lecturas existía una gran cantidad de ruido, el comportamiento fue satisfactorio. El algoritmo no requiere de calibración respecto a los parámetros de entrada para las probabilidades, por lo que es conveniente para diversos tipos de sensores y plataformas. La implementación del algoritmo de segmentación previo a la aplicación del RANSAC hace que los parámetros comúnmente necesarios y sensibles se puedan obtener fácilmente, haciéndolos dependientes por ejemplo del tamaño de la muestra del grupo segmentado, brindando mayor robustez y aplicabilidad al algoritmo.
La estimación de parámetros por medio de TLS brinda la posibilidad de obtener una recta más ajustada a los datos, describiendo de mejor manera el ambiente que ha sido escaneado y permitiendo una reconstrucción de mapas más acertada y con una precisión más fidedigna.
6. Financiamiento
El estudio presentado fue financiado por el programa de Posgrado de la Escuela de Ingeniería Eléctrica y Electrónica de la Universidad del Valle a través del programa de becas de asistentes de docencia.
Referencias
[1] R. Smith, M. Self and P. Cheeseman, "Estimating Uncertain Spatial Relationships in Robotics", Uncertainty in Artificial Intelligence 2, New York, USA: Elsevier Science Pub., pp. 435-461, 1988.
[2] A. Giannitrapani, A. Ross and A. Garulli, "Mobile robot SLAM for line-based environment representation", European Control Conference 2005, Siena, Italy, 2005.
[3] J. Tardos and J. Castellanos, "Laser-Based Segmentation and Localization for a Mobile Robot", Procs. of the 6th Int. Symposium, Vol. 6, New York, 1996.
[4] J. Van Dorpe, X. Eric and H. Van Brussel, "Exact Dynamic Map Building for a Mobile Robot using Geometrical Primitives Produced by a 2D Range Finder", In Proceedings of the IEEE International Conference in Robotics and Automation, Minneapolis, Minnesota, 1996.
[5] K. O. Arras and R. Y. Siegwart, "Feature Extraction and Scene Interpretation for Map-Based Navigation", Symposium on Intelligent Systems and Advanced Manufacturing, Pittsburgh, 1997.
[6] P. Jensfelt and H. I. Christensen, "Laser Based Position Acquisition and Tracking in an Indoor Environment", In Proceedings of the IEEE International, Leuven, Belgium, 1998.
[7] S. T. Pfster and S. I. Roumeliotis, "Weighted Line Fitting Algorithms for Mobile Robot Map Building and Efficient Data Representation", ICRA, Taipei, Taiwao, 2003.
[8] V. Nguyen, S. Gachter, A. Martinelli and T. Nicola, "A comparison of line extraction algorithms using 2D range data for indoor mobile robotics", Journal Autonomous Robots, Hingham, USA: Kluwer Academic Publishers, pp. 97-111, 2007.
[9] K. Fukunaga and L. Hostetler, "The estimation of the gradient of a density function, with applications in pattern recognition", IEEE Transactions on Information Theory, vol. 21, no. 1, pp. 32-40, enero 1975.
[10] Y. Cheng, "Mean shift, mode seeking, and clustering", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 17, no. 8, pp. 790-799, 1995.
[11] D. Comaniciu and P. Meer, "Mean shift: A robust approach toward feature space analysis", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, pp. 603-619, 2002.
[12] D. Comaniciu, V. Ramesh and P. Meer, "The Variable Bandwidth Mean Shift and Data-Driven Scale Selection", Proc. 8th Intl. Conf. on Computer Vision, Kauai, Hawaii, 2001.
[13] D. Comaniciu, V. Ramesh and P. Meer, "Kernel Based Object Tracking", IEEE Trans. Pattern Analysis Machine Intelligence, vol. 25, no. 26, pp. 564-577, 2003.
[14] J. Shlen, A Tutorial on Principal Component Analysis, La Jolla: Salk Insitute for Biological Studies, 2009.
[15] M. Fischler and R. Bolles, "Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography", Communications of the ACM, New York, ACM, 1981, pp. 381-395.
[16] P. Huber and J. Wiley, Robust statistics, New York: Wiley, 1981.
[17] P. Rousseeuw and M. Hubert, "Robust statistics for outlier detection", Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, New York: John Wiley and Sons, Inc., 2011, pp. 73-79.
[18] J. Mendel, Lessons in Estimation Theory for Signal Processing Communications, Idaho: Prentice Hall, 1995.
[19] Z. Zhengyou, "Parameter Estimation Techniques: A Tutorial with Application to Conic Fitting", Image and Vision Computing, vol. 15, pp. 59-76, 1997.
[20] C. Stewart, "Robust parameter estimation in computer vision", SIAM Reviews, vol. 41, pp. 513-537, 1999.
[21] C. Martínez, J. Castellanos and T. Juan, "Adaptive Scale Robust Segmentation for 2D Laser Scanner", International Conference on Intelligent Robots and Systems, Beijing, 2006.
[22] G. Golub and H. Van Loan, An Analysis of the Total Least Squares Problem, Ithaca: Cornell University, 1980.
[23] V. Huffel and S. Joos, Analysis and solution of the nongeneric total least squares problem, Philadelphia: Society for Industrial and Applied Mathematics, 1988.
[24] W. Kuo Lung and Y. Miin Shen, "Mean shift-based clustering", Pattern Recognition, vol. 40, no. 11, pp. 3035-3052, 2007.
[25] P. C. Benito, Integración de información de movimiento en la segmentación de secuencias de vídeo basada en el modelado de fondo, Madrid: Universidad Autónoma de Madrid, 2010.
[26] H. Abdi and W. Lynne, "Principal component analysis", Wiley Interdisciplinary Reviews: Computational Statistics, vol. 2, no. 4, pp. 433-459, 2010.
[27] J. Shlen, A Tutorial on Principal Component Analysis, La Jolla: Salk Insitute for Biological Studies, 2009.
[28] M. Zuliani, RANSAC for Dummies, Santa Barbara: University of California, 2009.
License
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.