DOI:
https://doi.org/10.14483/udistrital.jour.tecnura.2015.3.a06Publicado:
01-07-2015Número:
Vol. 19 Núm. 45 (2015): Julio - SeptiembreSección:
InvestigaciónComportamiento de las ecuaciones de Saint-Venant en 1D y aproximaciones para diferentes condiciones en régimen permanente y variable
Performance of the Saint Venant equations in 1d and approaches to different conditions in steady and variable state
Palabras clave:
ecuaciones de Saint-Venant, modelos matemáticos, onda dinámica, pendiente subcrítica, pendiente supercrítica (es).Palabras clave:
mathematical modeling, Saint-Venant equations, slope subcritical, supercritical slope, wave dynamics (en).Descargas
Referencias
Barati, R., Sajjad, R., & Akbari, G. (2012). Analysis of dynamic wave model for flood routing in natural rivers. Water Science and Engineering , 5 (3), 243-258.
Cea, L. (2008). Modelación matemática en lecho fijo del flujo en ríos. Modelos 1D y 2D en régimen permanente y variable. Jornadas Técnicas sobre Hidráulica Fluvial, CEDEX - Ministerio de Fomento. Madrid.
Chang, T. J., Kao, H. M., Chang, K. H., & Hsu, M. H. (2011). Numerical simulation of shallow water dam break flows in open channels using smoothed particle hydrodynamics. Journal Hydrology , 408, 78–90.
Chow, V. T., Maidment, D. R., & Mays, L. (1988). Applied Hydrology. Estados Unidos: Mac Graw Hill.
De Saint-Venant, B. (1871). Theorie du mouvement non permanent des eaux, avec application aux crues de rivieras at a l’introduction des marces dans leur lit. Compt Rend Acad Sci , 147–154.
Lighthill, M. J., & Whitham, G. B. (1955). On kinetic wave II: a theory of traffic flow on crowded roads. Proceedings of the Royal Society of London, Series A, 229, pp. 317- 345.
Macchione, F., & Morelli, M. (2003). Pactical aspect comparing shock-capturing schemes for dam break problems. Journal hydraulic engineering , 129 (3), 187-195.
Pino Vargas, E., Mejía Marcacuzo, J. A., & Chávarry Velarde, E. (2012). Un Modelo Numérico 1D en Volúmenes Finitos para la Solución de las Ecuaciones de Flujo e Infiltración del Riego por Gravedad en Melgas. Revista ECIPerú , 9 (1), 22-30.
Singh, V. P. (1996). Kinematic wave modeling in water resources: Sourface water hydrology. New York: John Wiley.
Tsai, C. W. (2003). Applicability of kinematic, noninertia, and quasi-steady dynamic wave models for bend-flow simulation. Journal of Hydraulic Engineering , 613-627.
White, M. F. (1991). Viscous Fluid Flow. Estados Unidos: University of Rhode Island.
Yao-Hsin, H. (2013). A characteristic particle method for the Saint-Venant equations. Computers & Fluids , 76, 58–72.
Zapata Gaviria, J. F. (2012). Propuesta metodológica para la conceptualización de sistemas de drenaje urbano. Revista EPM , 6, 20-31.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2015.3.a06
Investigación
Comportamiento de las ecuaciones de Saint-Venant en 1D y aproximaciones para diferentes condiciones en régimen permanente y variable
Performance of the Saint Venant equations in 1D and approaches to different conditions in steady and variable state
Gloria Estefany Amarís Castro*,
Thomas Edison Guerrero Barbosa**,
Edgar Antonio Sánchez Ortiz***
* Ingeniera civil, estudiante de la Maestría en Ingeniería Civil con énfasis en Recursos Hídricos, Universidad del Norte, Departamento de
Ingeniería Civil y Ambiental, Barranquilla, Colombia. Contacto: gloriacastro-18@hotmail.com
** Ingeniero civil, magíster en Ingeniería Civil. Docente Auxiliar, Universidad Francisco de Paula Santander Ocaña, Departamento de Ingeniería
Civil, Ocaña, Colombia. Contacto: teguerrerob@ufpso.edu.co
*** Licenciado en Física y Matemáticas, magíster en Educación. Director seccional, Universidad Francisco de Paula Santander Ocaña, Ocaña,
Colombia. Contacto: easanchezo@ufpso.edu.co
Fecha de recepción: 6 de septiembre de 2014 Fecha de aceptación: 6 de abril de 2015
Como citar: Amarís Castro, G. E., Guerrero Barbosa, T. E., & Sánchez Ortiz, E. A. (2015). Comportamiento de las ecuaciones de Saint-Venant en 1D y aproximaciones para diferentes condiciones en régimen permanente y variable. Revista Tecnura, 19(45), 75-87. doi: 10.14483/udistrital.jour.tecnura.2015.3.a06
RESUMEN
La importancia del comportamiento de las ecuaciones de Saint-Venant y sus implicaciones en el análisis del flujo aplicado a modelos de tránsito hidráulico es el tema principal de esta investigación. Partiendo de las aplicaciones y usos de dichos modelos matemáticos, se determina y se evalúa el comportamiento de estas ecuaciones en 1D y sus aproximaciones para diferentes condiciones posibles de una situación real mediante la experimentación numérica computacional para un tramo de un cauce con una sección hidráulica prismática, en casos en los cuales la pendiente del canal presenta tres tipos de condiciones: supercrítica, subcrítica y pendiente horizontal, para un caudal de referencia. El objetivo principal de esta investigación es encontrar una demostración de la aplicabilidad de las ecuaciones de Saint-Venant para diferentes condiciones de acercamiento a esta problemática desde el punto de vista de la solución de las ecuaciones de Saint-Venant en una dimensión. Se propone un esquema de solución simple que produzca soluciones útiles a las necesidades de la ingeniería, y se encuentra que dentro del análisis de redes de alcantarillado hay muchos factores que pueden afectar la solución de las ecuaciones de Saint-Venant.
Palabras clave: ecuaciones de Saint-Venant, modelos matemáticos, onda dinámica, pendiente subcrítica, pendiente supercrítica.
ABSTRACT
The importance of the behavior of the Saint Venant equations and its implications for flow analysis applied to models of hydraulic transit is the main theme of this research, where the basis of the applications and uses of these mathematical models is determined and the performance is evaluated these equations in 1D and its possible approaches for different conditions of a real situation using computational numerical experimentation for a section of a prismatic channel with a hydraulic section, in cases where the channel slope presents three types of conditions: supercritical, subcritical and horizontal slope for a design rate. The main objective of this research is to find a demonstration of the applicability of the Saint Venant equations for different conditions of approaching this problem from the point of view of the solution of the Saint Venant equations in one dimension. Scheme simple solution that produces useful solutions to the needs of engineering, finding that within the sewer network analysis there are many factors that can affect the solution of the Saint Venant equations.
Keywords: mathematical modeling, Saint-Venant equations, slope subcritical, supercritical slope, wave dynamics.
INTRODUCCIÓN
En Colombia los modelos de tránsito permanente son de uso común en las modelaciones en ingeniería. Software de uso frecuente como el Sistema de Análisis de Ríos, desarrollado por el Centro de Ingeniería Hidrológica de California, EUA (HEC-RAS, por su sigla en inglés), permite determinar la altura requerida para construir estructuras de control como puentes, diques, vertederos y obras de protección en aguas bajas, redes hídricas y flujo libre; sin embargo, cuando la lámina del flujo crece rápidamente, los errores de los esquemas no linealizados aumentan.
Las ecuaciones de Saint-Venant (1871) han demostrado ser un modelo matemático útil con aplicaciones en varias ramas de la ingeniería hidráulica y costera; estos modelos se basan en el desarrollo de ecuaciones diferenciales encargadas de modelar variación de caudal y nivel de un flujo en un espacio unidimensional y el tiempo de manera no permanente en canales abiertos. En general estas modelaciones se presentan en tres dimensiones, pero las aplicaciones prácticas suelen utilizar una aproximación unidimensional en la dirección de mayor relevancia, que usualmente suele ser a lo largo del canal en la dirección de flujo.
En la revisión bibliográfica se encuentran evidencias de otros estudios que se encargan de proponer diferentes escenarios con el fin de explicar el comportamiento del flujo mediante las ecuaciones de Saint-Venant y establecer su aplicabilidad para determinar el comportamiento del flujo.
En las modelaciones de flujo en canales de alta pendiente (So > 5%) se generan soluciones inestables debido a la alta acumulación de errores (Tsai, 2003). En estos casos generalmente se sugiere el uso de un esquema de solución mediante la formulación y desarrollo de la onda cinemática, de tal forma que considere la no linealidad en flujos bajo estas condiciones. Estas modelaciones matemáticas son consideradas como una aproximación a la realidad, por lo cual es primordial establecer las condiciones de frontera que permitan determinar las condiciones aproximadas del comportamiento del flujo y del canal, ya que cuanto más se adapten las ecuaciones de partida y la programación numérica para su resolución al fenómeno real que se está estudiando, mejores resultados se obtendrán.
Generalmente en los estudios hidráulicos, como es el caso de los efectos de la propagación de avenidas en ríos, cálculos de velocidades y niveles de agua, son usados métodos de abstracciones unidimensionales en régimen permanente gradualmente variado y fondo fijo, pues se les considera como una herramienta suficiente para determinar el comportamiento del río y se deja a un lado la evolución temporal en el proceso. Aplicaciones de partículas hidrodinámicas con modelos matemáticos basados en las ecuaciones de Saint-Venant en canales abiertos son mostradas por (Chang, Kao, Chang, & Hsu, 2011).
La onda dinámica se considera como el modelo de tránsito distribuido más completo existente, ya que tiene en cuenta todas las fuerzas que interactúan en el tránsito de la creciente (inerciales, presión, gravitacional, fricción) y tiene en cuenta los efectos de remanso en el cálculo; en su forma completa, estas ecuaciones se consideran de solución compleja aun con el uso de las más modernas herramientas computacionales (Cea, 2008).
A pesar de la complejidad de estas ecuaciones, son estudiadas con el fin de entenderlas y con esto mejorar las ideas en el campo de la mecánica de los fluidos en las soluciones de flujos particulares y para examinar leyes de modelamiento matemático (White, 1991).
Otros estudios aplicativos referentes a la implementación del esquema numérico en volúmenes finitos para las ecuaciones de flujo Saint-Venant han permitido conocer el perfil de flujo superficial y la infiltración en el suelo en sistemas de riego, como es el caso de Pino, Mejía y Chávarry (2012), quienes determinaron, tras un proceso de simulación de varios casos, que la pendiente longitudinal tiene un papel importante en el flujo para las melgas; según su modelo, la pendiente debe ser menor a 0,001 m/m. Las pendientes mayores generan flujos rápidos o supercríticos.
Al aplicar el análisis de flujo de régimen variable es imprescindible considerar las restricciones que permiten el desarrollo de las ecuaciones de Saint-Venant, por lo tanto es necesario utilizar un software que permita modelar las situaciones en que sea aplicable la suposición de onda cinemática como la onda dinámica.
Aplicaciones de las ecuaciones de Saint-Venant contrarias a los casos ya conocidos, como en redes fijas convencionales o métodos de partículas en movimiento, se evidencian en Yao-Hsin (2013), quien muestra una formulación a partir de la reasignación de partículas computacionales a lo largo de las curvas características. En la predicción de las variables de flujo para diferentes condiciones tiene gran importancia desarrollar modelos y simulaciones numéricas hidrodinámicas con precisión adecuada que permitan la correcta planificación de obras.
El objetivo principal de esta investigación es evaluar el comportamiento de las ecuaciones de Saint-Venant para condiciones en régimen permanente y variable, bajo diferentes escenarios de estudio y modificando las condiciones de frontera mediante condiciones de piscina nivelada, pendiente subcrítica y condición aguas abajo profundidad crítica, pendiente supercrítica y condición aguas abajo profundidad normal.
METODOLOGÍA
Teniendo en cuenta el concepto de onda cinemática como un modelo simplificado del flujo no permanente en canales abiertos y conociendo que las ondas dinámicas resuelven las ecuaciones completas, se concluiría que las ondas dinámicas resuelven las ecuaciones completas, pues se esperaría que la onda dinámica presentara mejor comportamiento que la onda cinemática debido a que la onda dinámica contiene términos inerciales (aceleración local y aceleración convectiva), fuerza gravitacional, fuerza de fricción; por el contrario, la onda cinemática únicamente contiene los términos de fuerza gravitacional y de fuerza de fricción pero según estudios realizados los últimos 100 cien años indican lo contrario. Lighthill y Whitham (1955) afirman que bajo las condiciones apropiadas para el flujo de avenida, las ondas dinámicas se atenúan muy rápidamente, y son las ondas cinemáticas, viajando a una velocidad menor, las que asumen el papel preponderante.
Tipos de tránsito hidráulico
Las ecuaciones de Saint-Venant tienen varias formas simplificadas, cada una de las cuales define un modelo de tránsito distribuido unidimensional (Zapata Gaviria, 2012). Aunque las fuerzas expresadas en la ecuación de momentum siempre están presentes en cualquier problema de hidrodinámica, se puede dar el caso de que no todas sean relevantes. Esto hace que sea posible tener varios tipos de tránsito hidráulico de crecientes, como se muestra en la ecuación (1).
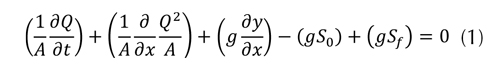
Modelo de onda cinemática
El modelo de onda cinemática es la mejor alternativa en la modelación del tránsito hidráulico en redes debido a la simplicidad de su estructura, buen comportamiento y representatividad ante una modelación, sin embargo el que desprecie ciertas condiciones como términos de aceleración local, aceleración convectiva y fuerzas de presión, limita en cierta medida al modelo para ciertas circunstancias de escenarios dependiendo del caso especifico (condiciones de pendiente y velocidad entre otras).
En este caso la ecuación de Saint Venant de conservación de momentum se reduce a la ecuación (2) y la ecuación (3).
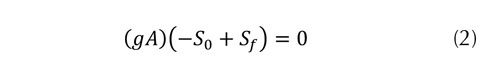
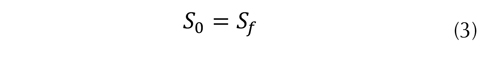
Lo anterior implica que el flujo puede ser tratado como "uniforme no permanente". Esto significa que no hay efectos transientes de curvas de remanso. En este caso existe un balance entre el efecto de la aceleración debido a la gravedad y el efecto de retraso de las fuerzas de fricción.
La celeridad de onda es la velocidad con la cual se mueve el frente de onda con respecto a los bordes del conducto. En el caso de la onda cinemática, los términos de aceleración y de presión son muy pequeños comparados con los gravitacionales y los de fricción; es decir, el movimiento de la onda está descrito más por la ecuación de continuidad que por la de momentum.
Esquema numérico
Las ecuaciones de Saint Venant para la onda cinemática son dos ecuaciones diferenciales parciales, una de continuidad y otra de momentum. La solución de las ecuaciones requiere de métodos numéricos directos, los cuales convierten las ecuaciones diferenciales en ecuaciones de diferencias finitas para la conservación de la masa y del momentum lineal, las cuales pueden ser lineales o no lineales. Los cálculos de las variables desconocidas se hacen simultáneamente en función del espacio y del tiempo. En el caso del tránsito hidráulico de crecientes, las variables desconocidas son: Q y A.
Si se tiene una función f(x) continua en un intervalo (a,b), el valor de f(x+Δx) puede ser calculado utilizando el valor de f(x), que se supone conocido, y las derivadas de la función f en el punto x conocido. Utilizando series de Taylor y resolviendo para f'(x), se obtiene la ecuación (4).
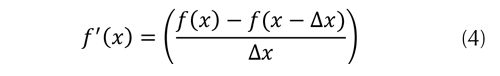
Esta ecuación puede ser utilizada para solucionar la ecuación diferencial parcial, en donde la derivada es función de los valores conocidos de la función inicial.
Solución por diferencias finitas
El esquema de diferencias finitas debe solucionar las ecuaciones de Saint Venant. La variable dependiente únicamente es Q. La ecuación de continuidad, por ser una ecuación diferencial parcial, se puede aplicar al método de las diferencias finitas, con el fin de conocer Q para cualquier lugar x del conducto en cualquier instante de tiempo.
La otra variable dependiente (y o A) se calcula utilizando Q(x,t) y una ecuación de resistencia fluida, tal como la ecuación de Gauckler Manning. Luego de un sencillo procedimiento matemático se llega a la ecuación (5).
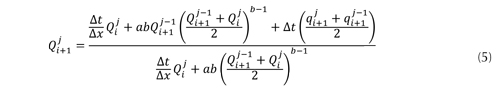
Donde los valores a y b dependen de la geometría del conducto, y los términos de Δx y Δt deben estar relacionados mediante la condición de Courant correspondiente a la ecuación (6).
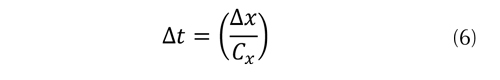
APLICACIÓN PARA EVALUAR LAS ECUACIONES DE SAINT-VENANT
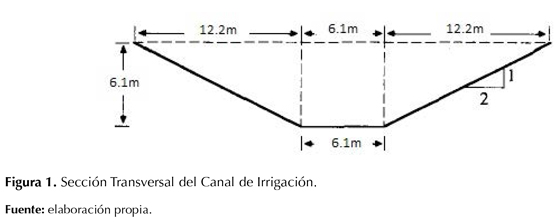
Mediante el uso de las ecuaciones de Saint-Venant y los métodos de solución tanto implícito como explícito, se procedió a desarrollar los siguientes casos de estudios y para cada uno se obtuvo resultados en una situación en particular. La sección transversal del canal de irrigación se muestra en la figura 1, así como otras características de esta se presentan a continuación:
- Tipo de cauce: canal prefabricado.
- Uso: irrigación.
- Forma de la sección transversal: trapezoidal.
- Relación de taludes laterales: 2H:1V.
- Base: 6,1 m.
- Longitud: 2743,2 m.
- Cota inicial: 29,1 m.s.n.m.
- Rugosidad (n de Manning): 0,025.
La pendiente longitudinal utilizada varió según las condiciones hidráulicas que se deseaban evaluar, tales como la propagación de la onda sobre una pendiente horizontal, subcrítica o supercrítica. En cuanto al cálculo del tránsito distribuido de la onda sobre el canal evaluado, fue necesario implementar una rutina (algoritmo) que lograra la resolución numérica de las ecuaciones diferenciales de momento y continuidad de una forma rápida y estable. Esta rutina fue elaborada en Matlab 2011 y consideró dentro de su estructura la posibilidad de evaluar diferentes condiciones de frontera, tales como: hidrograma y limnigrama en la frontera aguas arriba e hidrogramas, limnigramas, condiciones de flujo normal y flujo crítico sobre la frontera aguas abajo.
El análisis del escenario propuesto indica que el caudal pico mostrado en la gráfica del hidrograma de entrada es un tiempo de 3,65 hr (condiciones típicas de la ciudad de Barranquilla); para la programación es necesario que el tiempo de modelación sea superior por lo menos al caudal pico del hidrograma es por esto que se decidió tomar 5 h de tal forma que supere el caudal pico mostrado en el hidrograma; adicionalmente se utilizó un diferencial de tiempo (∆t) de 0,1 hrs y un diferencial de posición (∆x) de 305 m. Los casos sobre los cuales se evaluó la ecuación de Saint Venant se presentan a continuación.
Caso 1: flujo horizontal
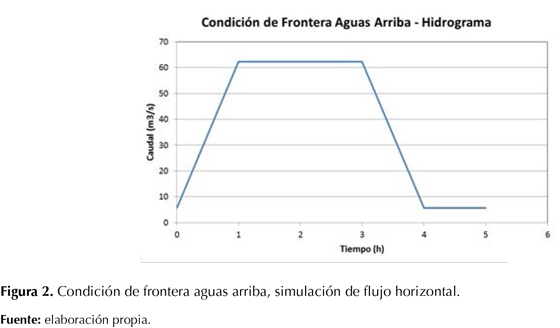
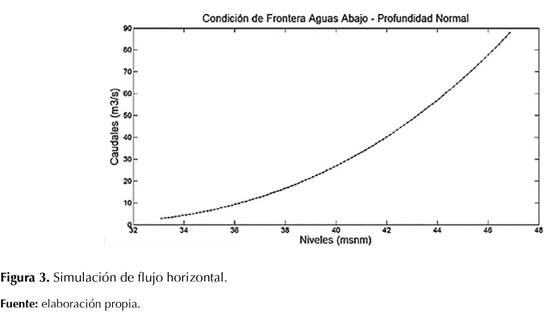
Para este escenario de modelación se planteó una pendiente de fondo de S0=0,0000005, suficientemente baja, simulando las condiciones de un embalse. Las condiciones de frontera para simulación fueron:
- Aguas arriba: hidrograma de caudales.
- Aguas abajo: profundidad normal.
A continuación se presentan las condiciones de frontera aguas arriba y aguas abajo definidas para la simulación de flujo horizontal correspondiente a las figuras 2 y 3.
Al igual que las simulaciones de los escenarios anteriores, esta se ejecutó con el modelo de onda dinámica, seleccionando como valor de θ=0,75. Para este caso las condiciones iniciales definidas son:
- Caudal inicial: 10 m3/s.
- Profundidad inicial: 7,119 m.
Caso 2: flujo subcrítico
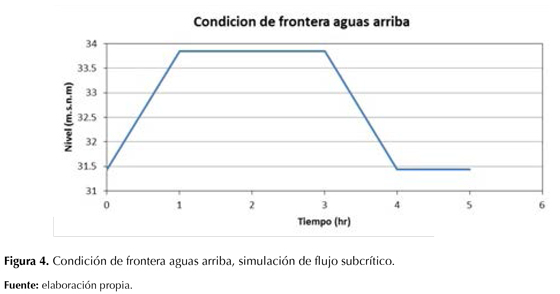
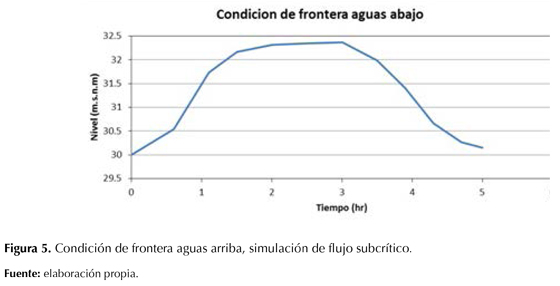
Se ha considerado un flujo subcrítico, con pendiente de fondo de S0=0,0005; las condiciones de frontera aplicadas en esta simulación fueron:
- Limnigrama de niveles aguas arriba.
- Limnigrama de niveles aguas abajo.
Las figuras 4 y 5 muestran las condiciones de frontera aguas arriba y aguas abajo utilizadas para esta simulación.
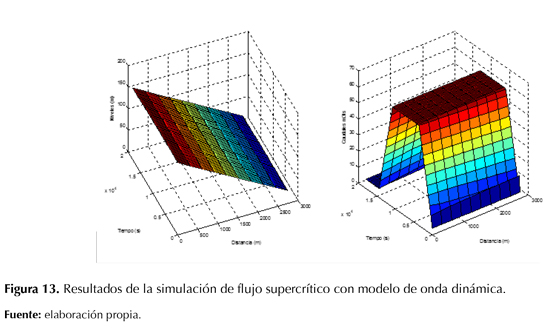
Caso 3: flujo supercrítico
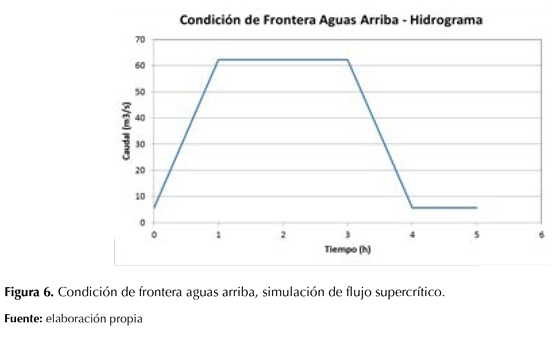
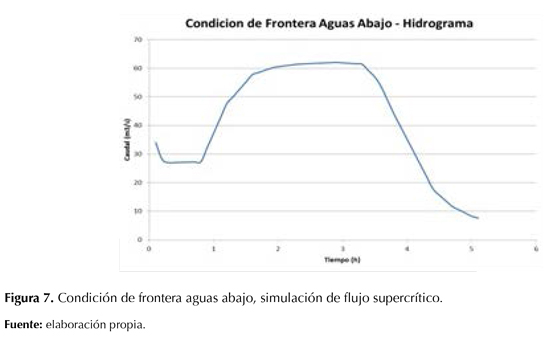
Se ha considerado un flujo supercrítico con pendiente de fondo de S0=0,05; las condiciones de frontera aplicadas en esta simulación fueron:
Hidrograma de caudales aguas arriba.
- Hidrograma de caudales aguas abajo.
Las figuras 6 y 7 muestran las condiciones de frontera aguas arriba y aguas abajo utilizadas para esta simulación.
RESULTADOS
Caso 1
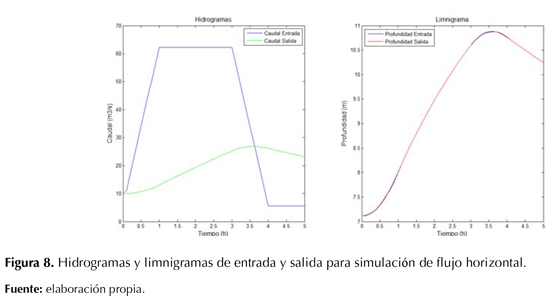
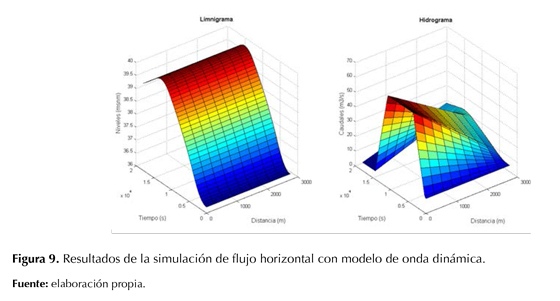
A continuación se presenta el tránsito del hidrograma de caudales y del limnigrama de profundidades a lo largo del canal para las condiciones iniciales y finales, como se ve en la figura 8. Respecto a los hidrogramas observamos que en el tiempo 3,65 h el caudal pico de la salida (26,82 m3/s) cruza el hidrograma de la entrada y a las 5 horas el caudal en la salida es de 23,3m3/s y en la entrada el caudal es de 5,66 m3/s. Mientras tanto, en el limnigrama notamos que la variación de la profundidad en la entrada es muy similar a la variación de la profundidad en la entrada.
Anteriormente observamos las variaciones de los caudales y las profundidades respecto al tiempo; ahora bien, en la figura 9 se presenta la variación de los caudales y las profundidades respecto al tiempo y al espacio.
Caso 2
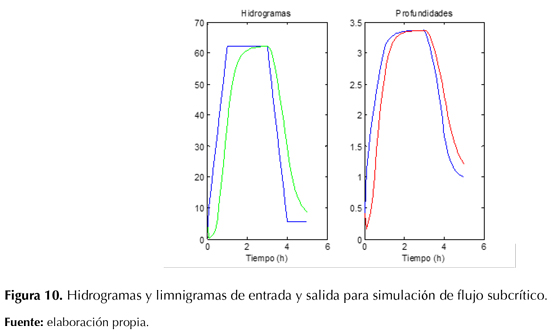
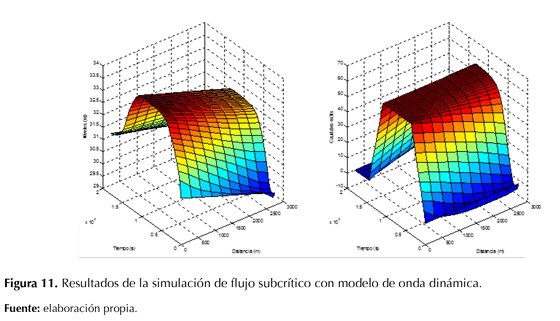
La simulación de este escenario se llevó a cabo con el modelo de onda dinámica. En la figura 10 se presenta el hidrograma de entrada, el hidrograma de salida, las profundidades de entrada y las profundidades de salida. En la figura 11 se muestra cómo transitan el hidrograma y el limnigrama a lo largo del canal.
El hidrograma de salida alcanza el mismo caudal pico que el hidrograma de entrada (62,3 m3/s) pico después de 4 horas de simulación. Se aprecia que el modelo de onda dinámica simula correctamente el escenario de flujo subcrítico unidimensional para el escenario de limnigramas como condiciones de frontera. Los resultados no tienen inconsistencias en el hidrograma de salida con un valor de θ= 0,75.
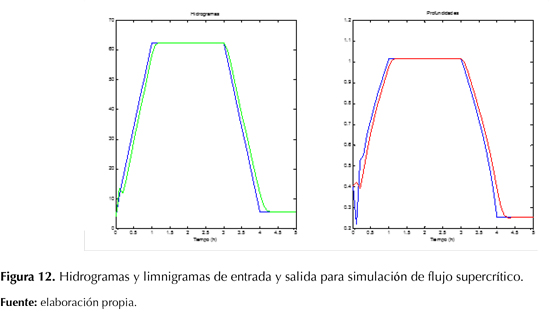
Caso 3
La simulación de este escenario se llevó a cabo con el modelo de onda dinámica. En la figura 12 se presenta el hidrograma de entrada, el hidrograma de salida, las profundidades de entrada y las profundidades de salida. En la figura 13 se muestra cómo transitan el hidrograma y el limnigrama a lo largo del canal. El hidrograma de salida alcanza el mismo caudal pico que el hidrograma de entrada (62,3 m3/s) pico en menos de 0,3 horas de simulación debido a la gran velocidad en la que se mueve la onda. Se pudo observar que el tiempo de respuesta del sistema a la onda fue tal que los hidrogramas de niveles y caudales de las fronteras están muy cercanos entre sí. Se aprecia que el modelo de onda dinámica simula correctamente el escenario de flujo supercrítico para las condiciones de frontera dadas. Los resultados presentan una ligera inestabilidad en el arranque de la simulación, y es debido a que el modelo para esos intervalos de tiempo no convergió en una solución adecuada, lo cual era de esperarse para el caso de flujo evaluado.
CONCLUSIONES
El modelo de la onda dinámica demuestra ser aplicable a todos los casos, a menos que sea posible demostrar que los modelos o aproximaciones de la onda difusa y la onda cinemática son adecuados para representar el flujo.
Las condiciones para las cuales son aplicables las ecuaciones de Saint-Venant que se basan en la solución de la ecuación de continuidad acompañada por la ecuación de momentum lineal son: para condiciones de pendiente menores al 10% y situaciones hidráulicas que cuenten con pendientes pronunciadas, se puede hacer uso del método de la onda cinemática;, si por el contrario las condiciones a modelar cuentan con pendientes suaves (terrenos planos con pendiente inferiores al 0,05%), se debe hacer uso del método de la onda dinámica, de tal manera que ajuste de forma adecuada a las condiciones del fenómeno que se desea modelar.
Durante el desarrollo de la investigación se demuestra que existen factores que afectan la solución de las ecuaciones, entre los cuales están el ∆x (variación de la distancia) que se escoja para el cálculo, las condiciones de frontera, la geometría y el tipo de estructura hidráulica.
Para verificar el efecto del ∆x, se modeló con el programa Matlab un tramo con una longitud de 2743,2 m y se variaron los ∆x para el cálculo. El uso de las ecuaciones simplificadas de la onda cinemática, en el tránsito de crecientes para canales de alta pendiente, se muestran bastante útiles, tal y como lo reportan Chow, Maidment y Mays (1988), Singh (1996), Tsai (2003), y Macchione yMorelli (2003).
El modelo basado en la simplificación de la onda dinámica permite simular los frentes de ondas manteniendo la continuidad en la masa y adicionalmente disminuyendo la atenuación en el caudal pico. Sin embargo, para condiciones de flujo en canales, donde se pueda generar un frente de onda, las ecuaciones de Saint-Venant no son válidas en las vecindades de la discontinuidad.
De acuerdo con los resultados obtenidos para cada aplicación, se debe cuestionar el uso de los softwares de manera que se tenga en cuenta en las modelaciones todos los parámetros que afectan las ecuaciones de Saint-Venant.
La evaluación y modelación del comportamiento del flujo es importante para la aplicación de la ingeniería hidráulica y costera, es por esto que las modelaciones que se realizan deben ajustarse a las situaciones reales encontradas en campo para definir las condiciones de frontera de la estructura hidráulica y sus limitaciones, con el fin de que las modelaciones simulen una situación cercana a la real presentada.
Los resultados sugieren que los efectos de los errores de los parámetros de entrada en los resultados de salida son más significativos en situaciones especiales, como los valores más bajos de coeficiente de rugosidad de Manning y una pendiente base más pronunciada en las características de un hidrograma de diseño, tal como lo sugiere Barti, Sajjad y Akbari (2012).
FINANCIAMIENTO
La investigación es resultado del financiamiento entregado por la Universidad Francisco de Paula Santander Ocaña (UFPSO) a través de la División de Investigación y Extensión (DIE) del proyecto titulado "Estudio del sistema de drenaje del campus de la Universidad Francisco de Paula Santander Ocaña y diseño de estructuras hidroeconómicas mediante el principio de incertidumbre".
REFERENCIAS
Barati, R., Sajjad, R., & Akbari, G. (2012). Analysis of dynamic wave model for flood routing in natural rivers. Water Science and Engineering , 5 (3), 243-258.
Cea, L. (2008). Modelación matemática en lecho fijo del flujo en ríos. Modelos 1D y 2D en régimen permanente y variable. Jornadas Técnicas sobre Hidráulica Fluvial, CEDEX-Ministerio de Fomento. Madrid.
Chang, T. J., Kao, H. M., Chang, K. H., & Hsu, M. H. (2011). Numerical simulation of shallow water dam break flows in open channels using smoothed particle hydrodynamics. Journal Hydrology , 408, 78-90.
Chow, V. T., Maidment, D. R., & Mays, L. (1988). Applied Hydrology. Estados Unidos: Mac Graw Hill.
De Saint-Venant, B. (1871). Theorie du mouvement non permanent des eaux, avec application aux crues de rivieras at a l'introduction des marces dans leur lit. Compt Rend Acad Sci , 147-154.
Lighthill, M. J., & Whitham, G. B. (1955). On kinetic wave II: a theory of traffic flow on crowded roads. Proceedings of the Royal Society of London, Series A, 229, pp. 317345.
Macchione, F., & Morelli, M. (2003). Pactical aspect comparing shock-capturing schemes for dam break problems. Journal hydraulic engineering , 129 (3), 187-195.
Pino Vargas, E., Mejía Marcacuzo, J. A., & Chávarry Velarde, E. (2012). Un Modelo Numérico 1D en Volúmenes Finitos para la Solución de las Ecuaciones de Flujo e Infiltración del Riego por Gravedad en Melgas. Revista ECIPerú , 9 (1), 22-30.
Singh, V. P. (1996). Kinematic wave modeling in water resources: Sourface water hydrology. New York: John Wiley.
Tsai, C. W. (2003). Applicability of kinematic, noninertia, and quasi-steady dynamic wave models for bend-flow simulation. Journal of Hydraulic Engineering , 613-627.
White, M. F. (1991). Viscous Fluid Flow. Estados Unidos: University of Rhode Island.
Yao-Hsin, H. (2013). A characteristic particle method for the Saint-Venant equations. Computers & Fluids, 76, 58-72.
Zapata Gaviria, J. F. (2012). Propuesta metodológica para la conceptualización de sistemas de drenaje urbano. Revista EPM , 6, 20-31.
Licencia
Esta licencia permite a otros remezclar, adaptar y desarrollar su trabajo incluso con fines comerciales, siempre que le den crédito y concedan licencias para sus nuevas creaciones bajo los mismos términos. Esta licencia a menudo se compara con las licencias de software libre y de código abierto “copyleft”. Todos los trabajos nuevos basados en el tuyo tendrán la misma licencia, por lo que cualquier derivado también permitirá el uso comercial. Esta es la licencia utilizada por Wikipedia y se recomienda para materiales que se beneficiarían al incorporar contenido de Wikipedia y proyectos con licencias similares.