Enseñanza de la derivada mediada por objetos de aprendizaje

Enseñanza de la derivada mediada por objetos de aprendizaje

Derived teaching mediated learning objects

El uso de tecnologías en la práctica docente

Recibido:22-05-2016
Modificado: 12-06-20166
Aprobado: 02-07-2016

Camilo Andrés Ortiz Daza

Ingeniero electrónico y de telecomunicaciones; estudiante de la Especialización en Multimedia para la Docencia, Universidad Cooperativa de Colombia, Sede Bogotá. Correo electrónico: ortizdaza9215@gmail.com

Fredys A. Simanca H

Ingeniero de sistemas; Especialista en Redes de Telecomunicaciones, Especialista en Multimedia para la Docencia, magíster en Informática Aplicada a la Educación; doctorando en Sociedad del Conocimiento. docente Investigador, Universidad Cooperativa de Colombia. Correo electrónico: fredys.simanca@campusucc.edu.co

Abstract:

This article aims to show a Learning Object (LO) built from a pedagogical and computer-based approach. The findings are directly obtained from the literature consulted, allowing to design learning objects based on constructivism, complying with the established indicators for the creation of LO, since some educational elements are only constructed from the point of view of computer science. Thus, the objective of the paper is to raise awareness among interested readers about the good use of information technology for the development of LO, in order to address and mitigate the difficulty of learning Differential Calculus, since it is still taught under a behaviorist and mechanistic approach generating desertion in diverse academic programs and in particular in engineering. Finally, the conclusions of the case are stated.

Key words

constructivism, teaching, mechanistic, learning objects.

Resumen

Este artículo pretende mostrar un Objeto de Aprendizaje (OA) construido a partir de un enfoque pedagógico e informático; los hallazgos son directamente obtenidos de la literatura consultada, permitiendo diseñar objetos de aprendizaje basados en el constructivismo, cumpliendo con los indicadores establecidos para la creación de OA, puesto que algunos elementos educativos solo se construyen a partir del punto de vista informático. De este modo, el objetivo del escrito es concientizar al lector interesado sobre el buen uso de la informática para el desarrollo de OA, con el fin de abordar y mitigar la dificultad del aprendizaje del cálculo diferencial, puesto que aún se sigue enseñando bajo un enfoque conductista y mecanicista generando deserción en diversos programas académicos y en particular en ingeniería; por último, se enuncian las conclusiones del caso.

Palabras clave:

constructivismo, didáctica, mecanicista, objetos de aprendizaje

1. INTRODUCCIÓN

Hoy en día los avances informáticos han permitido el desarrollo de una sociedad cada vez más interconectada y dependiente de la tecnología; los progresos tecnológicos en educación han tenido un crecimiento importante durante los últimos años en la formación semipresencial y virtual, esto comprende básicamente el desarrollo de OA y SE permitiéndole a los profesores mejorar sus procesos de enseñanza - aprendizaje. Estos deben ser elaborados mediante el uso de modelos pedagógicos con el fin de establecer una relación amigable, didáctica e interactiva entre el estudiante y los elementos; sin embargo, existe la problemática que refiere a la dificultad del aprendizaje principalmente del cálculo diferencial en carreras de modalidad presencial, debido a dos aspectos:

El primero, es una costumbre del profesor de matemáticas, en especial de cálculo diferencial, al momento de impartir una sesión de clase lo hace de manera conceptual, lógica y estructurada, más afín al análisis matemático; esto lo ha llevado a adoptar metodologías basadas en clases magistrales usando el marcador y el tablero para explicar los conceptos, reglas y teoremas que rigen la ciencia. Sin duda, esto ha generado un gran impacto sobre los estudiantes creando en ellos experiencias negativas relacionadas con el cálculo y la matemática en general, ocasionando que gran parte de ellos desarrollen cierto tipo de aversión a la disciplina o, peor aún, a generar posibles deserciones sobre todo en carreras de ingeniería. Por tal motivo, una sesión de clase magistral sobre cálculo diferencial demuestra que aún hoy en día se basa en un modelo tradicional y conductista, generando que los estudiantes entiendan los conceptos a medias o repitan y memoricen procedimientos sin entender su esencia.

Otro aspecto no menos importante es la ausencia de los recursos didácticos así como de herramientas informáticas implementadas en el aula, dicha ausencia de recursos convierte las clases de matemáticas en un “objeto” repetitivo, aburrido y de difícil entendimiento

¹; por ello, la problemática en cuestión ha sido objeto de investigaciones en educación concentrándose en fortalecer la didáctica en la enseñanza de la matemática, con el fin de desarrollar estrategias metodológicas, que pretenden solventar la dificultad del aprendizaje de esta ciencia. Sin embargo, aún existe una tímida participación de las tecnologías informáticas como un apoyo didáctico en las clases de matemáticas en modalidad presencial.

Siendo así, el objetivo del presente artículo es concientizar al lector interesado sobre la importancia y el uso adecuado de la informática para la construcción de OA que puedan ser implementados en la enseñanza del cálculo diferencial, ya que esto permitirá presentar los contenidos de formas más amigables para el estudiante contribuyendo significativamente a la didáctica; a su vez, se presenta solo el diseño de un OA orientado a la enseñanza del concepto de la derivada simplemente para evidenciar cómo puede usarse la informática con fines educativos.

2. MATERIALES Y MÉTODOS

La dificultad del aprendizaje en cálculo diferencial es estudiada bajo dos enfoques, el enfoque pedagógico y el enfoque informático; en el primero se realiza una breve descripción del modelo pedagógico conocido como constructivismo, mientras que en el segundo se busca presentar un OA elaborado por los autores del artículo a partir de la teoría consultada para su diseño.

2.1. El enfoque pedagógico

El entendimiento de las matemáticas es de vital importancia en carreras de ingeniería, particularmente en ingeniería electrónica; sus contenidos son en su gran mayoría netamente abstractos, donde las matemáticas y la física quizá se convierten en el eje central de la profesión, debido a que todos los argumentos son científicos y por lo tanto, se estructuran mediante un lenguaje matemático que ayuda a establecer definiciones y conceptos originados a través del estudio de la electrónica. Al ser la electrónica una rama de la física, se hace evidente que el estudio del concepto físico también sea un elemento a tener en cuenta en la carrera; dado esto, es conveniente considerar que el cálculo en general permite entender y comprender los fenómenos que ocurren en los circuitos electrónicos, por esta razón, los estudiantes de la disciplina deben tener una sólida formación en matemáticas desde el inicio de su carrera, es decir, del cálculo diferencial, con el fin de evitar la deserción [1].

Desafortunadamente, la falta de entendimiento del cálculo ocasiona, en buena medida, un aumento en el índice de deserción debido a que los estudiantes abandonan su carrera por causa de las falencias presentadas cuando cursan cálculo diferencial. A veces esto ocurre por la forma tradicional que tiene el maestro de presentar los contenidos de la asignatura, ya que lo hace adoptando una configuración magistral. Contrera afirma: “La configuración magistral, corresponde a la manera tradicional o clásica de enseñar matemáticas, basada en la presentación de los contenidos que esencialmente constituyen ejemplos, seguida de ejercicios de práctica o repetición de los procedimientos recién presentados”. Dicha configuración también suele ser conocida como mecanicista y los aspectos que la caracterizan son mencionados en [2], entre ellos se resaltan: la lista de problemas descontextualizados, las presentaciones defectuosas del contenido matemático, manipulación mecánica de los símbolos y procedimientos, etc.

Además, la falta de conocimiento de los procedimientos algebraicos, como es el caso de factorizar, racionalizar y de las propiedades básicas de los exponentes que son necesarios para reducir, simplificar, despejar, entre otros, señala una evidente falencia que afecta el dominio de los conceptos del cálculo diferencial, “Es por eso que el proceso de enseñanza - aprendizaje de la matemática constituye hoy en día un tema de interés mundial que, con diferentes matices, enfoques y concepciones, se estudia e investiga dada la insatisfacción generalizada que existe sobre el nivel de uso y manejo de la matemática en el desarrollo y dinámica del proceso de los profesionales, en particular de los ingenieros. De aquí que el mejoramiento de la calidad en su proceso de enseñanza - aprendizaje sea una aspiración generalizada”. [3].

Justamente en la enseñanza del cálculo diferencial se verifica dicha insatisfacción en los procesos de aprendizaje, puesto que hay ausencia de los recursos didácticos por parte del maestro, debilitando así todo el ejercicio educativo; en tal caso, el maestro aplica un modelo asociado a la escuela tradicional comúnmente llamado conductismo, donde se deja de lado los intereses propios del estudiante, sintiéndose impedido de recrear sus propias ideas y perdiendo con gran facilidad el interés por el aprendizaje de la ciencia.

A nivel epistemológico, en la escuela tradicional se desarrolla el modelo pedagógico heteroestructurante, mediante el cual el estudiante es considerado como una persona oscura, apagada y sin luz²[4]. En este modelo, los procesos de enseñanza - aprendizaje son bastante rígidos y se fundamentan en la disciplina, la repetitividad y la memorización de los conceptos y procedimientos impartidos por el maestro en una sesión de clase.

Hoy en día, fácilmente esto puede apreciarse en la clase de un profesor de cálculo diferencial, puesto que su metodología se basa en la escuela tradicional; comúnmente, el docente de matemáticas tiene como estrategia didáctica el uso y dominio del tablero, herramienta que le permite explicar los conceptos y teoremas pertinentes a alguna sesión de clase, donde los ejercicios a resolver por parte del estudiante se convierte en una estrategia conductista, ya que él se ve obligado a memorizar y mecanizar cada uno de los conceptos y procedimientos impartidos por su maestro [2].

Con el fin de contradecir la tesis anterior, ha de sugerirse dos posturas:

Por un lado, Becerra plantea que “Otro hecho no menos importante, digno de reportarse, es que la matemática, y en particular el cálculo, ha sido presentada a los estudiantes como un sistema conceptual lógico y estructurado, más acorde con el análisis matemático, aunque la matemática en su esencia es eso. Lo anterior no amerita para que deba ser presentada de esta manera, donde los estudiantes se ven impedidos de recrear ciertas ideas que están en el corazón de ella, dejando así muy poca participación de hacer matemáticas descubriendo, haciendo conjeturas, probando dichas conjeturas” [1].

Por otro lado, [3] plantea que “Este proceso de enseñanza del cálculo infinitesimal, en el contexto de la educación superior, constituye un proceso de naturaleza holística, consciente y dialéctica, en el que se establecen complejas relaciones que se dan en la actividad y en la comunicación de los sujetos implicados y donde el alumno, a partir de las cualidades que lo tipifican en la educación superior; se instruye, se educa y se desarrolla, esto es, se transforma a través de la integración de actividades de carácter académico, investigativo y laboral” [3].

Esto implica que, aunque el cálculo diferencial es un lenguaje simbólico, estructurado y lógico, afín al análisis matemático, claramente las dos posturas anteriormente citadas evidencian que no necesariamente debe enseñarse de tal forma, ya que esto pertenece a un modelo conductista, donde al estudiante prácticamente se le obliga a mecanizar cada uno de los conceptos y procedimientos implícitos en el estudio de la asignatura, más que el propio entendimiento de la misma.

Así, puede observarse que a pesar de que los estudiantes aprueben los cursos de cálculo, lo que en realidad están aprendiendo son solo rutinas, como es el caso de saber derivar, pero no aprenden lo fundamental, siendo esto las ideas que constituyen y construyen la esencia del maravilloso cálculo diferencial [1].

De este modo, y con base en las posturas citadas anteriormente, lo que debe establecerse con el fin de mejorar la calidad del proceso de enseñanza - aprendizaje en educación matemática, y particularmente al impartir la asignatura cálculo diferencial, es la adopción de un modelo pedagógico que permita recrear, descubrir, elaborar, investigar y probar las relaciones o conjeturas que el estudiante establezca a partir de dichas acciones, para que finalmente entienda el lenguaje de las matemáticas, así como su esencia, esto a su vez se logra con una comunicación asertiva entre el estudiante y su maestro. Debe ser un modelo que abarque un proceso de naturaleza holística puesto que “Su carácter holístico se presenta en su naturaleza totalizadora, porque cada una de las partes que forman parte del proceso, como objeto de estudio, está en constante interacción con las restantes, lo que hace que en cada una de estas se reflejen las cualidades del objeto como un todo, a la vez que en el todo se refleja el significado de cada una de las partes” [5].

En ese orden de ideas, el modelo pedagógico que dota al estudiante de una total libertad para explotar, reflexionar, indagar, recrear y actuar en el aprendizaje del cálculo diferencial, pertenece a las corrientes constructivistas, conformada por el modelo pedagógico autoestructurante. En él, el estudiante se encuentra en la capacidad de explorar lo que conoce sobre alguna realidad, creando esquemas que le permitan establecer una representación, una forma del mundo, generando así sus propias construcciones de lo que para él es la realidad. De esta manera, se concuerda con [4] al decir que “Los seres humanos construimos nuestras representaciones del mundo real y ellas, en consecuencia, no son copias de lo real, sino construcciones personales” [4].

En un modelo constructivista el estudiante interactúa en un grupo donde también está inmerso el maestro de forma análoga, él está envuelto en un espiral simétrico cuyos anillos siempre retornan al núcleo del mismo, este último es asociado directamente al estudiante; por esta razón, el maestro se convierte en un mediador entre el conocimiento y su estudiante, de esta manera mantiene la simetría de los anillos en la espiral formada por la interacción, estableciendo así una sociedad de conocimiento basado en [6]. Así que “desde el punto de vista constructivista los esquemas lógico-matemáticos básicos son abstraídos de la coordinación de la acción (reunir, sustraer, incluir, seriar, realizar conjuntos, correspondencias, etc.), y posteriormente, construidos doblemente en términos cada vez más abstractos, y de nuevo son aplicados a la organización lógico-matemática de la experiencia” [7].

En este caso, la construcción de esquemas originados del pensar, que en coordinación armoniosa con los movimientos del cuerpo permiten llegar a la acción, rigiéndose esta en varios procedimientos matemáticos, da origen a una realidad capaz de ser argumentada científicamente y de forma investigativa. Esto, sin duda, conlleva al estudiante a ser constructor de su propio conocimiento porque emplea su reflexión matemática como ejercicio para complementar su saber, donde ella, así como la retroalimentación, fortalecerán el conocimiento adquirido. En esta etapa es importante la intervención del maestro puesto que es el responsable de guiar a su estudiante durante todo el proceso formativo, así la retroalimentación hará énfasis en los “términos cada vez más abstractos” que adquiera el estudiante y que lo conducirá a la “organización lógico-matemática de la experiencia”.

En ese orden de ideas, la experiencia será el producto originado a partir de todos los esquemas construidos por el estudiante, dado en función del tiempo transcurrido durante el proceso formativo, en este caso todas las experiencias son positivas.

Por lo tanto, si un estudiante de cálculo diferencial adhiere en su interior esta ciencia como una realidad, entonces construirá esquemas que le permitirán encontrar relaciones que pueden ser argumentadas o refutadas conforme avanza y profundiza en el estudio de la ciencia. Este escenario le facilitará el crear sus propias construcciones de esa realidad, convirtiéndolo en un actor crítico de la ciencia desde su saber. Mediante la creación de esquemas, está claro que el estudiante será capaz de establecer una filosofía generándose preguntas que luego responderá y que, además, verificará probando sus hipótesis o refutándolas, será un ser consciente de su saber y del mundo que lo rodea, será el actor principal de su propio conocimiento construyendo el saber propio a partir de una filosofía matemática que, a su vez, le permitirá progresar significativamente en el proceso de aprendizaje.

Si bien se habló del constructivismo en este artículo como el enfoque pedagógico, es hora de abordar el enfoque informático.

2.2 El enfoque informático

Uno de los elementos desarrollados en beneficio de la educación es la creación de los OA y el SE, frecuentemente, son un soporte de acompañamiento en el proceso de enseñanza - aprendizaje en la educación semipresencial o virtual.

Se diseña un OA para enseñar el concepto de la derivada a partir del punto de vista geométrico y físico, este último visto como la velocidad y aceleración de una partícula; dicho objeto es elaborado con el fin de dar a conocer al lector cómo puede aplicarse la informática para desarrollar OA con fines educativos³, se escoge el concepto de la derivada ya que comúnmente el estudiante sabe derivar pero no conoce su significado.

El OA fue desarrollado con la herramienta Adobe Flash CS6 e incluye lenguaje de programación de animación ActionScritp 2.0 con el fin de entrelazar los fotogramas. La presentación del objeto se encuentra como un archivo ejecutable (con extensión .exe), apoyado con la herramienta Hotpotatoes versión 6.0 para la evaluación del tema visto; sin embargo, antes de ilustrar el objeto en sí, deben ser presentados algunos conceptos y definiciones con el fin de entender cómo funcionan los OA de forma más detallada y especifica.

2.3 Objetos de Aprendizaje (OA)

Esta tecnología surge en el año 1994 debido a la necesidad de compartir contenidos con fines educativos; algunos de los autores que incursionaron en su estudio y desarrollo fueron: Wiley, Polsani, el LTSC (Learning Technology Standards Committee), López, Downes, McGreal, Iriarte, Cabrera y Wayne Hodgins, este último incorpora el concepto de objeto de aprendizaje [8] y [9].

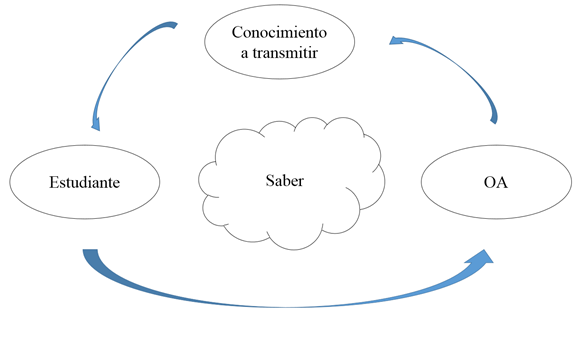
Un OA es un objeto virtual conformado por diversos elementos multimedia que sirve como recurso educativo para apoyar el proceso de enseñanza aprendizaje, es un elemento que contribuye a la didáctica para mejorar los contextos relacionados a la educación virtual y semipresencial. Así, un OA se convierte en la interfaz digital educativa entre humano e información, la cual establece una relación directa entre el estudiante con el conocimiento que se desea transmitir para así generar el saber de dicho conocimiento. Esto puede apreciarse en la Figura 1

Figura 1. OA como interfaz entre el conocimiento y el estudiante.

Fuente: elaboración propia.

En ese sentido, un OA debe cumplir ciertos requisitos con el fin de generar un impacto social en la comunidad educativa, dichos requisitos son: reusabilidad, granularidad, interoperabilidad, accesibilidad y durabilidad [9]; estos son definidos a continuación⁴:

• Reusabilidad: debe ser capaz de usarse en contextos y propósitos educativos diferentes para adaptarse y combinarse dentro de nuevas secuencias formativas [9].
• Granularidad: es el “resultado de agregar diversos componentes como; videos, audio, imagen, simulación, etc. Mientras más elementos independientes tiene un objeto mayor nivel de granularidad posee” [9].
• Interoperabilidad: es la capacidad que tiene el objeto para integrarse en diferentes plataformas de software y hardware [9].
• Accesibilidad: es la facilidad que tiene el objeto para ser identificado, buscado y encontrado, gracias al correspondiente etiquetado a través de diferentes descriptores (metadatos) que permitan la catalogación y almacenamiento en repositorios [9].
• Durabilidad: el OA debe permanecer intacto a las actualizaciones de software y hardware, para que, en caso de requerir cambios en los contenidos, no se necesiten grandes esfuerzos [9].

Los OA también son conocidos como Objetos Virtuales de Aprendizaje (OVA) ya que según el MEN citado en [10] un objeto virtual de aprendizaje (OVA), es un material estructurado de forma significativa, digital, dirigido al aprendizaje, que puede ser distribuido y consultado a través de internet; además, un OVA debe contar metadatos (fichas de registro) consistentes en listado de atributos que describen el uso del objeto y permiten su catalogación e intercambio. Bajo estos conceptos el Ministerio consideró la siguiente tipología de objetos: simuladores, cursos, multimedia, tutoriales, animaciones, videos, documentos interactivos y colecciones de imágenes estáticas.

2.4 Ilustración del OA

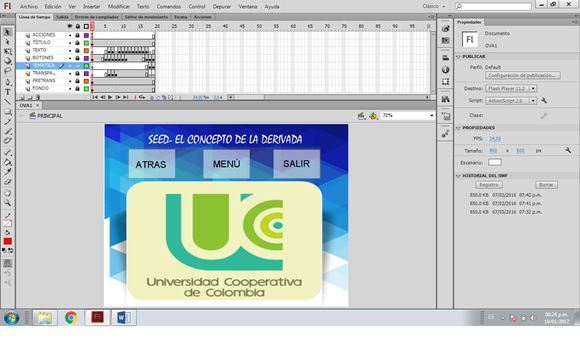
Como se dijo antes, el objeto fue desarrollado con la herramienta Adobe Flash CS6, su estructura comprende el lenguaje de programación ActionScritp 2.0, se usó la herramienta Hotpotatoes 6.0 como una alternativa de evaluación. Dicho OA fue creado con el ánimo de ilustrar el empleo de las herramientas informáticas antes mencionadas, así el lector podrá aplicar las mismas para elaborar los suyos. En la Figura 2 se ilustra la construcción del objeto.

Figura 2. Pantalla de Inicio de OA.

Fuente: Imagen de fondo: cortesía de la Universidad Cooperativa de Colombia.[12].

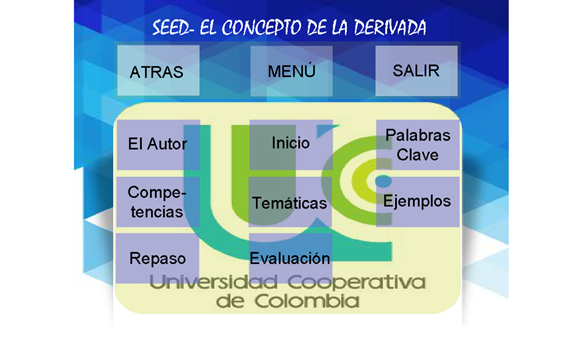
En su estructura, el objeto está compuesto por el logo de la Universidad Cooperativa de Colombia, que constituye el fondo de pantalla, al costado superior se encuentra el título del objeto⁵ y tres opciones que le permiten al estudiante navegar en él; la opción “menú” despliega todo el contenido del objeto con el fin de que el estudiante decida por dónde quiere comenzar, la opción “atrás” permite regresar a la pantalla anterior, finalmente, la opción “salir” le permite al estudiante salir de toda la presentación. El OA fue pensado con el fin de crear un escenario similar al de la presentación de navegación de los smartphone, puesto que se considera un ambiente familiar y amigable para los jóvenes de hoy en día. Al oprimir menú, las opciones que despliega son las que se muestran en la Figura 3.

Figura 3. Opciones del botón MENÚ.

Fuente: elaboración propia.

Cada una de las funciones desplegadas por la opción “menú” se explican a continuación:

• El autor: la función de esta opción es suministrar información básica del autor del OA tal como el nombre y el tipo de formación académica.
• Inicio: es una opción creada con fin de motivar al estudiante con un mensaje de bienvenida; además, tiene como propósito avisarle sobre los temas que se van a presentar dentro del objeto.
• Palabras clave: contiene algunas definiciones de conceptos clave presentados durante el desarrollo del contenido en sí.
• Competencias: esta opción le permite al estudiante conocer el propósito de la herramienta educativa.
• Temáticas: despliega todo el contenido de los temas tratados en el OA.
• Ejemplos: proporciona algunos ejemplos desarrollados paso a paso por el autor del OA.
• Repaso: pretende aclarar y concientizar al estudiante de los contenidos de OA.
• Evaluación: efectúa las pruebas de conocimiento pertinentes al caso.

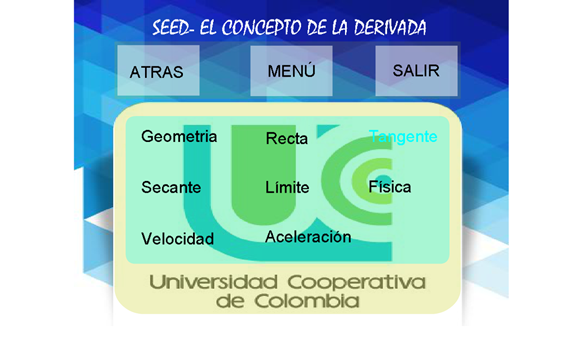
Por ejemplo, al oprimir la opción “palabras clave” se despliega la pantalla que se muestra en la Figura 4

Figura 4. Ventana que corresponde al botón palabras clave.

Fuente: elaboración propia.

Se observa que la palabra “tangente” se encuentra subrayada en color verde claro, esto indica que el estudiante se ha situado en dicha palabra; si realiza un clic sobre ella, la acción muestra la definición de la tangente, tal como se muestra en la Figura 5.

Figura 5. Producto de la acción clic sobre la palabra tangente.

Fuente: elaboración propia.

Los conceptos que definen cada una de las palabras claves son claros y concisos con el fin de no aburrir ni confundir al estudiante, todos los botones contienen animaciones y sonidos cuyo propósito es mantenerlo en un entorno amable, generando una didáctica en su proceso de aprendizaje.

En la Figura 6 se muestra la elaboración de las temáticas

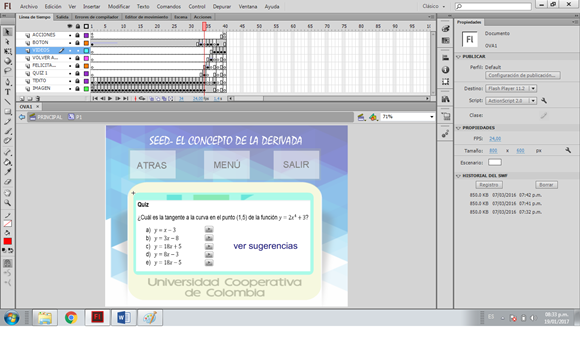
Figura 6. Diseño del Quiz.

Fuente: elaboración propia.

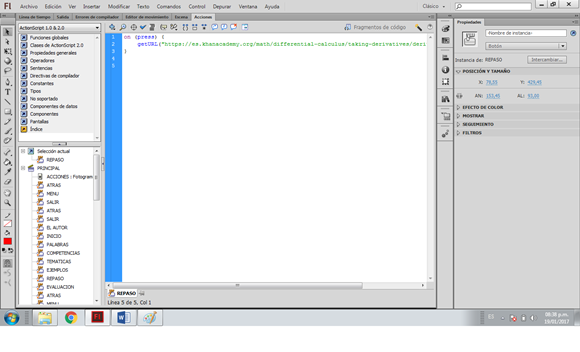
La opción “repaso” proporciona al estudiante el acceso a recursos académicos sobre el concepto de la derivada encontrados en la página de internet Khan Academy [13], los contenidos de dicha página son videos completamente en español elaborados por profesores de diferentes partes del mundo. El código que permite acceder a la página está inmerso en la opción puede apreciarse en la Figura 7.

Figura 7. Programación del botón repaso.

Fuente: elaboración propia.

Del mismo modo se ha programado la opción “evaluación”, puesto que debe exportar los diseños elaborados en Hotpotatoes 6.0⁶, como un archivo HTML. La presentación de la evaluación es de la forma que se observa en la Figura 8.

Figura 8. Evaluación propuesta por el OA, se elaboró con la herramienta educativa HotPotatoes 6.0.

Aunque la programación de los botoneslas opciones “repaso” y “evaluación” es idéntica a nivel de código, la diferencia radica en la conexión a internet, puesto que para acceder a los recursos de la página Khan Academy es evidente que el estudiante debe estar conectado a la red; sin embargo, para acceder a la evaluación del OA no es necesario dicha conexión porque el documento HTML generado por Hot potatoes 6.0 pertenece a los archivos que conforman toda la estructura del objeto.

2.5 Evaluación del OA

Para evaluar la pertinencia del objeto diseñado deben tenerse en cuenta los indicadores mencionados al comienzo del enfoque informático, ellos son: la reusabilidad, granularidad, interoperabilidad, accesibilidad y la durabilidad; de esta manera, se analizará el OA basado en cada uno de los indicadores propuestos.

• Reusabilidad: se considera que el objeto cumple con este indicador, debido a que puede ser usado como apoyo didáctico en el proceso de enseñanza – aprendizaje de la asignatura de cálculo diferencial en diferentes ramas del conocimiento en la universidad, he incluso en otros espacios educativos como lo es el último año de formación secundaria.
• Granularidad: el nivel de granularidad es aceptable, pero debe mejorarse, esto implica involucrar en la estructura del objeto muchos más recursos digitales como simuladores, juegos interactivos, entrenadores, entre otros.
• Interoperabilidad: los archivos generados en Flash pueden ser incorporados en plataformas virtuales de aprendizaje como Moodle [14]; además, el objeto se generó como un archivo ejecutable con el fin de facilitar flexibilidad e intercambio entre computadoras y dispositivos de almacenamiento, convirtiéndolo en un elemento portable y accesible, también puede ser exportado para sistemas operativos debido a la disponibilidad de las herramientas que ofrece Adobe Flash CS6 inmersas dentro del software [15].⁷
• Accesibilidad: aún el objeto no pertenece a ninguna base de datos ni está almacenado en repositorios, tampoco cuenta con algún logo o identificación que permita cierto tipo de catalogación, por tal motivo el objeto no cumple con este indicador [15].
• Durabilidad: por el momento, al ser el OA elaborado en Adobe Flash CS6 es posible realizar cambios y actualizaciones en su contenido, mejorando así el índice de granularidad; así mismo, mientras Flash continúe en vigencia el objeto puede ser fácilmente actualizable [16].

Otro indicador que no se ha descrito pero que es resulta evidente, es el hecho, de que sea educativo, esto implica diseñar un objeto con un enfoque pedagógico que, para el caso, será el constructivismo. Mediante este OA, el estudiante explora, se instruye y se educa bajo los lineamientos de los modelos auto – estructurantes ya que él observa, analiza, diseña y construye el saber a partir de esquemas mentales que le permiten a su vez recrear el conocimiento con base en la información que se muestra en el objeto, convirtiéndolo en el autor principal de todo el proceso de enseñanza – aprendizaje.

3. RECOMENDACIONES

Las recomendaciones serán orientadas con el fin de mejorar la interactividad entre el OA y el estudiante, es decir:

• Debe mejorarse significativamente el índice de granularidad, ello conlleva a la elaboración de juegos, videos, entrenadores, entre otros; así mismo es recomendable adaptar el uso del software Derive, creando un sistema embebido que le permita al estudiante, no solo usar el lápiz y papel para la elaboración de los ejercicios, sino que, a su vez, disponga de una herramienta que le permita comprobar sus resultados.
• Por otro lado, es importante que el OA se encuentre en repositorios o bases de datos de fácil acceso para la comunidad educativa, aunque no necesariamente debe ser indispensable.
• El OA debe someterse a una evaluación periódica donde el jurado esté conformado por expertos en informática y pedagogía con el fin de mejorar la calidad del producto, garantizando así la permanencia del mismo en los diversos entornos educativos, es decir, garantizando la reusabilidad y durabilidad del OA.
• Debe recordarse que al ser el OA una herramienta educativa, entonces éste tiene la misión de contribuir al mejoramiento de la didáctica del maestro durante todo el proceso de enseñanza aprendizaje.

4. RESULTADOS

Después de analizar los dos enfoques presentados en este artículo, los hallazgos obtenidos son los siguientes:

• De acuerdo con la pedagogía corriente del constructivismo, el OA, además de despertar el interés del estudiante, debe ser capaz de involucrarlo directamente sobre las temáticas del objeto, despertando su curiosidad, en afán de investigar más sobre los contenidos.
• Los contenidos de objeto deben ser presentados de forma amigable, de tal manera que el estudiante se sienta motivado para interactuar con este tipo de herramientas educativas
• La teoría del constructivismo indica que, en cada sesión de clase, ésta debe iniciarse con una pregunta; sin embargo, como el OA es un objeto en sí, por sí mismo no puede generar constructivismo, así que es necesario disponer de pedagogos expertos en el tema para su elaboración, con el fin de crear OA con un enfoque pedagógico constructivista. Así, que se considera conveniente presentar primero algo de contenido y después de ello abordar con una pregunta, tal conducta presenta un marco de referencia para el estudiante mediante el cual él puede empezar a crear sus propios esquemas.
• El OA también debe ser usado en grupo, con el fin de que los miembros que se encuentren más adelantados cooperen con el aprendizaje de sus demás compañeros, es decir, para generar un aprendizaje colaborativo
• Antes de desarrollar un objeto debe identificarse la necesidad que se pretende cubrir, así como al tipo de población que va dirigido⁸. Generalmente, los OA, así como los SE terminan siendo producto tecnológico de una investigación terminada.
• El objeto debe tener un diseño pertinente para el tipo de población al cual va dirigido, donde los colores, los sonidos, los botones, las animaciones, los contenidos, entre otros, dependen de que el estudiante se interese o no por el mismo
• La retroalimentación del maestro frente al estudiante es vital, puesto que él es el encargado de guiarlo, es en realidad quien se encarga de orientar el objeto hacia un enfoque constructivista, aunque este último debe ser diseñado y construido con sus fundamentos.
• Todos los objetos desarrollados con fines educativos deben ser sometidos a juicio por expertos en educación, informática, diseño, entre otros, para garantizar el impacto social que tendrá en el contexto educativo.
• Todos los objetos deben cumplir con los indicadores mencionados anteriormente en el enfoque informático de este artículo

5. DISCUSIÓN

Sin duda, los OA deben tener un enfoque pedagógico constructivista, en vía de mejorar los contenidos presentados habitualmente en el aula, ya que en la mayoría de casos el método de enseñanza se basa en la escuela tradicional, cuyas sesiones de clase son magistrales y mecanicistas. De este modo, los objetos tienen que regirse a una serie de lineamientos hallados en las diversas investigaciones de orden científico interesadas en el tema, es decir, que este recurso digital también debe ser estandarizado.

Por esta razón, se considera que los objetos desarrollados con fines educativos, y en especial para la enseñanza de la matemática, deben someterse a un juicio de expertos en pedagogía, informática, diseño, entre otros, para que el mismo genere un impacto social en el ámbito educativo.

Con el ánimo de discutir los hallazgos antes presentados, se han elegido cinco aspectos importantes de ellos. y son los siguientes:

• Los recursos multimedia: cuando estos son coherentemente utilizados en educación matemática, la granularidad del objeto tendrá un impacto considerablemente positivo sobre el estudiante, puesto que en dicho objeto él encontrará diversos recursos, invitándolo al deseo para la exploración de los contenidos. Por esta razón, cada elemento asociado al OA deber ser cuidadosamente elaborado, involucrando estratégicamente en su estructura, animaciones, sonidos, videos, imágenes, entre otros
• Los contenidos: se sugiere que, al momento de presentar los contenidos en el objeto, sea hecho mediante un enfoque constructivista, así, por ejemplo, la enseñanza del cálculo diferencial se convierte en una sesión más amigable e interactiva.
• La interactividad: este aspecto es muy importante, y debe ser abordado a partir del enfoque pedagógico e informático, pues debe ser función de la interactividad incentivar al estudiante en la exploración interminable de los contenidos, especialmente de las temáticas, los ejemplos y la evaluación.
• La motivación: los aspectos anteriormente mencionados conllevan a la motivación del estudiante, esto es muy importante en el aprendizaje del cálculo en general.
• Aprendizaje cooperativo: por último, dicho aprendizaje debe ser el resultado del constructivismo contenido en un objeto digital; el maestro también deberá pertenecer a tal movimiento, creando espacios de reflexión y retroalimentación, ya que finalmente depende de él, que sus estudiantes sean o no el eje central de todo el proceso de enseñanza – aprendizaje.

En este orden de ideas, se espera que el lector sea consciente de que el uso de la tecnología informática en el ámbito educativo, no solo requiere de sólidos conocimientos de herramientas informáticas, sino que, además, requiere de gran conocimiento pedagógico, así como de la ayuda y asesoría de varios expertos. Para la construcción del OA mostrado en el presente artículo fue utilizado el software Adobe Flash CS6, ya que ofrece bastantes recursos que contribuyen a la didáctica e invita a la interactividad; por tal motivo, Flash es comúnmente usado para el desarrollo de juegos, caricaturas animadas, animaciones web, entre otros, considerando que puede llegar a ser una poderosa herramienta en el beneficio de la educación.

6. CONCLUSIONES

El desarrollo del OA descrito permite concientizar al maestro sobre el uso de las herramientas informáticas, generando innovaciones tecnológicas en el aula y diseñadas pedagógicamente para contribuir a mejorar la didáctica en los contextos educativos en la enseñanza de la derivada; de esta manera se abandona la costumbre tradicional de enseñar el cálculo diferencial a través de métodos conductistas basados sesiones magistrales.

Los OA toman bastante fuerza en los procesos formativos semipresenciales o virtuales, pero poca relevancia en la formación presencial; por tal motivo, se invita al maestro de cálculo diferencial para que sea partícipe en el uso y desarrollo de dichos objetos, con el ánimo de mejorar la didáctica de la matemática y los procesos de enseñanza – aprendizaje en esta ciencia.

¹Se escribe objeto entre comillas con el fin de manifestar cierto desacuerdo con su significado al momento de hablar de matemáticas, puesto que, al debatir sobre ella, debe llegarse a la conclusión de que esta ciencia es una filosofía que ha perdurado hasta nuestros días, debido a que permite responder al por qué de los eventos y fenómenos que se dan en la naturaleza.

²En realidad, Julián de Zubiría se refiere a la escuela tradicional donde los estudiantes son llamados “alumnos”, sin embargo, se considera que esta visión es errónea debido a que el estudiante jamás será una persona apagada y sin luz. Solo hay que descubrir sus habilidades y esta función es responsabilidad del maestro.

³En la primera etapa de la investigación aún en ejercicio se ha desarrollado el OA con el ánimo de ilustrar la aplicación de la informática en la educación. Posteriormente, los autores procederán a efectuar las pruebas de campo y analizar los resultados obtenidos.

⁴Por favor revisar detalladamente el documento “Objetos de Aprendizaje. Características y Repositorios” especialmente las páginas 2 y 3 del mismo [11].

⁵SEED (Software Educativo para Enseñar a Derivar) es un SE en proceso de elaboración por parte del autor del presente artículo.

⁶Se elaboraron cuatro de los cinco modelos de evaluación propuestos por la herramienta, ellos son: JCloze, JCross, JQuiz y JMix. Con el fin de que aparezcan las evaluaciones en una sola página web se usó la herramienta The Matcher.

⁷Para hacerlo simplemente hay que abrir el objeto con extensión de flash (.fla) que se ha desarrollado, luego ir a archivo, configuración de publicación y elegir Proyector de MAC.

⁸El OA que soporta este artículo tiene un enfoque universitario y está pensado para estudiantes que inician su carrera en la Universidad en jornada nocturna.

REFERENCIAS

[1] E. Becerra y A. Medina, “Aplicación de un diseño modular para la enseñanza del cálculo diferencial” Ingeniere, vol 22, no 4, pp. 576- 586, octubre 2014.

[2] T. Florida, R. Ramírez “Formación matemática en la educación secundaria desde la perspectiva de los estudiantes que inician estudios en la Universidad de Costa Rica” Paradigma, vol 31, no. 2, pp. 129-154, 2014.

[3] J. M. Obregon, J. R. Ventura, J. R. Díaz, A. Estrabao and M. G. Valle, “El proceso de enseñanza - aprendizaje del cálculo infinitesimal: una caracterización epistemológica” Pedagogía niversitaria, vol. 22, no. 4, pp. 1-12, 2012

[4] J. De Zubiria, “Los modelos pedagógicos hacia una pedagogía díalogante”, Bogotá: Magisterio, 2006

[5] U. Mestre y P. R. Valdés, “Modelo de enseñanza - aprendizaje con tecnología multimedia para la modalidad de estudio semipresencial” Praxis Educativa, vol. 16, no. 14, pp. 35-41, 2011

[6] B. Amy y A. All, “Constructivism Theory Analysis And Application to Curricula”. Nursing Education Perspectives, vol. 31, no. 2, pp. 89-92, 2010.

[7] C. A. Londoño, “Avatares del Constructivismo: De KANT a PIAGET” Rhela, vol. 10, pp. 73- 96, 2008.

[8] D. M. Colomé, V. Estrada y J. P. Febls, “Ambiente tecnológico para la creación de objetos de aprendizaje en apoyo al proceso docente de las universidades cubanas” ACIMED, pp. 116-129, 2012.

[9] R. Cañizares, P. Feble y V. Estrada, “Los Objetos de aprendizaje, una tecnología necesaria para las instituciones de la educación superior en Cuba” ACIMED, pp. 102-115, 2012.

[10] E. Parra, “Propuesta de metodología de desarrollo de sofware para objetos virtuales de aprendiizaje - MESOVA” Revista Virtual Universidad Catolica del Norte, no 34, pp. 113-137, 2011.

[11] L. García, “Objetos de aprendizaje. Características y repositorio.” Editorial del BENED, 2005. [En línea] Disponible en: http://www. tecnoeducativos.com/descargas/objetos_virtuales_ deparedizaje.pdf

[12] UCC, “Universidad Cooperativa de Colombia”. [En línea] Disponible en: http://www.ucc.edu. co/Paginas/inicio.aspx

[13] KHANACADEMY, “Introducción a las derivadas” [En línea] Disponible en: https://es.khanacademy. org/math/differential-calculus/ taking-derivatives/derivative_intro

[14] Moodle, “Flash, s.f.” [En línea] Disponible en: https://docs.moodle.org/all/es/Flash

[15] La derivada, “Details, s.f.” [En línea] Disponible en: http://ova1final.weebly.com

[16] Adobe Systems Incorporated, “Adobe, s.f.” [En línea] Disponible en: http://www.adobe.com

Fuente: elaboración propia.