DOI:
https://doi.org/10.14483/2322939X.8016Publicado:
2014-12-19Número:
Vol. 11 Núm. 1 (2014)Sección:
Investigación y DesarrolloReconocimiento óptico de números escritos a mano usando funciones de base radial y sistema memético diferencial
Optical recognition of handwritten numbers using radial basis function and differential mimetic system
Palabras clave:
evolución diferencial, modelado difuso, algoritmo memético, reconocimiento óptico de números, redes neuronales de función de base radial (es).Palabras clave:
Differential evolution, Fuzzy modeling, mimetic algorithm, optical recognition of numbers, Radial Basis Function neural network (en).Descargas
Referencias
J. A. Navarro, “Sistemas de reconocimiento óptico de caracteres”, Revista del instituto tecnológico de informática, 9-11, 2009.
C. Sánchez, Reconocnimiento óptico de caracteres (OCR), Madrid, España: Universidad Carlos III, 2006.
Bang, Hwang, Recognition of unconstrained handwritten numerals by a radial basis function neural network classifier, Korea: Pohang University of Science and Technology, 1997.
UCI, University of California Irvine, 2010. Disponible en http://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
Haykin, Neural Networks: a comprehensive foundation, 1994, New York: Mc. Millan College publising company.
L. Wang, A course in fuzzy systems and control. Upper Saddle River, NJ: Prentice-Hall, 1996.
M. Melgarejo, Sintonización de sistemas difusos mediante un algoritmo memético adaptativo, en XVIII Congreso internacional de ingeniería eléctrica, electrónica, de sistemas y ramas afines, 2011.
M. Melgarejo, Sintonización de sistemas difusos utilizando evolución diferencial, en XVIII Congreso internacional de ingeniería eléctrica, electrónica, de sistemas y ramas afines, 2011.
L. Wang, J. Mendel, “Back‐ Propagation Fuzzy System As Nonlinear Dynamic System Identifiers”, IEEE International
Conference on Fuzzy Systems, 1992.
L. Hongmin, Y. Zhixi, Applying multiple agents to Fuzzy collaborative filtering. North University o China, 2, 2009.
H. Al Hamad, “Use an Efficient Neural Network to Improve the Arabic Handwriting Recognition”, in International Conference on Systems, Control, Signal Processing and Informatics, 2013.
Y. S. Hwang, Sung-Yang, “Recognition of Unconstrained Handwritten Numerals by a Radial Basis Function Neural
Network Classifier”, Pattern Recognition Letters, 657-664, 1997.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas
Descargas
RECONOCIMIENTO ÓPTICO DE NÚMEROS ESCRITOS A MANO USANDO FUNCIONES DE BASE RADIAL Y SISTEMA MEMÉTICO DIFERENCIAL
OPTICAL RECOGNITION OF HANDWRITTEN NUMBERS USING RADIAL BASIS FUNCTION AND DIFFERENTIAL MIMETIC SYSTEM
Fecha de recepción: febrero 2014
Fecha de aceptación: marzo 2014
Oscar Manuel Piragauta Gómez
Estudiante de Ingeniería Electrónica de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: ompiragautag@correo.udistrital.edu.co
Omar David Bello Santos
Estudiante de Ingeniería Electrónica de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: odbellos@correo.udistrital.edu.co
Bryan Montes Castañeda
Estudiante de Ingeniería Electrónica de la Universidad Distrital Francisco José de Caldas, Bogotá, Colombia. Contacto: bmontesc@correo.udistrital.edu.co
Resumen
El problema de reconocimiento óptico de números escritos a mano ha sido trabajado desde diferentes técnicas obteniendo buenos resultados. En el presente artículo se proponen sistemas difusos con algoritmos genéticos, más específicamente meméticos para realizar esta tarea. Los resultados obtenidos con este método son comparados con redes neuronales de aprendizaje semi-supervisado, donde fueron utilizadas redes con funciones de base radial (RBF). Al realizar la comparación es posible observar que este tipo de redes neuronales ofrecen ventajas en cuanto a tasas de error y tiempo de obtención del sistema de reconocimiento frente a los métodos basados en sistemas difusos.
Palabras Clave
evolución diferencial, modelado difuso, algoritmo memético, reconocimiento óptico de números, redes neuronales de función de base radial.
Abstract
Optical recognition of handwritten numbers was worked by different methods, with satisfactory results. In this paper, we propose fuzzy systems with genetic algorithms, specifically memetic, to do this task. Results with this method are compared with neuronal network of semi-supervised learning, where we was used networks with radial base functions (RBF). To make the comparison, is possible observed that this kind of neuronal network offers advantages regarding error rates and time-to-results of the recognition system, compared with methods based in fuzzy systems.
Keywords:
Differential evolution, Fuzzy modeling, mimetic algorithm, optical recognition of numbers, Radial Basis Function neural network
Introducción
El reconocimiento óptico de caracteres o OCR —por sus siglas en inglés, Optical Characters Recognition— es un proceso que tiene como objetivo digitalizar y reconocer los caracteres de un determinado alfabeto o simbología contenidos en diferentes fuentes de texto, como puede ser una hoja impresa por un procesador de palabras o texto escrito a mano por un humano, donde este último tiene el mayor nivel de dificultad para su reconocimiento por la diversa caligrafía de cada individuo; además de otros factores como el tamaño y la similitud en tres símbolos.
En la actualidad, el OCR es muy utilizado y estudiado para mejorar la calidad de varios servicios como el reconocimiento de textos manuscritos para su almacenamiento en forma de datos [1]. Uno de los problemas más importantes que enfrenta el reconocimiento óptico de caracteres es el de segmentación de los caracteres para su obtención uno a uno [2].
Todos los algoritmos OCR se basan en una serie de pautas que se deben seguir para lograr diferenciar texto. Existen cuatro etapas que son: 1) binarización, en ella se digitaliza y umbraliza los caracteres y se realiza su respectivo almacenamiento en una imagen binaría (blanco y negro). 2) Fragmentación o segmentación, este es el proceso más complicado y clave para el reconocimiento de los caracteres, aquí la imagen es segmentada carácter por carácter para poder trabajar con cada uno de ellos individualmente. 3) Reducción de los componentes, generalmente es usada para eliminar la información irrelevante que puede alterar el reconocimiento de los caracteres. 4) Comparación de caracteres, en esta etapa se comparan los caracteres obtenidos de los procesos anteriores con patrones definidos y conocidos para su reconocimiento; generalmente el resultado está dado por la mayor coincidencia con los patrones [2]. Esta última etapa será estudiada en el presente artículo mediante técnicas de inteligencia computacional con sistemas difusos y redes neuronales.
En el campo de la inteligencia computacional aplicada al reconocimiento de caracteres se puede encontrar una amplia gama de opciones, que en sí son propuestas aisladas y no proveen una comparación de las ventajas y diferencias de los métodos disponibles.
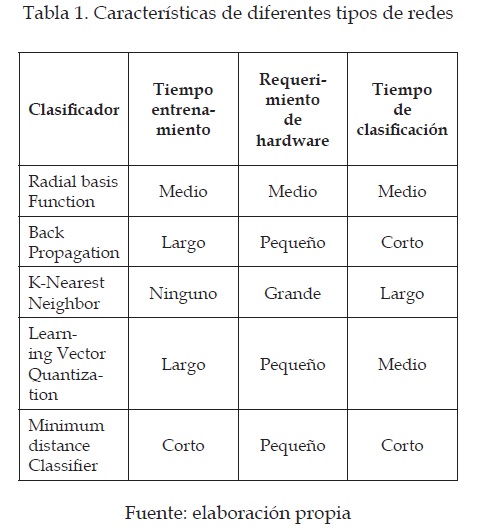
Las principales características de los métodos descritos, de los métodos de clasificación de patrones, como el reconocimiento de los números manuscritos, se pueden resumir en una tabla (ver tabla 1) [3].
Se entiende el requerimiento de hardware como la cantidad de memoria RAM usada por el computador. Tenemos entonces que RBF no tiene grandes requerimientos de hardware y permite un tiempo de entrenamiento corto; con lo que es posible sintonizar los parámetros del sistema para obtener los mejores resultados posibles sin tomar demasiado tiempo.
1. Metodología
En esta sección se presenta la base de datos utilizada para implementar el presente estudio. Los métodos de lógica difusa y de redes neuronales son también explicados en detalle sobre su implementación.
1.1. Base de datos
La base de datos utilizada para la identificación óptica de números hechos a mano se encuentra en el repositorios de la UCI [4], en ella ya está elaborada la etapa de binarización, fragmentación y reducción de información. Esta base datos fue realizada por 43 personas, donde cada una de ellas escribió más de un dígito
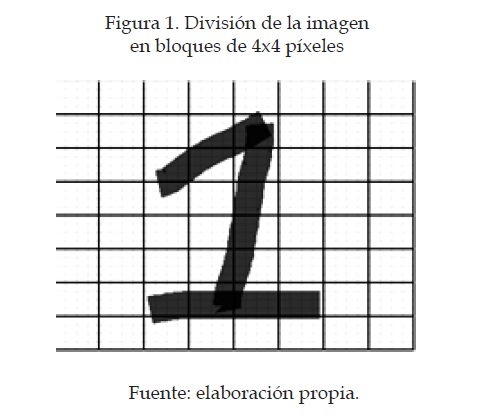
Los números escritos se segmentaron en mapas de 32x32 píxeles. Cada carácter se dividió en matrices de 4x4 píxeles, como se muestra en la figura 1, esto quiere decir que cada carácter tiene una línea de datos de 8x8 para un total de 64 datos, de los cuales cada uno tiene la información de un bloque de 4x4.
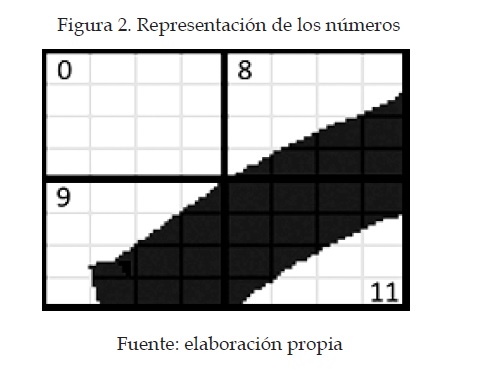
En cada dato de los 64 que contiene un carácter, se almacena la información de cuántos píxeles en los bloques de 4x4 tienen un nivel de brillo igual a cero —un nivel de brillo igual a cero equivale a una tonalidad oscura—, lo que quiere decir que el máximo valor para cada dato será 16 (figura 2).
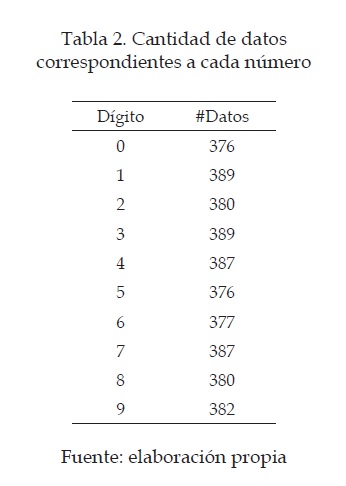
La cantidad de datos correspondientes a cada número se muestra en la tabla 2, en donde se tiene un total de 3823 datos de números del 0 al 9.
Al obtener la base de datos se realizó una normalización dividiendo cada valor de los datos entre el máximo valor, en este caso 16, lo que proporciona una base de datos más manejable y lista para trabajar con los algoritmos propuestos.Figura 3
De los 3823 datos se tomó el 70 % de la base de datos para el entrenamiento (2676 datos) y el 30 % restante para validación (1147 datos), lo que garantiza que el método no sea sobreentrenado [5].
1.2 Sistema Difuso Genético a partir de Algoritmo Evolutivo de Tercera Generación Memético (MA)
Para el reconocimiento de los números escritos a mano se consideró el uso de una primera metodología basada en la clasificación con un sistema difuso sintonizado con algoritmos genéticos entrenado con aprendizaje supervisado. A continuación se describen las partes que componen el reconocedor a partir de esta metodología.
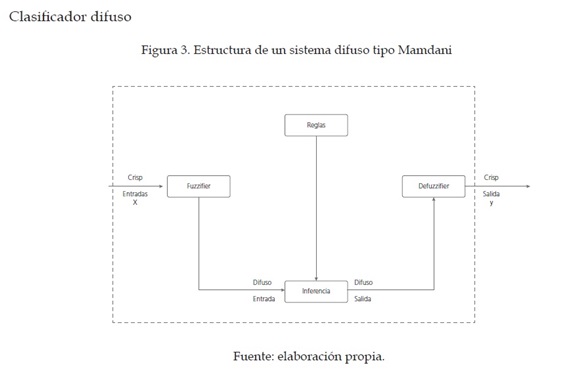
La clasificación de los caracteres está basada en un sistema de inferencia difuso en donde un conjunto de reglas lingüísticas son trasformadas en un mapeo no lineal, y de esta forma lograr un aproximador universal [6]. La configuración utilizada en el presente trabajo se conoce como de tipo Mamdani, ya que presenta en su estructura un fuzzificador, un mecanismo de inferencia difusa con su respectiva base de reglas difusas y un defuzzificador, como se muestra en la figura 3. La expresión matemática de un sistema de inferencia difusa tipo Mamdani se muestra a continuación (ecuación 1), donde sus conjuntos difusos son de tipo gaussiano para N entradas y M reglas.
La complejidad de estos sistemas difusos depende del número de entradas y reglas difusas planteadas, ya que la cantidad de conjuntos difusos en el antecedente y de centros en el consecuente dependen de estos dos factores; para este caso en particular se tiene 64 entradas y un total de 10 reglas que están dadas por el total de números a reconocer.
Sintonización del sistema difuso a partir del algoritmo evolutivo de tercera generación Memético (MA)
Como se ha expuesto en [7], un algoritmo memético es un algoritmo híbrido que incorpora el conocimiento o aprendizaje a un determinado algoritmo evolutivo en cada una de las poblaciones existentes en cada generación. Para esto se realizará una hibridación y, de esta forma, generar el algoritmo memético entre el algoritmo evolutivo diferencial expuesto en [8] y un aprendizaje supervisado típico [9] utilizando el algoritmo de Backpropagation. En otras palabras, se realizó una sintonización en la inferencia difusa basándonos en un algoritmo de evolución diferencial con búsqueda local, lo llamaremos algoritmo evolutivo memético diferencial (MDE).
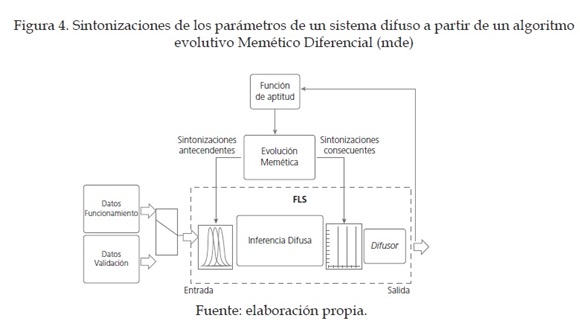
La estructura general trabajada para la sintonización es la que se muestra en la figura 4 [8]. Los valores que se encuentran en cada cromosoma de cada uno de los individuos de la población son los 64 centros en cada atributo, y sus respectivas desviaciones estándar; por esto, cada individuo de la población tendrá 128 genes
Para generar la familia de individuos de la primera generación, se tomó cada centro de número como individuos principales; a partir de ellos se genera aleatoriamente los demás individuos, los cuales son variaciones de estos individuos principales. En general, se tiene una población de 30 individuos correspondiente a cada número, para un total de 300 individuos.
La probabilidad de cruce para todos los parámetros de los principales individuos fue de 0.9, de este valor se sacó la probabilidad de cruce de los demás individuos de la población, dependiendo qué tan lejos esté de estos individuos principales así:
PROB = 0.9 * e -abs(indi1-indix) (2)
PROB es la probabilidad de un individuo x indi1 es el individuo principal indix es el individuo x
Para generar la mutación en el algoritmo se utilizó la variante del DE (diferencial evolutivo), en donde se tomó como mejor individuo el principal. El factor de mutación F se tomó con el valor de 0.8. Los valores de probabilidad de cruce, factor de mutación y número de individuos se tomaron de [8].
Sistema difuso a partir de red de funciones de base radial (RBF)
La segunda está basada en una red neuronal de funciones de base radial RBF entrenada con aprendizaje semi-supervisado.
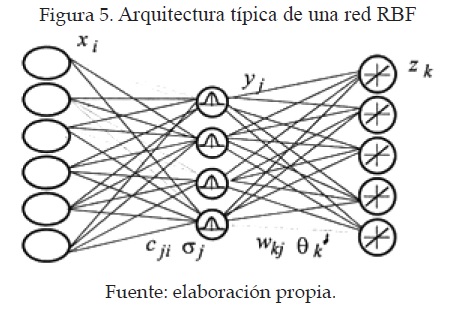
- Redes de Función de Base Radial (RBF) Este tipo de redes se caracteriza por tener un aprendizaje o entrenamiento híbrido, este tipo de redes neuronales tienen tres capas: una de entrada, una única capa oculta y una capa de salida, como se muestra en la figura 5.
Aunque la arquitectura pueda recordar a la un MLP, la diferencia fundamental está en que las neuronas de la capa oculta en vez de calcular una suma ponderada de las entradas y aplicar un sigmoide, calculan la distancia euclidiana entre el vector de pesos sinápticos (centroide) y la entrada, y sobre esta distancia se aplica una función de tipo radial con forma gaussiana.
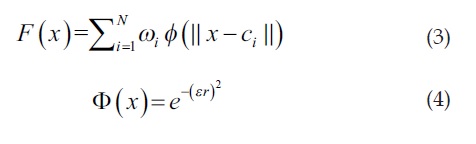
En la ecuación (3) se puede ver la función general de una red RBF, donde a cada neurona le corresponde una función de base radial Φ(x) y un peso de salida ωi.
- Aprendizaje semisupervisado de la Red RBF
El aprendizaje consiste en la determinación de los centros, desviaciones y pesos de las neuronas de la capa oculta a la capa de salida. Como las capas de la red realizan diferentes tareas, se separan los parámetros de la capa oculta de la capa de salida para optimizar el proceso. De esta forma, los centros y las desviaciones siguen un proceso guiado por una optimización en el espacio de entrada, mientras que los pesos siguen una optimización basado en las salidas que se desean obtener.
Para el aprendizaje de la capa oculta se usa un aprendizaje no supervisado, donde se obtienen el número de funciones, sus centros y su respectiva dispersión o radio. Existen diferentes métodos conocidos, uno de ellos es el algoritmo k-means descrito en [10], el cual es un algoritmo no supervisado de agrupamiento de datos, donde k es el número de grupos que se desea encontrar y corresponde al número de neuronas en la capa oculta.
Una vez fijados los valores de los centros en el paso anterior, se ajusta el ancho de cada neurona. Los anchos son los parámetros de dispersión que aparecen en cada una de las funciones gaussianas. De esta forma, dan una medida de cuando una muestra activa una neurona oculta para que dé una salida significativa, estas dispersiones de cada neurona deben ser calculadas de manera que presenten el menor solapamiento posible entre sí.
Después de obtener el número de funciones de base radial con sus respectivas características es realizada una fase supervisada. Aquí son calculados los pesos y umbrales de las neuronas de salida de la red. El objetivo es minimizar las diferencias entre las salidas de la red y las salidas deseadas. Hay dos métodos para realizar esta fase: realizado un proceso de optimización a través del método de mínimos cuadrados, el cual, al finalizar el proceso de entrenamiento, obtiene como resultado el valor de los pesos sinápticos de la red que soluciona el problema de clasificación.
Resultados
Los resultados son presentados en el orden de acuerdo con el modelo mostrado en la metodología. Después de ello se realizó una comparación entre las técnicas y finalmente se discuten los resultados del presente trabajo con otros encontrados en la literatura.
Resultados del Sistema Memético Diferencial
Los resultados arrojados por el algoritmo se estudiaron después de realizar alrededor de 80 pruebas para obtener representación estadística. El error de clasificación era observado en función del número de generaciones requeridas. Con esto, el algoritmo memético diferencial logró disminuir el error de clasificación hasta un valor del 6.3 %. Además, fue disminuido considerablemente el número de generaciones para llegar a dicho valor en comparación a otros algoritmos evolutivos.
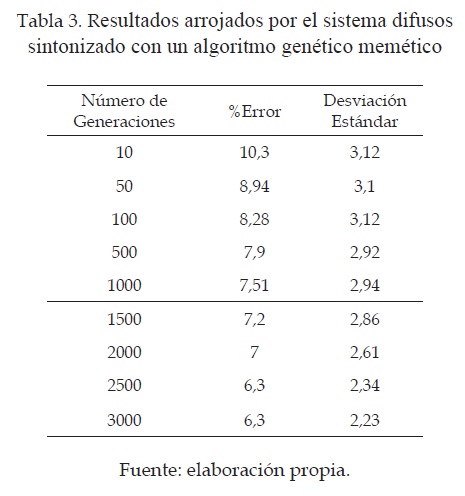
En la tabla 3 se pueden observar los resultados arrojados por el algoritmo memético, donde se varió el número de generaciones para observar los resultados del porcentaje de error y su respectiva desviación estándar.
Como es posible observar en la tabla 3, los resultados obtenidos con el sistema difuso construido a partir de algoritmos genéticos obtuvieron muy buenos resultados. El porcentaje de error se logró disminuir hasta un 6.3 % con el inconveniente del costo computacional, ya que para obtener este error fueron necesarias 2500 generaciones.
Resultados obtenidos de la red RBF
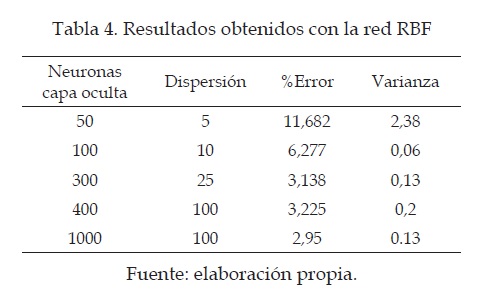
Para la implementación de la red neuronal de funciones de base radial fue modificado el número de neuronas en la capa oculta, y también la dispersión para la función Gaussiana utilizada. Los resultados obtenidos son mostrados en la tabla 4.
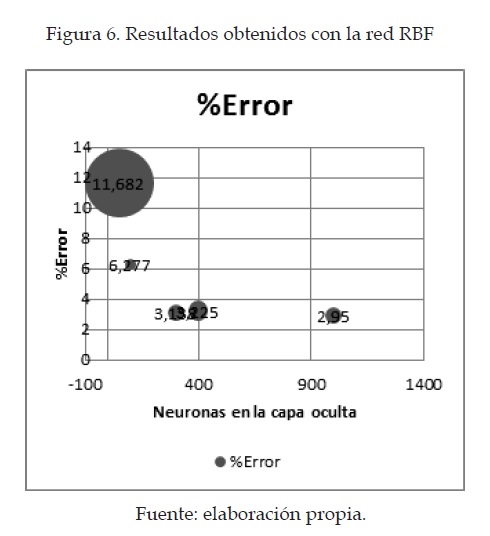
En la figura 6 se pueden observar los resultados obtenidos de forma gráfica. Es posible ver el número de neuronas en la capa oculta, el error y la dispersión. En los resultados con mayor dispersión se puede ver un círculo de mayor radio comparado con los demás datos. Los mejores resultados que relacionan el costo computacional y el porcentaje de error fueron obtenidos para una red RBF con 300 neuronas en la capa oculta. El porcentaje de error para este caso fue de 3.138 %, con una varianza bastante baja; lo que indica que la red neuronal tiene resultados consistentes, haciendo el método estable frente al problema de reconocimiento. En la tabla 3 se puede ver que se obtuvieron mejores resultados con 1000 neuronas en la capa oculta, pero la mínima diferencia que presenta está en porcentaje de error y varianza, con respecto a la de 300 neuronas no justifica el costo computacional necesario para obtener este resultado, por esta razón en las pruebas siguientes se decidió tomar la red RBF de 300 neuronas.
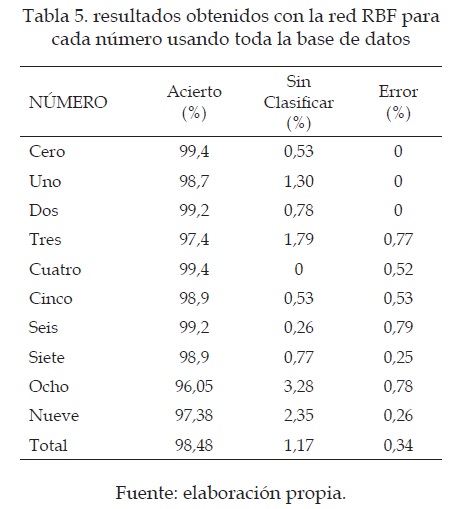
En base a los resultados, se decidió sacar el porcentaje de error para cada número en particular, pero esta vez para toda la base de datos. También se quiso observar si la red neuronal confundía números entre sí, y cuales confundía; los resultados obtenidos son los que se muestran en la tabla 5. Allí es mostrada la tasa de clasificación para cada número, el porcentaje de valores no clasificados y el porcentaje de los errores cometidos por la red.
De estos resultados (tabla 5) se puede observar que los números que mejor clasifica la red RBF son el cero y el cuatro, donde el porcentaje de error es ligeramente superior al 0.5 %, donde la red no pudo clasificar correctamente a todos los datos presentados. También se puede ver que el número que tiene un mayor error de clasificación es el ocho, con un error cercano al 4%, este carácter es confundido con otro carácter, lo que hace que se cuente como un error.
En general es posible ver que los resultados para todo el sistema son de 1.51 %, partiendo del hecho de que un 1.17 % son de números que la red no clasificó erradamente sino que consideró que no podía clasificarlos
Comparación de los resultados para las metodologías propuestas
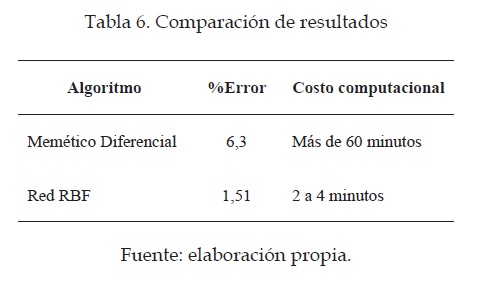
Los resultados expuestos anteriormente muestran que para el modelo de reconocimiento basado en la red neuronal, el porcentaje de error es más bajo, como se muestra en la tabla 6, y el costo computacional demandado por la red RBF es menor que el obtenido a través del sistema memético diferencial. Mientras la red RBF toma unos tres minutos en entrenar la red neuronal y arrojar resultados, el algoritmo memético pude tomar horas en dar un resultado satisfactorio.
Es claro que el sistema difuso igualmente resolvió el problema disminuyendo el porcentaje de error considerablemente y lo hizo mucho mejor que con otros algoritmos probados.
Discusión de los resultados
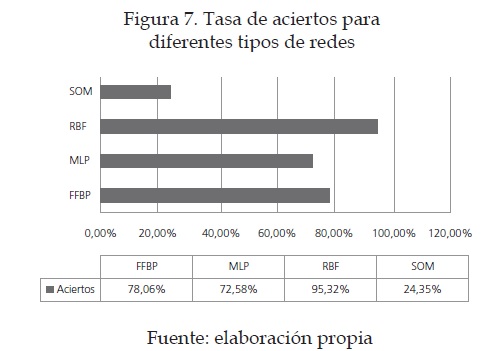
Analizando los resultados obtenidos en [11] se puede concluir que, entre los diferentes tipos de redes neuronales, los mejores resultados se obtuvieron con RBF y los peores con SOM, lo cual hizo más coherente desarrollar nuestra red neuronal bajo este modelo. Figura 7
Adicionalmente, bajo la misma base de datos y en la misma máquina, el tiempo de entrenamiento y validación del RBF es de una cuarta parte del MLP y la mitad del SOM. Esto nos permite afirmar aún más la idea de trabajar con RBF. Cabe notar que la base de datos usada es diferente a la usada en el presente trabajo, pero tiene características interesantes como estilos muy poco elegantes en cuanto a caligrafía, lo que hace particularmente difícil clasificar el dígito en alguna categoría. Encontraron especial dificultad en los dígitos cero (0), tres (3), cuatro (4) y siete (7) [12].
Conclusiones
El objetivo propuesto para este artículo fue satisfactoriamente cumplido, con los dos métodos con los cuales fue abordado el problema se obtuvieron muy buenos resultados, llegando casi al 99 % de clasificación exitosa de toda la base de datos, como es el caso de la red RBF, con el sistema memético diferencial fueron obtenidos resultados cercanos al 95 % en la tasa de clasificación.
Como conclusión final es bueno resaltar que para este caso en particular —el reconocimiento óptico de números escritos a mano— es mejor usar una red RBF, que un sistema memético diferencial, con los resultados expuestos se pudo entrever que el porcentaje de clasificación de la red RBF es ligeramente más efectivo que el sistema difuso genético, agregando como parte fundamental los costos computacionales que son requeridos para el desarrollo e implementación de cada uno de ellos.
Referencias
[1] J. A. Navarro, “Sistemas de reconocimiento óptico de caracteres”, Revista del instituto tecnológico de informática, 9-11, 2009.
[2] C. Sánchez, Reconocnimiento óptico de caracteres (OCR), Madrid, España: Universidad Carlos III, 2006.
[3] Bang, Hwang, Recognition of unconstrained handwritten numerals by a radial basis function neural network classifier, Korea: Pohang University of Science and Technology, 1997.
[4] UCI, University of California Irvine, 2010. Disponible en http://archive.ics. uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
[5] Haykin, Neural Networks: a comprehensive foundation, 1994, New York: Mc.Millan College publising company.
[6] L. Wang, A course in fuzzy systems and control. Upper Saddle River, NJ: Prentice-Hall, 1996.
[7] M. Melgarejo, Sintonización de sistemas difusos mediante un algoritmo memético adaptativo, en XVIII Congreso internacional de ingeniería eléctrica, electrónica, de sistemas y ramas afines, 2011.
[8] M. Melgarejo, Sintonización de sistemas difusos utilizando evolución diferencial, en XVIII Congreso internacional de ingeniería eléctrica, electrónica, de sistemas y ramas afines, 2011.
[9] L. Wang, J. Mendel, “Back‐ Propagation Fuzzy System As Nonlinear Dynamic System Identifiers”, IEEE International Conference on Fuzzy Systems, 1992.
[10] L. Hongmin, Y. Zhixi, Applying multiple agents to Fuzzy collaborative filtering. North University o China, 2, 2009.
[11] H. Al Hamad, “Use an Efficient Neural Network to Improve the Arabic Handwriting Recognition”, in International Conference on Systems, Control, Signal Processing and Informatics, 2013.
[12] Y. S. Hwang, Sung-Yang, “Recognition of Unconstrained Handwritten Numerals by a Radial Basis Function Neural Network Classifier”, Pattern Recognition Letters, 657-664, 1997.


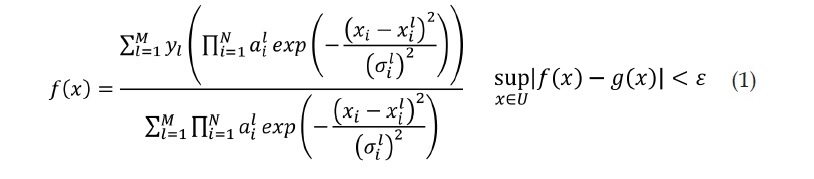
2.png)



